Study of Thermal Stress Fluctuations at the Die-Attach Solder Interface Using the Finite Element Method
Abstract
:1. Introduction
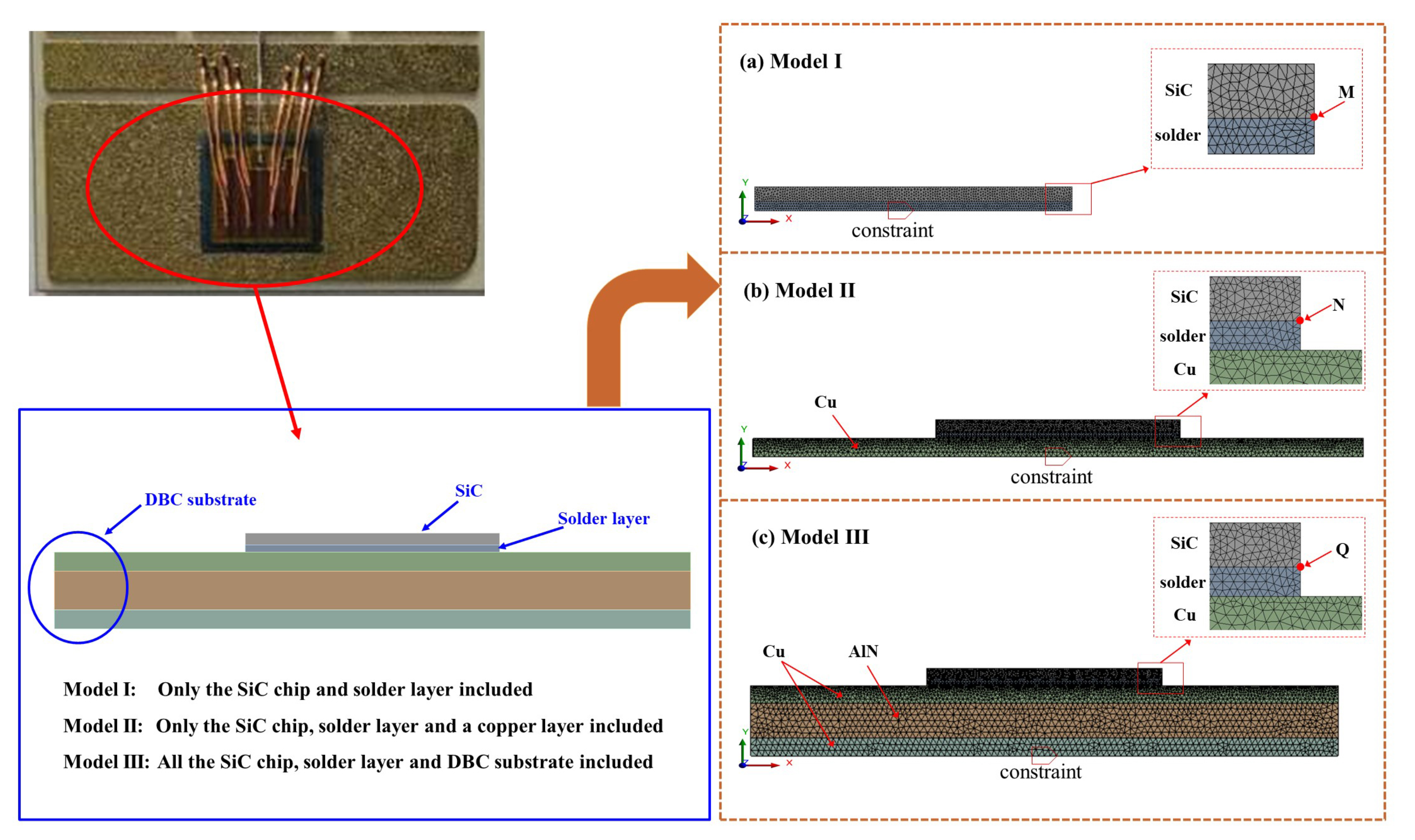
2. Finite Element Modeling
2.1. Finite Element Model Structure
2.2. Material Properties
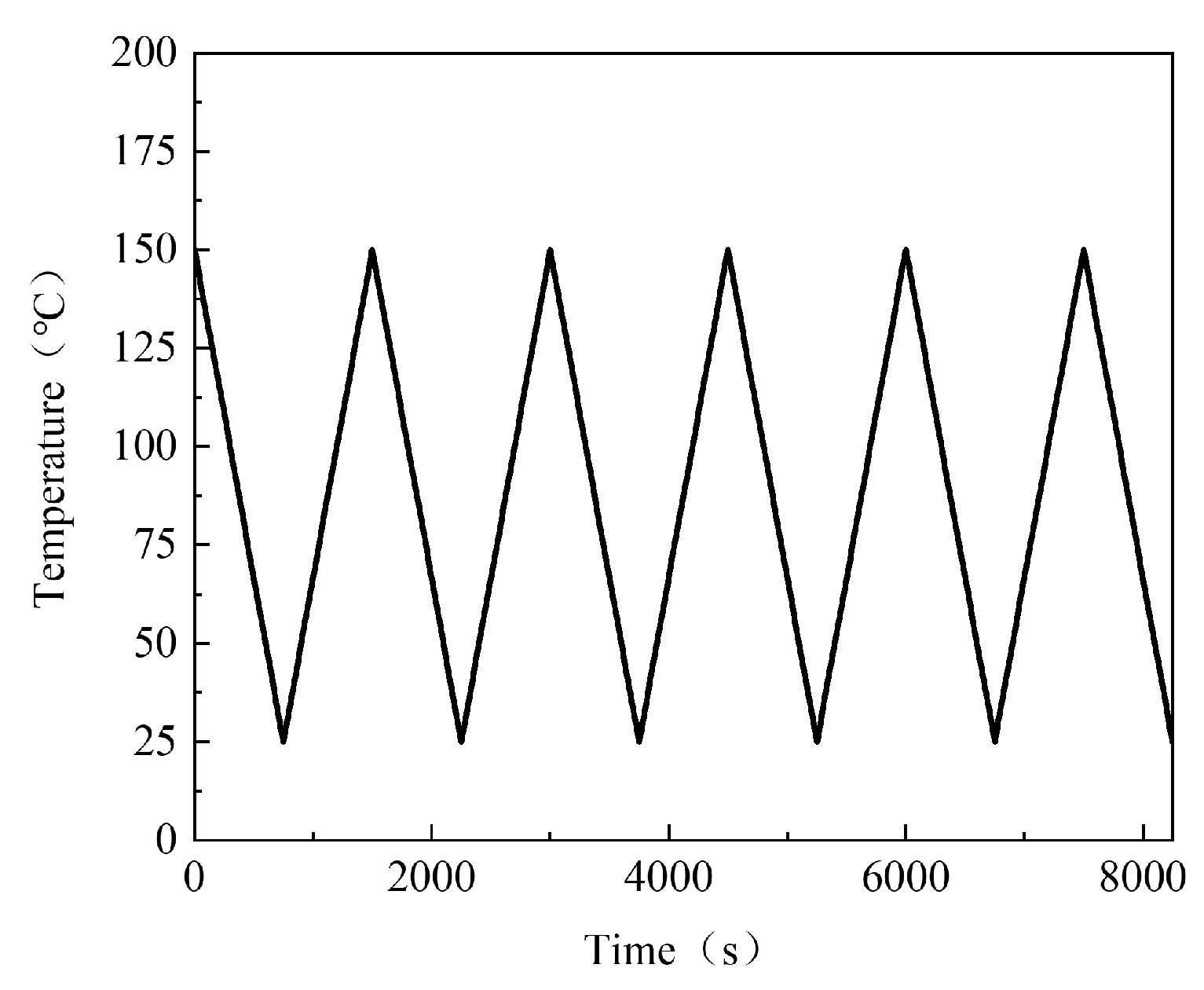
2.3. Load and Boundary Conditions
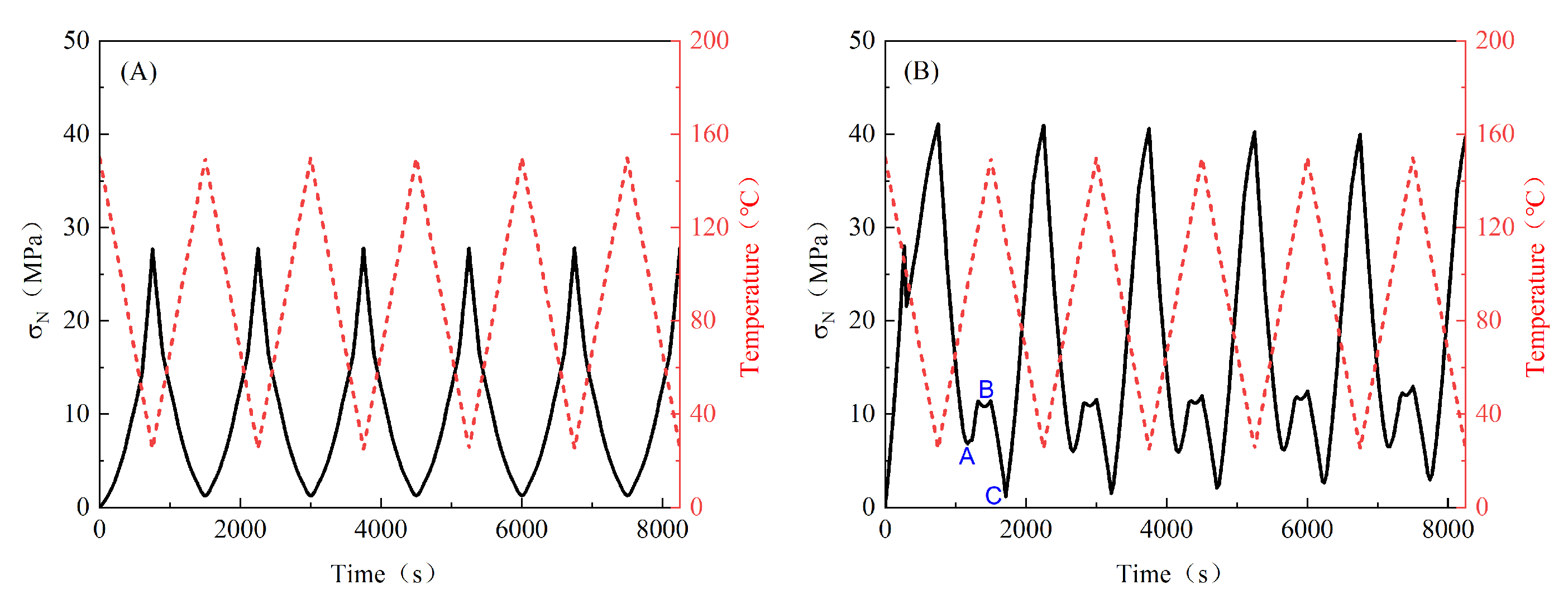
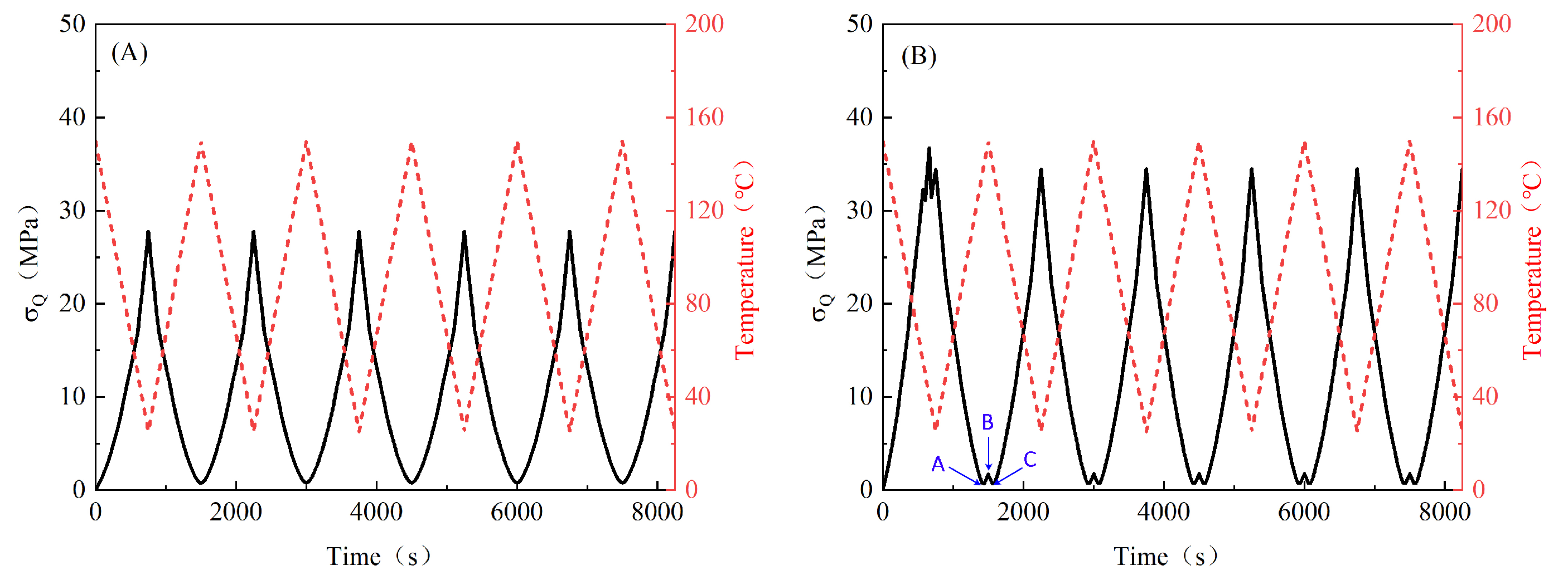
3. Results and Discussion
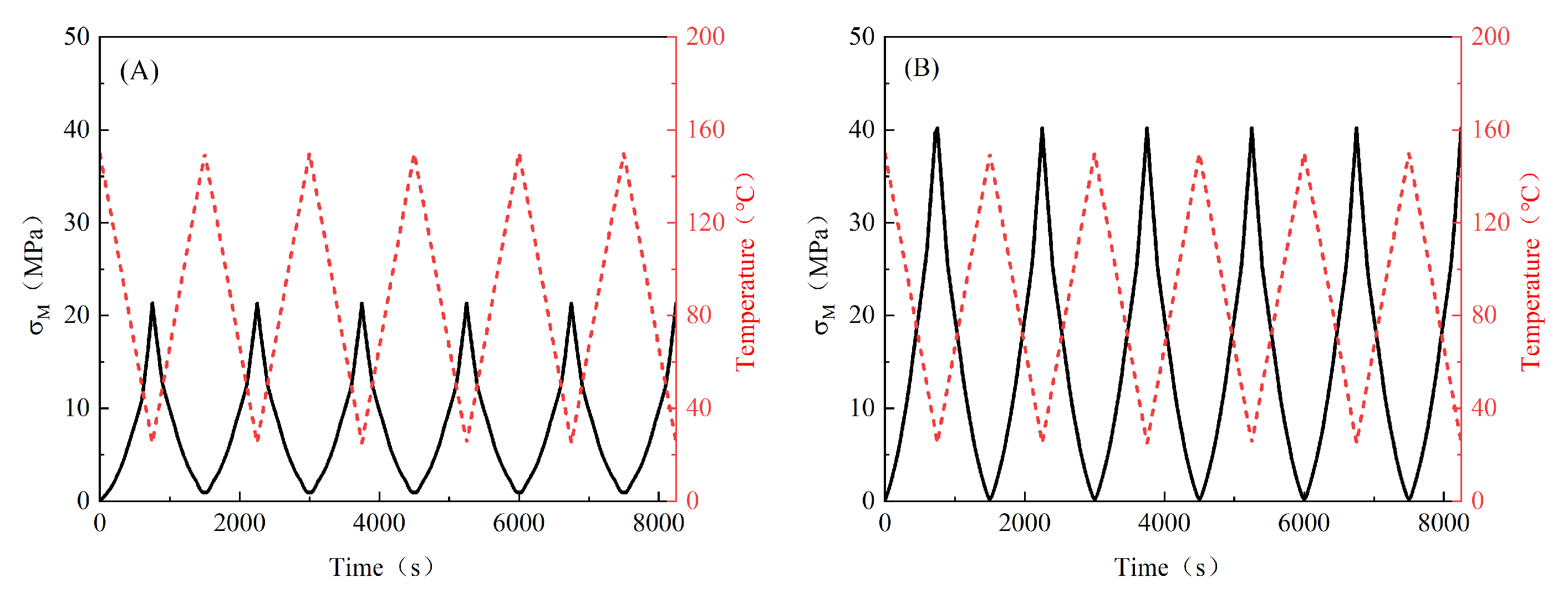
3.1. Effects of Boundary Conditions
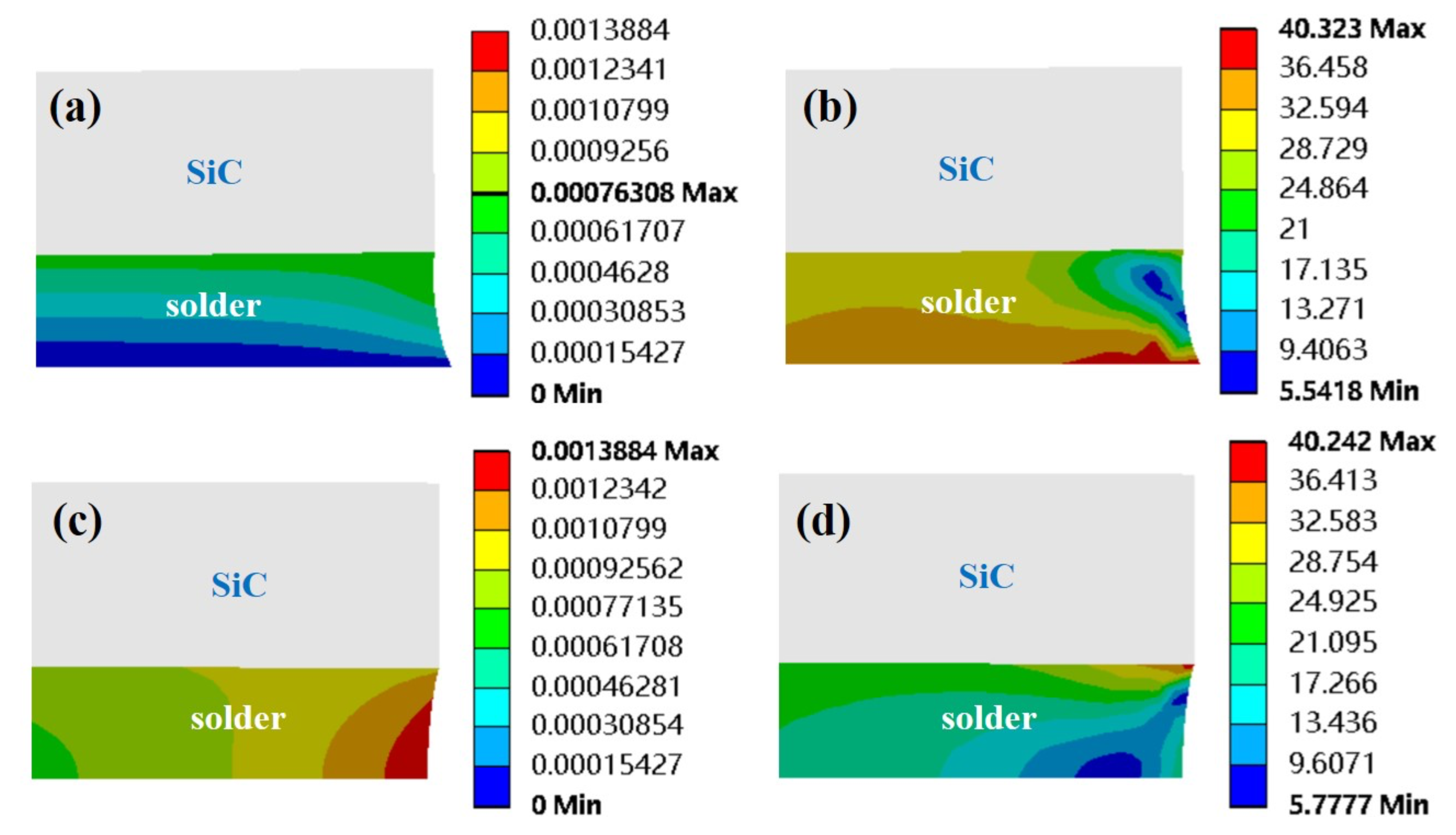
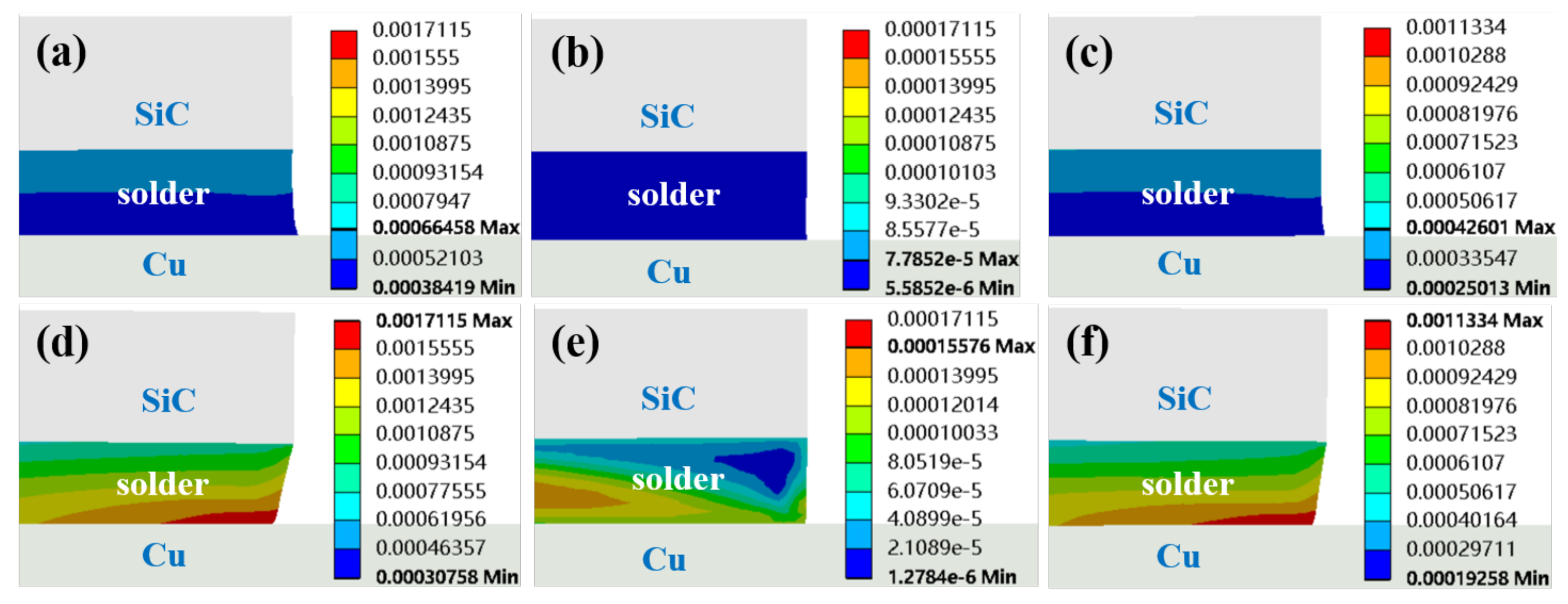
3.2. Effects of Modeling Scope
3.3. Effects of Substrates
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ballestín-Fuertes, J.; Muñoz-Cruzado-alba, J.; Sanz-Osorio, J.F.; Laporta-Puyal, E. Role of wide bandgap materials in power electronics for smart grids applications. Electronics 2021, 10, 677. [Google Scholar] [CrossRef]
- Jiang, C.; Guo, W.; Fan, J.; Qian, C.; Fan, X.; Zhang, G. Optimization of reflow soldering process for white LED chip-scale-packages on substrate. In Proceedings of the International Conference on Electronic Packaging Technology, Harbin, China, 16–19 August 2017; pp. 1309–1313. [Google Scholar]
- Otiaba, K.C.; Bhatti, R.S.; Ekere, N.N.; Mallik, S. Finite element analysis of the effect of silver content for Sn-Ag-Cu alloy compositions on thermal cycling reliability of solder die attach. Eng. Fail. Anal. 2013, 28, 192–207. [Google Scholar] [CrossRef]
- Barbagallo, C.; Rizzo, S.A.; Scelba, G.; Scarcella, G.; Cacciato, M. On the lifetime estimation of SiC power MOSFETs for motor drive applications. Electronics 2021, 10, 324. [Google Scholar] [CrossRef]
- Alves, L.F.S.; Lefranc, P.; Jeannin, P.-O.; Sarrazin, B.; Crebier, J.-C. Analysis of the multi-steps package (MSP) for series-connected SiC-MOSFETs. Electronics 2020, 9, 1341. [Google Scholar] [CrossRef]
- Fan, J.; Hu, A.; Pecht, M.; Chen, W.; Fan, X.; Xu, D.; Zhang, G. Fatigue damage assessment of LED chip scale packages with finite element simulation. In Proceedings of the International Conference on Electronic Packaging Technology, Shanghai, China, 8–11 August 2018; pp. 1642–1648. [Google Scholar]
- Mokhtar, N.Z.M.; Salleh, M.A.A.M.; Sandu, A.V.; Ramli, M.M.; Chaiprapa, J.; Vizureanu, P.; Ramli, M.I.I. Effect of electromigration and thermal ageing on the Tin whiskers’ formation in thin Sn–0.7Cu–0.05Ga lead (Pb)-free solder joints. Coatings 2021, 11, 935. [Google Scholar] [CrossRef]
- Yamamoto, M.; Shohji, I.; Kobayashi, T.; Mitsui, K.; Watanabe, H. Effect of small amount of Ni addition on microstructure and fatigue properties of Sn-Sb-Ag lead-free solder. Materials 2021, 14, 3799. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Huang, Y.; Tian, Y. Microstructure of Ag nano paste joint and its influence on reliability. Crystals 2021, 11, 1537. [Google Scholar] [CrossRef]
- Huang, C.M.; Raj, A.; Osterman, M.; Pecht, M. Assembly options and challenges for electronic products with lead-free exemption. IEEE Access 2020, 8, 134194–134208. [Google Scholar] [CrossRef]
- Kang, M.S.; Kim, D.S.; Shin, Y.E. The effect of epoxy polymer addition in Sn-Ag-Cu and Sn-Bi solder joints. Materials 2019, 16, 960. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Depiver, J.A.; Mallik, S.; Amalu, E.H. Thermal fatigue life of ball grid array (BGA) solder joints made from different alloy compositions. Eng. Fail. Anal. 2021, 125, 105447. [Google Scholar] [CrossRef]
- Song, F.; Lo, J.C.; Lam, J.K.; Jiang, T.; Lee, S. A comprehensive parallel study on the board level reliability of SAC, SACX and SCN solders. In Proceedings of the Electronic Components and Technology Conference, Lake Buena Vista, FL, USA, 27–30 May 2008; pp. 146–154. [Google Scholar]
- Chen, Y.L.; Jia, J.Y.; Fu, H.Z.; Zhi, Z. Analysis of the BGA solder Sn-3.0Ag-0.5Cu crack interface and a prediction of the fatigue life under tensile stress. Int. J. Fatigue 2016, 87, 216–224. [Google Scholar] [CrossRef]
- Huang, X.G.; Han, Z.Y. Interface singular field analysis and thermal fatigue failure of solder joint in a stacked electronic modules. J. Mater. Sci. Mater. Electron. 2016, 27, 8299–8311. [Google Scholar] [CrossRef]
- ZHan, Y.; Huang, X.G. GA-BP in thermal fatigue failure prediction of microelectronic chips. Electronics 2019, 8, 542. [Google Scholar]
- Chen, C.; Choe, C.; Zhang, Z.; Kim, D. Low-stress design of bonding structure and its thermal shock performance (−50 to 250 °C) in SiC/DBC power die-attached modules. J. Mater. Sci. Mater. Electron. 2018, 29, 14335–14346. [Google Scholar] [CrossRef]
- ZYang, T.; Peng, B.; Gao, L. Research on the thermal fatigue life of CQFN packaging. In Proceedings of the International Conference on Electronic Packaging Technology, Shanghai, China, 8–11 August 2018; pp. 662–666. [Google Scholar]
- Psota, B.; Szendiuch, I. Modeling of microelectronic structures and packages using ANSYS software. In Proceedings of the International Spring Seminar on Electronics Technology, Tratanska Lomnica, Slovakia, 11–15 May 2011; pp. 354–357. [Google Scholar]
- Xie, X.; Bi, X.; Li, G. Thermal-mechanical fatigue reliability of PbSnAg solder layer of die attachment for power electronic devices. In Proceedings of the International Conference on Electronic Packaging Technology & High Density Packaging, Beijing, China, 10–13 August 2009; pp. 1181–1185. [Google Scholar]
- Zhang, L.; Han, J.; He, C.; Guo, Y. Reliability behavior of lead-free solder joints in electronic components. J. Mater. Sci. Mater. Electron. 2013, 24, 172–190. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, L.; Wu, F.; Xia, W.; Liu, H. Effect of interface structure on fatigue life under thermal cycle with SAC305 solder joints. In Proceedings of the International Conference on Electronic Packaging Technology, Dalian, China, 11–14 August 2013; pp. 959–964. [Google Scholar]
- Waidhas, B.; Proschwitz, J.; Pietryga, C.; Wagner, T. Study of the board level reliability performance of a large 0.3 mm pitch wafer level package. In Proceedings of the Electronic Components and Technology Conference, Las Vegas, NV, USA, 28–31 May 2019; pp. 1159–1164. [Google Scholar]
- Kim, Y.; Ahn, C.W.; Choi, J.J.; Ryu, J.; Kim, J.W.; Yoon, W.H.; Park, D.S.; Yoon, S.Y.; Ma, B.; Hahn, B.D. Next generation ceramic substrate fabricated at room temperature. Sci. Rep. 2017, 7, 6637. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, S.S.; Yan, L.C.; Gao, K.W.; Yang, H.S. Finite element analysis of the effect of TiC or graphite modified composite fillers on the thermal residual stress of AMB ceramic substrates. Ceram. Int. 2019, 45, 19098–19104. [Google Scholar] [CrossRef]
- Xu, L.; Liu, Y.; Liu, S. Modeling and simulation of power electronic modules with microchannel coolers for thermo-mechanical performance. Microelectron. Reliab. 2014, 54, 2824–2835. [Google Scholar] [CrossRef]
- Chen, G.; Zhao, X.; Wu, H. A critical review of constitutive models for solders in electronic packaging. Adv. Mech. Eng. 2017, 9, 1687814017714976. [Google Scholar] [CrossRef] [Green Version]
- Depiver, J.A.; Mallik, S.; Amalu, E.H. Effective solder for improved thermo-mechanical reliability of solder joints in a ball grid array (BGA) soldered on printed circuit board (PCB). J. Electron. Mater. 2021, 50, 263–282. [Google Scholar] [CrossRef]
- Li, Y.M.; Zhao, T.Y.; Liu, J.; Huang, B.Z. Research for viscoplastic behaviors of SAC405 Pb-free solder. Adv. Mater. Res. 2013, 690, 2686–2689. [Google Scholar] [CrossRef]
- Chaboche, J.L. Constitutive equations for cyclic plasticity and cyclic viscoplasticity. Int. J. Plast. 1989, 5, 247–302. [Google Scholar] [CrossRef]
- Amalu, E.H.; Ekere, N.N. Modelling evaluation of Garofalo-Arrhenius creep relation for lead-free solder joints in surface mount electronic component assemblies. J. Manuf. Syst. 2016, 39, 9–23. [Google Scholar] [CrossRef]
- Cougo, B.; Morais, L.M.F.; Segond, G.; Riva, R.; Tran Duc, H. Influence of PWM methods on semiconductor losses and thermal cycling of 15-kVA three-phase SiC inverter for aircraft applications. Electronics 2020, 9, 620. [Google Scholar] [CrossRef] [Green Version]
- Chang, K.C.; Lii, M.J.; Hsu, S.; Liu, H.C.; Lai, Y.K.; Tsai, S.H.; Hsu, C.H. A novel metal scheme and bump array design configuration to enhance advanced Si packages CPI reliability performance by using finite element modeling technique. In Proceedings of the Electronic Components and Technology Conference, Las Vegas, NV, USA, 28–31 May 2019; pp. 397–404. [Google Scholar]
- Curamik. Curamik Ceramic Substrates DBC Technology—Design Rules; Rogers Corporation: Chandler, AZ, USA, 2015. [Google Scholar]
- Uchibori, C.J.; Lee, M.; Zhang, X.; Ho, P.S.; Nakamura, T. Impact of Cu/low-k interconnect design on chip package interaction in flip chip package. AIP Conf. Proc. 2009, 1143, 185–196. [Google Scholar]
- Kondo, S.; Yu, Q.; Shibutani, T.; Shiratori, M. New reliability assessment method for solder joints in BGA package by considering the interaction between design factors. In Proceedings of the International Workshop on Thermal Investigation of ICs and Systems, Budapest, Hungary, 17–19 September 2007; pp. 26–31. [Google Scholar]
- Hong, R.H.; Wang, J. Board level WLCSP 3D thermal stress analysis by submodeling of FEA. In Proceedings of the International Conference on Electronic Packaging Technology & High Density Packaging, Xi’an, China, 16–19 August 2010; pp. 762–766. [Google Scholar]
- Xue, T.; Zhu, Y.; Ming, X.; Zhang, G. Analysis on thermo-mechanical reliability of TSV interposer and solder joint. In Proceedings of the International Conference on Electronic Packaging Technology, Changsha, China, 11–14 August 2015; pp. 144–147. [Google Scholar]
- Deshpande, A.; Jiang, Q.; Dasgupta, A. Effect of microscale heterogeneities and stress state on the mechanical behavior of solder joints. In Proceedings of the Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems, Lake Buena Vista, FL, USA, 26–29 May 2020; pp. 1024–1028. [Google Scholar]
- Ni, C.Y.; Liu, D.S.; Chen, C.Y. Procedure for design optimization of a T-cap flip chip package. Microelectron. Reliab. 2002, 42, 1903–1911. [Google Scholar] [CrossRef]


| Material | Density (kg/m3) | Special Heat Capacity (J/kg·K) | Thermal Conductivity (W/m·K) | Elastic Modulus (GPa) | Poisson Ratio | CTE (ppm/K) |
|---|---|---|---|---|---|---|
| SiC | 3200 | 690 | 370 | 501 | 0.45 | 3.4 |
| SAC405 | 7410 | 236 | 62 | 25 °C: 8.21 50 °C: 6.33 75 °C: 5.65 100 °C: 4.62 155 °C: 2.58 | 0.38 | 26.0 |
| Cu | 8900 | 390 | 383 | 110 | 0.34 | 17.5 |
| AlN | 3300 | 750 | 170 | 310 | 0.20 | 4.5 |
| Temperature (°C) | Yield Strength (MPa) | C1 (MPa) | γ1 | C2 (MPa) | γ2 |
|---|---|---|---|---|---|
| 20 | 211 | 54,041 | 962 | 721 | 1.1 |
| 50 | 208 | 52,880 | 1000 | 700 | 1.1 |
| 150 | 201 | 45,760 | 1100 | 600 | 1.1 |
| Substrate CTE (ppm/K) | σN (MPa) | Deviation from the Least Value (%) | ||
|---|---|---|---|---|
| Main Stress Peak | Stress Recovery Peak | Main Stress Peak | Stress Recovery Peak | |
| 8.5 | 37.5 | 4.6 | 0.0 | 0.0 |
| 13.0 | 39.4 | 7.9 | 5.1 | 71.7 |
| 17.5 | 39.7 | 13.0 | 5.9 | 182.6 |
| 22.0 | 41.3 | 17.0 | 10.1 | 269.6 |
| 26.5 | 43.6 | 18.5 | 16.3 | 302.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, L.; Yao, J.; Dai, Y.; Zhang, S.; Bai, W.; Gao, K.; Yang, H.; Wang, Y. Study of Thermal Stress Fluctuations at the Die-Attach Solder Interface Using the Finite Element Method. Electronics 2022, 11, 62. https://doi.org/10.3390/electronics11010062
Yan L, Yao J, Dai Y, Zhang S, Bai W, Gao K, Yang H, Wang Y. Study of Thermal Stress Fluctuations at the Die-Attach Solder Interface Using the Finite Element Method. Electronics. 2022; 11(1):62. https://doi.org/10.3390/electronics11010062
Chicago/Turabian StyleYan, Luchun, Jiawen Yao, Yu Dai, Shanshan Zhang, Wangmin Bai, Kewei Gao, Huisheng Yang, and Yanbin Wang. 2022. "Study of Thermal Stress Fluctuations at the Die-Attach Solder Interface Using the Finite Element Method" Electronics 11, no. 1: 62. https://doi.org/10.3390/electronics11010062
APA StyleYan, L., Yao, J., Dai, Y., Zhang, S., Bai, W., Gao, K., Yang, H., & Wang, Y. (2022). Study of Thermal Stress Fluctuations at the Die-Attach Solder Interface Using the Finite Element Method. Electronics, 11(1), 62. https://doi.org/10.3390/electronics11010062






