Time Delay Estimation Control of Permanent Magnet Spherical Actuator Based on Gradient Compensation
Abstract
:1. Introduction
2. Structure and Dynamic Model of PMSpA
2.1. Mechanical Structure of PMSpA
2.2. Dynamic Modeling
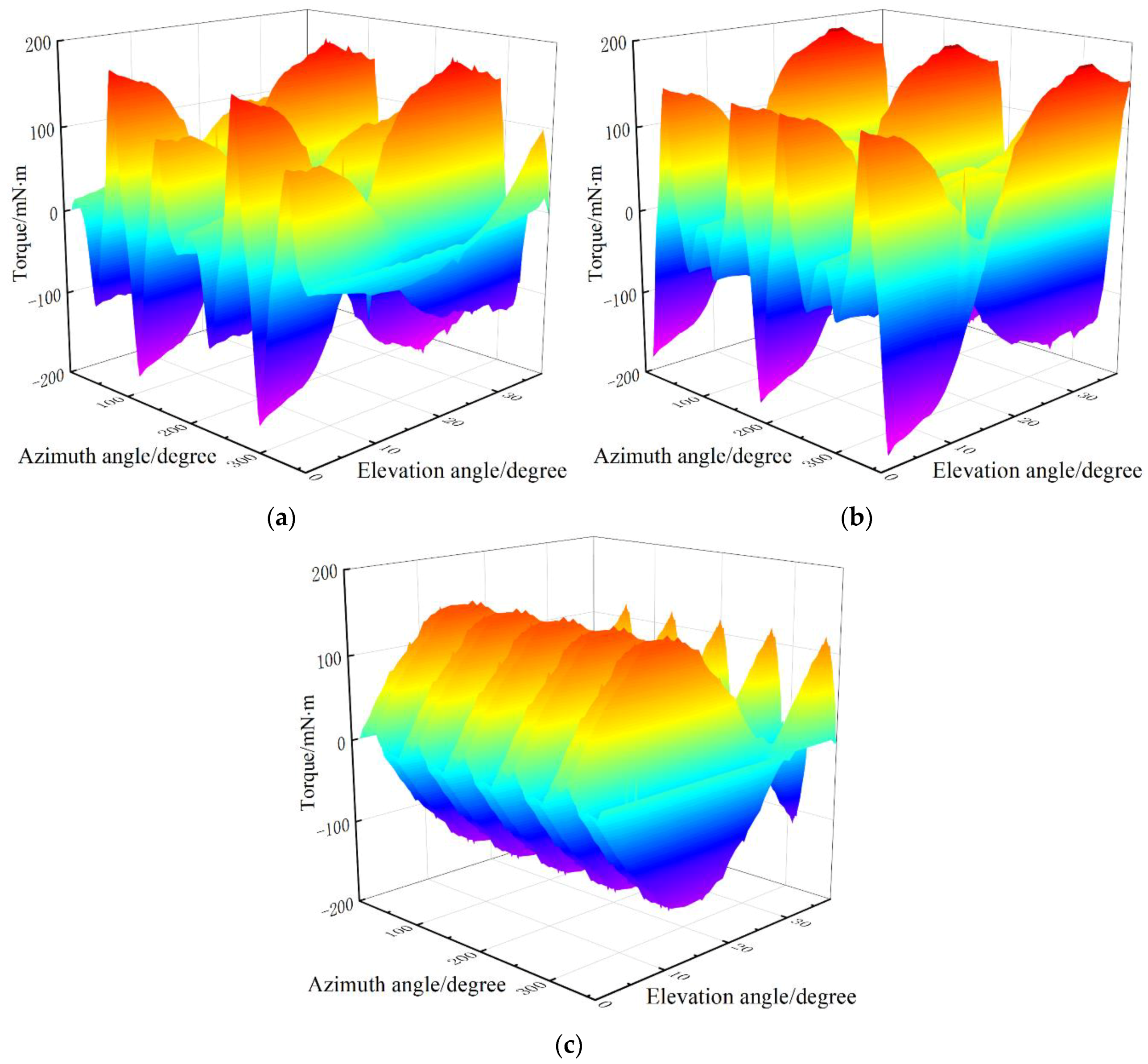
2.3. Torque Modeling
3. Design of Controller
3.1. TDC Controller
3.2. TDC Controller with Gradient Compensation
4. Simulations
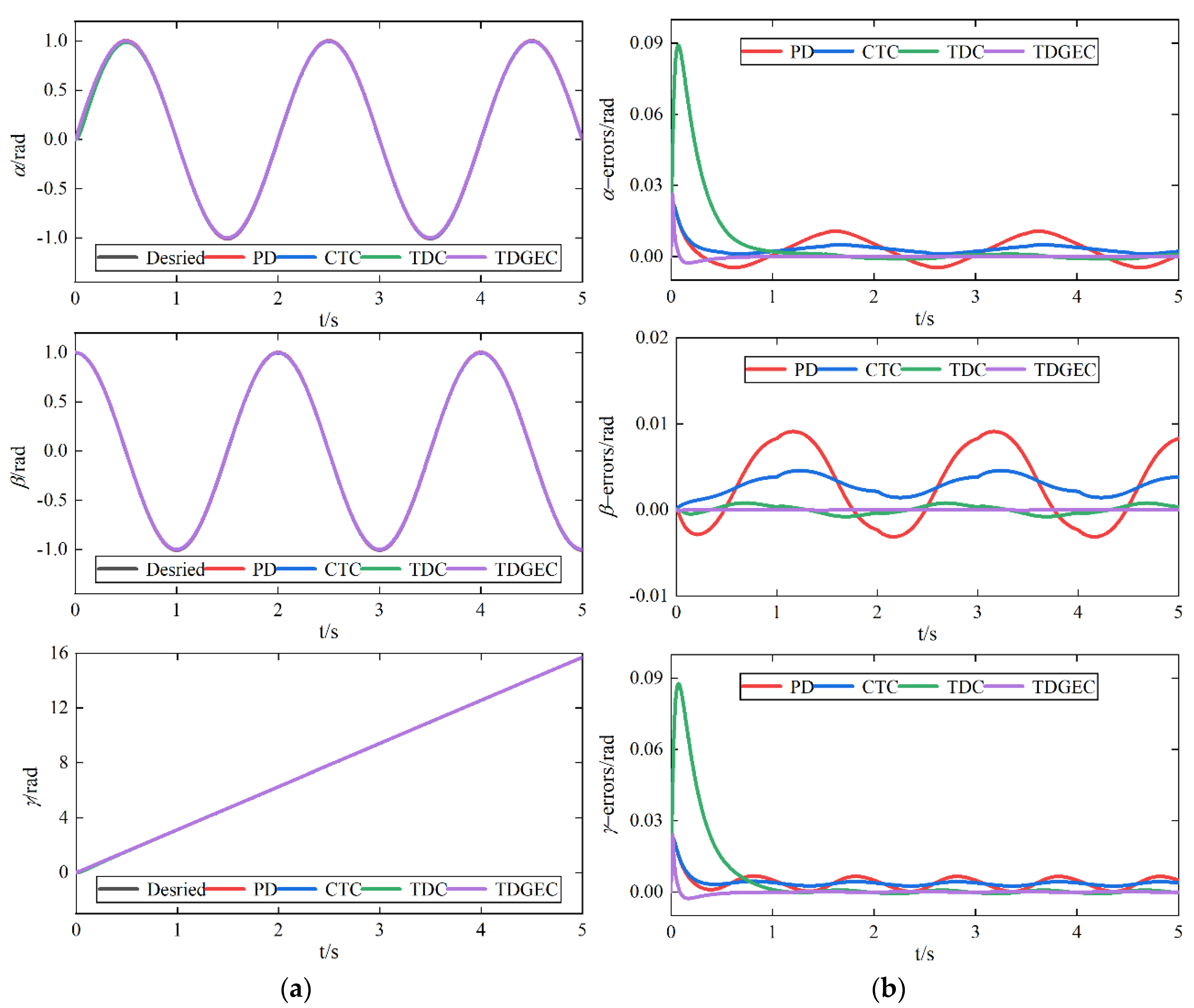
4.1. Simulation under Different Modeling Errors
4.2. Simulation under Different Load Torque
5. Experiment Evaluation
5.1. Experimental Platform and Principle
5.2. Experiment and Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| xyz | Stator coordinate system |
| dqp | Rotor coordinate system |
| α, β, γ | Euler angles |
| Rrot | Rotation matrix |
| Inertial matrix of PMSpA | |
| Coriolis matrix of PMSpA | |
| θ = [α, β, γ]T | Euler angle vector |
| Fq | Nonlinear disturbance |
| d | Load torque |
| u ∈ R3 | Control torque |
| Id, Iq Ip | Main moments of inertia of the PMSpA |
| A positive definite martix | |
| All the complex nonlinear terms in the dynamic model of PMSpA | |
| The estimated value of | |
| θij | Deflection angle |
| f(θij) | Torque characteristic curve |
| Sri | Position vectors of the coils |
| Srj | Position vectors of the PMs |
| Ii | Current of coils |
| ux, uy, uz | Spin torque, pitch torque, and yaw torque |
| fxi, fyi, fzi | Torque components along xyz |
| e | Position tracking error of the PMSpA |
| Expected Euler angle trajectory of the PMSpA | |
| Kp, Kd | Diagonal gain matrix of the PD controller |
| L | System sampling time |
| λ | Time delay estimation error |
| Gradient compensation term | |
| Estimated error value of λ | |
| Cost function of λ | |
| KGC diag(KGC1,…, KGCn) | Gain matrix of the gradient compensator |
| V | Lyapunov function |
| w | Load moment coefficient |
| r | Modeling error coefficient |
| Desired tracking trajectories |
Appendix A
Appendix B
References
- Yang, L.; Chen, I.M.; Lim, C.K.; Yang, G.; Lin, W.; Lee, K.M. Design and analysis of a permanent magnet spherical actuator. IEEE-ASME Trans. Mechatron. 2008, 13, 239–248. [Google Scholar] [CrossRef]
- Wright, S.E.; Mahoney, A.W.; Popek, K.M.; Abbott, J.J. The Spherical-Actuator-Magnet Manipulator: A Permanent-Magnet Robotic End-Effector. IEEE Trans. Robot. 2017, 33, 1013–1024. [Google Scholar] [CrossRef]
- Li, Z.; Gao, S.H.; Zhang, H.M. Wireless power transmission for multi-degree-of-freedom motor applications based on magnetic field coupling. IEICE Electron. Express. 2019, 16, 20190330. [Google Scholar] [CrossRef]
- Fernandes, J.F.P.; Branco, P.J.C. The Shell-Like Spherical Induction Motor for Low-Speed Traction: Electromagnetic Design, Analysis, and Experimental Tests. IEEE Trans. Ind. Electron. 2016, 63, 4325–4335. [Google Scholar] [CrossRef]
- Bai, K.; Xu, R.Y.; Lee, K.M.; Dai, W.; Huang, Y.A. Design and Development of a Spherical Motor for Conformal Printing of Curved Electronics. IEEE Trans. Ind. Electron. 2018, 65, 9190–9200. [Google Scholar] [CrossRef]
- Maeda, S.; Hirata, K.; Niguchi, N. Dynamic Analysis of an Independently Controllable Electromagnetic Spherical Actuator. IEEE Trans. Magn. 2013, 49, 2263–2266. [Google Scholar] [CrossRef]
- Yan, L.; Wu, Z.W.; Jiao, Z.X.; Chen, C.Y.; Chen, I.M. Equivalent energized coil model for magnetic field of permanent-magnet spherical actuators. Sens. Actuator A Phys. 2015, 229, 68–76. [Google Scholar] [CrossRef]
- VanNinhuijs, B.; Motoasca, T.E.; Gysen, B.L.J.; Lomonova, E.A. Modeling of Spherical Magnet Arrays Using the Magnetic Charge Model. IEEE Trans. Magn. 2013, 49, 4109–4112. [Google Scholar] [CrossRef]
- Son, H.S.; Lee, K.M. Open-Loop Controller Design and Dynamic Characteristics of a Spherical Wheel Motor. IEEE Trans. Ind. Electron. 2010, 57, 3475–3482. [Google Scholar] [CrossRef]
- Son, H.S.; Lee, K.M. Control system design and input shape for orientation of spherical wheel motor. Control. Eng. Pract. 2014, 24, 120–128. [Google Scholar] [CrossRef]
- Chen, W.H.; Zhang, L.; Yan, L.; Liu, J.M. Design and control of a three degree-of-freedom permanent magnet spherical actuator. Sens. Actuator A Phys. 2012, 180, 75–86. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, W.H.; Liu, J.M.; Wen, C.Y. A Robust Adaptive Iterative Learning Control for Trajectory Tracking of Permanent-Magnet Spherical Actuator. IEEE Trans. Ind. Electron. 2015, 63, 291–301. [Google Scholar] [CrossRef]
- Nguyen, K.D. On the adaptive control of spherical actuators. Trans. Inst. Meas. Control. 2019, 41, 816–827. [Google Scholar] [CrossRef]
- Xia, C.L.; Guo, C.; Shi, T.N. A Neural-Network-Identifier and Fuzzy-Controller-Based Algorithm for Dynamic Decoupling Control of Permanent-Magnet Spherical Motor. IEEE Trans. Ind. Electron. 2010, 57, 2868–2878. [Google Scholar] [CrossRef]
- Guo, X.W.; Pan, K.D.; Wang, Q.J.; Wen, Y. Robust Adaptive Sliding-Mode Control of a Permanent Magnetic Spherical Actuator with Delay Compensation. IEEE Access 2020, 8, 128096–128105. [Google Scholar] [CrossRef]
- Yan, L.; Zhang, L.; Zhu, B.; Zhang, J.Y.; Jiao, Z.X. Single neural adaptive controller and neural network identifier based on PSO algorithm for spherical actuators with 3D magnet array. Rev. Sci. Instrum. 2017, 88, 105001. [Google Scholar] [CrossRef] [PubMed]
- Youcef, T.K.; Ito, O. A Time Delay Controller for Systems with Unknown Dynamics. J. Dyn. Syst. Meas., Control. 1990, 112, 133–142. [Google Scholar] [CrossRef]
- Chang, P.H.; Park, S.H. On improving time-delay control under certain hard nonlinearities. Mechatronics 2003, 13, 393–412. [Google Scholar] [CrossRef]
- Jin, M.L.; Kang, S.H.; Chang, P.H. Robust Compliant Motion Control of Robot with Nonlinear Friction Using Time-Delay Estimation. IEEE Trans. Ind. Electron. 2008, 55, 258–269. [Google Scholar] [CrossRef]
- Baek, J.; Jin, M.; Han, S. A New Adaptive Sliding-Mode Control Scheme for Application to Robot Manipulators. IEEE Trans. Ind. Electron. 2016, 63, 3628–3637. [Google Scholar] [CrossRef]
- Baek, J.; Kwon, W.; Kim, B.; Han, S. A Widely Adaptive Time-Delayed Control and Its Application to Robot Manipulators. IEEE Trans. Ind. Electron. 2019, 66, 5332–5342. [Google Scholar] [CrossRef]
- Jin, M.L.; Kang, S.H.; Chang, P.H.; Lee, J. Robust Control of Robot Manipulators Using Inclusive and Enhanced Time Delay Control. IEEE-ASME Trans. Mechatron. 2017, 22, 2141–2152. [Google Scholar] [CrossRef]
- Jiang, S.R.; Wang, Y.Y.; Ju, F.; Chen, B.; Wu, H.T. A new fuzzy time-delay control for cable-driven robot. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419835017. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Jewell, G.W.; Howe, D. Analysis, design and control of a novel spherical permanent-magnet actuator. IEE Proc.—Electr. Power Appl. 1998, 145, 61–71. [Google Scholar] [CrossRef]
- Li, H.L.; Li, G.L.; Wang, Q.J.; Ju, B.; Wen, Y. Friction torque field distribution of a permanent-magnet spherical motor based on multi-physical field coupling analysis. IET Electr. Power Appl. 2021, 15, 1045–1055. [Google Scholar] [CrossRef]
- Lee, K.M.; Vachtsevanos, G.; Kwan, C. Development of a spherical stepper wrist motor. J. Intell. Rob. Syst. 1988, 1, 225–242. [Google Scholar] [CrossRef]
- Xia, C.L.; Li, H.F.; Shi, T.N. 3-D magnetic feld and torque analysis of a novel Halbach array permanent-magnet spherical motor. IEEE Trans. Magn. 2008, 44, 2016–2020. [Google Scholar] [CrossRef]
- Wen, Y.; Li, G.L.; Wang, Q.J.; Guo, X.W. Robust Adaptive Sliding-Mode Control for Permanent Magnet Spherical Actuator with Uncertainty Using Dynamic Surface Approach. J. Electr. Eng. Technol. 2019, 14, 2341–2353. [Google Scholar] [CrossRef]
- Hsia, T.C.; Gao, L.S. Robot manipulator control using decentralized linear time-invariant time-delayed joint controllers. In Proceedings of the IEEE International Conference on Robotics and Automation, Cincinnati, OH, USA, 13–18 May 1990; pp. 2070–2075. [Google Scholar] [CrossRef]










| Parameters | Unit | Value |
|---|---|---|
| Radius of the stator | mm | 115 |
| Radius of the rotor | mm | 64 |
| Height of coils | mm | 25 |
| Inner radius of coils | mm | 4 |
| Ampere-turns coils | A | 1200 |
| Radius of PMs | mm | 10 |
| Length of air gap | mm | 1 |
| Material of PM | NdFe35 | |
| Maximum pitch angle | degree | 37.5 |
| AMSSE (rad) | PD | CTC | TDC | TDGEC |
|---|---|---|---|---|
| α | 0.0107 | 4.94 × 10−3 | 8.98 × 10−4 | 5.02 × 10−5 |
| β | 0.0091 | 4.56 × 10−3 | 7.85 × 10−4 | 2.82 × 10−5 |
| γ | 6.56 × 10−3 | 4.31 × 10−3 | 7.61 × 10−4 | 5.07 × 10−5 |
| AMSSE (rad) | PD | CTC | TDC | TDGEC |
|---|---|---|---|---|
| α | 0.0161 | 0.0104 | 8.90 × 10−4 | 4.61 × 10−5 |
| β | 0.0146 | 0.0101 | 6.98 × 10−4 | 2.56 × 10−5 |
| γ | 0.0123 | 0.0101 | 7.06 × 10−4 | 4.71 × 10−5 |
| PD | TDC | TDGEC | |
|---|---|---|---|
| Kp | diag{0.02,0.02,0.02} | diag{0.05,0.05,0.05} | diag{0.05,0.05,0.05} |
| Kd | diag{0.005,0.005,0.005} | diag{0.02,0.02,0.02} | diag{0.02,0.02,0.02} |
| - | diag{0.003,0.004,0.004} | diag{0.003,0.004,0.004} | |
| KGC | - | - | diag{0.08,0.08,0.08} |
| PD | TDC | TDGEC | ||||
|---|---|---|---|---|---|---|
| α | β | α | β | α | β | |
| SSE (degree) | 0.814 | 0.714 | 0.614 | 0.494 | 0.414 | 0.246 |
| AME (degree) | 1.869 | 1.635 | 1.449 | 1.247 | 0.743 | 0.799 |
| Standard deviation (degree) | 0.487 | 0.327 | 0.590 | 0.532 | 0.319 | 0.240 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zhang, R.; Li, G.; Wang, Q.; Wen, Y. Time Delay Estimation Control of Permanent Magnet Spherical Actuator Based on Gradient Compensation. Electronics 2022, 11, 66. https://doi.org/10.3390/electronics11010066
Wang X, Zhang R, Li G, Wang Q, Wen Y. Time Delay Estimation Control of Permanent Magnet Spherical Actuator Based on Gradient Compensation. Electronics. 2022; 11(1):66. https://doi.org/10.3390/electronics11010066
Chicago/Turabian StyleWang, Xiuqin, Rui Zhang, Guoli Li, Qunjing Wang, and Yan Wen. 2022. "Time Delay Estimation Control of Permanent Magnet Spherical Actuator Based on Gradient Compensation" Electronics 11, no. 1: 66. https://doi.org/10.3390/electronics11010066
APA StyleWang, X., Zhang, R., Li, G., Wang, Q., & Wen, Y. (2022). Time Delay Estimation Control of Permanent Magnet Spherical Actuator Based on Gradient Compensation. Electronics, 11(1), 66. https://doi.org/10.3390/electronics11010066






