Comprehensive Overview of Backpropagation Algorithm for Digital Image Denoising
Abstract
:1. Introduction
- The MLP’s capacity was chosen to be large enough to accommodate a suitable number of hidden layers and hidden layer neurons;
- The image patch size was selected to ensure that a noisy image patch has sufficient information to recover a noise-free version of the original input image;
- The chosen training set was large enough to allow for on-the-fly generation of training samples by corrupting noise-free patches with noise.
2. Artificial ANNs
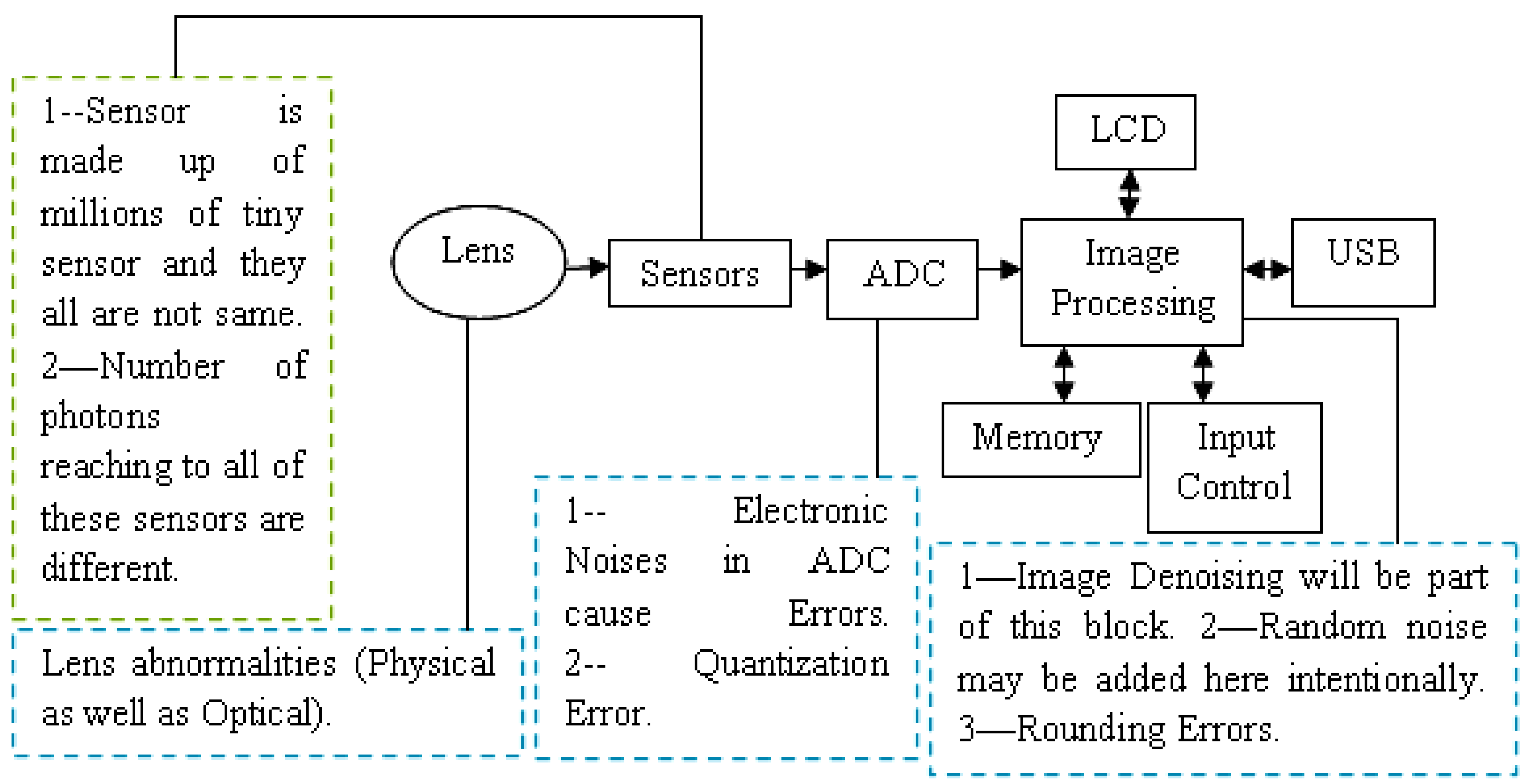
3. Problem Specific Approach for ANNs Development
- Phase 1 (problem description and formulation): This phase is primarily reliant on a thorough grasp of the problem, especially the “cause-effect” relationships. Before deciding on a modelling technique, the advantages of ANNs over alternative techniques (if available) should be weighed;
- Phase 2 (System Design): This is the initial phase in the actual ANN design, in which the modeller selects the appropriate type of ANN and learning algorithm for the task. Data collecting, data preprocessing to fit the type of ANN utilised, statistical data analysis, and data splitting into three unique subsets are all part of this phase (training, test, and validation subsets);
- Phase 3 (System Realisation): This phase entails training the network with the training and test subsets while also analysing the prediction error to gauge network performance. The design and performance of the final network can be influenced by the optimal selection of numerous parameters (e.g., network size, learning rate, number of training cycles, tolerable error, etc.). If practicable, breaking the problem down into smaller sub-problems and building an ensemble of networks could improve overall system accuracy. The modeller is now back in phase 2;
- Phase 4 (System Verification): Although network construction includes ANN testing against test data while training is in progress, it is best to practise (if data permits) using the validation subset to assess the best network for its generalisation capabilities. The goal of verification is to ensure that the ANN-based model can appropriately respond to cases that have never been utilised in network construction. Comparing the performance of the ANN-based model to that of other methodologies (if available) such as statistical regression and expert systems is also part of this phase.
- Phase 5 (System Implementation): This phase entails integrating the network into a suitable operating system, such as a hardware controller or computer software. Before releasing the integrated system to the end user, it should be thoroughly tested.
- Phase 6 (System Maintenance): This phase entails upgrading the produced system as the environment or system variables change (e.g., new data), which necessitates a new development cycle.
4. Multi-Layer Perceptron ANNs
5. Supervise Learning Algorithm
- Input to neuron j of layer l;
- Weight from layer (l−1) neuron i (means weights of previous layer neuron i) to layer l neuron j;
- Sigmoidal transfer function;
- Bias of neuron j of layer l;
- Output of neuron j in layer l;
- Target value of neuron j of the output layer.
5.1. The Error Calculation
5.2. Output Layer Neurons
5.3. Hidden Layer Neurons
5.4. ANN Parameter
5.4.1. Number of Hidden Layer Neurons
5.4.2. Learning Rate ()
5.4.3. Momentum
5.4.4. Training Type
5.4.5. Epoch
5.4.6. Minimum Error (Only for Training by Minimum Error)
5.5. Delta Learning Rule
5.6. Gradient Descent (GD) Learning Rule
5.7. Gradient Descent Backpropagation with Momentum (GDM)
- For each training pattern in ANNs, feedforward propagation simply calculates the output values;
- Backward propagation is where an erroneous signal is sent backward from the output layer to the input layer. The backpropagated error signal is used to alter the weights.
6. Results
7. Importance of ANN in Various Fields
- ANNs can learn and model non-linear and complicated interactions, which is critical because many of the relationships between inputs and outputs in real life are non-linear and complex;
- ANNs can generalise—after learning from the original inputs and their associations, the model may infer unknown relationships from unknown data, allowing it to generalise and predict on unknown data;
- ANN does not impose any limits on the input variables, unlike many other prediction algorithms (such as how they should be distributed). Furthermore, several studies demonstrated that ANNs could better predict heteroskedasticity, or data with high volatility and non-constant variance, because of their capacity to learn latent links in the data without imposing any predefined relationships.
- Image Processing and Character Recognition: ANNs play an important role in image and character recognition because of their ability to take in a large number of inputs, process them, and infer hidden as well as complex, non-linear correlations. Character recognition, such as handwriting recognition, has a wide range of applications in fraud detection and even national security assessments. Image recognition is a rapidly evolving field with numerous applications ranging from social media facial recognition to cancer detection in medicine to satellite data processing for agricultural and defense uses. Deep ANNs [6,7], which form the backbone of “deep learning”, have now opened up all of the new and revolutionary developments in computer vision, speech recognition, and natural language processing—prominent examples being self-driving cars, thanks to ANN research [16,17,20,40];
- Forecasting: Forecasting is widely used in everyday company decisions (such as sales, the financial allocation between products, and capacity utilisation), economic and monetary policy, and finance and the stock market. Forecasting difficulties are frequently complex; for example, predicting stock prices is a complicated problem with many underlying variables (some known, some unseen). Traditional forecasting models have flaws when it comes to accounting for these complicated, non-linear relationships. Given its capacity to model and extract previously overlooked characteristics and associations, ANNs can provide a reliable alternative when used correctly. ANN also has no restrictions on the input and residual distributions, unlike classical models. For example, recent breakthroughs in the use of LSTM and Recurrent ANNs for forecasting are driving more research on the subject [4,5,6,11,40].
8. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Banhom, M.R.; Katsaggelos, A.K. Digital Image Denoising. IEEE Signal Process. Mag. 1997, 14, 24–41. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, T.; Hu, J.; Xu, D.; Xie, G. End-to-End Background Subtraction via a Multi-Scale Spatio-Temporal Model. IEEE Access 2019, 7, 97949–97958. [Google Scholar] [CrossRef]
- Jain, A.K. Fundamentals of Digital Image Processing. In Control of Color Imaging Systems; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar] [CrossRef]
- Thakur, R.S.; Yadav, R.N.; Gupta, L. State-of-art analysis of image denoising methods using convolutional neural networks. IET Image Process. 2019, 13, 2367–2380. [Google Scholar] [CrossRef]
- Bouwmans, T.; Javed, S.; Sultana, M.; Jung, S.K. Deep neural network concepts for background subtraction:A systematic review and comparative evaluation. Neural Netw. 2019, 117, 8–66. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.; Zhang, X.; Ke, X.; Liu, C.; Xu, X.; Zhan, X.; Wang, C.; Ahmad, I.; Zhou, Y.; Pan, D.; et al. HOG-ShipCLSNet: A Novel Deep Learning Network with HOG Feature Fusion for SAR Ship Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5210322. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X. ShipDeNet-20: An Only 20 Convolution Layers and <1-MB Lightweight SAR Ship Detector. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1234–1238. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X. Squeeze-and-Excitation Laplacian Pyramid Network with Dual-Polarization Feature Fusion for Ship Classification in SAR Images. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4019905. [Google Scholar] [CrossRef]
- Kushwaha, S.; Singh, R.K. Study of Various Image Noises and Their Behavior. Int. J. Comput. Sci. Eng. 2015, 3, 2347–2693. [Google Scholar]
- Protter, M.; Elad, M. Image Sequence Denoising via Sparse and Redundant Representations. IEEE Trans. Image Process. 2010, 18, 842–861. [Google Scholar] [CrossRef]
- Zhao, C.; Basu, A. Dynamic Deep Pixel Distribution Learning for Background Subtraction. IEEE Trans. Circuits Syst. Video Technol. 2020, 30, 4192–4206. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X.; Ke, X. Quad-FPN: A Novel Quad Feature Pyramid Network for SAR Ship Detection. Remote Sens. 2021, 13, 2771. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Orr, G.; Muller, K. Efficient Backprop. In ANNs, Tricks of the Trade, Lecture Notes in Computer Science LNCS 1524; Springer: Berlin/Heidelberg, Germany, 1998; Available online: http://leon.bottou.org/papers/lecun-98x (accessed on 5 April 2022).
- Elad, M.; Aharon, M. Image Denoising Via Sparse and Redundant Representations over Learned Dictionaries. IEEE Trans. Image Process. 2006, 15, 3736–3745. [Google Scholar] [CrossRef] [PubMed]
- Kushwaha, S.; Rai, A. IoT with AI: Requirements and Challenges. Gorteria 2022, 35, 105–114. [Google Scholar]
- Kushwaha, S.; Singh, R.K. Optimization of the proposed hybrid denoising technique to overcome over-filtering issue. Biomed. Eng. Biomed. Tech. 2019, 64, 601–618. [Google Scholar] [CrossRef] [PubMed]
- Kushwaha, S.; Singh, R.K. Robust denoising technique for ultrasound images by splicing of low rank filter and principal component analysis. Biomed. Res. 2018, 29, 3444–3455. [Google Scholar] [CrossRef] [Green Version]
- Burger, H.C.; Schuler, C.J.; Harmeling, S. Image denoising with multi-layer perceptrons, part 1: Comparison with existing algorithms and with bounds. arXiv 2012, arXiv:1211.1544. [Google Scholar]
- Luisier, F.; Blu, T.; Unser, M. Image denoising in mixed poisson—gaussian noise. IEEE Trans. Image Process. (TIP) 2011, 20, 696–708. [Google Scholar] [CrossRef] [Green Version]
- Kushwaha, S. An Efficient Filtering Approach for Speckle Reduction in Ultrasound Images. Biomed. Pharmacol. J. 2017, 10, 1355–1367. [Google Scholar] [CrossRef]
- Levin, A.; Nadler, B. Natural Image Denoising: Optimality and Inherent Bounds. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Washington, DC, USA, 20–25 June 2011; pp. 2833–2840. [Google Scholar]
- Kushwaha, S.; Singh, R.K. Performance Comparison of Different Despeckled Filters for Ultrasound Images. Biomed. Pharmacol. J. 2017, 10, 837–845. [Google Scholar] [CrossRef]
- Gnana Sheela, K.; Deepa, S.N. Review on methods to fix number of hidden neurons in ANNs. Math. Probl. Eng. 2013, 2013, 11. [Google Scholar]
- Rosenblatt, X.F. Principles of Neurodynamics: Perceptrons and the Theory of Brain Mechanism; Spartan Books: Washington, DC, USA, 1961. [Google Scholar]
- Kushwaha, S.; Singh, R.K. An Efficient Approach for Denoising Ultrasound Images using Anisotropic Diffusion and Teaching Learning Based Optimization. Biomed. Pharmacol. J. 2017, 10, 805–816. [Google Scholar] [CrossRef]
- Kushwaha, S. Mathematical Analysis of Robust Anisotropic Diffusion Filter for Ultrasound Images. Int. J. Comput. Sci. Eng. 2016, 4, 152–160. [Google Scholar]
- Zeng, A.K.D.; Zhu, M. Combining background subtraction algorithms with convolutional neural network. J. Electron. Imaging 2019, 28, 013011. [Google Scholar] [CrossRef]
- Zhao, C.; Hu, K.; Basu, A. Universal Background Subtraction Based on Arithmetic Distribution Neural Network. IEEE Trans. Image Process. 2022, 31, 2934–2949. [Google Scholar] [CrossRef] [PubMed]
- Basheer, I.A.; Hajmeer, M. Artificial ANNs: Fundamentals, computing, design, and application. ELSEVIER J. Microbiol. Methods 2000, 43, 3–31. [Google Scholar] [CrossRef]
- Asokan, A.; Anitha, J. Adaptive Cuckoo Search based optimal bilateral filtering for denoising of satellite images. ISA Trans. 2020, 100, 308–321. [Google Scholar] [CrossRef]
- Erhan, D.; Courville, A.; Bengio, Y. Understanding Representations Learned in Deep Architectures; Technical Report 1355; Université de Montréal/DIRO: Montreal, QC, Canada, 2010; pp. 1–25. [Google Scholar]
- Bengio, Y.; Glorot, X. Understanding the difficulty of training deep feedforward ANNs. In Proceedings of the Artificial Intelligence and Statistics Conference (AISTATS), Sardinia, Italy, 13–15 May 2010; Volume 9, pp. 249–256. [Google Scholar]
- Kushwaha, S.; Singh, R.K. Study and Analysis of Various Image Enhancement Method using MATLAB. Int. J. Comput. Sci. Eng. 2015, 3, 15–20. [Google Scholar]
- Lim, L.A.; Keles, H.Y. Learning multi-scale features for foreground segmentation. Pattern Anal. Appl. 2020, 23, 1369–1380. [Google Scholar] [CrossRef] [Green Version]
- Artificial ANNs/Competitive Models. Available online: www.wikibooks.org/wiki/Artificial_Neural_Networks/Competitive_Models (accessed on 5 April 2022).
- Chang, H.H.; Lin, Y.J.; Zhuang, A.H. An Automatic Parameter Decision System of Bilateral Filtering with GPU-Based Acceleration for Brain MR Images. J. Digit. Imaging 2019, 32, 148–161. [Google Scholar] [CrossRef]
- Dao, V.N.P.; Vemuri, V.R. A performance comparison of different back propagation ANNs methods in computer network intrusion detection. Differ. Equ. Dyn. Syst. 2002, 10, 201–214. [Google Scholar]
- Kumar, M.; Mishra, S.K. A Comprehensive Review on Nature Inspired Neural Network based Adaptive Filter for Eliminating Noise in Medical Images. Curr. Med. Imaging 2020, 16, 278–287. [Google Scholar] [CrossRef] [PubMed]
- Engelbrecht, A.P. Computational Intelligence: A Introduction, 2nd ed.; John Wiley and Sons Ltd.: Chichester, UK, 2007. [Google Scholar]
- Liu, S.; Chang, R.; Zuo, J.; Webber, R.J.; Xiong, F.; Dong, N. Application of Artificial ANNs in Construction Management: Current Status and Future Directions. Appl. Sci. 2021, 11, 9616. [Google Scholar] [CrossRef]






| Advantages | Disadvantages |
|---|---|
| For specific requirements, the hidden layer structure can be put up in a variety of ways. | The model’s intricacy may result in over-fitting or under-fitting. |
| Multiple goal outputs can be set without increasing the challenge greatly. | There are no specific network design principles or recommendations. |
| There are a variety of challenges that can be classified as complex regression problems or classification tasks. | Low learning rate and local optimal. |
| Multivariable and non-linear issues. | Extrapolation beyond the data range performs poorly. |
| Problems arising from a lack of knowledge or experience. | Difficulty in expressing the decision’s rationale. |
| The link between factors is unclear. | Weight and other essential factors are difficult to determine. |
| Gaussian Noise Standard Deviation | Test Image Number | Performance Comparison of Different Filters for All Images | |||||
|---|---|---|---|---|---|---|---|
| [16] | [17] | [4] | [5] | [6] | [11] | ||
| σ = 10 | (a) | 35.12 | 35.67 | 35.48 | 36.82 | 36.51 | 36.11 |
| (b) | 40.14 | 44.56 | 44.65 | 45.02 | 44.91 | 43.52 | |
| (c) | 38.52 | 40.15 | 39.88 | 40.12 | 41.25 | 40.44 | |
| (d) | 34.65 | 34.44 | 33.22 | 33.48 | 34.14 | 34.95 | |
| (e) | 32.55 | 32.15 | 32.89 | 33.69 | 32.78 | 33.11 | |
| [16] | [17] | [4] | [5] | [6] | [11] | ||
| σ = 30 | (a) | 29.11 | 30.91 | 30.94 | 31.28 | 31.23 | 30.25 |
| (b) | 35.49 | 39.47 | 39.55 | 39.85 | 38.89 | 40.12 | |
| (c) | 34.15 | 34.56 | 34.68 | 35.57 | 35.68 | 35.90 | |
| (d) | 28.34 | 28.18 | 28.74 | 29.38 | 29.47 | 29.89 | |
| (e) | 27.39 | 27.35 | 26.55 | 26.48 | 27.68 | 27.88 | |
| [16] | [17] | [4] | [5] | [6] | [11] | ||
| σ = 40 | (a) | 28.56 | 28.42 | 28.65 | 29.54 | 28.52 | 28.70 |
| (b) | 33.23 | 37.54 | 37.56 | 37.61 | 37.89 | 39.22 | |
| (c) | 32.24 | 32.56 | 32.45 | 32.78 | 33.11 | 33.78 | |
| (d) | 28.36 | 28.67 | 28.91 | 27.22 | 28.11 | 28.89 | |
| (e) | 25.27 | 25.67 | 25.88 | 25.48 | 26.14 | 26.32 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, A.; Kushwaha, S.; Alarfaj, M.; Singh, M. Comprehensive Overview of Backpropagation Algorithm for Digital Image Denoising. Electronics 2022, 11, 1590. https://doi.org/10.3390/electronics11101590
Singh A, Kushwaha S, Alarfaj M, Singh M. Comprehensive Overview of Backpropagation Algorithm for Digital Image Denoising. Electronics. 2022; 11(10):1590. https://doi.org/10.3390/electronics11101590
Chicago/Turabian StyleSingh, Abha, Sumit Kushwaha, Maryam Alarfaj, and Manoj Singh. 2022. "Comprehensive Overview of Backpropagation Algorithm for Digital Image Denoising" Electronics 11, no. 10: 1590. https://doi.org/10.3390/electronics11101590
APA StyleSingh, A., Kushwaha, S., Alarfaj, M., & Singh, M. (2022). Comprehensive Overview of Backpropagation Algorithm for Digital Image Denoising. Electronics, 11(10), 1590. https://doi.org/10.3390/electronics11101590






