1. Introduction
Artificial intelligence (AI) has become the focus of social attention. At present, the Al semiconductors field is in full bloom and storage is a major basic function of chips. If AI chips pursue performance, the memory itself must be fast enough and the bandwidth be large enough to exchange data quickly, which is inseparable with the progress of SRAM [
1]. At the same time, the manufacturing process of integrated circuits (IC) has entered the nanoscale stage, and the small size and low voltage make circuit nodes more and more sensitive to the impact of space high-energy particles. Data security and reliability have been of concern. With the exploration of space, integrated circuit devices have been gradually applied to aerospace devices. The aerospace microprocessors widely use static random access memory (SRAM) to store data and instructions, because of the advantages of high read/write rate and low power consumption [
2]. The rapidly changing radiation environment in space causes errors in memory [
3], which have different degrees of impact, and seriously affect the performance and life of SRAM, which seriously threatens the regular operation of various spacecraft [
4]. Therefore, it becomes more and more essential to improve the radiation resistance of SRAM.
SRAM usually adds ECC for error correction and error detection in anti-radiation reinforcement. In the process of rectifying soft mistakes, ECC technology does not require unique and sophisticated design in layout and storage unit circuit structure, and it is compatible with commercial memory. As a result, ECC is frequently utilized at this level for error repair and detection. However, the ECC reinforcement design usually brings new problems: timing violations, area increase, and power consumption increase [
5]. The constraints on timing, area, and power consumption are becoming larger and larger with the continued increase of chip-scale and operating frequency. Taking into account various indicators and improving the energy-efficiency and hardware-cost ratio is a fundamental challenge for the current SRAM reinforcement technology.
Although the frequency and range of memory increase, the system still spends most of its time running without errors. However, each memory access must suffer performance, power, and area cost for error coverage in traditional error detection and correction techniques. For instance, suppose we wish to prevent multi-bit errors using robust ECC, each word must hold additional bits for ECC detection, and each access must suffer the delay and power cost of accessing, computing, and comparing the codewords. So to a certain extent, traditional memory protection techniques are not suitable for detecting and recovering from failures because of the high overhead involved. Suppose we can decouple the none-error operation in the normal situation from the error-occurred operation in the uncommon case, and only pay the error protection expense when an error is detected. In that case, we can accomplish both minimal overhead and error prevention.
This paper proposes a design based on a two-dimensional error coding scheme, TECED, to detect and correct the coding error of SRAM (both horizontal and vertical). The main contributions of this paper are as follows:
We reduce the number of detection Units by combining the traditional word-for-word horizontal error code (just for detecting errors and possible small-scale correcting error) with the cross-word vertical error code (for only error correcting), to cut down the energy consumption of ECC;
We have implemented and optimized the two-dimensional error correction codes on the hardware, and thus realizing the potential of two-dimensional error correction codes;
We define the energy-efficiency and hardware-cost ratio as the ratio of the evaluating indicator of the whole system. Comparing with the convention evaluation index, the energy-efficiency and hardware-cost ratio focuses on the system being able to maximize the overall performance of IC instead of a particular index. Compared with the traditional Hamming code widely used at this stage, we can obtain the application range of two-dimensional error coding with a more efficient cost ratio and the evaluation shows that the TECED reduces at most fifty percent of the area overhead and twenty-eight point five percent power consumption of the memory at a specific storage capacity.
The remainder of this paper is organized as follows:
Section 2 presents the background and related work.
Section 3 shows 2D error encoding and its implementation,
Section 4 discusses the experimental results.
Section 5 brings our efforts to a close.
2. Related Work and Background
2.1. Related Work
Errors in memory can lead to the erroneous execution of a program; there are several techniques to mitigate these failures in electronic devices, such as improving process technology [
6,
7,
8,
9], using hardened memory cells [
10,
11,
12], triple-modular redundancy (TMR) [
13,
14,
15], or error-correction codes. However, ECC technology does not need to complete special and complex design in layout and storage unit circuit structure in the process of repairing soft errors, and has good compatibility with commercial memory. Therefore, ECC is usually used for error correction and error detection at this stage. Its idea is to increase the difference between codewords by adding redundant bits. When an error occurs in one codeword, it will not be mistakenly identified as another codeword, to achieve the purpose of fault tolerance.
Lanuzza et al. [
16] suggest applying hamming codes to a data word created by frame bit interleaving to repair burst mistakes in SRAM-based FPGAs. The bit interleaving approach minimizes the likelihood of several bit-faults occurring in the same data word, improving rectification efficiency. However, the quantity of bit interleaving limits the error correction, therefore it may not be acceptable if a high error correction efficiency is required.
Argyrides et al. [
17] propose the Matrix Code (MC) system, which uses hamming codes in conjunction with parity codes to detect and repair numerous faults in an FPGA configuration frame. A matrix of subwords is created from a frame word. Computing hamming codes for each row, giving Single Error Correction Double Error Detection (SECDED) and computing parity codes for each column are used to repair errors. As a result, this approach is ineffective in dealing with MBUs since the ECC algorithm does not identify more than two faults in a row.
In [
18] the Bose–Chaudhuri–Hocquenghem (BCH) code has been proposed for multi-level memory, allowing fast correction of arbitrary 1-bit, 2-bit errors, and 3-bit errors. The ECC codes used in all these files are derived from Hamming codes or BCH codes. Sunita M. S. and colleagues investigated the use of a factorized algorithm to recognize and resolve distinct types of mistakes in memory-dependent matrix codes. With many bit flips, the system boosts memory yield [
19]. It will usually be associated with correcting burst errors, which are located in persistent groups of information bits, affected by external radiation. The downside is that when multiple errors occur on multiple lines, only a few errors are adjusted, others remain uncorrected. Due to the algorithm’s structure, the bit-interleaved Hamming code or BCH code can theoretically be extended to detect and correct more faults. However, the hardware cost will increase rapidly, so the number of faults detected and corrected in the current literature is small. Therefore, due to its simple structure, low area, and low power consumption, 2D error-correction codes have also been applied in other fields. In [
20], 2D error-correction codes have been applied to reinforce multiple faults of on-chip network links, significantly reducing the link cost. Anwesh Varada et al. proposed using two-dimensional even-check codes in Ternary Content Addressable Memory (TCAM) architecture, which can correct one-bit errors and detect up to 3-bit errors in each block while simultaneously achieving a certain degree of power and area reduction [
21]. In the above literature they cannot balance the electrical timing, area and power consumption constraints. Therefore, we propose to use two-dimensional error correction code in the SRAM design.
2.2. Background
2.2.1. Hamming Code
The most commonly used error correction code is the Hamming code. R.W. Hamming proposed the Hamming code in 1950 to correct one error or detect two errors. it is widely used because of its better performance, simplicity, and ease of implementation. The Hamming code needs to satisfy the inequality (1), where
k represents the data bit,
r represents the check digit, and
n represents the total code length.
As long as this inequality is satisfied, the Hamming code can achieve one-bit error correction or two-bit error detection. For example, encoding every 4 bits of data into a Hamming (7,4) code by adding 3 parity bits is one of the most widely adopted and very efficient bit error correction codes, with low space overhead, and provides high reliability [
22]. Mythrai et al. improved the encoder and decoder of Hamming code using the memory implemented by the 8T-bit unit, and improved the advantages of high speed and energy saving of the Hamming code [
23].
2.2.2. Decimal Matrix Codes
The decimal algorithm is used in Decimal Matrix Codes (DMC), and Neethu V et al. discovered that DMC uses encoder reuse routines to ensure fault-tolerant memory safety [
24]. The usage of DMC has increased the capability of error detection and correction. DMC has the drawback of requiring a large number of redundant bits. The word in Hamming codes has an extra equality bit. The word in extended Hamming codes has an extra equality bit. It can be done by obtaining the segment’s load attribute. Hamming codes may fail to notice numerous faults when they occur. Single error correction double Adjacent error detection (SEC-DAED) [
25] Hamming codes are displayed as 16, 32, and 64 bit words. Babitha Antony and her colleagues talk about modifying the Hamming code. By directly altering the bits in memory and reordering the Hamming matrix, upscaling discovery of neighboring faults can be accomplished [
26]. The improved Hamming code can recognize double and triple adjacent faults as well as resolve single and double adjacent errors. It is commonly used to organize code in order to fix any subset of double mistakes.
3. Two-Dimensional Error Correction Code and Its Realization Method
3.1. Overview
We propose using two-dimensional error correction code techniques on SRAM for the fast, error-free operation of common errors. The key to 2D error coding is the combination of lightweight horizontal per-word error coding and vertical column error coding. The horizontal and vertical coding can be an error detection code (EDC) or an error correction code (ECC). So we only use vertical codes for correcting errors, and keep them in the background, so they have a minimal overhead impact in the absence of errors.
In order to demonstrate how 2D error code works, 2D error coding and Hamming code are compared and described below. The first is to compare two protection methods’ error covering and memory requirements for 8 × 8 memory arrays.
Figure 1a shows an ECC for a traditional Hamming code that can be used in contemporary memory arrays.
Figure 1b shows an array using 2D error encoding, which is the same as using Hamming code to complete the function of correcting one and checking one, in which each parity bit calculates the parity in the word. Although the scheme only uses parity check code, the mixture of EDC in the X and Y instructions can identify the position of the erroneous bit. Logically, once the erroneous bits are identified, they can be corrected by simple bit reversal in the binary system.
3.2. Failure Analysis
Figure 2 shows different error types. The following will analyze the error correction ability of two-dimensional error coding under different error types. In type 1 and type 2, no matter if the error occurs in the same row or different rows, as shown in
Figure 2a,b, 2D error codes can detect the occurrence of errors through the horizontal parity check code and correct them through the vertical parity check code. The correction process is to simply reverse the data. In type 3, since the error occurs in the same column, as shown in
Figure 2c; although the 2D error code can detect the occurrence of the error, because there are two errors in the same column, there is no abnormality in the vertical parity code. Corrected by the vertical parity check code, in type 4, both horizontal and vertical coding cannot detect errors due to multi-bit errors, as shown in
Figure 2d, so errors cannot be detected.
3.3. Implementing 2D Error Code in SRAM
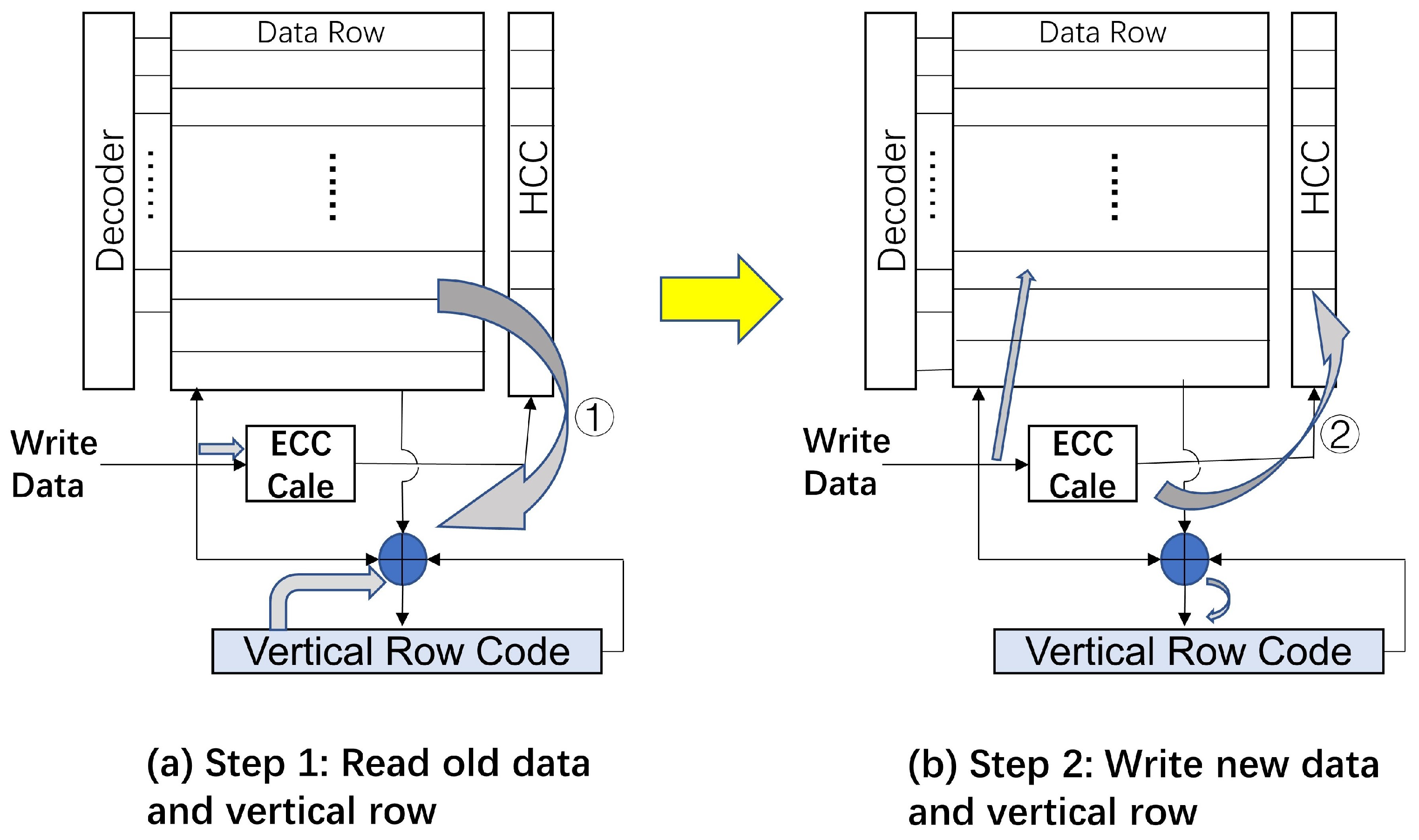
The anatomy of the SRAM data subarray that implements the 2D error code and the manner of replacing the vertical code at write time are depicted in
Figure 3a. Next, we describe how 2D coding schemes operate with and without error.
3.3.1. No Errors Occurred
The horizontal and vertical codes are updated on every writer without errors. The update of the horizontal code is based solely on the statistics to be written, and the update of the vertical code needs to read the old data and XOR with the new data word (step 1), as shown in
Figure 3b, then calculate and update Vertical parity, so the SRAM converts each write operation into a “write-after-read” operation, performing the write of the new data after reading the old data. The “write-after-read” operation will increase all write operations’ latency and power consumption. The performance impact on SRAM demonstrates itself as extra port contention. Luckily, SRAM is usually multi-ported and has free memory bandwidth most of the time. The memory controller conservatively issues “write-after-read” commands for write hits and write misses, even if old data is only utilized to update vertical parity when written, to ease update logic and reduce delays in SRAM port planning. Since the tag subarray is always read on SRAM access, a separate “write-after-read” operation is not required because the tag subarray is always read on SRAM access. It has no directly performance impact because the vertical parity update circuitry can be parallelized and eliminated from the SRAM access critical path. The access time and cycle time of the SRAM subarray are unaffected by the vertical parity update rate as long as it matches the data access rate of the SRAM. Accessing the main array is slower than updating a register-like vertical parity row, so the rate can be readily matched in reality.
3.3.2. In Error Condition
In the case of a single error that can be corrected, it can be corrected by a simple inversion. The controller will initiate a 2D recovery process if the level code identifies an uncorrectable fault. The controller reads all info units that share the vertical parity row with the error data row, and XORs their content altogether, resulting in the error row’s original value which is then written back to the right position. If a 1-bit error at the same memory location for many lines shows a significant fault along the column, recover and review the vertical code to pinpoint the failed column to restart the horizontal repair operation.
4. Experiments and Results
The experiment focuses on evaluating the cost-effectiveness of protecting SRAM by two-dimensional error-correcting codes and Hamming codes. Since the cost-effectiveness ratio is reflected in the ratio of error correction capability to overhead, we compare the two-dimensional error correction code and Hamming at the same level for error correction capability, and correct one-bit errors. In this case, we only need to correct the overhead of the two protection schemes compared to minimize the overhead, to achieve the overall optimal effect and find the best application range of the two-dimensional error correction code. Among them, the hardware overhead is reflected in the area, timing, and power overhead, which will be explained and elaborated on separately through experiments. The experimental object is a single port high density SRAM, which is synthesized by the Design Compiler of S company under the CMOS 40 nm technology. The activity is 0.5, the operating voltage is 1 V, and the operating frequency is 1000 MHz. The proposed 2D error correction codes have been implemented in HDL and mapped to the 40nm library. Then, we implemented varying sizes of protected memories as an example to evaluate the overheads of the schemes. Existing Hamming codes have also been implemented to show the benefits of the 2D codes. We selected the setting of synthesis to put max effort into optimizing power, area overhead and latency to demonstrate the benefit of power/area which can be achieved by the error tolerant memories.
4.1. Hardware Cost Analysis
First, let us compare the area overhead of the array using 2D error coding and Hamming code in the case of different memory capacities.
Figure 4 shows the hardware redundancy ratio of the two codes in the case of mux = 1, 2, 4, and 8; on the curve is the point where the additional area overhead of the two codes accounts for the same, the abscissa represents the depth, the ordinate represents the word capacity(/bit), and the area under the curve shows that the redundancy of the two-dimensional error code is smaller than that of the Hamming code, and the upper area is the Hamming code with a smaller proportion. The redundancy ratio represents the additional area overhead of SRAM, so this indicator will be used as one of the important judgment factors for using two different codes when evaluating the capacity. After comparison, it can be concluded that, compared with Hamming code, 2D error-correction codes can achieve a fifty percent reduction in area overhead with moderate depth and word capacity (ranging from about 16 to 64 for depth and word capacity). Hamming code requires a large amount of extra storage overhead per word in the case of large depth and word capacity, and generates big power consumption and latency costs in calculation or access.
The proposed technique outperforms traditional Hamming codes in terms of decoding complexity and the number of parity bits per word. The reduced decoding complexity means that access times can be reduced. The 2D error correction code involves the problem of replacing the vertical code, and each time writing a word to the array, we have to read out the relevant bit first to update the vertical code. Due to the modest size of the vertical code array, the power, latency and area overhead associated with updating the vertical parity check code are small. Additionally, to reduce update delay, vertical update circuitry can be pipelined in tandem with conventional memory operations.
It can be seen from the above that the advantage of Hamming code in ECC is that only one read is required in the process of access and error protection. However in some scales of SRAM, the proportion of extra redundancy is large, and the area overhead of hardware is significant. However, the advantage of two-dimensional error coding lies in the use of parity-check coding; the coding is simple and stable. The hardware overhead is small, but based on the characteristics of SRAM, we will find that SRAM requires more reading times for error correction after errors occur. Since an error every few days is very rare, the recovery process’ overhead has little effect on overall performance. According to the American Physical Data Center statistics, between 1980 and 1990, the United States launched a total of 39 synchronous satellites. The number of failures of these satellites due to the single event effect was 621, and an error occurred every fifteen hours on average [
27], so we can consider 2D errors. It is tolerable that the code requires many reads when performing error correction.
4.2. Power Consumption Analysis
As an indicator to evaluate its performance, there is a more important point–power consumption. In this section, we will intuitively evaluate the performance of Hamming codes and 2D error codes by analyzing and comparing the power consumption. Power consumption can be divided into static power consumption and dynamic power consumption, and the total power consumption is equal to the sum of static power consumption and dynamic power consumption. Since the static power consumption exists even when no switching occurs, even when the circuit is waiting, minimizing the static power consumption is a fundamental goal in the design process. Dynamic power consumption is reflected in the writing and reading of data in SRAM. We will evaluate the total power consumption of Hamming code versus 2D error encoding. In the experimental results, the read and write power consumption of SRAM is tiny compared with its own static power consumption, which is almost negligible, so we get the average power consumption comparison of the two; as shown in
Figure 5, we selected comparing the power of SRAMs with different capacities in mux = 4, 8 and bank = 1, 2. The orange column above the blue column represents the larger power consumption of Hamming code than the two-dimensional error code, and the lower one is the Hamming code. The clear code is smaller than the two-dimensional error code. The clear comparison in the figure shows that the 2D error encoding consumes less power at most of the capacities selected in the figure. By comparison, two-dimensional error correction codes can reduce power consumption by up to 28.5% compared with Hamming codes. Therefore, this power consumption evaluation provides an excellent reference for the design and manufacture of SRAM of corresponding capacity. Based on the above results, we can select a moderate-capacity SRAM according to the needs and use the two-dimensional error correction code solution for reinforcement, to achieve high cost-efficiency.
5. Conclusions
In recent years, the rapid development of transistor technology makes SRAM more prone to soft errors. Electrical timing, area and power consumption has become the main constraint of digital system design. We cannot only focus on one index and ignore other indexes in a design. Against the background of the increasing chip-scale and work frequency, focusing on only one index will lead to other overall imbalances, which will affect the performance of the system. We propose a design named TECED, achieving higher energy-efficiency and lower hardware cost by using a two-dimensional error correction code. This paper evaluates the applicability of 2D error coding in different capacity ranges in the 40nm process. The evaluation shows that the TECED reduces the area and power consumption of the memory within a specific storage capacity compared with the traditional Hamming code, which will provide an important reference for the future SRAM design.
Author Contributions
Literature search, Z.C.; Conceptualization, J.L., B.L. and X.C.; Data curation, Z.C.; Project administration, J.L. and X.C.; Formal analysis, Y.Z., X.C. and C.L.; Investigation, Y.Z., J.L. and B.L.; Methodology, J.L., B.L., X.C. and C.L.; Resources, B.L. and C.L.; Software, Z.C. and B.L.; Supervision, Y.Z. and C.L.; Visualization, Z.C.;Writing—original draft, Z.C. and Y.Z.; Writing—review and editing, Z.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Key Laboratory Fund, College of Computer, National University of Defense Technology grant No. WDZC20215250109.
Data Availability Statement
The data presented in this study are available on request from corresponding authors.
Acknowledgments
This work was supported by Key Laboratory Fund, College of Computer, National University of Defense Technology under grant No. WDZC20215250109.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ma, S.; Wu, T.; Chen, X.; Wang, Y.; Tang, H.; Yao, Y.; Wang, Y.; Zhu, Z.; Deng, J.; Wan, J.; et al. An artificial neural network chip based on two-dimensional semiconductor. Sci. Bull. 2022, 67, 270–277. [Google Scholar] [CrossRef]
- Du, B.; Desogus, M.; Sterpone, L. Analysis and mitigation of SEUs in ARM-based SoC on Xilinx Virtex-V SRAM-based FPGAs. In Proceedings of the 2015 11th Conference on Ph.D. Research in Microelectronics and Electronics (PRIME), Glasgow, UK, 29 June–2 July 2015; pp. 236–239. [Google Scholar]
- Sanyong, Z. A SEU/MBU tolerant SRAM bit cell based on multi-input gate. In Proceedings of the 2017 4th International Conference on Electrical and Electronic Engineering (ICEEE), Ankara, Turkey, 8–10 April 2017; pp. 251–255. [Google Scholar]
- Dyer, C.; Hands, A.; Ryden, K.; Lei, F. Extreme Atmospheric Radiation Environments and Single Event Effects. IEEE Trans. Nucl. Sci. 2018, 65, 432–438. [Google Scholar] [CrossRef] [Green Version]
- Guo, J.; Zhu, L.; Liu, W.; Huang, H.; Liu, S.; Wang, T.; Xiao, L.; Mao, Z. Novel Radiation-Hardened-by-Design (RHBD) 12T Memory Cell for Aerospace Applications in Nanoscale CMOS Technology. IEEE Trans. Very Large Scale Integr. Syst. 2017, 25, 1593–1600. [Google Scholar] [CrossRef]
- Hubert, G.; Li Cavoli, P.; Federico, C.; Artola, L.; Busto, J. Effect of the Radial Ionization Profile of Proton on SEU Sensitivity of Nanoscale SRAMs. IEEE Trans. Nucl. Sci. 2015, 62, 2837–2845. [Google Scholar] [CrossRef]
- Rostand, N.; Hubert, G.; Martinie, S. SEU Prediction for Very Integrated Circuits based on Advanced Physical Considerations. In Proceedings of the 2019 19th European Conference on Radiation and Its Effects on Components and Systems (RADECS), Montpellier, France, 16–20 September 2019; pp. 1–6. [Google Scholar]
- Clemente, J.A.; Hubert, G.; Fraire, J.; Franco, F.J.; Villa, F.; Rey, S.; Baylac, M.; Puchner, H.; Mecha, H.; Velazco, R. SEU Characterization of Three Successive Generations of COTS SRAMs at Ultralow Bias Voltage to 14.2-MeV Neutrons. IEEE Trans. Nucl. Sci. 2018, 65, 1858–1865. [Google Scholar] [CrossRef] [Green Version]
- Shuming, C.; Bin, L.; Biwei, L.; Zheng, L. Temperature Dependence of Digital SET Pulse Width in Bulk and SOI Technologies. IEEE Trans. Nucl. Sci. 2008, 55, 2914–2920. [Google Scholar] [CrossRef]
- Hu, C.; Yue, S.; Lu, S. Design of a novel 12T radiation hardened memory cell tolerant to single event upsets (SEU). In Proceedings of the 2017 2nd IEEE International Conference on Integrated Circuits and Microsystems (ICICM), Nanjing, China, 8–11 November 2017; pp. 182–185. [Google Scholar]
- Shinghal, K.; Saxena, A.; Misra, R.; Agarwal, A. Radiation Hardened Memories for Satellites. In Proceedings of the 2019 4th International Conference on Internet of Things: Smart Innovation and Usages (IoT-SIU), Ghaziabad, India, 18–19 April 2019; pp. 1–5. [Google Scholar]
- Dou, Z.; Yan, A.; Zhou, J.; Hu, Y.; Chen, Y.; Ni, T.; Cui, J.; Girard, P.; Wen, X. Design of a Highly Reliable SRAM Cell with Advanced Self-Recoverability from Soft Errors. In Proceedings of the 2020 IEEE International Test Conference in Asia (ITC-Asia), Ghaziabad, India, 18–19 April 2019; pp. 35–40. [Google Scholar]
- Kjar, R.A.; Peterson, B.E.; Blandford, J.T. Radiation Hardened 64-BIT CMOS/SOS RAM. IEEE Trans. Nucl. Sci. 1976, 23, 1728–1731. [Google Scholar] [CrossRef]
- Foucard, G.; Peronnard, P.; Velazco, R. Reliability limits of TMR implemented in a SRAM-based FPGA: Heavy ion measures vs. fault injection predictions. In Proceedings of the 2010 11th Latin American Test Workshop, Punta del Este, Uruguay, 28–31 March 2010; pp. 1–5. [Google Scholar]
- Flores dos Santos, A.; Tambara, L.A.; Kastensmidt, F.L. Evaluating the efficiency of using TMR in the high-level synthesis design flow of SRAM-based FPGA. In Proceedings of the 2017 IEEE 8th Latin American Symposium on Circuits Systems (LASCAS), Bariloche, Argentina, 20–23 February 2017; pp. 1–4. [Google Scholar]
- Lanuzza, M.; Zicari, P.; Frustaci, F.; Perri, S.; Corsonello, P. A self-hosting configuration management system to mitigate the impact of Radiation-Induced Multi-Bit Upsets in SRAM-based FPGAs. In Proceedings of the 2010 IEEE International Symposium on Industrial Electronics, Bari, Italy, 4–7 July 2010; pp. 1989–1994. [Google Scholar]
- Argyrides, C.; Pradhan, D.K.; Kocak, T. Matrix Codes for Reliable and Cost Efficient Memory Chips. IEEE Trans. Very Large Scale Integr. Syst. 2011, 19, 420–428. [Google Scholar] [CrossRef]
- Badack, C.; Kern, T.; Gössel, M. Modified DEC BCH codes for parallel correction of 3-bit errors comprising a pair of adjacent errors. In Proceedings of the 2014 IEEE 20th International On-Line Testing Symposium (IOLTS), Platja d’Aro, Spain, 7–9 July 2014; pp. 116–121. [Google Scholar]
- Sunita, M.S.; Kanchana, B. Matrix Code Based Multiple Error Correction Technique for N-Bit Memory Data. Int. J. VLSI Des. Commun. Syst. 2013, 4, 29–37. [Google Scholar]
- Chen, X.; Lu, Z.; Lei, Y.; Wang, Y.; Chen, S. Multi-bit transient fault control for NoC links using 2D fault coding method. In Proceedings of the 2016 Tenth IEEE/ACM International Symposium on Networks-on-Chip (NOCS), Nara, Japan, 31 August–2 September 2016; pp. 1–8. [Google Scholar]
- Varada, A.; Agrawal, S. An Efficient SRAM-Based Ternary Content Addressable Memory (TCAM) with Soft Error Correction. In Proceedings of the 2021 5th International Conference on Electronics, Materials Engineering Nano-Technology (IEMENTech), Kolkata, India, 24–26 September 2021; pp. 1–6. [Google Scholar]
- Hamming, R.W. Error detecting and error correcting codes. Bell Labs Tech. J. 2014, 29, 147–160. [Google Scholar] [CrossRef]
- Kavitha, S.; Singh, P.; Shah, A.P.; Vishwakarma, S.K.; Reniwal, B.S. Energy Efficient, Hamming Code Technique for Error Detection/Correction Using In-Memory Computation. In Proceedings of the 2021 25th International Symposium on VLSI Design and Test (VDAT), Surat, India, 16–18 September 2021; pp. 1–4. [Google Scholar]
- Neethu, V.; Anju, S.L. A New Methodology for Error Detection and Correction to Realize Fault Tolerant Memory. Int. J. Sci. Res. 2013, 4, 1689–1694. [Google Scholar]
- Sánchez-Macián, A.; Reviriego, P.; Maestro, J.A. Hamming SEC-DAED and Extended Hamming SEC-DED-TAED Codes Through Selective Shortening and Bit Placement. IEEE Trans. Device Mater. Reliab. 2014, 14, 574–576. [Google Scholar] [CrossRef]
- Antony, B.; Divya, S. Modified Hamming Codes with Double Adjacent Error Correction along with Enhanced Adjacent Error Detection. Int. J. Innov. Res. Comput. Commun. Eng. 2015, 3, 7706–7713. [Google Scholar]
- Wallmark, J.; Marcus, S. Maximum packing density and minimum size of semiconductor devices. In Proceedings of the 1961 International Electron Devices Meeting, Washington, DC, USA, 26–28 October 1961; p. 34. [Google Scholar]
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).