Anti-Jerk Optimal Preview Control Strategy to Enhance Performance of Active and Semi-Active Suspension Systems
Abstract
:1. Introduction
2. Research Motivation
3. Problem Formulation
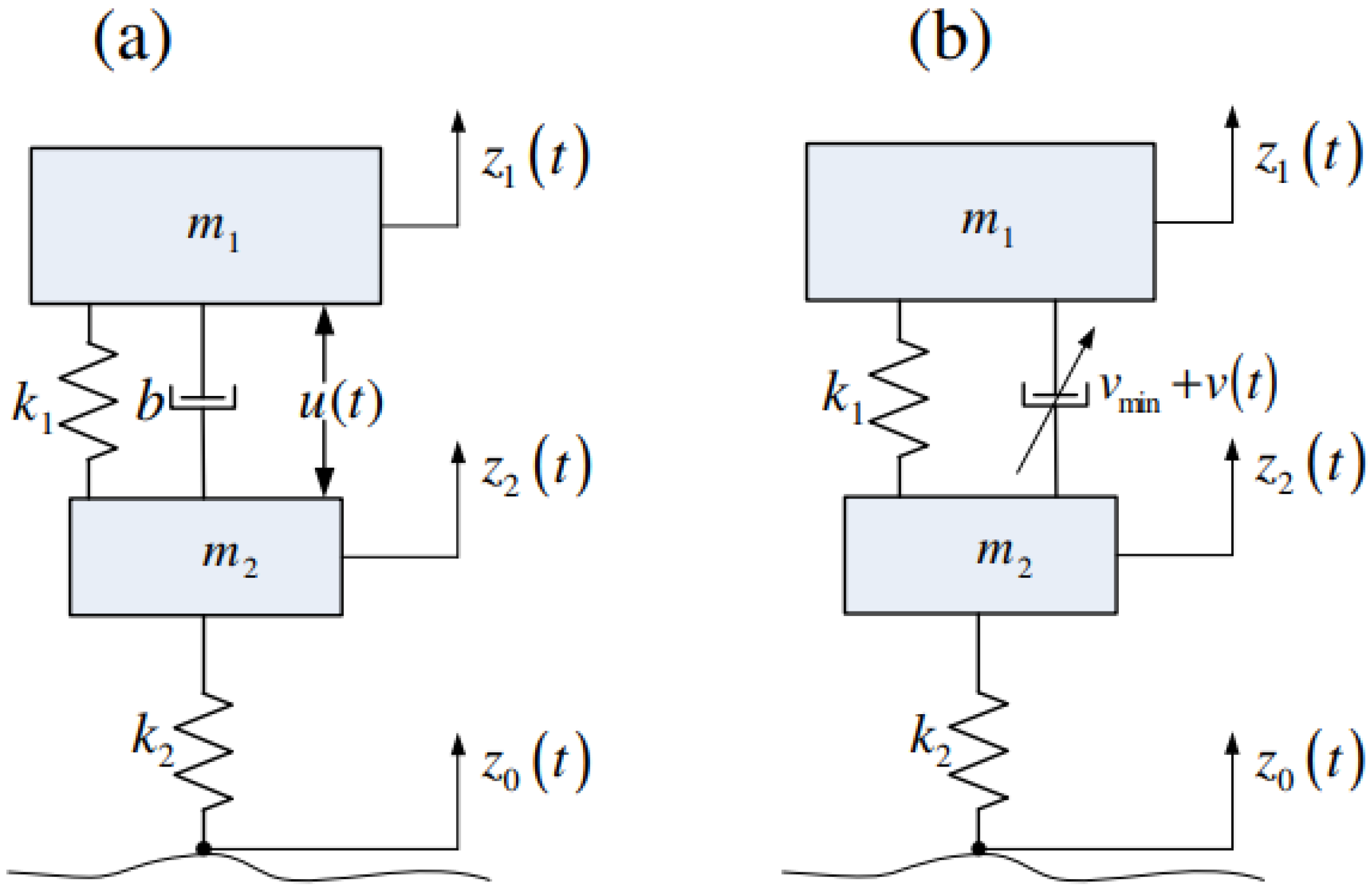
3.1. Quarter-Car Mathematical and Dynamic Models
3.2. Formulation for Optimal Control Design
4. Controller Design
4.1. Active Suspension System
4.2. Semi-Active Suspension System
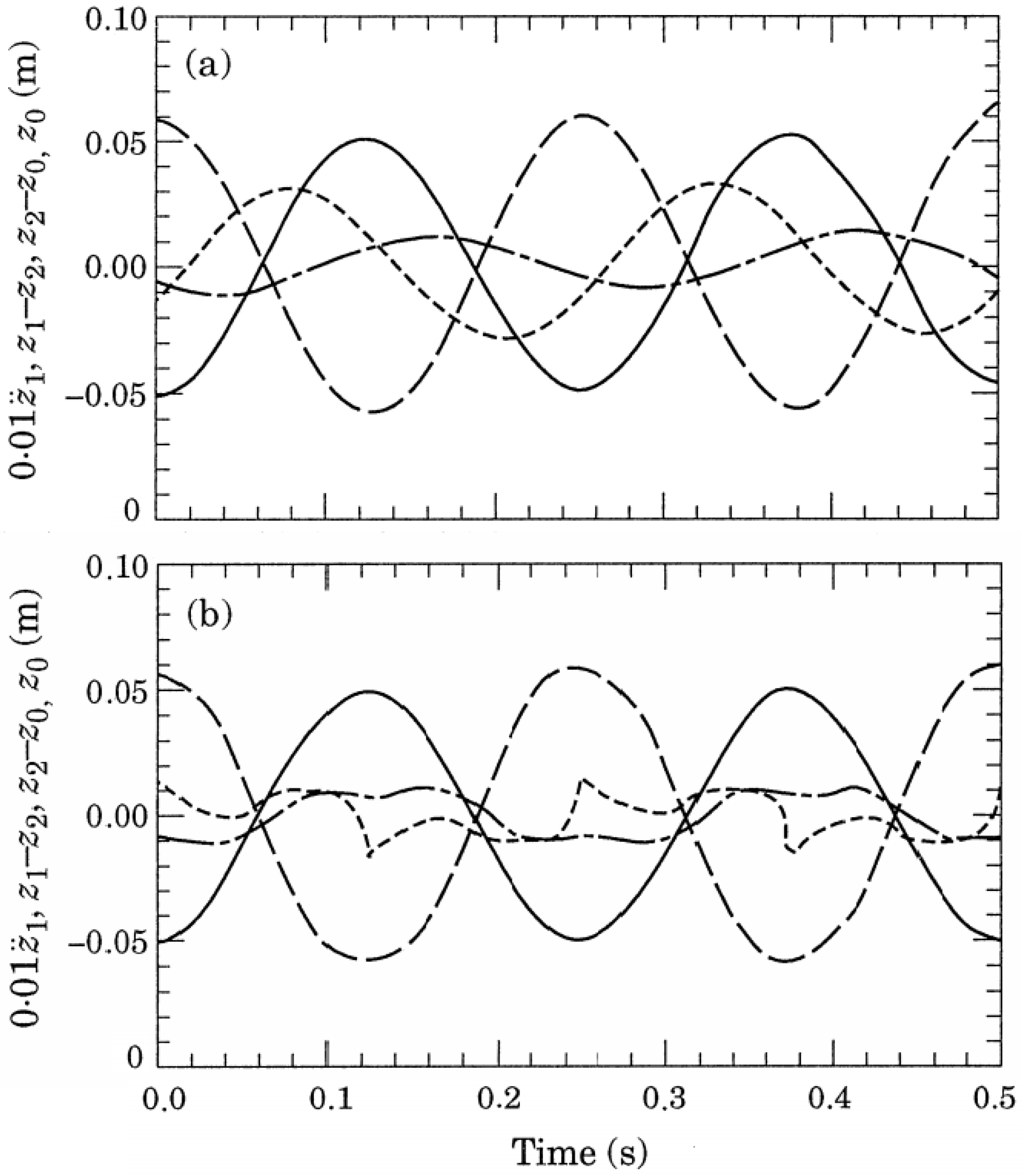
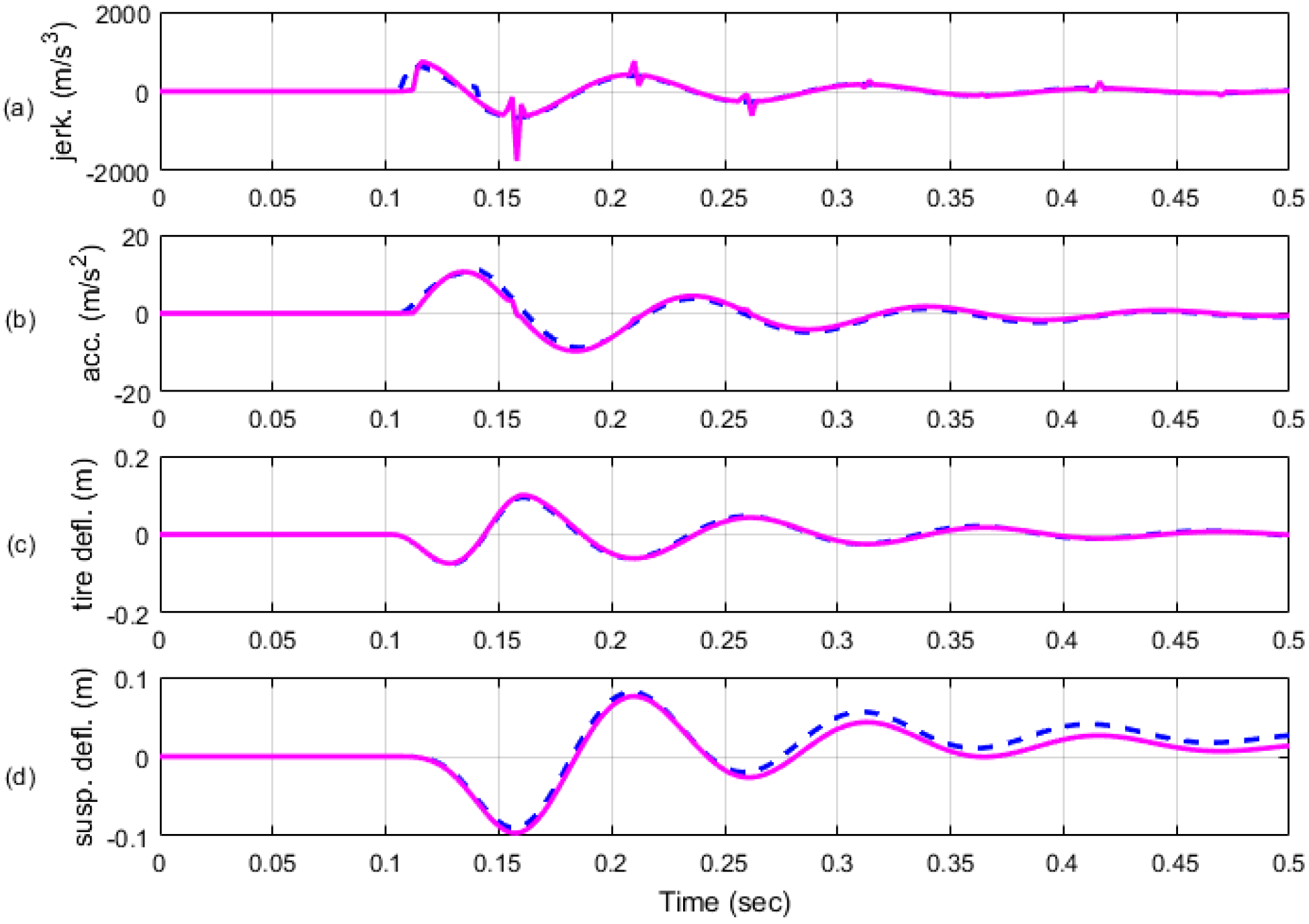
5. Analysis of Simulation Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ahmad, E.; Iqbal, J.; Arshad Khan, M.; Liang, W.; Youn, I. Predictive Control Using Active Aerodynamic Surfaces to Improve Ride Quality of a Vehicle. Electronics 2020, 9, 1463. [Google Scholar] [CrossRef]
- Van der Sande, T.; Gysen, B.; Besselink, I.; Paulides, J.; Lomonova, E.; Nijmeijer, H. Robust control of an electromagnetic active suspension system: Simulations and measurements. Mechatronics 2013, 23, 204–212. [Google Scholar] [CrossRef]
- Rath, J.J.; Defoort, M.; Sentouh, C.; Karimi, H.R.; Veluvolu, K.C. Output-Constrained Robust Sliding Mode Based Nonlinear Active Suspension Control. IEEE Trans. Ind. Electron. 2020, 67, 10652–10662. [Google Scholar] [CrossRef]
- Zhou, C.; Liu, X.; Chen, W.; Xu, F.; Cao, B. Optimal sliding mode control for an active suspension system based on a genetic algorithm. Algorithms 2018, 11, 205. [Google Scholar] [CrossRef] [Green Version]
- Formentin, S.; Karimi, A. A data-driven approach to mixed-sensitivity control with application to an active suspension system. IEEE Trans. Ind. Inform. 2012, 9, 2293–2300. [Google Scholar] [CrossRef] [Green Version]
- Kilicaslan, S. Control of active suspension system considering nonlinear actuator dynamics. Nonlinear Dyn. 2018, 91, 1383–1394. [Google Scholar] [CrossRef]
- Liu, C.; Chen, L.; Yang, X.; Zhang, X.; Yang, Y. General theory of skyhook control and its application to semi-active suspension control strategy design. IEEE Access 2019, 7, 101552–101560. [Google Scholar] [CrossRef]
- Desai, R.M.; Jamadar, M.E.H.; Kumar, H.; Joladarashi, S.; Rajasekaran, S.; Amarnath, G. Evaluation of a commercial MR damper for application in semi-active suspension. SN Appl. Sci. 2019, 1, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Soliman, A.; Kaldas, M. Semi-active suspension systems from research to mass-market—A review. J. Low Freq. Noise Vib. Act. Control. 2021, 40, 1005–1023. [Google Scholar] [CrossRef] [Green Version]
- Hać, A. Optimal linear preview control of active vehicle suspension. Veh. Syst. Dyn. 1992, 21, 167–195. [Google Scholar] [CrossRef]
- Qin, Y.; Xiang, C.; Wang, Z.; Dong, M. Road excitation classification for semi-active suspension system based on system response. J. Vib. Control. 2018, 24, 2732–2748. [Google Scholar] [CrossRef]
- Qin, Y.; Langari, R.; Wang, Z.; Xiang, C.; Dong, M. Road excitation classification for semi-active suspension system with deep neural networks. J. Intell. Fuzzy Syst. 2017, 33, 1907–1918. [Google Scholar] [CrossRef]
- Paulides, J.J.; Encica, L.; Lomonova, E.A.; Vandenput, A.J. Design considerations for a semi-active electromagnetic suspension system. IEEE Trans. Magn. 2006, 42, 3446–3448. [Google Scholar] [CrossRef] [Green Version]
- Tanahashi, H.; Shindo, K.; Nogami, T.; Oonuma, T. Toyota Electronic Modulated Air Suspension for the 1986 Soarer; Technical Report; SAE Technical Paper; SAE International: Warrendale, PA, USA, 1987. [Google Scholar]
- Youn, I.; Hać, A. Semi-active suspensions with adaptive capability. J. Sound Vib. 1995, 180, 475–492. [Google Scholar] [CrossRef]
- Emura, J.; Kakizaki, S.; Yamaoka, F.; Nakamura, M. Development of the semi-active suspension system based on the sky-hook damper theory. SAE Trans. 1994, 103, 1110–1119. [Google Scholar]
- Ma, X.; Wong, P.K.; Zhao, J. Practical multi-objective control for automotive semi-active suspension system with nonlinear hydraulic adjustable damper. Mech. Syst. Signal Process. 2019, 117, 667–688. [Google Scholar] [CrossRef]
- Yoon, D.S.; Kim, G.W.; Choi, S.B. Response time of magnetorheological dampers to current inputs in a semi-active suspension system: Modeling, control and sensitivity analysis. Mech. Syst. Signal Process. 2021, 146, 106999. [Google Scholar] [CrossRef]
- Bender, E. Optimum Linear Preview Control with Application to Vehicle Suspension. ASME J. Basic Eng. 1968, 90, 213–221. [Google Scholar] [CrossRef]
- Hac, A.; Youn, I. Optimal Semi-Active Suspension with Preview Based on a Quarter Car Model. J. Vib. Acoust. 1992, 114, 84–92. [Google Scholar] [CrossRef]
- Thompson, A.; Pearce, C. RMS values for force, stroke and deflection in a quarter-car model active suspension with preview. Veh. Syst. Dyn. 2003, 39, 57–75. [Google Scholar] [CrossRef]
- Birla, N.; Swarup, A. Optimal preview control: A review. Optim. Control. Appl. Methods 2015, 36, 241–268. [Google Scholar] [CrossRef]
- Göhrle, C.; Schindler, A.; Wagner, A.; Sawodny, O. Model predictive control of semi-active and active suspension systems with available road preview. In Proceedings of the 2013 European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1499–1504. [Google Scholar]
- Jin, T.; Liu, Z.; Sun, S.; Ren, Z.; Deng, L.; Yang, B.; Christie, M.D.; Li, W. Development and evaluation of a versatile semi-active suspension system for high-speed railway vehicles. Mech. Syst. Signal Process. 2020, 135, 106338. [Google Scholar] [CrossRef]
- Thompson, A.; Pearce, C.E.M. Direct computation of the performance index for an optimally controlled active suspension with preview applied to a half-car model. Veh. Syst. Dyn. 2001, 35, 121–137. [Google Scholar] [CrossRef]
- Zhen, Z.; Jiang, S.; Jiang, J. Preview Control and Particle Filtering for Automatic Carrier Landing. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2662–2674. [Google Scholar] [CrossRef]
- Zhen, Z.; Jiang, S.; Ma, K. Automatic carrier landing control for unmanned aerial vehicles based on preview control and particle filtering. Aerosp. Sci. Technol. 2018, 81, 99–107. [Google Scholar] [CrossRef]
- Zhou, H.; Gao, J.; Liu, H. Vehicle speed preview control with road curvature information for safety and comfort promotion. Proc. Inst. Mech. Eng. Part J. Automob. Eng. 2021, 235, 1527–1538. [Google Scholar] [CrossRef]
- Yim, S. Design of a preview controller for vehicle rollover prevention. IEEE Trans. Veh. Technol. 2011, 60, 4217–4226. [Google Scholar] [CrossRef]
- Choi, H.D.; Lee, C.J.; Lim, M.T. Fuzzy preview control for half-vehicle electro-hydraulic suspension system. Int. J. Control. Autom. Syst. 2018, 16, 2489–2500. [Google Scholar] [CrossRef]
- Hrovat, D.; Hubbard, M. Optimum Vehicle Suspensions Minimizing rms Rattlespace, Sprung-Mass Acceleration and Jerk. J. Dyn. Syst. Meas. Control. 1981, 103, 228–236. [Google Scholar] [CrossRef]
- Hrovat, D.; Hubbard, M. A comparison between jerk optimal and acceleration optimal vibration isolation. J. Sound Vib. 1987, 112, 201–210. [Google Scholar] [CrossRef]
- Rutledge, D.; Hubbard, M.; Hrovat, D. A two DOF model for jerk optimal vehicle suspensions. Veh. Syst. Dyn. 1996, 25, 113–136. [Google Scholar] [CrossRef]




| Weighting Constants | Targets | 1st Set | 2nd Set |
|---|---|---|---|
| Suspension deflection | |||
| Tire deflection | |||
| Sprung-mass acceleration | 1 | ||
| Sprung-mass jerk | 1 | 0 |
| Active System | E | E | E | E | |
|---|---|---|---|---|---|
| set | |||||
| set |
| Semi-Active System w/Preview | E | E | E | E | |
|---|---|---|---|---|---|
| set | |||||
| set |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Youn, I.; Ahmad, E. Anti-Jerk Optimal Preview Control Strategy to Enhance Performance of Active and Semi-Active Suspension Systems. Electronics 2022, 11, 1657. https://doi.org/10.3390/electronics11101657
Youn I, Ahmad E. Anti-Jerk Optimal Preview Control Strategy to Enhance Performance of Active and Semi-Active Suspension Systems. Electronics. 2022; 11(10):1657. https://doi.org/10.3390/electronics11101657
Chicago/Turabian StyleYoun, Iljoong, and Ejaz Ahmad. 2022. "Anti-Jerk Optimal Preview Control Strategy to Enhance Performance of Active and Semi-Active Suspension Systems" Electronics 11, no. 10: 1657. https://doi.org/10.3390/electronics11101657
APA StyleYoun, I., & Ahmad, E. (2022). Anti-Jerk Optimal Preview Control Strategy to Enhance Performance of Active and Semi-Active Suspension Systems. Electronics, 11(10), 1657. https://doi.org/10.3390/electronics11101657







