Multiplication and Accumulation Co-Optimization for Low Complexity FIR Filter Implementation

Abstract

In multiplierless finite impulse response (FIR) filters, the product accumulation block (PAB) could be the major contributor to hardware complexity, especially for high-order filters. In this paper, an optimization scheme where the constant multiplication block and the PAB are jointly optimized at the bit-level is proposed to minimize the hardware complexity. In the proposed joint optimization, the multiple constant multiplications (MCM) block is rearranged into several MCM sub-blocks. The products are summed locally before accumulation to reduce the word-length of the structural adders. It is shown that the symmetric property of linear phase FIR filters can be utilized in some cases to further reduce the complexity of the constant multiplications. Quantitative analyses are also presented to study the relationship between the optimum group size and the coefficient values as well as the filter orders. It is shown that there is no fixed optimum structure for filters with different coefficient word-lengths and filter orders, and each filter needs to be optimized specifically to achieve the minimum hardware complexity. Implementation results are presented to validate the effectiveness of the proposed method.

1. Introduction

Digital filtering is one of the most important functions in digital signal processing (DSP) systems. Finite impulse response (FIR) filters are widely used in many DSP applications due to their guaranteed stability and linear phase properties [1]. However, compared with infinite impulse response (IIR) filters, the computational complexity of FIR filters are much higher [2,3,4]. Therefore, it is crucial to reduce the complexity of FIR filters. Extensive research has been conducted in the past several decades. Since multipliers are expensive in terms of circuit area and computational delay, many works focus on the design of FIR filter coefficients. One of the approaches is to reduce the number of non-zero filter coefficients, which is always referred to as a sparse FIR filter design [5,6,7,8]. Since multipliers can be omitted if the corresponding coefficients are zero, the overall complexity can be reduced by increasing the sparsity of the filter. In addition, FIR filters can also be implemented using a number system other than binary for complexity reduction. A typical example is the residue numeral system (RNS)-based FIR filter implementation [9]. Moreover, there are also some works focusing on a hybrid filter structure for complexity reduction [10,11,12]. For the VLSI implementation of FIR filters with fixed coefficients, a multiplierless design is a more general technique to reduce the hardware and time complexities [13,14,15,16,17,18,19,20,21,22,23]. In the multiplierless implementation of FIR filters, the constant multiplications are generally implemented by optimized shift-add networks. The adders in the shift-add network are usually referred to as multiplication block adders. Besides multiplication block adders, another type of adder, known as structural adders [22], exists to implement the product accumulation block (PAB) of the FIR filter.

The problem of minimizing the multiplication block has been intensively studied. Various optimization techniques have been proposed [24,25,26,27,28,29,30,31] to extract the common subexpressions (partial products) in the coefficients and reuse them within the coefficient multiplication as well as across all the multiplications for a direct form filter structure (shown in Figure 1a) or a transposed direct form (TDF) filter structure (shown in Figure 1b). Most of the multiplication block design algorithms focus on the TDF filter structure, where the input sample is concurrently multiplied by all the filter coefficients, forming a multiple constant multiplication (MCM) block. With the help of MCM design algorithms, the constant multiplications in TDF FIR filters can be implemented very efficiently.

Although the optimization of structural adders in the PABs is generally ignored by most researchers, it is noted that this part can be the major contributor to the overall hardware complexity. The number of structural adders is the same as the filter order and cannot be reduced. The naturally pipelined PAB in the TDF structure is advantageous to achieving low critical path delay, but it results in an increase in hardware complexity. As product words are added one by one along the accumulation line, the word-lengths of structural adders increase monotonically. The direct form structure, on the other hand, contains a PAB without any delay element, which could be implemented by a binary adder-tree of relatively less complexity. Therefore, a hybrid structure is a proper choice to reduce the PAB complexity and subsequently the overall complexity of FIR filters without sacrificing too much delay. In [11], the matrix MCM is proposed to minimize the adder cost of constant multiplications in hybrid-form FIR filters. In [12], different types of hybrid-form structures are discussed and evaluated. However, no optimization schemes have been investigated in the existing literature to reduce the bit-level complexity of the multiplication block as well as the PAB in hybrid-form FIR filters. Moreover, the symmetric property of linear phase FIR filters has not been utilized in such optimizations.

In this paper, a design scheme where the multiplication block and the PAB are jointly optimized at bit-level is proposed to minimize the hardware complexity of the multiplierless implementation of FIR filters. In the proposed joint optimization, the MCM block is partitioned into several MCM sub-blocks. The product words are summed locally before accumulation to reduce the word-length of structural adders. In particular, when the MCM block is partitioned into two MCM sub-blocks, the symmetric property of linear phase FIR filters can be utilized by carefully grouping the product terms to further reduce the complexity of constant multiplications. An exhaustive search algorithm, which minimizes the total complexity of the constant multipliers and PAB, is proposed to determine the optimum partition of the MCM block. The relationship between the coefficient word-length as well as filter order and the optimum structure is also studied.

The rest of the paper is organized as follows. Section 2 presents the complexity reduction of PAB. Section 3 discusses the joint optimization of PAB and the multiplication block. The quantitative analysis of the optimum group size is presented in Section 4, and conclusions are drawn in Section 5.

2. Complexity Reduction of the Product Accumulation Block

2.1. Complexity of FIR Filters at the Bit Level

Instead of the word-level adder count, a more accurate estimation of hardware complexity is the number of full adders. According to [32,33], the number of full adders needed to implement a shift-add operation can be estimated as

$$W_{{\mathrm{MBA}}_i}=W_X+\lceil {log}_2{f}_i\rceil -l_i,$$

(1)

where $W_X$ is the word-length of the filter input, $f_i$ is the generated fundamental and $l_i$ is the number of left-shifts in this shift-add operation. Since shifts can be implemented by proper wiring, the complexity of the MCM block can be measured in terms of the total number of full adders needed, which is given by

$$W_{\mathrm{MBA}}=\sum _{i=1}^M{W}_{{\mathrm{MBA}}_i}=\sum _{i=1}^{M_r+M_a}(W_X+\lceil {log}_2{f}_i\rceil -l_i).$$

(2)

Here, $M=M_r+M_a$ is the number of shift-add operations in the multiplication block, where $M_r$ is the number of required fundamentals that are reduced from the given coefficients and $M_a$ is the number of additional fundamentals that are inserted to implement the required fundamentals. Therefore, both $M_a$ ($M_r$ is fixed for a given coefficient set) and $W_{{\mathrm{MBA}}_i}$ need to be minimized to reduce the complexity of the multiplier.

In FIR filters, the PAB consists of two parts: (i) the structural adders and (ii) the registers. The number of full adders needed to implement the ith structural adder in an Nth order filter is

$$W_{{\mathrm{SA}}_i}=W_X+\lceil {log}_2\sum _{k=i}^N\left|h_k\right|\rceil -s_i, \mathrm{for} 0\le i<N,$$

(3)

where $h_k$ represents the kth filter coefficient and $s_i$ is the number of left-shifts needed to generate $h_i$ from the corresponding fundamental. The total number of full adders needed is therefore the sum of N structural adders. The number of bit-registers needed for each register, denoted by $W_{{\mathrm{Reg}}_i}$, can be estimated in the same manner, except that the number of left-shifts $s_i$ will not affect the number of bit-registers. Note that either in the direct form structure or the TDF structure, the number of structural adders and registers are fixed.

2.2. Optimization of the Product Accumulation Block

In Equation (3), the first term $W_X$ and the third term $s_i$ are fixed for a tap. In the TDF structure, each product is added to the accumulation result of the previous tap. Therefore, the second term in Equation (3) needs to include the coefficients of all the previous taps to guard the range expansion. For the hybrid FIR filter structure, the MCM block can be rearranged into L MCM sub-blocks. In this work, the structure has two different forms depending on the value of L.

2.2.1. Structure for $L=2$

The filter coefficients for linear phase FIR filters are symmetric, i.e., $|h_i| = |h_{N-i}|$ for $0\le i\le \lfloor N/2\rfloor$. For $L=2$, this property of the linear phase FIR filter can be utilized by grouping the symmetrical coefficients into the same MCM sub-block [34].

Unlike the conventional hybrid-form implementation, which groups every other two coefficients from $h_0$ till the end, we can start from $h_1$ and $h_N$, and group every other two coefficients in both directions, i.e., $\{h_1, h_2\}$, $\{h_3, h_4\}$ so on and so forth and $\{h_N, h_{N-1}\}$, $\{h_{N-2}, h_{N-3}\}$ so on and so forth, and leave $h_0$ un-grouped. Let us use the filter in Figure 2 to illustrate the grouping. As shown in Figure 2, the structure can be transformed from the TDF structure using the retiming technique. Note that the delay elements for the input in each group are drawn individually in Figure 2 for the convenience of explanation. In practical implementations, these elements can be shared.

In this structure, the products except $h_0$ are locally summed with their neighbours before accumulation. The adders used to sum products before accumulation is referred to as local structural adders (LSAs). Note that the combinational hardware complexity of this structure is less than that of the TDF structure because the word-length of the LSAs is smaller than that of its corresponding structural adders (in TDF structure) due to the range reduction. For example, in Figure 2, the word-length of the adder used to sum the products of $h_1$ and $h_2$ is

$$\begin{array}{c}\hfill W_{h_1,h_2}=W_X+\lceil {log}_2\left(\right|h_1|+|h_2\left|\right)\rceil -max(s_1,s_2),\end{array}$$

(4)

while the word-length of its corresponding structural adder in the TDF form is

$$\begin{array}{c}\hfill W_{h_1,h_2}=W_X+\lceil {log}_2\sum _{k=2}^8\left|h_k\right|\rceil -s_2.\end{array}$$

(5)

The word-length is reduced because the range expansion of the sum is reduced from $\lceil {log}_2{\sum }_{k=2}^8\left|h_k\right|\rceil$ bits to $\lceil {log}_2\left(\right|h_1|+|h_2\left|\right)\rceil$ bits.

The structure for $L=2$ can also be explained using the transfer function, which is given by

$$\begin{array}{cc}\hfill H\left(z\right)& =\sum _{i=0}^8{h}_i{z}^{-i}\hfill \\ \hfill & =h_0+\sum _{i=0}^3\left(z^{-(2i+1)}(h_{2i+1}+h_{2i+2}{z}^{-1})\right).\hfill \end{array}$$

(6)

It can also be expressed in matrix form as

$$H\left(z\right)=h_0+{\left[\begin{array}{c}{z}^{-1}\\ z^{-3}\\ z^{-5}\\ z^{-7}\end{array}\right]}^T\left[\begin{array}{cc}{h}_1& h_2\\ h_3& h_4\\ h_5& h_6\\ h_7& h_8\end{array}\right]\left[\begin{array}{c}1\\ z^{-1}\end{array}\right]$$

(7)

The constant matrix vector multiplication (CMVM) in Equation (7) can be optimized using MCM algorithms or CMVM algorithms [12]. Note that in this structure, symmetric coefficient pairs are grouped into the same MCM sub-block in the CMVM. For example, in Equation (7), the CMVM consists of two MCM sub-blocks. It can be observed that the symmetric coefficient pairs in the original filter coefficient set, for example $\{h_1, h_7\}$ and $\{h_3, h_5\}$ in the first column, are grouped into the same MCM sub-block. Since in MCMs or CMVMs, duplicated coefficients are implemented once and reused across the block, only two coefficients, $h_1$ and $h_3$, need to be implemented for the MCM sub-block of the first column, leading to reduced hardware complexity. The stand alone coefficient in Equations (6) and (7), $h_0$, can be grouped together with the first column of the coefficient matrix.

2.2.2. Structure for $L\ge 2$

For $L\ge 2$, the symmetric pairs of filter coefficients can no longer be grouped into the same MCM sub-block to reduce the number of unique coefficients. Therefore, the filter coefficients can be simply grouped from $h_0$ to $h_N$ with a group size of L. The structure for $L\ge 2$ can be transformed from the TDF structure in the same way as $L=2$ using retiming techniques. The transfer function $H\left(z\right)$ for $L\ge 2$ can be expressed in the matrix form as

$${\left[\begin{array}{c}{z}^0\\ z^{-L}\\ \dots \\ z^{-N+L}\end{array}\right]}^T\left[\begin{array}{cccc}{h}_0& h_1& \dots & h_{L-1}\\ h_L& h_{L+1}& \dots & h_{2L-1}\\ \dots & \dots & \dots & \dots \\ h_{N-L+1}& h_{N-L+2}& \dots & h_N\end{array}\right]\left[\begin{array}{c}1\\ z^{-1}\\ \dots \\ z^{-L+1}\end{array}\right]$$

(8)

The filter structure based on Equation (8) is shown in Figure 3, which is a Type II hybrid-form structure according to the classification in [12]. The constant multiplications in Figure 3 can be designed using MCM algorithms or CMVM algorithms. Note that a binary adder tree can be used to implement the LSAs in each group to reduce the word-length of adders.

3. Joint Optimization of the Product Accumulation Block and Multiplication Block

In this section, the generalized bit-level complexity model of LSAs is proposed. The relationship between the group size L and the area complexity of PAB and constant multipliers are analyzed. Based on that, the joint optimization of the PAB and the multiplication block is proposed to reduce the overall combinational hardware complexity, followed by the register complexity analysis.

3.1. Bit-Level Complexity Reduction of LSAs

To estimate the number of full adders of LSAs, the shifts in products as well as sums generated by LSAs need to be defined. For the products, the shifts are simply the number of left-shift bits needed to generate the coefficients from the corresponding fundamentals. For the sums generated by the LSAs, the shifts can be recursively defined as

Definition 1.

The shift of a sum generated by an LSA is the smaller shift among the shifts of two input addends.

Let us use the LSAs shown in Figure 4 as an example. According to the definition, the shifts of the sums generated by LSA-1 and LSA-2 are $min(2,4)=2$ and $min(3,5)=3$, respectively. Therefore, the sum generated by LSA-3 is $min(2,3)=2$.

Basically, the shift-add operations of LSAs are the same as the shift-add operations in the MCM block except that both of the operands of LSAs may be left-shifted. Therefore, all the shifts (positive odd fundamentals are shifted to generate the corresponding coefficients) should be considered in the bit-level complexity estimation of LSAs. The number of full adders needed for an LSA that sums two products are given by Equation (4). The generalized form of the number of full adders needed for LSAs can be expressed as

$$W_{\mathrm{LSA}}=W_X+\sum _{h_k\in A}|k_k|-max(s_a, s_b),$$

(9)

where A is the set of coefficients corresponding to the products that the LSA is used to sum, while $s_a$ and $s_b$ are the shifts of the two inputs of the LSA.

As shown in Equation (9), the word-length of LSAs need to only cover the range expansion in the current group of coefficients, while the word-length of structure adders have to cover the range expansion of all the previous taps. Therefore, the overall complexity can be reduced even when the number of adders does not change. For example, the first four coefficients of the 121-tap filter in [23] are 6, $-13$, 22 and −28. If $L=4$ and $W_X=8$, the word-length of the three LSAs and one structural adder shown in Figure 5a are 12-bit, 12-bit, 14-bit and 25-bit, respectively, while the word-length of the four structural adders of the TDF structure in Figure 5b are 23-bit, 24-bit, 25-bit and 24-bit. The overall reduction for this group can only be as much as 33 full adders. However, it should be noted that as i (the subscript of coefficient $h_i$) increases, the differences in word-length between LSAs and structural adders decrease due to reduced range expansion.

3.2. Relationship between L and Complexity of the PAB

In the structure of $L=2$, every two coefficients are grouped and locally summed such that half of the structural adders in the TDF structure are reduced to LSAs with smaller word-length. Generally, the proportion of structural adders that are reduced to LSAs can be expressed as

$$P=\frac{L-1}{L}=1-\frac{1}{L}$$

(10)

It is obvious that P increases with the increase in group size L, i.e., more structural adders can be reduced to LSAs. Theoretically, the hardware complexity of the PAB reduces monotonically with the increase in L. However, it should be noted that the word-lengths of LSAs need to extend accordingly (with the increase in depth in the binary adder tree) to keep the range expansion of the local sums. Therefore, the complexity reduction of PAB is limited when L is larger than certain values.

The reduction in the number of LSAs by sharing the common subexpressions across the rows in the constant matrix depends highly on the CMVM algorithms, and there is no clear relationship with the group size L. For a given filter coefficient set, the number of rows decreases with the increase in group size L, while the number of LSAs in each group increases. The increase in the number of rows and the number of LSAs in each group is beneficial for the sharing of LSAs. Generally, a small L value is more suitable for row-oriented CMVM algorithms that work better for matrices with more rows, and a large L value is more suitable for column-oriented CMVM algorithms that work better for matrices with more columns.

3.3. Relationship between L and Complexity of the Constant Multipliers

It is noted that the grouping of coefficients into MCM sub-blocks has a negative effect on the overall complexity of the constant multipliers (excluding the LSAs in CMVM). Unlike the LSAs (which can be shared across the rows in CMVM), the partial products of constant multiplications can only be shared within the sub-blocks where the subset of coefficients is multiplied with the same input. Partitioning the MCM block into sub-blocks reduces the number of coefficients in each sub-block, diminishing the shareability of partial products, leading to an increase in the complexity of the design. For $L=1$, i.e., the conventional TDF structure, all the coefficients reside in a single MCM block, which maximizes the sharing of partial products. This is one of the main reasons that the TDF structure is more popular for multiplierless FIR filter implementation. With the increase in L, the overall hardware complexity of the constant multipliers increases accordingly due to the reduction in shareability of partial products.

3.4. Joint Optimization

The direct form structure and the TDF structure are two special cases of $L=N$ and $L=1$. It has been shown that the group size L affects both the complexity of the constant multipliers and the PAB. However, the relationship between the overall complexity and L is filter-dependent, i.e., both the filter order and the filter coefficient values will affect the optimum group size L for a specific filter. Therefore, the total combinational hardware complexity is a function of L, and there is no fixed optimum structure for all the filters. For a given filter, the overall combinational complexity can be expressed as

$$C_{\mathrm{T}}\left(L\right)=C_{\mathrm{MBA}}\left(L\right)+C_{\mathrm{LSA}}\left(L\right)+C_{\mathrm{SA}}\left(L\right),$$

(11)

where $C_{\mathrm{MBA}}\left(L\right)$ is the complexity of the shift-add network of the constant multiplications, which can be estimated using the model in [33], $C_{\mathrm{LSA}}\left(L\right)$ is the complexity of all the LSAs, which can be estimated using Equation (9), and $C_{\mathrm{SA}}\left(L\right)$ is the complexity of all the SAs, which can be estimated using Equation (3). Based on Equation (11), an exhaustive search algorithm in Algorithm 1 is proposed to determine the optimum structure for the implementation of a given filter.

Algorithm 1 The exhaustive search algorithm

Input:  Filter coefficients Output:  The optimum structure 1: forL = 1 to N do 2:     Compute the constant matrix 3:     *Design the CMVM block using constant multiplication algorithms 4:     Compute $C_{\mathrm{T}}\left(L\right)$ by evaluating (11) 5:     $L_{\mathrm{Opt}}={arg}_{L}min\left(C_{\mathrm{T}}\left(L\right)\right)$ 6:     Partition the coefficients with group size of $L_{\mathrm{Opt}}$ 7: end for * The design of CMVM block is independent of the algorithm. Different CMVM algorithms can be used here.

In Algorithm 1, if $L_{\mathrm{Opt}}=2$, the structure discussed in Section 2.2.1 is used to take advantage of the symmetry property of filter coefficients; otherwise, the generalized structure in Section 2.2.2 should be used. Note that there is no constraint on the CMVM technique and any constant multiplication optimization algorithms can be used. Generally, high-order filters tend to have the least hardware complexity with a relatively larger L since the PABs contribute the major part of hardware complexity, while for low-order filters, even the TDF structure ($L=1$) can be the optimum structure since the overhead introduced by partitioning the coefficients may be larger than the benefits.

3.5. Bit-Level Delay Analysis

The delay of the shift-add-based constant multiplication block consists of two parts: (i) the horizontal propagation delay and (ii) the vertical propagation delay. The horizontal delay, which is caused by the propagation of carries within the adders, can be simply estimated by the word-length of the final result minus the corresponding shift. The vertical delay, which is caused by the signal propagation across adder stages, can be estimated by the adder depth. A more precise estimation of the critical path delay can be found in [30]. Since LSAs are not registered as the structural adders in the TDF structure, extra delay may be introduced.

Let us consider the computation of a group with two-stage LSAs, as shown in Figure 6. Unlike the conventional TDF structure, adder stages exist between the constant multiplication block and the structural adders. Since the range of the accumulation results of the structural adders is not affected by the partition of the MCM block, $W_{\mathrm{SA}}$ is the same as that of the TDF structure. Therefore, the horizontal delay of this tap is the same as that of the TDF structure. The vertical delay is incremented by the number of LSA adder stages. If the binary adder tree is used for LSAs, the total increment of delay can be expressed as

$$D_{\Delta }=T_v·\lceil {log}_{2}L\rceil ,$$

(12)

where $T_v$ is the vertical propagation delay of a full adder. Therefore, the delay increment is $\lceil {log}_{2}L\rceil$ vertical full adder delays instead of the delay of $\lceil {log}_{2}L\rceil$ word-level adders.

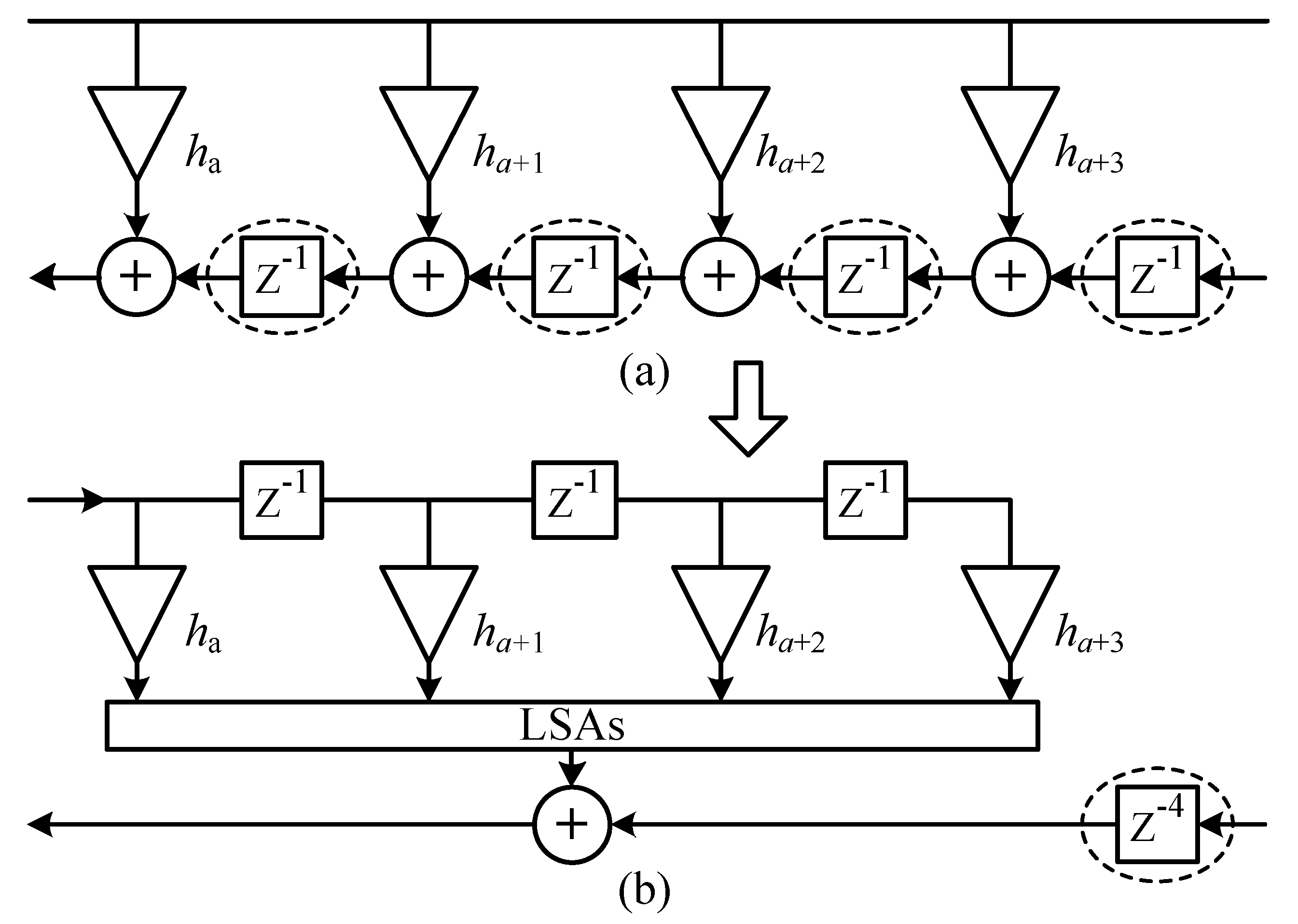
3.6. Bit-Level Register Complexity Analysis

The number of word-level registers of the structures in Figure 3 can be estimated as

$$R_w=L·(\lceil \frac{N+1}{L}\rceil -1)+L,$$

(13)

which is the same as that of TDF structures if $N+1$ is an integer multiple of L. However, the register complexity at bit-level is reduced compared to the TDF structure. Let us consider the transformation from the TDF structure to the structure in Figure 7. As can be seen, the original registers (in dashed circles in Figure 7a) in the TDF structure are moved to the input of the structural adder (in dashed circles in Figure 7b) such that the range of the register input is reduced. Therefore, the overall bit-registers for each group are reduced (the registers for the input can be shared by all the groups of coefficients such that the overhead is negligible). Moreover, as L increases, more registers are transferred to the input line, which has a word-length of only $W_X$. Therefore, the overall register complexity of the filter decreases with the increase in L. The structure with $L=N$, i.e., the direct form structure, has the least register complexity.

4. Quantitative Analysis of the Relationship between Optimum $L$ and Filter Coefficient Values as Well as Filter Order

It is known that the optimum structure of a filter depends on the coefficient values and the filter order. In this section, a quantitative analysis is presented to show the relationship between the optimum group size L and coefficient values as well as filter order in the proposed joint optimization scheme. Note that the algorithms are coded in MATLAB in this work. In the design examples, the CMVM blocks are designed in two steps: (i) apply RAG-n to each MCM sub-block and use the algorithm [33] for further bit-level optimization and (ii) identify and share the length-2 common subexpressions (subexpressions with two variables) across the MCM sub-blocks. An input word-length of $W_X=8$ is used in all the implementations. To the best of the authors’ knowledge, this is the first time that the PAB and the multiplication block are jointly optimized at bit-level for low-complexity FIR filter implementation. The conventional TDF structure is therefore used as the reference structure for comparison. The direct form structure is not considered due to its order-dependent critical path, which makes it unsuitable for high-speed applications.

In the first experiment, we analyze the implementation of a 151-tap filter and a 418-tap order filter [35]. The full adder complexity of the TDF structure and the structure of joint optimization are presented in

Table 1. Hardware complexity of two benchmark filters.

Filter	# Taps	CWL	# Unique	GS	# FA			FA Saving	Delay Increment
					PAB	MB	Total
A	151	15	70	$L_{\mathrm{TDF}}=1$	3479	690	4169	−	−
				$L_{\mathrm{Opt}}=2$	2975	781	3756	9.9%	$T_v$
B	418	12	29	$L_{\mathrm{TDF}}=1$	7479	246	7725	−	−
				$L_{\mathrm{Opt}}=6$	5328	774	6102	21.0%	$3·T_v$

CWL: coefficient word-length; PAB: product accumulation block; MB: multiplication block; T_v: vertical full adder delay; GS: group size.

, where “CWL" in the third column is the word-length of the largest coefficient and “# Unique" in the fourth column is the number of unique fundamentals, which are reduced from the coefficients. The “# FA PAB" and “# FA MB" in the fifth and sixth columns represent the number of full adders needed for the PAB and the constant multiplication block, respectively. The $L_{\mathrm{Opt}}$ is the optimum group size found by the joint optimization. As can be seen, the full adder cost of the PAB can be significantly reduced at the expense of increased constant multiplication complexity. Since the PAB contributes the major part of the hardware complexity, the overall full adder cost is reduced significantly. The reduction in hardware complexity for filter A and filter B are 9.9% and 21.0%, respectively.

Figure 8a,b show the relationship between the full adder cost and the group size L for filter A and filter B, respectively. Generally, the full adder cost of the PAB decreases with the increase in L. However, as can be seen, for filter A, the reduction in full adder cost of the PAB is almost flat for $L>2$ after the significant drop from $L=1$ to $L=2$, while for filter B, the reduction is notable until $L>6$. This is because the range expansion of the local accumulation results in each group diminishes word-length saving for LSAs. The order of filter B is considerably higher than that of filter A, leading to more reducible structural adders. Moreover, the larger coefficient word-length of filter A may result in a reduction in the difference between the word-length of LSAs and their corresponding structural adders in the TDF structure.

Generally, the full adder complexity of all the constant multipliers grows with the increase in L. However, as can be seen, the complexity of constant multipliers as well as its slope of increment of filter A is larger than than that of filter B. This is because the coefficient word-length of filter A is larger. Although the coefficient value is not the only factor of complexity of constant multipliers (larger coefficients do not necessarily result in more complex constant multipliers), it has a positive effect on the complexity of constant multipliers from a statistical point of view. As shown in Table 1, filter A has 70 unique fundamentals that need to be implemented, while filter B has only 29, even though the order of filter A is considerably lower than that of filter B.

Therefore, it can be concluded that the total full adder cost of the filter will increase after the optimum value of L since the reduction in the PAB cannot compensate for the increase in the multiplication block, and the optimum value of L is affected by the coefficient word-length as well as the filter order.

In order to study the impact of the filter coefficient word-length, we present the complexity of four 418-tap low-pass filters with coefficient word-lengths of 12-bit, 16-bit, 20-bit and 24-bit (used for different stopband attenuations) [35]. Figure 9 shows the total full adder cost of these four filters for different L values. The optimum L values and full adder reduction compared to the TDF structure are listed in

Table 2. Results for 418-tap filters with different word-lengths.

Coef WL	12-Bit	16-Bit	20-Bit	24-Bit
# Unique	29	102	187	208
$L_{\mathrm{Opt}}$	6	3	3	1
% FA Reduction	21.0%	9.1%	2.0%	0%
Delay Increment	$3·T_v$	$2·T_v$	$2·T_v$	0

WL: word-length.

. The optimum values of L for 12-bit, 16-bit, 20-bit and 24-bit filters are 6, 3, 3 and 1, respectively. It is interesting to note that a 4-bit increase in word-length from 12 to 16 bits results in a large reduction in FA adder saving. The main reason is that, for filters with a smaller word-length, the overall hardware complexity is also smaller, such that the percentage of FA reduction will be larger. Moreover, in this case, the optimum L is also changed, which may also affect the optimization of the PAB block. As can be seen, with the increase in the coefficient word-length from 12-bit to 24-bit, the optimum values of L are reduced from 6 to 1 and the full adder cost saving is reduced from 21.0% to 0, i.e., the TDF structure is the optimum structure for the 24-bit filter. Therefore, it can be concluded that for filters with a very long coefficient word-length, the TDF structure is the optimum structure in terms of complexity. This is because with the increase in coefficient word-length, the complexity of the constant multipliers increases such that the reduction in the PAB can no longer compensate for the complexity increase in constant multipliers due to the long coefficient word-length.

In the third experiment, we present the optimum L of 25 different filters [35] with orders from dozens to hundreds in

Table 3. Results for filters with different orders.

# Filter Taps	Coef WL	# Unique	${\mathit{L}}_{\mathbf{Opt}}$	% FA Reduction	Delay Increment
30	10	28	2	1.8	$T_v$
32	7	10	1	0.0	0
34	11	10	1	0.0	0
36	8	5	2	8.0	$T_v$
37	8	5	2	12.4	$T_v$
49	9	11	2	10.9	$T_v$
59	10	14	2	7.7	$T_v$
60	13	26	1	0.0	0
61	15	30	2	6.2	$T_v$
63	10	17	2	7.3	$T_v$
67	15	28	2	9.6	$T_v$
80	15	36	1	0.0	0
105	9	10	2	17.1	$T_v$
108	9	23	3	5.5	$2·T_v$
119	15	53	2	11.4	$T_v$
121	14	42	2	12.5	$T_v$
151	15	70	2	11.0	$T_v$
222	12	44	3	11.6	$2·T_v$
240	15	82	3	5.3	$2·T_v$
279	12	30	4	20.9	$2·T_v$
418	12	29	6	26.6	$3·T_v$
441	14	86	2	19.0	$T_v$
516	12	27	7	30.7	$3·T_v$
631	12	28	8	34.8	$3·T_v$
695	12	32	8	35.9	$3·T_v$

WL: word-length.

. As can be seen, generally high-order filters tend to have a larger optimum value of L. However, as discussed, the optimum value of L depends on both the coefficient values and the filter order. In Figure 10, we plot the optimum values of L and the percentage of full adder reduction (compared to TDF structure) with respect to “# Filter Taps/Coef WL”. As can be seen, both the optimum values of L and the percentage of full adder reduction are almost linear with “# Filter Taps/Coef WL”, i.e., high-order filters with small coefficient word-lengths tend to have large complexity reductions by the proposed joint optimization.

Another interesting finding is that for filters with orders less than 100, the optimum structure is either the TDF structure ($L=1$) or the structure with $L=2$. This is because for low-order filters, the proportion of the complexity of constant multipliers is much higher than that of high-order filters. Therefore, the complexity overhead introduced by the multiplication block can be significant compared to the overall complexity of the filter. In the structure for $L=2$, the symmetric property of coefficients is utilized to minimize the complexity overhead of constant multipliers.

5. Implementation Results

In this section, the implementation results are presented to demonstrate the effectiveness of the proposed method. Filter B in Table 1, i.e., the 418-tap filter with 12-bit word-length, is used as the benchmark filter to compare different methods. All the designs are implemented using verilogHDL and synthesized using the Synopsys Design Compiler based on 40 nm CMOS technology. The input to the filter is 8-bit for all the designs.

Table 4. Area comparison of the 418-tap filter with a 12-bit word-length (40 nm CMOS technology).

Algorithm	Area ($\mathsf{\mu }$m${}^{\mathbf{2}}$) under Different Clock Frequencies
	200 MHz			300 MHz			400 MHz
	Comb	Ncomb	Total	Comb	Ncomb	Total	Comb	Ncomb	Total
MCM_only	1356	-	1356	2097	-	2097	3427	-	3427
C1 [36]	32,086	34,313	66,399	40,577	35,360	75,938	42,699	35,108	77,808
Hcub [28]	31,966	34,314	66,280	40,553	35,348	75,901	42,885	34,932	77,818
MBPG [37]	32245	34,313	66,558	40,594	35,351	75,946	43,495	34,936	78,431
MINAS [38]	32047	34,313	66,361	40,804	35,347	76,151	43,047	34,702	77,750
NRSCSE [39]	32184	34,313	66,497	38,922	35,356	74,278	43,109	34,815	77,924
Proposed (L = 2)	25,906	33,208	59,114	31,462	33,955	65,417	37,340	33,936	71,277

Comb: combinational; Ncomb: non-combinational.

presents the area comparison of different implementations of the filter, where various algorithms, i.e., C1 [36], Hcub [28], MBPG [37], MINAS [38] and NRSCSE [39], are used to design the MCM block of the filter. Note that the first row of Table 4 shows the area of the MCM block only (designed using C1). As we can see, for this filter, the MCM block designed with a sophisticated algorithm only consumes a very small portion of the total chip area. Moreover, since the PAB part consumes the major part of chip area, there is little difference between filters designed using different MCM algorithms. As for the proposed method, since the PAB part is taken into consideration during the optimization, a significant amount of area can be saved. In addition, as we can observe from the table, the area saving becomes smaller with the increment of clock frequency. This is because extra delays are introduced to optimize the computational complexity, making the synthesis tool pay for more area to achieve a higher clock rate.

Table 5. Power comparison of the 418-tap filter with a 12-bit word-length (40 nm CMOS technology).

Algorithm	Power ($\mathsf{\mu }$W) under Different Clock Frequencies
	200 M	300 M	400 M
C1 [36]	122.9	202.1	262.9
Hcub [28]	122.5	201.1	258.5
MBPG [37]	121.6	201.3	265.5
MINAS [38]	121.5	204.2	254.4
NRSCSE [39]	122.0	197.0	256.8
Proposed (L = 2)	93.8	154.6	197.6

presents the power consumption of different filter implementations. As we can see, similar to the area comparison, the power consumption of the filter design using the proposed method is significantly lower than other methods. The main reason, as we have analyzed, is the computational complexity reduction.

6. Conclusions

Most of the literature on multiplierless design and implementation of FIR filters concentrates on the efficient design of MCM blocks. However, the PAB, which is often ignored, can be the major contributor to hardware complexity, especially for high-order filters. A design scheme is therefore proposed to minimize the hardware complexity of multiplierless FIR filters by optimizing the multiplication block and PAB jointly at bit-level. In the proposed joint optimization, the single MCM block is rearranged into several MCM sub-blocks. The products of input and coefficient values are summed locally before being accumulated to reduce the word-lengths of structural adders. The symmetric property of linear phase FIR filters can be utilized to further reduce the complexity of constant multipliers when the MCM block is partitioned into two MCM sub-blocks. Moreover, an exhaustive search algorithm is proposed to determine the optimum partition of the MCM block. Quantitative analyses are presented to study the relationship between the optimum group size L and the coefficient values as well as the filter orders in the proposed joint optimization scheme. It is shown that there is no fixed optimum structure for filters with different coefficient word-lengths and filter orders, and each filter needs to be optimized specifically to achieve the lowest hardware complexity.

We need to mention that there are certain limitations to the proposed method. The first one is the modeling of complexity and delay. In our work, we analyze the complexity and delay based on FA, but it is well-known that modern synthesis tools are smart enough to optimize area and timing at a finer-grain level. Therefore, FA-based modeling may not be accurate enough to find the optimum structure. Another limitation is that for low-order filters, the complexity of the MCM part may occupy a significant portion of the overall complexity, such that the overhead introduced by the MCM part may undermine the overall benefits.