Marker-Based 3D Position-Prediction Algorithm of Mobile Vertiport for Cabin-Delivery Mechanism of Dual-Mode Flying Car
Abstract
:1. Introduction
2. Position-Prediction Technology for Cabin Delivery of the Mobile Station
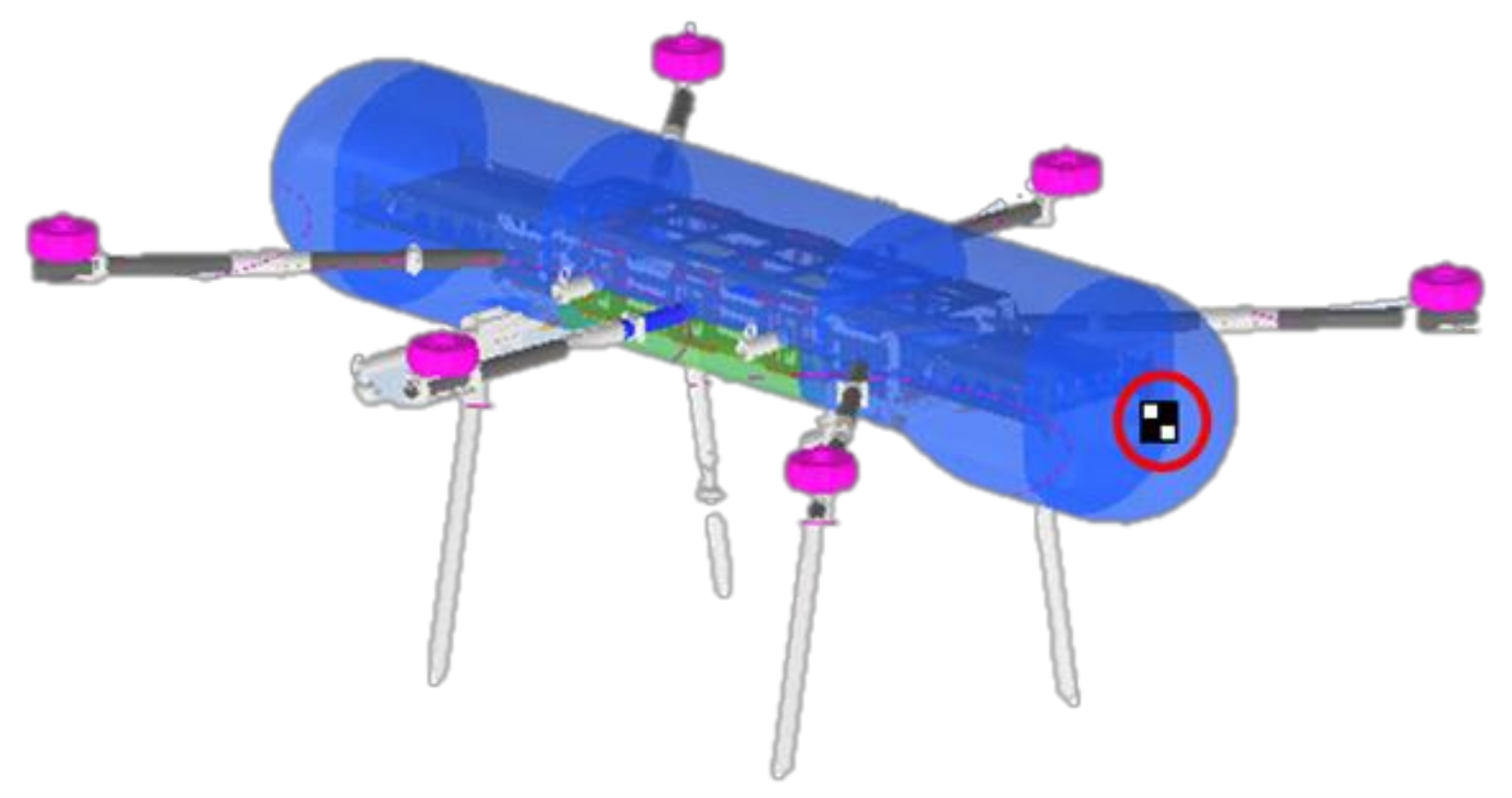
2.1. Marker-Based AEV’s Position-Information Acquisition (Local Localization)
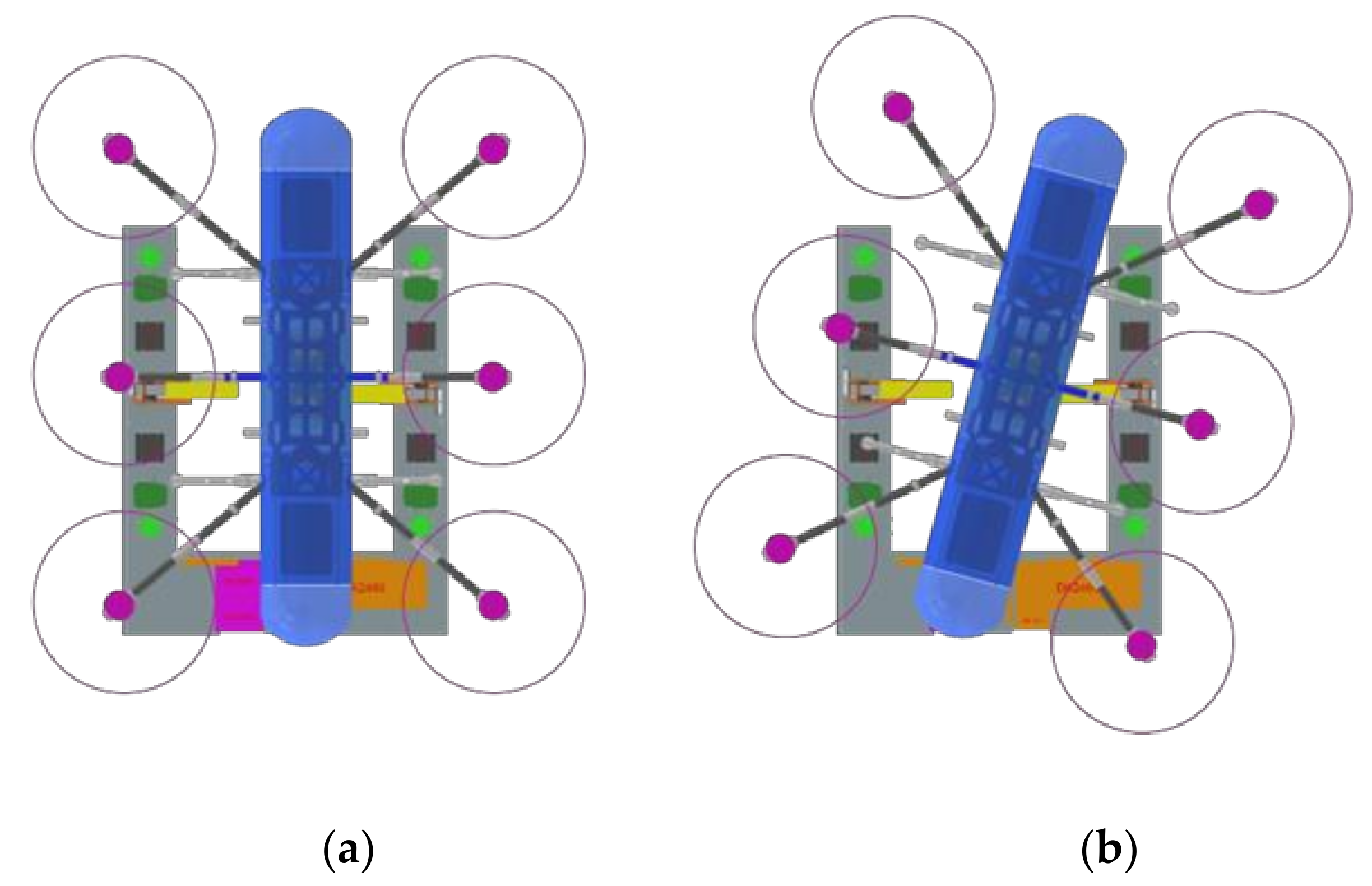
2.2. Precision Correction of the Mobile Station Based on Markers
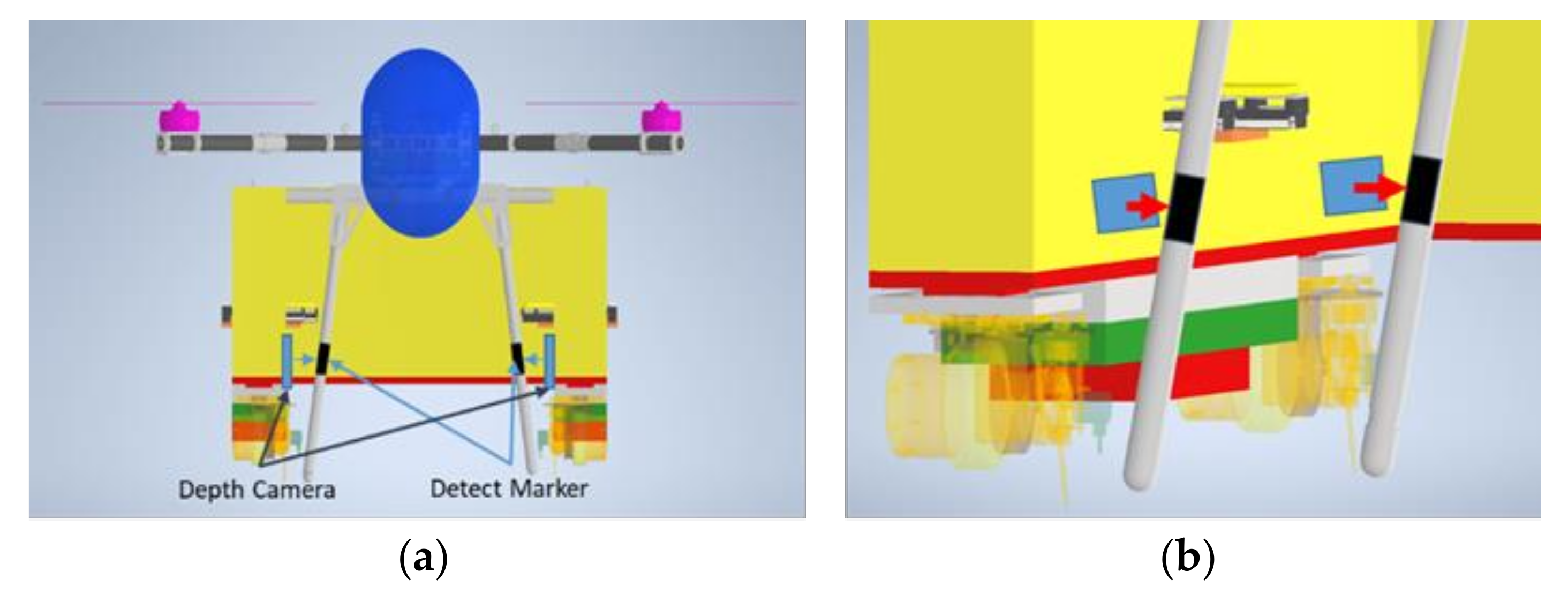
2.3. Docking between the AEV and Cabin Using the Marker-Based Mobile Station
3. Experiment
3.1. Experiment Environment
3.2. Marker-Based AEV’s Position Information
3.3. Precision Correction of the Mobile Station Based on Markers
3.4. Docking between the AEV and Cabin Using the Marker-Based Mobile Station
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Geissinger, A.; Laurell, C.; Sandström, C. Digital Disruption beyond Uber and Airbnb—Tracking the long tail of the sharing economy. Technol. Forecast. Soc. Chang. 2020, 155, 119323. [Google Scholar] [CrossRef]
- Straubinger, A.; Rothfeld, R.; Shamiyeh, M.; Büchter, K.-D.; Kaiser, J.; Plötner, K.O. An overview of current research and developments in urban air mobility—Setting the scene for UAM introduction. J. Air Transp. Manag. 2020, 87, 101852. [Google Scholar] [CrossRef]
- Thipphavong, D.P.; Apaza, R.; Barmore, B.; Battiste, V.; Burian, B.; Dao, Q.; Verma, S.A. Urban air mobility airspace integration concepts and considerations. In Proceedings of the 2018 Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 25 June 2018; p. 3676. [Google Scholar]
- Silva, C.; Johnson, W.R.; Solis, E.; Patterson, M.D.; Antcliff, K.R. VTOL urban air mobility concept vehicles for technology development. In Proceedings of the 2018 Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 25 June 2018; p. 3847. [Google Scholar]
- Fu, M.; Rothfeld, R.; Antoniou, C. Exploring preferences for transportation modes in an urban air mobility environment: Munich case study. Transp. Res. Rec. 2019, 2673, 427–442. [Google Scholar] [CrossRef] [Green Version]
- Vascik, P.D.; Hansman, R.J. Scaling constraints for urban air mobility operations: Air traffic control, ground infrastructure, and noise. In Proceedings of the 2018 Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 25 June 2018; p. 3849. [Google Scholar]
- Brown, A.; Harris, W.L. Vehicle design and optimization model for urban air mobility. J. Aircr. 2020, 57, 1003–1013. [Google Scholar] [CrossRef]
- Balac, M.; Rothfeld, R.L.; Hörl, S. The prospects of on-demand urban air mobility in Zurich, Switzerland. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019. [Google Scholar]
- Shamiyeh, M.; Rothfeld, R.; Hornung, M. A performance benchmark of recent personal air vehicle concepts for urban air mobility. In Proceedings of the 31st Congress of the International Council of the Aeronautical Sciences, Belo Horizonte, Brazil, 9–14 September 2018. [Google Scholar]
- Moore, M. 21st century personal air vehicle research. In Proceedings of the AIAA International Air and Space Symposium and Exposition, The Next 100 Years, Dayton, OH, USA, 14–17 July 2003; p. 2646. [Google Scholar]
- Lewe, J.H.; Ahn, B.; DeLaurentis, D.; Mavris, D.; Schrage, D. An integrated decision-making method to identify design requirements through agent-based simulation for personal air vehicle system. In AIAA’s Aircraft Technology, Integration, and Operations (ATIO) 2002 Technical Forum; The Ohio State University: Columbus, OH, USA, 2002; p. 5876. [Google Scholar]
- Lee, J.-H.; Cho, G.-H.; Lee, J.-W. Development and prospect of personal air vehicle as next generation transportation. J. Korean Soc. Aeronaut. Space Sci. 2006, 34, 101–108. [Google Scholar]
- Kohout, L.; Schmitz, P. Fuel cell propulsion systems for an all-electric personal air vehicle. In Proceedings of the AIAA International Air and Space Symposium and Exposition, The Next 100 Years, Dayton, OH, USA, 14–17 July 2003; p. 2867. [Google Scholar]
- Cha, J.; Yun, J.; Hwang, H.-Y. Initial sizing of a roadable personal air vehicle using design of experiments for various engine types. Aircr. Eng. Aerosp. Technol. 2021, 93, 1–14. [Google Scholar] [CrossRef]
- Yi, T.H.; Kim, K.T.; Ahn, S.M.; Lee, D.S. Technical development trend and analysis of futuristic personal air vehicle. Curr. Ind. Technol. Trends Aerosp. 2011, 9, 64–76. [Google Scholar]
- Ahn, B.; DeLaurentis, D.; Mavris, D. Advanced personal air vehicle concept development using powered rotor and autogyro configurations. In AIAA’s Aircraft Technology, Integration, and Operations (ATIO) 2002 Technical Forum; The Ohio State University: Columbus, OH, USA, 2002; p. 5878. [Google Scholar]
- Rice, S.; Winter, S.R.; Crouse, S.; Ruskin, K.J. Vertiport and air taxi features valued by consumers in the United States and India. Case Stud. Transp. Policy 2022, 10, 500–506. [Google Scholar] [CrossRef]
- Shao, Q.; Shao, M.; Lu, Y. Terminal area control rules and eVTOL adaptive scheduling model for multi-vertiport system in urban air Mobility. Transp. Res. Part C Emerg. Technol. 2021, 132, 103385. [Google Scholar] [CrossRef]
- Daskilewicz, M.; German, B.; Warren, M.; Garrow, L.A.; Boddupalli, S.-S.; Douthat, T.H. Progress in vertiport placement and estimating aircraft range requirements for eVTOL daily commuting. In Proceedings of the 2018 Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 25 June 2018; p. 2884. [Google Scholar]
- Lim, E.; Hwang, H. The selection of vertiport location for on-demand mobility and its application to Seoul metro area. Int. J. Aeronaut. Space Sci. 2019, 20, 260–272. [Google Scholar] [CrossRef]

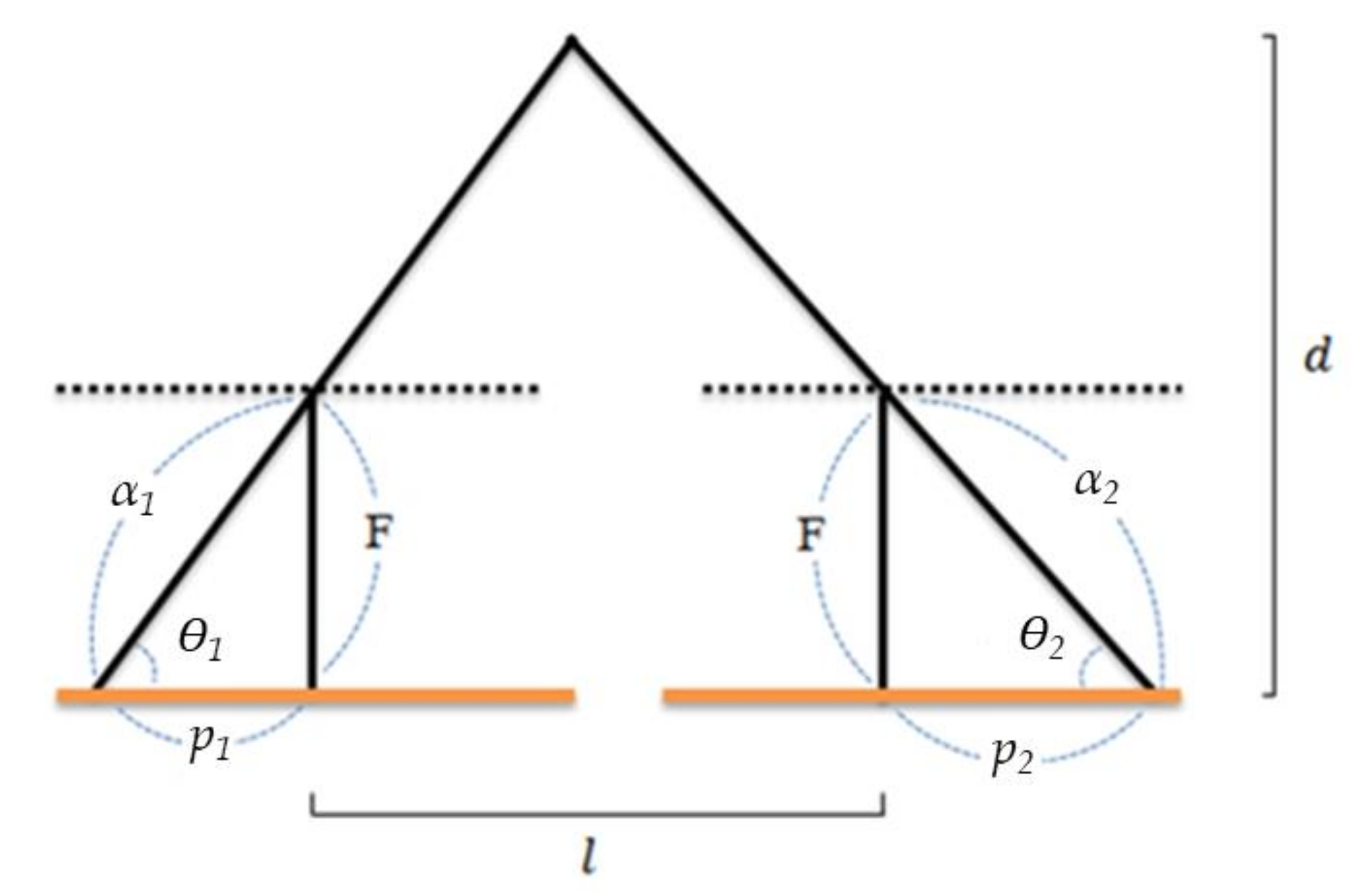













| Parameter Name | Parameter Description |
|---|---|
| The angle between the camera object and the target | |
| d | Distance between the camera and object |
| l | Distance between cameras |
| P | Pixel distance on the camera |
| α | The hypotenuse of focal length triangle |
| F | Camera’s focal length |
| Distance (m) | AVG. Error (m) | Max Error (m) |
|---|---|---|
| 2.5 | 0.05 | 0.08 |
| 4 | 0.07 | 0.08 |
| 7 | 0.11 | 0.13 |
| 11 | 0.16 | 0.19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bae, H.; Lee, J.; Lee, K. Marker-Based 3D Position-Prediction Algorithm of Mobile Vertiport for Cabin-Delivery Mechanism of Dual-Mode Flying Car. Electronics 2022, 11, 1837. https://doi.org/10.3390/electronics11121837
Bae H, Lee J, Lee K. Marker-Based 3D Position-Prediction Algorithm of Mobile Vertiport for Cabin-Delivery Mechanism of Dual-Mode Flying Car. Electronics. 2022; 11(12):1837. https://doi.org/10.3390/electronics11121837
Chicago/Turabian StyleBae, Hyansu, Jeongwook Lee, and Kichang Lee. 2022. "Marker-Based 3D Position-Prediction Algorithm of Mobile Vertiport for Cabin-Delivery Mechanism of Dual-Mode Flying Car" Electronics 11, no. 12: 1837. https://doi.org/10.3390/electronics11121837
APA StyleBae, H., Lee, J., & Lee, K. (2022). Marker-Based 3D Position-Prediction Algorithm of Mobile Vertiport for Cabin-Delivery Mechanism of Dual-Mode Flying Car. Electronics, 11(12), 1837. https://doi.org/10.3390/electronics11121837






