A Passive but Local Active Memristor and Its Complex Dynamics
Abstract
:1. Introduction
2. A Six-Lobe Locally Active Memristor with a Continuous and Derivable State Equation
2.1. Dynamic Route Map of the Memristor
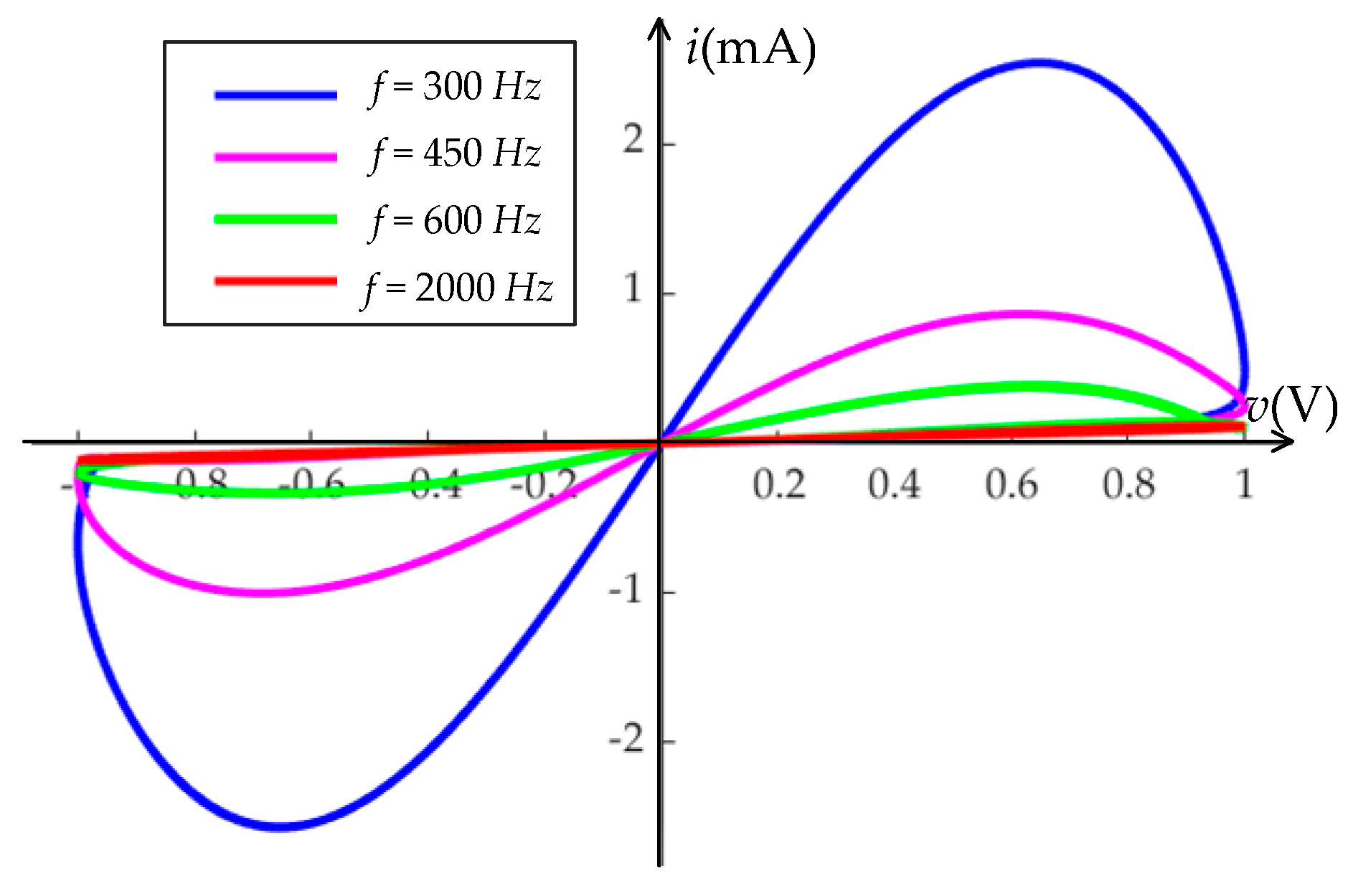
2.2. Hysteresis Characteristics of Memristor
2.3. Local Activity
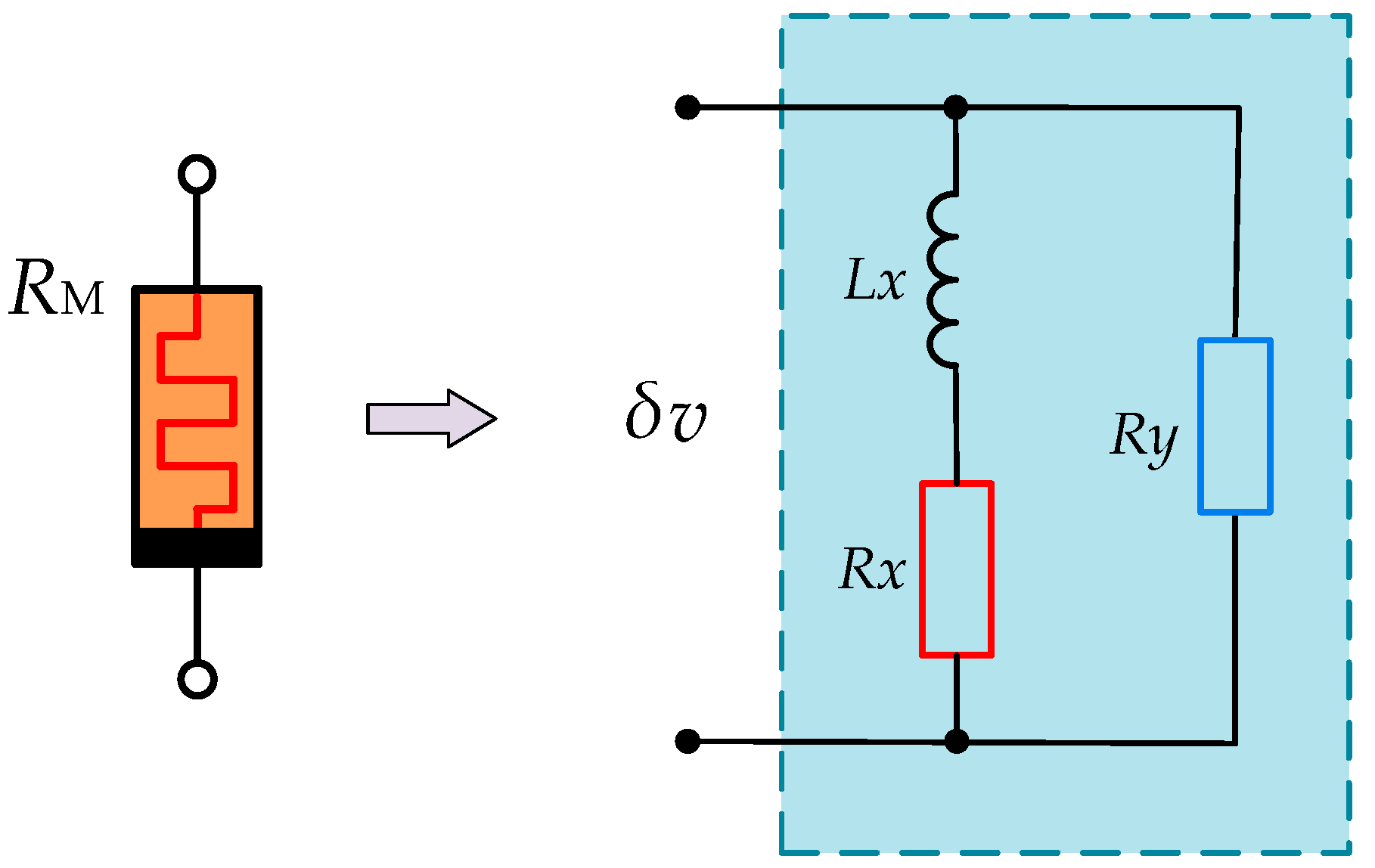
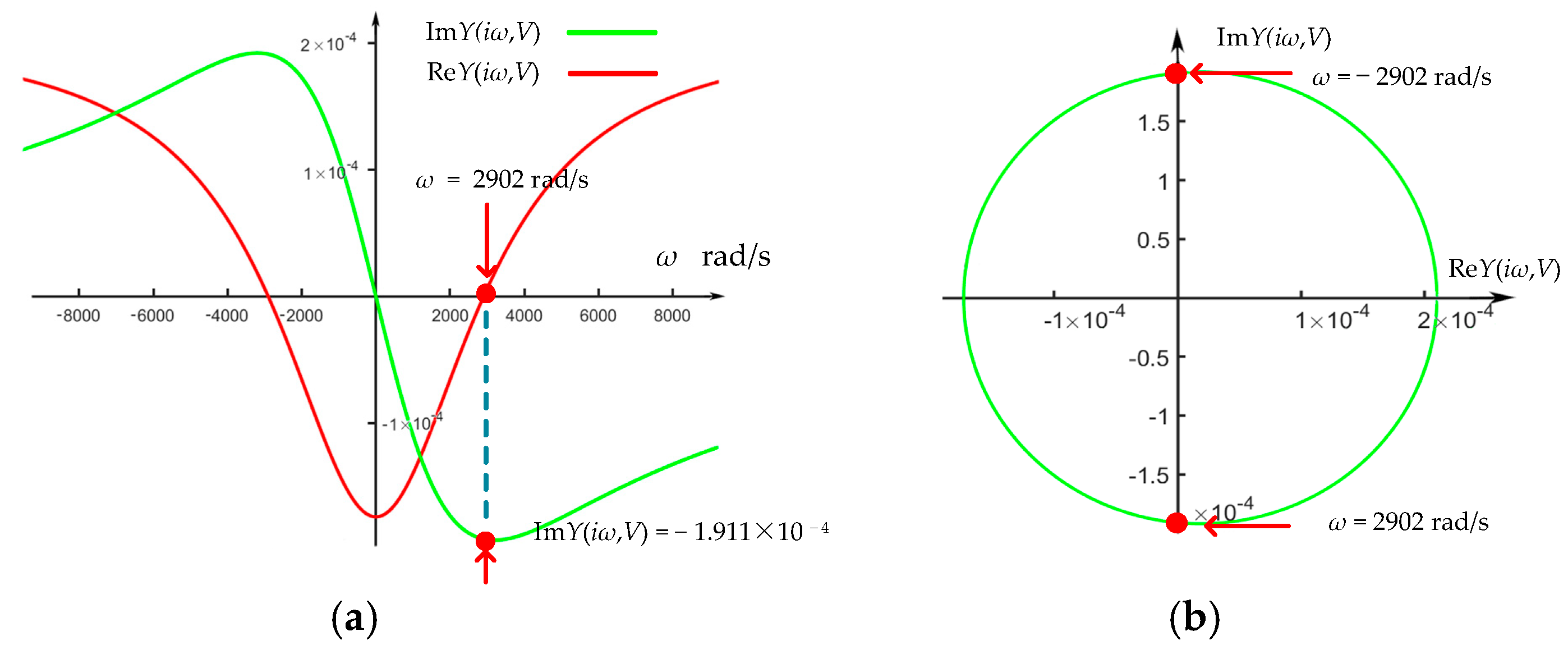
3. Small-Signal Analysis for Locally Active Region
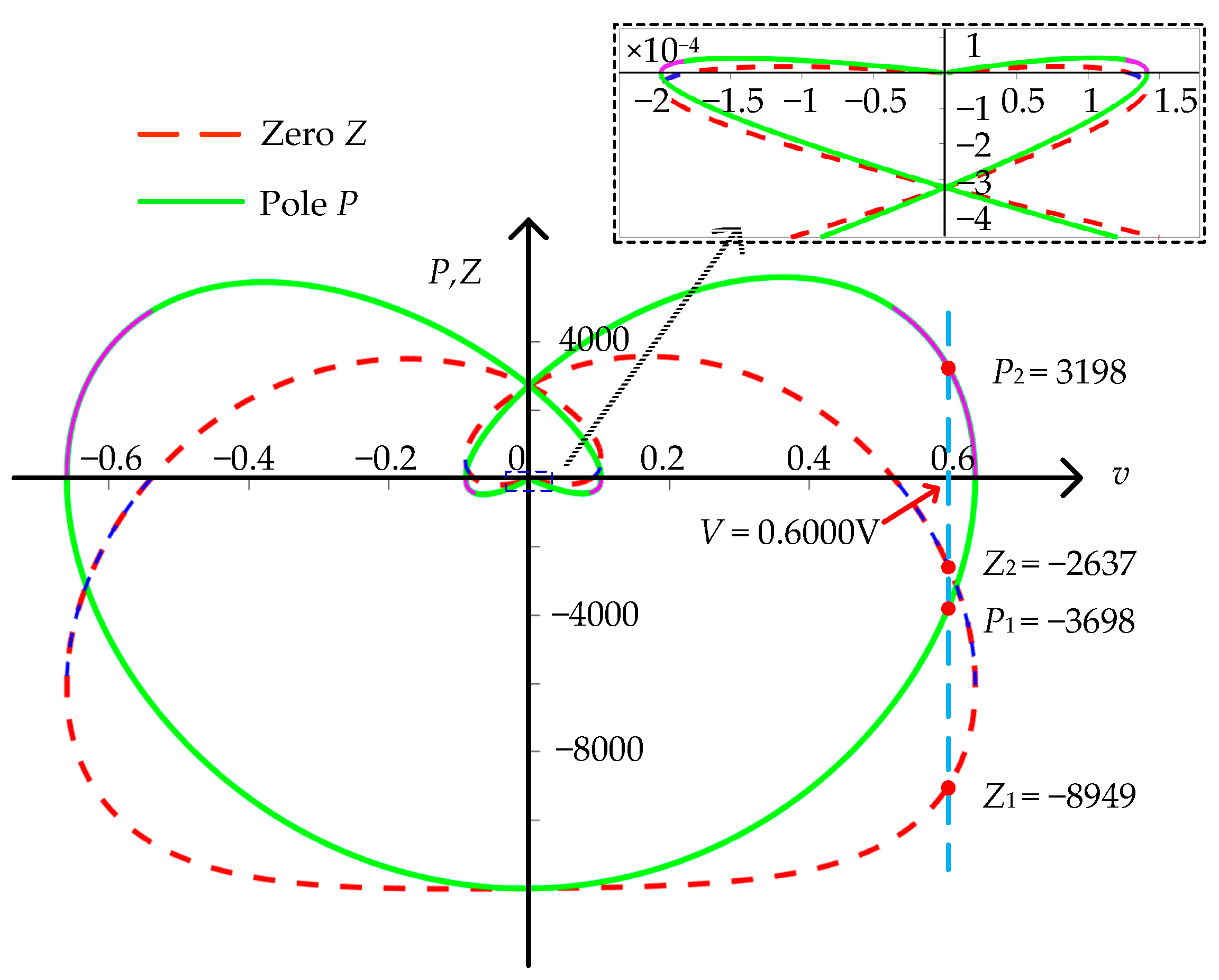
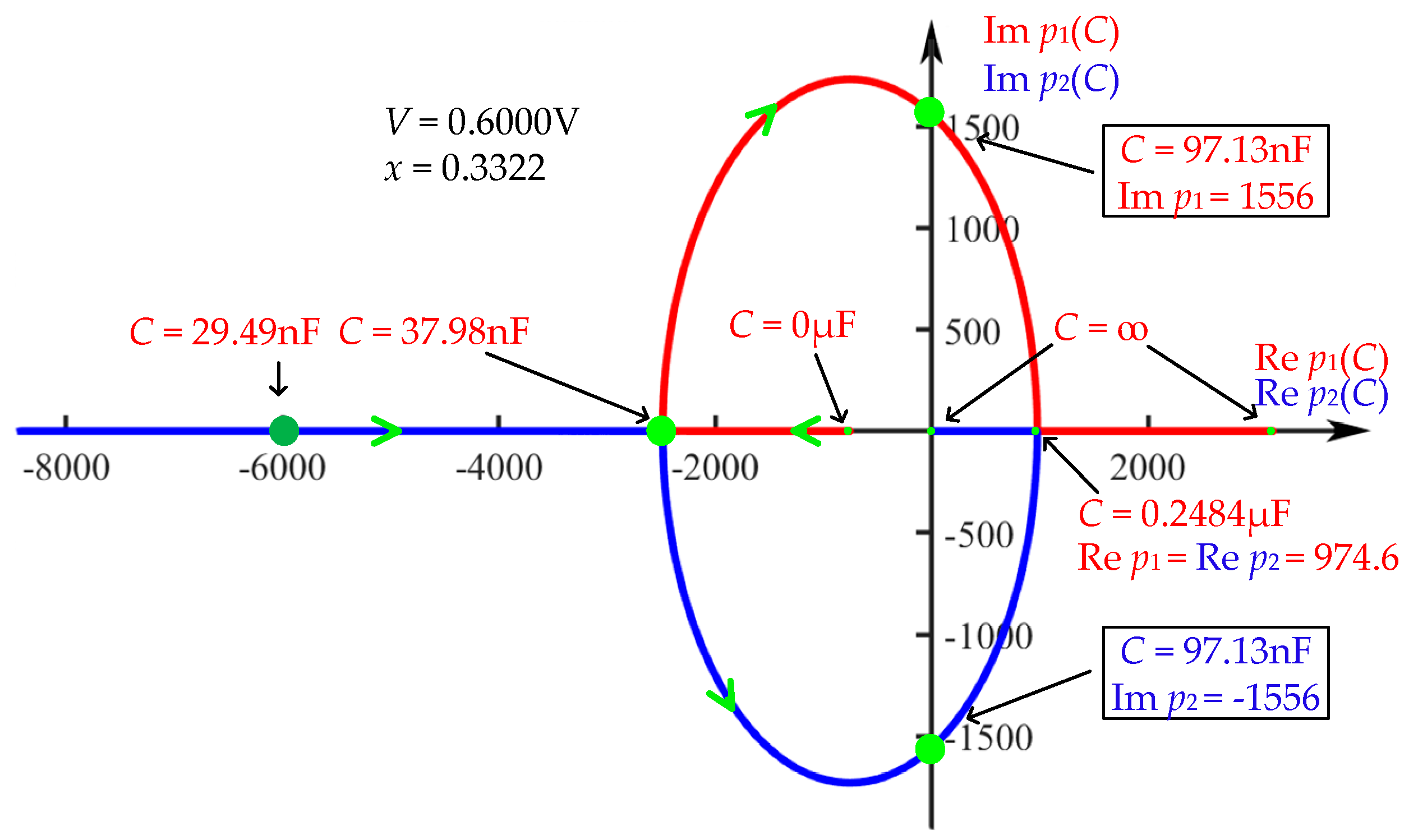
3.1. Zero-Pole Analysis of Memristor
3.2. Frequency Response of the Memristor
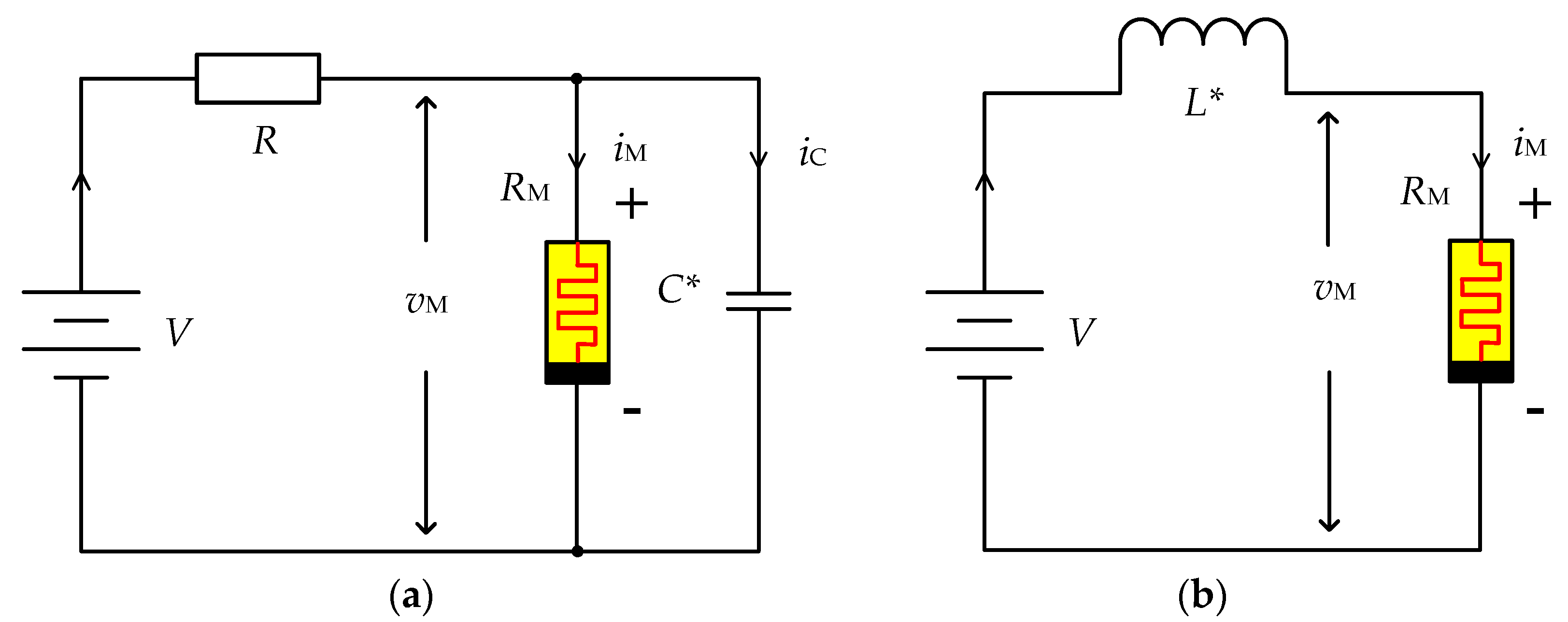
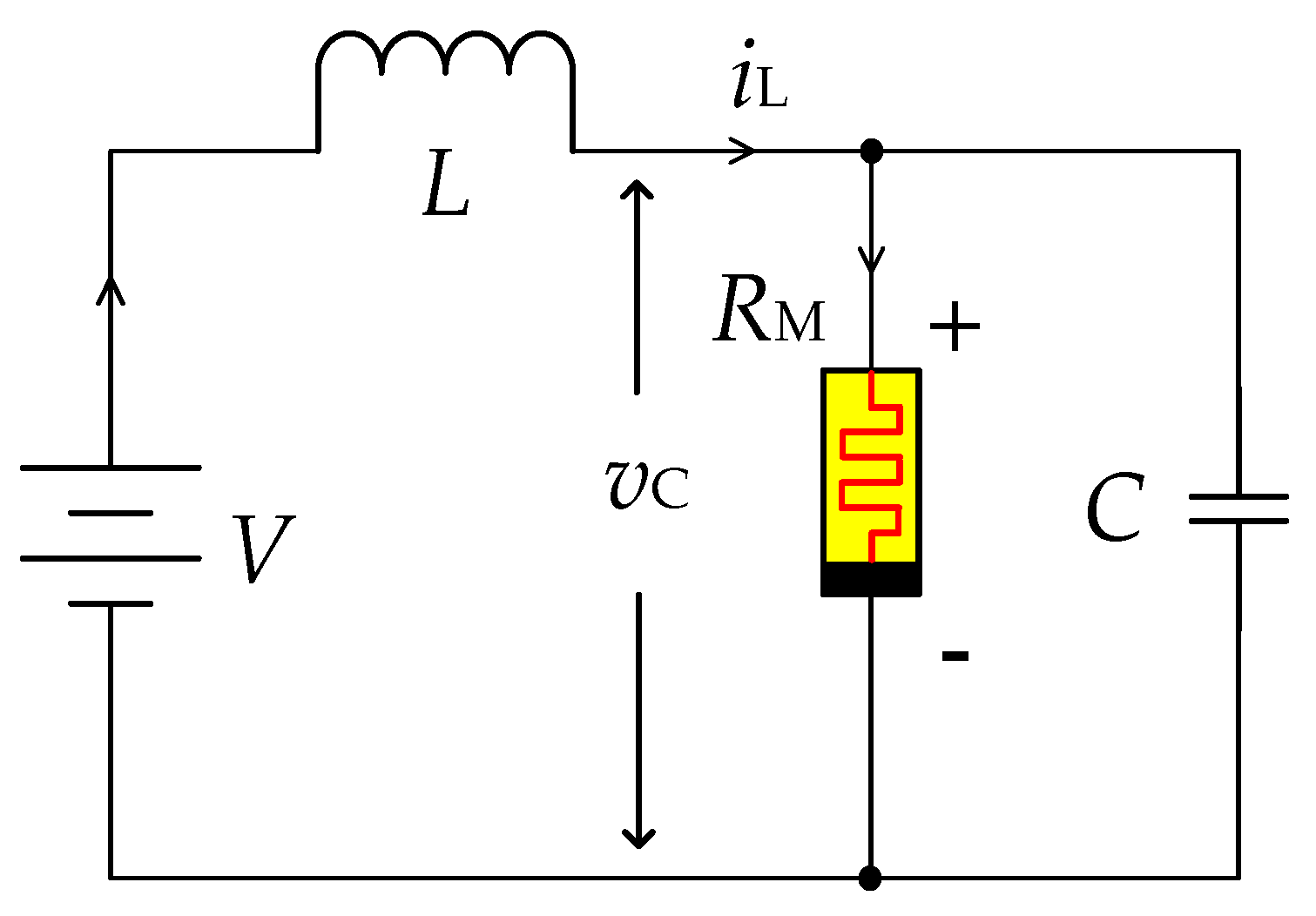
4. Second-Order Periodic Circuit of Memristor
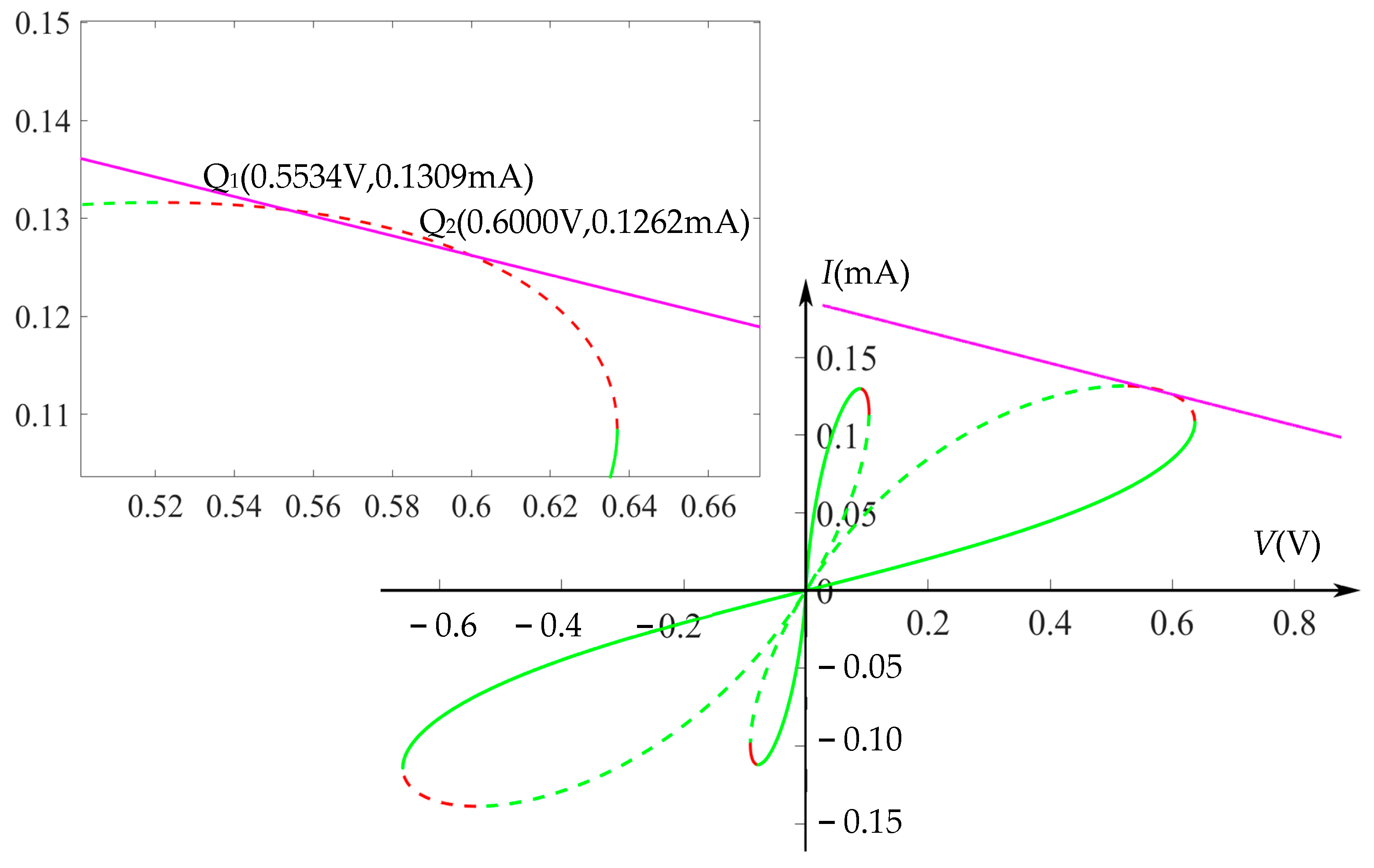
4.1. Properties of the Memristive Circuit in the Unstable Locally Active Region of the Memristor
4.2. Properties of the Memristive Circuit in the Stable Locally Active Region of the Memristor
5. Memristor-Based Third-Order Chaotic Circuit
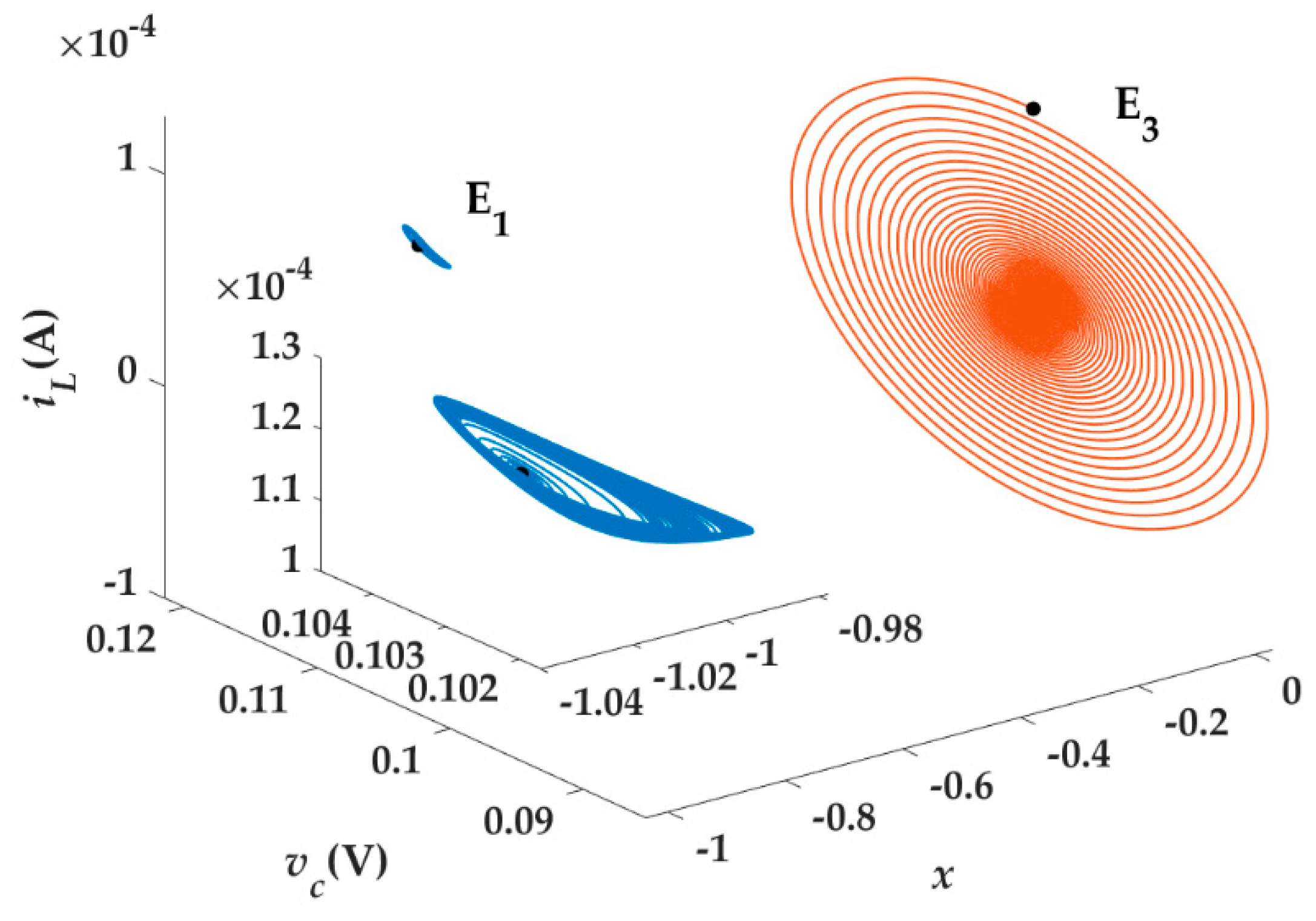
5.1. System Equilibrium Points
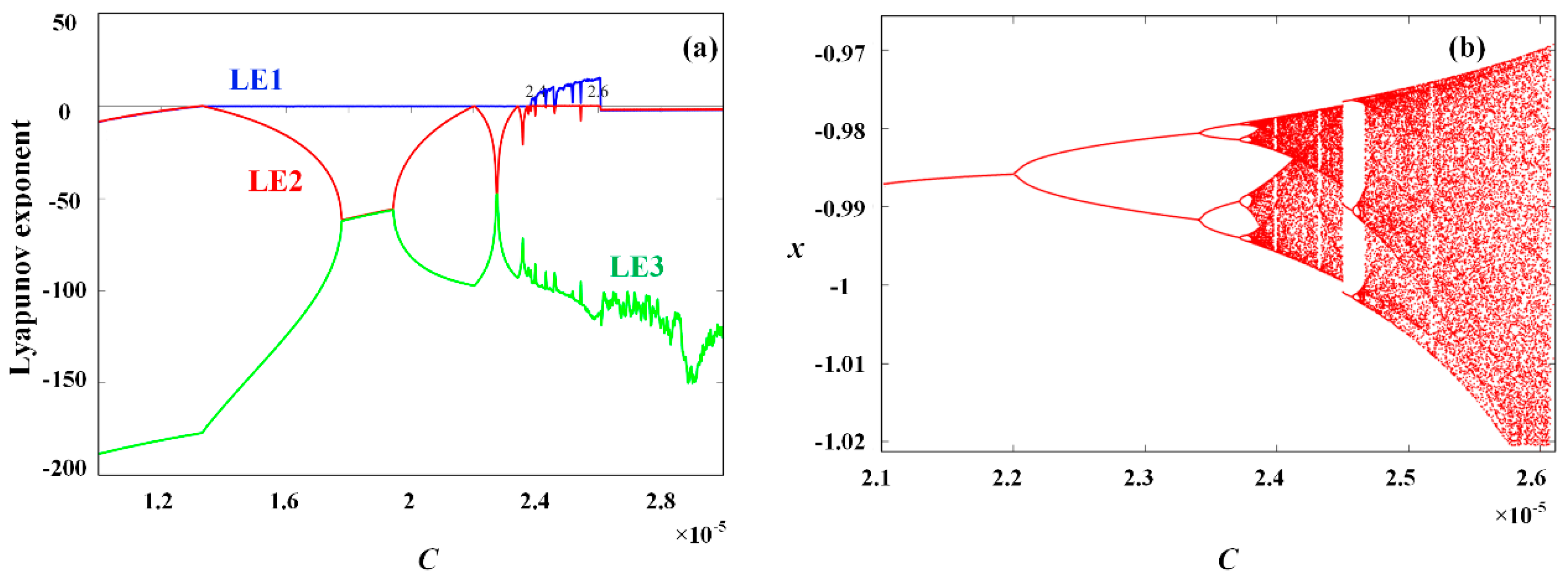
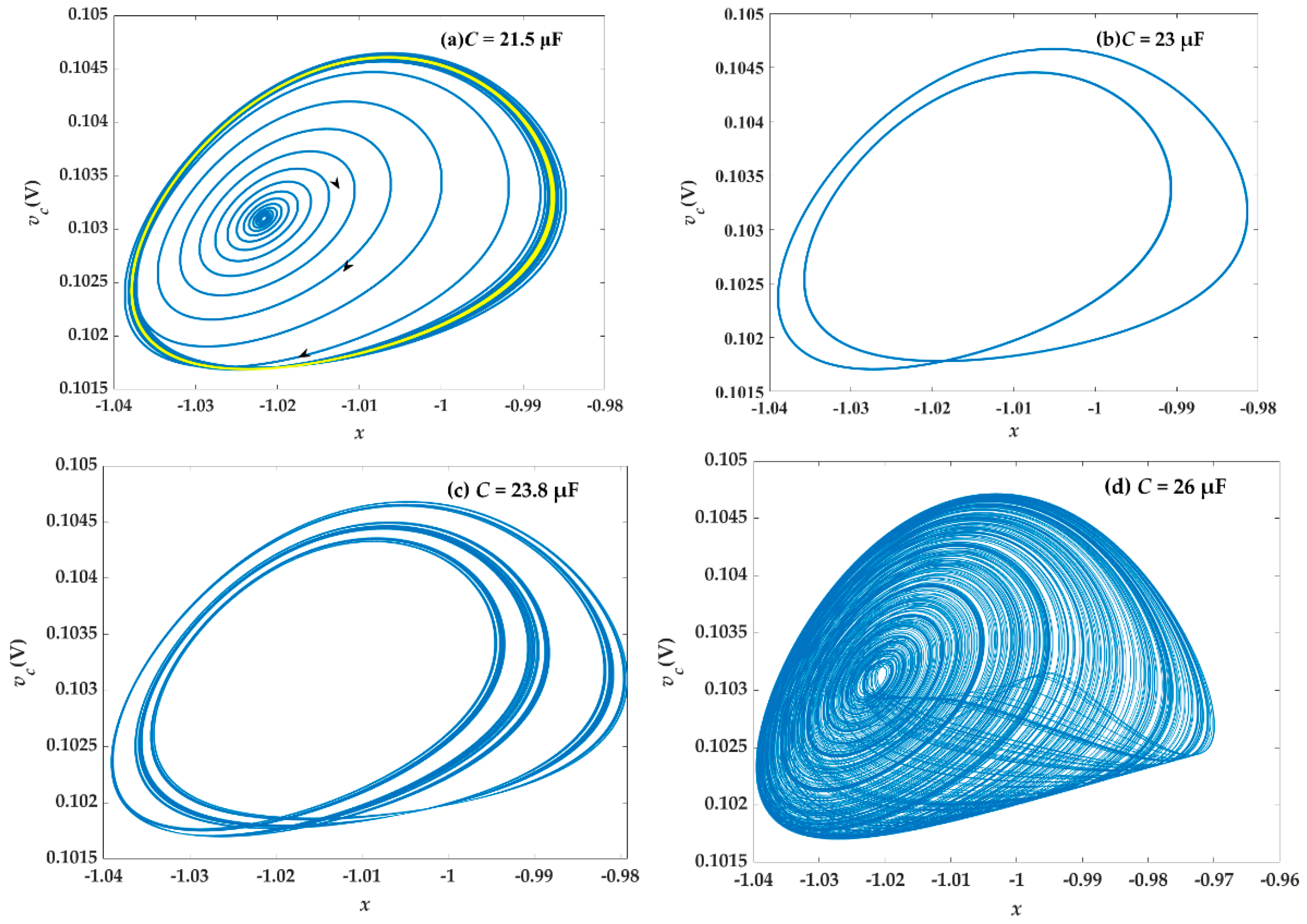
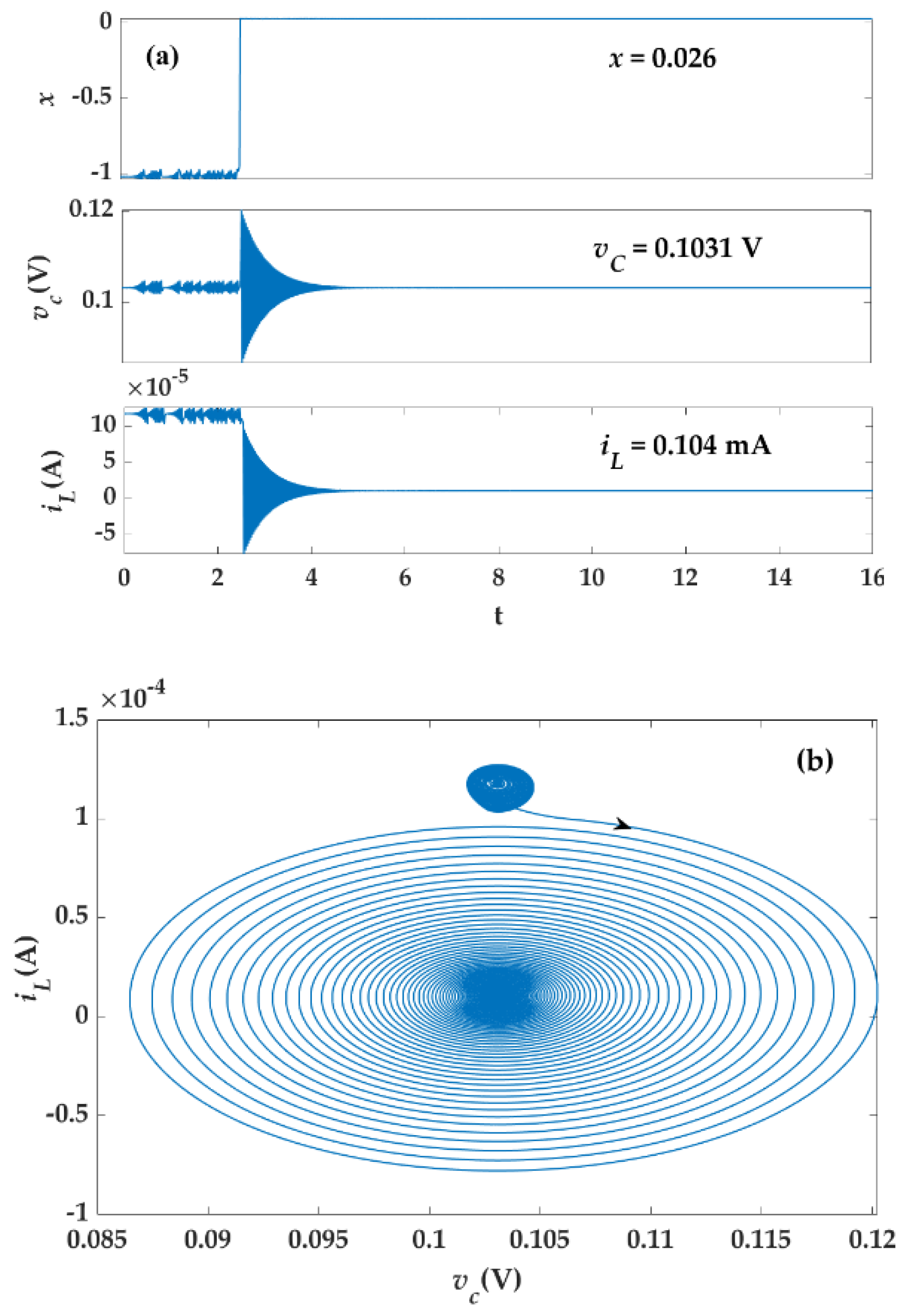
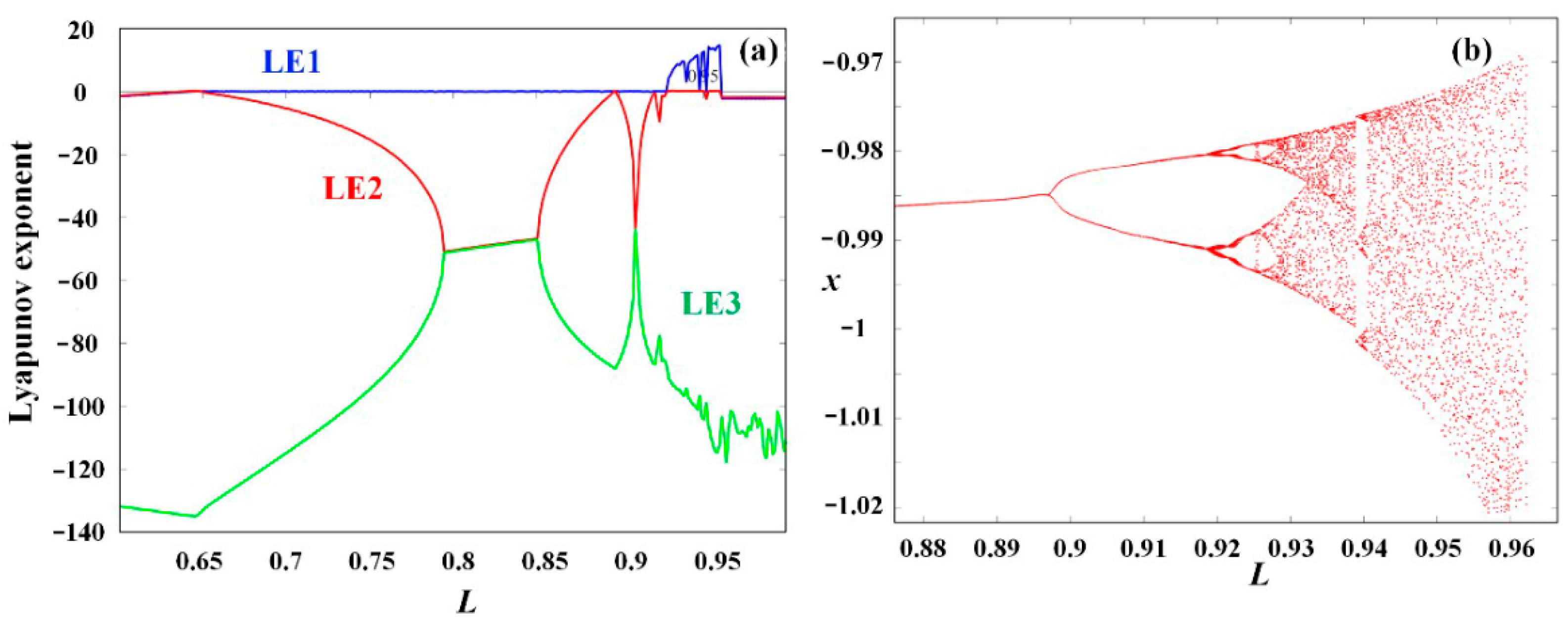
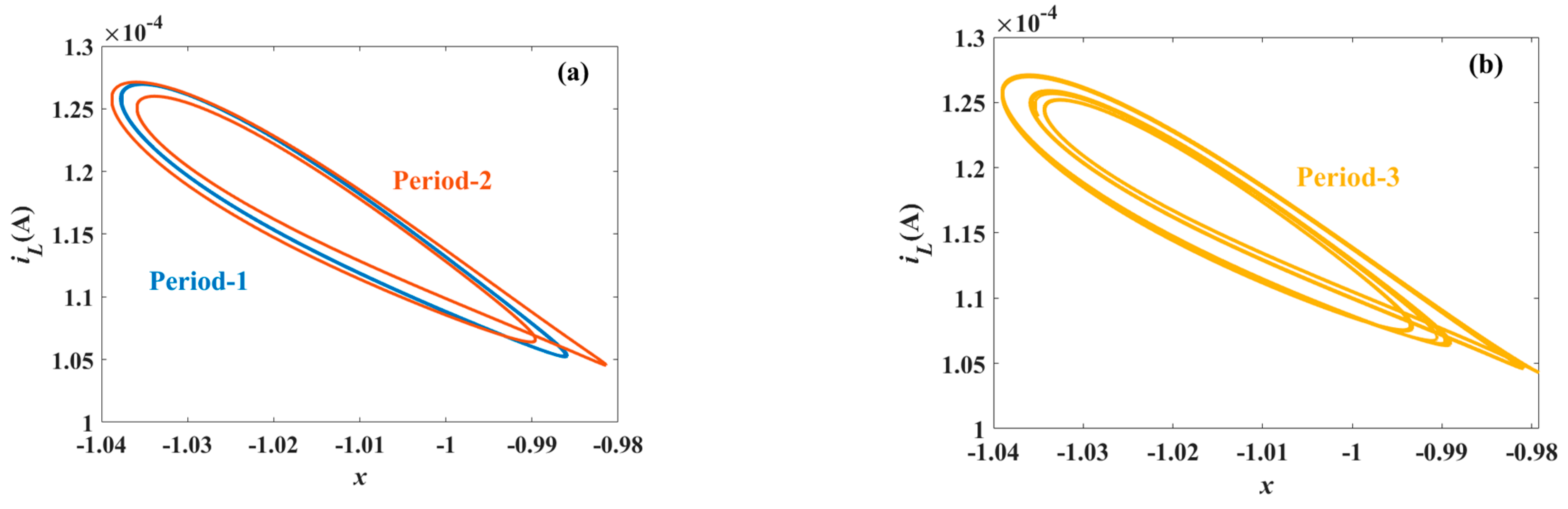
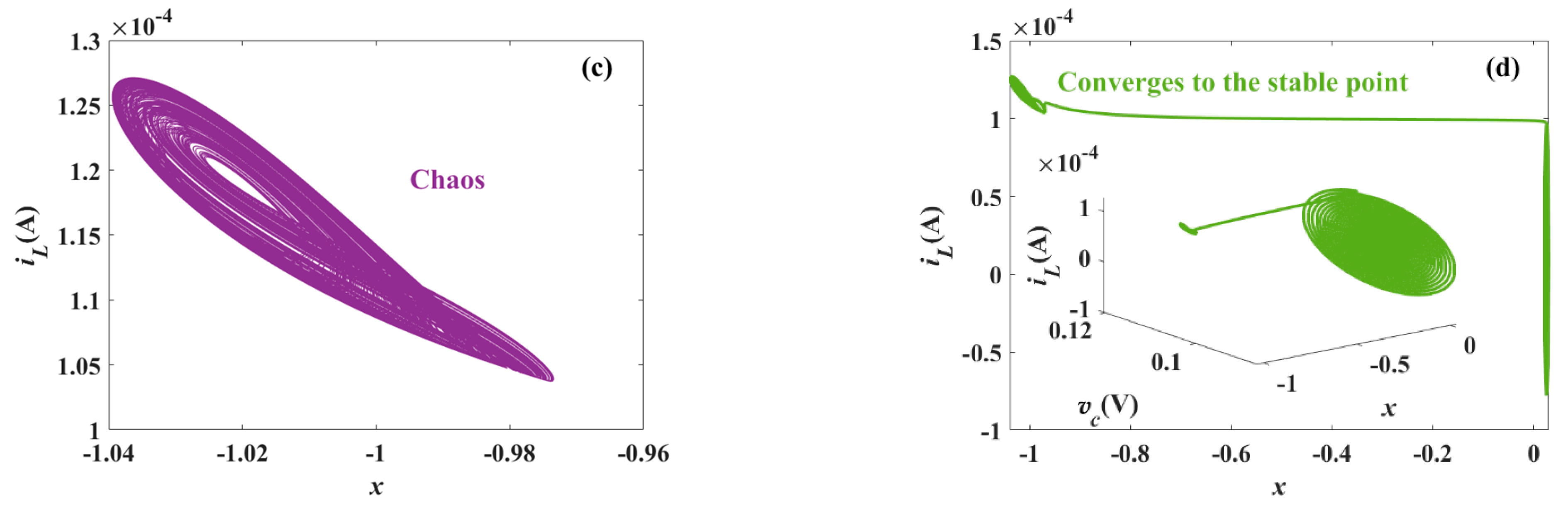
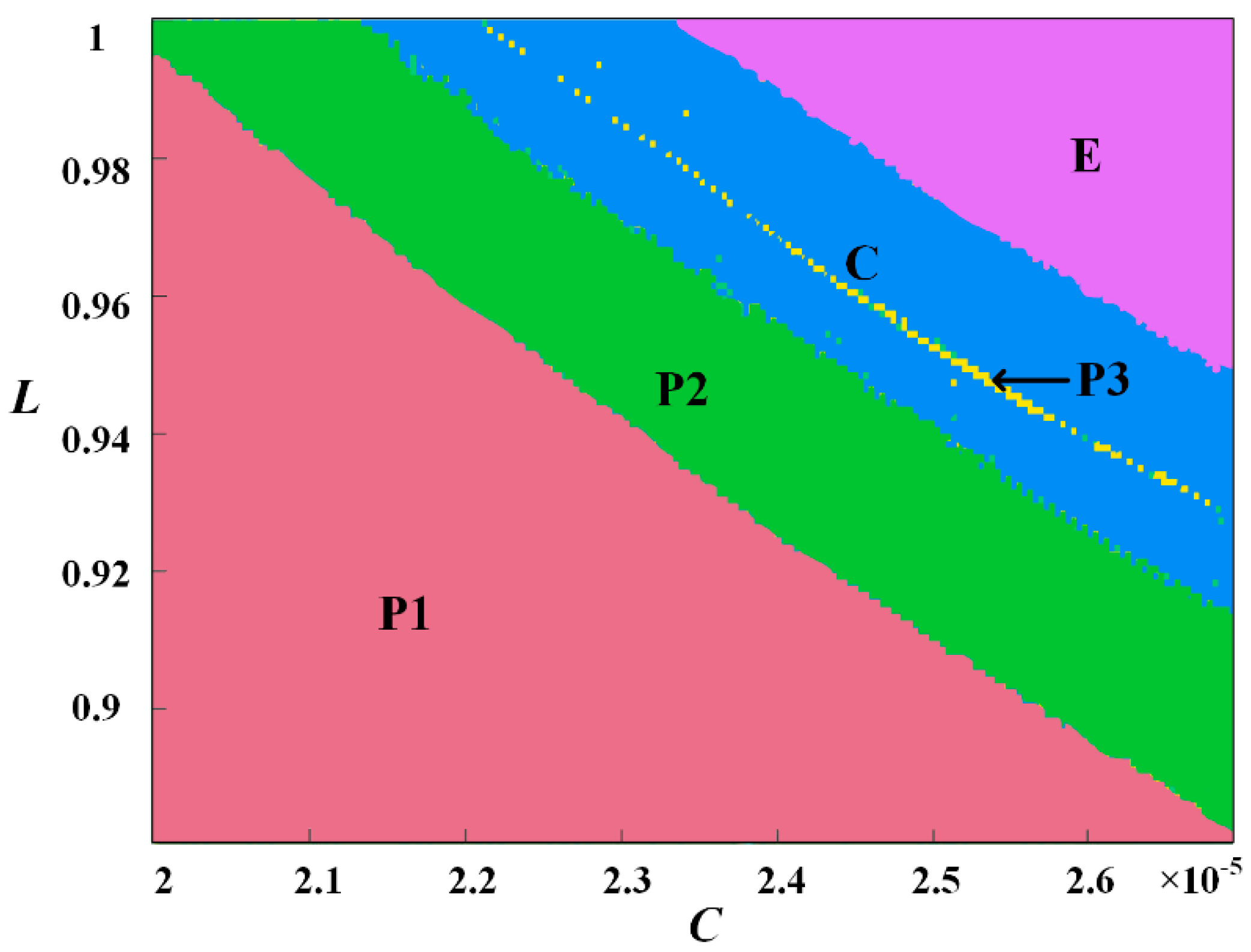
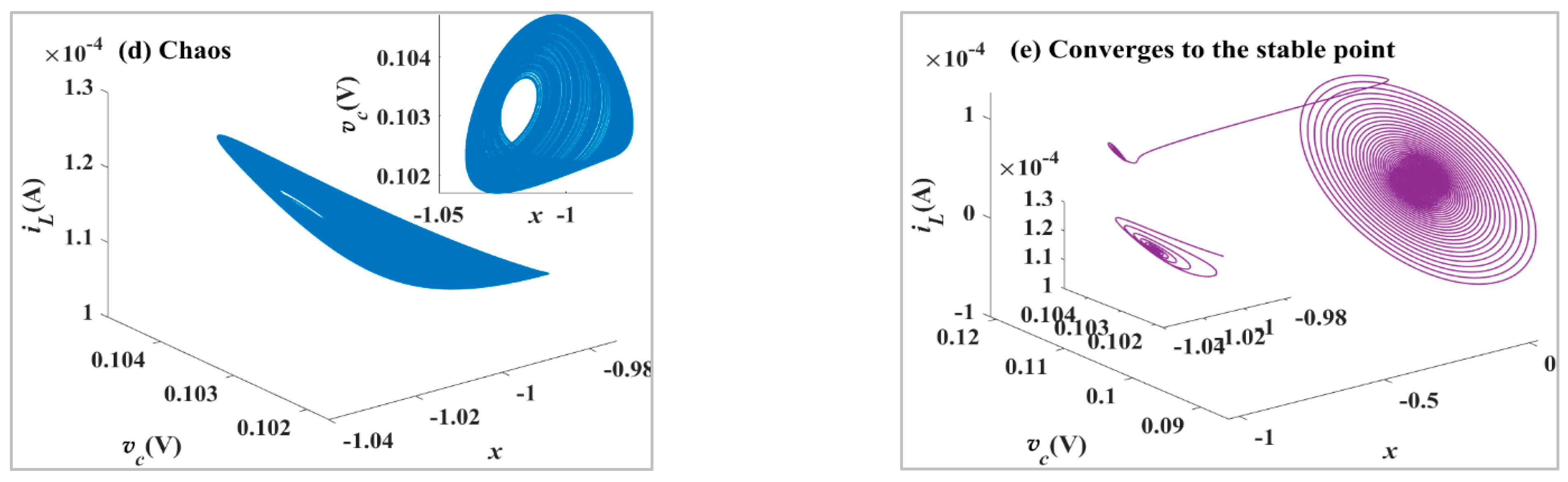
5.2. Influence of Parameters L and C on System Dynamics
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chua, L. Local activity is the origin of complexity. Int. J. Bifurcat. Chaos 2011, 15, 3435–3456. [Google Scholar] [CrossRef] [Green Version]
- Mannan, Z.I.; Choi, H.; Kim, H. Chua corsage memristor oscillator via Hopf bifurcation. Int. J. Bifurcat. Chaos 2016, 26, 1630009. [Google Scholar] [CrossRef]
- Dong, Y.; Wang, G.; Chen, G. A Bistable Nonvolatile Locally-active Memristor and its Complex Dynamics. Commun. Nonlinear Sci. Numer. Simul. 2020, 84, 105203. [Google Scholar] [CrossRef]
- Mannan, Z.I.; Yang, C.; Kim, H. Oscillation with 4-lobe Chua corsage memristor. IEEE Circuits Syst. Mag. 2018, 18, 14–27. [Google Scholar] [CrossRef]
- Mannan, Z.I.; Yang, C.; Adhikari, S.P. Exact Analysis and Physical Realization of the 6-Lobe Chua Corsage Memristor. Complexity 2018, 2018, 8405978. [Google Scholar] [CrossRef]
- Jin, P.; Wang, G.; Iu, H.H.C. A Locally-Active Memristor and its Application in Chaotic Circuit. IEEE Trans. Circuits Syst. II Express Briefs 2017, 65, 246–250. [Google Scholar] [CrossRef]
- Gu, W.; Wang, G.; Dong, Y.; Ying, J. Nonlinear dynamics in non-volatile locally-active memristor for periodic and chaotic oscillations. Chin. Phys. B 2020, 29, 110503. [Google Scholar] [CrossRef]
- Ying, J.; Liang, Y.; Wang, J.; Dong, Y.; Wang, G.; Gu, M. A tristable locally-active memristor and its complex dynamics. Chaos Solitons Fractals 2021, 148, 111038. [Google Scholar] [CrossRef]
- Liang, Y.; Wang, G.; Chen, G.; Dong, Y.; Yu, D.; Iu, H.H.C. S-Type Locally active memristor-based periodic and chaotic oscillators. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 5139–5152. [Google Scholar] [CrossRef]
- Ascoli, A.; Slesazeck, S.; Tetzlaff, R.; Maehne, H.; Mikolajick, T. Unfolding the local activity of a memristor. In Proceedings of the 2014 14th International Workshop on Cellular Nanoscale Networks and their Applications (CNNA), Notre Dame, IN, USA, 29–31 July 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–2. [Google Scholar]
- Chua, L.O. Five non-volatile memristor enigmas solved. Appl. Phys. A Mater. Sci. 2018, 124, 563. [Google Scholar] [CrossRef]
- Adhikari, S.P.; Sah Kim, M.P.H.; Chua, L.O. Three fingerprints of memristor. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 3008–3021. [Google Scholar] [CrossRef]
- Chua, L. If it’s pinched it’s a memristor. Semicond. Sci. Technol. 2014, 29, 1–42. [Google Scholar] [CrossRef]
- Mannan, Z.I.; Choi, H.; Rajamani, V.; Kim, H.; Chua, L.O. Chua Corsage Memristor: Phase Portraits, Basin of Attraction, and Coexisting Pinched Hysteresis Loops. Int. J. Bifurc. Chaos 2017, 27, 1730011. [Google Scholar] [CrossRef]
- Kumar, S.; Strachan, J.P.; Williams, R.S. Chaotic dynamics in nanoscale NbO2 Mott memristors for analogue computing. Nature 2017, 548, 318–321. [Google Scholar] [CrossRef] [PubMed]
- Sandri, M. Numerical calculation of Lyapunov exponents. Math. J. 1996, 6, 78–84. [Google Scholar]

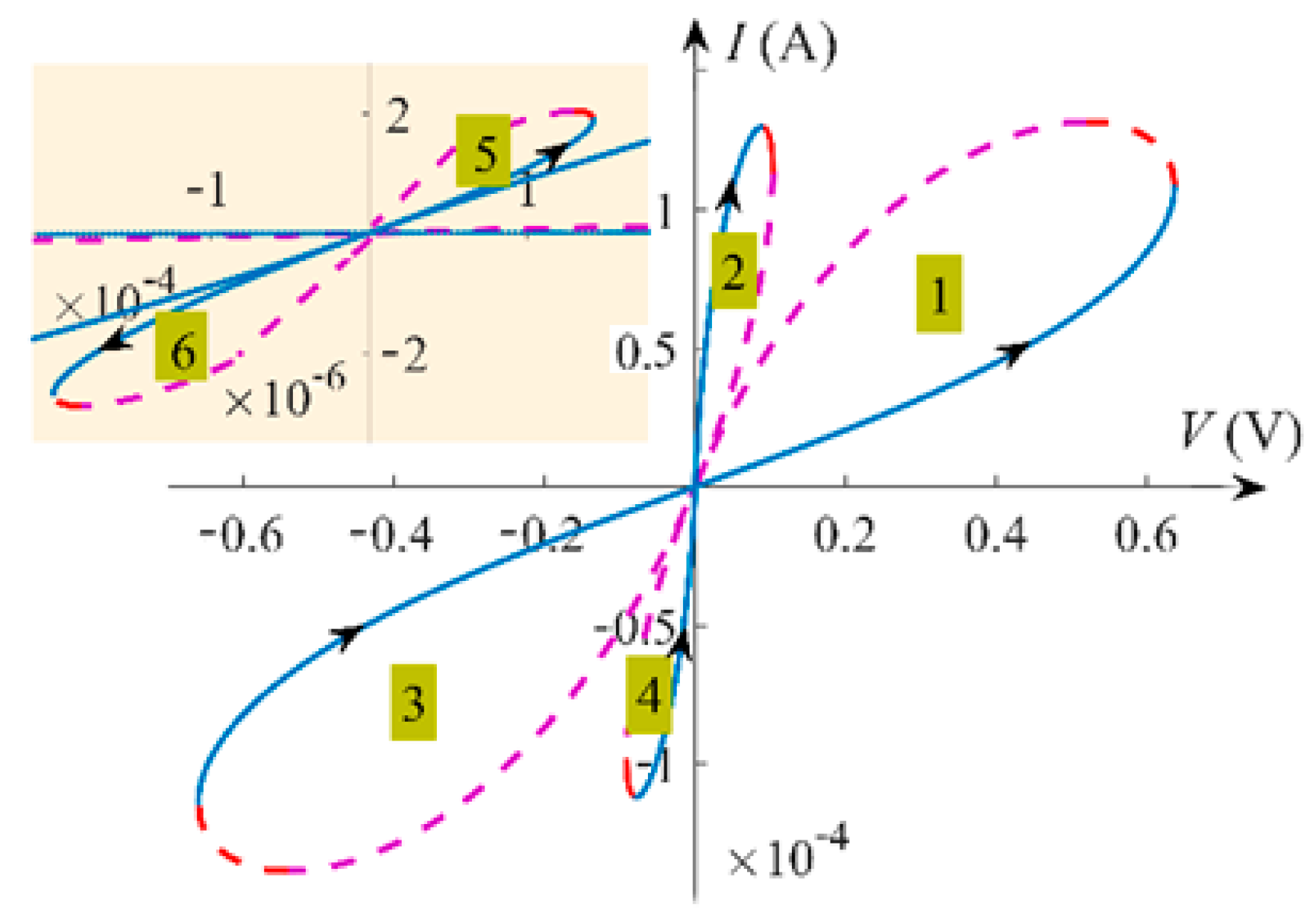



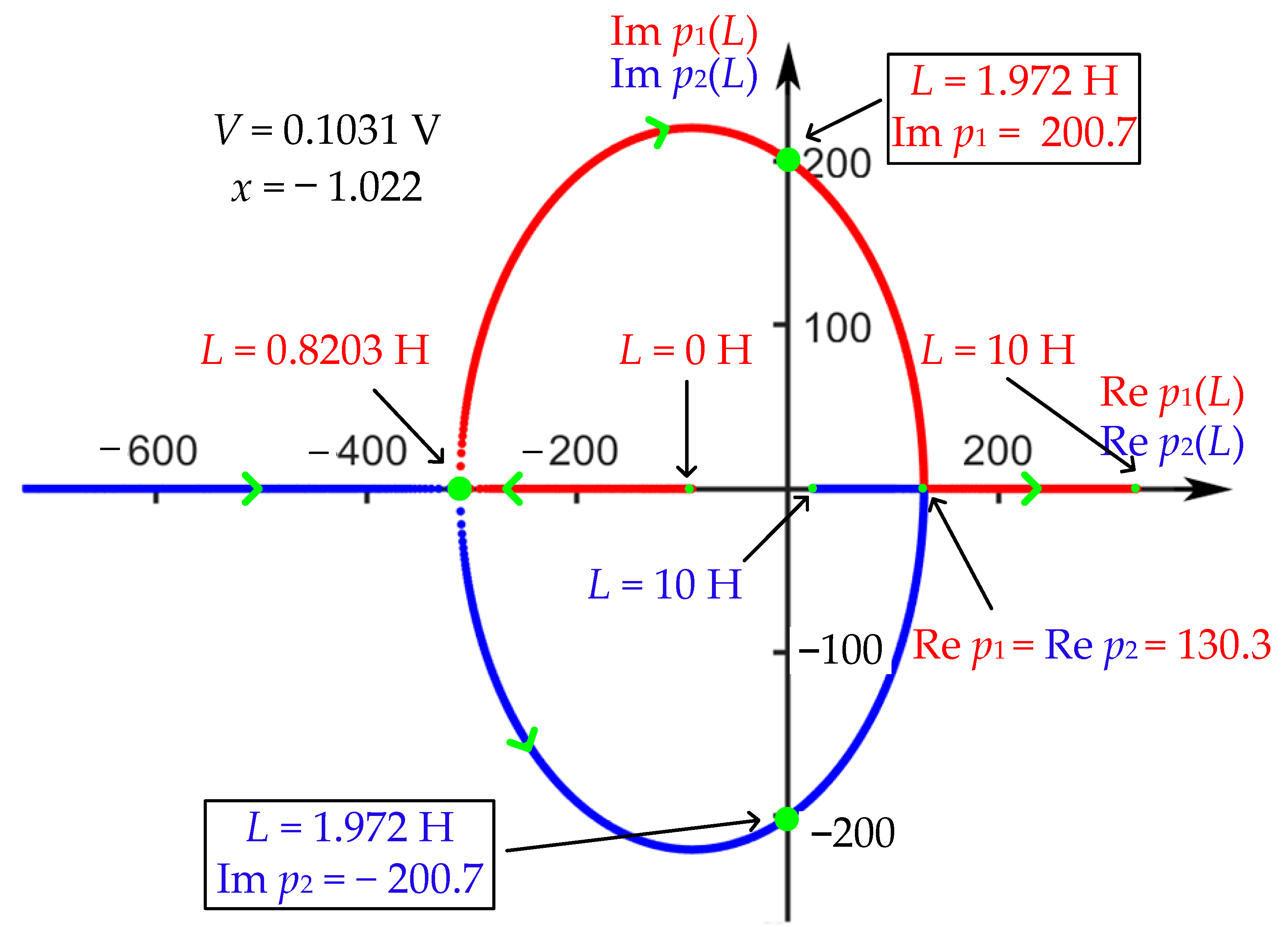



| Range of x | Lobe | Corresponding Voltage (V) | Corresponding Current I (mA) | Stability |
|---|---|---|---|---|
| (−3.979, −3.667) | 6 | (−1.816 × 10−4, −1.989 × 10−4) | (−2.894 × 10−6, −2.694 × 10−6) | Unstable |
| (−1.169, −1.000) | 2 | (0.08855, 0.1034) | (1.298 × 10−4, 1.138 × 10−4) | Stable |
| (−0.3963, −0.2702) | 3 | (−0.5395, −0.6600) | (−1.387 × 10−4, −1.140 × 10−4) | Unstable |
| (0.2649, 0.3909) | 1 | (0.6369, 0.5206) | (1.084 × 10−4, 1.316 × 10−4) | Unstable |
| (0.9921, 1.152) | 4 | (−0.09095, −0.07837) | (−9.862 × 10−5, −1.119 × 10−4) | Stable |
| (3.653, 3.954) | 5 | (1.414 × 10−4, 1.295 × 10−4) | (1.902 × 10−6, 2.038 × 10−6) | Unstable |
| Lobe | Equivalent Circuit Lx | P | Z | Energy Storage Element |
|---|---|---|---|---|
| 1 | > 0 | > 0 | < 0 | Parallel capacitance |
| 2 | < 0 | < 0 | > 0 | Series inductance |
| 3 | > 0 | > 0 | < 0 | Parallel capacitance |
| 4 | < 0 | < 0 | > 0 | Series inductance |
| 5 | > 0 | > 0 | < 0 | Parallel capacitance |
| 6 | > 0 | > 0 | < 0 | Parallel capacitance |
| Equilibrium Point | Characteristic Value | Equilibrium Points Types | ||
|---|---|---|---|---|
| λ1 | λ2 | λ3 | ||
| E1 | −157.01 | 9.55 + 156.13i | 9.55–156.13i | Saddle focus |
| E2 | 144.14 | −45.92 + 159.2i | −45.92–159.2i | Saddle focus |
| E3 | −11810 | −2 + 204i | −2–204i | Stable focus |
| E4 | 4273.2 | −8.1 + 204.2i | −8.1–204.2i | Saddle focus |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Liu, J.; Zhou, W.; Dong, Y.; Jin, P.; Ying, J.; Wang, G. A Passive but Local Active Memristor and Its Complex Dynamics. Electronics 2022, 11, 1843. https://doi.org/10.3390/electronics11121843
Li F, Liu J, Zhou W, Dong Y, Jin P, Ying J, Wang G. A Passive but Local Active Memristor and Its Complex Dynamics. Electronics. 2022; 11(12):1843. https://doi.org/10.3390/electronics11121843
Chicago/Turabian StyleLi, Fupeng, Jingbiao Liu, Wei Zhou, Yujiao Dong, Peipei Jin, Jiajie Ying, and Guangyi Wang. 2022. "A Passive but Local Active Memristor and Its Complex Dynamics" Electronics 11, no. 12: 1843. https://doi.org/10.3390/electronics11121843
APA StyleLi, F., Liu, J., Zhou, W., Dong, Y., Jin, P., Ying, J., & Wang, G. (2022). A Passive but Local Active Memristor and Its Complex Dynamics. Electronics, 11(12), 1843. https://doi.org/10.3390/electronics11121843






