Dependence of Temperature Rise on the Position of Catheters and Implants Power Sources Due to the Heat Transfer into the Blood Flow
Abstract
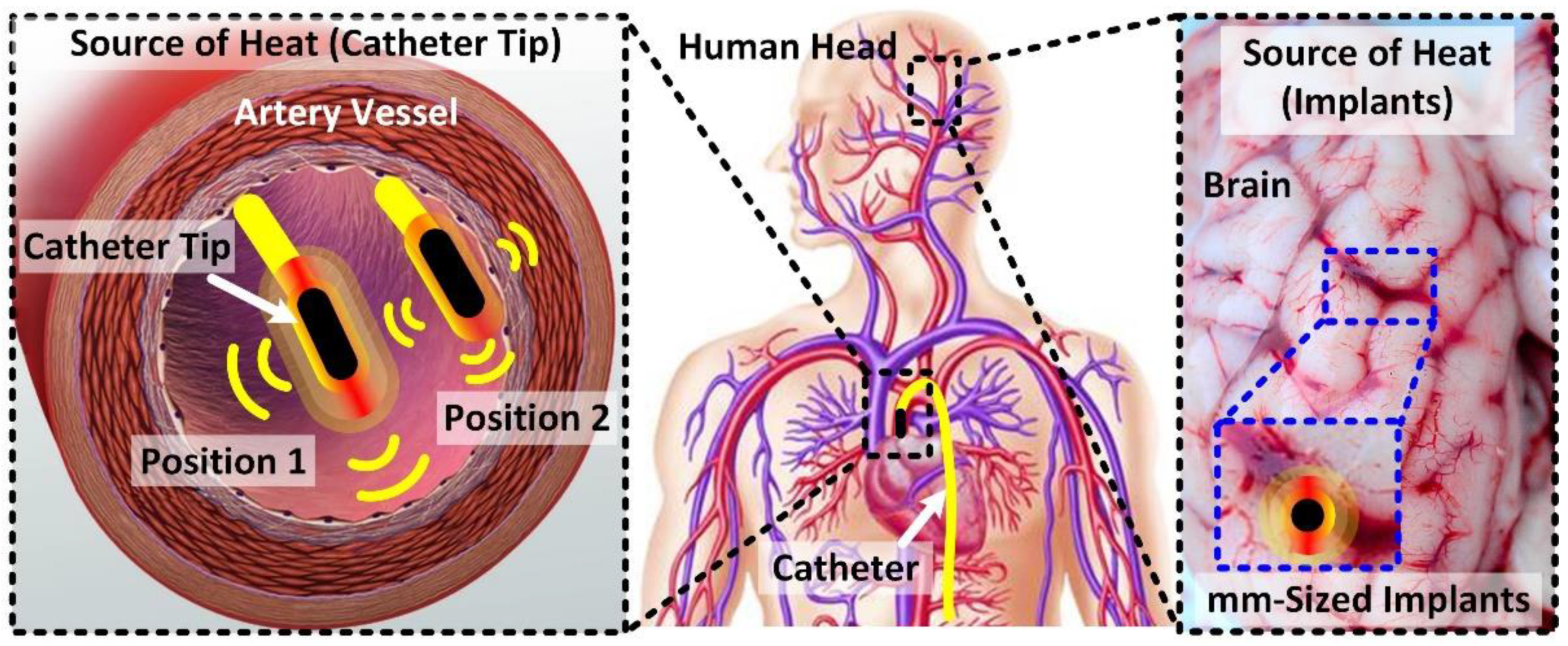
:1. Introduction
2. System Modeling
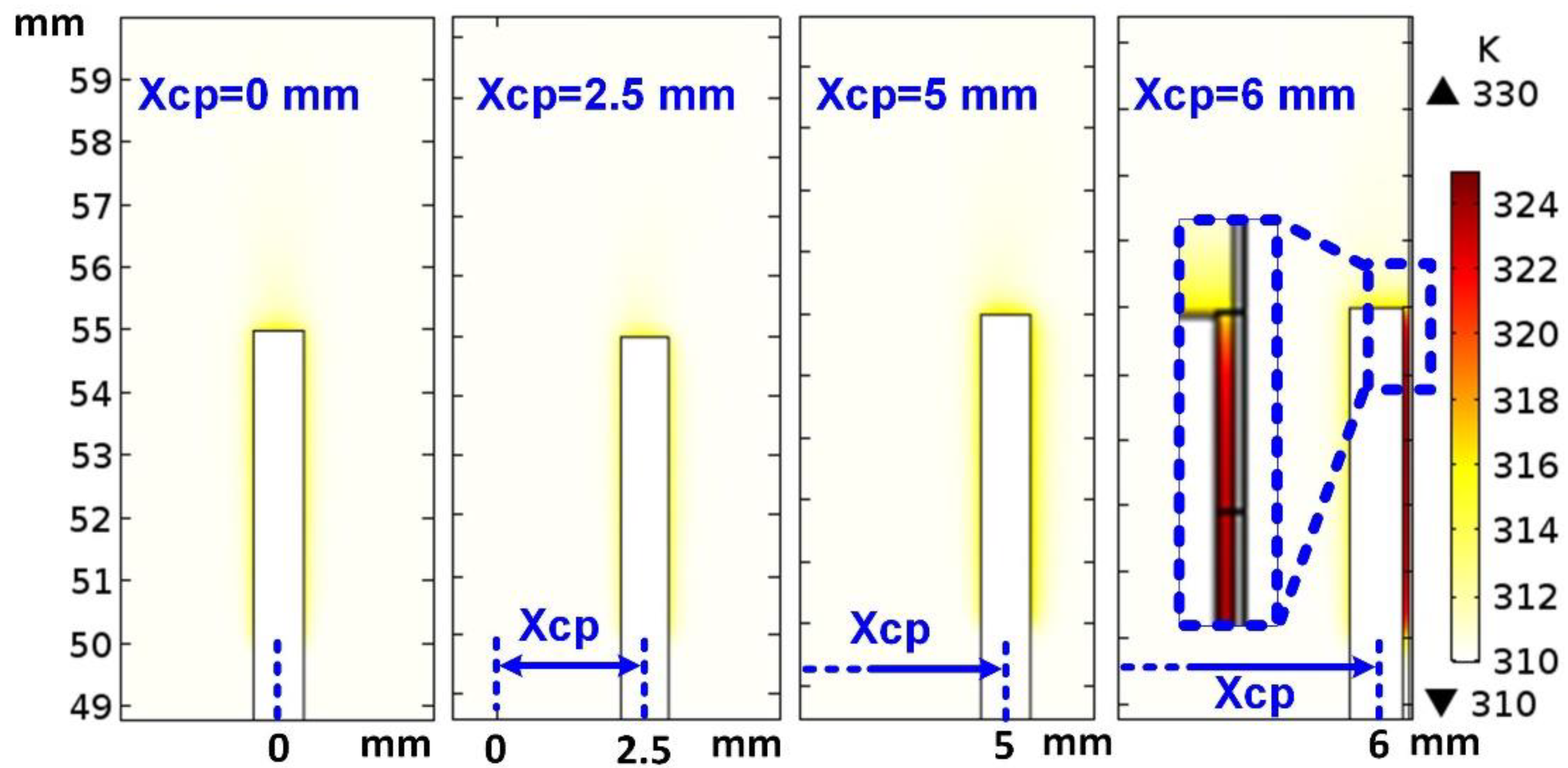
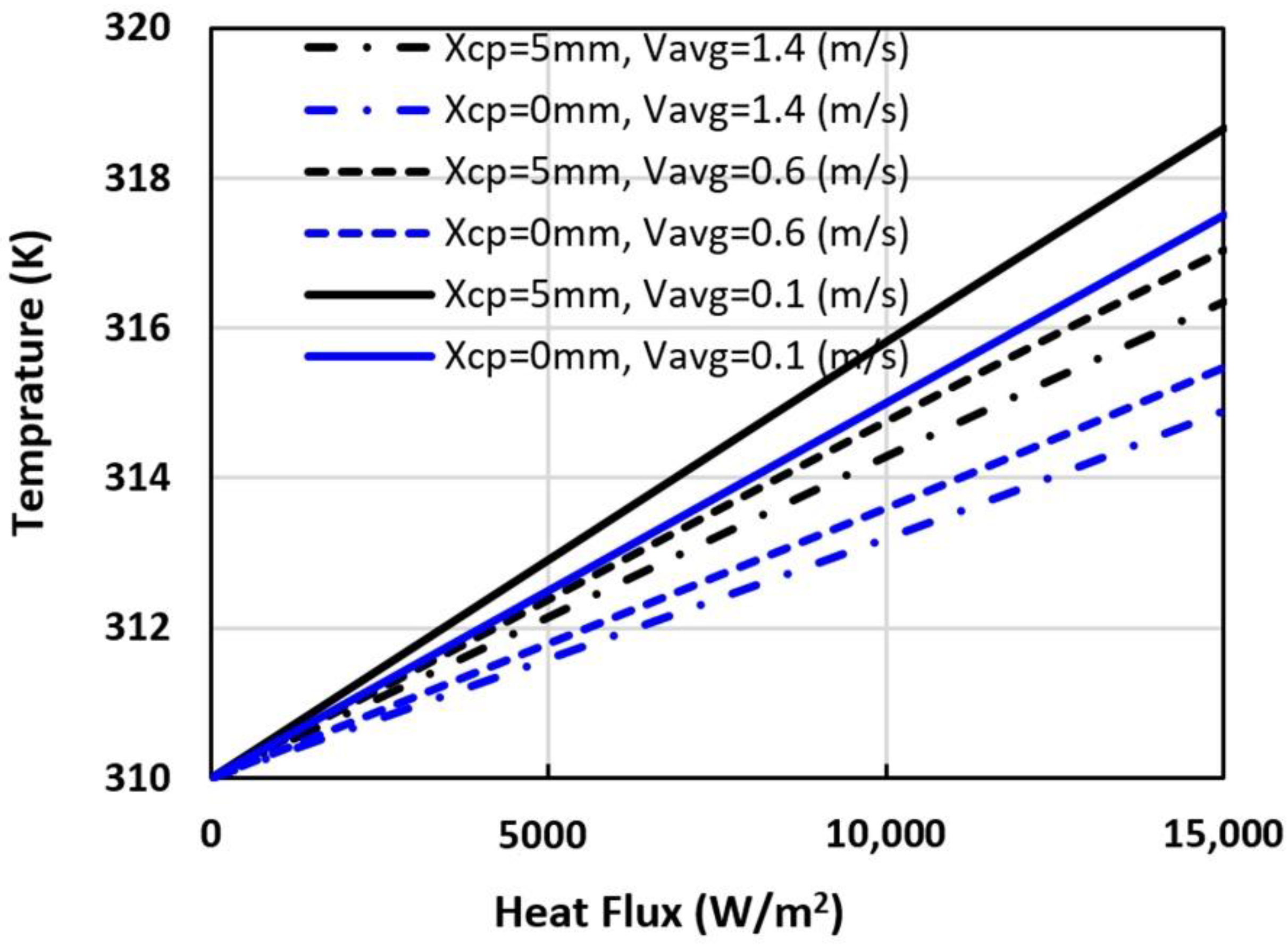
3. Simulation Results
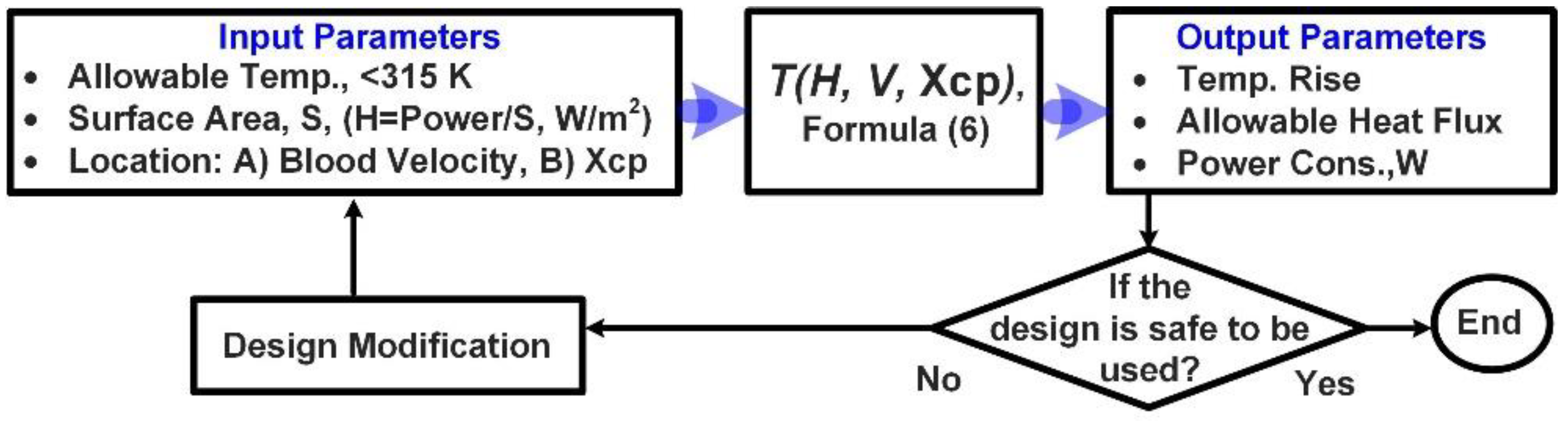
4. Design Rule and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Djongyang, N.; Tchinda, R.; Njomo, D. Thermal comfort: A review paper. Renew. Sustain. Energy Rev. 2010, 14, 2626–2640. [Google Scholar] [CrossRef]
- Katić, K.; Li, R.; Zeiler, W. Thermophysiological models and their applications: A review. Build. Environ. 2016, 106, 286–300. [Google Scholar] [CrossRef] [Green Version]
- Choi, J.H.; Loftness, V. Investigation of human body skin temperatures as a bio-signal to indicate overall thermal sensa-tions. Build. Environ. 2012, 58, 258–269. [Google Scholar] [CrossRef]
- Witzmann, F.A. Temperature regulation and exercise physiology. In Medical Physiology: Principles for Clinical Medicine, 3rd ed.; Rhoades, R.A., Bell, D.R., Eds.; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2009. [Google Scholar]
- Hochstein, S.; Rauschenberger, P.; Weigand, B.; Siebert, T.; Schmitt, S.; Schlicht, W.; Převorovská, S.; Maršík, F. Assessment of physical activity of the human body considering the thermodynamic system. Comput. Methods Biomech. Biomed. Eng. 2016, 19, 923–933. [Google Scholar] [CrossRef] [PubMed]
- Yi, L.; Fengzhi, L.; Yingxi, L.; Zhongxuan, L. An integrated model for simulating interactive thermal processes in hu-man–clothing system. J. Therm. Biol. 2004, 29, 567–575. [Google Scholar] [CrossRef]
- Boregowda, S.C.; Choate, R.E.; Handy, R. Entropy Generation Analysis of Human Thermal Stress Responses. Int. Sch. Res. Not. 2012, 2012, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Ruggera, P.S.; Witters, D.M.; Von Maltzahn, G.; Bassen, H.I. In vitro assessment of tissue heating near metallic medical implants by exposure to pulsed radio frequency diathermy. Phys. Med. Biol. 2003, 48, 2919–2928. [Google Scholar] [CrossRef] [PubMed]
- Wolf, P.D. Thermal Considerations for the Design of an Implanted Cortical Brain–Machine Interface (BMI). In Indwelling Neural Implants: Strategies for Contending with the In Vivo Environment; Chapter 3; Reichert, W.M., Ed.; CRC Press/Taylor & Francis: Boca Raton, FL, USA, 2008. [Google Scholar]
- Lazzi, G. Thermal effects of bioimplants. IEEE Eng. Med. Boil. Mag. 2005, 24, 75–81. [Google Scholar] [CrossRef] [PubMed]
- Holopainen, R. A Human Thermal Model for Improved Thermal Comfort; VTT Technical Research Centre of Finland: Espoo, Finland, 2012. [Google Scholar]
- Patel, V.; Light, E.; Herickhoff, C.; Grant, G.; Britz, G.; Wilson, C.; Palmeri, M.; Smith, S. Intracranial Dual-Mode IVUS and Hyperthermia Using Circular Arrays: Preliminary Experiments. Ultrasonic Imaging 2013, 35, 17–29. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, J.; Kim, S.; Hwang, G.; Kwon, K.; Jeon, S.; Bae, H.-M. Reference-Less Time-Division Duplex Transceiver IC for a Renal Denervation System. IEEE J. Solid-State Circuits 2019, 54, 1657–1668. [Google Scholar] [CrossRef]
- Beiert, T.; Schrickel, J.W. Catheter ablation of cardiac arrhythmias. Herzschr Elektrophys 2019, 30, 330–335. [Google Scholar] [CrossRef] [PubMed]
- Ram, C.V.S. Status of Renal Denervation Therapy for Hypertension: Still in Search of the Magic Bullet. Circulation 2019, 139, 601–603. [Google Scholar] [CrossRef] [PubMed]
- Singh, V.; Roy, A.; Castro, R.; McClure, K.; Dai, R.; Agrawal, R.; Greenberg, R.J.; Weiland, J.D.; Humayun, M.S.; Lazzi, G. On the Thermal Elevation of a 60-Electrode Epiretinal Prosthesis for the Blind. IEEE Trans. Biomed. Circuits Syst. 2008, 2, 289–300. [Google Scholar] [CrossRef] [PubMed]
- Lauder, L.; Böhm, M.; Mahfoud, F. The current status of renal denervation for the treatment of arterial hypertension. Prog. Cardiovasc. Dis. 2021, 65, 76–83. [Google Scholar] [CrossRef] [PubMed]
- Tekes, C.; Karaman, M.; Degertekin, F.L. Optimizing circular ring arrays for forward- looking IVUS imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 2596–2607. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gurun, G.; Tekes, C.; Zahorian, J.; Xu, T.; Satir, S.; Karaman, M.; Hasler, J.; Degertekin, F.L. Single-chip CMUT-on-CMOS front-end system for real-time volumetric IVUS and ICE imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 239–250. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- DiBona, G.F.; Esler, M. Translational medicine: The antihypertensive effect of renal denervation. Am. J. Physiol. Integr. Comp. Physiol. 2010, 298, R245–R253. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jung, G.; Tekes, C.; Rashid, M.W.; Carpenter, T.M.; Cowell, D.; Freear, S.; Degertekin, F.L.; Ghovanloo, M.; Degertekin, L. A Reduced-Wire ICE Catheter ASIC With Tx Beamforming and Rx Time-Division Multiplexing. IEEE Trans. Biomed. Circuits Syst. 2018, 12, 1246–1255. [Google Scholar] [CrossRef] [PubMed]
- Mirbozorgi, S.A.; Tekes, C.; Pirouz, A.; Kocaturk, O.; Lederman, R.; Ghovanloo, M.; Degertekin, F.L. A feasibility study for MRI guided CMUT-based intracardiac echocardiography catheters. In 2017 IEEE International Ultrasonics Symposium (IUS); IEEE: Washington, DC, USA, 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Zangooei, H.; Mirbozorgi, S.A.; Mirbozorgi, S. Thermal Analysis of Heat Transfer from Catheters and Implantable Devices to the Blood Flow. Micromachines 2021, 12, 230. [Google Scholar] [CrossRef] [PubMed]
- Shaik, E. Numerical Simulations of Blood Flow in Arteries Using Fluid-Structure Interactions. Ph.D. Thesis, Wichita State University, Wichita, KS, USA, 2007. [Google Scholar]
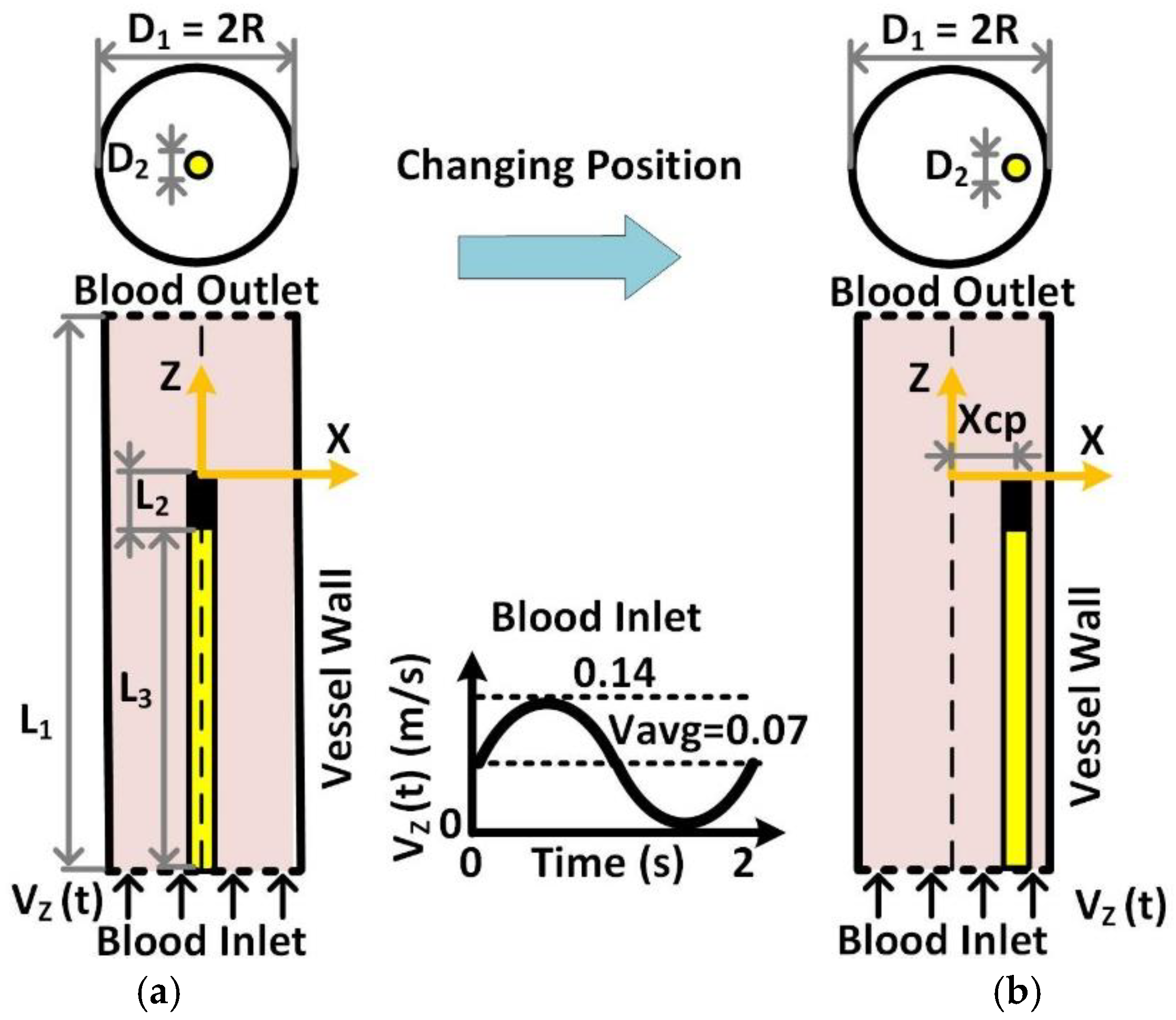



| Parameters | Value (mm) | Description |
|---|---|---|
| D1 | 13 | Diameter of the Blood Vessel |
| D2 | 0.8 | Diameter of the Catheter |
| Xcp | 0–6 | Position from Center |
| L1 | 80 | Length of the Blood Vessel |
| L2 | 5 | Length of the Catheter Tip, Probe/Implant |
| L3 | 50 | Length of the Catheter |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zangooei, H.; Mirbozorgi, S.A.; Mirbozorgi, S. Dependence of Temperature Rise on the Position of Catheters and Implants Power Sources Due to the Heat Transfer into the Blood Flow. Electronics 2022, 11, 1878. https://doi.org/10.3390/electronics11121878
Zangooei H, Mirbozorgi SA, Mirbozorgi S. Dependence of Temperature Rise on the Position of Catheters and Implants Power Sources Due to the Heat Transfer into the Blood Flow. Electronics. 2022; 11(12):1878. https://doi.org/10.3390/electronics11121878
Chicago/Turabian StyleZangooei, Hossein, Seyed Ali Mirbozorgi, and Seyedabdollah Mirbozorgi. 2022. "Dependence of Temperature Rise on the Position of Catheters and Implants Power Sources Due to the Heat Transfer into the Blood Flow" Electronics 11, no. 12: 1878. https://doi.org/10.3390/electronics11121878
APA StyleZangooei, H., Mirbozorgi, S. A., & Mirbozorgi, S. (2022). Dependence of Temperature Rise on the Position of Catheters and Implants Power Sources Due to the Heat Transfer into the Blood Flow. Electronics, 11(12), 1878. https://doi.org/10.3390/electronics11121878







