The electromagnetic power flow around simple loop antennas is analyzed in this section. The introduced error estimators are applied, and the field regions are investigated. As a practical example, the coupling behavior of an electrically large loop antenna is examined.
4.1. Loop Antennas
This section analyzes the power flow and the proposed error estimators for the field regions of a simple loop antenna in the xy-plane. The overall circumference C of the loop antenna is given with , , and . Hence, electrically short and electrically large loop antennas are presented, which results in non-uniform current distributions for the electrically large loop antenna. The loops are excited at an angle of , with a finite feed-gap of . Hence, effects based on the feed-gap are also considered. Consequently, a symmetry will be seen regarding the xy-plane and the xz-plane. For the Poynting vector visualization, the vectors are plotted at a random seed of points; hence, non-symmetric behavior in the quiver-plots is only due to visualization reasons.
In
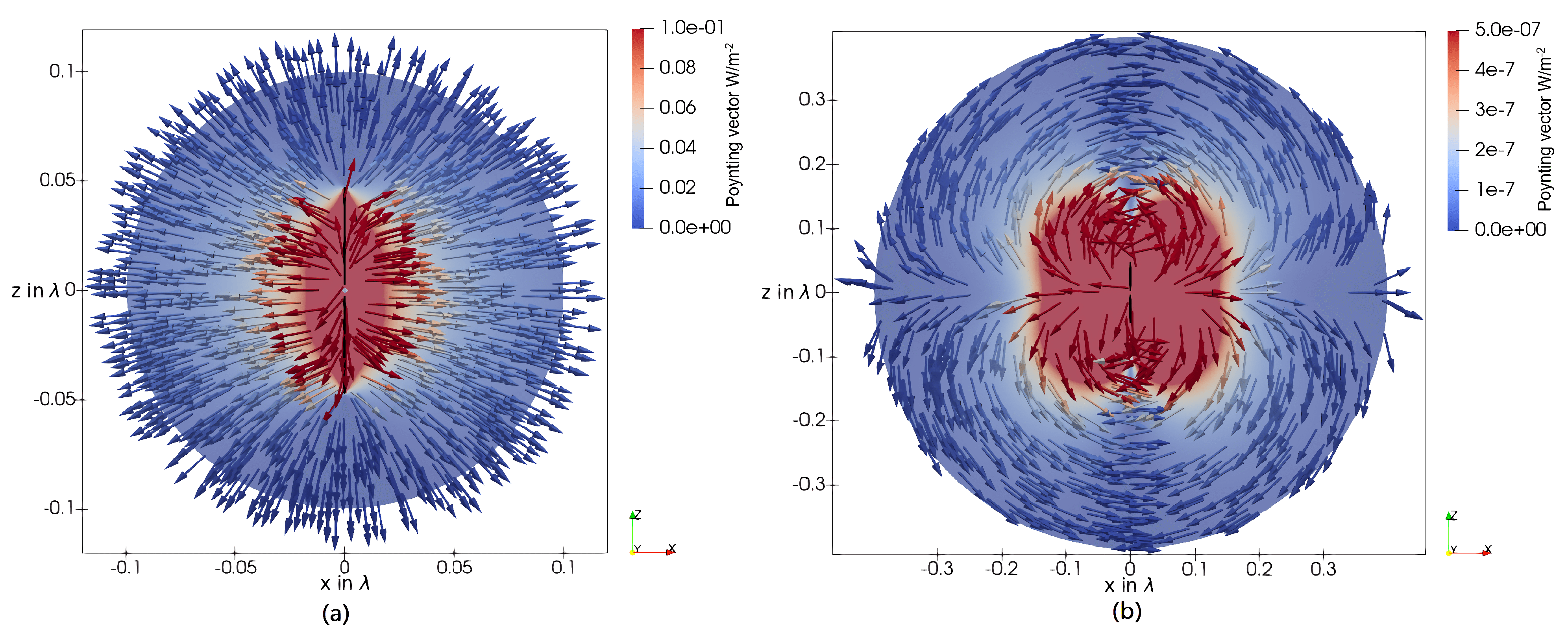
Figure 17, the real part and the imaginary part of the Poynting vector in the coordinate planes around a
loop antenna are shown. As seen in the xy-plane in
Figure 17a, the real part of the Poynting vector also has non-radial parts. Hence, a transition zone can be observed. For higher distances to the antenna origin, these non-radial components vanish, and a rotationally symmetrical behavior can be observed in the xy-plane. In the xz-plane in
Figure 17c, a net power flow in the
-direction around the antenna can be seen. This power flow is directed from the
direction to the
direction. Again, this non-radial net power flow vanishes at higher distances, and pure radial components can be seen. The same occurs for the magnetic dipole; for the angles
and
, the real part of the energy flow vanishes at higher distances. Consequently, a donut-shaped directivity pattern can be expected.
When investigating the imaginary part of the Poynting vector in the yz-plane, shown in
Figure 17b, it can be seen that there is a fluctuating power flow in the four quadrants of this plane between the directions
,
, and the direction
. As for small dipoles, the shape of the magnitude of the imaginary part of the Poynting vector forms a kidney shape. In the xz-plane in
Figure 17c, two separate regions with a dominant imaginary part of the Poynting vector can be seen, with a null in between. This behavior can be explained as a combination of the loop’s inductive behavior and the feeding point’s capacitive behavior.
Figure 18 shows the directivity (a) and the FF error-estimator
6 in the xy-plane (b), yz-plane (c), and zx-plane (d) for a loop antenna with the circumference of
. Again, it can be observed that the highest FF error is present between nulls and lobes of the directivity pattern. Hence, a quite-low error can be seen in the xy-plane, where the main lobe is present. At the FF boundary for small antennas
, the error decreased to about 0.01. Following this, the FF boundary proposed from the literature can be used without any restrictions. The maximum directivity
is the same as for a magnetic dipole as well as for a Hertzian dipole. Additionally, the directivity pattern behaves the same as for small dipole antennas.
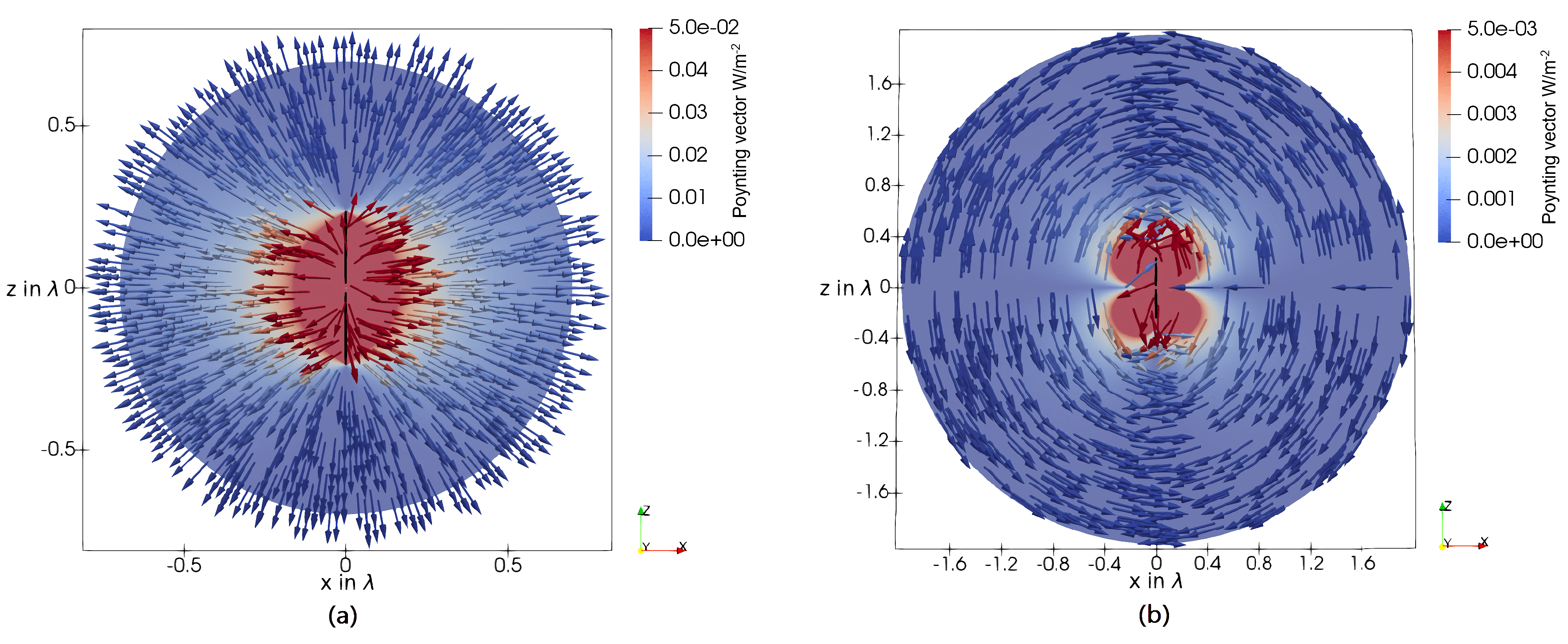
In
Figure 19, the real and the imaginary part of the Poynting vector in the coordinate planes around a
loop antenna are shown. Compared to the loop antenna with a circumference of
in
Figure 17, barely any differences can be seen. This can be explained as the
loop antenna is the border case for being electrically small. However, similar field behavior is still observable, as for the electrically very small antenna. For the real part, barely no difference can be seen. As a consequence, the directivity has to also behave the same. When comparing the imaginary part of the power flow, it can be seen that in the xz-plane in
Figure 17c, the second reactive region at
increased. This can be explained due to the not-uniform current distribution along the antenna structure. As for very small loop antennas, in the yz plane
Figure 17b, a kidney-shaped behavior of the magnitude of the imaginary part of the Poynting vector can be seen.
Figure 20 shows the directivity (a) and the FF error-estimator
6 in the xy-plane (b), yz-plane (c), and zx-plane (d) for a loop antenna with the circumference of
. No difference can be observed compared to the
loop antenna qualitatively. As a circumference of
can still be seen as electrically short, the directivity pattern and the maximum directivity
are the same.
In
Figure 21, the real and the imaginary part of the Poynting vector in the coordinate planes around a
loop antenna are shown. For the real part of the Poynting vector, the most significant difference can be observed in the yz-plane in
Figure 21b, as the behavior changes and the net power flow in the y-direction decreases faster than in the z-direction, other than for smaller loop antennas. As for larger distances, the net power flow in the y-direction decreases, and the directivity pattern also has to change, compared to small loop antennas.
A more significant change can be observed for the imaginary part of the Poynting vector. In the xy-plane in
Figure 21a, it can be seen that the high-reactive regions are not circular-shaped anymore. This is due to the nonuniform current distribution on the electrically large antenna. For a loop antenna with a circumference of about half a wavelength, on the exciting point at
, a voltage maximum is located, and on the other side at
, a current maximum. Hence, two separate high-reactive regions exist, a capacitive region at around
and an inductive region at around
. This can be explained by transmission-line theory, as for
, a voltage-maximum and for
, a current-maximum is present. Additionally, the behavior in the xz-plane in
Figure 21c changed, caused by the same reason.
Figure 22 shows the directivity (a) and the FF error-estimator
6 in the xy-plane (b), yz-plane (c), and zx-plane (d) for a loop antenna with the circumference of
. The directivity in
Figure 22a differs essentially from an electrically short dipole. The power flow shifted from the y-direction towards the z-direction. Additionally, no null in the directivity pattern is observable. The maxima are located in the positive and negative x-direction. Hence, an almost rotationally symmetrical behavior along the x-axis can be seen. The xy-plane and xz-plane of the error-estimator
6 behave qualitatively the same. In
Figure 22c, it can be seen that the maximum error lies in the yz-plane. As for smaller loop antennas or dipole antennas, this is again between two maxima of the directivity pattern. At the FF boundary for small antennas
, the error decreased to about 0.01. Hence, the proposed FF boundary can be seen as reliable.
In
Figure 23, the proposed reactive NF region is shown for loop antennas with the circumference (a)
, (b)
, (c)
, and (d)
. The regions have been derived with the error estimator
11, postulating
. Hence, the oscillating power flow normal to the enclosing surface equals the time-averaged power flow.
By investigating
Figure 23 in detail, it can be seen that the reactive NF region of electrically small loop antennas in (a) and (b) have an almost spherical structure with a radius of
. For the loop antenna with a circumference of
, a toroidal-like behavior with a bulge at the positive and negative z-axis can be observed. Nevertheless, a sphere can still be seen as a good approximation.
Two main regions can be observed when the loop antenna is electrically large, as for the
loop antenna in
Figure 23c. One region is around the xy-plane between
and
for negative x-values. Here, a current maximum on the conducting structure occurs, and following, mainly inductive behavior can be expected. The second region can be seen from
to
for
. As for
, the voltage maximum can be observed. This region can be seen as highly capacitive. Still, the overall reactive NF region can be approximated by a sphere with the radius
.
Figure 23d shows a
loop antenna. As can be seen, a sphere cannot approximate the reactive NF region for electrically large antennas bigger than half a wavelength. For this type of antenna, mainly a toroid-shape behavior around the conducting structure can be seen. At the position where current or voltage maximums occur, the reactive NF region is more pronounced.
4.2. Coupling Behavior of an Electrically Large Loop Antenna
This section analyzes the coupling behavior of a loop antenna with the circumference of . Therefore, first, the reactive NF region is examined in more detail. Second, an electrically small dipole antenna (the coupling mechanism is mainly capacitive) and an electrically small loop antenna (the coupling mechanism is mainly inductive) are placed near the antenna and the induced voltage is analyzed.
In
Figure 24, the reactive NF region of a
loop antenna is shown. Two main regions can be observed: one with a negative imaginary part of the normal component of the Poynting vector (blue) and one with a positive imaginary part (red). As the blue region is close to the current maximum on the current structure, higher inductive coupling behavior can be expected. The red region is close to a potential maximum—consequently, higher capacitive coupling behavior can be expected.
Figure 25 shows the simulation setup to analyze the coupling behavior. Here, the analyzed
loop antenna is excited. Then, an additional electrically small, open-circuited loop antenna is placed above the excited loop to sense the inductive coupling. In the second setup, an electrically small dipole antenna is placed above the excited loop antenna, to mainly sense the capacitive coupling.
In
Figure 26, the induced voltage on the loop probe (a) and dipole probe (b) are shown. As seen in the loop probe, the maximum of the induced voltage can be observed for negative x-values. As already discussed, this area is mainly inductive. The following behavior could be expected. Around the feed-gap of the excited loop, mainly capacitive behavior is expected. Hence, also the induced voltage on the loop probe is significantly smaller. Additionally, two positions with a voltage minimum can be observed. These minima occur as at these positions, half of the probe loop’s area overlaps the inside of the excited loop, and the other half of the area is outside the excited loop. Hence, the magnetic flux cancels, which is called zero-coupling behavior.
For the dipole probe, inverse behavior can be observed. Here, the maximum is given above the feed-gap of the excited loop. This behavior can be explained, as the voltage along the conducting structure is maximized at this position. Additionally, the highest capacitive coupling behavior can be observed. At negative x-values, the excited loop has a voltage minimum and shows mainly inductive behavior. Hence, the capacitive coupling is minor.
Therefore, by introducing the surface-based NF boundary and categorizing the surface, using the sign of the imaginary part of the Poynting vector, advanced predictions regarding the coupling behavior can be given.