A Microscopic Platoon Stability Model Using Vehicle-to-Vehicle Communication

Abstract

With Vehicle-to-Vehicle (V2V) communication capability, vehicle platoon on the highway helps to reduce traffic congestion. However, the dynamic nature of vehicles imposes challenges on the V2V-based platoon management. In this paper, by considering the characteristics of a Vehicular Ad-hoc Network (VANET), a microscopic platoon management scheme is proposed to deal with three basic dynamic platoon maneuvers, namely merging, splitting, and speed-change. The congestion detection feature of VANET is used as a scale for platoon merging, splitting, and speed selection. Real-time congestion is detected if the number of vehicles in a given road segment exceeds the occupancy rate or the time headway is less than the thresholds. In the proposed platoon management scheme, platoon maintenance is triggered in congestion detection. Finally, a VANET-based platoon platform is built by using Network Simulator Version 2 (NS2) network simulation to assess the performance over some real road traces generated by Simulation of Urban MObility (SUMO). It is shown that V2V-based dynamic vehicle platoon management provides an inexpensive technique to cope with the dynamic platoon management requirement.

1. Introduction

The constant increase in traffic volume has raised severe traffic congestion issues worldwide [1]. Vehicle platooning improves vehicle safety, mileage, and driving time while mitigating traffic congestion and reducing pollution and passenger blood pressure [2]. A platoon is a group of vehicles that can travel very closely together, safely at high speed. [3]. Vehicle platoon is an improved version of adaptive cruise control (ACC) [4,5] that matches the vehicle’s movement to the distance, velocity, and direction of the car ahead. Grouping vehicles on highways can save fuel, fit more cars on the road, and improve road safety [6,7]. In addition, platoon allows the driver to relax and do other things while queuing up to long-distance destinations. The cooperation between the queue members improves with the help of Vehicular Ad-hoc Networks (VANETs) [8,9].

VANETs help to form and preserve a platoon structure and allow each vehicle to exchange traffic information with neighboring cars. Over the past few years, VANET-based platoons have been extensively studied. Most of the studies related to traffic dynamic control and performance optimization [10,11,12,13,14,15]. The authors in [10,11] proposed two schemes, namely microscopic congestion detection protocol (MCDP) and infrastructure-based vehicular congestion detection (IVCD), for dynamic traffic congestion detection and avoidance. The first scheme MCDP [10], estimates the traffic density from vehicle-to-vehicle (V2V) communications and avoids it by helping the drivers to select an appropriate speed. In contrast, IVCD [11] estimates the traffic congestion from the base station using vehicle-to-infrastructure (V2I) communications. The schemes mentioned above, i.e., MCDP and IVCD, dynamically assess the road traffic from frequent beacon messages and regulate the traffic to avoid congestion. In the same context, an intelligent route Internet-of-Vehicles (IoV)-based congestion detection and avoidance (IoV-based CDA) scheme is proposed to perform: (i) congestion detection and (ii) congestion avoidance in a particular area of interest, i.e., intersection point [12]. In the same context, Zahid and Anis proposed a dynamic traffic monitoring protocol called SmartFlow [14] for congestion detection and assessing the drivers to avoid long delays on traffic signals. In this paper, in the light of the work done in [10,11,12,13,14,15], we adopt the dynamic traffic management features and applied to the VANET-based dynamic platoon management. It is challenging to maintain the time headway and inter-vehicle spacing for a dynamic platoon in the cases of platoon merging, splitting, and speed-change [16]. In [17], technical issues regarding vehicle platooning are discussed to highlight obstacle detection and collision avoidance. A hierarchical architecture is proposed in [18] to include the guidance, management, and traffic control layers for platoon management. A simulation environment is built in [19] for platoons of autonomous vehicles over Simulation of Urban MObility (SUMO). However, no actual platoon management protocol was proposed to consider coordination among vehicles in maneuvers. For multiple platoons, existing works mainly studied platoon merging and splitting. Several significant projects have proposed the inter-platoon coordination model [20,21,22,23]. Based on the existing platoon works [20,21,22,23] and the dynamic traffic management [10,11,12,13,14,15], devising a dynamic platoon management scheme to suit a dynamic traffic nature effectively is imperative. Many research efforts focused on maintaining platoon stability and providing valuable driving guidance. Even though some progress has been made, the following questions need further exploration.

• Firstly, it is unclear how different vehicle dynamic parameters and the typical platoon dynamics (merging, splitting, and speed-change) affect the stability of the VANET-based platoon structure. The inherent relationship between the platoon stability probability and the observed transportation parameters, for instance, traffic density, relative vehicle speed, the deviation in relative vehicle speed, and the time headway of the platoon. It is necessary to provide insightful guidance on the design mechanism to maintain a stable platoon in the presence of different kinds of disturbance.
• Secondly, most of the existing research focused only on maintaining a stable platoon (e.g., constant inter-vehicle distance) rather than addressing the adverse effects of traffic variations. Traffic disturbances lead to frequent, sudden acceleration or deceleration, which lead to an uncomfortable passenger experience and to more fuel consumption [24]. A practical method to mitigate these negative impacts is essential and highly desirable.

To this end, we first focus on the stability probability analysis of dynamic VANET-based platoon. By doing so, the dominating factors that affect the platoon stability probability can be characterized. On this basis, microscopic dynamic platoon management design is proposed to maintain a relatively stable dynamic platoon in the presence of traffic merging, splitting, and changes in speed. The main contributions of this paper are two-fold.

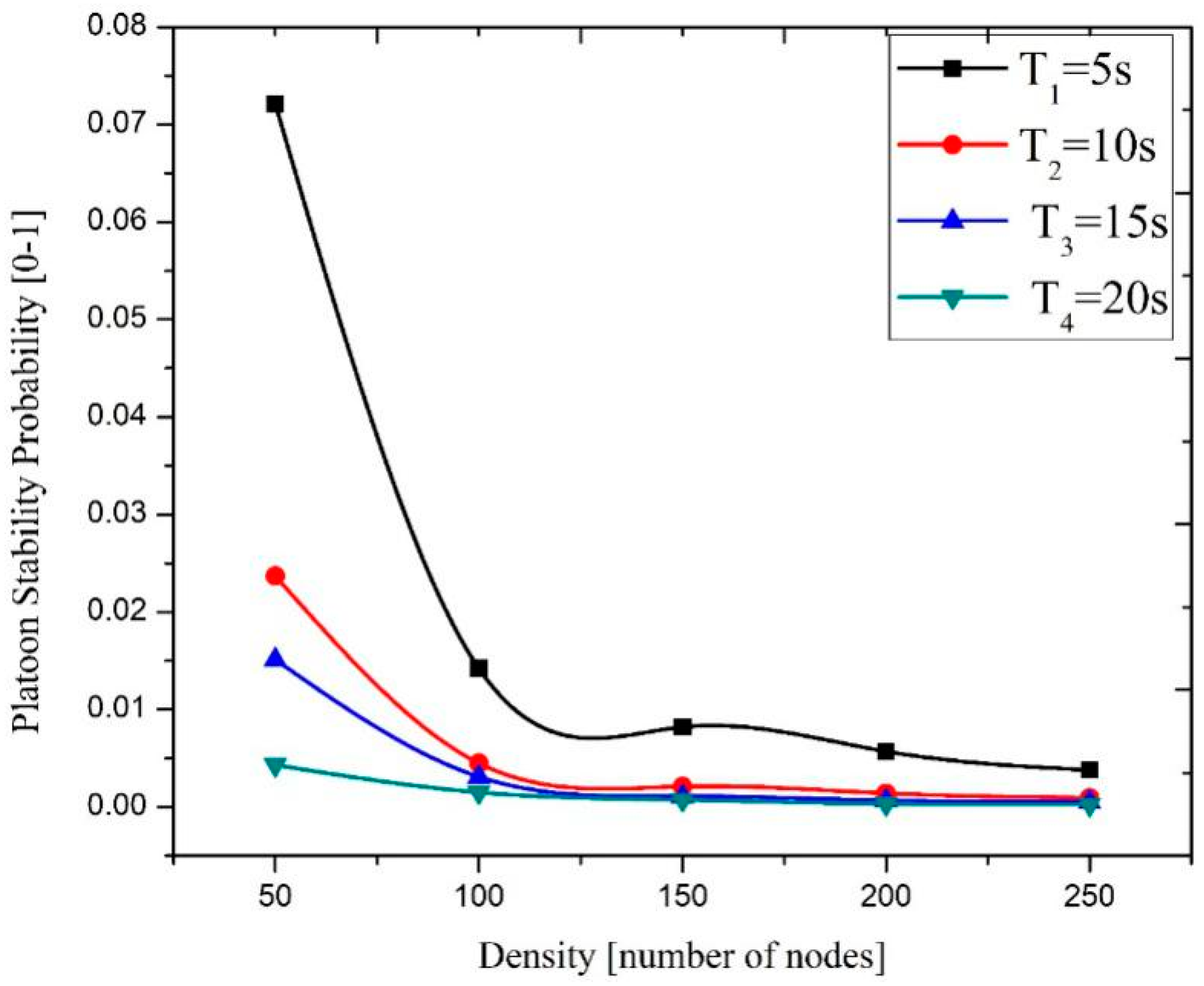
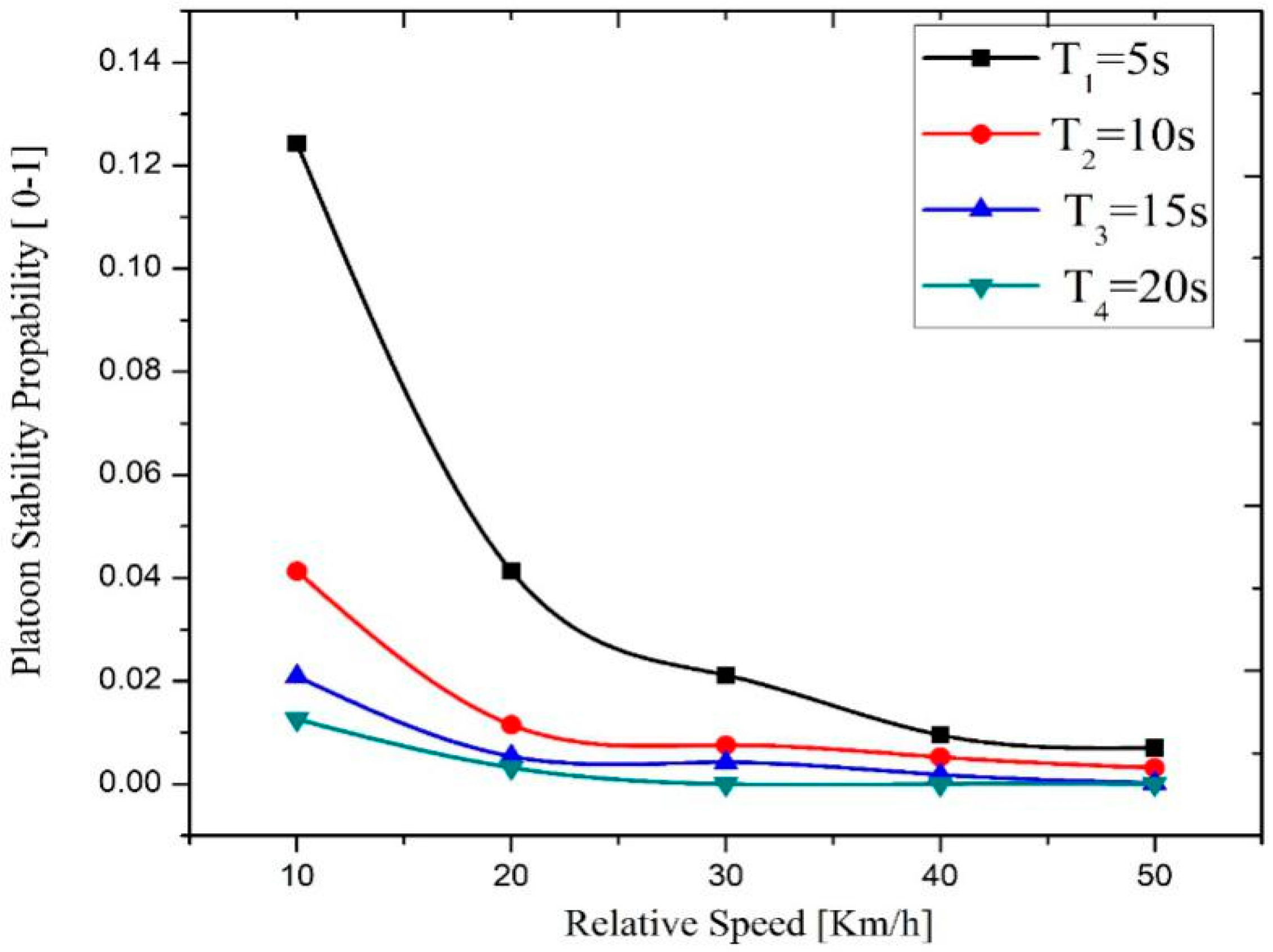
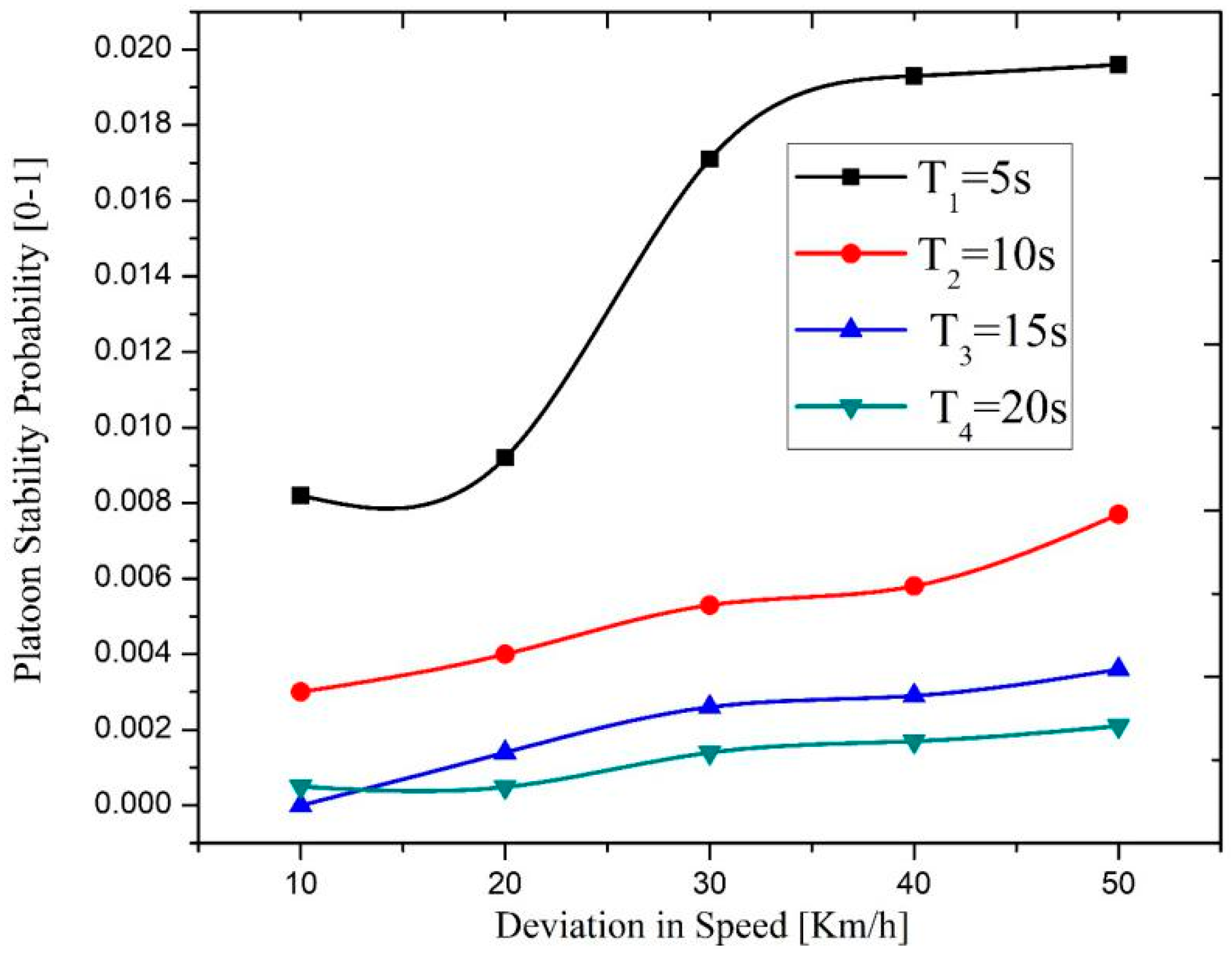
• We derive the stability probability of the VANET-based dynamic platoon system to reveal the inherent relationship between the platoon stability and key transportation parameters (traffic density, relative speed, and time headway). It is shown that increasing the average relative speed, vehicle density, and time headway degrade platoon stability. However, it raises the standard deviation of the relative speed, decreases the equivalent relative velocity, and thus improves the platoon stability probability. Therefore, these parameters cannot be ignored when designing the dynamic platoon management mechanism.
• A microscopic platoon management design is proposed to deal with three basic dynamic platoon maneuvers: merging, splitting, and speed-change. Each vehicle counts its neighbors from iterative beacon messages and estimates the time spacing between the consecutive cars. It is shown that by keeping a reasonable time headway, we can retain the desired dynamic platoon stability.

The remainder of the paper is organized as follows. Platoon stability analysis is presented in Section 2. In Section 3, a VANET-based dynamic platoon management model is presented. The experimental part is presented in Section 4. An additional explanation related to experiments is added in Section 5. The paper is concluded in Section 6.

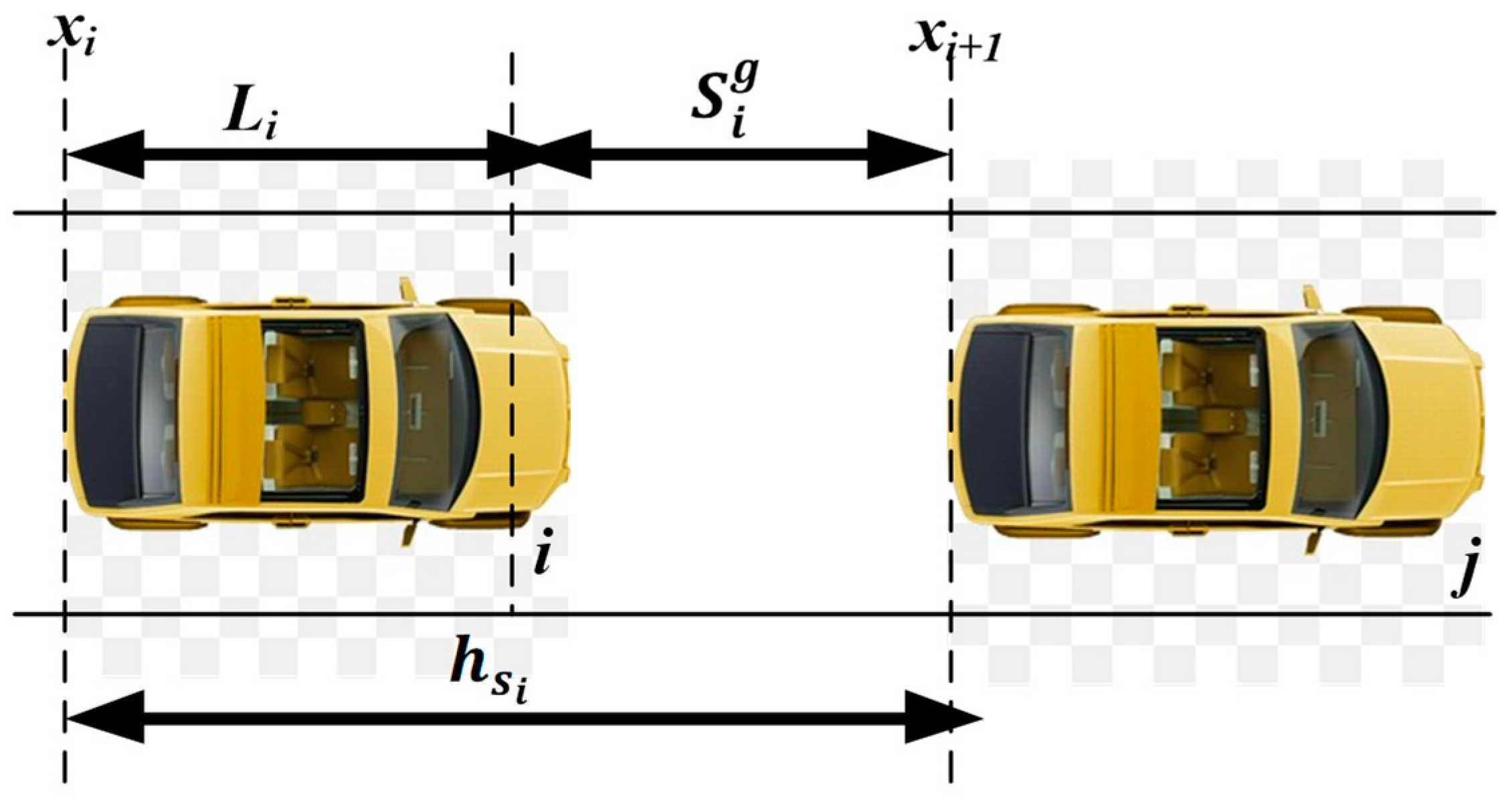
2. System Model and Platoon Stability Formulation

We consider a unidirectional and uninterrupted one-way highway with N subsegments $\left\{s_1, s_2,\dots \dots \dots s_N\right\}$, where $s_i$ indicates the ith road segment. The vehicle arrival rates at all road segments are assumed to be Poisson distributed with mean ${\frac{1}{{\lambda }_{ }}}_{ }$ per unit time and each road segment $s_i$ has a constant arrival rate ${\lambda }_{i }\left(i=1, 2, 3,\cdots N\right)$ with unit vehicle per hour (veh/h). The speed of the vehicle typically follows the normal distribution $N\left(\mu , {\sigma }^2\right)$ with mean $\mu$ and variance $\sigma$² [25]. The occurrence probability of each speed is $P_i=\frac{{\lambda }_i}{\lambda }$, where $\lambda ={\displaystyle \sum }_{i=1}^N{\lambda }_i$ [26]. The inter-vehicle distance (IVD) X specifies the distance between neighboring vehicles. It is shown in [27] that IVD is independent and identically distributed as follows:

$$P_{ }\left(X>x\right)=1-F_X\left(x\right)=e^{-\lambda {\displaystyle \sum }_{i=1}^N\frac{P_i}{v_i}x}$$

(1)

where $F_X(x$) is the corresponding probability distribution function (PDF) of inter-vehicle distances. On the basis of the IVD, the time-headway distribution of all vehicles can be characterized by:

$$P_{ }\left(T>t\right)=1-F_T\left(t\right)=e^{-\lambda {\displaystyle \sum }_{i=1}^N\frac{P_i}{v_i}t}$$

(2)

where $F_T(t$) is the corresponding PDF of time headway. The time-headway $T$ between two successive vehicles is dependent on the transportation parameters such as the average vehicle arrival rate ${\lambda }_{i }$ (or the speed occurrence probability) and the vehicle speed. Later in Section 3, it is illustrated that time-headway is an important parameter to assess the platoon stability. It is important to explore the impact of the transportation parameters of vehicle density, deviation in speed $\sigma$ as well as $T$ on the platoon stability probability.

Definition 1.

Platoon stability is the probability that a specific time gap (time headway) among platoon vehicles will be maintained under transportation safety requirements. A platoon is said to be stable if the gap between the cars or headway lies within the threshold of safe transportation. In case of any disturbance, the platoon will split or merge with other platoon segments to maintain safe transportation regulations.

We focused on the inter-vehicle spaces and the time required to cover the inter gap in the proposed platoon stability model. Since the inter-vehicle spacing and time is related to the speed. Thus, all the mathematical work uses time, distance, and speed as primary input parameters of different functions. As shown in Figure 1, a vehicle $i$ has a certain space headway $h_{s_i}$ to its predecessor, composed of the space gap $S_i^{g }$ to vehicle j and its own length $L_i$:

$$h_s{}_i=S_i^{g }+L_i{}_{ }$$

(3)

In the same way, the vehicle $i$ also has a time headway $h_{t_i}$ (expressed in seconds) consisting of a time gap $t_{i }^g$ and the car occupancy time $O_i$

$$h_{t_i}=t_{i }^g+O_i$$

(4)

and it can be linked to the vehicle’s relative speed $∆v_{ij}{}_{ }$ as follows:

$$\frac{h_S{}_i}{h_t{}_i}=\frac{h_i^g{}_{ }}{t_i^g{}_{ }}=\frac{L_i{}_{ }}{O_i{}_{ }}=∆v_{ij}$$

(5)

The average relative speed can be estimated as:

$$\widehat{∆v}=\frac{1}{N}{\displaystyle \sum }_{i,j=1}^N\left|\overrightarrow{∆v_{ij}{}_{ }}\right|$$

(6)

Let us assume that every vehicle enters a highway segment at a different speed. In [26], the vehicle speed is modeled as Gaussian distribution, and it is further assumed that the speed of every vehicle remains constant for a specific time duration. The speed is assigned to a vehicle and its PDF can be written as:

$$f\left(v\right)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{{\left(v-\mu \right)}^2}{2{\sigma }^2}}$$

(7)

The distribution of time headway $h_t$ depends on the following two factors: (1) Relative speed $∆v_{ij}$ of vehicle $V_i$ and $V_j \left(2\right)$ Spacing headway $h_{s_i}$. Let $h_{T_p}$ be the predicted time headway and we have:

$$h_{T_p}=\frac{h_{s_i}}{∆v_{ij}}$$

(8)

Considering the average relative speed and the average spacing headway of the entire platoon, $h_{T_p}$ can be given by:

$$h_{T_p}=\frac{\frac{1}{\mathrm{n}}{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{h}}_{{\mathrm{s}}_{\mathrm{i}}}}{\widehat{∆v}}$$

(9)

To calculate time headway stability probability, the probability density function of time headway time $h_{t_i}$ is given by:

$$f(t_i)=\frac{h_{S_i}}{\Delta v_{ij}{h}_{t_i}^2\sqrt{2\pi }\sigma }{e}^{-{\left(\frac{h_{S_i}}{h_{t_i}}-{\mu }_{ij}\right)}^2/2{\sigma }_{ij}^2}$$

(10)

The PDF $f\left(t_i\right)$ shows the probability that vehicle $i$ will be stable for time $t$ in terms of time headway. In (10), ${\mu }_{ij}$ and ${\sigma }_{ij}^2$ represent the mean and variance of the relative speed $∆v_{ij}$ among platoon consecutive vehicles, respectively. Given the time headway $T$ within period [t, $t+h_{T_p}$], the stability probability of platoon can be computed as below:

$$f\left(T\right)={{\displaystyle \int }}_t^{t+h_{T_p}}f\left(h_{t_i}\right) dt if h_{T_p}\ge {\tau }_0$$

(11)

where ${\tau }_0$ is the minimum safety time headway threshold. The platoon stability probability $f\left(T\right)$ of time headway $T$ among any two vehicles at time t for a specific time interval $h_{T_p}$. When the platoon comprises a set of $N$ vehicles and $f_i\left(T\right)\left(i=1,2,\dots N\right)$ represents the stability probability between two consecutive vehicles, then the stability probability of the entire platoon will be:

$$f\left(T\right)=N{{\displaystyle \int }}_t^{t+h_{Tp}}f\left(h_{t_i}\right) dt if h_{Tp}\ge {\tau }_0$$

(12)

Here, the probability of an individual vehicle’s stability is multiplied to get the net stability of the whole platoon. The product rule of probability is applied because each vehicle’s stability is independent of the other. From the probability and statistics rules, the probability of two independent events co-occurring is calculated by multiplying the individual probabilities of each isolated event.

3. Proposed V2V-Based Platoon Stability

A microscopic V2V-based platoon management system is introduced in this paper by integrating transportation with communication. In practice, with V2V communication capabilities, the vehicles in a platoon improve highway safety and traffic flow throughput. The proposed V2V platoon management system operates in a fully decentralized mode, independent of any additional information, such as traffic data from local authorities. Every vehicle reacts autonomously and directly communicates with each other. As shown in Figure 2, the platoon management system consists of a controller that adapts to the disruption scenario and considers both platoon dynamics and VANET requirements. Macroscopic vehicles’ parameters are collected microscopically for platoon stability. The time headway estimation is enabled by measuring distinct neighbors and spacing (inter-vehicle distance). Furthermore, in case of traffic disturbance, every vehicle calculates its estimated speed from the received micro-beacons to retain a predefined constant time gap between platoon vehicles.

3.1. Beacon Message Dissemination

• In VANETS, every vehicle periodically disseminates its basic information through beacon messages with neighboring vehicles. The disseminated beacon messages are very important for platoon maintenance and vehicle coordination. It is assumed that all vehicles in the platoon are capable of V2V and V2I communications within DSRC range. The information dissemination is divided into two parts. i.e., (i) primary parameter exchange (ii) platoon control message.
• Primary parameter exchange: The vehicles in the platoon periodically exchange micro-beacon messages with each other, and the cars abstract the position, speed, acceleration, direction, and additional information embedded in these micro-beacon messages to calculate neighbors within its DSRC communication range [28]. The newly introduced transportation control domain of periodic beacon messages is given in

  Table 1. Micro-beacons message contents.

  Content	Description
  V_ID	Vehicle identifier
  Session Time Ts	Message generation time
  Speed S	Vehicle’s speed (Read from odometer)
  Direction d	Vehicle’s direction (Obtained from Navigator system)
  Acceleration a	Rate of change of vehicle speed (Read from odometer)
  Platoon ID Pid	Platoon identity on highway
  Position p	Vehicle’s Position (GPS)
  Road Type H	Obtained from Transportation Department
  Constant Time headway ${\tau }_{0 }$	Desire time headway
  Vl	Vehicle length

  . Every vehicle calculates its distinct neighbors in the same platoon ID (P_id) and the headway/time gap T between each other.
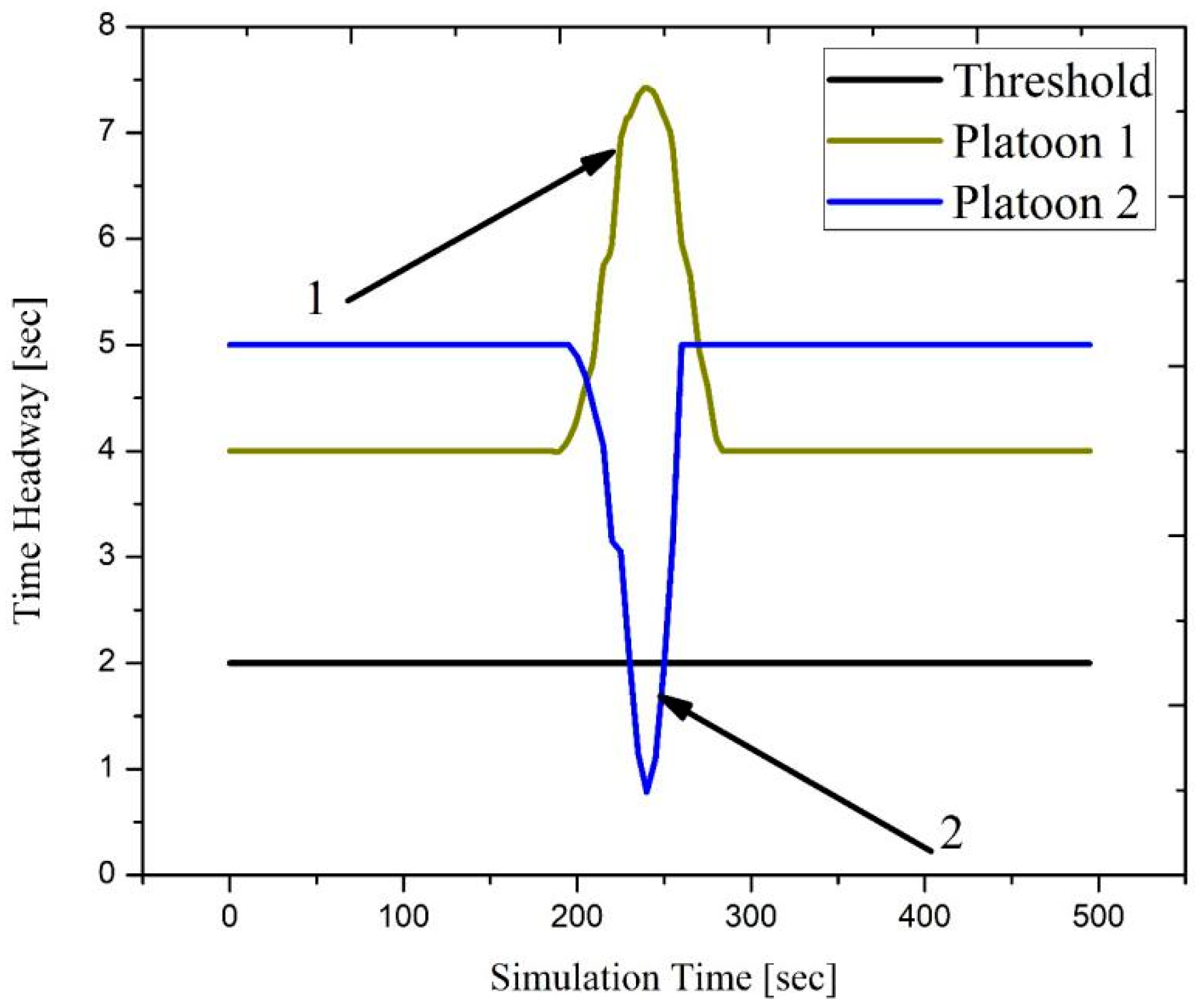
• Platoon control message: This message is multicast to all platoon vehicles to control the moving speed during platoon disturbance. The proposed technique tries to retain constant headway by acceleration or declaration to accomplish maneuvers. As long as T is significant or lower than some predefined threshold τ₀ (for instance, τ₀ = 2), the proposed approach starts broadcasting the platoon control messages and estimating the moving speed v_est to maintain a constant inter-platoon time headway.

3.2. Dynamic Platoon Management

In a platoon, the driver must cooperate to manage and control speed during vehicle merging or splitting to retain a constant platoon headway. Therefore, the vehicles collect transportation information from beacon messages to estimate time headway. Basically, time headway estimation is carried out after primary information exchange. Each car in the platoon calculates distinct neighbors in the platoon and estimates the space gap between vehicles (spacing) based on DSRC range and $N_c$. Finally, each car within platoon can calculate the time-gap/headway time T as below:

$$T=\frac{1}{v_h}\left[\frac{R_{DSRC}}{N_c}-\frac{{{\displaystyle \sum }}_{V=1}^{N_c}{V}_l}{N_c}\right]$$

(13)

where $v_h$ is the speed limit of the corresponding platoon, and $\frac{{{\displaystyle \sum }}_{V=1}^{N_c}{V}_l}{N_c}$ corresponds to the mean length of vehicles in a platoon. In Figure 3, $t_i$ delineates the random variable representing the time-headway time between two consecutive vehicles. In this scenario, the platoon will be stable if the time-headway is equal to ${\tau }_0$. This illustrates that the time-headway between any two neighboring vehicles should be equal to ${\tau }_0$ for platoon stability. Let $P_s$ be the stability probability of the VANET-based platoon. Then, we have:

$$P_s=P_T \{t_1\ge {\tau }_0, t_2\ge {\tau }_0,t_3\ge {\tau }_0,\dots ,t_{n-1}\ge {\tau }_0\}$$

(14)

As $t_i$ is independent and identically distributed $\left(i.i.d\right)$ random variable, we have

$$P_s={{\displaystyle \prod }}_{i=1}^{n-1}{P}_T\left\{t_i\ge {\tau }_0\right\}={{\displaystyle \prod }}_{i=1}^{n-1}[\left(1-\alpha \right)\ast P_T\left\{t_i\ge {\tau }_0\right\}+\alpha \ast P_T\left\{t_i\ge {\tau }_0\right\}]$$

(15)

where α describes the ratio of the platoons in the given network. The platoon stability is defined as the time-headway $T$ among the vehicles and theoretically, platoon stability can be guaranteed if the following condition is satisfied.

$$P_s=\{\begin{array}{c}1 if T={\tau }_{0 }\\ \\ 0 otherwise\end{array}$$

(16)

All vehicles in platoon assess the traffic conditions (merging, splitting, and speed changes) based on the calculated time headway $T_{ }$ and then the moving speed can be estimated according to the underlying traffic status

$$v_{est}=\frac{1}{T} \left(\frac{R}{N_c}-\frac{{{\displaystyle \sum }}_{V=1}^{N_c}{V}_l}{N_c}\right)$$

(17)

here $v_{est }$ is the suggested speed to the driver according to the time-headway $T$ and R is the transmission range of DSRC.

4. Results

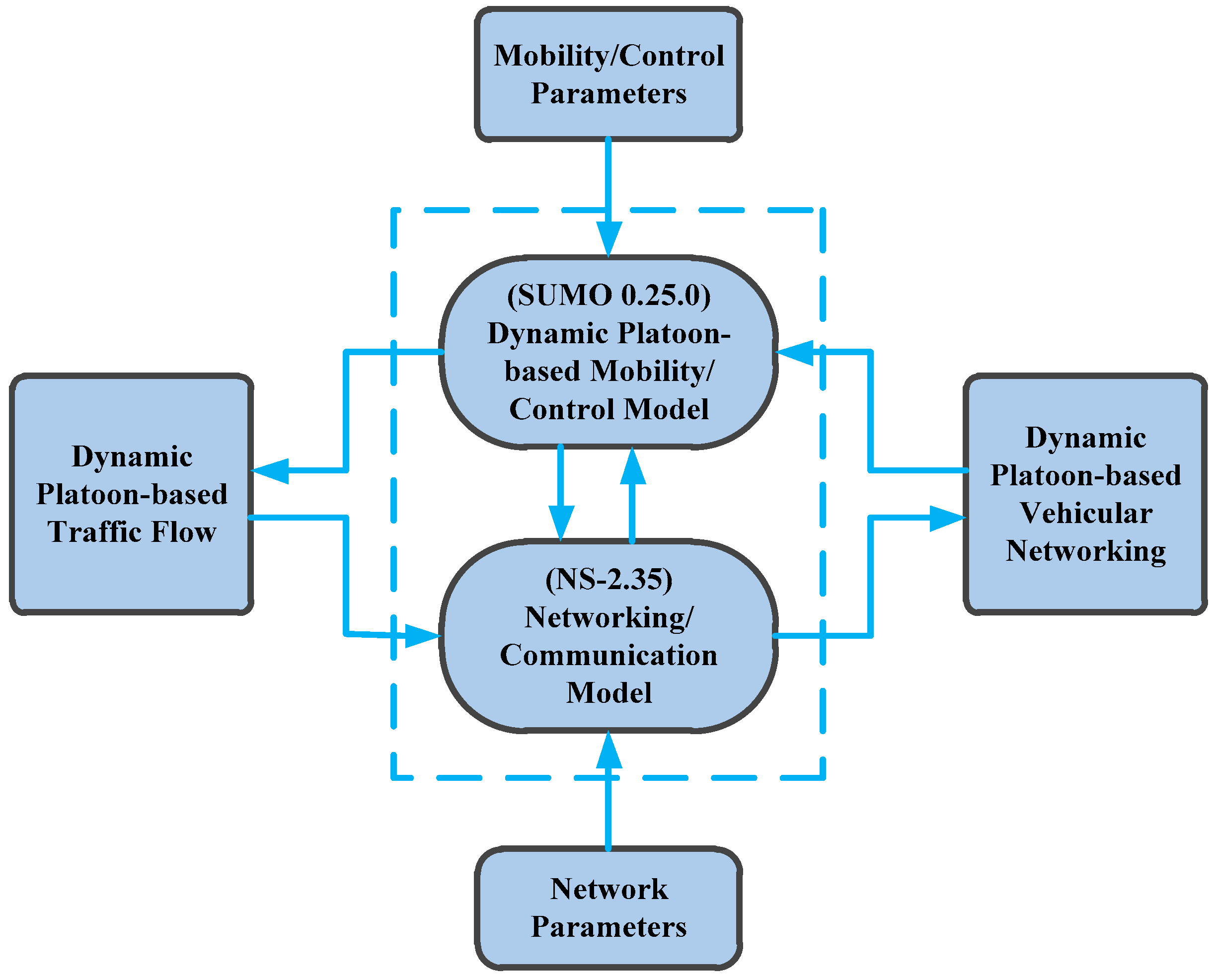
4.1. Environment Setup

We assess the platoon stability of the proposed platoon management protocol on a unidirectional two-lane highway with a speed limit of 100 km/h. The traffic is generated by the Monte Carlo simulation in Matlab R2015b [29]. We assume homogeneous vehicles and penetration of platooned-enabled vehicles. The speed of all cars follows the normal distribution. The maximal and the minimal inter-vehicle spacing are reasonably approximated by exponential distributions, while the arrival and departure of vehicles follow the Poisson distribution. We assume the DSRC range of 1000 m for every car in the platoon. The assumed parameters in experiments are summarized in

Table 2. Parameter setting for performance evaluation.

Parameter	Value
Safety headway	τ0 = 2
Transmission range	DSRCrange = 1000 m
Vehicle’s length	Car_length = 5 m, Bus_length = 10 m
Number of lanes	2
Number of vehicles	50 to 250 randomly generated
Speed limit	100 km/h
Simulation runs	50
Simulation time	500 s
Propagation model	Two ray ground

. All the simulation in this work is performed with SUMO and NS2 (NS-2.25).

4.2. Platoon Stability Analysis

The platoon stability probability with different traffic densities is illustrated in Figure 4, where four time-headways, i.e., 5 s, 10 s, 15 s, and 20 s are considered. It is shown that vehicle density has an inverse relation with platoon stability. The stability of the platoon decreases in dense traffic while increases in sparse traffic. For instance, when T₁ = 5 s, the platoon stability probability is 0.072 for 50 vehicles, while 0.0038 for 250 vehicles. When the traffic exceeds 150 vehicles, the platoon stability probabilities are very close to 0. It indicates that a long platoon is difficult to maintain through V2V communications. Similarly, the time-headways have an inverse relation with the platoon’s stability. As discussed in Section 3, the excessive control beacon messages among neighboring vehicles significantly complicate the management of the platoon. With more vehicles in a platoon, the number of hops also increases, which subsequently causes more Medium Access Control (MAC) contention over the leader vehicle.

In a platoon, the difference between any two neighboring vehicles is normally adjudicated on the basis of relative headway, space headway, and time headway. The platoon stability with relative speed is illustrated in Figure 5, where we assume fixed vehicle density (100 vehicles). It is observed that for a fixed number of vehicles, if the relative speed increases, space headway among vehicles also increases. The relative speed is directly proportional to the space headway, which degrades the platoon stability probability. Two vehicles may have a very fast speed, but their relative speed may be very small, therefore platoon stability is not affected too much.

On the other hand, the platoon stability improves in a dynamic platoon when the standard deviation of relative speed increases. The effect of speed deviation on platoon stability is presented in Figure 6. It is concluded that for a fixed number of vehicles, the increased deviation in speed improves the platoon stability probability. Additionally, increasing the standard deviation of the vehicle speed decreases the equivalent speed, which also improves platoon stability probability. While increasing the average relative speed increases the equivalent speed, which degrades platoon stability probability. In Figure 7, it is shown that time headway is inversely proportional to platoon stability probability. From the relative speed dependency to spacing policy, with a large headway-time, vehicles are moving with more considerable inter-vehicle distances than those with smaller headway-time.

4.3. Dynamic Platoon Management Analysis

To assess the proposed V2V-based dynamic platoon, a federated simulation architecture is built by integrating the traffic simulator (i.e., SUMO) and network simulator (i.e., NS2), as shown in Figure 8. Since all vehicles in the platoon are platoon-enabled, each car from lane 1 changes to lane 0 for merging and then becomes a part of a platoon. In the platoon, the vehicles remain on line 0, and upon splitting, they move to lane 1. Figure 9 shows two platoons in lane 0, including a platoon of seven vehicles with a time headway of 4 s and a platoon of five cars with a time headway of 5 s, two non-platoon vehicles, and a merging car.

We inspect dynamic platoon stability performance through the splitting and merging maneuvers in 7 and 5 vehicle platoons that are moving at the speed of 40 m/s. Figure 10 illustrates the time-headway statistics of platoon splitting and merging scenarios.

The splitting maneuver begins at simulation time $\mathcal{T}=199$ s (mark 1), and vehicles of the platoon change their time gap from T = 4 s to T = 7.458 s. As a result, platoon vehicles accelerate to maintain T = 4 s. Subsequently, the merging maneuver starts at time $\mathcal{T}=203$ s marked with 2. Platoon vehicles change their time headway setting to T = 0.7855 s. As a result, platoon vehicles decelerate to maintain T = 5 s. Figure 10 illustrates how the time gap between neighboring vehicles gradually gets wider in splitting (mark 1) and gradually closes in merging (mark 2).

5. Discussion and Challenges

5.1. Relevant Discussion

Platoon stability is vital for a long and safe journey. From the results, we conclude that the stability of a platoon is dependent on four factors: (i) vehicle density, (ii) relative speed, (iii) deviation in speed, and (iv) time headway. In a highly dense vehicular network, the stability of the platoon is disturbed, as mentioned in the results section (Figure 4). Additionally, platoon maintenance becomes challenging because of the high control message overhead. Platoon splitting seems reasonable to control the MAC contention problem in V2V communication and the severe overhead signaling.

Moreover, it is also observed that enormous headway time corresponds to lower platoon stability because vehicles drive with somewhat longer headway time. The followers’ vehicles remain behind in the platoon for a long time. In this situation, the ratio of splitting vehicles increases. Similarly, relative speed variance increases lead to a decrease in correlation [30]. If the time headway interval between neighboring vehicles is long enough, cars in the platoon travel freely. As an outcome, the time headway between adjacent vehicles should be independent, with their correlation close to zero. Based on the result, we also noticed that relative speed is also a function of platoon stability. If the relative speed of two vehicles increases, the stability of their connectivity in platoon decreases. Since the relative speed is related to the space headway, enormous relative speed leads to tremendous space headway. Subsequently, the vast space headway increases the inter-distances among the vehicles, which may lead to poor communication. As a result, the platoon will lead to splitting, aiming to reduce the space headway for better communication. Our results proposed that relative speed and time headway are appropriate platoon measurements.

The deviation in speed is also related to the stability of the platoon. The high variation in speed increases the stability of the platoon. The relationship between speed deviation and platoon stability also depends on the time headway, as shown in Figure 6. The time headway is also a function of platoon stability. Figure 7 represents that time headway negatively explains the stability of the platoon. The work done in [10,11,12,14] also uses the dynamic properties of VANETs for traffic monitoring and management. The schemes mentioned above assess the traffic density from the periodic beacon messages. If the threshold of traffic density exceeds a particular limit, congestion detects, and the methods in [10,11,12,14] re-route or suggest speed to the driver to avoid the congestion. Similarly, our proposed platoon stability scheme detects the level of stability in terms of density, speed, and time headway. In case of low stability under the above constraints, it splits or merges the platoon, as shown in Figure 10.

5.2. Challenges

Vehicle-to-everything (V2X) communications relate to information interchange between vehicles and other parts of the intelligent transportation system, including cars, pedestrians, Internet gateways, traffic lights, signals, etc. Dedicated short-range communications (DSRC) and cellular networks are the two leading technologies used in V2X communications. Many issues are linked with IEEE 802.11p [31] based V2X communication systems, including limited mobility, minimal support for advanced use cases (fully automated cars), limited coverage range, reliability, and latency [32]. The cellular-V2X (C-V2X) based on 5G significantly improves the performance of VANETs in terms of latency, reliability, throughput, packet loss, and many other metrics [33,34,35]. Thus, the adoption of C-V2X will significantly improve the connectivity of the platoon due to the advanced 5G technology. In this paper, we used the traditional IEEE 802.11p [36,37], which may lead to the issues mentioned above. The proposed model is a base for a stable platoon and can be extended to C-V2X in the future, aiming to overcome the problems related to the dis-connectivity of VANETs.

6. Conclusions and Future Direction

This paper proposed a dynamic platoon management system with three fundamental maneuvers: merging, splitting, and speed-change. The outcome of this research has presented an analytical model to find the stability probability of an inter-vehicle communications (IVC)-enabled platoon with microscopic parameters. In particular, to sum up, analytically characterized the effects of time headway on the platoon stability probability and dynamic platoon. Implementing this system in a Linux operating system, a novel integrated real-time simulation platform based on SUMO and NS2 reveals the effectiveness of a dynamic platoon management system. Through a simulation study, it can be concluded that the proposed scheme provides a method to ensure traffic flow stability in a dynamic nature vehicles platoon. The impact of transportation parameters, such as vehicle density, relative speed, deviation in relative speed, and time headway, was investigated. Assuming relative speed and density to be varying parameters, the experimental results disclose the dependence of vehicle relative speed and vehicle density on the dynamic platoon stability probability. The results obtained from the proposed model would be fruitful for a network engineer building a self-organizing dynamic platoon in intelligent transport systems. The findings provide guidance regarding the impact of notable performance measuring parameters, such as vehicle arrival rate, vehicle density, relative speed, the standard deviation of relative velocity, and time headway of vehicle on dynamic platoon stability probability. Based on the nature of V2V, we conclude that the proposed system is an inexpensive dynamic platoon management system for the intelligent transportation system. The dynamic splitting and merging feature enhance the proposed system’s applicability to a smart city. The proposed platooning mechanism is highly applicable on city roads, where frequent arrival and departure of vehicles are in practice. The community can get many benefits from this proposal. It can be either applied to the autonomous vehicles and the smart city or it can extend advanced C-V2X based technology. The proposed model will be extended to C-V2X in the future, aiming to overcome the problems related to the dis-connectivity of VANETs.