Optical Modelling of Planar and Fibre Perovskite Solar Cells
Abstract
:1. Introduction
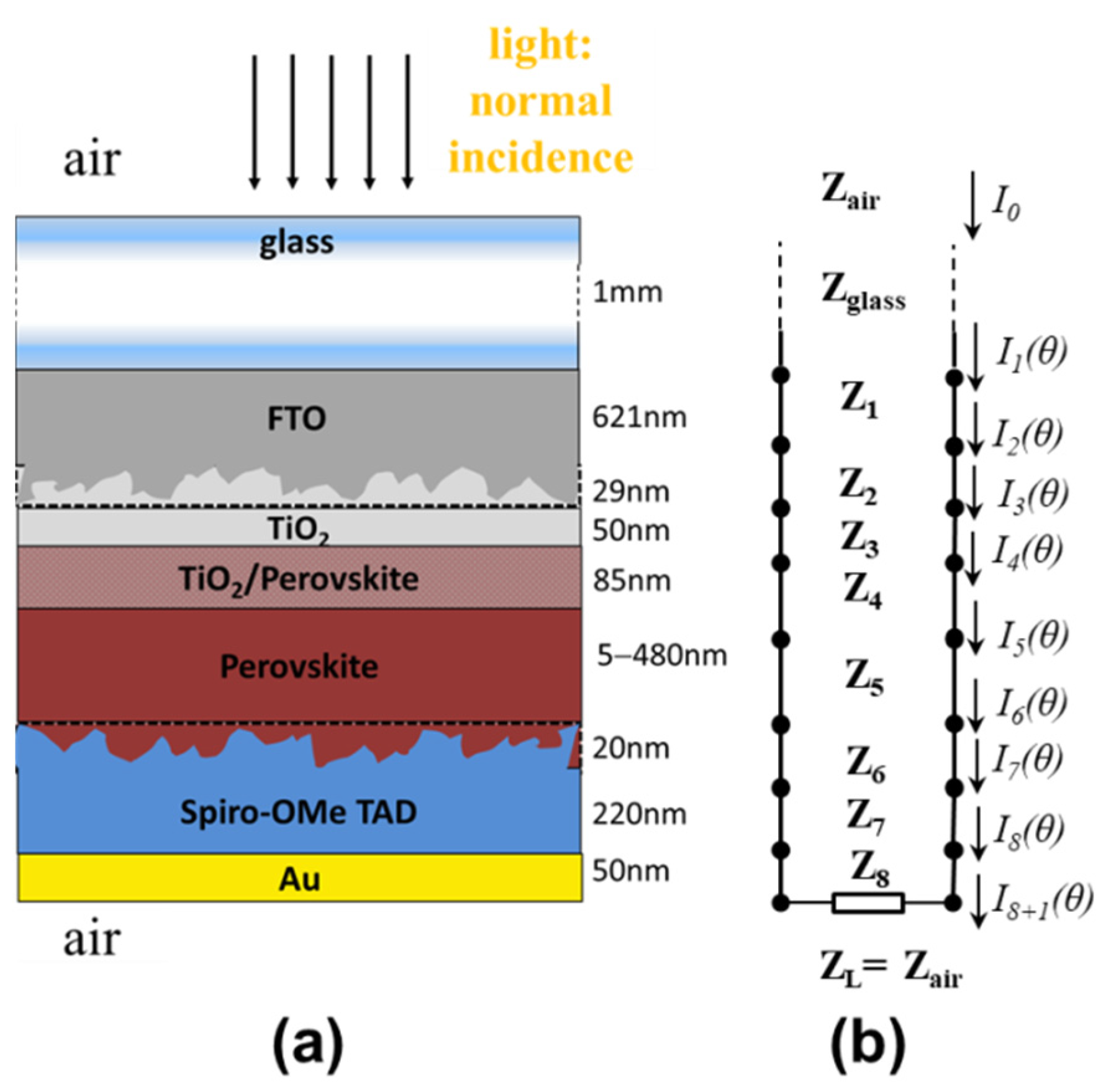
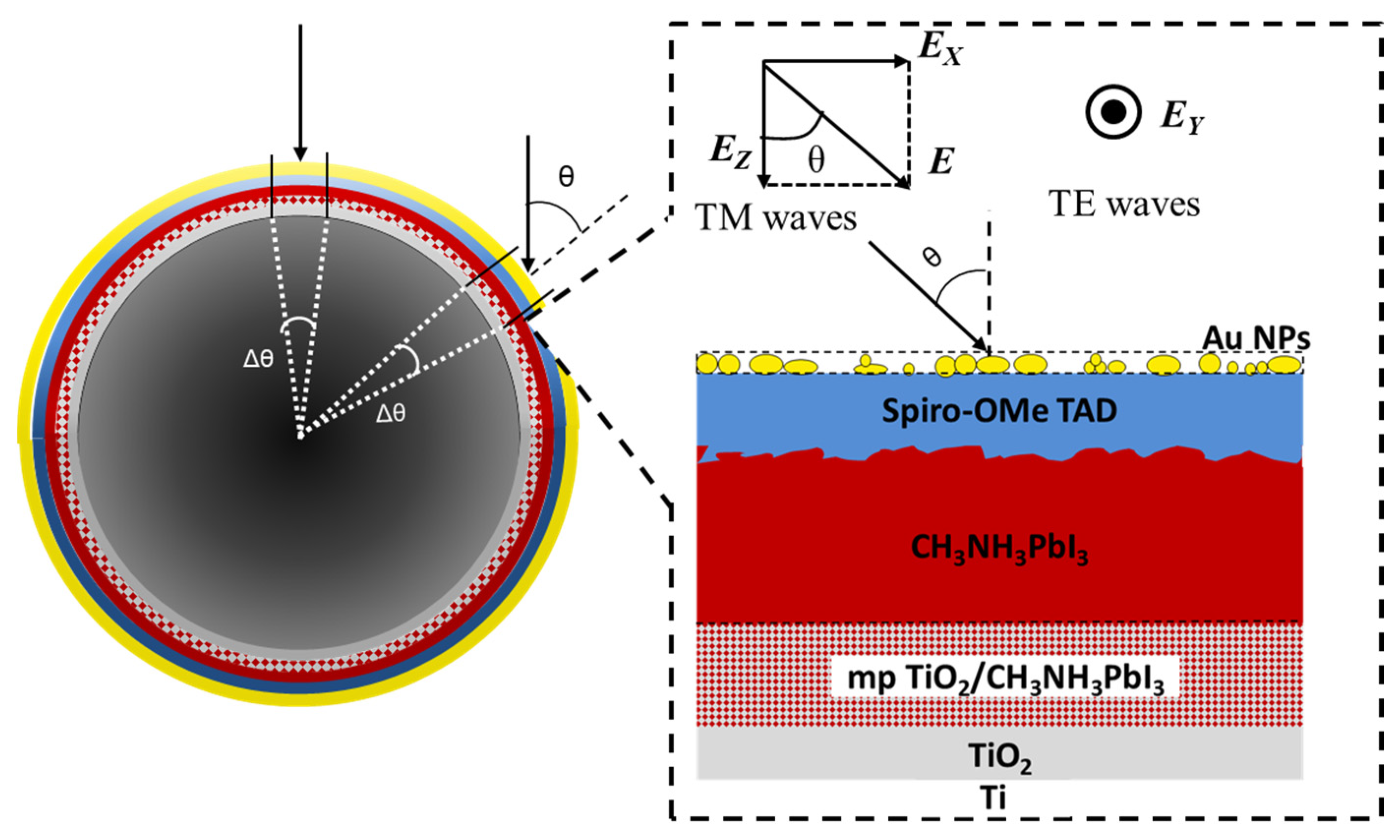
2. The Modelled PCS Structure
3. Modelling Method
4. Optical Simulation Results and Discussion
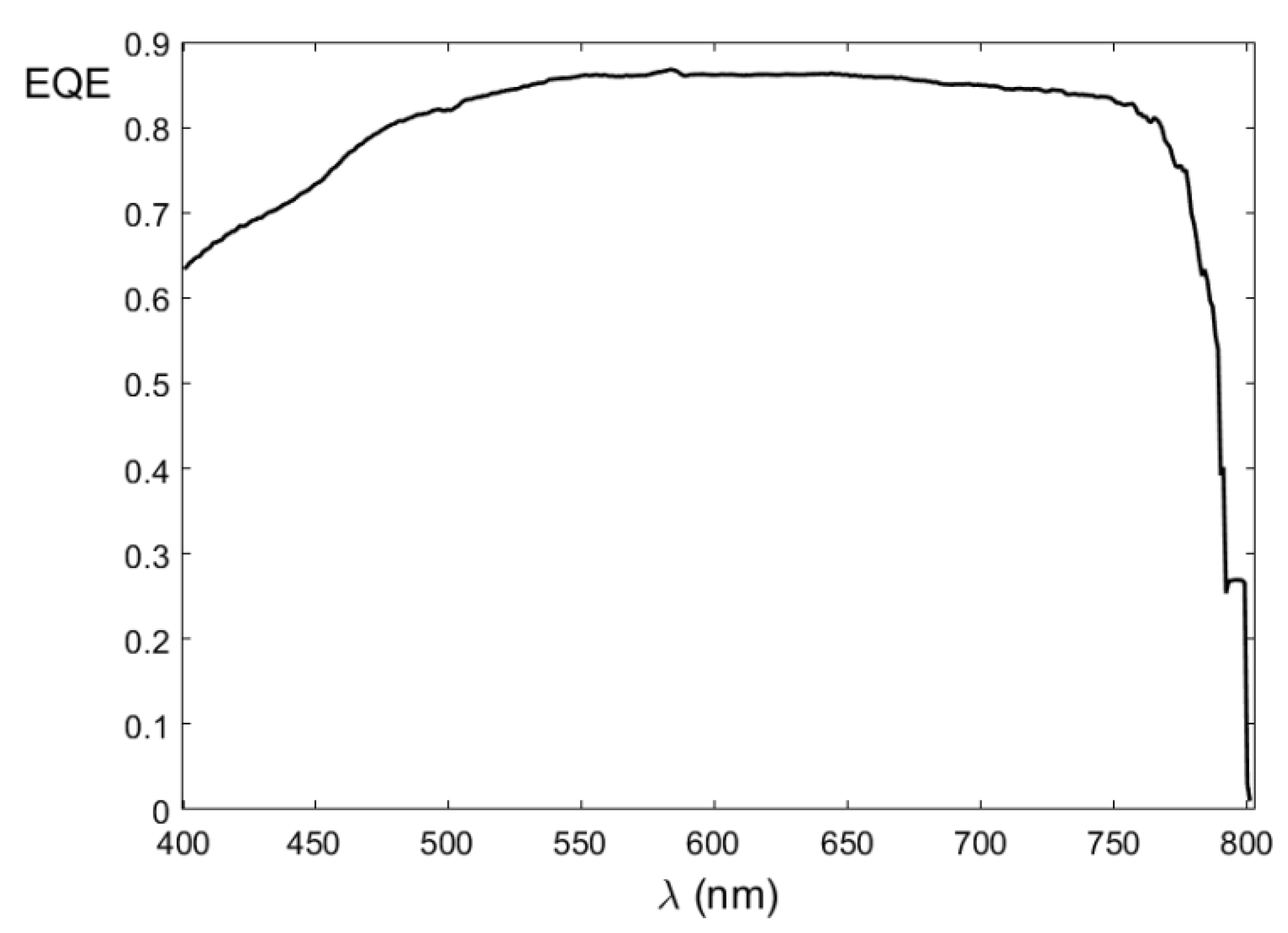
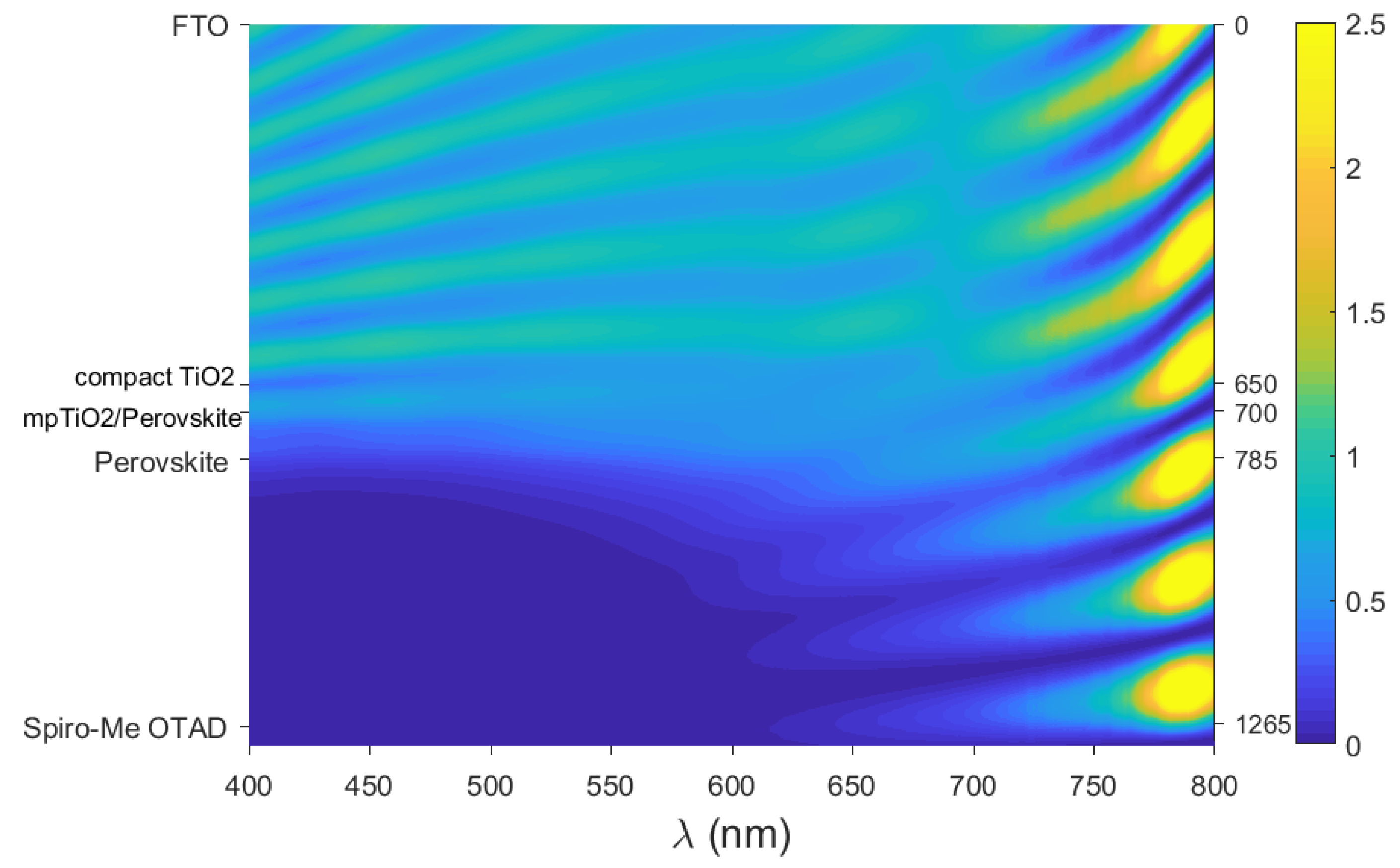
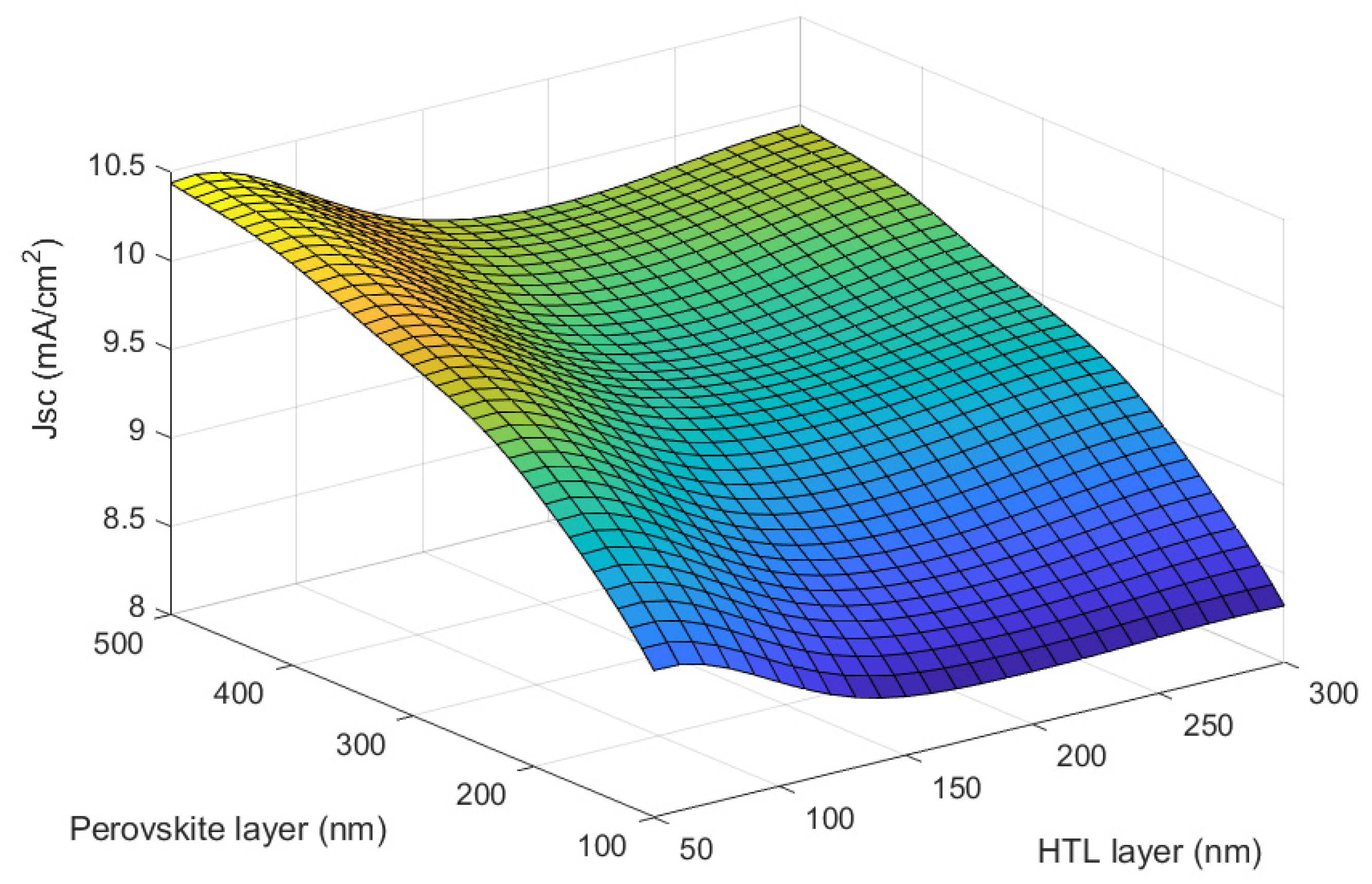
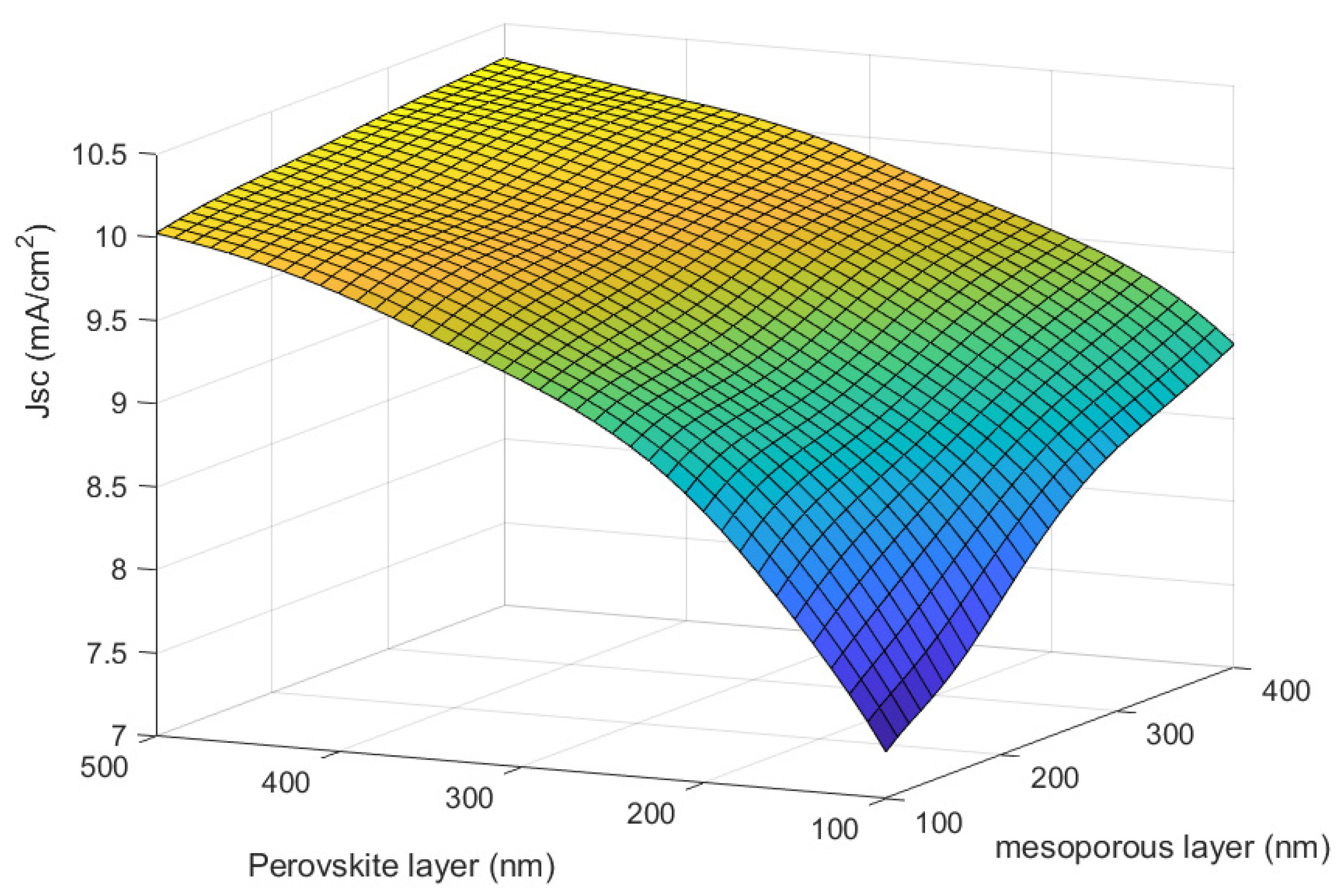
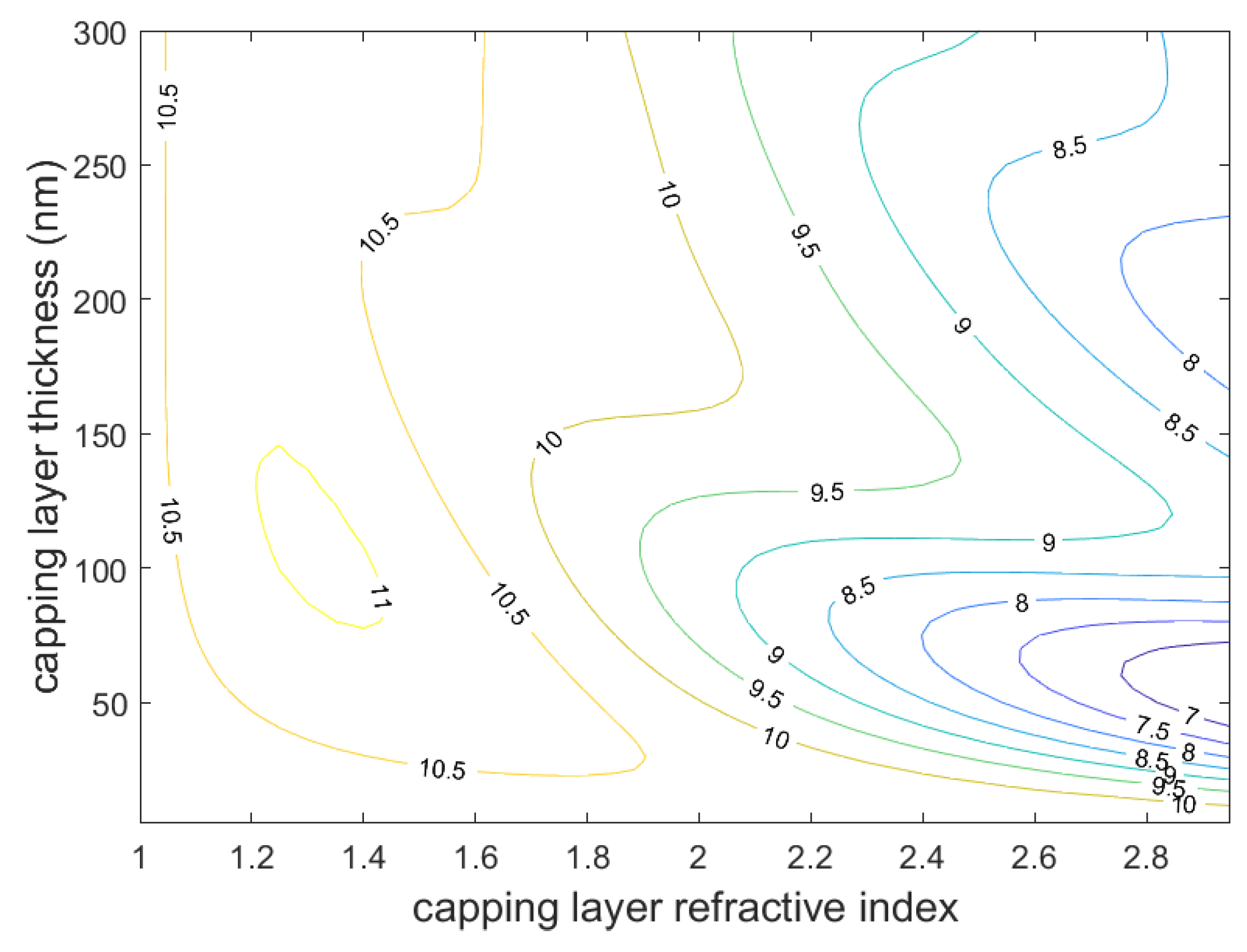
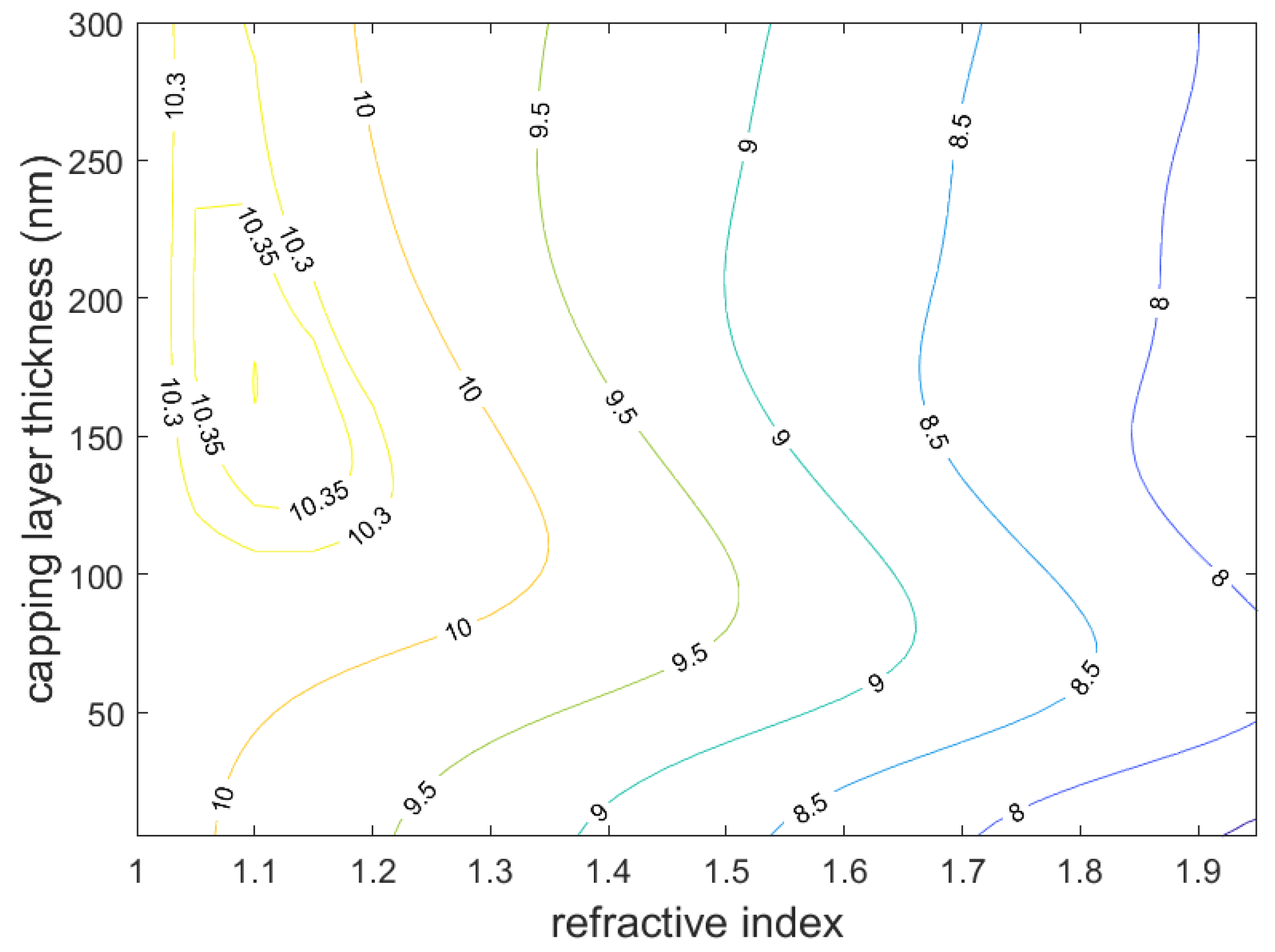
4.1. The Planar Structure
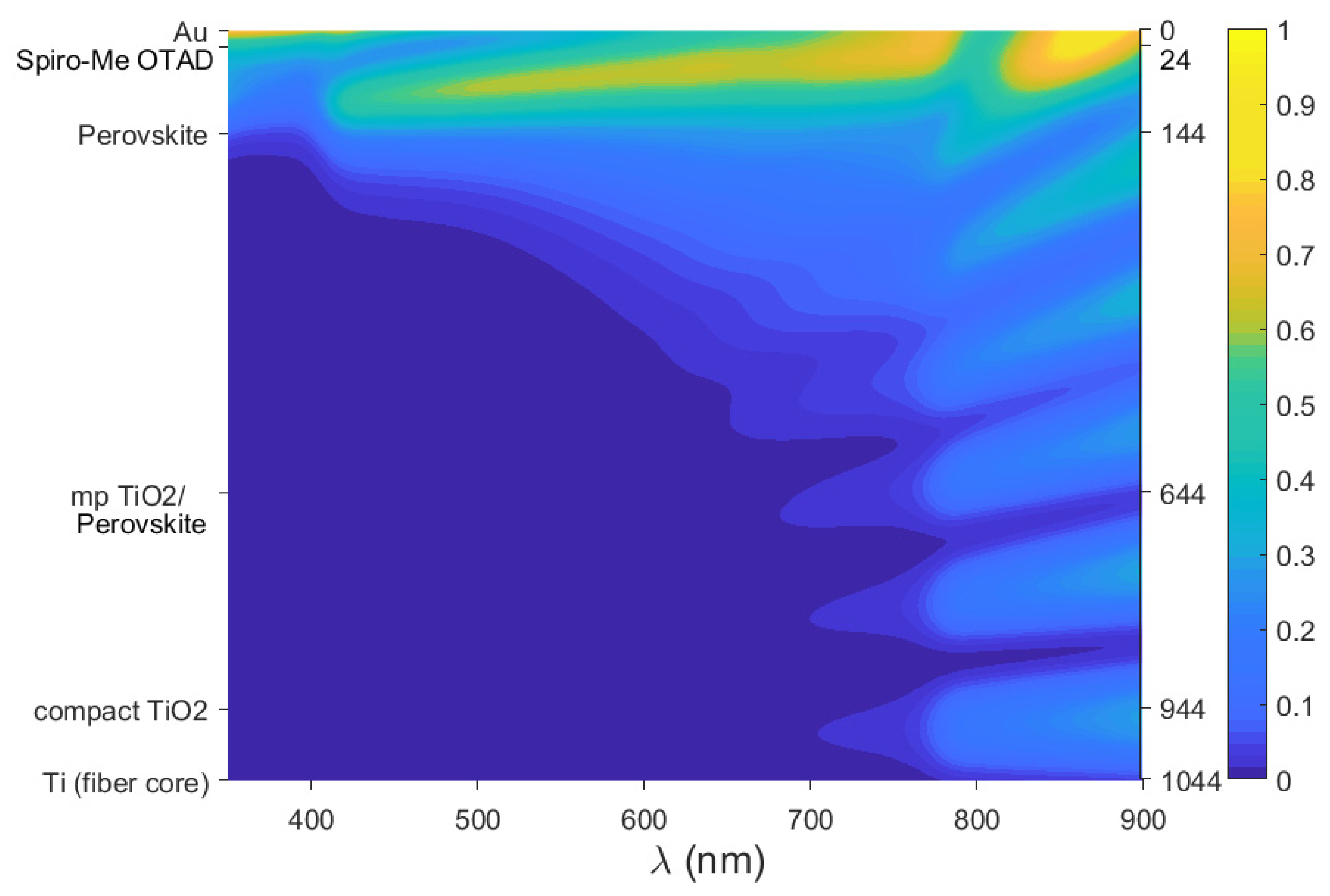
4.2. The Cylindrical Structure
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Petrova-Koch, V.; Hezel, R.; Goetzberger, A. High-Efficient Low-Cost Photovoltaics, Recent Developments, 2nd ed.; Springer Nature: Basel, Switzerland, 2020. [Google Scholar]
- Jenat, A.K.; Kulkami, A.; Miyasaka, T. Halide Perovskite Photovoltaics: Background, Status, and Future Prospects. Chem. Rev. 2019, 119, 3036–3103. [Google Scholar] [CrossRef] [PubMed]
- Saeed, M.A.; Cheng, S.; Biswas, S.; Kim, S.H.; Kwon, S.-K.; Kim, H.; Kim, Y.-H.; Shim, J.W. Remarkably high performance of organic photovoltaic devices with 3,9-bis(2-methylene-(3-(1,1-dicyanomethylene)-indanone))-5,5,11,11-tetrakis(4-hexyl meta-phenyl)-dithieno[2,3-d:2′,3′-d]-s-indaceno[1,2-b:5,6-b′]dithiophene)-ethylhexyloxy] photoactive acceptor under halogen light illumination. J. Power Sources 2022, 518, 230782. [Google Scholar]
- Saeed, M.A.; Kang, H.C.; Yoo, K.; Asiam, F.K.; Lee, J.J.; Shim, J.W. Cosensitization of metal-based dyes for high-performance dye-sensitized photovoltaics under ambient lighting conditions. Dye. Pigment. 2021, 194, 109624. [Google Scholar] [CrossRef]
- Li, F.; Wang, H.; Kufer, D.; Liang, L.; Yu, W.; Alarousu, E.; Ma, C.; Li, Y.; Liu, Z.; Liu, C.; et al. Ultrahigh Carrier Mobility Achievedin Photoresponsive Hybrid Perovskite Films via Coupling with Single-Walled Carbon Nanotubes. Adv. Mater. 2017, 29, 1602432. [Google Scholar] [CrossRef] [PubMed]
- Sichert, J.A.; Tong, Y.; Mutz, N.; Vollmer, M.; Fischer, S.; Milowska, K.Z.; Cortadella, R.C.; Nickel, B.; Cardenas-Daw, C.; Urban, A.S.; et al. Quantum size efect in organometal halide perovskitenanoplatelets. Nano Lett. 2015, 15, 6521–6527. [Google Scholar] [CrossRef]
- Balilonda, A.; Li, Q.; Tebyetekerwa, M.; Tusiime, R.; Zhang, H.; Jode, R.; Zabihi, F.; Yang, S.; Ramakrisna, S.; Zhu, M. Perovskite Solar Fibers: Current Status, Issues and Challenges. Adv. Fiber Mater. 2019, 1, 101–125. [Google Scholar] [CrossRef] [Green Version]
- Junxiang, Z.; Zhuanpei, W.; Xuelian, L.; Jie, Y.; Chenhui, S.; Yongpeng, L.; Jianli, C.; Qun, G.; Bin, W. Flexible Platinum-Free Fiber-Shaped Dye Sensitized Solar Cell with 10.28% Efficiency . ACS Appl. Energy Mat. 2019, 2, 2870–2877. [Google Scholar]
- Ball, J.M.; Stranks, S.D.; Hörantner, M.T.; Hüttner, S.; Zhang, W.; Crossland, E.J.W.; Ramirez, I.; Riede, M.; Johnston, M.B.; Richard, H.; et al. Optical properties and limiting photocurrent of thin-film perovskite solar cells. Energy Environ. Sci. 2015, 8, 602–609. [Google Scholar] [CrossRef]
- Anaya, M.; Lozano, G.; Calvo, M.E.; Zhang, W.; Johnston, M.B.; Snaith, H.J.; Míguez, H. Optical Description of Mesostructured Organic–Inorganic Halide Perovskite Solar Cells. J. Phys. Chem. Lett. 2015, 6, 48–53. [Google Scholar] [CrossRef] [Green Version]
- Wahid, S.; Islam, M.; Rahman, M.S.S.; Alam, M.K. Transfer Matrix Formalism-Based Analytical Modeling and Performance Evaluation of Perovskite Solar Cells. IEEE Trans. Electron Devices 2017, 64, 5034–5041. [Google Scholar] [CrossRef]
- Rani, S.; Kumar, A.; Ghosh, D.S. Optical Designing of Perovskite Solar Cells. IEEE J. Photovolt. 2022, 12, 595–601. [Google Scholar] [CrossRef]
- Stathopoulos, N.A.; Savaidis, S.P.; Botsialas, A.; Ioannidis, Z.C.; Georgiadou, D.G.; Vasilopoulou, M.; Pagiatakis, G. Reflection and transmission calculations in a multilayer structure with coherent, incoherent, and partially coherent interference, using the transmission line method. Appl. Opt. 2015, 54, 1492–1504. [Google Scholar] [CrossRef] [PubMed]
- Moshonas, N.; Pagiatakis, G.; Papagiannis, P.; Savaidis, S.P.; Stathopoulos, N.A. Application of the transmission line method for the study of highly nonlinear multilayer optical structures. Opt. Eng. 2014, 53, 115106. [Google Scholar] [CrossRef]
- Correa-Baena, J.P.; Anaya, M.; Lozano, G.; Tress, W.; Domanski, K.; Saliba, M.; Matsui, T.; Jacobssom, T.J.; Calvo, M.E.; Abate, A.; et al. Unbroken Perovskite: Interplay of Morphology, Electro-optical Properties, and Ionic Movement. Adv. Mater. 2016, 38, 521–527. [Google Scholar] [CrossRef]
- Refractive Index Database. Available online: https://refractiveindex.info/?shelf=main&book=Au&page=Johnson (accessed on 25 April 2022).
- Moulé, A.J.; Snaith, H.J.; Kaiser, M.; Klesper, H.; Huang, D.M.; Grätzel, M.; Meerholz, K. Optical description of solid-state dye-sensitized solar cells. I. Measurement of layer optical properties. J. Appl. Phys. 2009, 106, 073111. [Google Scholar]
- Hsienwei, H.; Dong, B.; Chen, B.; Gao, X.; Zou, D. High performance fiber-shaped perovskite solar cells based on lead acetate precursor. Sustain. Energy Fuels 2018, 2, 79–84. [Google Scholar]
- Springer, J.; Poruba, A.; Vanecek, M. Improved three-dimensional optical model for thin-film silicon solar cells. J. Appl. Phys. 2004, 96, 5329–5337. [Google Scholar] [CrossRef]
- Wang, S.; Cabreros, A.; Yang, Y.; Hall, A.S.; Valenzuela, S.; Luo, Y.; Correa-Baena, J.P.; Kim, M.C.; Fjeldberg, Ø.; Fenning, D.P.; et al. Impacts of the Hole Transport Layer Deposition Process on Buried Interfaces in Perovskite Solar Cells. Cell. Rep. Phys Sci. 2020, 1, 100103. [Google Scholar] [CrossRef]
- Moshonas, N.; Stathopoulos, N.A.; O’Connor, B.T.; Bedeloglu, A.C.; Savaidis, S.P.; Vasiliadis, S. Optical modeling of fiber organic photovoltaic structures using a transmission line method. Appl. Opt. 2017, 56, 9351–9358. [Google Scholar] [CrossRef]
- Stathopoulos, N.A.; Palilis, L.C.; Yesayan, S.R.; Savaidis, S.P.; Vasilopoulou, M.; Argitis, P. A transmission line model for the optical simulation of multilayer structures and its application for oblique illumination of an organic solar cell with anisotropic extinction coefficient. J. Appl. Phys. 2011, 110, 114506. [Google Scholar] [CrossRef]
- Moulé, A.J.; Bonekamp, J.B.; Meerholz, K. The effect of active layer thickness and composition on the performance of bulk heterojunction solar cell. J. Appl. Phys. 2006, 100, 094503. [Google Scholar] [CrossRef]
- Pettersson, L.A.A.; Roman, L.S.; Inganas, O. Modeling photocurrent action spectra of photovoltaic devices based on organic thin films. J. Appl. Phys. 1999, 86, 487–496. [Google Scholar] [CrossRef]
- Huang, D.M.; Snaith, H.J.; Grätzel, M.; Meerholz, K.; Moul, A.J. Optical description of solid-state dye-sensitized solar cells. II. Device optical modeling with implications for improving efficiency. J Appl. Phys. 2009, 106, 073112. [Google Scholar] [CrossRef]
- 2.2 mm 7–8 Ohm/SqFTO TEC 7 Coated Glass Substrates. Available online: https://www.msesupplies.com/products/fluorine-doped-tin-oxide-fto-coated-tec-7-7-ohm-sq-glass-tec7-fto-can-customize-pattern-as-required?variant=19974123652 (accessed on 27 April 2022).
- Cojocaru, L.; Uchida, S.; Jayaweera, P.V.V.; Kaneko, S.; Wang, H.; Nakazaki, J.; Kubo, T.; Segawa, H. Effect of TiO2 Surface Treatment on the Current–Voltage Hysteresis of Planar-Structure Perovskite Solar Cells Prepared on Rough and Flat Fluorine-Doped Tin Oxide Substrates. Energy Technol. 2017, 5, 1762–1766. [Google Scholar] [CrossRef] [Green Version]
- Wenger, S.; Schmid, M.; Rothenberger, G.; Gentsch, A.; Grätzel, M.; Schumacher, J.O. Coupled Optical and Electronic Modeling of Dye-Sensitized Solar Cells for Steady-State Parameter Extraction. J. Phys. Chem. C 2011, 115, 10218–10229. [Google Scholar] [CrossRef] [Green Version]
- Essalhi, Z.; Hartiti, B.; Lfakir, A.; Siadat, M.; Thevenin, P. Optical properties of TiO2 Thin films prepared by Sol Gel method. J. Mater. Environ. Sci. 2016, 7, 1328–1333. [Google Scholar]
- Evtushenko, Y.M.; Romashkin, S.V.; Trofimov, N.S.; Chekhlova, T.K. Optical properties of TiO2 thin films. Phys. Procedia 2015, 73, 100–107. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Meng, S.; Qin, L.; Lu, H. Optical properties of anatase and rutile TiO2 studied by GGA + U. Chin. Phys. B 2017, 26, 3–8. [Google Scholar]
- Abdellatif, S.; Sharifi, P.; Kirah, K.; Ghannam, R.; Khalil, A.S.G.; Erni, D.; Marlow, F. Refractive index and scattering of porous TiO2 films. Micropor. Mesopor. Mat. 2018, 264, 84–91. [Google Scholar] [CrossRef] [Green Version]
- Lansåker, P. Gold-Based Nanoparticles and Thin Films: Applications to Green Nanotechnology. Ph.D. Thesis, Uppsala Universitet, Upsala, Sweden, 2012. [Google Scholar]
- Rai, V.N.; Srivastava, A.K.; Mukherjee, C.; Deb, S.K. Surface enhanced absorption and transmission from dye coated gold nanoparticles in thin films. Appl. Opt. 2012, 51, 2606–2615. [Google Scholar] [CrossRef]
- Summonte, C.; Maccagnani, P.; Maurizi, A.; Pizzochero, G.; Bolognini, G. Simulation of the optical properties of gold nanoparticles on sodium alginate. In Proceedings of the European Optical Society Annual Meeting (EOSAM), Rome, Italy, 13–17 September 2021. [Google Scholar]
- Haiss, W.; Nguyen, T.K.; Thanh, N.T.K.; Aveyard, J.; Fernig, D.G. Determination of Size and Concentration of Gold Nanoparticles from UV–Vis Spectra. Anal. Chem. 2007, 79, 4215–4221. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Yan, K.; Peng, M.; Yu, X.; Chen, S.; Chen, B.; Dong, B.; Gao, X.; Zou, D. Fiber-shaped perovskite solar cells with 5.3% efciency. J. Mater. Chem. A 2016, 4, 3901–3906. [Google Scholar] [CrossRef]
- Kim, G.W.; Shindea, D.P.; Taiho, P. Thickness of the hole transport layer in perovskite solar cells: Performance versus reproducibility. RSC Adv. 2015, 120, 99356–99360. [Google Scholar] [CrossRef]
- Moshonas, N.; Stathopoulos, N.A. Optical modeling of thin film perovskite solar cells. In Novel Optical Materials and Applications; Optical Society of America: Washington, DC, USA, 2020; p. JTu4C-21. [Google Scholar]
- Zhang, W.; Anaya, M.; Lozano, G.; Calvo, M.E.; Johnston, M.B.; HernánMíguez, H.; Snaith, H.J. Highly Efficient Perovskite Solar Cells with Tunable Structural Color. Nano Lett. 2015, 15, 1698–1702. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Katagiri, K.; Yamazaki, S.; Inumaru, K.; Koumoto, K. Anti-reflective coatings prepared via layer-by-layerassembly of mesoporous silica nanoparticles andpolyelectrolytes. Polym. J. 2015, 47, 190–194. [Google Scholar] [CrossRef]
- Deka, S.; Mohammed, W. Enhancement of light absorption using Nanoparticles Embedded Double layer Anti-Reflection Coating. Eng. J. 2020, 24, 53–63. [Google Scholar] [CrossRef]
- Martínez-Hernández, M.E.; Goicoechea, J.; Rivero, P.J.; Arregui, F.J. In Situ Synthesis of Gold Nanoparticles in Layer-by-Layer Polymeric Coatings for the Fabrication of Optical Fiber Sensors. Polymers 2022, 14, 776. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, H.; Wang, L.; Yang, K.; Cang, L.; Liu, X.; Wei Huang, W. Highly Stable and Efficient Mesoporous and Hollow Silica Antireflection Coatings for Perovskite Solar Cells. ACS Appl. Energy Mater. 2020, 3, 4484–4491. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moshonas, N.; Stathopoulos, N.A.; Pagiatakis, G. Optical Modelling of Planar and Fibre Perovskite Solar Cells. Electronics 2022, 11, 2041. https://doi.org/10.3390/electronics11132041
Moshonas N, Stathopoulos NA, Pagiatakis G. Optical Modelling of Planar and Fibre Perovskite Solar Cells. Electronics. 2022; 11(13):2041. https://doi.org/10.3390/electronics11132041
Chicago/Turabian StyleMoshonas, Nikolaos, Nikolaos A. Stathopoulos, and Gerasimos Pagiatakis. 2022. "Optical Modelling of Planar and Fibre Perovskite Solar Cells" Electronics 11, no. 13: 2041. https://doi.org/10.3390/electronics11132041
APA StyleMoshonas, N., Stathopoulos, N. A., & Pagiatakis, G. (2022). Optical Modelling of Planar and Fibre Perovskite Solar Cells. Electronics, 11(13), 2041. https://doi.org/10.3390/electronics11132041





