Trigger-Based K-Band Microwave Ranging System Thermal Control with Model-Free Learning Process
Abstract
:1. Introduction
- Feasible triggered thermal system control design with obvious communication burden reduction;
- No original thermodynamic information required when faced with disturbed system model uncertainty;
- Suitable for real autonomous management of space platforms with long-term mission life;
- Thermal control strategies can be selected from nominal control, triggered control, and model-free learning process, according different orbiting period.
2. Thermal System Design for Precise Ranging System
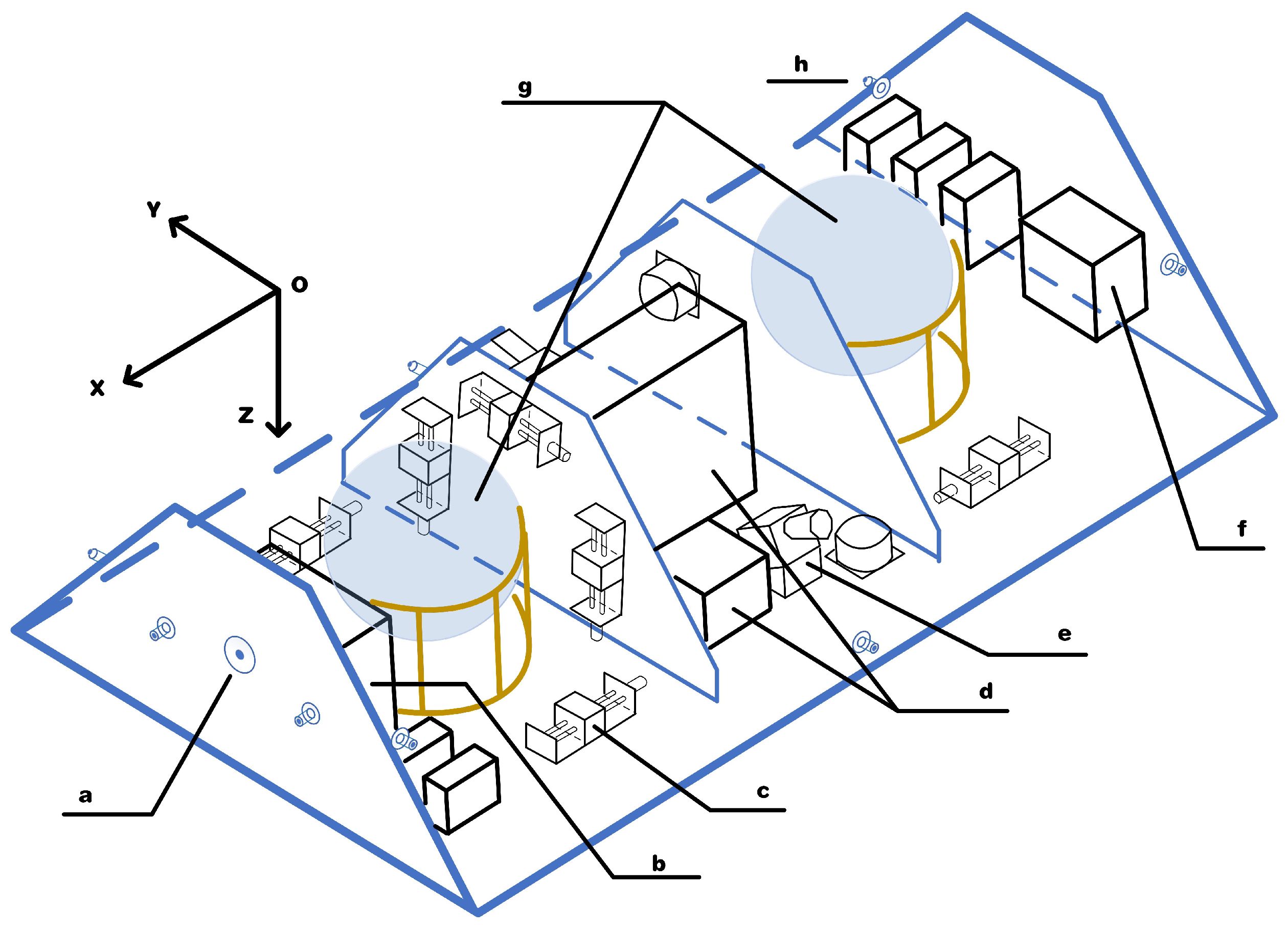
2.1. Thermal Structure of Deployed Satellite
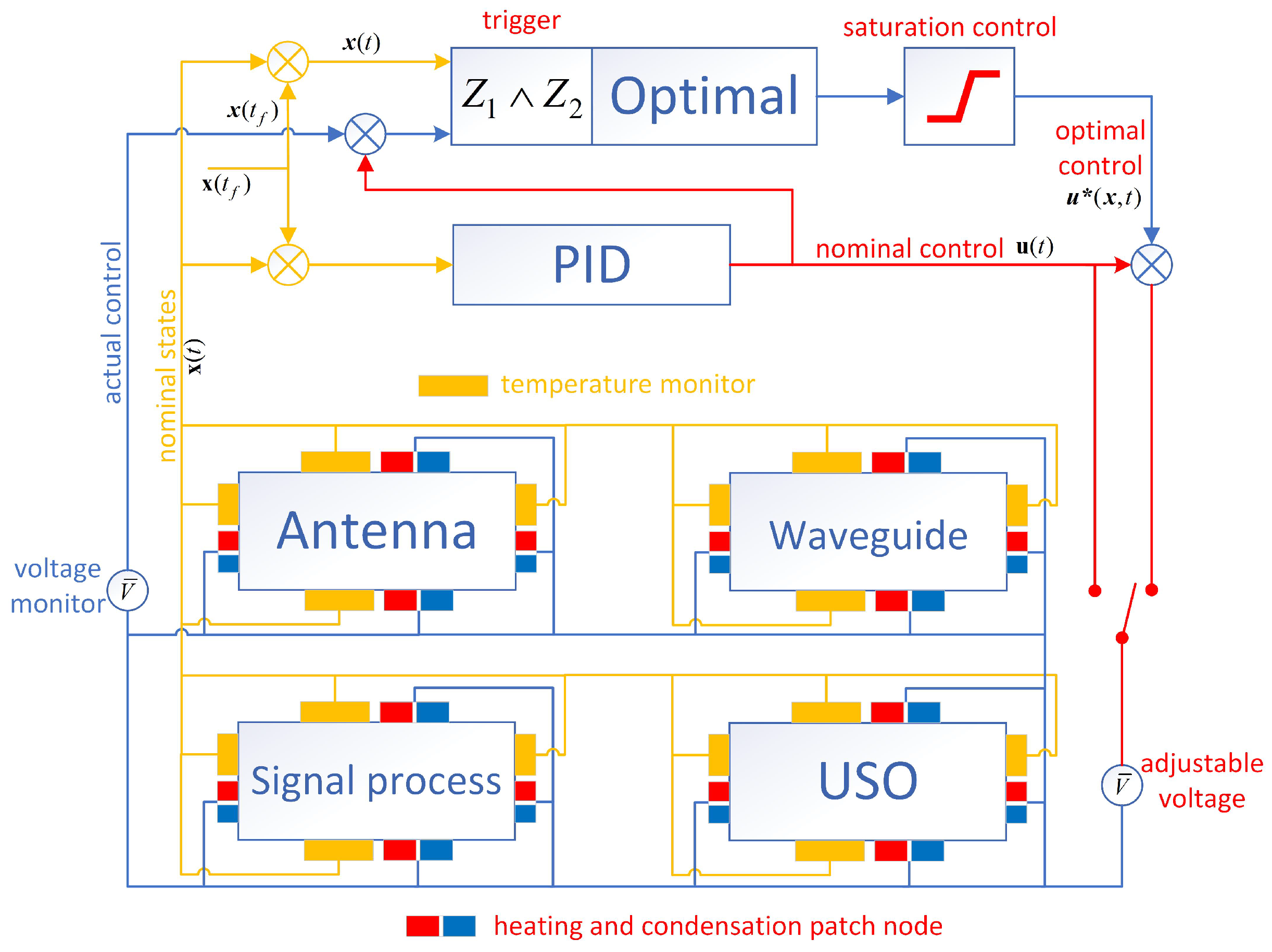
2.2. Payload Thermal Dynamic Modeling and Nominal PID Control
2.3. Trigger-Based Precise Optimal Thermal Control with Saturation Constraint
2.4. Trigger Condition Analysis
2.5. Stability Analysis of Trigger Control
3. Model-Free Reinforcement Learning Formulation
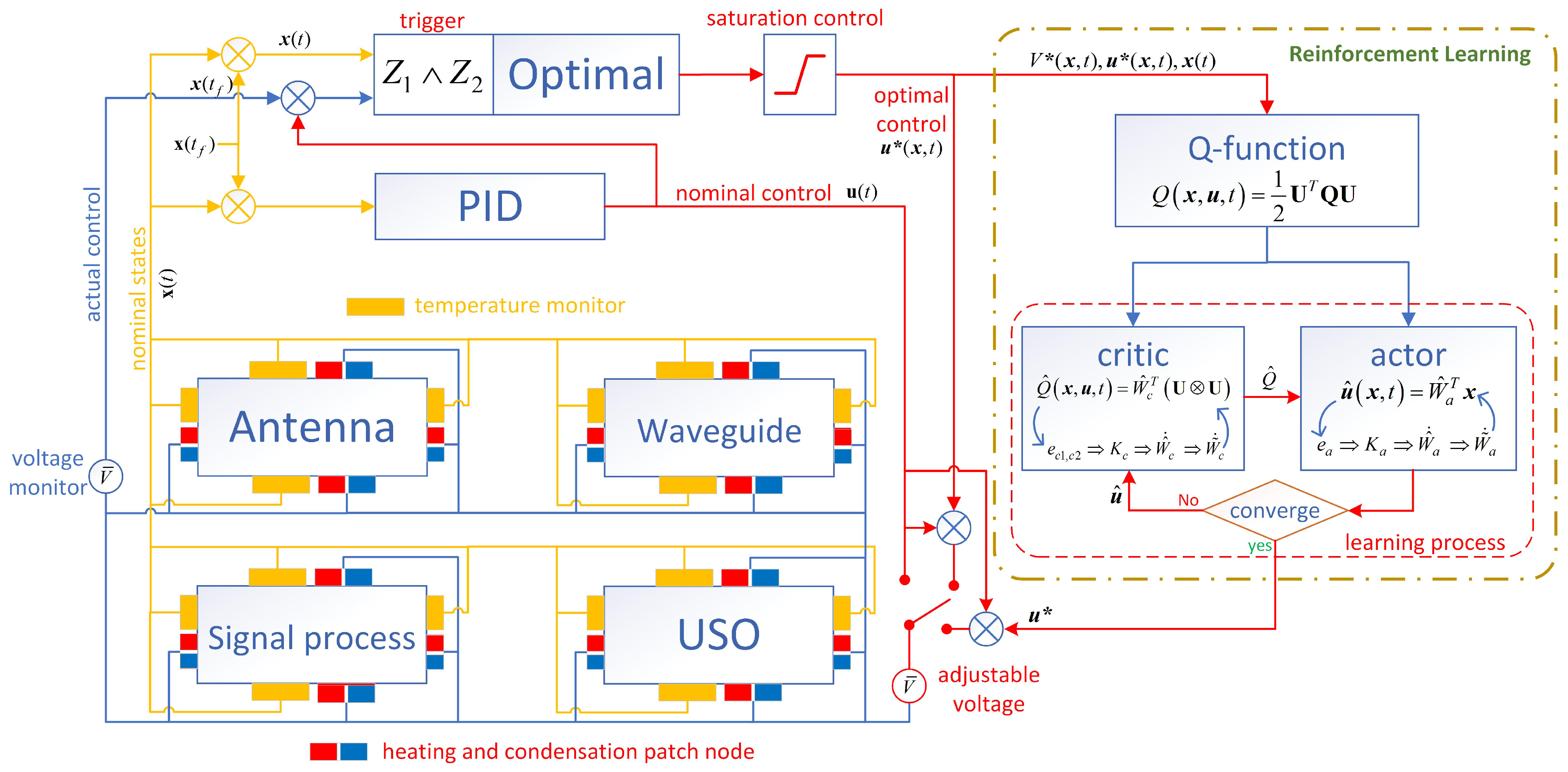
3.1. Reinforcement Learning Structure
3.2. Reinforcement Learning Structure
3.3. Critic/Actor Structure
3.4. Learning Process
4. Experiment Test and Simulation
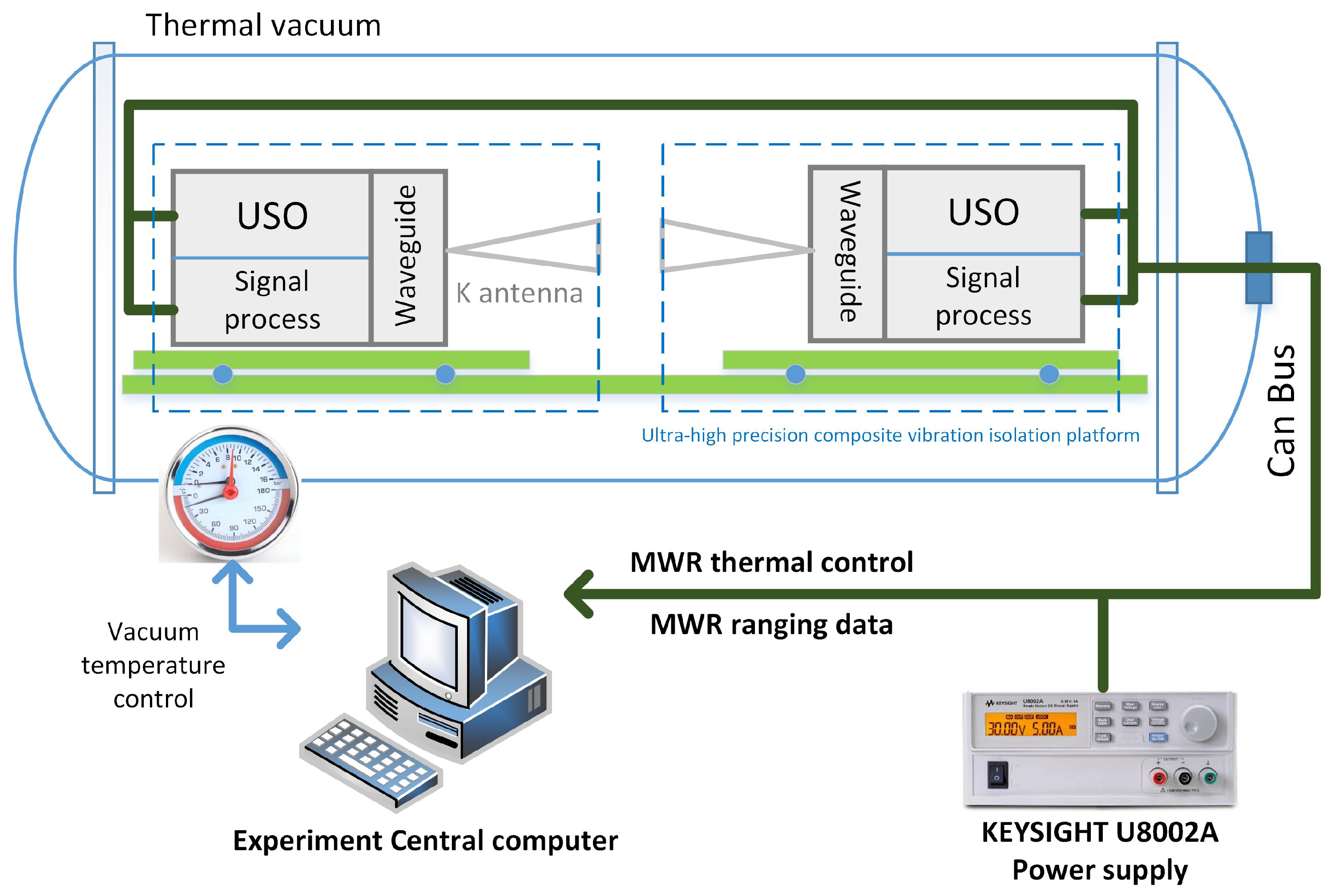
4.1. Laboratory Experiment Environment
4.2. Performance of Passive and Nominal Thermal Control
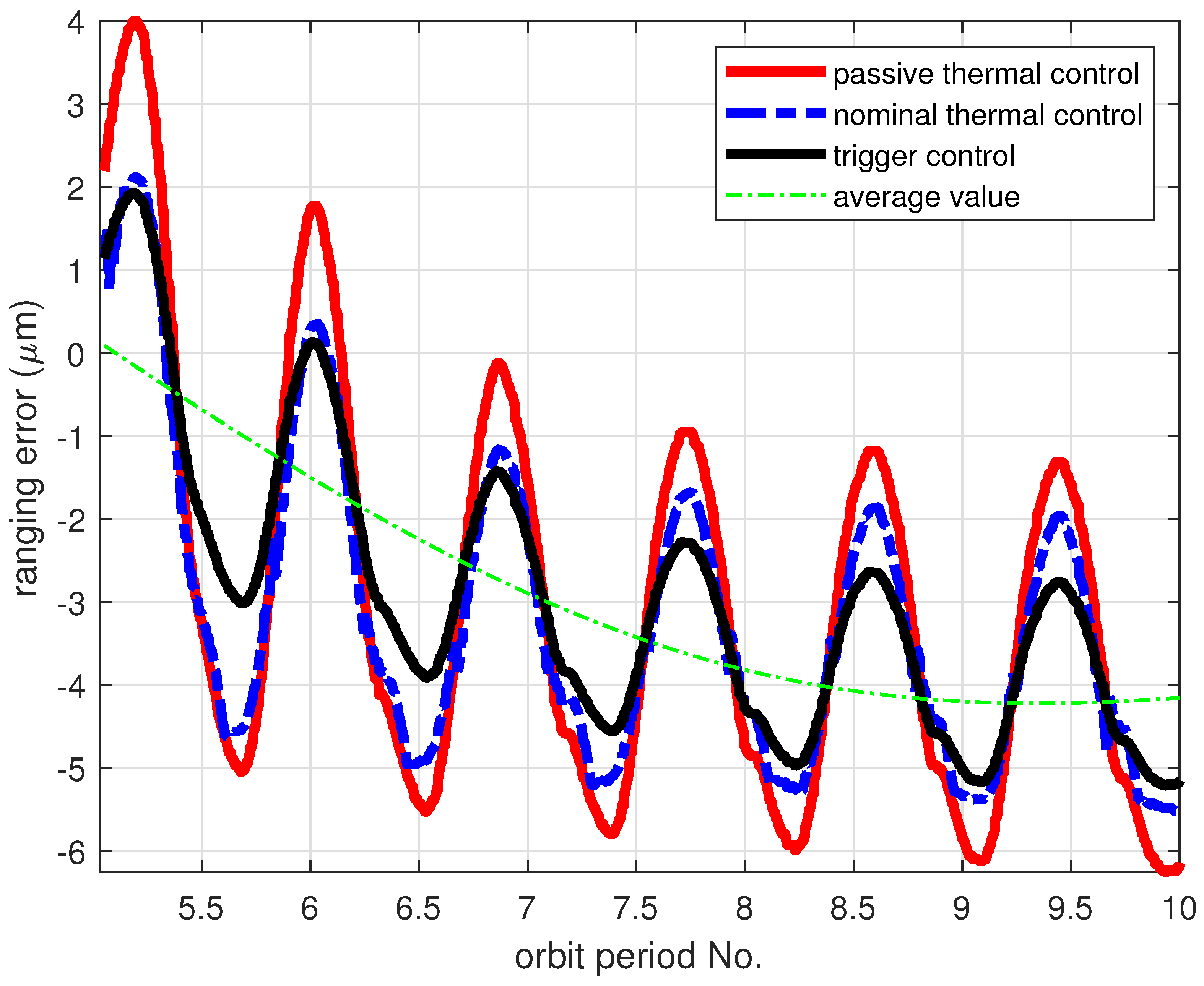
4.3. Performance of Trigger Control
4.4. Performance of Learning Process
4.5. Time-Delay Performance of MWR Ranging System
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| RMS | Root mean square |
| MWR | Microwave ranging |
| ETC | Event-triggered control |
| STC | Self-triggered control |
| LMI | Linear matrix inequality |
| ADP | Adaptive dynamic programming |
| ApDP | Approximate dynamic programming |
| RL | Reinforcement learning |
| USO | Ultra-stable crystal oscillator |
| CFRP | Carbon fiber reinforced plastic |
| MLI | Multi-layer insulation |
| A/D converter | Analog-to-digital converter |
| FPGA | Field Programmable Gate Array |
| DSP | Digital Signal Processing |
| MEMS | Micro-Electro-Mechanical System |
| PWM | Pulse-width modulating |
| PID | Proportion Integration Differentiation |
| HJB function | Hamilton–Jacobi–Bellman function |
| PE | Persistently exciting |
| RAAN | Right Ascension of Ascending Node |
| TDC | Time-delay/Celsius degree |
Symbols
| saturation control | |
| positive constants for triggering error | |
| the triggered time of event k | |
| signal transmitting period since | |
| function of | |
| trigger period of | |
| function |
| estimation and error of critic approximate weight | |
| estimation and error of actor approximate weight | |
| critic approximation error | |
| actor approximation error | |
| critic/actor approximation error function | |
| user defined function of generalized states | |
| constant gain of convergence rate | |
| constant of exponential converges function |
Appendix A
References
- Landerer, F.W.; Flechtner, F.M.; Save, H.; Webb, F.H.; Bandikova, T.; Bertiger, W.I.; Bettadpur, S.V.; Byun, S.H.; Dahle, C.; Dobslaw, H.; et al. Extending the global mass change data record: GRACE Follow-On instrument and science data performance. Geophys. Res. Lett. 2020, 47, e2020GL088306. [Google Scholar] [CrossRef]
- Bryant, R.; Moran, M.S.; McElroy, S.A.; Holifield, C.; Thome, K.J.; Miura, T.; Biggar, S.F. Data continuity of Earth observing 1 (EO-1) Advanced Land I satellite image (ALI) and Landsat TM and ETM+. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1204–1214. [Google Scholar] [CrossRef]
- Totani, T.; Ogawa, H.; Inoue, R.; Das, T.K.; Wakita, M.; Nagata, H. Thermal design procedure for micro- and nanosatellite pointing to earth. J. Thermophys. Heat Transf. 2014, 28, 524–533. [Google Scholar] [CrossRef]
- Reiss, P.; Hager, P.; Bewick, C. New methodologies for the thermal modeling of CubeSats. In Proceedings of the 26th Annual AIAA/USU Conference on Small Satellites, Logan, UT, USA, 13–16 August 2012; pp. 1–12. [Google Scholar]
- Jiang, X.; Han, Q.L.; Liu, S.; Xue, A. A New H∞ Stabilization Criterion for Networked Control Systems. IEEE Trans. Autom. Control 2008, 53, 1025–1032. [Google Scholar] [CrossRef]
- Astrom, K.J.; Bernhardsson, B.M. Comparison of Riemann and Lebesgue sampling for first order stochastic systems. In Proceedings of the 41st IEEE Conference on Decision and Control, Las Vegas, NV, USA, 10–13 December 2002; Volume 2, pp. 2011–2016. [Google Scholar]
- Pan, H.; Chang, X.; Zhang, D. Event-triggered adaptive control for uncertain constrained nonlinear systems with its application. IEEE Trans. Ind. Inform. 2019, 16, 3818–3827. [Google Scholar] [CrossRef]
- Liu, W.; Huang, J. Event-triggered global robust output regulation for a class of nonlinear systems. IEEE Trans. Autom. Control 2017, 62, 5923–5930. [Google Scholar] [CrossRef]
- Xing, L.; Wen, C.; Liu, Z.; Su, H.; Cai, J. Event-Triggered Output Feedback Control A Cl. Uncertain Nonlinear Systems. IEEE Trans. Autom. Control 2018, 64, 290–297. [Google Scholar] [CrossRef]
- Wang, R.; Si, C.; Ma, H.; Hao, C. Global event-triggered inner-outer loop stabilization of under-actuated surface vessels. Ocean Eng. 2020, 218, 108228. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, S.; Liu, J.F. Economic model predictive control with triggered evaluations: State and output feedback. J. Process Control 2014, 24, 1197–1206. [Google Scholar] [CrossRef]
- Shahid, M.I.; Ling, Q. Event-triggered distributed dynamic output-feedback dissipative control of multi-weighted and multi-delayed large-scale systems. ISA Trans. 2020, 96, 116–131. [Google Scholar] [CrossRef]
- Azimi, M.M.; Afzalian, A.A.; Ghaderi, R. Decentralized stabilization of a class of large scale networked control systems based on modified event-triggered scheme. Int. J. Dyn. Control 2021, 9, 149–159. [Google Scholar] [CrossRef]
- Li, F.; Cao, X.; Zhou, C.; Yang, C. Event-triggered asynchronous sliding mode control of CSTR based on Markov Model. J. Frankl. Inst. 2021, 358, 4688–4704. [Google Scholar] [CrossRef]
- Wang, W.; Tong, S. Distributed adaptive fuzzy event-triggered containment control of nonlinear strict-feedback systems. IEEE Trans. Cybern. 2019, 50, 3973–3983. [Google Scholar] [CrossRef] [PubMed]
- Su, X.; Liu, Z.; Lai, G.; Zhang, Y.; Chen, C.P. Event-triggered adaptive fuzzy control for uncertain strict-feedback nonlinear systems with guaranteed transient performance. IEEE Trans. Fuzzy Syst. 2019, 27, 2327–2337. [Google Scholar] [CrossRef]
- Abhinav, S.; Rajiv, K.M. Control of a nonlinear continuous stirred tank reactor via event triggered sliding modes. Chem. Eng. Sci. 2018, 187, 52–59. [Google Scholar]
- Tang, X.T.; Deng, L. Multi-step output feedback predictive control for uncertain discrete-time T-S fuzzy system via event-triggered scheme. Automatica 2019, 107, 362–370. [Google Scholar] [CrossRef]
- Li, S.; Ahn, C.K.; Guo, J.; Xiang, Z. Neural-Network Approximation-Based Adaptive Periodic Event-Triggered Output-Feedback Control of Switched Nonlinear Systems. IEEE Trans. Cybern. 2020, 51, 4011–4020. [Google Scholar] [CrossRef]
- Liu, D.; Yang, G.H. Neural Network-Based Event-Triggered MFAC for Nonlinear Discrete-Time Processes. Neurocomputing 2018, 272, 356–364. [Google Scholar] [CrossRef]
- Xing, X.; Liu, J. Event-triggered neural network control for a class of uncertain nonlinear systems with input quantization. Neurocomputing 2021, 440, 240–250. [Google Scholar] [CrossRef]
- Yang, X.; Wei, Q.L. Adaptive Critic Designs for Optimal Event-Driven Control of a CSTR System. IEEE Trans. Ind. Inform. 2020, 17, 484–493. [Google Scholar] [CrossRef]
- Yang, X.; He, H. Event-Driven H∞-Constrained Control Using Adaptive Critic Learning. IEEE Trans. Cybern. 2020, 51, 4860–4872. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Zhu, Y.; Dong, N.; Wei, Q.L. Decentralized Event-Driven Constrained Control Using Adaptive Critic Designs. IEEE Trans. Neural Netw. Learn. Syst. 2021; 1–15, Early Access. [Google Scholar] [CrossRef] [PubMed]
- Seuret, A.; Prieur, C.; Tarbouriech, S.; Zaccarian, L. Event-triggered control with LQ optimality guarantees for saturated linear systems. IFAC Proc. Vol. 2013, 46, 341–346. [Google Scholar] [CrossRef] [Green Version]
- Tarbouriech, S.; Garcia, G.; da Silva, J.M.G., Jr.; Queinnec, I. Stability and Stabilization of Linear Systems with Saturating Actuators; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Wu, W.; Reimann, S.; Liu, S. Event-triggered control for linear systems subject to actuator saturation. IFAC Proc. Vol. 2014, 47, 9492–9497. [Google Scholar] [CrossRef] [Green Version]
- Åarzén, K.E. A simple event-based PID controller. IFAC Proc. Vol. 1999, 32, 8687–8692. [Google Scholar] [CrossRef]
- Heemels, W.P.; Gorter, R.J.; Van Zijl, A.; Van den Bosch, P.P.; Weiland, S.; Hendrix, W.H.; Vonder, M.R. Asynchronous measurement and control: A case study on motor synchronization. Control Eng. Pract. 1999, 7, 1467–1482. [Google Scholar] [CrossRef]
- Velasco, M.; Fuertes, J.; Marti, P. The self triggered task model for real-time control systems. In Proceedings of the Work-in-Progress Session of the 24th IEEE Real-Time Systems Symposium (RTSS03), Cancun, Mexico, 3–5 December 2003; Volume 384, pp. 67–70. [Google Scholar]
- Heemels, W.; Johansson, K.H.; Tabuada, P. An introduction to event-triggered and self-triggered control. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 3270–3285. [Google Scholar]
- Yi, X.; Liu, K.; Dimarogonas, D.V.; Johansson, K.H. Dynamic event-triggered and self-triggered control for multi-agent systems. IEEE Trans. Autom. Control 2018, 64, 3300–3307. [Google Scholar] [CrossRef]
- Wang, X.; Lemmon, M.D. Self-Triggered Feedback Control Systems with Finite-Gain L2 Stability. IEEE Trans. Autom. Control 2009, 54, 452–467. [Google Scholar] [CrossRef]
- Almeida, J.; Silvestre, C.; Pascoal, A.M. Self-triggered state-feedback control of linear plants under bounded disturbances. Int. J. Robust Nonlinear Control 2015, 25, 1230–1246. [Google Scholar] [CrossRef]
- Peng, C.; Han, Q.L. On designing a novel self-triggered sampling scheme for networked control systems with data losses and communication delays. IEEE Trans. Ind. Electron. 2015, 63, 1239–1248. [Google Scholar] [CrossRef]
- Buşoniu, L.; de Bruin, T.; Tolić, D.; Kober, J.; Palunko, I. Reinforcement learning for control: Performance, stability, and deep approximators. Annu. Rev. Control 2018, 46, 8–28. [Google Scholar] [CrossRef]
- Vamvoudakis, K.G. Q-learning for continuous-time linear systems: A model-free infinite horizon optimal control approach. Syst. Control Lett. 2017, 100, 14–20. [Google Scholar] [CrossRef]
- Fortunato, M.; Azar, M.G.; Piot, B.; Menick, J.; Osband, I.; Graves, A.; Mnih, V.; Munos, R.; Hassabis, D.; Pietquin, O.; et al. Noisy networks for exploration. arXiv 2017, arXiv:1706.10295. [Google Scholar]
- Asadi, K.; Littman, M.L. An alternative softmax operator for reinforcement learning. In Proceedings of the International Conference on Machine Learning, Sydney, NSW, Australia, 6–11 August 2017; PMLR 2017. pp. 243–252. [Google Scholar]
- Engel, Y.; Mannor, S.; Meir, R. Reinforcement learning with Gaussian processes. In Proceedings of the 22nd International Conference on Machine Learning, Bonn, Germany, 7–11 August 2005; pp. 201–208. [Google Scholar]
- Sutton, R.S.; McAllester, D.; Singh, S.; Mansour, Y. Policy gradient methods for reinforcement learning with function approximation. Adv. Neural Inf. Process. Syst. 2000, 12, 1057–1063. [Google Scholar]
- Jha, S.K.; Roy, S.B.; Bhasin, S. Direct adaptive optimal control for uncertain continuous-time LTI systems without persistence of excitation. IEEE Trans. Circuits Syst. II Express Briefs 2018, 65, 1993–1997. [Google Scholar] [CrossRef]
- Tu, S.; Recht, B. Least-squares temporal difference learning for the linear quadratic regulator. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; PMLR 2018. pp. 5005–5014. [Google Scholar]
- Umenberger, J.; Schön, T.B. Learning convex bounds for linear quadratic control policy synthesis. Adv. Neural Inf. Process. Syst. 2018, 31. Available online: https://proceedings.neurips.cc/paper/2018/hash/f610a13de080fb8df6cf972fc01ad93f-Abstract.html (accessed on 3 July 2022).
- Lee, D.; Hu, J. Primal-dual Q-learning framework for LQR design. IEEE Trans. Autom. Control 2018, 64, 3756–3763. [Google Scholar] [CrossRef]
- Konda, V.R.; Tsitsiklis, J.N. On actor-critic algorithms. SIAM J. Control Optim. 2003, 42, 1143–1166. [Google Scholar] [CrossRef]
- Lee, D.; Lin, C.J.; Lai, C.W.; Huang, T. Smart-valve-assisted model-free predictive control system for chiller plants. Energy Build. 2021, 234, 110708. [Google Scholar] [CrossRef]
- Qiu, S.; Li, Z.; Fan, D.; He, R.; Dai, X.; Li, Z. Chilled water temperature resetting using model-free reinforcement learning: Engineering application. Energy Build. 2022, 255, 111694. [Google Scholar] [CrossRef]
- Wang, X.; Gong, D.; Jiang, Y.; Mo, Q.; Kang, Z.; Shen, Q.; Wu, S.; Wang, D. A Submillimeter-Level Relative Navigation Technology for Spacecraft Formation Flying in Highly Elliptical Orbit. Sensors 2020, 20, 6524. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wu, S.; Gong, D.; Shen, Q.; Wang, D.; Damaren, C. Evaluation of Precise Microwave Ranging Technology for Low Earth Orbit Formation Missions with Beidou Time-Synchronize Receiver. Sensors 2021, 21, 4883. [Google Scholar] [CrossRef]
- Min, G. Satellite Thermal Control Technology; China Astronautics Press: Beijing, China, 1991; Volume 249. (In Chinese) [Google Scholar]
- Choi, M. Thermal assessment of swift instrument module thermal control system and mini heater controllers after 5+ Years in Flight. In Proceedings of the 40th International Conference on Environmental Systems, Barcelona, Spain, 11–15 July 2010. AAAA 2010-6003. [Google Scholar]
- Choi, M. Thermal Evaluation of NASA/Goddard Heater Controllers on Swift BAT, Optical Bench and ACS. In Proceedings of the 3rd International Energy Conversion Engineering Conference, San Francisco, CA, USA, 15–18 August 2005. AAAA 2005-5607. [Google Scholar]
- Granger, J.; Franklin, B.; Michalik, M.; Yates, P.; Peterson, E.; Borders, J. Fault-Tolerant, Multiple-Zone Temperature Control; NASA Tech Briefs: New York, NY, USA, 1 September 2008; No. NPO-45230.
- Lewis, F.L.; Syrmos, V. Optimal Control; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Bradtke, S.J.; Barto, A.G. Linear least-squares algorithms for temporal difference learning. Mach. Learn. 1996, 22, 33–57. [Google Scholar] [CrossRef] [Green Version]
- Jiao, Z.; Wang, D.; Liu, X.; Ren, S.; Yang, S.; Zhong, X. Test and research on time delay stability of micron microwave ranging system. Space Electron. Technol. 2021, 18, 58–63. (In Chinese) [Google Scholar]




| Payload | Materials 1 | Heat Capacity (J/kg·K) | Block mass (kg) | Thermal conductivity (W/m·K) | Heating Patch Surface Area (mm × mm) | Nominal Heat/Cool Power (W) | Saturation Heat/Cool Power (W) |
|---|---|---|---|---|---|---|---|
| antenna | magaluma 5086 | 9.00 × 10 | 1.45 | 127 | 50 × 20 | 8 | 3.5 |
| waveguide | nickel alloy GH4169 | 6.15 × 10 | 0.50 | 23.6 | 20 × 10 | 4 | 3.5 |
| signal process | aluminum alloy AZ91D | 8.80 × 10 | 2.14 | 51 | 80 × 30 | 8 | 3.5 |
| USO | aluminum alloy AZ91D | 8.80 × 10 | 0.67 | 51 | 60 × 30 | 5 | 3.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zhu, H.; Shen, Q.; Wu, S.; Wang, N.; Liu, X.; Wang, D.; Zhong, X.; Zhu, Z.; Damaren, C. Trigger-Based K-Band Microwave Ranging System Thermal Control with Model-Free Learning Process. Electronics 2022, 11, 2173. https://doi.org/10.3390/electronics11142173
Wang X, Zhu H, Shen Q, Wu S, Wang N, Liu X, Wang D, Zhong X, Zhu Z, Damaren C. Trigger-Based K-Band Microwave Ranging System Thermal Control with Model-Free Learning Process. Electronics. 2022; 11(14):2173. https://doi.org/10.3390/electronics11142173
Chicago/Turabian StyleWang, Xiaoliang, Hongxu Zhu, Qiang Shen, Shufan Wu, Nan Wang, Xuan Liu, Dengfeng Wang, Xingwang Zhong, Zhu Zhu, and Christopher Damaren. 2022. "Trigger-Based K-Band Microwave Ranging System Thermal Control with Model-Free Learning Process" Electronics 11, no. 14: 2173. https://doi.org/10.3390/electronics11142173
APA StyleWang, X., Zhu, H., Shen, Q., Wu, S., Wang, N., Liu, X., Wang, D., Zhong, X., Zhu, Z., & Damaren, C. (2022). Trigger-Based K-Band Microwave Ranging System Thermal Control with Model-Free Learning Process. Electronics, 11(14), 2173. https://doi.org/10.3390/electronics11142173







