Cellular Positioning in an NLOS Environment Applying the COPSO-TVAC Algorithm
Abstract
:1. Introduction
1.1. Related Works
1.2. Contribution and Structure
- The cellular positioning problem in the mixed LOS/NLOS environment is formulated as the ML estimation problem, using TOA measurements obtained from a minimum set of available BSs, in situations when IAD estimators are not applicable.
- The COPSO-TVAC algorithm, as an improved variant of the PSO-TVAC algorithm, has been proposed to efficiently optimize the objective function of the ML estimator with a minimum population size.
- The proposed method includes the hybridization of PSO with three techniques to create a quality initial PSO population and maintain the balance between exploration and exploitation: opposite learning, chaos search procedure based on chaotic maps, and the adaptive change of the acceleration coefficients [34,35,36,37,38,39,40,41,42,43,44].
- The simulation results show the effectiveness of the COPSO-TVAC algorithm for different numbers of NLOS BSs and the NLOS error levels in the suburban and the urban environment, compared to the standard PSO and PSO-TVAC metaheuristic algorithms [22,24,36], as well as compared to the conventional algorithms such as the TSLS [13] and gradient-based algorithms [7,8].
- The proposed algorithm attains the CRLB accuracy and has better convergence and statistical characteristics than the PSO and the PSO-TVAC algorithm. Based on these facts, it can be concluded that the modifications proposed in this paper can improve the overall optimization performance.
2. ML Estimator in NLOS Scenario
3. PSO Algorithm and the Proposed Modified Versions
3.1. PSO Algorithm
| Algorithm 1 PSO Algorithm for Optimization Problem (22) |
|
3.2. PSO-TVAC Algorithm
| Algorithm 2 PSO-TVAC Algorithm for Optimization Problem (22) |
|
3.3. COPSO-TVAC Algorithm
4. CRLB in NLOS Environment
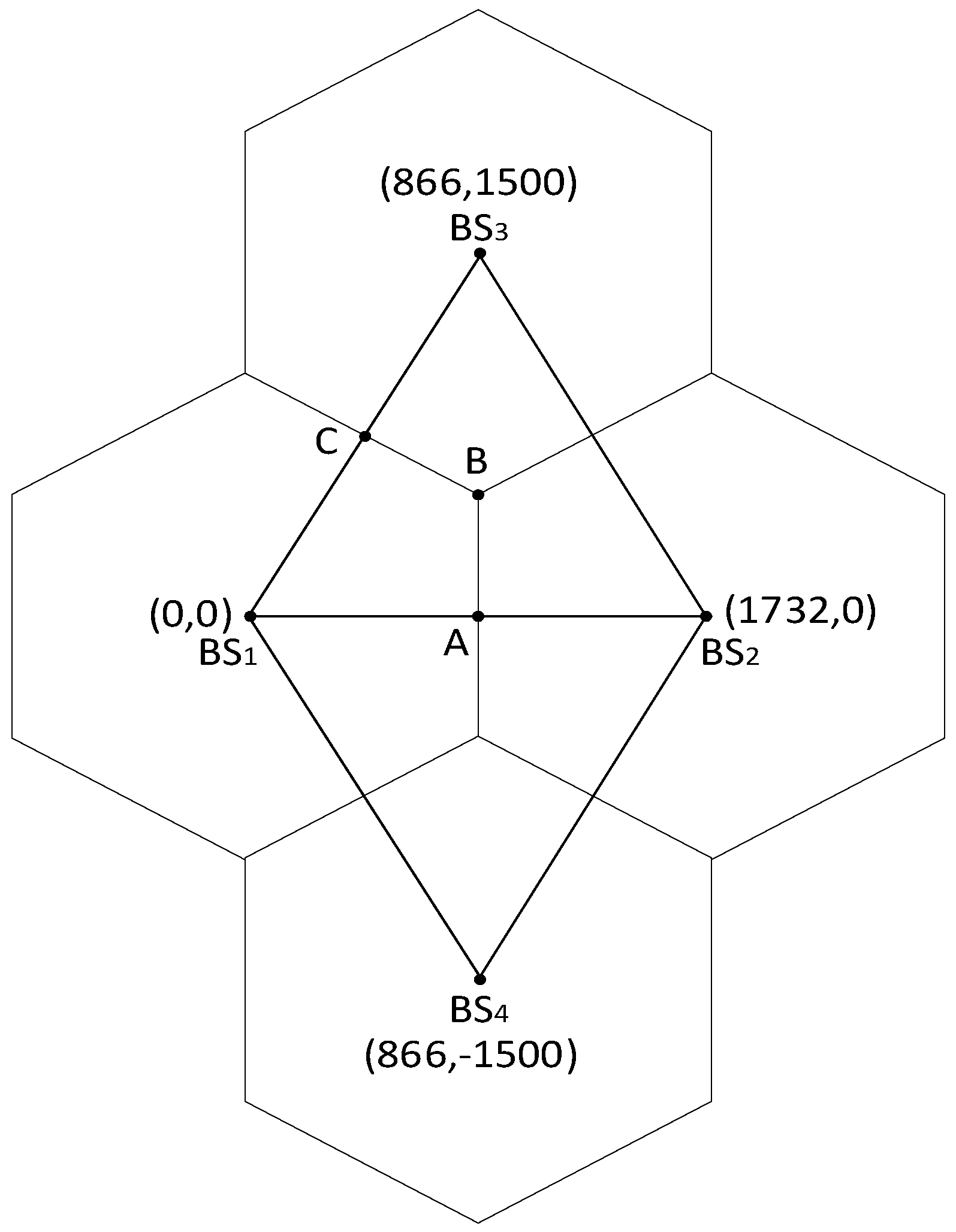
5. Simulation Results and Discussion
| Algorithm 3 COPSO-TVAC algorithm for optimization problem (22) |
|
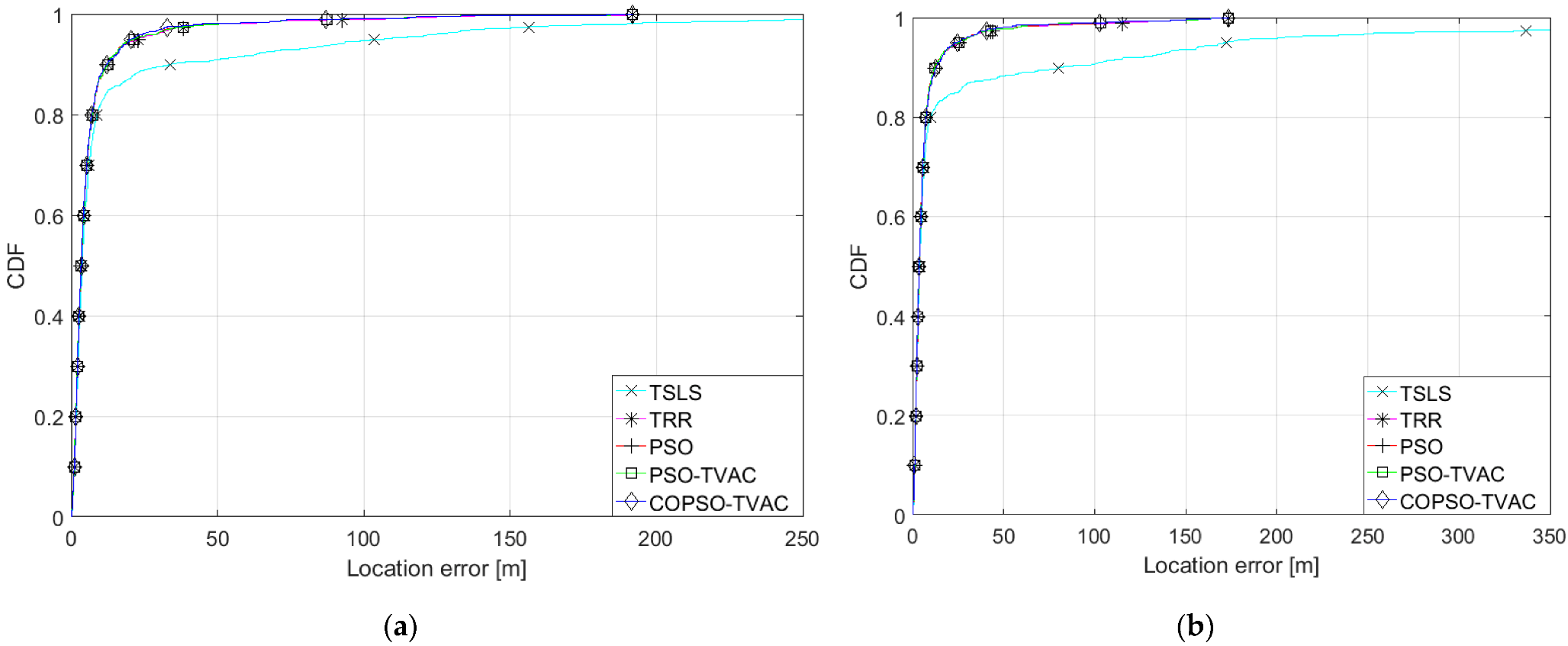
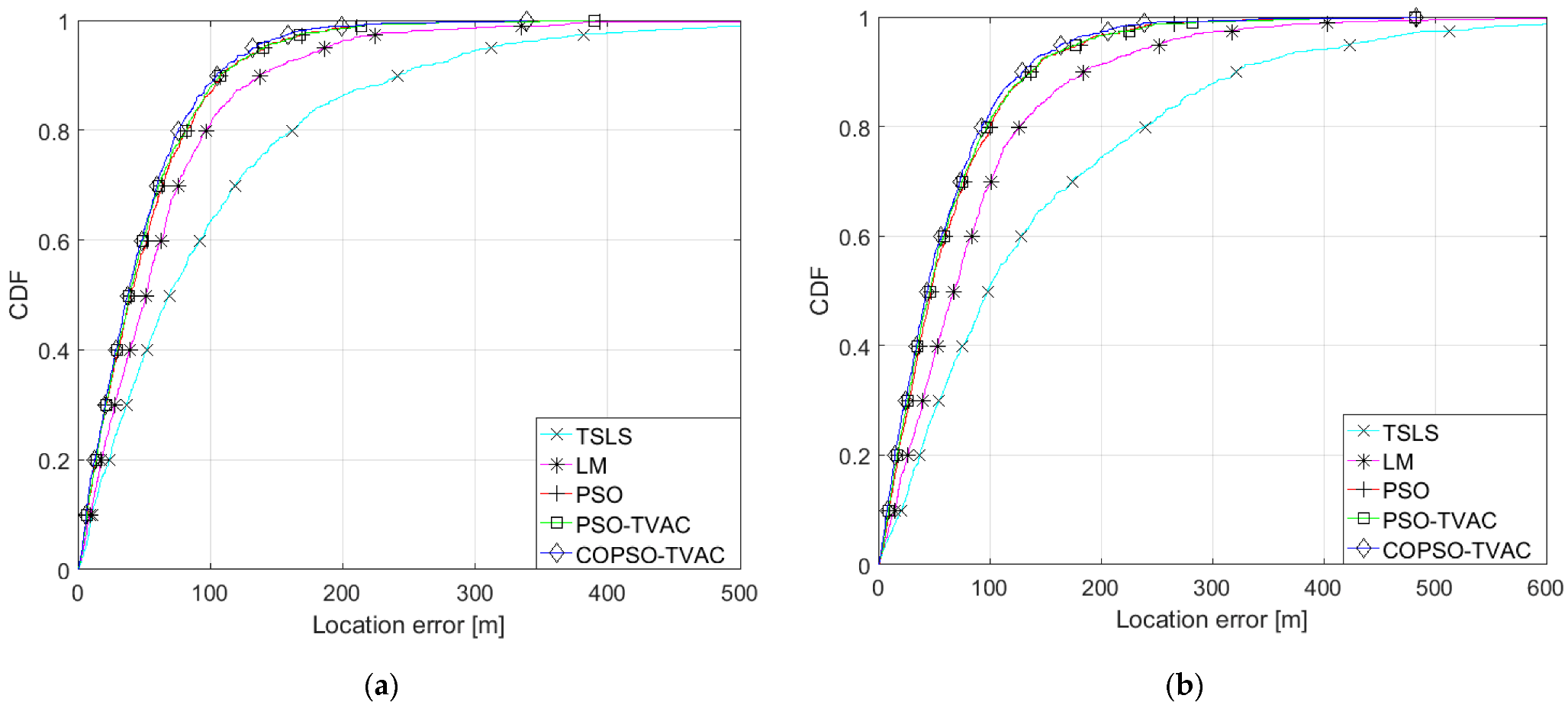
5.1. Localization Performance
5.2. Convergence Properties
5.3. Statistical Comparison of the Proposed Metaheuristic Algorithms
5.4. Computational Complexity of the Considered Algorithms
6. Conclusions and Future Scope
Author Contributions
Funding
Conflicts of Interest
References
- Silventoinen, M.I.; Rantalainen, T. Mobile station emergency locating in GSM. In Proceedings of the 1996 IEEE International Conference on Personal Wireless Communications, New Delhi, India, 21–21 February 1996; pp. 232–238. [Google Scholar]
- Chan, Y.T.; Tsui, W.Y.; So, H.C.; Ching, P.C. Time-of-arrival based localization under NLOS conditions. IEEE Trans. Veh. Technol. 2006, 55, 17–24. [Google Scholar] [CrossRef]
- Cong, L.; Zhuang, W. Non-line-of-sight error mitigation in TDOA mobile location. In Proceedings of the GLOBECOM’01, IEEE Global Telecommunications Conference (Cat. No.01CH37270), San Antonio, TX, USA, 25–29 November 2001; pp. 680–684. [Google Scholar]
- Qi, Y. Wireless Geolocation in a Non-Line-of-Sight Environment. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, November 2003. [Google Scholar]
- Mensing, C.; Plass, S. Positioning algorithms for cellular networks using TDOA. In Proceedings of the 2006 IEEE International Conference on Acoustics, Speech and Signal Processing, Toulouse, France, 14–19 May 2006; pp. 513–516. [Google Scholar]
- Ouyang, R.W.; Wong, A.K. An Enhanced ToA-based Wireless Location Estimation Algorithm for Dense NLOS Environments. In Proceedings of the 2009 IEEE Wireless Communications and Networking Conference, Budapest, Hungary, 5–8 April 2009; pp. 1–6. [Google Scholar]
- Wang, Y.; Wu, Q.; Zhou, M.; Yang, X.; Nie, W.; Xie, L. Single base station positioning based on multipath parameter clustering in NLOS environments. EURASIP J. Adv. Signal Process. 2021, 2021, 20. [Google Scholar] [CrossRef]
- Ruble, M.; Guvenc, I. Wireless localization for mmWave networks in urban environments. EURASIP J. Adv. Signal Process. 2018, 2018, 35. [Google Scholar] [CrossRef] [PubMed]
- Riba, J.; Urruela, A. A non-line-of-sight mitigation technique based on ML-detection. In Proceedings of the 2004 IEEE International Conference on Acoustics, Speech and Signal Processing, Montreal, QC, Canada, 17–21 May 2004; pp. 151–153. [Google Scholar]
- Chen, P.C. A non-line-of-sight error mitigation algorithm in location estimation. In Proceedings of the WCNC, 1999 IEEE Wireless Communications and Networking Conference (Cat. No.99TH8466), New Orleans, LA, USA, 21–24 September 1999; pp. 316–320. [Google Scholar]
- Cheung, K.W.; So, H.C.; Ma, W.K.; Chan, Y.T. Least squares algorithms for time-of-arrival-based mobile location. IEEE Trans. Signal Process. 2004, 52, 1121–1130. [Google Scholar] [CrossRef] [Green Version]
- Yu, K.; Guo, Y.J. NLOS Error Mitigation for Mobile Location Estimation in Wireless Networks. In Proceedings of the 2007 IEEE 65th Vehicular Technology Conference—VTC2007-Spring, Dublin, Ireland, 22–25 April 2007; pp. 1071–1075. [Google Scholar]
- Kocur, D.; Švecova, M.; Kažimir, P. Determining the Position of the Moving Persons in 3D Space by UWB Sensors using Taylor Series Based Localization Method. Acta Polytech. Hung. 2019, 16, 45–63. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Z.; O’Dea, B. A TOA-based location algorithm reducing the errors due to non-line-of-sight (NLOS) propagation. IEEE Trans. Veh. Technol. 2003, 52, 112–116. [Google Scholar] [CrossRef]
- Venkatesh, S.; Buehrer, R.M. NLOS mitigation using linear programming in UWB location-aware networks. IEEE Trans. Veh. Technol. 2007, 56, 3182–3198. [Google Scholar] [CrossRef]
- Venkatesh, S.; Buehrer, R.M. A linear programming approach to NLOS mitigation in sensor networks. In Proceedings of the 2006 5th International Conference on Information Processing in Sensor Networks, Nashville, TN, USA, 19–21 April 2006; pp. 301–308. [Google Scholar]
- Yu, K.; Guo, Y.J. Improved Positioning Algorithms for Nonline-of-Sight Environments. IEEE Trans. Veh. Technol. 2008, 57, 2342–2353. [Google Scholar]
- Yang, X.S. Engineering Optimization: An Introduction with Metaheuristic Application, 1st ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010; pp. 1–28. [Google Scholar]
- Yang, X.S. Nature-Inspired Optimization Algorithms, 1st ed.; Elsevier, Inc.: London, UK, 2014; pp. 1–42. [Google Scholar]
- Campos, R.S.; Lovisolo, L. Genetic algorithm optimized DCM positioning. In Proceedings of the 2013 10th Workshop on Positioning, Navigation and Communication (WPNC), Dresden, Germany, 20–21 March 2013; pp. 1–5. [Google Scholar]
- Chen, C.S.; Lin, J.M.; Lee, C.T.; Lu, C.D. The Hybrid Taguchi-Genetic Algorithm for Mobile Location. Int. J. Distrib. Sens. Netw. 2014, 10, 489563. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.S. A non-line-of-sight error mitigation method for location estimation. Int. J. Distrib. Sens. Netw. 2017, 13, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Enqing, D.; Yanze, C.; Xiaojun, L. A novel three-dimensional localization algorithm for Wireless Sensor Networks based on Particle Swarm Optimization. In Proceedings of the 2011 18th International Conference on Telecommunications, Ayia Napa, Cyprus, 8–11 May 2011; pp. 55–60. [Google Scholar]
- Lukic, S.; Simic, M. NLOS Error Mitigation in Cellular Positioning using PSO Optimization Algorithm. Int. J. Electr. Eng. Comput. IJEEC 2018, 2, 48–56. [Google Scholar]
- Chen, C.S.; Huang, J.F.; Huang, N.C.; Chen, K.S. MS Location Estimation Based on the Artificial Bee Colony Algorithm. Sensors 2020, 20, 5597. [Google Scholar] [CrossRef]
- Yiang, J.; Liu, M.; Chen, T.; Gao, L. TDOA Passive Location Based on Cuckoo Search Algorithm. J. Shanghai Jiaotong Univ. (Sci.) 2018, 23, 368–375. [Google Scholar]
- Cheng, J.; Xia, L. An Effective Cuckoo Search Algorithm for Node Localization in Wireless Sensor Network. Sensors 2016, 16, 1390. [Google Scholar] [CrossRef] [Green Version]
- Tuba, E.; Tuba, M.; Beko, M. Two Stage Wireless Sensor Node Localization Using Firefly Algorithm. In Smart Trends in Systems, Security and Sustainability; Yang, X.S., Nagar, A.K., Joshi, A., Eds.; Springer: Singapore, 2018; Volume 18, pp. 113–120. [Google Scholar]
- Shi, Y.; Eberhart, R.C. Particle swarm optimization: Developments, applications and resources. In Proceedings of the 2001 Congress on Evolutionary Computation (IEEE Cat. No.01TH8546), Seoul, Korea, 27–30 May 2001; pp. 81–86. [Google Scholar]
- Shi, Y.; Eberhart, R.C. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation, IEEE World Congress on Computational Intelligence (Cat. No.98TH8360), Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Zhang, X.; Zou, D.; Shen, X. A Novel Simple Particle Swarm Optimization Algorithm for Global Optimization. Mathematics 2018, 6, 287. [Google Scholar] [CrossRef] [Green Version]
- Liang, J.J.; Qin, A.K.; Suganthan, P.N.; Baskar, S. Comprehensive Learning Particle Swarm Optimizer for Global Optimization of Multimodal Functions. IEEE Trans. Evol. Comput. 2006, 10, 281–295. [Google Scholar] [CrossRef]
- Tanweer, M.R.; Suresh, S.; Sundararajan, N. Dynamic mentoring and self-regulation based particle swarm optimization algorithm for solving complex real-world optimization problems. Inf. Sci. 2016, 326, 1–24. [Google Scholar] [CrossRef]
- Ratnaweera, A.; Halgamuge, S.K.; Watson, H.A. Self-Organizing Hierarchical Particle Swarm Optimizer with Time-Varying Acceleration Coefficients. IEEE Trans. Evol. Comput. 2004, 8, 240–255. [Google Scholar] [CrossRef]
- Chaturvedi, K.T.; Pandit, M.; Srivastava, L. Particle swarm optimization with time-varying acceleration coefficients for non-convex economic power dispatch. Int. J. Electr. Power Energy Syst. 2009, 31, 249–257. [Google Scholar] [CrossRef]
- Fang, J.; Feng, J. Using PSO-TVAC to improve the performance of DV-Hop. Int. J. Wirel. Mob. Comput. 2018, 14, 358–361. [Google Scholar] [CrossRef]
- Zhang, H.; Shen, J.H.; Zhang, T.N.; Li, Y. An improved chaotic particle swarm optimization and its application in investment. In Proceedings of the 2008 International Symposium on Computational Intelligence and Design, Wuhan, China, 17–18 October 2008; pp. 124–128. [Google Scholar]
- Tian, D. Particle Swarm Optimization with Chaos-based Initialization for Numerical Optimization. Intell. Autom. Soft Comput. 2018, 24, 331–342. [Google Scholar] [CrossRef]
- Feng, Y.; Teng, G.F.; Wang, A.X.; Yao, Y.M. Chaotic Inertia Weight in Particle Swarm Optimization. In Proceedings of the Second International Conference on Innovative Computing, Information and Control (ICICIC 2007), Kumamoto, Japan, 5–7 September 2007; p. 475. [Google Scholar]
- Arasomwan, A.M.; Adewumi, A.O. An Investigation into the Performance of Particle Swarm Optimization Algorithm with Various Chaotic Maps. Math. Probl. Eng. 2014, 2014, 178959. [Google Scholar] [CrossRef]
- Wang, H.; Li, H.; Liu, Y.; Li, C.; Zeng, S. Opposition-based particle swarm algorithm with cauchy mutation. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 4750–4756. [Google Scholar]
- Mahdavi, S.; Rahnamayan, S.; Deb, K. Opposition-based learning: A literature review. Swarm Evol. Comput. 2018, 39, 1–23. [Google Scholar] [CrossRef]
- Dong, N.; Wu, C.H.; Ip, W.H.; Chen, Z.Q.; Chan, C.Y.; Yung, K.L. An opposition-based chaotic GA/PSO hybrid algorithm and its application in circle detection. Comput. Math. Appl. 2012, 64, 1886–1902. [Google Scholar] [CrossRef] [Green Version]
- Gao, W.; Liu, S.; Huang, L. Particle swarm optimization with chaotic opposition-based population and stochastic search technique. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 25185–25199. [Google Scholar] [CrossRef]
- Venkatraman, S.; Caffery, J.; You, H.R. A novel ToA location algorithm using LOS range estimation for NLOS environments. IEEE Trans. Veh. Technol. 2004, 53, 1515–1524. [Google Scholar] [CrossRef]
- Del Peral-Rosado, J.A.; Lopes-Salcedo, J.A.; Zanier, F.; Seco-Granados, G. Position Accuracy of Joint Time-Delay and Channel Estimators in LTE Networks. IEEE Access 2018, 6, 25185–25199. [Google Scholar] [CrossRef]
- Greenstein, L.J.; Erceg, V.; Yeh, Y.S.; Clark, M.V. A new path-gain/delay-spread propagation model for digital cellular channels. IEEE Trans. Veh. Technol. 1997, 46, 477–485. [Google Scholar] [CrossRef]
- Guvenc, I.; Cong, C.C. A Survey on TOA Based Wireless Localization and NLOS Mitigation Techniques. IEEE Commun. Surv. Tutor. 2009, 11, 107–124. [Google Scholar] [CrossRef]
- Mezura-Montes, E.; Flores-Mendoza, J.I. Improved Particle Swarm Optimization in Constrained Numerical Search Space. In Nature Inspired Algorithms for Optimization. Studies in Computational Intelligence, 1st ed.; Chiong, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 193, pp. 299–332. [Google Scholar]
- Joines, J.A.; Houck, C.R. On the Use of Non-Stationary Penalty Function to Solve Nonlinear Constrained Optimization Problems with GA’s. In Proceedings of the First IEEE Conference on Evolutionary Computation, IEEE World Congress on Computational Intelligence, Orlando, FL, USA, 26–29 June 1994; pp. 579–584. [Google Scholar]
- Optimization and Data Fitting—DTU Informatics. Available online: http://www2.imm.dtu.dk/pubdb/edoc/imm5938.pdf (accessed on 28 September 2021).
- Jativa, E.R.; Sanchez, D.; Vidal, J. NLOS Mitigation Based on TOA for Mobile Subscriber Positioning System by Weighting Measures and Geometrical Restrictions. In Proceedings of the 2015 Asia-Pacific Conference on Computer Aided System Engineering, Quito, Ecuador, 14–16 July 2015; pp. 325–330. [Google Scholar]
- Kay, S.; Eldar, Y.C. Rethinking biased estimation [Lecture Note]. IEEE Signal Process. Mag. 2008, 25, 133–136. [Google Scholar] [CrossRef]
- Cakir, O.; Kaya, I.; Yazgan, A.; Cakir, O.; Tugcu, E. Emitter Location Finding using Particle Swarm Optimization. Radioengineering 2014, 23, 252–258. [Google Scholar]
- Derrac, J.; Garcia, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametrical statistical test as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]


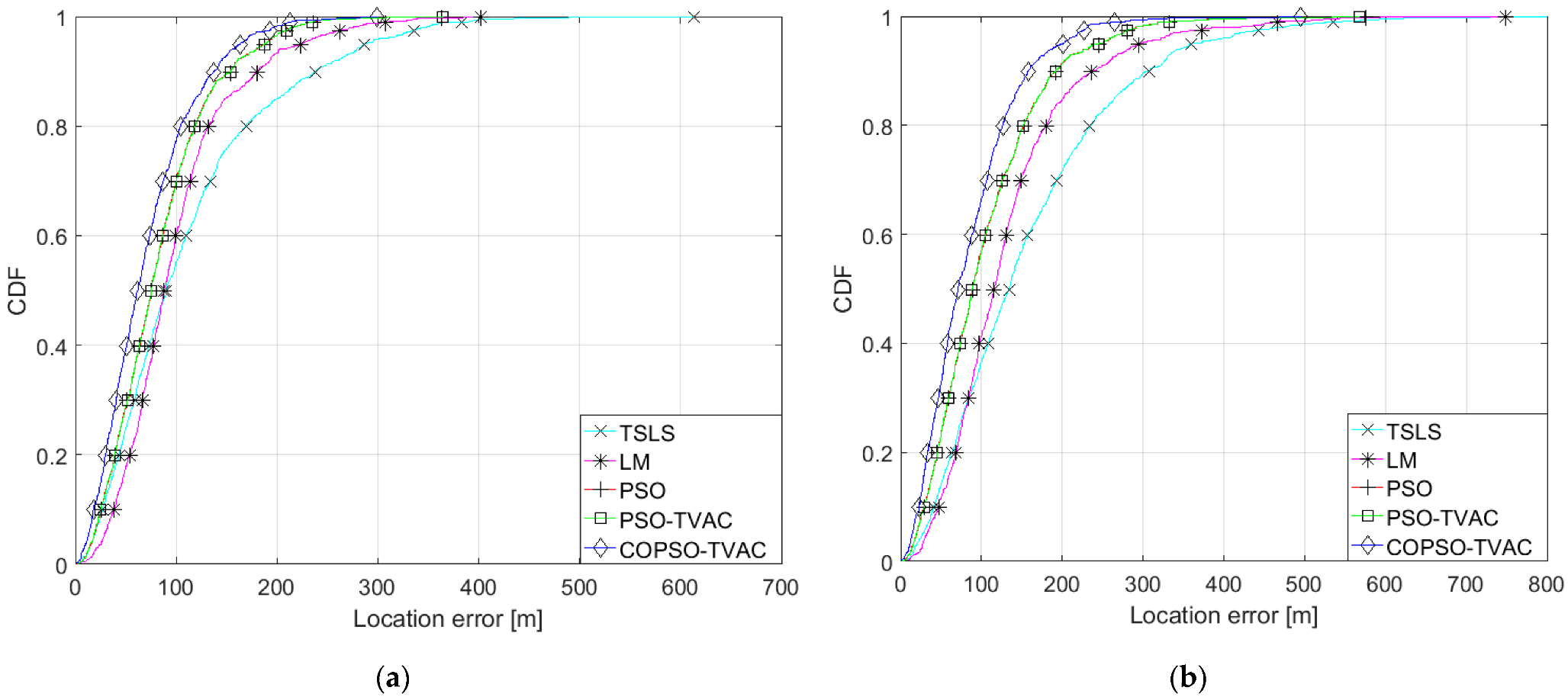
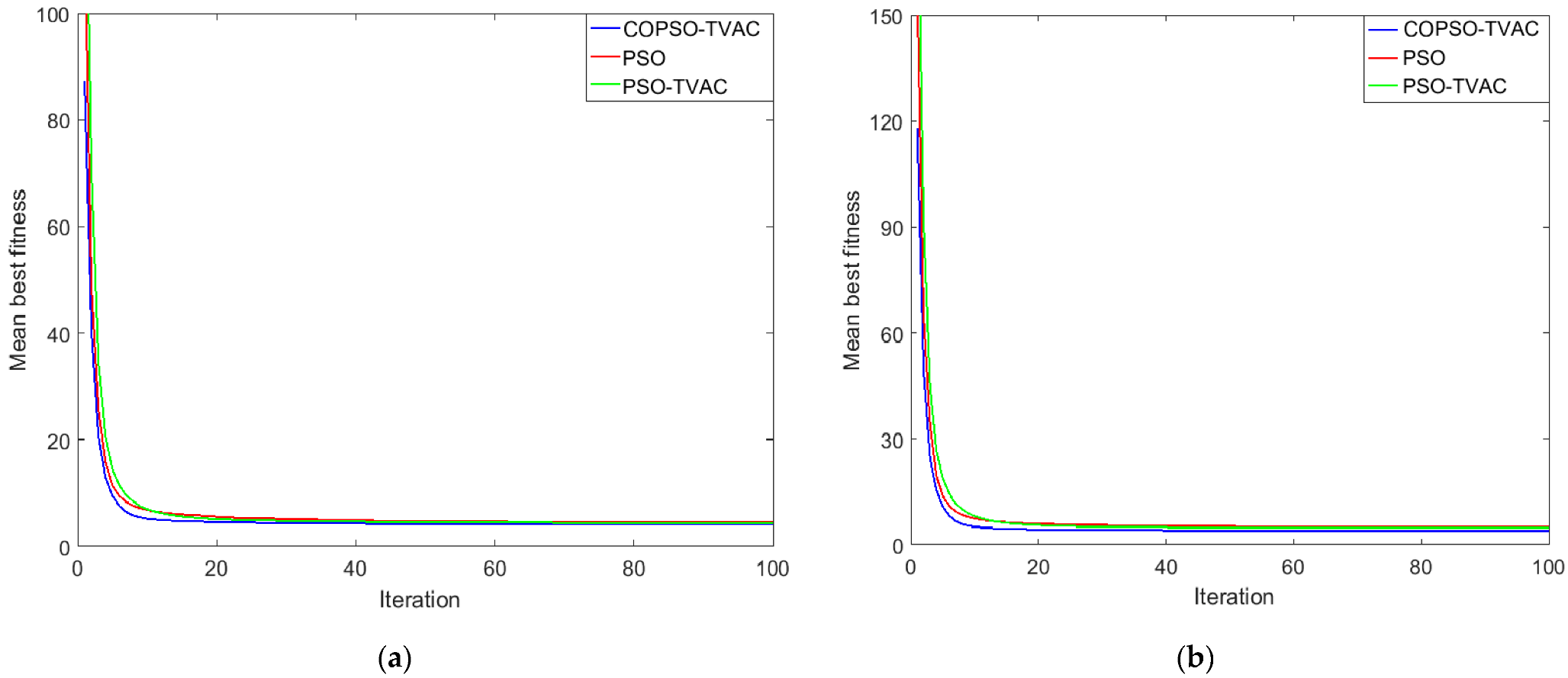
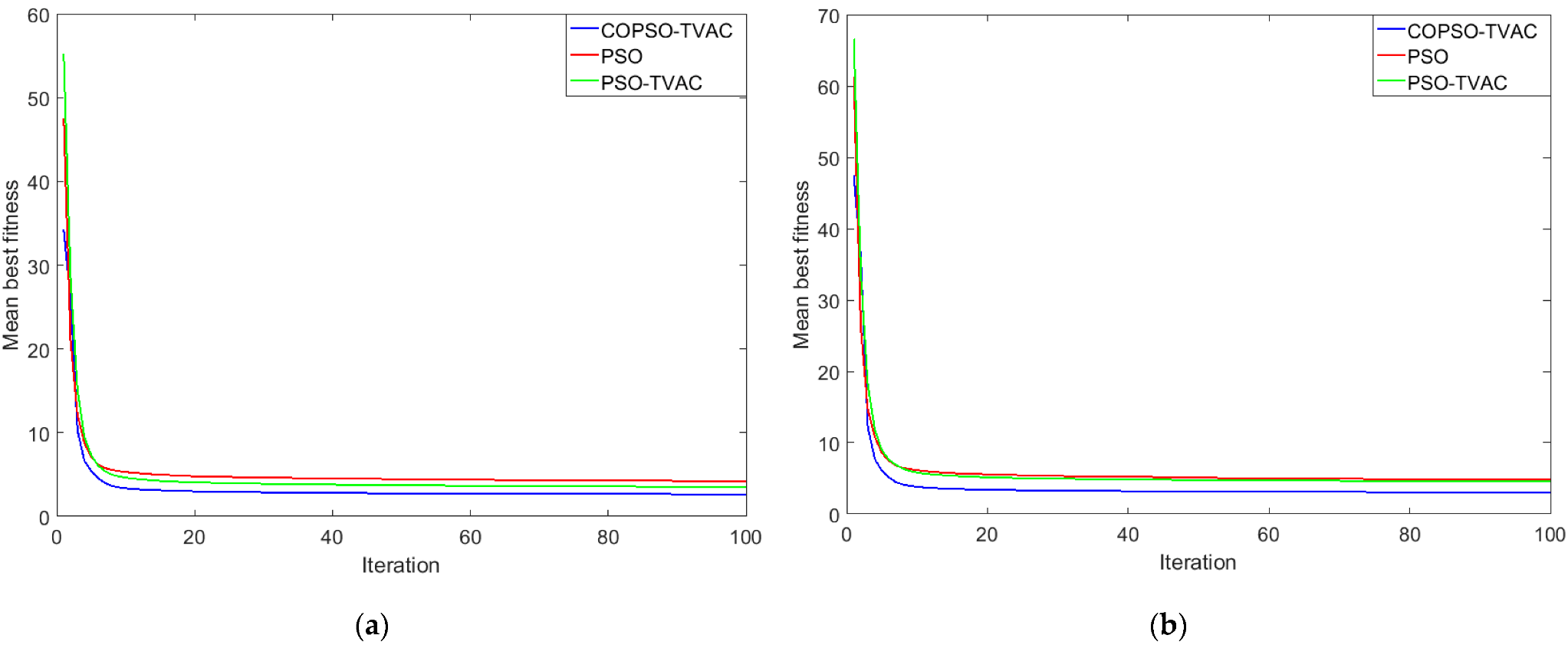
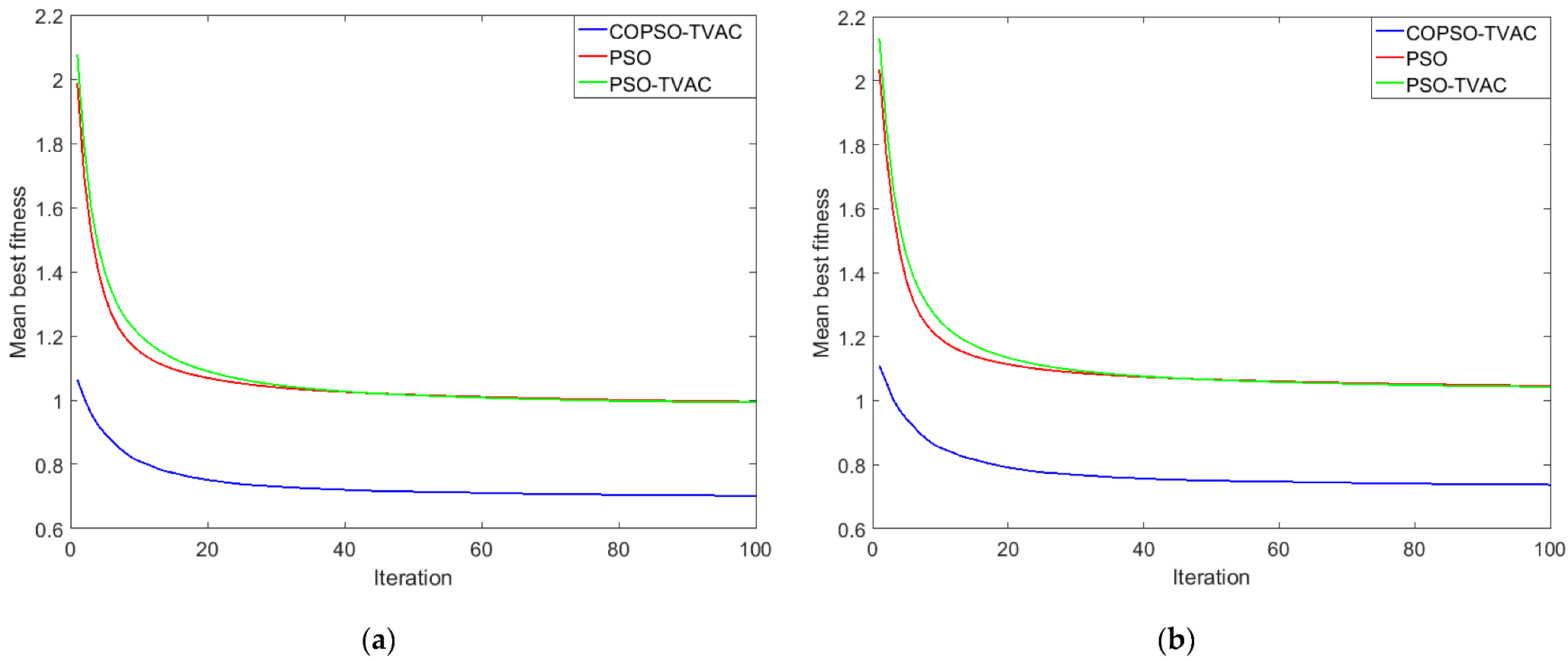
| Simulation Parameter | PSO | PSO-TVAC | COPSO-TVAC |
|---|---|---|---|
| Population size (N) | 20 | 20 | 20 |
| Dimension of the search space (n) | 4–6 | 4–6 | 4–6 |
| Sample size (M) | 50 | 50 | 50 |
| Maximum iteration number (T) | 100 | 100 | 100 |
| Value of factor k1 | 0.015 | 0.015 | 0.015 |
| Value of factor k2 (suburban) | 100.06 | 100.06 | 100.06 |
| Value of factor k2 (urban) | 133.42 | 133.42 | 133.42 |
| Cognitive acceleration coefficient (c1) | 2 | - | - |
| Social acceleration coefficient (c2) | 2 | - | - |
| Initial value of cognitive coefficient (c1i) | - | 2.5 | 2.5 |
| Final value of cognitive coefficient (c1f) | - | 0.5 | 0.5 |
| Initial value of social coefficient (c2i) | - | 0.5 | 0.5 |
| Final value of social coefficient (c2f) | - | 2.5 | 2.5 |
| Initial value of LDIW/CDIW factor (ωmax) | 0.9 | 0.9 | 0.9 |
| Final value of LDIW/CDIW factor (ωmin) | 0.4 | 0.4 | 0.4 |
| Weighting factor kp | 0.15 | 0.15 | 0.15 |
| Initial value of a logistic map in (44) and (45) | - | - | 0.7 |
| Number of NLOS BSs | RAMMSE | RMSE | ||||
|---|---|---|---|---|---|---|
| TSLS | TRR/LM | PSO | PSO-TVAC | COPSO-TVAC | ||
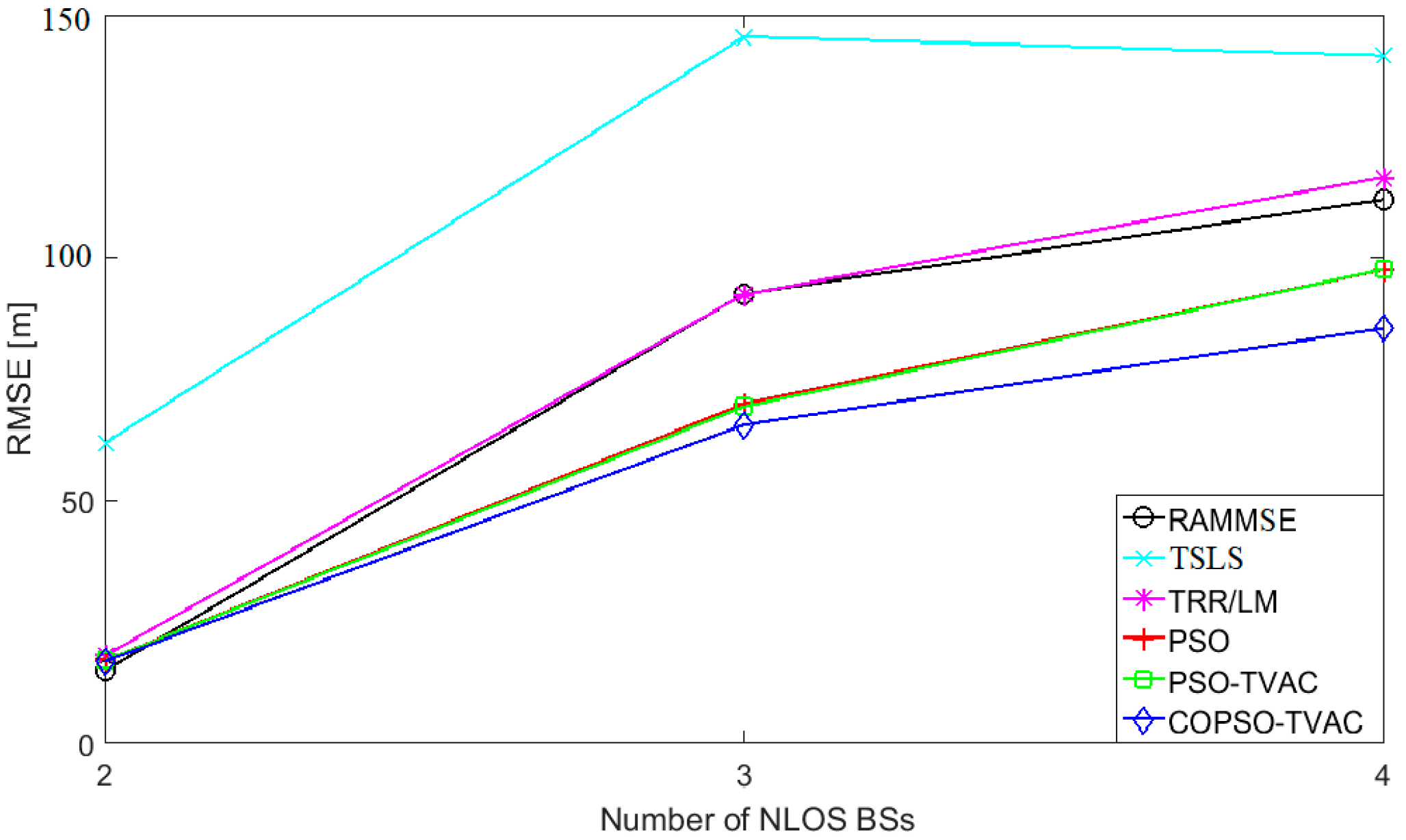
| 2 | 14.93 | 61.80 | 18.05 | 17.08 | 17.07 | 16.89 |
| 3 | 92.53 | 145.44 | 92.42 | 69.91 | 69.30 | 65.56 |
| 4 | 111.95 | 141.60 | 116.51 | 97.47 | 97.54 | 85.43 |
| Number of NLOS BSs | RAMMSE | RMSE | ||||
|---|---|---|---|---|---|---|
| TSLS | TRR/LM | PSO | PSO-TVAC | COPSO-TVAC | ||
| 2 | 16.92 | 111.87 | 18.89 | 18.26 | 18.06 | 17.84 |
| 3 | 122.99 | 203.31 | 128.47 | 87.47 | 87.17 | 82.17 |
| 4 | 149.08 | 193.81 | 159.02 | 126.43 | 126.38 | 103.45 |
| Algorithm | Scenario | Mean Ranking | Rank | |||||
|---|---|---|---|---|---|---|---|---|
| 2 NLOS BSs Suburban | 2 NLOS BSs Urban | 3 NLOS BSs Suburban | 3 NLOS BSs Urban | 4 NLOS BSs Suburban | 4 NLOS BSs Urban | |||
| PSO | 2.68 | 2.68 | 2.74 | 2.78 | 2.49 | 2.52 | 2.64 | 3 |
| PSO-TVAC | 1.83 | 1.77 | 1.76 | 1.76 | 1.75 | 1.81 | 1.78 | 2 |
| COPSO-TVAC | 1.48 | 1.53 | 1.49 | 1.45 | 1.74 | 1.65 | 1.55 | 1 |
| Friedman p value | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | ||
| Algorithm | Configuration | ||
|---|---|---|---|
| 2 NLOS BSs | 3 NLOS BSs | 4 NLOS BSs | |
| TSLS | 3.03 | 3.16 | 3.20 |
| TRR | 29.50 | - | - |
| LM | - | 32.68 | 34.94 |
| PSO | 11.15 | 12.99 | 13.42 |
| PSO-TVAC | 11.39 | 13.58 | 14.24 |
| COPSO-TVAC | 12.04 | 13.88 | 14.88 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lukić, S.; Simić, M. Cellular Positioning in an NLOS Environment Applying the COPSO-TVAC Algorithm. Electronics 2022, 11, 2300. https://doi.org/10.3390/electronics11152300
Lukić S, Simić M. Cellular Positioning in an NLOS Environment Applying the COPSO-TVAC Algorithm. Electronics. 2022; 11(15):2300. https://doi.org/10.3390/electronics11152300
Chicago/Turabian StyleLukić, Stevo, and Mirjana Simić. 2022. "Cellular Positioning in an NLOS Environment Applying the COPSO-TVAC Algorithm" Electronics 11, no. 15: 2300. https://doi.org/10.3390/electronics11152300
APA StyleLukić, S., & Simić, M. (2022). Cellular Positioning in an NLOS Environment Applying the COPSO-TVAC Algorithm. Electronics, 11(15), 2300. https://doi.org/10.3390/electronics11152300






