Delay Compensation Control Strategy for Electric Vehicle Participating in Frequency Regulation Based on MPC Algorithm
Abstract
:1. Introduction
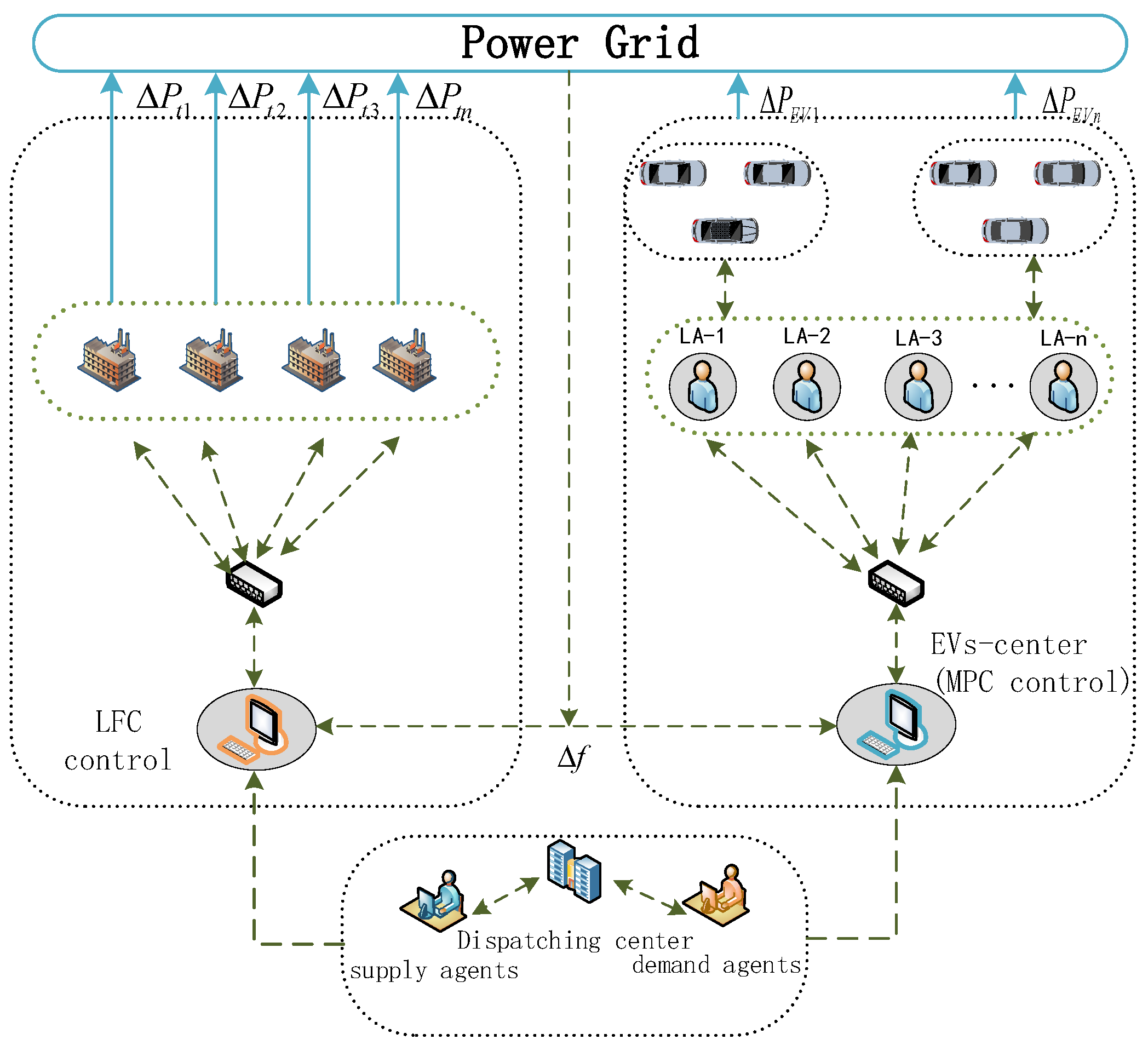
2. MPC-Based Electric Vehicle Frequency Regulation Framework
3. Frequency Control Strategy of Electric Vehicles Based on MPC
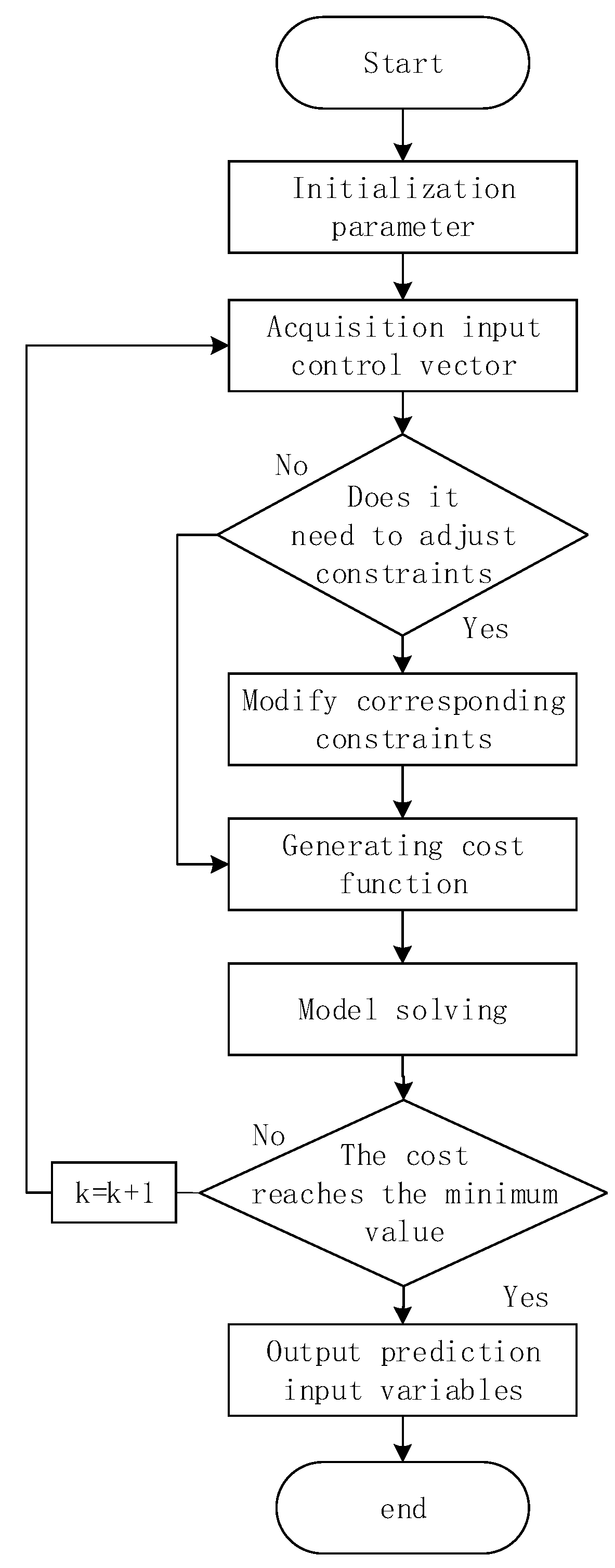
3.1. Model Predictive Control Theory Introduction
3.2. Electric Vehicle Aggregation Model Construction
3.3. Frequency Control Strategy of Electric Vehicles Based on MPC
4. Electric Vehicle Frequency Regulation Delay Compensation Strategy
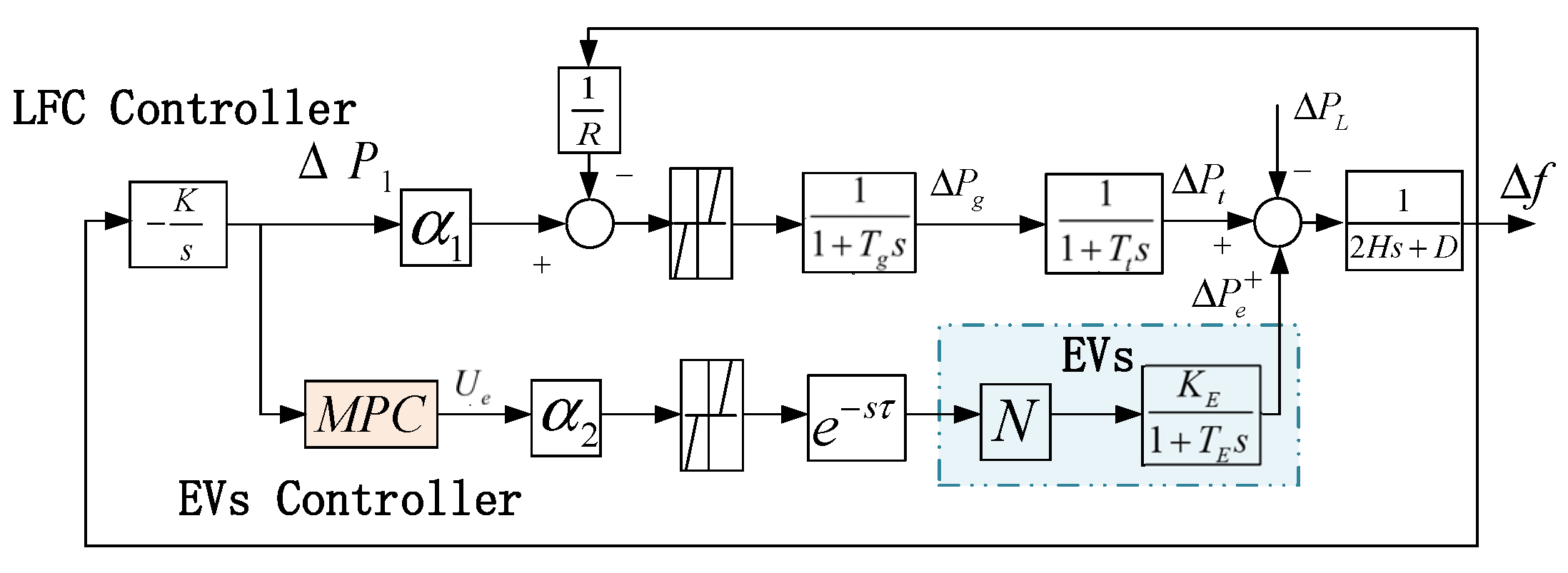
4.1. The Effects of Communication Delays on the Participation of EVs in Frequency Regulation
4.2. Active Compensation Strategy for Frequency Regulation Delay of Electric Vehicles
5. Simulation Results and Analysis
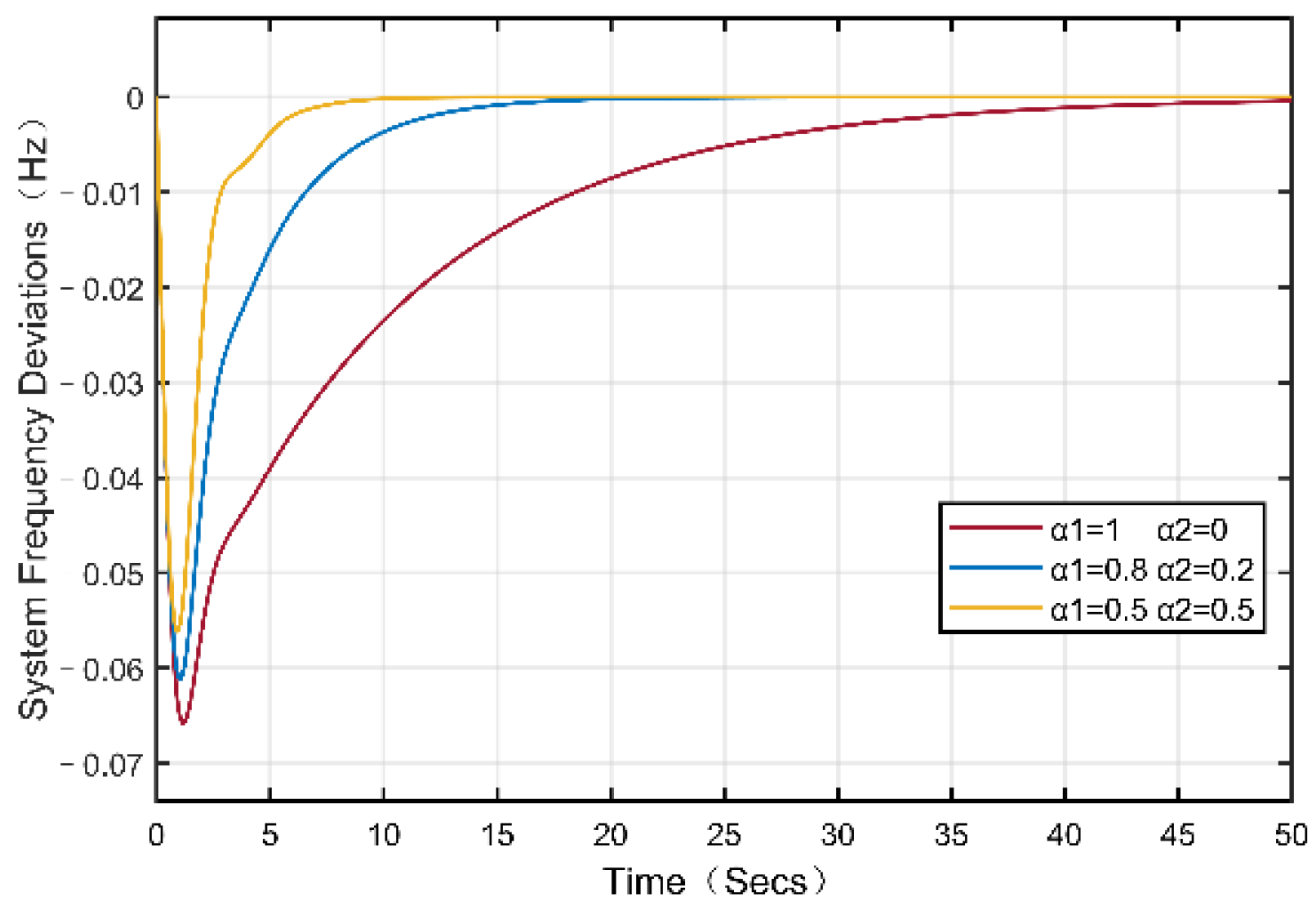
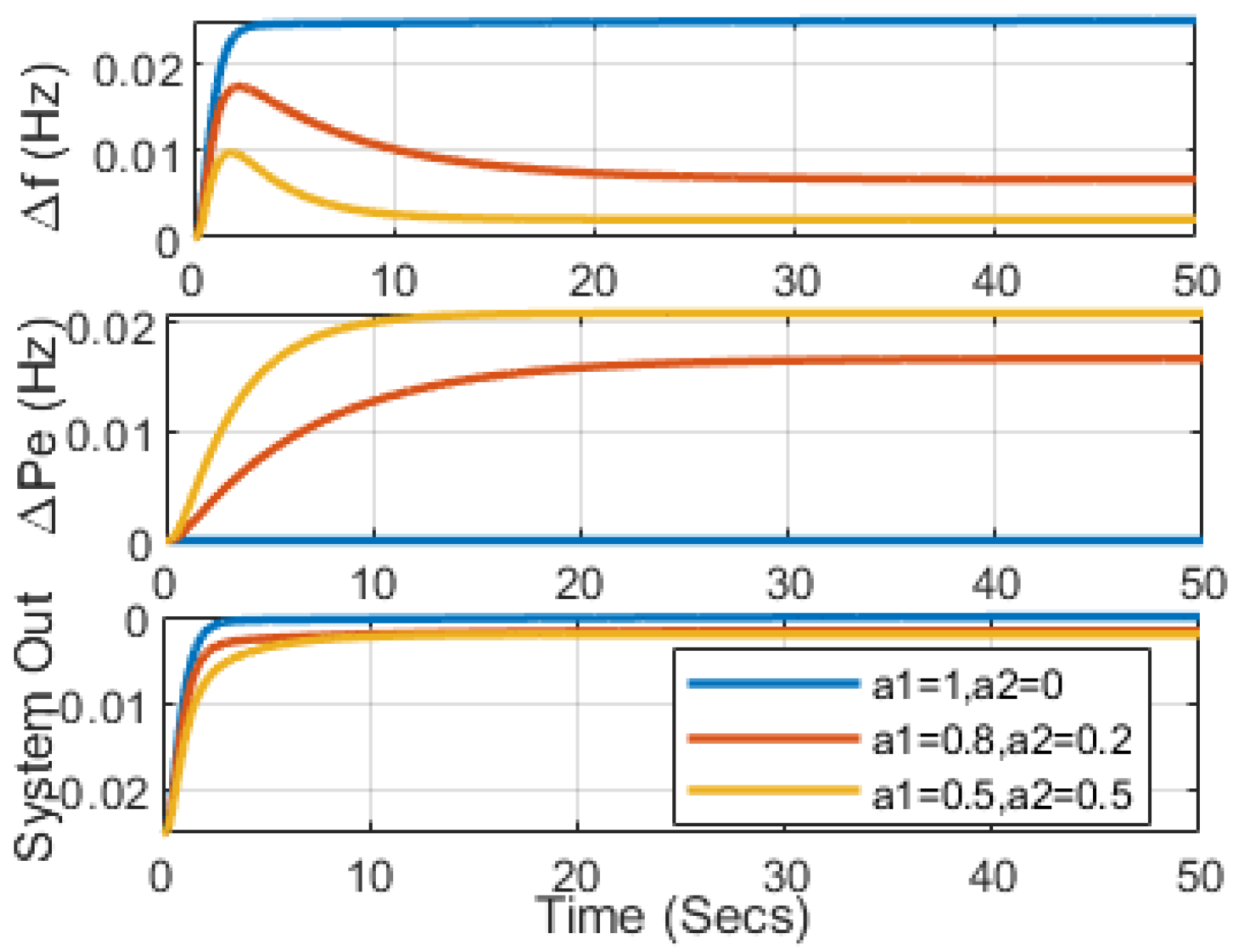
5.1. Effect of Aggregated EV Involved in Dynamic Response on System Frequency Stability
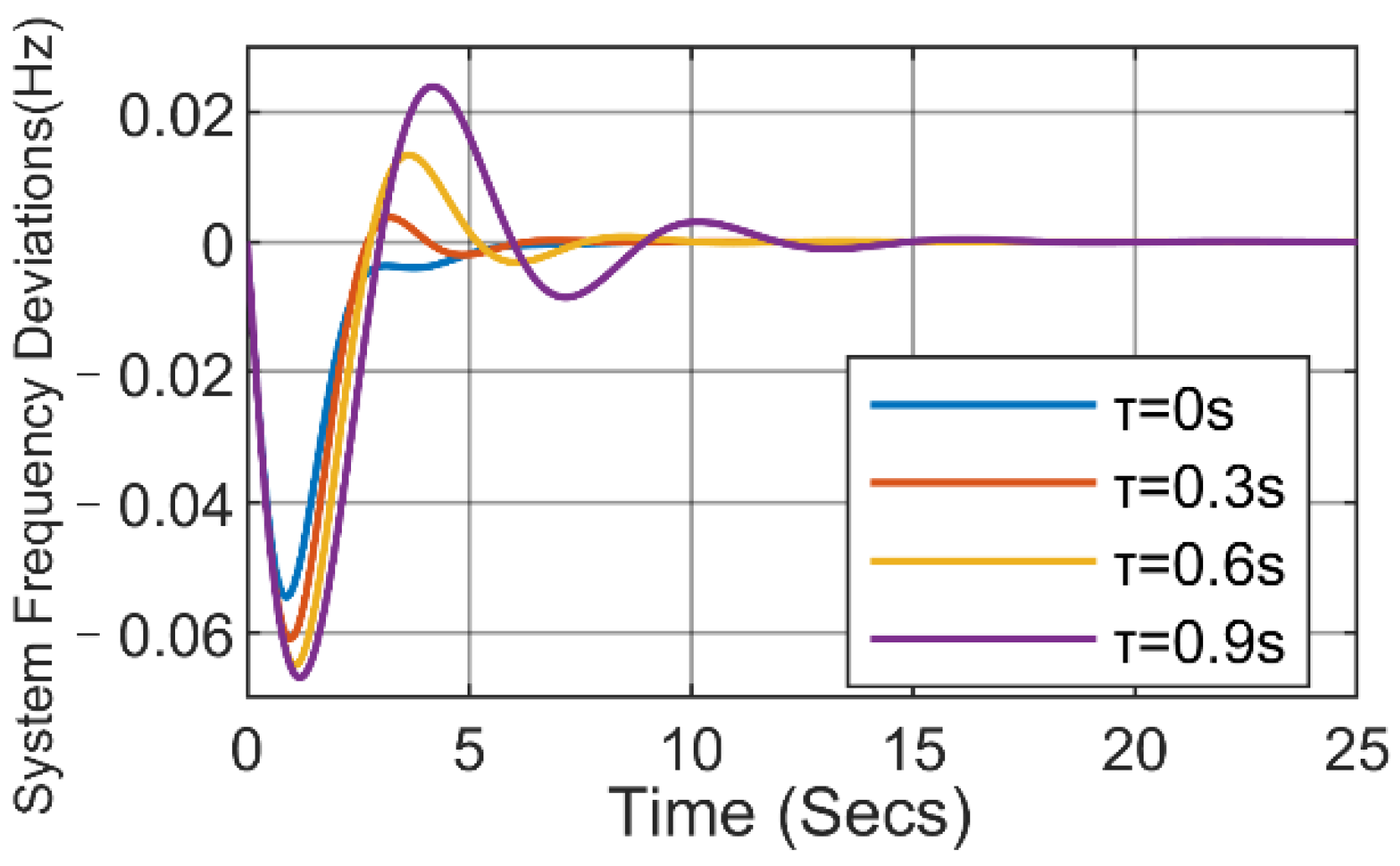
5.2. The Effect of Communication Delay on the Power System Frequency Response
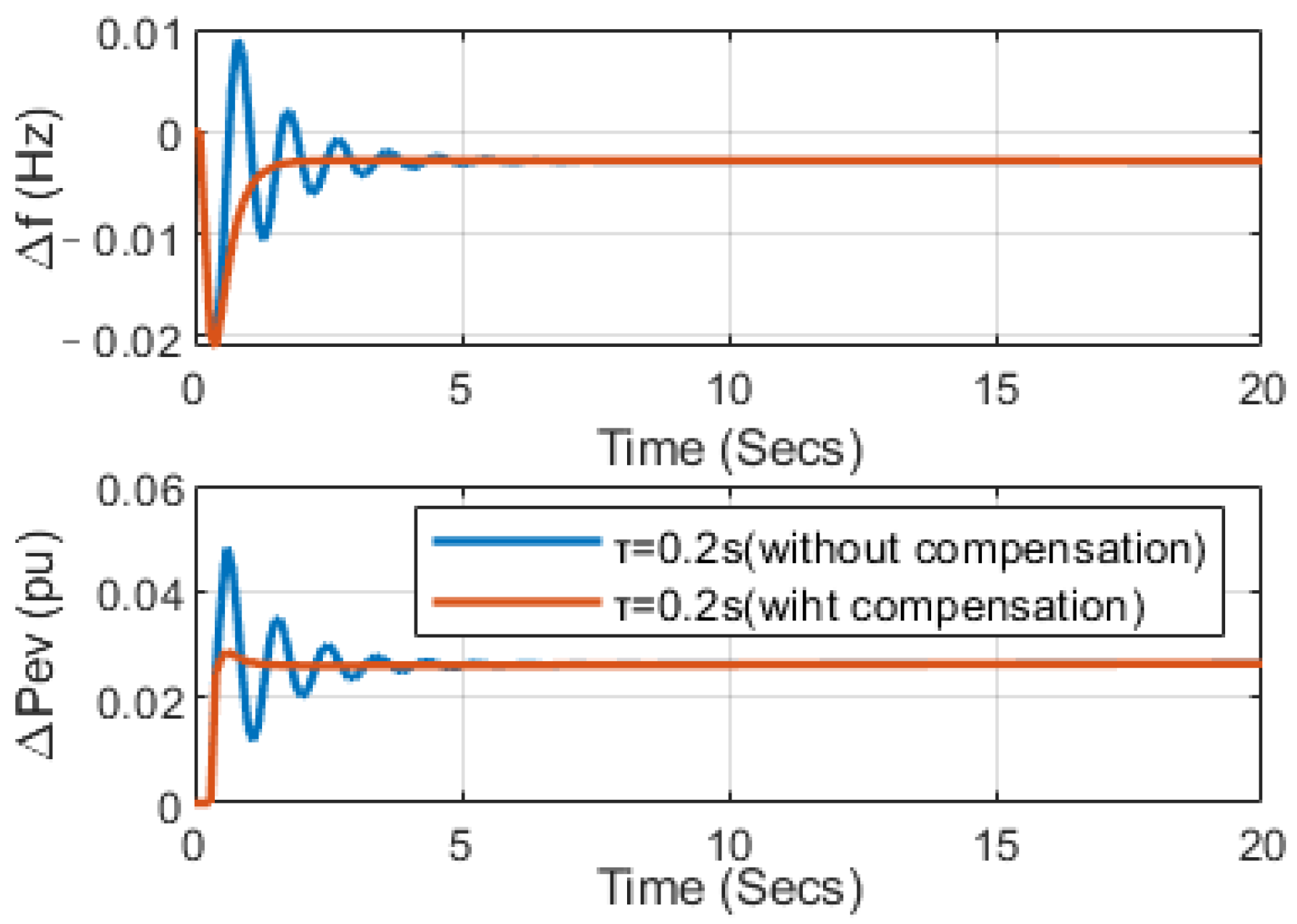
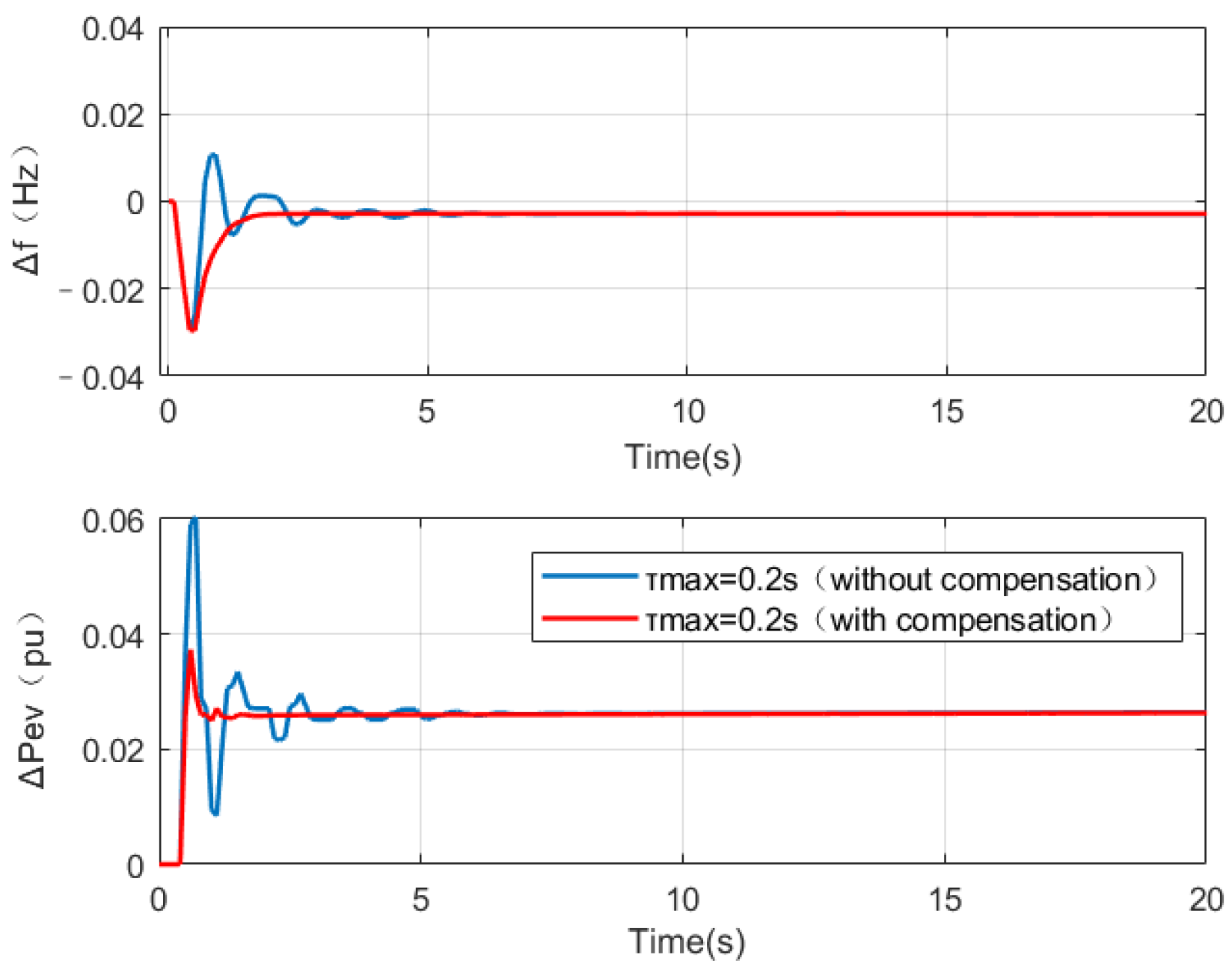
5.3. Comparison Effect of System Performance with or without Delay Compensation
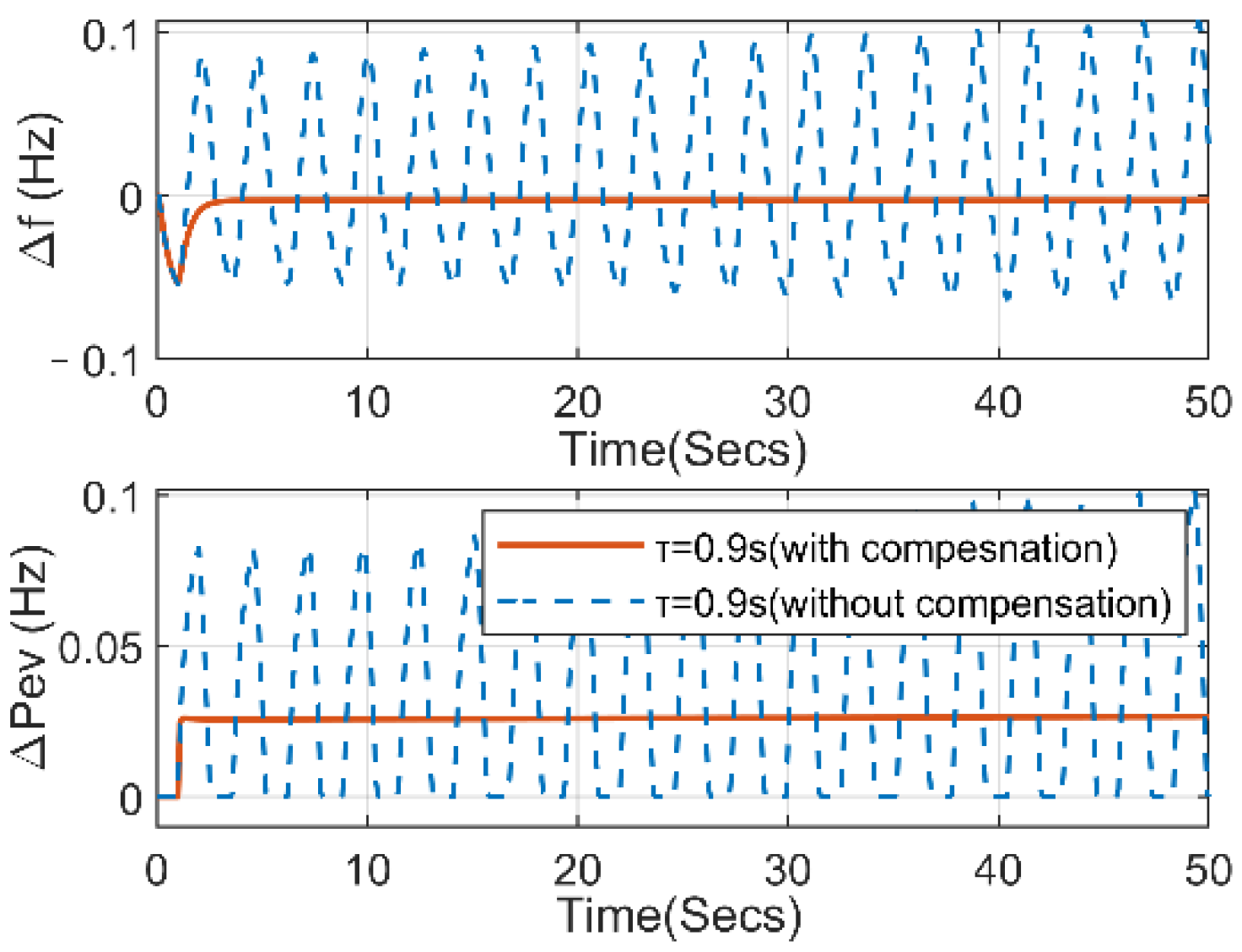
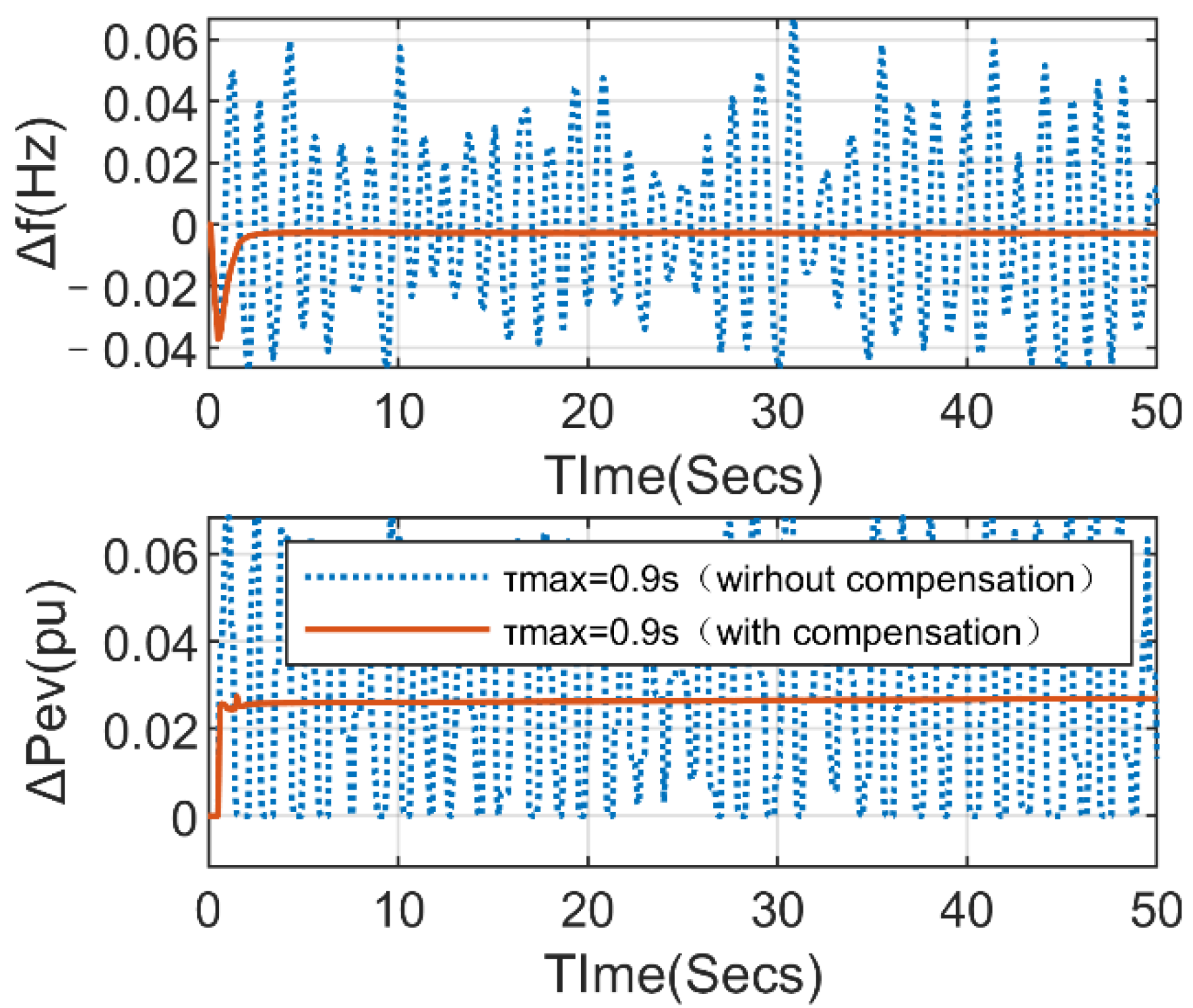
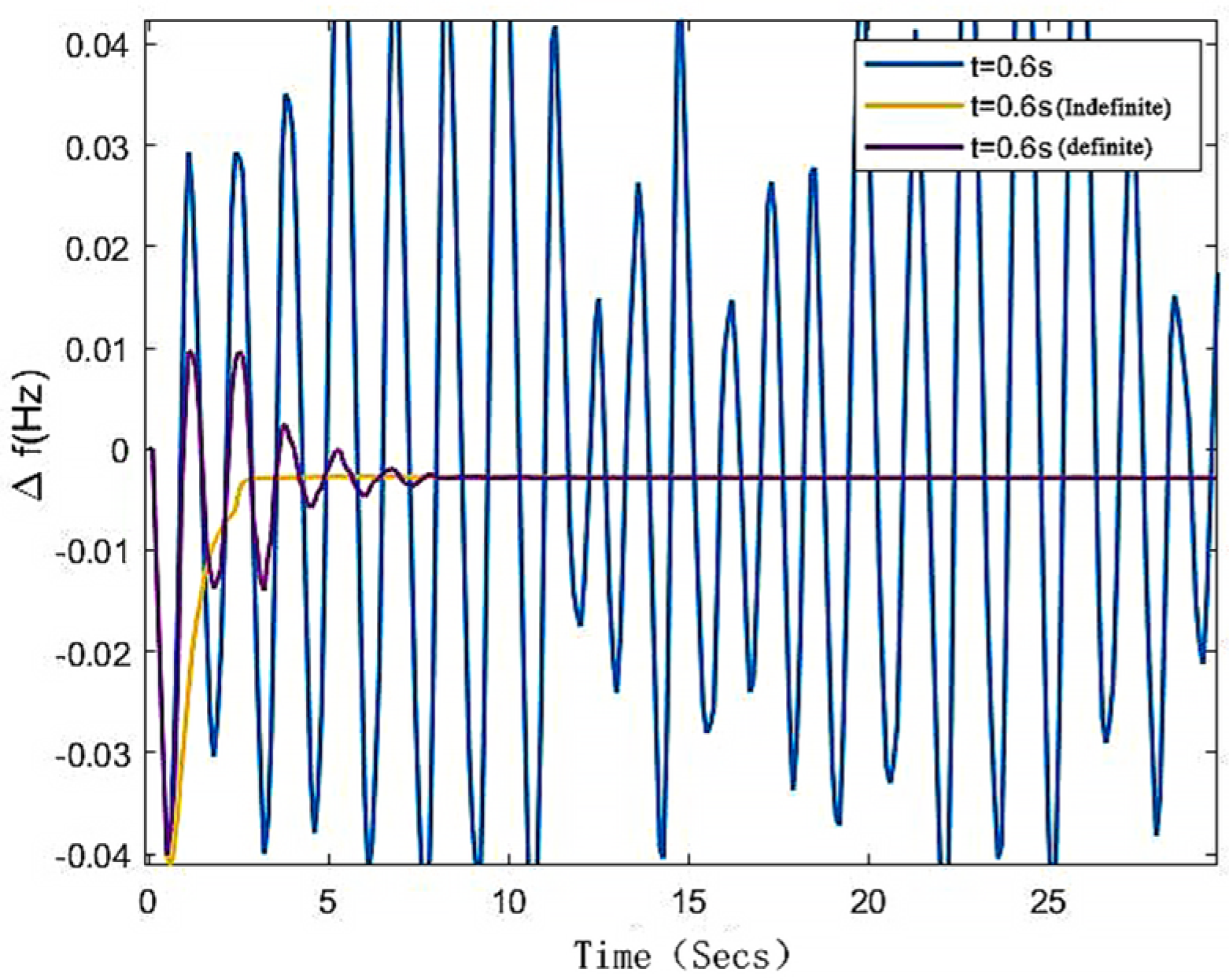
5.4. Dynamic Performance of Systems with Random and Variable Delays under Different Compensation Strategies
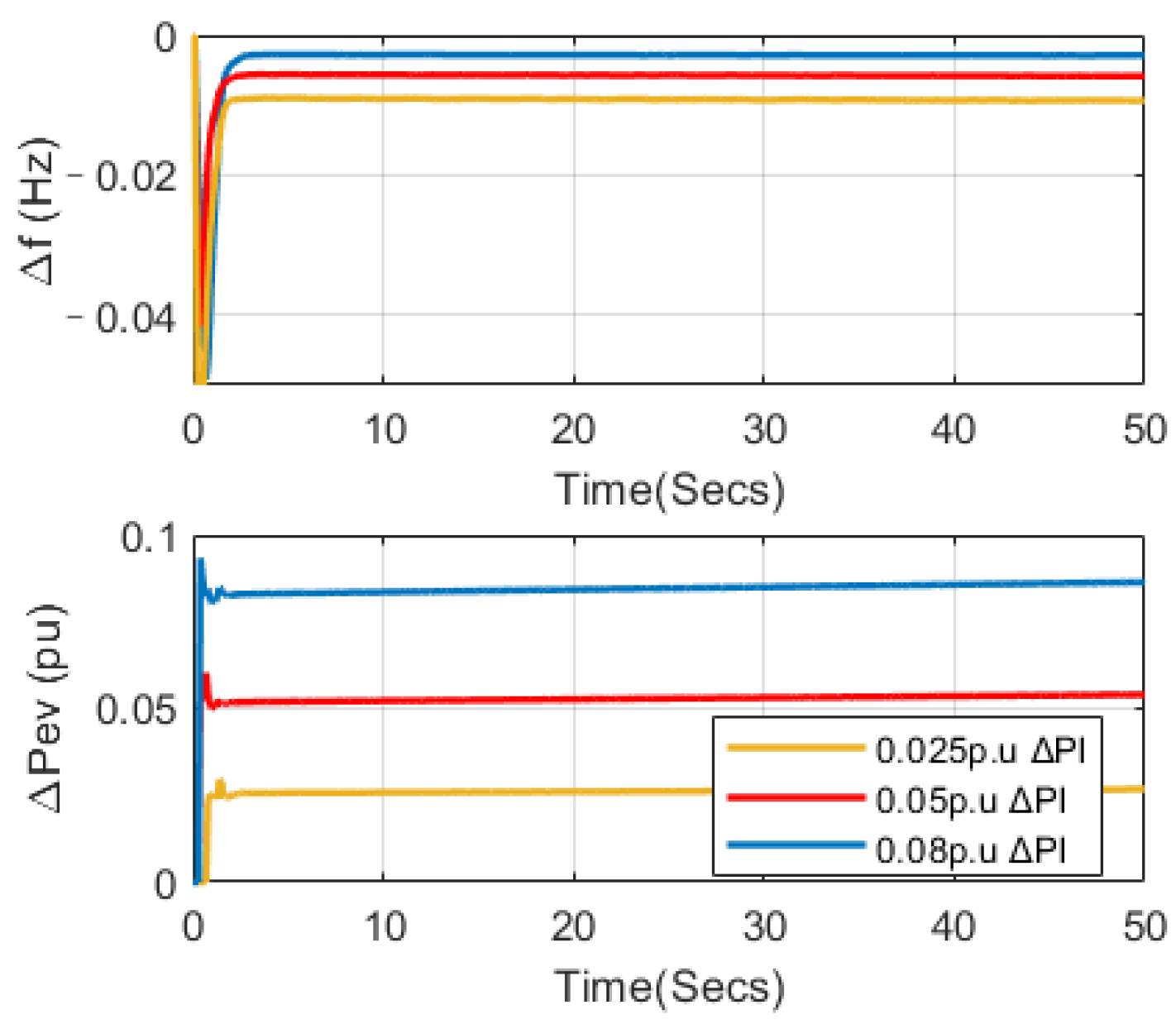
5.5. Dynamic Performance of a System with a Delay Compensation Strategy under Different Load Disturbances
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Barreto, R.; Faria, P.; Vale, Z. Electric Mobility. An Overview of the Main Aspects Related to the Smart Grid. Electronics 2022, 11, 1311. [Google Scholar] [CrossRef]
- Smil, V. Decarbonization Algebra: The COP26 Calls for Impossibly Steep Cuts in Carbon Emissions: Numbers Don’t Lie. IEEE Spectr. 2022, 59, 20–21. [Google Scholar] [CrossRef]
- Nana, O. Bonsu. Towards a circular and low-carbon economy: Insights from the transitioning to electric vehicles and net zero economy. J. Clean. Prod. 2020, 256, 120659. [Google Scholar]
- Antoniadou-Plytaria, K.; Steen, D.; Carlson, O.; Mohandes, B.; Ghazvini, M.A.F. Scenario-based Stochastic Optimization for Energy and Flexibility Dispatch of a Microgrid. IEEE Trans. Smart Grid 2022. [Google Scholar] [CrossRef]
- Kroposki, B. Integrating high levels of variable renewable energy into electric power systems. J. Mod. Power Syst. Clean Energy 2017, 5, 831–837. [Google Scholar] [CrossRef] [Green Version]
- Amamra, S.-A.; Marco, J. Vehicle-to-Grid Aggregator to Support Power Grid and Reduce Electric Vehicle Charging Cost. IEEE Access 2019, 7, 178528–178538. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, H.; Yang, J. Model Switching Frequency of Electrohydraulic-Power-Coupled Electric Vehicles with Different Delay Control Times. Electronics 2022, 11, 1299. [Google Scholar] [CrossRef]
- Zhang, C.-K.; Jiang, L.; Wu, Q.H.; He, Y.; Wu, M. Delay-Dependent Robust Load Frequency Control for Time Delay Power Systems. IEEE Trans. Power Syst. 2013, 28, 2192–2201. [Google Scholar] [CrossRef]
- Liu, F.; Li, Y.; Cao, Y.; She, J.; Wu, M. A Two-Layer Active Disturbance Rejection Controller Design for Load Frequency Control of Interconnected Power System. IEEE Trans. Power Syst. 2016, 31, 3320–3321. [Google Scholar] [CrossRef]
- Jin, L.; Zhang, C.-K.; He, Y.; Jiang, L.; Wu, M. Delay-Dependent Stability Analysis of Multi-Area Load Frequency Control with Enhanced Accuracy and Computation Efficiency. IEEE Trans. Power Syst. 2019, 34, 3687–3696. [Google Scholar] [CrossRef]
- Rehmani, M.H.; Reisslein, M.; Rachedi, A.; Erol-Kantarci, M.; Radenkovic, M. Integrating Renewable Energy Resources into the Smart Grid: Recent Developments in Information and Communication Technologies. IEEE Trans. Ind. Inform. 2018, 14, 2814–2825. [Google Scholar] [CrossRef]
- Alam, S.; Al-Ismail, F.S.; Salem, A.; Abido, M.A. High-Level Penetration of Renewable Energy Sources into Grid Utility: Challenges and Solutions. IEEE Access 2020, 8, 190277–190299. [Google Scholar] [CrossRef]
- Cao, Y.; Zhong, Y.; Peng, X.; Pan, S. Energy Efficiency Maximization for Hybrid-Powered 5G Networks with Energy Cooperation. Electronics 2022, 11, 1605. [Google Scholar] [CrossRef]
- Ko, K.S.; Sung, D.K. The Effect of EV Aggregators with Time-Varying Delays on the Stability of a Load Frequency Control System. IEEE Trans. Power Syst. 2018, 33, 669–680. [Google Scholar] [CrossRef]
- Huang, C.; Yue, D.; Xie, X.; Xie, J. Anti-Windup Load Frequency Controller Design for Multi-Area Power System with Generation Rate Constraint. Energies 2016, 9, 330. [Google Scholar] [CrossRef]
- Guille, C.; Gross, G. A conceptual framework for the(V2G) implementation. Energy Policy 2009, 11, 4379–4390. [Google Scholar] [CrossRef]
- Larsen, E.; Chandrashekhara, D.K.; Ostergard, J. Electric Vehicles for Improved Operation of Power Systems with High Wind Power Penetration. In Proceedings of the Energy 2030 Conference, Atlanta, GA, USA, 17–18 November 2008; pp. 1–6. [Google Scholar]
- Medina, J.; Muller, N.; Roytelman, I. Demand response and distribution grid operations: Opportunities and challenges. IEEE Trans. Smart Grid 2010, 1, 193–198. [Google Scholar] [CrossRef]
- Li, J.; Ai, X.; Hu, J. Supple-mentary Frequency Regulation Strategy Considering Electric Vehicles. In Proceedings of the 2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 10–22 October 2018; pp. 1–9. [Google Scholar]
- Annamraju, A.; Nandiraju, S. Coordinated control of conventional power sources and PHEVs using jaya algorithm optimized PID controller for frequency control of a renewable penetrated power system. Prot. Control Mod. Power Syst. 2019, 4, 343–355. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Yang, W.; Hu, Y.; Dzung, P.Q. Frequency Regulation at a Wind Farm Using Time-Varying Inertia and Droop Controls. IEEE Trans. Ind. Appl. 2019, 55, 213–224. [Google Scholar] [CrossRef]
- Zhong, J.; He, L.; Li, C.; Cao, Y.; Wang, J.; Fang, B.; Zeng, L.; Xiao, G. Coordinated control for large-scale EV charging facilities and energy storage devices participating in frequency regulation. Appl. Energy 2014, 123, 253–262. [Google Scholar] [CrossRef]
- Fan, H.; Jiang, L.; Zhang, C.K.; Mao, C.X. Frequency regulation of multi-area power systems with plug-in electric vehicles considering communication delays. IET Gener. Transm. Distrib. 2016, 14, 3481–3491. [Google Scholar] [CrossRef] [Green Version]
- Zhao, N.; Gorbachev, S.; Yue, D.; Kuzin, V.; Dou, C.; Zhou, X.; Dai, J. Model predictive based frequency control of power system incorporating air-conditioning loads with communication delay. Int. J. Electr. Power Energy Syst. 2022, 138, 107856. [Google Scholar] [CrossRef]
- Peng, C.; Zhang, J. Delay-distribution-dependent load frequency control of power systems with probabilistic interval delays. IEEE Trans. Power Syst. 2015, 4, 3309–3331. [Google Scholar] [CrossRef]
- Ahmed, M.; Zheng, Y.; Amine, A.; Fathiannasab, H.; Chen, Z.W. The role of artificial intelligence in the mass adoption of electric vehicles. Joule 2021, 5, 2296–2322. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Yang, F.; Hu, W.; Zhang, Z.; Zhou, X. Delay Compensation Control Strategy for Electric Vehicle Participating in Frequency Regulation Based on MPC Algorithm. Electronics 2022, 11, 2341. https://doi.org/10.3390/electronics11152341
Yang Z, Yang F, Hu W, Zhang Z, Zhou X. Delay Compensation Control Strategy for Electric Vehicle Participating in Frequency Regulation Based on MPC Algorithm. Electronics. 2022; 11(15):2341. https://doi.org/10.3390/electronics11152341
Chicago/Turabian StyleYang, Zhichun, Fan Yang, Wei Hu, Zhixuan Zhang, and Xia Zhou. 2022. "Delay Compensation Control Strategy for Electric Vehicle Participating in Frequency Regulation Based on MPC Algorithm" Electronics 11, no. 15: 2341. https://doi.org/10.3390/electronics11152341
APA StyleYang, Z., Yang, F., Hu, W., Zhang, Z., & Zhou, X. (2022). Delay Compensation Control Strategy for Electric Vehicle Participating in Frequency Regulation Based on MPC Algorithm. Electronics, 11(15), 2341. https://doi.org/10.3390/electronics11152341




