A Hierarchical Random Graph Efficient Sampling Algorithm Based on Improved MCMC Algorithm
Abstract
:1. Introduction
- (1)
- A novel algorithm for sampling hierarchical random graphs is proposed. The algorithm allows two candidate states to be generated and takes the one with the maximum likelihood in the Markov process to speed up the traversal of hierarchical random graph sets.
- (2)
- By means of competition, eliminate the worse of the two candidate states to avoid producing multiple Markov chains. At the same time, this method indirectly leads to the Markov chain with more detailed balance.
2. Related Work
3. TST-MCMC Algorithm
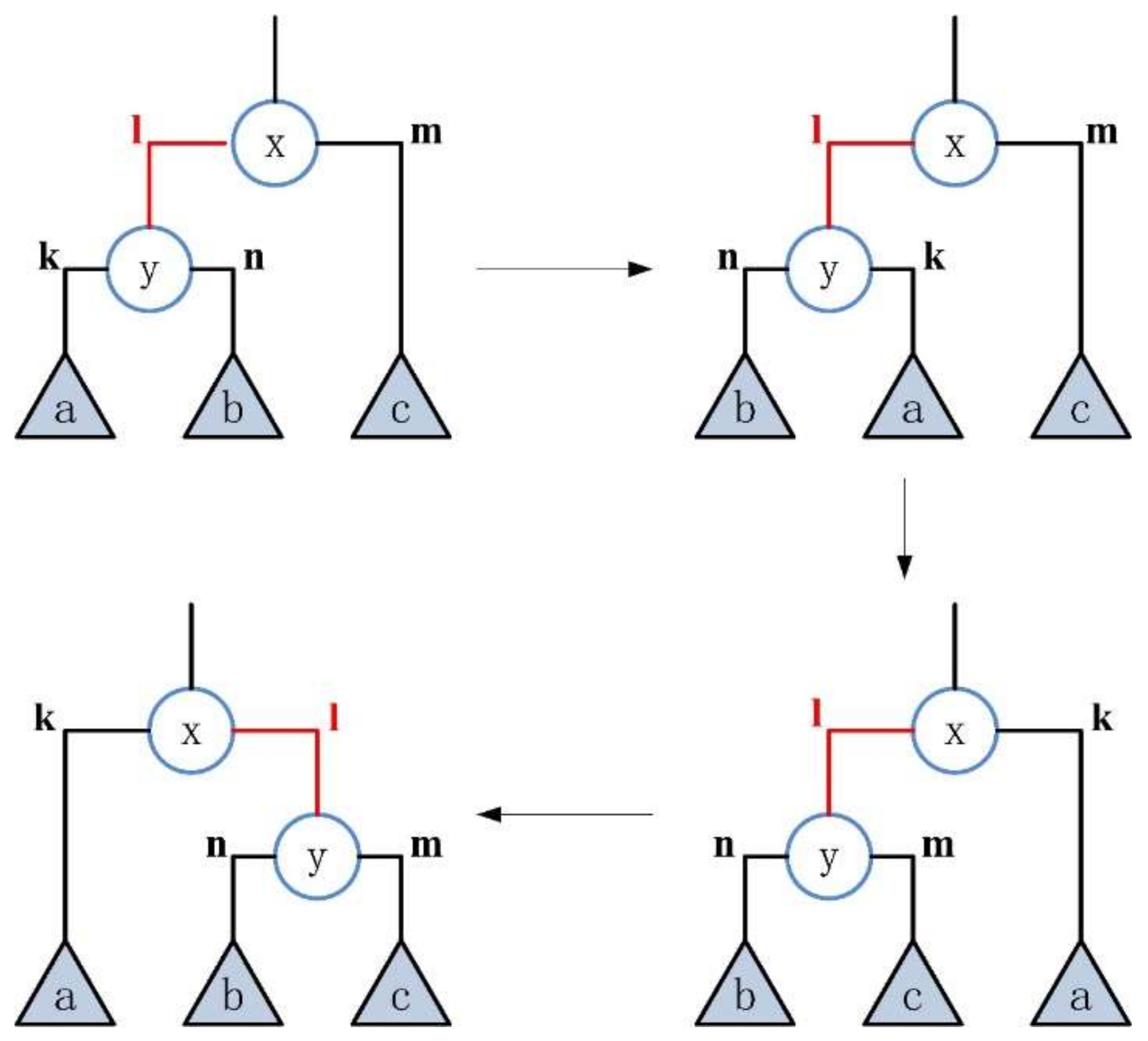
3.1. Subtree Rearrangement
- 1.
- The type of inner edge is “left”
- transformation
- transformation
- 2.
- The type of inner edge is “right”
- transformation
- transformation
3.2. TST-MCMC Algorithm
3.3. Performance Analysis
| Algorithm 1 TST-MCMC |
| Let be the observed Graph. Build the initial HRG Compute likelihood of While (true) ←Randomly select two different internal nodes(non-root) Transform the dendrogram according to Compute likelihood of according to Equation (2) Transform the dendrogram according to Compute likelihood of according to Equation (2) ≥ 0 then Randomly generate a value ∈[0,1] then Record the current dendrogram structure else Keep intact else Randomly generate value ∈[0,1] then Record the current dendrogram structure else Keep intact |
3.4. Example
4. Experiments and Analysis
4.1. Experimental Setup
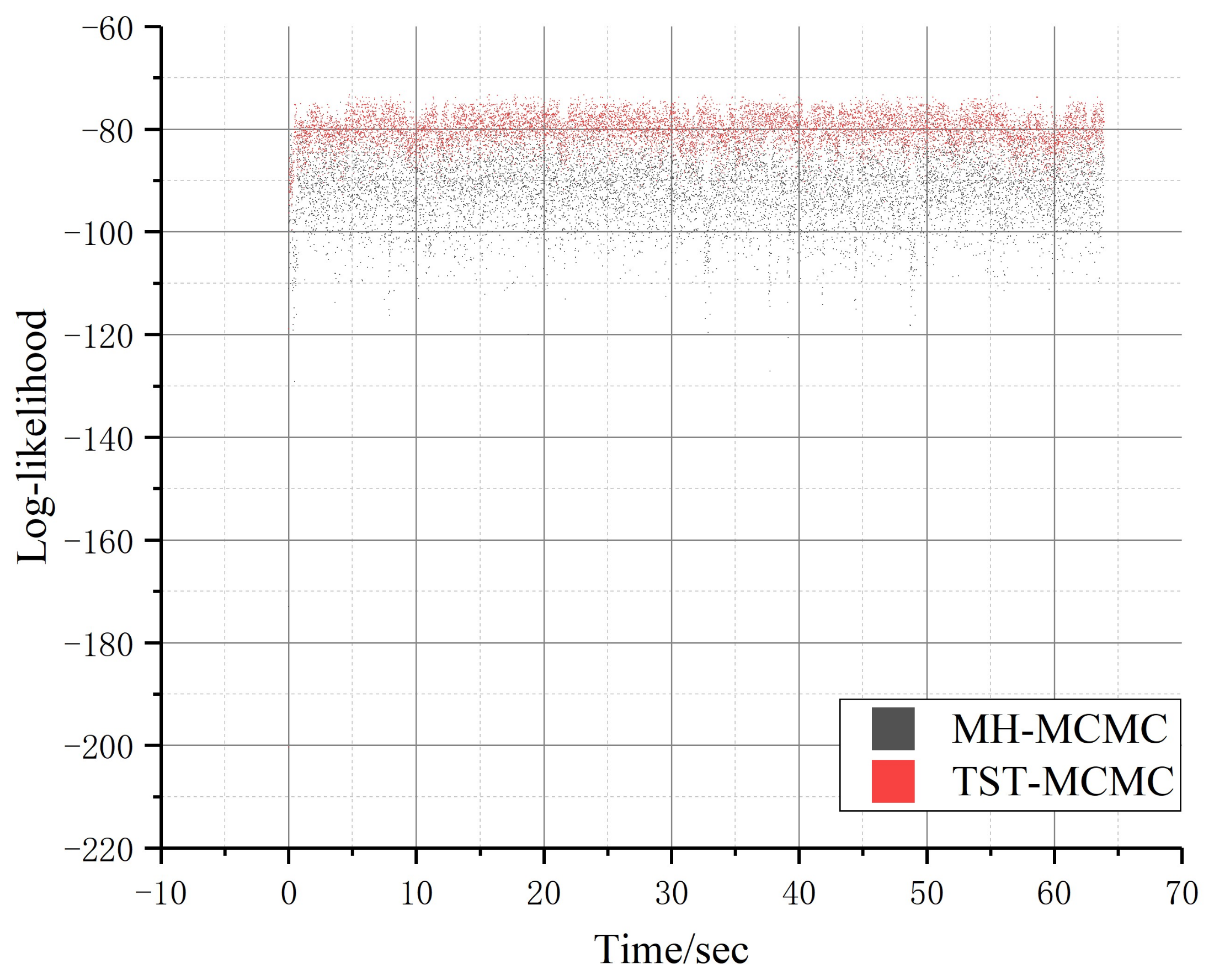
4.2. Experimental Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Watts, D.; Strogatz, S. Collective Dynamics of Small World Networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Barabasi, A.-L.; Albert, R. Emergence of Scaling in Random Networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Girvan, M.; Newman, M. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kernighan, B.; Lin, S. An Efficient Heuristic Procedure for Partitioning Graphs. Bell Syst. Tech. J. 1970, 49, 291. [Google Scholar] [CrossRef]
- Pothen, A.; Simon, H.; Liou, K.-P. Partitioning Sparse Matrices with Eigenvectors of Graphs. SIAM J. Matrix Anal. Appl. 1990, 11, 430–452. [Google Scholar] [CrossRef]
- Kanungo, T.; Mount, D.; Netanyahu, N.; Piatko, C.; Silverman, R.; Wu, A. A Local Search Approximation Algorithm for k-Means Clustering. Comput. Geom. 2004, 28, 89–112. [Google Scholar] [CrossRef]
- Park, H.-S.; Jun, C.-H. A simple and fast algorithm for K-medoids clustering. Expert Syst. Appl. 2009, 36, 3336–3341. [Google Scholar] [CrossRef]
- Zhang, X.-K.; Ren, J.; Song, C.; Jia, J.; Zhang, Q. Label propagation algorithm for community detection based on node importance and label influence. Phys. Lett. A 2017, 381, 2691–2698. [Google Scholar] [CrossRef]
- Azaouzi, M.; Romdhane, L. An evidential influence-based label propagation algorithm for distributed community detection in social networks. Procedia Comput. Sci. 2017, 112, 407–416. [Google Scholar] [CrossRef]
- Ravasz, E.; Somera, A.L.; Mongru, D.A.; Oltvai, Z.N.; Barabasi, A.L. Hierarchical organization of modularity in metabolic networks. Science 2002, 297, 1551–1555. [Google Scholar] [CrossRef] [Green Version]
- Zhou, C.; Zemanova, L.; Zamora, G.; Hilgetag, C.C.; Kurths, J. Hierarchical organization unveiled by functional connectivity in complex brain networks. Phys. Rev. Lett. 2006, 97, 238103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sales-Pardo, M.; Guimera, R.; Moreira, A.; Amaral, A.L. Extracting the Hierarchical Organization of Complex Systems. Proc. Natl. Acad. Sci. USA 2007, 104, 15224–15229. [Google Scholar] [CrossRef] [Green Version]
- Brzoska, L.; Fischer, M.; Lentz, H.H.K. Hierarchical Structures in Livestock Trade Networks-A Stochastic Block Model of the German Cattle Trade Network. Front. Vet. Sci. 2020, 7, 281. [Google Scholar] [CrossRef] [PubMed]
- Robaina-Estevez, S.; Nikoloski, Z. Flux-based hierarchical organization of Escherichia coli’s metabolic network. PLoS Comput. Biol. 2020, 16, e1007832. [Google Scholar] [CrossRef] [Green Version]
- Jin, D.; Liu, J.; Jia, Z.X.; Liu, D.Y. K-nearest-neighbor network based data clustering algorithm. Pattern Recogn. Artif. Intell. 2010, 23, 546–551. [Google Scholar]
- Newman, M. Fast algorithm for detecting community structure in networks. Phys. Rev. E. 2004, 69, 066133. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, J.; Wang, D.; Zhao, W.; Feng, S.; Zhang, Y. A community mining algorithm based on core nodes expansion. J. Shandong Univ. 2016, 51, 106–114. (In Chinese) [Google Scholar]
- Guimerà, R.; Sales-Pardo, M.; Amaral, L. Modularity from Fluctuations in Random Graphs and Complex Networks. Phys. Rev. E 2004, 70, 025101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reichardt, J.; Bornholdt, S. Statistical Mechanics of Community Detection. Phys. Rev. E 2006, 74, 016110. [Google Scholar] [CrossRef] [Green Version]
- Fortunato, S.; Barthelemy, M. Resolution limit in community detection. Proc. Natl. Acad. Sci. USA 2007, 104, 36–41. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Good, B.H.; de Montjoye, Y.-A.; Clauset, A. Performance of modularity maximization in practical contexts. Phys. Rev. E 2010, 81, 046106. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Clauset, A.; Moore, C.; Newman, M.E.J. Structural inference of hierarchies in network. In Proceedings of the ICML Workshop on Statistical Network Analysis, Pittsburgh, PA, USA, 29 June 2006. [Google Scholar]
- Clauset, A.; Moore, C.; Newman, M.E. Hierarchical structure and the prediction of missing links in networks. Nature 2008, 453, 98–101. [Google Scholar] [CrossRef] [PubMed]
- Lin, P.Y.; Liu, J.Y. Evaluation and calibration of ultimate bond strength models for soil nails using maximum likelihood method. Acta Geotech. 2020, 15, 1993–2015. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Siems, T. Markov Chain Monte Carlo on finite state spaces. Math. Gaz. 2020, 104, 281–287. [Google Scholar] [CrossRef]
- Martino, L. A Review of Multiple Try MCMC algorithms for Signal Processing. Digit. Signal Processing 2018, 75, 134–152. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.S.; Liang, F.; Wong, W.H. The Multiple-Try Method and Local Optimization in Metropolis Sampling. J. Am. Stat. Assoc. 2000, 95, 121–134. [Google Scholar] [CrossRef]
- Martino, L.; Elvira, V.; Camps-Valls, G. Group Importance Sampling for particle filtering and MCMC. Digit. Signal Processing 2018, 82, 133–151. [Google Scholar] [CrossRef] [Green Version]
- Luengo, D.; Martino, L.; Bugallo, M.; Elvira, V.; Särkkä, S. A survey of Monte Carlo methods for parameter estimation. EURASIP J. Adv. Signal Processing 2020, 2020, 25. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef] [Green Version]
- Tabarzad, M.A.; Hamzeh, A. A heuristic local community detection method (HLCD). Appl. Intell. 2017, 46, 62–78. [Google Scholar] [CrossRef]
- Chua, F.C.T.; Lim, E.P. Modeling Bipartite Graphs Using Hierarchical Structures. In Proceedings of the 2011 International Conference on Advances in Social Networks Analysis and Mining, Kaohsiung, Taiwan, 25–27 July 2011. [Google Scholar]
- Allen, D.; Moon, H.; Huber, D.; Lu, T.-C. Hierarchical Random Graphs for Networks with Weighted Edges and Multiple Edge Attributes. In Proceedings of the 2011 International Conference on Data Mining, Las Vegas, NV, USA, 18–21 July 2011. [Google Scholar]
- Wu, D.D.; Hu, X.; He, T. Exploratory Analysis of Protein Translation Regulatory Networks Using Hierarchical Random Graphs. BMC Bioinform. 2010, 11 (Suppl. S3), S2. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fountain, T.; Lapata, M. Taxonomy induction using hierarchical random graphs. In Proceedings of the 2012 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Montreal, QC, Canada, 3–8 June 2012. [Google Scholar]
- Yang, Y.L.; Guo, H.; Tian, T.; Li, H.F. Link Prediction in Brain Networks Based on a Hierarchical Random Graph Model. Tsinghua Sci. Technol. 2015, 20, 306–315. [Google Scholar] [CrossRef]
- Gao, T.; Li, F.; Chen, Y.; Zou, X. Local Differential Privately Anonymizing Online Social Networks Under HRG-Based Model. IEEE Trans. Comput. Soc. Syst. 2018, 5, 1009–1020. [Google Scholar] [CrossRef]
- Mossel, E.; Vigoda, E. Phylogenetic MCMC algorithms are misleading on mixtures of trees. Science 2005, 309, 2207–2209. [Google Scholar] [CrossRef] [Green Version]
- Zachary, W.W. An Information Flow Model for Conflict and Fission in Small Groups. J. Anthropol. Res. 1977, 33, 452–473. [Google Scholar] [CrossRef] [Green Version]
- Jordi, D.; Alex, A. Community detection in complex networks using extremal optimization. Phys. Rev. E 2005, 72, 027104. [Google Scholar]
- Von Mering, C.; Krause, R.; Snel, B.; Cornell, M.; Oliver, S.G.; Fields, S.; Bork, P. Comparative assessment of large-scale data sets of protein-protein interactions. Nature 2002, 417, 399–403. [Google Scholar] [CrossRef]
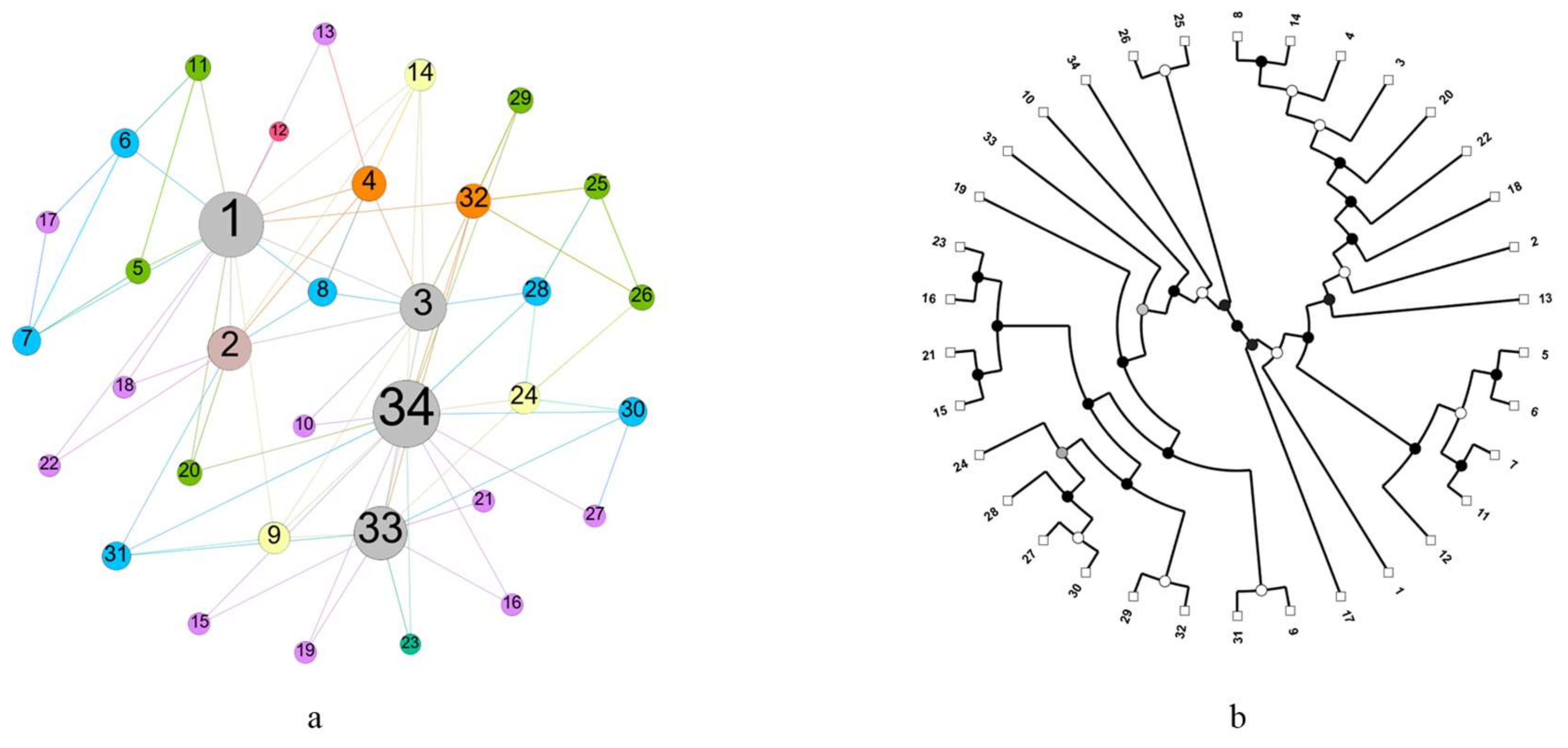
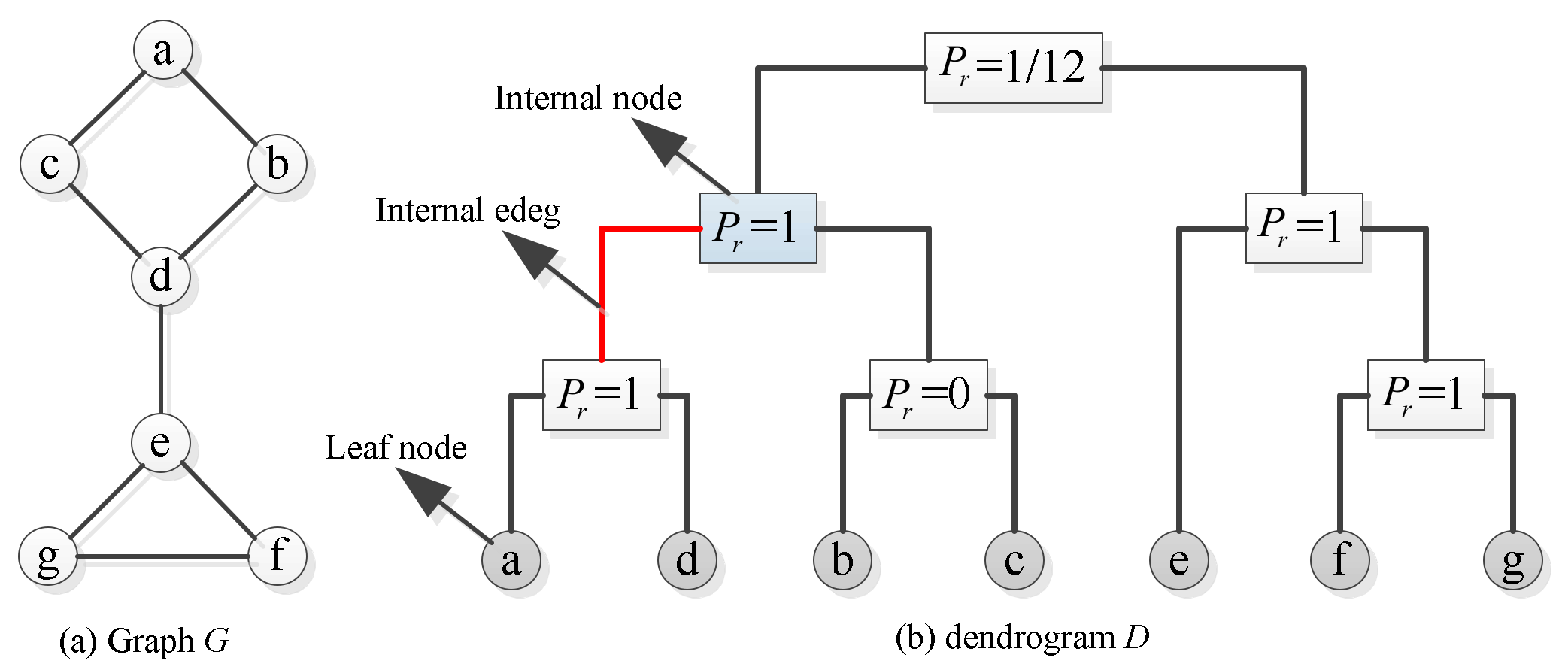










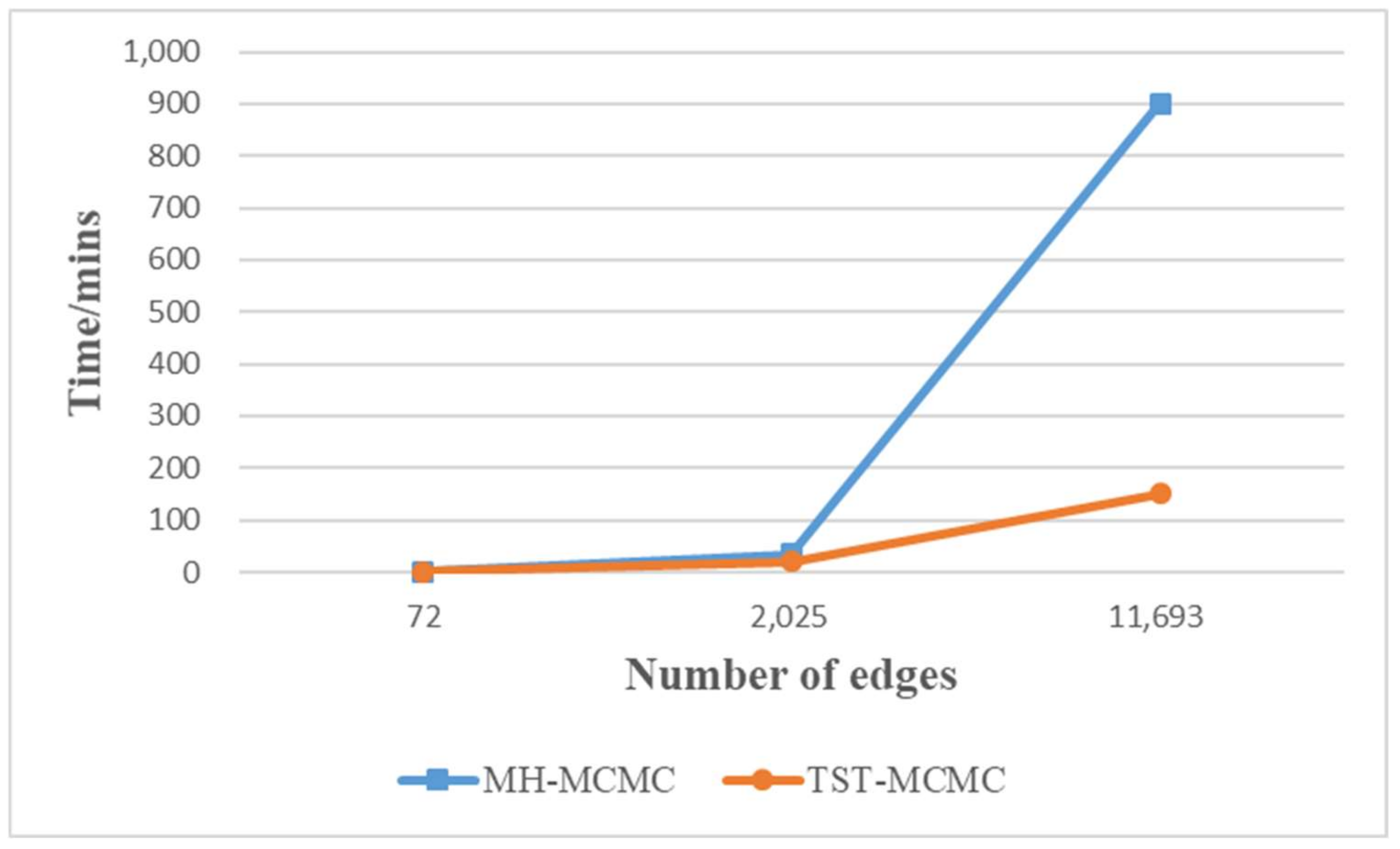
| Name | Nodes | Edges | Directed | Weight |
|---|---|---|---|---|
| Zachary Karate Club | 34 | 72 | undirected | unweighted |
| Metabolic | 453 | 2025 | undirected | unweighted |
| Yeast | 2375 | 11,693 | undirected | unweighted |
| Target | MH-MCMC | TST-MCMC | Difference |
|---|---|---|---|
| Mean | −4468.61 | −4314.27 | 154.34 |
| Standard deviation | 45.41 | 47.02 | 1.61 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tie, Z.; Zhu, D.; Hong, S.; Xu, H. A Hierarchical Random Graph Efficient Sampling Algorithm Based on Improved MCMC Algorithm. Electronics 2022, 11, 2396. https://doi.org/10.3390/electronics11152396
Tie Z, Zhu D, Hong S, Xu H. A Hierarchical Random Graph Efficient Sampling Algorithm Based on Improved MCMC Algorithm. Electronics. 2022; 11(15):2396. https://doi.org/10.3390/electronics11152396
Chicago/Turabian StyleTie, Zhixin, Dingkai Zhu, Shunhe Hong, and Hui Xu. 2022. "A Hierarchical Random Graph Efficient Sampling Algorithm Based on Improved MCMC Algorithm" Electronics 11, no. 15: 2396. https://doi.org/10.3390/electronics11152396






