1. Introduction
Quantum key distribution (QKD), based on the uncertainty principle and the No-Cloning theorem, theoretically has higher security than the existing information security schemes [
1]. However, the generated key itself has no substantive information. Only when it is encrypted by the encryption algorithm as a key can the information required by both sides of the communication be transmitted [
2,
3,
4,
5]. The encrypted key needs to be transmitted in the public channel, which inevitably leads to the risk of information disclosure. In order to delete the leaked information from the negotiation key containing the leaked information, Bennet et al. proposed an important privacy amplification step in the post-processing of quantum communication [
6,
7], which realizes the unconditional security of the quantum key distribution system by compressing the negotiation key into an absolutely secure final key [
8,
9,
10].
A common PA is to compress a string of keys through a universal hash function, and then eliminate the information leaked to attacker Eve. In this way, the security key can be obtained. The hash function is usually selected as the Toeplitz matrix, whose element is 0 or 1 [
11]. Some researchers use a variety of acceleration software methods provided by fast Fourier transform (FFT) [
12] to realize the privacy amplification algorithm through CPU and GPU software [
13]. Its experimental efficiency is relatively good and can achieve a considerable processing rate. In [
12], the researchers propose a FFT PA scheme on commercial CPU platform. The long input weak secure key is divided into many blocks, then PA procedures are parallel implemented for all sub-key blocks, and afterwards the outcomes are merged as the final secure key, but FFT also needs to consume a lot of computing resources. Moreover, for the practical quantum key distribution system, these methods of using CPU software to realize the PA algorithm have hidden dangers in security. There may be various unknown backdoors and vulnerabilities in this system, which greatly affect the work of quantum key distribution system. Therefore, researchers propose to use a field programmable gate array (FPGA) platform to implement the privacy amplification algorithm. The algorithm implemented by FPGA is a pure hardware logic circuit with low security risks. In [
14], Lu et al. proposed a PA algorithm implemented on FPGA platform. By constructing the required Toeplitz matrix on FPGA and using the characteristics of FPGA to calculate the Toeplitz matrix in parallel, they succeed in improving the running speed of the algorithm and the maximum safe coding rate of the system. In addition, the algorithm can also achieve any number of input key bits in a certain length, which is helpful for the implementation of future PA algorithms [
15]. In [
16], Toeplitz matrix is divided into several sub blocks, and FPGA is used to process the sub blocks in parallel to improve the operation speed. However, it only considers the reconstruction of the Toeplitz matrix, and does not involve the adequate processing of the negotiated key with the Toeplitz matrix. In view of the high requirements of hardware resources and low computing speed of Toeplitz matrix, researchers put forward some effective schemes to improve it. In [
17], they propose a privacy amplification algorithm based on LFSR to save storage space and speed up operation process. For the storage of elements in the Toeplitz matrix, only one register is needed, which greatly saves hardware storage resources. In [
18], Bai et al. proposed a PA algorithm based on Toeplitz matrix, which uses LFSR to save storage space and speed up the privacy amplification process. The continuous state transformation of LFSR is constructed. The results of each LFSR state are accumulated at the same time of LFSR state transition. Repeat the above steps through block iteration to obtain the final key. Because the operations of different accumulators are independent, the calculation of the final key is parallel, and the speed of the algorithm can be improved. However, due to the characteristics of its sequential transformation to produce the whole Toeplitz matrix, the rate of generating the final key is still inevitably affected.
In this paper, we propose a PA algorithm based on Cellular Automata (CA) and block structure. CA is used to generate a pseudorandom sequence with good random characteristics. The sequence performs a bit operation with the negotiation key and accumulates in blocks, so as to realize the function of compressing the longer key into the final key. Unlike the algorithm of dynamically generating Toeplitz matrix using LFSR, CA does not need to generate random sequences bit by bit like LFSR. Due to the characteristics of CA, it can generate many new random sequences in parallel, which improves the operation speed and can generate keys of any length. The National Institute of Standards and Technology (NIST) randomness test [
19] and avalanche test show that the final key generated by the algorithm also has good randomness performance and a good avalanche effect [
20,
21].
The rest of this paper is organized as follows.
Section 2 introduces some relevant principles used in this paper, including privacy amplification and Cellular Automata.
Section 3 introduces the algorithm and its implementation proposed in this paper.
Section 4 is the analysis of the experimental results. Finally,
Section 5 is presented.
3. Proposed Algorithm
No matter how the designer optimizes it, the PA based on Toeplitz matrix needs to find a balance between resource consumption and time consumption, which will inevitably be greatly affected by the Toeplitz matrix itself required by the compression function. Therefore, we use CA, a tool that can generate pseudorandom sequences with good randomness, to replace Toeplitz matrix and realize the compression process from negotiation key to final key, so as to improve the speed of PA algorithm. Based on this idea, we propose a high-speed PA algorithm with memory-saving using CA.
Table 2 gives some notations involved in the algorithm.
Figure 2 depicts the process of the proposed PA algorithm.
As can be seen from
Figure 2,
n bits negotiation key
T is firstly divided into
K groups
with length
M. After dividing the negotiation key, process the group negotiation key in turn. For example, for the group negotiation key
with length
M, we further divide it into
C blocks and each block with length
N. To make
M satisfy
, it is necessary to add a zero sequence of
bits after the original negotiation key
T. The core of the algorithm is to use CA to generate multiple pseudorandom sequences with good randomness at the same time, and successfully compress the group negotiation key of length
M into the final key
of length
N through operation. After obtaining the result of the final key, we use the idea of iteration to take the current
N bits final key
as the initial value of CA used in the next group, the same algorithm is used to obtain the next
N bits final key. The above steps are repeated until all the group negotiation keys are processed and the final required
bits final key
H is generated.
Figure 3 shows the processing flow of the algorithm. The specific process of the algorithm will be described in detail below.
Step 1: Set the parameters according to the requirements, such as the length N of CA and the reciprocal C of the compression rate of the final key. After setting the parameters, divide the received n bits negotiation key T into small groups with length M. The last may not meet the requirement of length M. If the length does not meet the requirement, we will add a sufficient number of zeros m in the last group to make it meet the requirement of length.
Step 2: Initialize CA and set its running rules. In order to make the pseudorandom sequence generated by CA have good randomness, we need to adopt appropriate rules. Our algorithm selects rule 150 shown in
Table 1 among the 256 rules of ECA. Under this rule, the sequence space-time map generated by CA has obvious chaotic characteristics. As for the choice of the initial value of CA, we select the fixed first
N bits of
e,
,
or
.
Step 3: We further divide the group negotiation key with length M into blocks with length N, and then we combine these blocks with the N bits sequence generated by CA to perform bit and operation. The specific operation is that the first N length block is combined with the initial value of the CA , denoted as and the result is put into the N bits accumulator. After the first block operation, using the characteristics of the CA, we can update the N bits data of the CA at the same time, and the updated result performs bit and operation with the negotiation key of the next N length block . The result is also put into the N bits accumulator and performs modulo-2 addition with the previous result. Repeat the above steps until the C blocks M length negotiation key is calculated, we can take the value of the accumulator as the final key . Using the idea of iteration, we take the result of the final key as the N bits initial value of the next CA, repeat the above process again, and finally complete the calculation of the last group to obtain the final key .
Step 4: After all the negotiation keys are calculated, we can get the final key with K blocks length of N, and we combine it into a final security key H. Because the final key of the algorithm is obtained in blocks, using this feature, we can output the final result of the privacy amplification process in real time, which improves the data throughput of the hardware implementation.
We summarize the proposed PA algorithm as follow:
The proposed PA algorithm can be regarded as an -family of hash functions as follows. We associate a hash function h such that for any message of binary length M, is defined as .
The
-balanced hash function is defined [
11] as follows.
Definition 1. A family of hash functions is called -balanced if Theorem 1. For any values of N and M the above defined family of hash functions is -balanced for .
Proof. To show that the family is -balanced, notice that any non-zero message of length M and any string c of length N, iff . Since generated by ECA under rule 150 has random characteristics, the vector assumes this value c with probability of , and therefore happens with at most this probability. □
4. Experimental Results
The amount of computing resources consumed, the rate of generating the final key, the randomness of generating the final key, and the sensitivity to the change of the input key are four important indicators to evaluate the performance of a PA algorithm. In addition, we will also test the influence of the initial value of CA on the experimental results. In order to evaluate the algorithm we proposed in this paper, we carried out simulation experiments on Matlab R2020a platform, and analyzed the experimental results with [
12,
18] in these four aspects.
The computer used in this simulation experiment is configured as AMD Ryzen 5 5600 h with Radeon graphics 3.30 GHz, 16.0 GB memory and win11 operating system.
4.1. Analysis of Memory
The length of the negotiation key is usually long enough, due to the finite scale effect [
32,
33]. However, with the increase of the length of the negotiation key, the memory of Toeplitz matrix based PA will increase, and the storage of Toeplitz matrix elements is an obstacle.
If the algorithm in [
12] is used, the privacy amplification process is carried out by dividing the Toeplitz matrix into several sub matrices and using FFT fast operations on these sub matrices. Using this method, we need to store the information with the size of
bits.
If the method in [
18] is used and the Toeplitz matrix is generated by LFSR, we need to store the
N bits LFSR state and
N bits accumulator, and need
bits to complete the whole PA process,
bits in all. However, when
N is large, finding the irreducible polynomial of length
N is a troublesome problem.
In our algorithm, the state of CA changes iteratively by itself. When the size of CA is N, only N bits need to be stored, and we need bits to store the final key. With only bits, the whole PA process can be completed without looking for the irreducible polynomial required by LFSR.
4.2. Analysis of Final Key Generation Rate
In order to verify the advantages of this scheme, we will compare the key generation rates of different schemes under the same conditions. Firstly, we set several different negotiation key lengths from 0.64 million bits to 5.12 million bits, which is convenient for calculation. The compression ratio
is set to 0.1, the length of CA is set to 128 bits, the length of LFSR is the same as that of CA [
18], and the size of sub block meets the requirements of each algorithm.
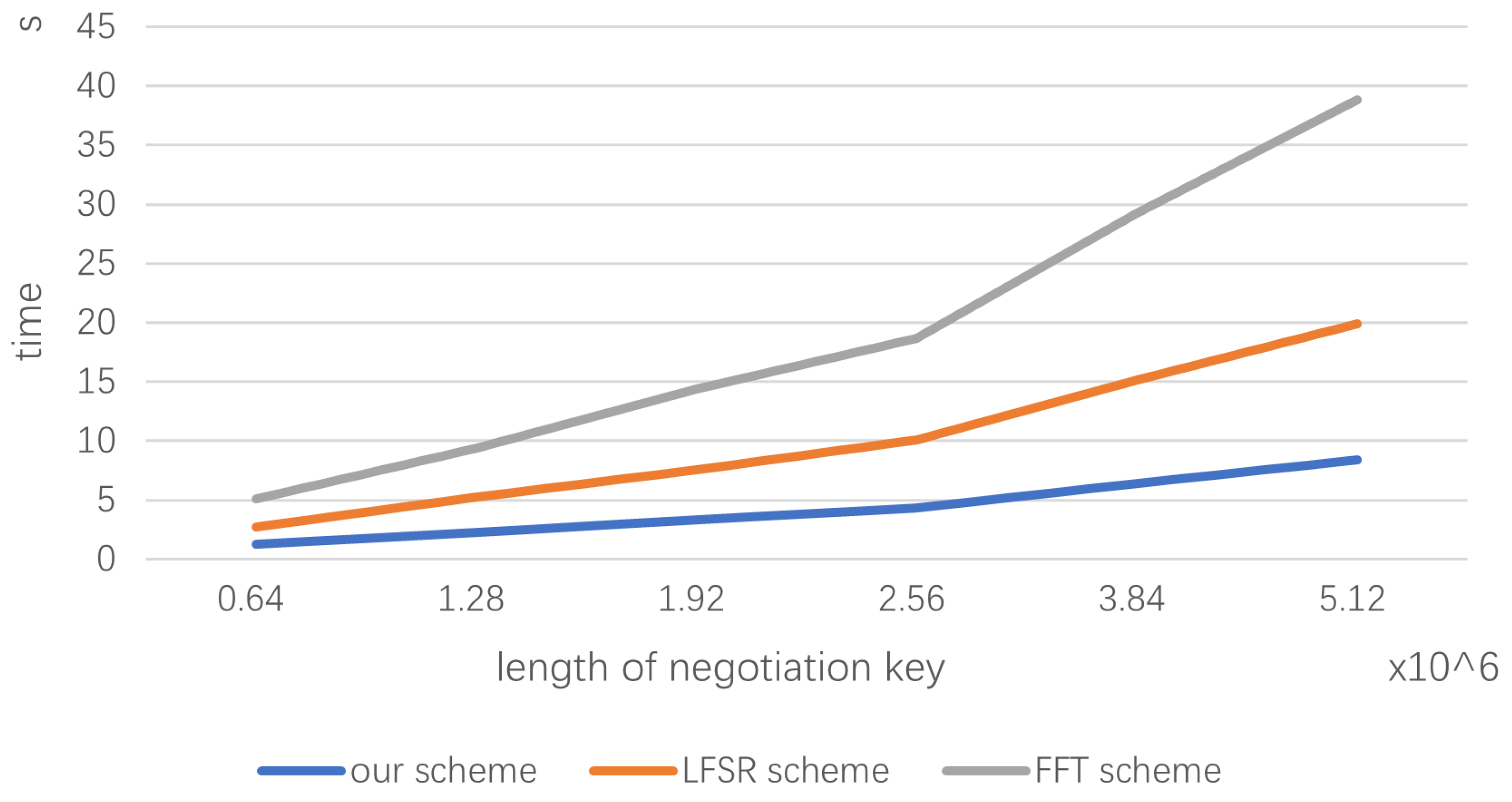
The experimental results are shown in
Figure 4. We can see that under the experimental conditions we set, the time consumption of the PA algorithm using CA is almost half that of the block LFSR algorithm [
18] and a quarter of that of the FFT algorithm [
12]. It can be seen that under certain conditions, the proposed PA algorithm has advantages in key generation rate and algorithm execution speed.
However, other factors will affect the execution speed of the algorithm and the generation rate of the key. Therefore, we then changed the conditions of the compression rate to 0.1, 0.2 and 0.5, respectively, and observed the impact of different compression rates on several algorithms (the length of the experimental negotiation key is 1.28 million bits). The results are shown in the
Table 3.
It can be seen from the table that the change of compression rate has little impact on several algorithms, because the change of compression rate will affect the size of the data to be processed, but the change of data size does not account for the overall negotiation key size, so the compression rate only has a slight impact on the execution time of the algorithm.
Finally, we investigate the effect of block length on the running time of the algorithm. Due to the influence of algorithm design, we only compare the block LFSR and CA algorithms. The block length of negotiation key in the two scheme is that of the length of CA and LFSR. Observe the effects of different lengths of CA and LFSR on the operation speed of the two algorithms (the length of the experimental negotiation key is 1.28 million bits and the compression rate is 0.1). The results are shown in the
Table 4.
It can be seen that with the increase of the length of pseudorandom sequence generators such as CA and LFSR, the execution time of the PA algorithm using CA changes slightly, while the time consumption of the block LFSR PA algorithm [
18] increases with the increase of the block length, which shows that the PA algorithm using CA is less sensitive to the block length. The CA with appropriate length can be selected according to the actual needs, while the LFSR can only select the LFSR with a fixed range to meet the appropriate length due to the difficulty of finding the higher-order primitive polynomial and the high sensitivity to the change of block length. We can find that the PA algorithm using CA has advantages in this aspect.
4.3. Randomness Analysis of Final Key
For the randomness analysis of the final key, we choose to use NIST test tools [
19] to analyze the final binary key.
We set the length of the negotiation key to 1.28 million bits and the compression rate to 0.1. We test the final key generated by CA with the length of 64 bits, 128 bits and 256 bits, respectively, and analyze the influence of CA with different length on the randomness of the key. The results are shown in the
Table 5 below.
From the data analysis shown in the
Table 5, the longer the length of CA, the more binary digital sequences can be represented by it, so the randomness of the pseudorandom sequences generated by it is stronger. When it is applied to the PA algorithm, the randomness of the final key generated by it with the length of CA is also similar to the pseudorandom sequence of CA. With the increase of the length of CA, the randomness of the final key increases slightly. It can be seen that although the three lengths of CA based PA algorithms have different sizes in each NIST test project, on the whole, the
p value of CA with large length is greater than that of CA with shorter length.
Moreover, because our algorithm uses the iterative structure, the initial value of the next CA is determined by the accumulation of the previous register, rather than the continuous transformation of the first initial value of the CA, which strengthens the correlation between the iterative block structures.
4.4. Avalanche Analysis of Final Key
Avalanche effect is an ideal characteristic of hash algorithm. Avalanche effect means that even the smallest change in the input (for example, reversing one binary bit) will lead to drastic changes in the results generated by the algorithm. Strict avalanche criterion is the formalization of avalanche effect. The criterion points out that when any input at the input is reversed, each bit in the output has a 0.5 probability of changing [
30]. In order to amplify the influence of interference on eavesdropper Eve, we need the final key to have good avalanche characteristics. If the key does not show a certain degree of avalanche characteristics, we can think that its randomness is poor.
Therefore, we conduct an avalanche test on the final key obtained by our algorithm. The length of the negotiation key we use is 1.28 million bits, the compression rate is 0.1, and the length of CA is 128 bits. Change the input 1, 2, 3, 4 and 5 binary bits, respectively, and observe the percentage of the number of bits of the final key flipped in the total length. The corresponding results are given in the
Table 6.
As can be seen from
Table 6, due to the iterative structure used in the algorithm, the overall connection of the final key is strong. The reversal of one input can cause the reversal of about 50% of the digit value of the whole final key. From the data in the table, we can get that the final key generated by the PA algorithm proposed in this paper has a good avalanche effect.
4.5. Influence of CA Initial Value
In this paper, CA is used to replace LFSR in the process of privacy amplification. For the chaotic CA used in this paper, its initial value sensitivity and complex system model are the sources of its randomness. Therefore, we need to test the influence of the initial value changed in a wide range on the experimental results to ensure that the proposed algorithm is universal for most of the initial value selection.
Avalanche effect reflects randomness to a certain extent and is more intuitive. We conduct avalanche test on the final key obtained from different CA initial values. We can change the initial value by changing the proportion
R of 1 s in the CA initial values. In this experiment, the selected
R is 0.1, 0.5 and 0.9, respectively. The length of the negotiation key we use is 1.28 million bits, the compression rate is 0.1, and the length of CA is 128 bits. Change the input 1, 2, and 3 binary bits, and observe the percentage of the number of bits of the final key flipped in the total length. The corresponding results are given in
Table 7.
From
Table 7, we can see that the avalanche effect is still good and still tends to be close to the strict avalanche criterion when the final key generated by the proposed PA algorithm changes the initial value of CA in a large range. We can get from it that the initial value selection of CA has little effect on the final key generated by the proposed algorithm.
5. Conclusions
In this paper, a high-speed PA algorithm for QKD system is proposed. CA is used to to construct a hash function for the secure key distribution. Different from using LFSR-based PA to establish Toeplitz matrix by sequential shift, the algorithm proposed in this paper uses CA, which can simultaneously iterate the sequence of N bits CA length, and calculate the input of a multi bits negotiation key at the same time, the speed of the algorithm is then improved. This algorithm also uses the idea of block iteration to process the overall negotiation key block by block, and strengthen the correlation of each block generated key through iteration. Finally, the analysis results show that the algorithm saves hardware memory resources and improves the running speed. The final shared key also has good randomness performance.
The algorithm proposed in this paper can carry out the parallel processing of multi bits negotiation key input, and it improves the speed. However, when processing the block negotiation keys, we still need to wait for the update and iteration of the CA itself, and the waiting time will slow down the running speed of the algorithm. Therefore, in order to further improve the generation rate based on the algorithm in this paper, when the hardware resources are sufficient, we can choose the improved scheme of exchanging resources for time, that is, increasing the number of CA. When the initial values are the same, at the same time, the multi block negotiation key is processed in parallel to improve the speed of the algorithm.
The security of a classical cryptosystem depends on the security of the key. The key can be distributed by the QKD system in this paper. The key of block cipher and public key cipher is usually very short, ranging from 128 bits to 4096 bits, the last corresponding bits of the final key can be used as the key. Another advantage of this algorithm is that the key generated in real time can be directly used as the encryption key of the classical stream cipher system, so as to achieve the effect of One-Time-Pad.
In addition, the CA can be implemented in FPGA to further improve the processing efficiency, which will be studied in the future.