Improved Belief Propagation List Decoding for Polar Codes
Abstract
:1. Introduction
- We optimize the permutation of factor graph for message iteration to achieve higher reliability of the decoding, which also reduces the complexity of the algorithm.
- We propose the metrics of bit reliability and decoding path reliability for the current codeword and the current iteration, which make the path expansion and pruning more accurate.
- The proposed algorithm flips one bit at a time and employs the flip-iteration-metric-expansion mechanism to further improve the decoding performance.
2. Polar Codes and Belief Propagation Decoder
2.1. Polar Codes
2.2. Belief Propagation Decoder
3. Design of Factor Graph Permutating for the IBPL Decoder
4. Design of Path Extension and Pruning for the IBPL Decoder
4.1. Design of Path Extension for the IBPL Decoder
4.2. Design of Path Pruning for the IBPL Decoder
| Algorithm 1 The proposed IBPL decoder. |
|
5. Simulation Results
5.1. Performance Comparison for Different Permutations of Factor Graph
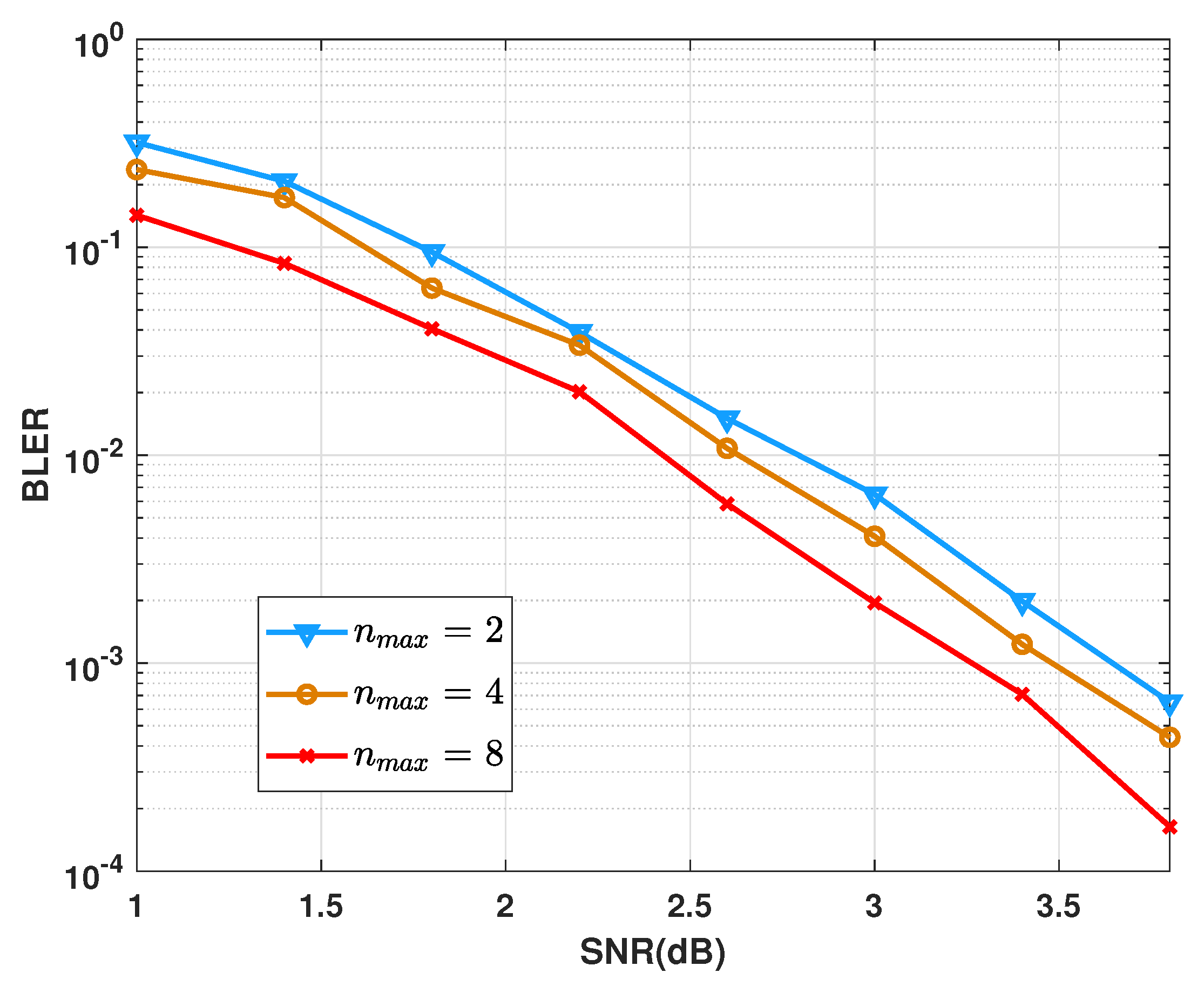
5.2. Performance Comparison of BP, BP-Flip, SCL and IBPL Decoding Algorithms
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| BPM | Bit parity-check metric |
| DPM | Decoding path metric |
| BCB | 2-right-port basic computational block |
| PPN | Parity-check passed node |
| BPPM | Bit parity-check path metric |
| FBER | Frozen-bit error rate |
References
- Arikan, E. Channel polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels. IEEE Trans. Inf. Theory 2009, 55, 3051–3073. [Google Scholar] [CrossRef]
- Liu, G.; Jiang, D. 5G: Vision and requirements for mobile communication system towards year 2020. Chin. J. Eng. 2016, 2016, 5974586. [Google Scholar] [CrossRef] [Green Version]
- Hu, W.; Zhang, M.; Li, Z.; Popov, S.; Leeson, M.; Xu, T. High-dimensional feature based non-coherent detection for multi-intensity modulated ultraviolet communications. J. Light. Technol. 2022, 40, 1879–1887. [Google Scholar] [CrossRef]
- Alamdar-Yazdi, A.; Kschischang, F.R. A simplified successive-cancellation decoder for polar codes. IEEE Commun. Lett. 2011, 15, 1378–1380. [Google Scholar] [CrossRef]
- Sarkis, G.; Gross, W.J. Increasing the tThroughput of polar decoders. IEEE Commun. Lett. 2013, 17, 725–728. [Google Scholar] [CrossRef]
- Sarkis, G.; Giard, P.; Vardy, A.; Thibeault, C.; Gross, W.J. Fast polar decoders: Algorithm and implementation. IEEE J. Sel. Areas Commun. 2014, 32, 946–957. [Google Scholar] [CrossRef] [Green Version]
- Tal, I.; Vardy, A. List decoding of polar codes. IEEE Trans. Inf. Theory 2015, 61, 2213–2226. [Google Scholar] [CrossRef]
- Arikan, E. A performance comparison of polar codes and reed-mullercodes. IEEE Commun. Lett. 2008, 12, 447–449. [Google Scholar] [CrossRef]
- Arikan, E. Polar codes: A pipelined implementation. In Proceedings of the 4th International Symposium on Broadband Communication (ISBC), Melaka, Malaysia, 11–14 July 2010; pp. 11–14. [Google Scholar]
- Hussami, N.; Korada, S.; Urbanke, R. Performance of polar codes for channel and source coding. In Proceedings of the 2009 IEEE International Symposium on Information Theory, Seoul, Korea, 28 June–3 July 2009; pp. 1488–1492. [Google Scholar]
- Elkelesh, A.; Ebada, M.; Cammerer, S.; ten Brink, S. Belief propagation decoding of polar codes on permuted factor graphs. In Proceedings of the 2018 IEEE Wireless Communications and Networking Conference (WCNC), Barcelona, Spain, 15–18 April 2018; pp. 1–6. [Google Scholar]
- Doan, N.; Hashemi, S.A.; Mondelli, M.; Gross, W.J. On the decoding of polar codes on permuted factor graphs. In Proceedings of the 2018 IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, United Arab Emirates, 9–13 December 2018; pp. 1–6. [Google Scholar]
- Elkelesh, A.; Ebada, M.; Cammerer, S.; Ten Brink, S. Belief propagation list decoding of polar codes. IEEE Commun. Lett. 2018, 22, 1536–1539. [Google Scholar] [CrossRef] [Green Version]
- Ren, Y.; Shen, Y.; Zhang, Z.; You, X.; Zhang, C. Efficient belief propagation polar decoder with loop simplification based factor graphs. IEEE Trans. Veh. Technol. 2020, 69, 5657–5660. [Google Scholar] [CrossRef]
- Yu, Y.; Pan, Z.; Liu, N.; You, X. Belief propagation bit-flip decoder for polar codes. IEEE Access 2019, 7, 10937–10946. [Google Scholar] [CrossRef]
- Shen, Y.; Song, W.; Ren, Y.; Ji, H.; You, X.; Zhang, C. Enhanced belief propagation decoder for 5G polar codes with bit-flipping. IEEE Trans. Circuits Syst. II Exp. Briefs 2020, 67, 901–905. [Google Scholar] [CrossRef]
- Ji, H.; Shen, Y.; Song, W.; Zhang, Z.; You, X.; Zhang, C. Hardware implementation for belief propagation flip decoding of polar codes. IEEE Trans. Circuits Syst. 2021, 68, 1330–1341. [Google Scholar] [CrossRef]
- Cavus, E.; Daneshrad, B. A performance improvement and error floor avoidance technique for belief propagation decoding of LDPC codes. In Proceedings of the 2005 IEEE 16th International Symposium on Personal, Indoor and Mobile Radio Communications, Berlin, Germany, 11–14 September 2005; Volume 4, pp. 2386–2390. [Google Scholar]
- Shen, Y.; Song, W.; Ji, H.; Ren, Y.; Ji, C.; You, X.; Zhang, C. Improved belief propagation polar decoders with bit-flipping algorithms. IEEE Trans. Commun. 2020, 68, 6699–6713. [Google Scholar] [CrossRef]
- Qin, M.; Guo, J.; Bhatia, A.; i Fàbregas, A.G.; Siegel, P.H. Polar code constructions based on LLR evolution. IEEE Commun. Lett. 2017, 21, 1221–1224. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Q.; Pan, X.; Ye, Z.; Gong, C. A simplified belief propagation decoder for polar codes. In Proceedings of the IEEE International Wireless Symposium (IWS 2014), Xi’an, China, 24–26 March 2014; pp. 1–4. [Google Scholar]
- Zhang, Y.; Liu, A.; Pan, X.; Ye, Z.; Gong, C. A modified belief propagation polar decoder. IEEE Commun. Lett. 2014, 18, 1091–1094. [Google Scholar] [CrossRef]
- Marvin, G.; Ahmed, E.; Jannis, C.; Stephan, B. A polar subcode approach to belief propagation list decoding. arXiv 2022, arXiv:2205.06631. [Google Scholar]
- Geiselhart, M.; Elkelesh, A.; Ebada, M.; Cammerer, S.; ten Brink, S. CRC-aided belief propagation list decoding of polar codes. In Proceedings of the 2020 IEEE International Symposium on Information Theory (ISIT), Los Angeles, CA, USA, 21–26 June 2020; pp. 395–400. [Google Scholar]









| Parameter | Values |
|---|---|
| Channel model | AWGN |
| Modulation mode | BPSK |
| Length of codeword, N | 128, 256 |
| Code rate | |
| Maximum number of decoding paths, | 4 |
| Maximum iteration number for path extension of the proposed IBPL decoder, | 5 |
| Maximum iteration number for inner BP decoding of the proposed IBPL decoder, | 20 |
| Maximum iteration number for BP decoders of other schemes, | 100 |
| Permutation | The Number of FNs (Rate) |
|---|---|
| s-descending | 216 () |
| Random | 298 () |
| Cyclic-shift | 328 () |
| Proposed -ascending | 446 () |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Huang, J.; Sun, C. Improved Belief Propagation List Decoding for Polar Codes. Electronics 2022, 11, 2458. https://doi.org/10.3390/electronics11152458
Li H, Huang J, Sun C. Improved Belief Propagation List Decoding for Polar Codes. Electronics. 2022; 11(15):2458. https://doi.org/10.3390/electronics11152458
Chicago/Turabian StyleLi, Huan, Jingxuan Huang, and Ce Sun. 2022. "Improved Belief Propagation List Decoding for Polar Codes" Electronics 11, no. 15: 2458. https://doi.org/10.3390/electronics11152458
APA StyleLi, H., Huang, J., & Sun, C. (2022). Improved Belief Propagation List Decoding for Polar Codes. Electronics, 11(15), 2458. https://doi.org/10.3390/electronics11152458







