Abstract
In multiplexed sequencing, the identification of DNA sequencing barcodes can effectively reduce the probability of sample misassignment. However, the great quantity of sequence data requires a high-throughput identification method. Therefore, based on a barcode identification scheme combining cyclic shifting with dynamic programming (DP), this paper proposes, implements and tests a hardware accelerator that can accelerate barcode identification. In the accelerator, considering that the computational complexity of the DP algorithm can be expressed as the multiplication of the lengths of both involved sequences, we design a systolic array structure with simplified processing element (PE) and a parallel circuit architecture to identify the insertion and deletion errors based on the traceback. The accelerator is implemented on a field-programmable gate array (FPGA), and its performance is compared with that of software implemented on a general-purpose computer. The experimental results indicate that, compared with the software implementation, the accelerator can achieve speedups of two orders of magnitude for longer barcodes.
1. Introduction
Next-generation sequencing (NGS) technologies can generate up to one billion reads of DNA sequence per slide, which continuously increase at a rapid pace [1,2]. Multiplexed nanopore sequencing has become an essential strategy to effectively utilize the rising sequencing capacity of NGS technologies [3]. In the multiplexing strategy, specific sample tags, also termed barcodes [4,5], are added to DNA fragments from multiple samples and used to separate sequencing reads belonging to different samples after sequencing. However, DNA barcodes are often corrupted by insertions, deletions, and substitutions during DNA synthesis and sequencing, resulting in sample index misassignments [6]. Therefore, some barcode construction and identification methods with different error correction capacity have been proposed in the past.
Conventional construction and identification methods for DNA barcodes are based on Hamming distance [7,8], Levenshtein distance [9,10], watermark code [11], etc. Recently, in [12], a scheme that combines a pseudorandom sequence with a cyclic block code was proposed to construct barcodes while the cyclic shifting and DP algorithm were used to identify barcodes. This scheme had the advantages of a low complexity and high robustness. However, if we still rely on software tools to realize these approaches, it will fail to meet the high-throughput sequencing requirement due to the fact that more and more sequencing reads need to be sorted and separated [13,14,15]. Compared to central processing units (CPUs), FPGAs provide a higher bit-level data parallelism and can customize hardware according to the requirements, which leads to a higher computing speed [16,17]. Therefore, taking the scheme proposed in [12] as an example, this paper designs and implements an FPGA-based hardware accelerator.
The cyclic shifting and DP algorithm are the important components of the accelerator. The cyclic shifting can be realized by a shift register in hardware. As a commonly used algorithm for sequence alignment, the DP algorithm has the computational complexity of the square of the length of the sequences, so it is crucial to accelerate the algorithm [18]. Recently, an FPGA used to realize a linear systolic array (LSA) to accelerate sequence alignment attracted extensive attention, and a series of studies were conducted. The general structures of the LSA were introduced in [19,20,21,22], but there were some deficiencies in these works. On one hand, the iterative equation of the sequence alignment algorithm was directly mapped to the PE. On the other hand, the above works did not describe the implementation of the identification of insertions and deletions in detail.
In this paper, a hardware accelerator for a barcode identification algorithm with a high robustness and low complexity is implemented and evaluated. Aiming at the quadratic complexity of the DP algorithm in the identification scheme, we propose an optimization strategy to improve the mapping efficiency of the PE by simplifying the mapping circuit of the iterative equations. Meanwhile, according to the traceback algorithm, a parallel circuit is designed to simultaneously mark and correct insertion and deletion errors on barcodes. The function simulation and performance verification platform are designed and built, and the comparison between a CPU platform and an FPGA acceleration platform is completed. The hardware results indicate that the accelerator has a significantly higher identification speed of sequencing barcodes than the software version of the same algorithm running on the general-purpose computer.
2. Background
This section reviews the related works, including the barcode identification scheme proposed in [12] and the DP algorithm for identifying an insertion/deletion (indel).
2.1. Sequencing Barcode Identification Method
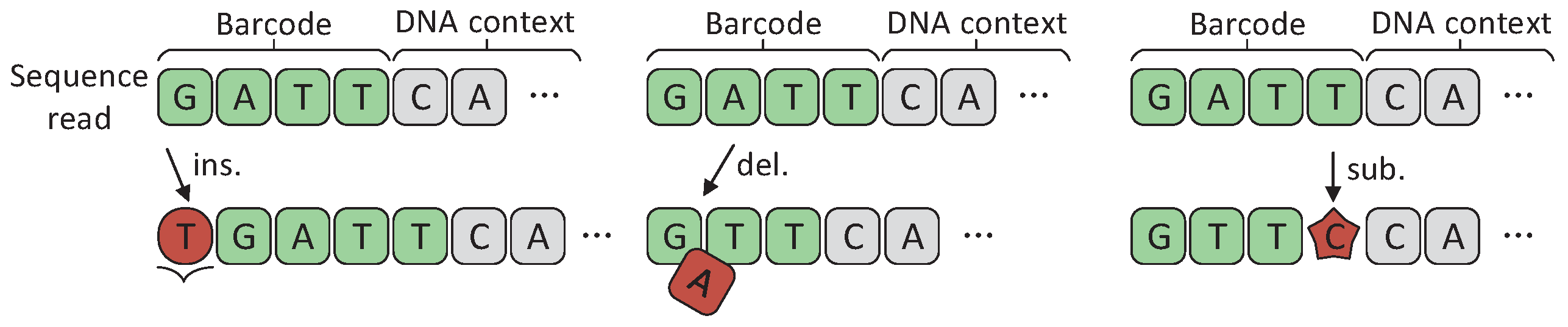
In multiplexed sequencing, DNA barcodes are added to each DNA fragment as special sample tags. After sequencing, sequencing reads belonging to different samples are separated by identifying barcodes. However, the insertions, deletions, and substitutions may occur randomly on barcodes due to the defects in DNA synthesis and sequencing, as shown in Figure 1. NGS technologies itself have error rates of ∼ [10]. For nanopore sequencing, the sequencing reads are quite long. Correspondingly, its sequencing error rate is very high (15.1%), of which indels are the main error type (10%) and the rest consists of substitutions (5.1%) [23]. These errors confuse the source of samples, which in turn reduces the accuracy of sequencing. Therefore, DNA barcodes need to be designed to resist insertion, deletion, and substitution errors, which is important for improving the sequencing accuracy of NGS.
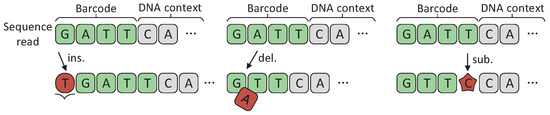
Figure 1.
Insertion/deletion/substitution errors on DNA sequencing barcodes.
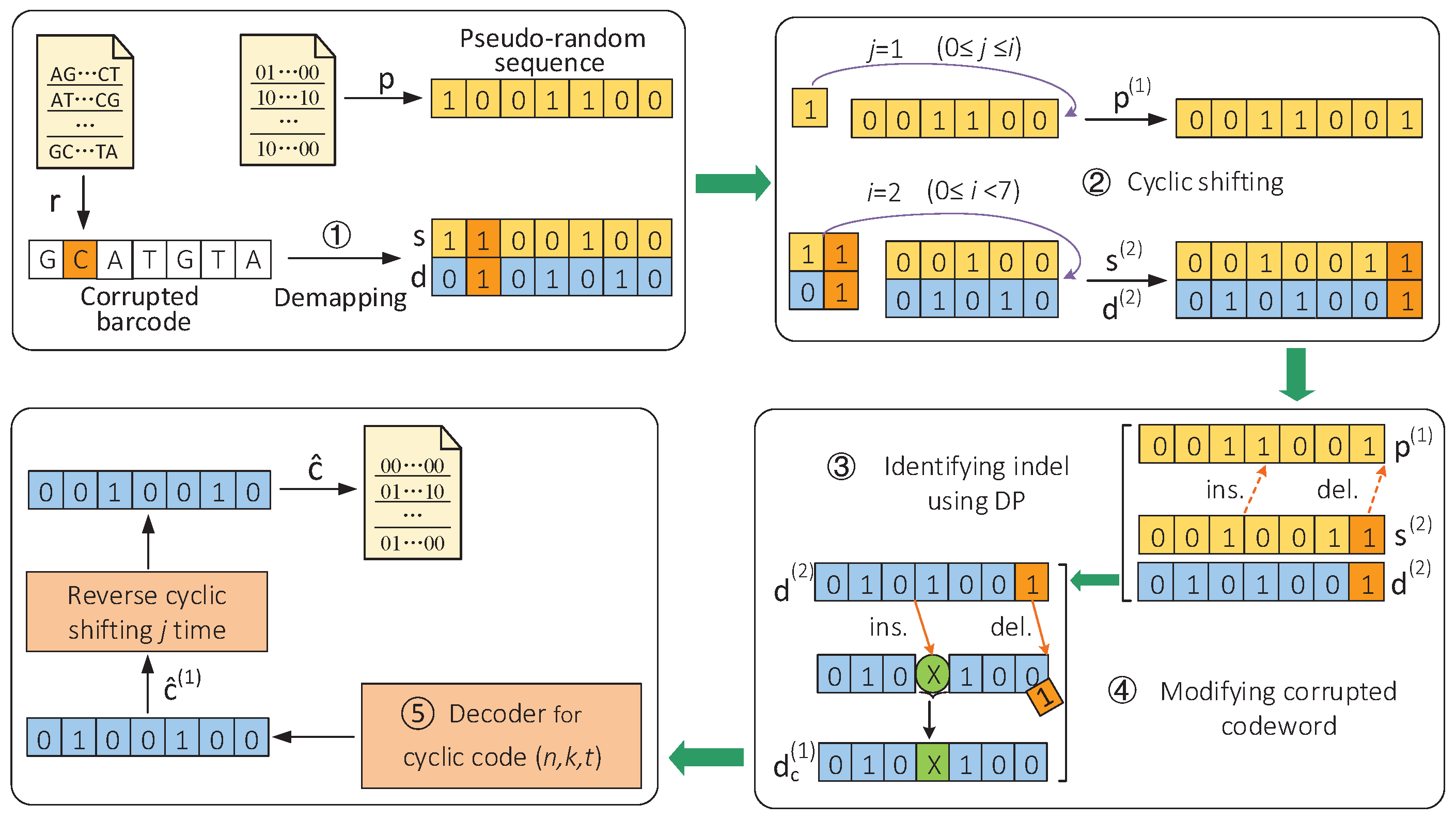
Aiming at various types of errors introduced during multiplexed nanopore sequencing, a new DNA barcode construction scheme was proposed in [12], which combined a pseudorandom sequence with a cyclic block code and converted them into bases by bit pairs. Here, the pseudorandom sequence acted as a hidden component of sequencing barcodes to identify indels and the cyclic block code was used against the substitution errors. For the barcode generated by the above construction scheme, an identification method using cyclic shifting and DP was proposed. The specific process of decoding barcodes in this scheme is summarized in Figure 2. We took the constructed barcode “GATGCTA” as an example, and it was assumed that a base “C” was inserted into the second position of the barcode and the base “C” at the fifth position of the barcode was deleted during sequencing.
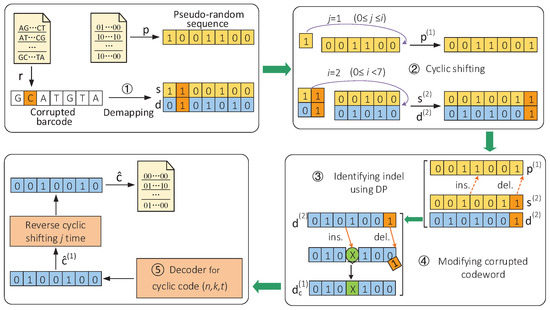
Figure 2.
Sequencing barcode identification scheme based on cyclic shifting and DP algorithm [12]. (Reprinted with permission from ref. [12]. Copyright 2022 Springer Nature.)
The decoding process of the corrupted barcode is described below. Specifically, we read the corrupted barcode r and the known pseudorandom sequence p from the text files as the input of the identification scheme. First, the corrupted barcode r is demapped into the corrupted sequence s and the corrupted codeword d. Subsequently, we found that when s and d are cyclically shifted to the left i = 2 times, the inserted base is moved to the end. When we cyclically shift the pseudorandom sequence p to the left j = 1 time and use DP to compare the and , it can identify the positions of an indel and modify the codeword . Then, the modified codeword is sent to the decoder for decoding. Finally, the decoded codeword is cyclically reverse-shifted to obtain the final result ĉ, which was output to a text file. Using the information bits of the codeword ĉ, the sequencing reads are assigned to their respective samples. The above method is summarized in Algorithm 1. (Adapted with permission from ref. [12]. Copyright 2022 Springer Nature.)
| Algorithm 1 Barcode identification algorithm in [12] |
|
2.2. DP Algorithm for Identifying Indel
The essence of the DP algorithm is to find an optimal path from the target sequence to the reference sequence and judge the position of an indel through this path. The basic process of identifying indels using DP algorithms can be described as follows. First, we build a two-dimensional matrix. Next, we use an iterative equation to calculate the value of the edit distance between the two sequences and store it in the matrix. Then, we use the backtracking algorithm to find an optimal path in the two-dimensional matrix. Finally, we use the optimal path to determine the position of indels in the target sequence.
In the barcode identification scheme, the DP algorithm is exploited to calculate the edit distance and obtain the optimum alignment for the sequences s and p. Based on the optimum alignment, the positions of insertions and deletions can be determined [24]. It can be seen that the edit distance calculation and the optimum path backtracking are the key links that affect the complexity of the DP algorithm [25].
Assuming that the lengths of two sequences A and B are, respectively, m and n, and the elements in the sequence are, respectively, denoted as and (, ), the specific process of using DP to realize the indel identification is as follows.
- 1.
- Calculate the edit distance between sequence elements and ; the calculation equation iswhere = = 1 and = 0 if = , otherwise = 1 [26]. The initial values of the iterative equation are given by and for and .
- 2.
- Backtrack from to to find the optimum path (i,j), which can be expressed as
- 3.
- Use the optimum path (i,j) to get the vector (i,j) that marks the indel positions, as follows
- 4.
- Based on the marker vector (i,j), the insertion and deletion errors on the corrupted sequence can be corrected.
Observing the above iterative equation for calculating edit distance, we can see that the time and space complexity of the DP algorithm are both . The general method to reduce the time complexity of the algorithm is to establish the LSA structure [27,28]. Since the performance of the LSA mainly depends on the number of PEs and the clock frequency of the PE [29], a simplified design of the PE can improve the performance of the LSA to a certain extent.
3. Barcode Identification Accelerator
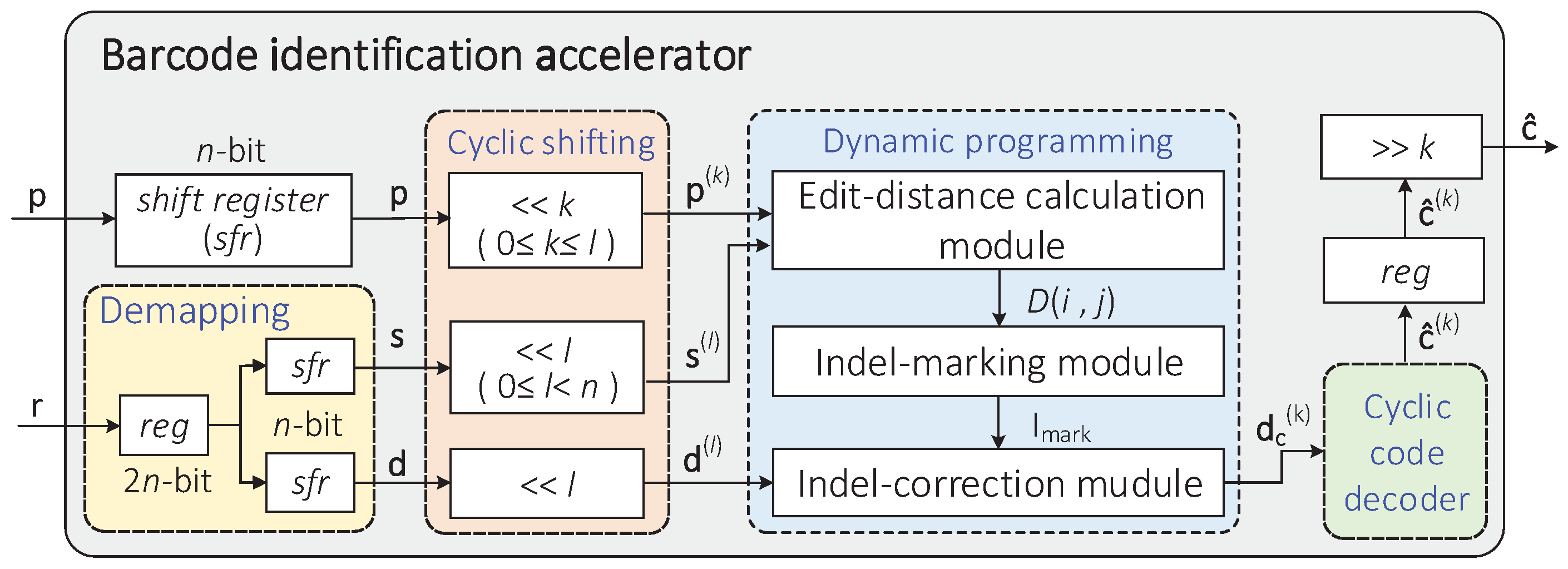
Based on the barcode identification method proposed in [12], the overall architecture of the hardware accelerator designed in this paper is illustrated in Figure 3. The accelerator consists of several modules, including demapping, cyclic shifting, dynamic programming, cyclic code decoder, and so on. The input of the accelerator includes an n-bit predetermined pseudorandom sequence p and a -bit corrupted barcode r converted from n-nt bases (strings), and the output is the final result obtained by cyclically shifting the decoded codeword to the right k times.
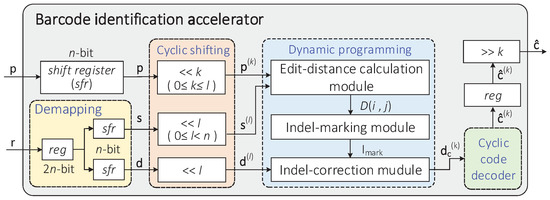
Figure 3.
Hardware architecture of the sequencing barcode identification accelerator.
The specific process of hardware implementation is explained as follows. The working state of each module is controlled by a finite state machine.
- 1.
- The -bit barcode r = is transformed into the sequence s = and code d = through the demapping module;
- 2.
- In the cyclic shifting module, it is assumed that the code d and the sequence s have been cyclically shifted to the left l times () to obtain the sequence and codeword . Meanwhile, the predetermined sequence p has been cyclically shifted to the left k times () to obtain the sequence ;
- 3.
- The shifted sequences , , and code are input into the dynamic programming module. Through the processing of this module, the indel identification of code is realized by calculating the edit distance of the sequences s and p and backtracking the optimal path, and we get the modified codeword ;
- 4.
- Subsequently, the remaining substitution errors on the codeword are decoded by the cyclic code decoder. If the decoded codeword meets the condition, that is, all syndromes equal to zero, it is cyclically shifted to the right k times as the final output result. Otherwise, the accelerator returns to the cyclic shifting module.
- 5.
- In the cyclic shifting module, if , we cyclically shift the sequence to the left once, and then perform indel identification. When , if , the sequence and the codeword are cyclically shifted to the left once, and then indel identification is performed; otherwise, the accelerator directly outputs the final decoding result .
Considering that the computational complexity of the DP algorithm in this paper is , with the increase of the number of cyclic shifts, the overall operation efficiency of the barcode identification algorithm will be seriously affected. Therefore, the hardware acceleration of the dynamic programming module is described in detail in this paper. Specifically, the hardware circuit of this module includes three submodules: (a) an edit-distance calculation module; (b) an insertion-and-deletion-errors-marking module, called indel-marking module; and (c) an insertion-and-deletion-errors-correction module, called indel-correction module.
3.1. Dynamic Programming Module
This section details the hardware acceleration of the dynamic programming module, mainly including an LSA structure with the simplified PE and a parallel circuit for identifying insertion and deletion errors.
3.1.1. Edit-Distance Calculation Module
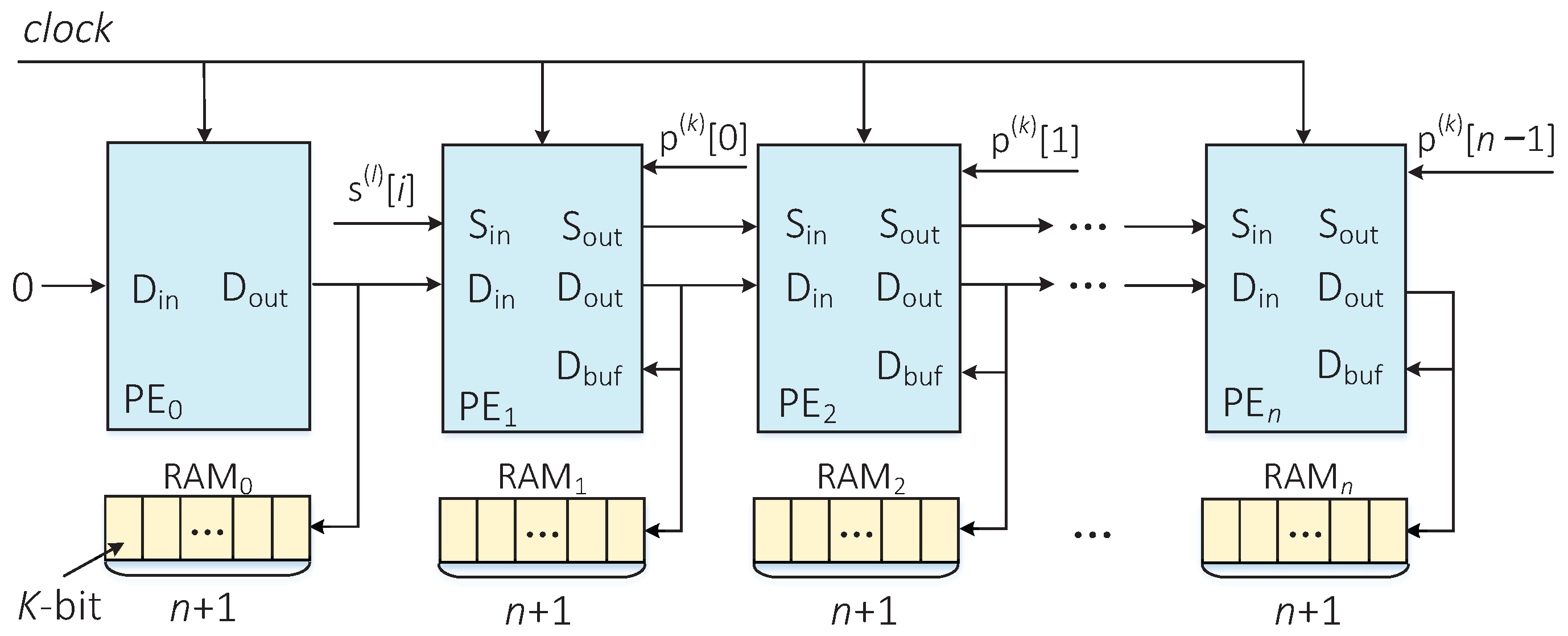
To realize hardware acceleration of the DP algorithm, an LSA structure was constructed to implement the parallel computation of the edit distance between the predetermined sequence and the corrupted sequence . All of the edit distance values can be stored in a two-dimensional array of size . Figure 4 describes the LSA structure constructed in this paper. The number of PE in the LSA is determined by the length n of the pseudorandom sequence p. The PEs are placed horizontally, and each PE is responsible for calculating a column of elements in the two-dimensional array.
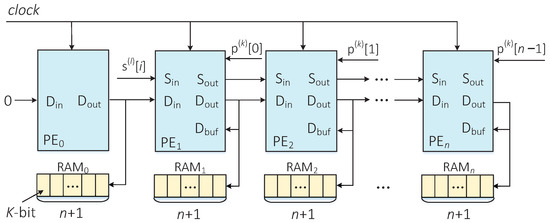
Figure 4.
LSA structure for parallel calculation of edit distances.
PE is responsible for the calculation of the first column element in the two-dimensional array, and its accumulation operation can be implemented with a simple accumulator. In the first clock cycle, an initial value is assigned to the port of each PE, which comes from the corresponding first row element in the two-dimensional array. The start and end signals of two adjacent PEs are always separated by one clock cycle. In each clock cycle, all PEs calculate the edit distance in parallel. After clock cycles, the minimum edit distance is output by PE.
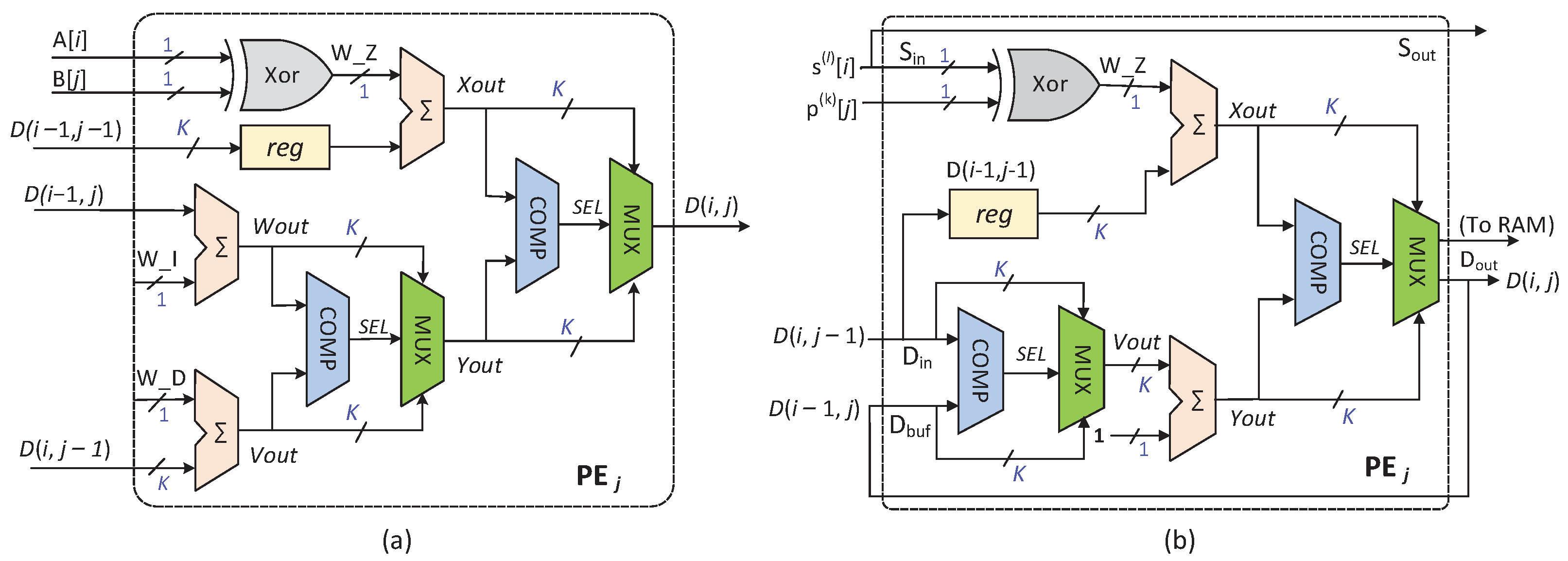
The architecture of the PEs except PE is illustrated in Figure 5. In previous works, researchers directly mapped the iterative equation to PE [19,20]. Such a PE is shown in Figure 5a. Obviously, the directly mapped PE contains three addition operations and two comparison operations. On this basis, we propose a simplified PE architecture, as depicted in Figure 5b. The design of this architecture is also based on Formula (1), but the mapping circuit of the equation is simplified. Specifically, we adjust the execution order of the comparison operation and the addition operation, thereby reducing the number of adders in the circuit when directly mapping the iterative equation and improving the mapping efficiency of the PE. The redesigned PE architecture first performs the comparison operation between and , then performs the comparison operation between and , and finally outputs the minimum value .
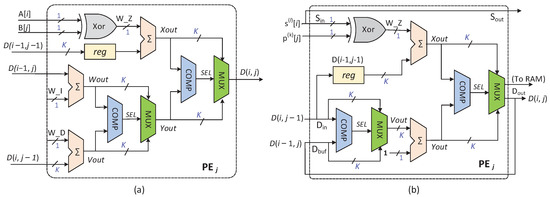
Figure 5.
Details of the PEs except PE: (a) directly mapped PE; (b) simplified PE.
Figure 5b describes the PE responsible for calculating the editing distance of the elements in the column. Two sequences are simultaneously sent to PE for alignment, and all the needed data for the PE come from itself and other PEs in the systolic array. The details are as follows:
- PE sequentially receives in every clock cycle and sends it to PE in the next clock cycle. Similarly, PE receives the 1-bit from PE and outputs it to PE in the following clock cycle;
- The elements in every column correspond to one bit, respectively, in the sequence . In other words, as far as PE is concerned, the corresponding bit in the sequence (i.e., ) is constant, and it is only read at the beginning of the process;
- At the clock cycle, the input of PE is the output result of the same PE in the clock cycle. Moreover, the input and of PE are the output results of the PE in the and clock cycles, respectively;
- The calculated result is not only the input of PE, but also stored in a random access memory (RAM) with a width of K bits and depth of , where n is the sequence’s length, and it satisfies .
3.1.2. Indel-Marking Module
According to the intermediate calculation results stored in RAM, the indel-marking module searches the optimum path by traceback and marks the position where the indel appears on the sequence . Contrary to the process of calculating the edit distance, the traceback needs to find the optimal path starting from the lower right corner element of the two-dimensional array. The execution time of this module is related to the length n of the pseudorandom sequence and the number N of indel errors. Since each search for a traceback point takes one clock cycle, the number of clocks required to find the entire traceback path is T = .
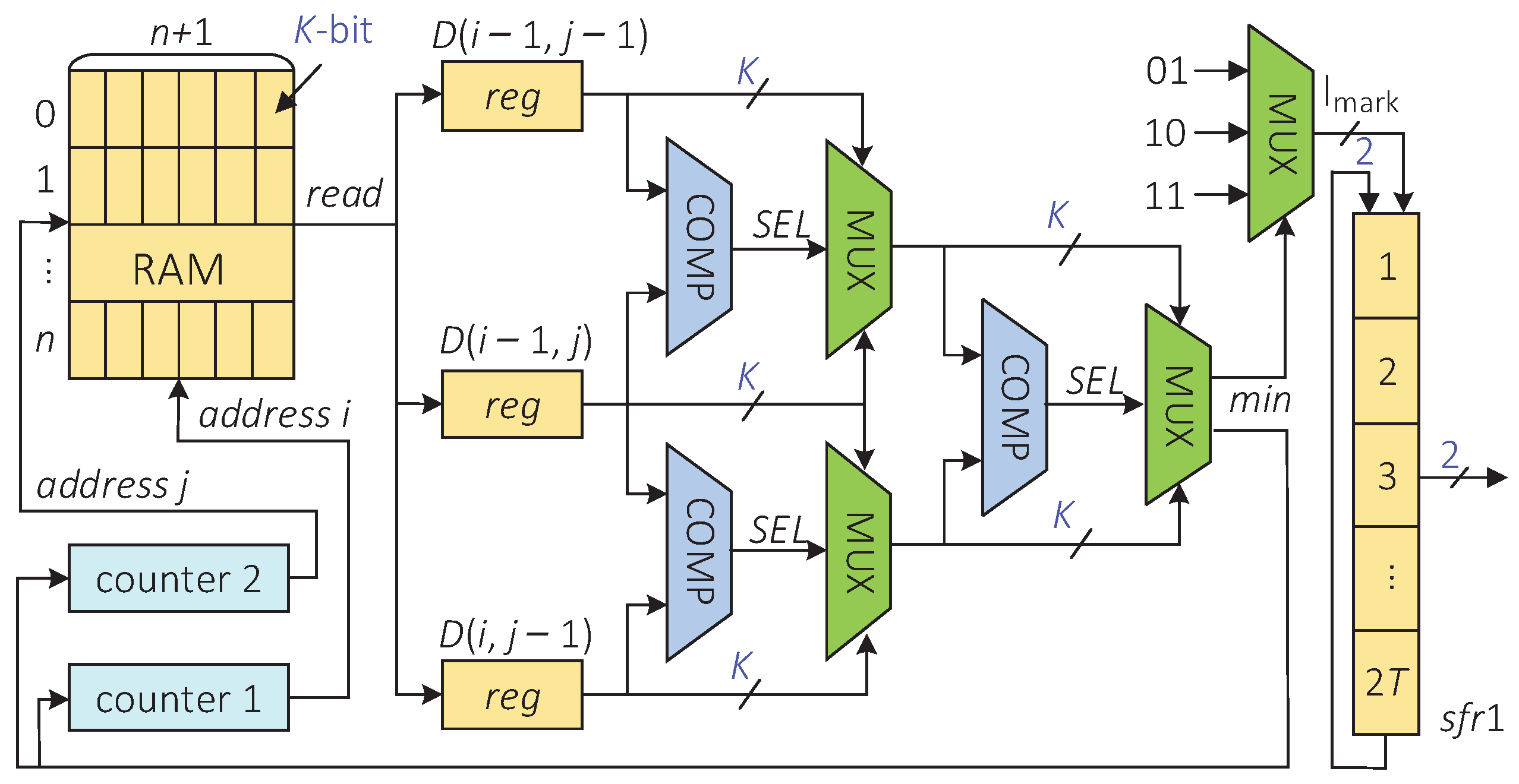
The hardware architecture of the indel-marking module is shown in Figure 6, and the implementation of this architecture is divided into the following three steps. First, starting from the RAM and taking the RAM as the reference element, the minimum value of the three elements is selected in the order from the upper left(RAM), left(RAM), to top(RAM). Then, the insertion, deletion, and substitution or correct transmission are detected according to the current position where the minimum value is located. Finally, the element with the minimum value is taken as the next reference cell, and the previous two steps are repeated until the traversal reaches RAM[0][0].
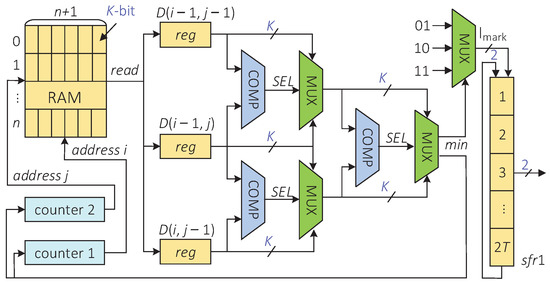
Figure 6.
The hardware architecture of the indel-marking module.
Specifically, the rules of the second step are described as follows.
- If is the minimum, it means that an insertion error appears in the sequence at the position to i. In this case, the shift register sfr1 writes 2-bit data “01” in the upper direction;
- If is the minimum, it indicates that a deletion error appears in the sequence at the position to i. In this case, the shift register sfr1 writes 2-bit data “10” in the upper direction;
- If is the minimum, it means that the data are transmitted correctly or there is a substitution error in the sequence at position . In this case, the shift register sfr1 writes 2-bit data “11” in the upper direction.
The traceback process finishes after T clock cycles. At this time, the shift register sfr1 stores -bit data. These data contain the position information of insertions and deletions.
3.1.3. Indel-Correction Module
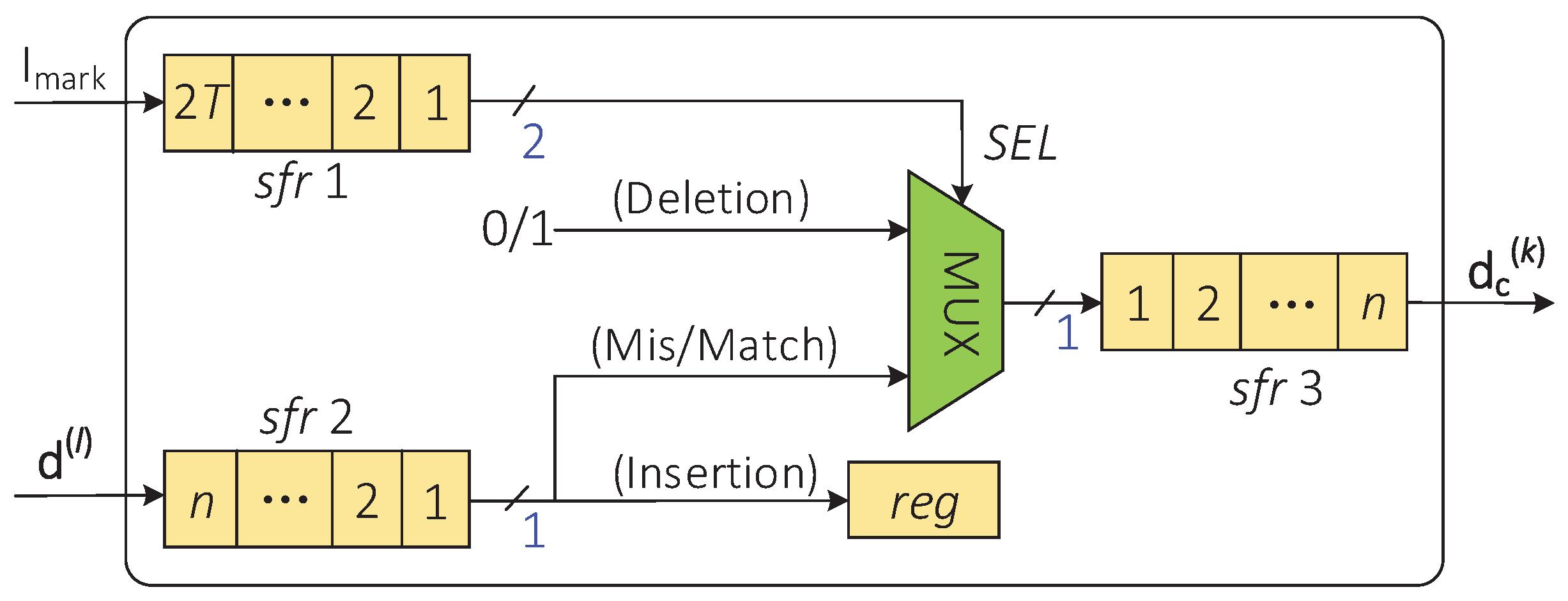
The indel-correction module corrects the insertion and deletion errors on the corrupted codeword according to the error locations provided by the indel-marking module. Therefore, the indel-marking module and the indel-correction module can be implemented in parallel on hardware. Figure 7 describes the hardware implementation architecture of the indel-correction module. The locations of the insertion and deletion errors on the sequence are stored in the shift register sfr1, and the corrupted codeword is stored in the shift register sfr2.
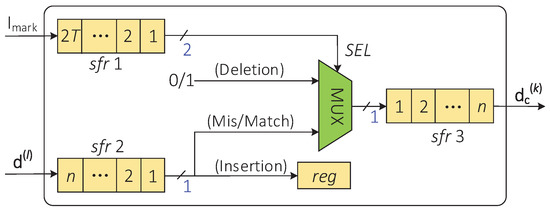
Figure 7.
The hardware architecture of the indel-correction module.
At the same clock pulse, if the output data of the sfr1 are “11”, sfr2 will shift out one bit of the data and these data will be written to the high position of the shift register sfr3. If the output data element of the sfr1 are “10”, sfr2 will stay still, and random data (i.e., “0” or “1”) will be written into the sfr3. If the output data of sfr1 are “01”, sfr2 will shift out one bit of the data to an additional register and sfr3 will stay still. After T clock cycles, the piece of data stored in sfr3 is the corrected codeword .
For the dynamic programming module, the total number of clock cycles required to calculate edit distance, mark indels, and correct indels is . Compared with the serial computation amount of in the software implementation, the computing time is greatly shortened.
3.2. Cyclic Code Decoder
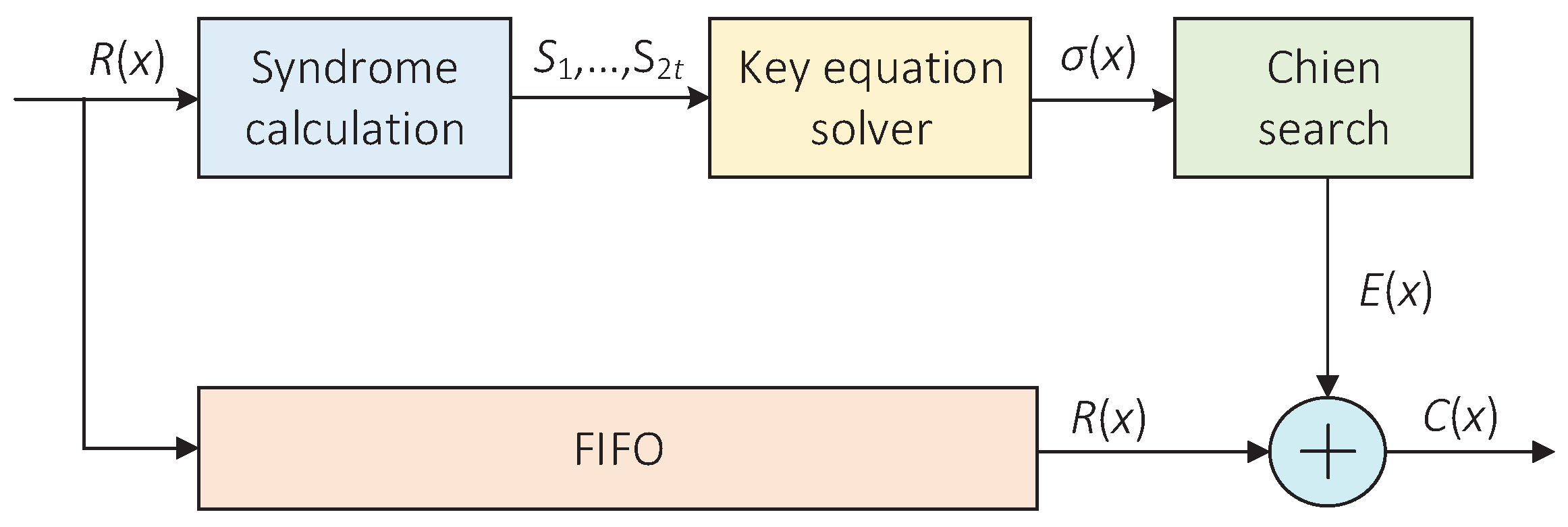
The cyclic code decoder is another key error correction module in the accelerator. Due to the use of cyclic block codes in barcodes, the remaining substitution errors can be corrected. In this paper, the Bose–Chaudhuri–Hocquenghem (BCH) codes consistent with the software program were chosen as the coding scheme. BCH codes have been proven to be excellent error-correcting codes with relatively strong error-correcting capability, which are simple to encode and decode [30]. Figure 8 shows the overall architecture of a BCH decoder, which mainly includes three blocks, namely, the syndrome calculation block, the key equation solver(KES) block and the Chien search block.
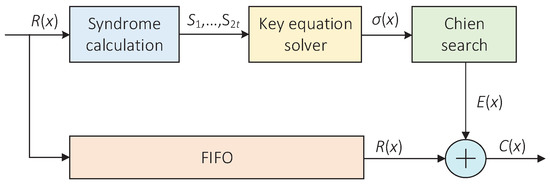
Figure 8.
The architecture of the BCH decoder.
In the accelerator, the BCH decoder is responsible for correcting the remaining substitution errors on the codeword . In the meantime, the syndrome output by the syndrome calculation block can be used to judge whether the codeword is correct. If all the syndromes are zero, the judgment condition is satisfied and the codeword is error-free; otherwise, it is not satisfied. The most important and complicated part of the BCH decoder is the KES block. It requires a lot of hardware resources to calculate the error locator polynomial. In this paper, the inversionless Berlekamp–Massey (IBM) algorithm [31] was adopted as the iterative decoding algorithm because it had a relatively low hardware implementation complexity. Meanwhile, its execution speed and device utilization can be improved by parallel processing methods. Thus, this paper adopted and implemented a BCH decoder with a high-speed parallel architecture [32].
4. Results
This section focuses on the implementation results of the accelerator. We comprehensively evaluate the accelerator’s function and performance from three aspects: robustness, resource utilization, and acceleration effect.
4.1. Performance Verification
To verify the accuracy and robustness of the barcode identification accelerator, the same noisy channel model was adopted in hardware. It included two different error scenarios (random scenario and context scenario) and a simplified channel model of insertion/deletion/substitution (IDS) [33,34].
The two scenarios were generalized as follows. For the random scenario, the same number of insertion and deletion occurred on the barcode, so the length of the barcode was unchanged. For the context scenario, the number of insertions or deletions that occurred on the barcode varied, and the length of the barcode was thus changed [6]. To simulate various errors introduced on the barcode, the sequencing process was modeled as a noisy channel model similar to that in communication systems. In this channel, barcodes were inserted, deleted, and substituted with a certain probability. The channel was described by three parameters: insertion probability , deletion probability , and substitution probability . We validated the robustness of the barcode identification scheme by estimating the identification error rate (i.e., the probability that a corrupted barcode is decoded incorrectly).
The software simulation was realized by using the software program in [12]. This program includes the generation of a barcode, the setting of the sequencing channel and the identification of the barcode. In the software program, cyclic codes and predetermined pseudorandom sequences were combined bit by bit to form sequencing barcodes. After the generated barcodes passed through the noisy channel, the corrupted barcodes were obtained. In the sequencing channel, we could choose different error scenarios and set different mutation probability of barcodes. Taking the corrupted barcodes as input, the software simulation and hardware implementation of the barcode identification were performed.
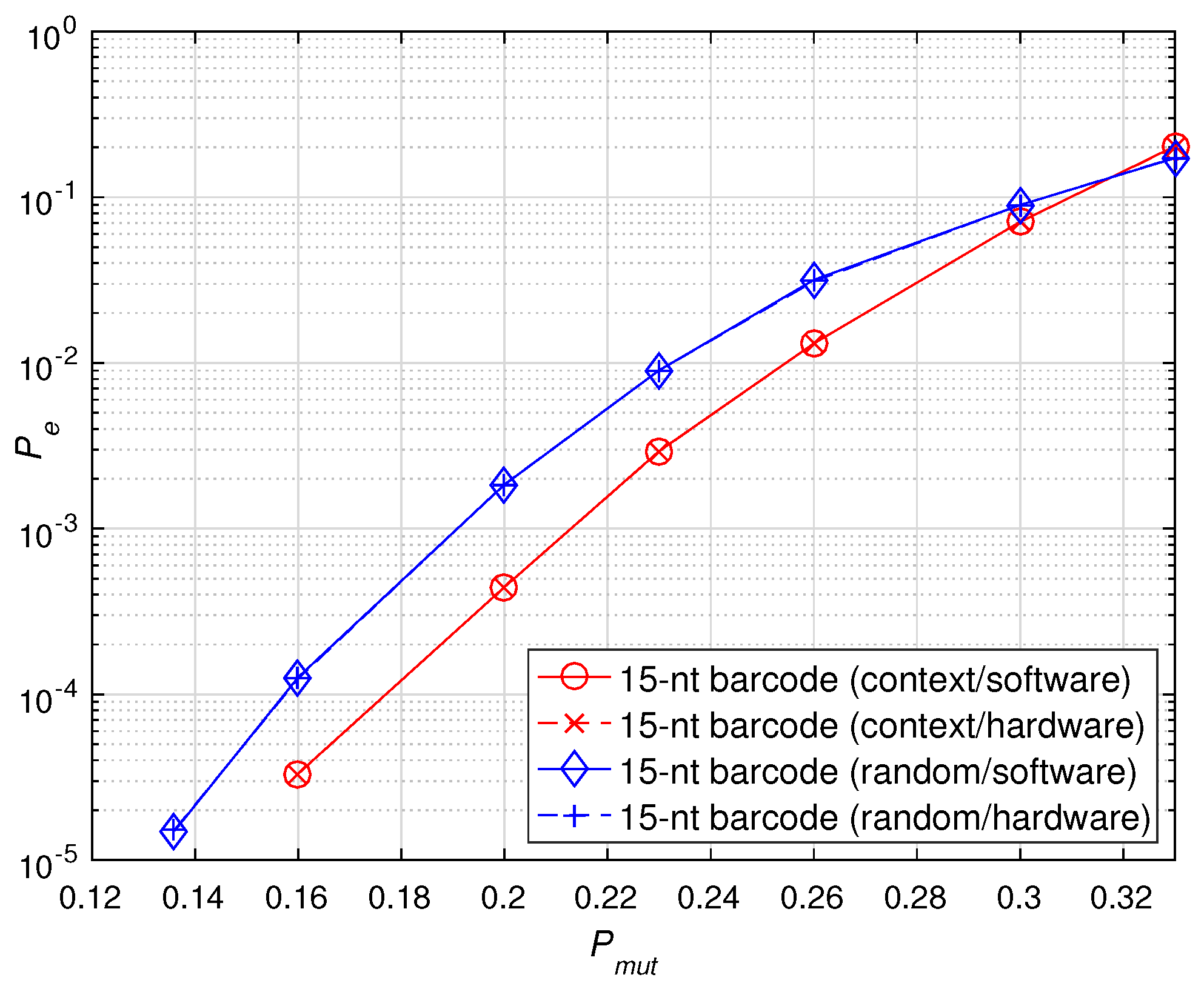
First, we investigated the identification error rate of the hardware implementation and software simulation for the 15-nt sequencing barcode constructed with BCH(15, 5, 3) in the two different scenarios. For each scenario, 200 barcodes were randomly selected from the relevant database for validation. The mutation probability of each base on the barcode was , where = + + . The simulation results are shown in Figure 9. The experimental results show that the hardware implementation results are consistent with the software simulation results regardless of the random scenario or the context scenario. Therefore, it is verified that the accelerators can be applied to two different error scenarios and achieve the same performance as the software simulation for different error scenarios.
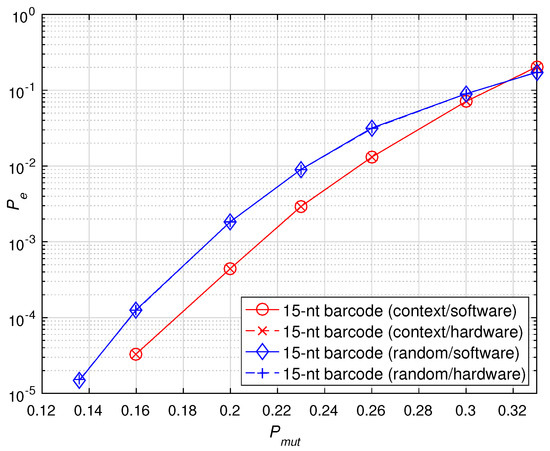
Figure 9.
Performance verification of software and hardware implementations of sequencing barcodes under different error scenarios.
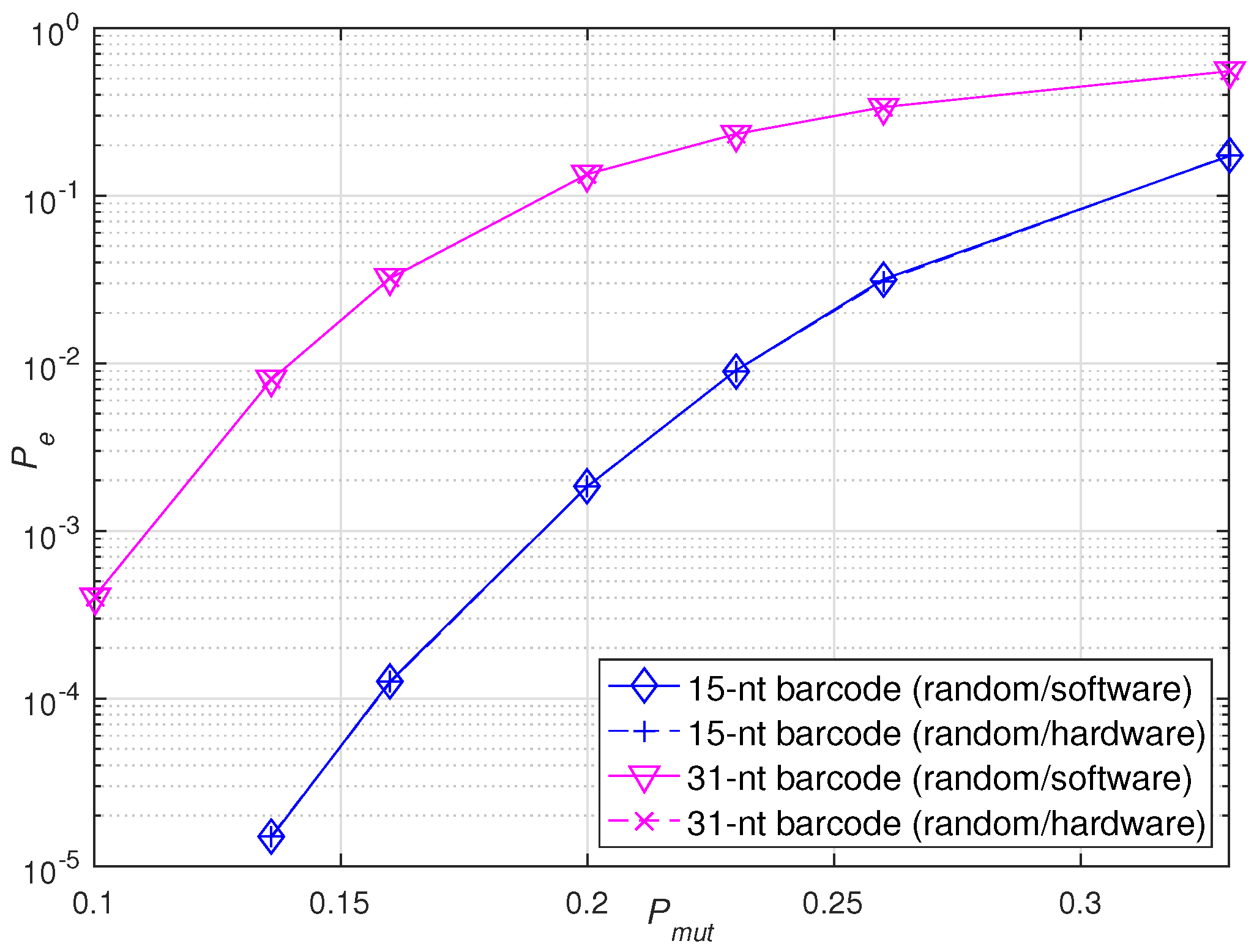
Then, to verify the robustness of the hardware accelerators, two types of barcodes were constructed by BCH codes with the same error correction ability but different lengths. Specifically, the 31-nt barcodes were constructed with BCH(31,16,3) and the 15-nt barcodes were constructed with BCH(15,5,3). For each length, 200 barcodes were randomly selected from the relevant database for hardware and software validation. The simulation experiment was performed under the same error scenario. Figure 10 shows the identification error rate of the sequencing barcodes implemented by hardware and software in the random scenario under different mutation probabilities . It is observed that the hardware accelerators built for barcodes of different lengths can also achieve the same robustness as that of software simulations under the same error scenario.
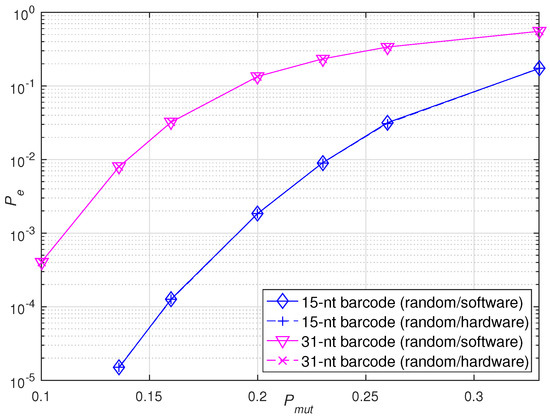
Figure 10.
Performance verification of software and hardware implementations of sequencing barcodes with different lengths under the same error scenario.
4.2. Hardware Implementation Results
We wrote Verilog codes for accelerators with barcode lengths of 12-nt, 15-nt, and 31-nt. All designs were mapped on a Virtex-6 XC6VLX240T FPGA using the Xilinx ISE 14.7 development suite. This family was only used because of its availability and the fact that we did not need to change the core code to use different chips. Using larger or newer FPGAs should enable longer barcode identification and yield better results. The accelerator took the FPGA chip as the core and realized the communication between a host CPU and the FPGA through the PCIe. The PCIe interface controller was implemented based on Xilinx PCIe IP. On the CPU side, corrupted barcodes and pseudorandom sequences were transferred from the main memory via direct memory access (DMA). On the FPGA side, two asynchronous FIFOs were used to buffer the input data.
Taking the 12-nt, 15-nt, and 31-nt sequencing barcodes constructed from BCH(12, 4, 2), BCH(15, 5, 3), and BCH(31, 16, 3) codes as an example, we observed the implementation results of the three accelerators on the FPGA. Among them, BCH(12, 4, 2) was a shorted cyclic BCH code, which was generated using BCH(15,7,2). The overall on-chip resource utilization and maximum clock frequency of the three accelerators are listed in Table 1. It is seen that each of these three types of accelerators occupies a small amount of logic resources of the FPGA, and the maximum frequency of the accelerator designed for barcodes of length 15 can reach 228.7 MHz. However, it is apparent that for larger barcodes, the FPGA resources consumed by the accelerator increase significantly.

Table 1.
The implementation results of the three accelerators.
In addition, we compared the runtime of software and hardware for barcodes identification. To obtain the runtime of the pure software implementation, the original software code was run on a computer configured with an Intel Core i7-10700 microprocessor (eight-core, sixteen-thread, 4.8 GHz) and main memory with a capacity of 16 GB. The software solution came from the software program in [12], which compiles and runs directly in Visual Studio 2019. The hardware execution time was the time from the hardware startup to the output of the decoded result to the memory. The time required by the CPU and FPGA to identify barcode sequences of different lengths is listed in Table 2, where the FPGA clocked at 100 MHz. For each length, 200,000 barcodes with the mutation probability were randomly selected from the relevant database for identification. To improve the accuracy of the results, the identification of each length was performed three times and the running time was averaged.

Table 2.
Comparison of the runtime for different lengths of sequencing barcodes identification based on CPU and FPGA.
It can be observed in Table 2 that the accelerator is approximately 70–180× faster than the C implementation for representative input sizes, and this performance improvement increases with the length of the barcode. As a result, for longer barcodes, hardware-based accelerators outperform the software by two orders of magnitude in terms of the identification speed.
It was also important to compare the current implementation with the methods described in other literature works. In multiplex sequencing, the traditional DNA barcode design and identification methods are mostly realized by software. For example, Costea et al. [35] reported a fully customizable, fast, and accurate software package called TagGD (Tag Generator and Demultiplexer); Tambe et al. [36] proposed a software tool for identifying and correcting barcodes in single cell genomics, etc. The above methods were compared with the work in this paper, as shown in Table 3. Since different platforms use different processors, algorithms, and datasets, the number of barcode reads that can be processed per second was used to evaluate the processing speed of different software and hardware solutions. It should be noted that for a given method, the longer the barcodes are, the longer the processing time is required. The comparison shows that although the barcodes identified by our hardware accelerator are the longest, the processing speed of the barcodes is the fastest.

Table 3.
Comparison with other previous approaches.
5. Conclusions
In this paper, we presented the design and implementation of an FPGA-based hardware accelerator for a highly robust sequencing barcode identification algorithm. Considering that the DP algorithm in the identification scheme had the time complexity of , a systolic array structure was proposed, which improved the mapping efficiency of a PE by simplifying the circuit structure when the iterative equation was mapped to the PE. Moreover, according to the two-dimensional array stored in RAM, a parallel circuit using traceback to identify insertion and deletion errors was designed. The simulation results on an FPGA indicated that the accelerators constructed for sequencing barcodes with different lengths could achieve a speedup of about 70–180× compared to the general-purpose computer platform. Our future work will mainly focus on the hardware acceleration of sequencing barcode identification algorithms based on graphic processing unit (GPU).
Author Contributions
Conceptualization, W.C. and W.H.; methodology, W.H.; software, W.H.; validation, W.H.; formal analysis, W.C.; investigation, W.C., H.Z. and Y.Z.; writing—original draft preparation, W.C. and W.H.; writing—review and editing, W.C., W.H., Y.Z. and H.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy restrictions.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FPGA | Field-programmable gate array |
| NGS | Next-generation sequencing |
| DNA | Deoxyribonucleic acid |
| CPU | Central processing unit |
| DP | Dynamic programming |
| PE | Processing element |
| LSA | Linear systolic array |
| RAM | Random-access memory |
| BCH | Bose–Chaudhuri–Hocquenghem |
| KES | Key equation solver |
| IBM | Inversionless Berlekamp–Massey |
| GPU | Graphics processing unit |
References
- Hardwick, S.A.; Deveson, I.W.; Mercer, T.R. Reference standards for next-generation sequencing. Nat. Rev. Genet. 2017, 18, 473–484. [Google Scholar] [CrossRef] [PubMed]
- Hu, T.; Chitnis, N.; Monos, D.; Dinh, A. Next-generation sequencing technologies: An overview. Hum. Immunol. 2021, 82, 801–811. [Google Scholar] [CrossRef] [PubMed]
- Krishnan, A.R.; Sweeney, M.; Vasic, J.; Galbraith, D.W.; Vasic, B. Barcodes for DNA sequencing with guaranteed error correction capability. Electron. Lett. 2011, 47, 236–237. [Google Scholar] [CrossRef]
- Abeynayake, S.W.; Fiorito, S.; Dinsdale, A.; Whattam, M.; Crowe, B.; Sparks, K.; Campbell, P.R.; Gambley, C. A rapid and cost-effective identification of invertebrate pests at the borders using MinION sequencing of DNA barcodes. Genes 2021, 8, 1138. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Han, M.; Zhou, J.; Ge, Q.; Wang, P.; Zhu, S.; Song, L.; Yuan, Y. An artificial chromosome for data storage. Natl. Sci. Rev. 2021, 8, nwab028–nwab037. [Google Scholar] [CrossRef]
- Chen, W.; Wang, L.; Han, M.; Han, C.; Li, B. Sequencing barcode construction and identification methods based on block error-correction codes. Sci. China Life Sci. 2020, 63, 1580–1592. [Google Scholar] [CrossRef]
- Hamady, M.; Walker, J.J.; Harris, J.K.; Gold, N.J.; Knight, R. Error-correcting barcoded primers for pyrosequencing hundreds of samples in multiplex. Nat. Methods 2008, 5, 235–237. [Google Scholar] [CrossRef]
- Bystrykh, L.V. Generalized DNA barcode design based on hamming codes. PLoS ONE 2012, 7, e36852. [Google Scholar] [CrossRef]
- Buschmann, T.; Bystrykh, L.V. Levenshtein error-correcting barcodes for multiplexed DNA sequencing. BMC Bioinform. 2013, 14, 272–281. [Google Scholar] [CrossRef]
- Hawkins, J.A.; Jones, S.K.; Finkelstein, I.J.; Press, W.H.; Callan, C.G.; Troyanskaya, O.G.; Weissman, J.S. Indel-correcting DNA barcodes for high-throughput sequencing. Proc. Natl. Acad. Sci. USA 2018, 115, e6217–e6226. [Google Scholar] [CrossRef]
- Kracht, D.; Schober, S. Insertion and deletion correcting DNA barcodes based on watermarks. BMC Bioinform. 2015, 16, 50. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Wang, P.; Wang, L.; Zhang, D.; Han, M.; Han, M.; Song, L. Low-complexity and highly robust barcodes for error-rich single molecular sequencing. 3 Biotech 2021, 11, 78. [Google Scholar] [CrossRef] [PubMed]
- Goenka, S.D.; Gorzynski, J.E.; Shafin, K.; Fisk, D.G.; Pesout, T.; Jensen, T.D.; Monlong, J. Accelerated identification of disease-causing variants with ultra-rapid nanopore genome sequencing. Nat. Biotechnol. 2022, 40, 1035–1041. [Google Scholar] [CrossRef] [PubMed]
- Gorzynski, J.E.; Goenka, S.D.; Shafin, K.; Jensen, T.D.; Fisk, D.G.; Grove, M.E. Ultrarapid nanopore genome sequencing in a critical care setting. N. Engl. J. Med. 2022, 386, 700–702. [Google Scholar] [CrossRef]
- Pomerantz, A.; Peñafiel, N.; Arteaga, A.; Bustamante, L.; Pichardo, F.; Coloma, L.A.; Prost, S. Real-time DNA barcoding in a rainforest using nanopore sequencing: Opportunities for rapid biodiversity assessments and local capacity building. Gigascience 2018, 7, giy033. [Google Scholar] [CrossRef]
- Awad, M. FPGA supercomputing platforms: A survey. In Proceedings of the International Conference on Field Programmable Logic, Prague, Czech Republic, 31 August–2 September 2009; pp. 564–568. [Google Scholar]
- Leiserson, C.E.; Thompson, N.C.; Emer, J.S.; Kuszmaul, B.C.; Tao, B.S. There is plenty of room at the top: What will drive computer performance after Moore’s law. Science 2020, 368, e9744. [Google Scholar] [CrossRef]
- Stivala, A.; Stuckey, P.J.; Banda, M.G.D.L.; Hermenegildo, M.; Wirth, A. Lock-free parallel dynamic programming. J. Parallel Distrib. Comput. 2010, 70, 839–848. [Google Scholar] [CrossRef]
- Guo, X.; Hong, W.; Devabhaktuni, V. A systolic array-based FPGA parallel architecture for the BLAST algorithm. ISRN Bioinform. 2012, 2012, 195658. [Google Scholar] [CrossRef]
- Casale-Brunet, S.; Bezati, E.; Mattavelli, M. Design space exploration of dataflow-based Smith-Waterman FPGA implementations. In Proceedings of the 2017 IEEE International Workshop on Signal Processing Systems (SiPS), Lorient, France, 3–5 October 2017; pp. 1–6. [Google Scholar]
- Shah, H.A.; Hasan, L.; Koo, I. Optimized and portable FPGA-based systolic cell architecture for Smith-Waterman-based DNA sequence alignment. J. Inf. Commun. Converg. Eng. 2016, 14, 26–34. [Google Scholar] [CrossRef][Green Version]
- Koliogeorgi, K.; Voss, N.; Fytraki, S.; Xydis, S.; Soudris, D. Dataflow acceleration of Smith-Waterman with traceback for high throughput next generation sequencing. In Proceedings of the 2019 29th International Conference on Field Programmable Logic and Applications (FPL), Barcelona, Spain, 8–12 September 2019; pp. 74–80. [Google Scholar]
- Jain, M.; Koren, S.; Miga, K.H.; Quick, J.; Rand, A.C.; Sasani, T.A. Nanopore sequencing and assembly of a human genome with ultra-long reads. Nat. Biotechnol. 2018, 36, 338–345. [Google Scholar] [CrossRef]
- Kruskal, J.B. An overview of sequence comparison: Time warps, string edits, and macromolecules. SIAM Rev. 1983, 25, 201–237. [Google Scholar] [CrossRef]
- Nawaz, Z.; Nadeem, M.; Someren, H.V.; Bertels, K. A parallel FPGA design of the Smith-Waterman traceback. In Proceedings of the 2010 International Conference on Field-Programmable Technology, Beijing, China, 8–10 December 2010; pp. 454–459. [Google Scholar]
- Tithi, J.J.; Crago, N.C.; Emer, J.S. Exploiting spatial architectures for edit distance algorithms. In Proceedings of the 2014 IEEE International Symposium on Performance Analysis of Systems and Software (ISPASS), Monterey, CA, USA, 23–25 March 2014; pp. 23–34. [Google Scholar]
- Benkrid, K.; Liu, Y.; Benkrid, A.S. A highly parameterized and efficient FPGA-based skeleton for pairwise biological sequence alignment. IEEE Trans. Very Large Scale Integr. VLSI Syst. 2009, 17, 561–570. [Google Scholar] [CrossRef]
- Rucci, E.; Garcia, C.; Botella, G.; Giusti, A.D.; Naiouf, M.; Prieto-Matias, M. Swifold: Smith-Waterman implementation on FPGA with OpenCL for long DNA sequences. BMC Syst. Biol. 2018, 12, 96. [Google Scholar] [CrossRef] [PubMed]
- Gok, M.; Yilmaz, C. Efficient cell designs for systolic Smith-Waterman implementations. In Proceedings of the 16th International Conference on Field Programmable Logic and Applications, Madrid, Spain, 28–30 August 2007; pp. 1–4. [Google Scholar]
- Reed, I.S.; Shih, M.T. VLSI design of inverse-free Berlekamp-Massey algorithm. IEE Proc. E (Comput. Digit. Tech.) 1991, 138, 295–298. [Google Scholar] [CrossRef]
- Chen, C.; Han, Y.S.; Wang, Z.; Bai, B. A new inversionless Berlekamp-Massey algorithm with efficient architecture. In Proceedings of the 2019 IEEE International Workshop on Signal Processing Systems (SiPS), Nanjing, China, 20–23 October 2019; pp. 48–53. [Google Scholar]
- Hwang, T. Parallel decoding of binary BCH codes. Electron. Lett. 1991, 27, 2223–2225. [Google Scholar] [CrossRef]
- Davey, M.C.; Mackay, D.J.C. Reliable communication over channels with insertions, deletions, and substitutions. IEEE Trans. Inf. Theory 2001, 42, 687–698. [Google Scholar] [CrossRef]
- Ezpeleta, J.; Krsticevic, F.J.; Bulacio, P.; Tapia, E. Designing robust watermark barcodes for multiplex long-read sequencing. BMC Bioinform. 2017, 33, 807–813. [Google Scholar] [CrossRef][Green Version]
- Costea, P.I.; Lundeberg, J.; Akan, P. Tag GD: Fast and accurate software for DNA tag generation and demultiplexing. PLoS ONE 2013, 8, e57521. [Google Scholar] [CrossRef]
- Tambe, A.; Pachter, L. Barcode identification for single cell genomics. BMC Bioinform. 2019, 20, 32–41. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).