Smart, Fast, and Low Memory Beam-Steering Antenna Configurations for 5G and Future Wireless Systems
Abstract
:1. Introduction
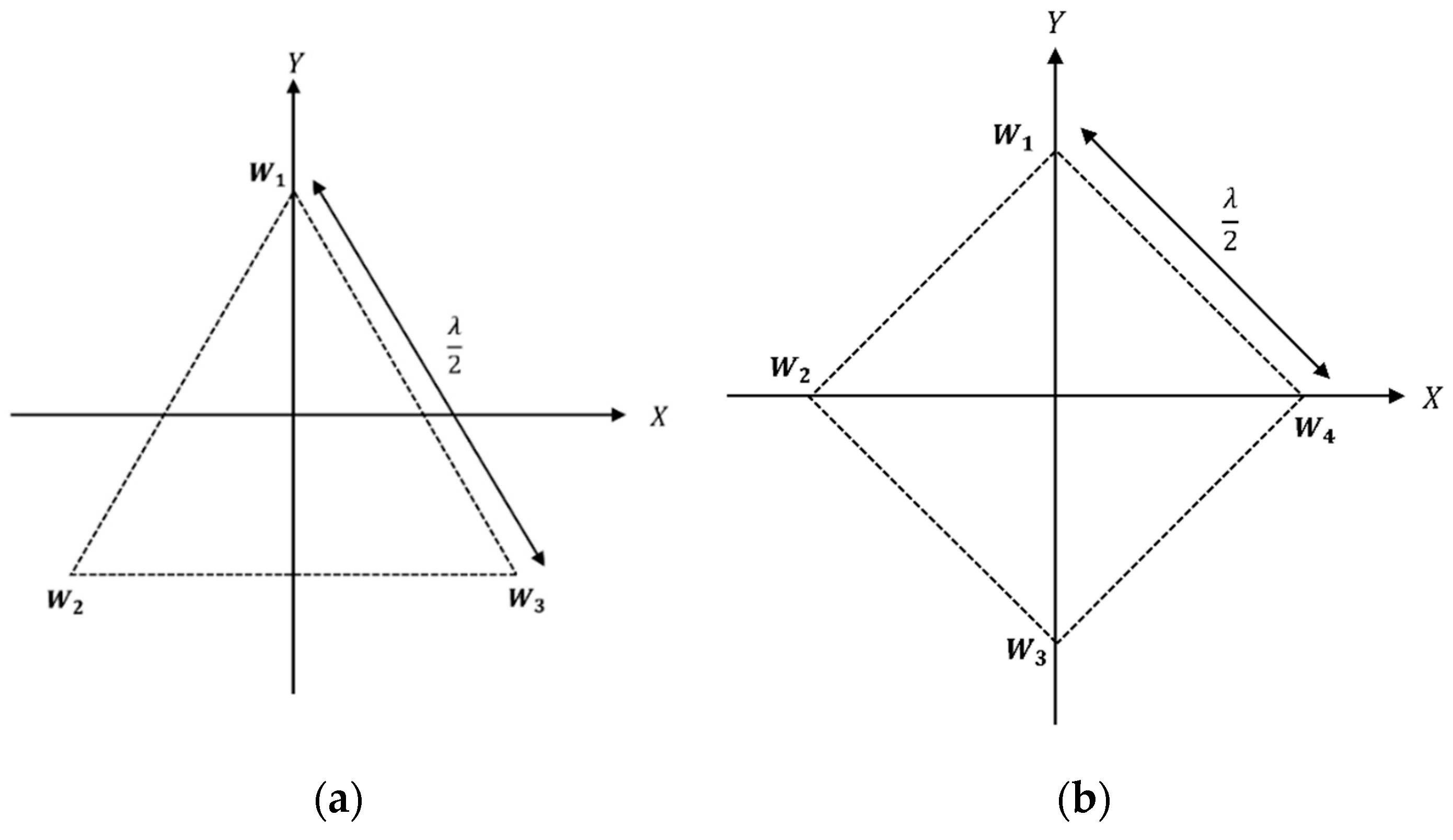
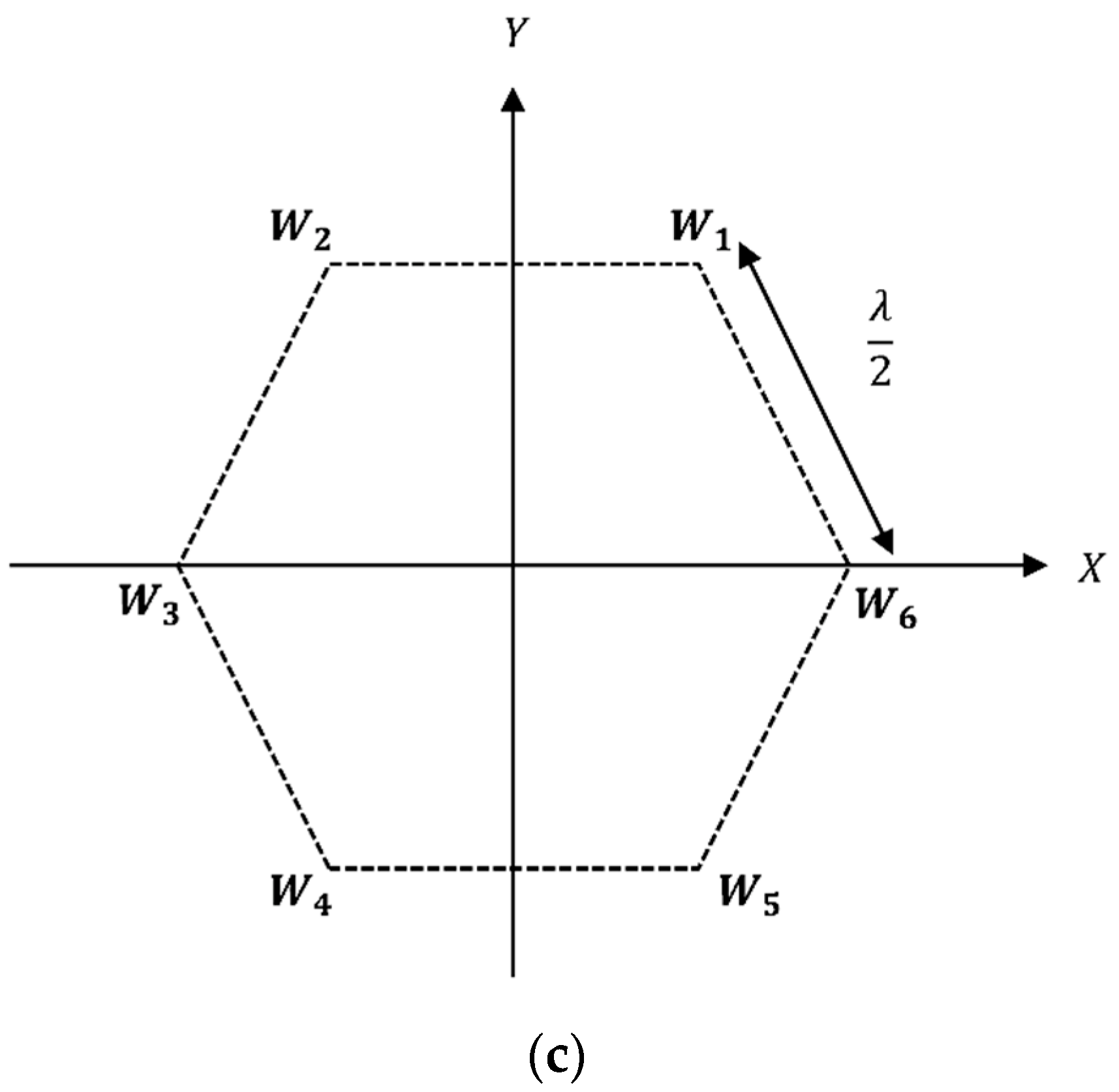
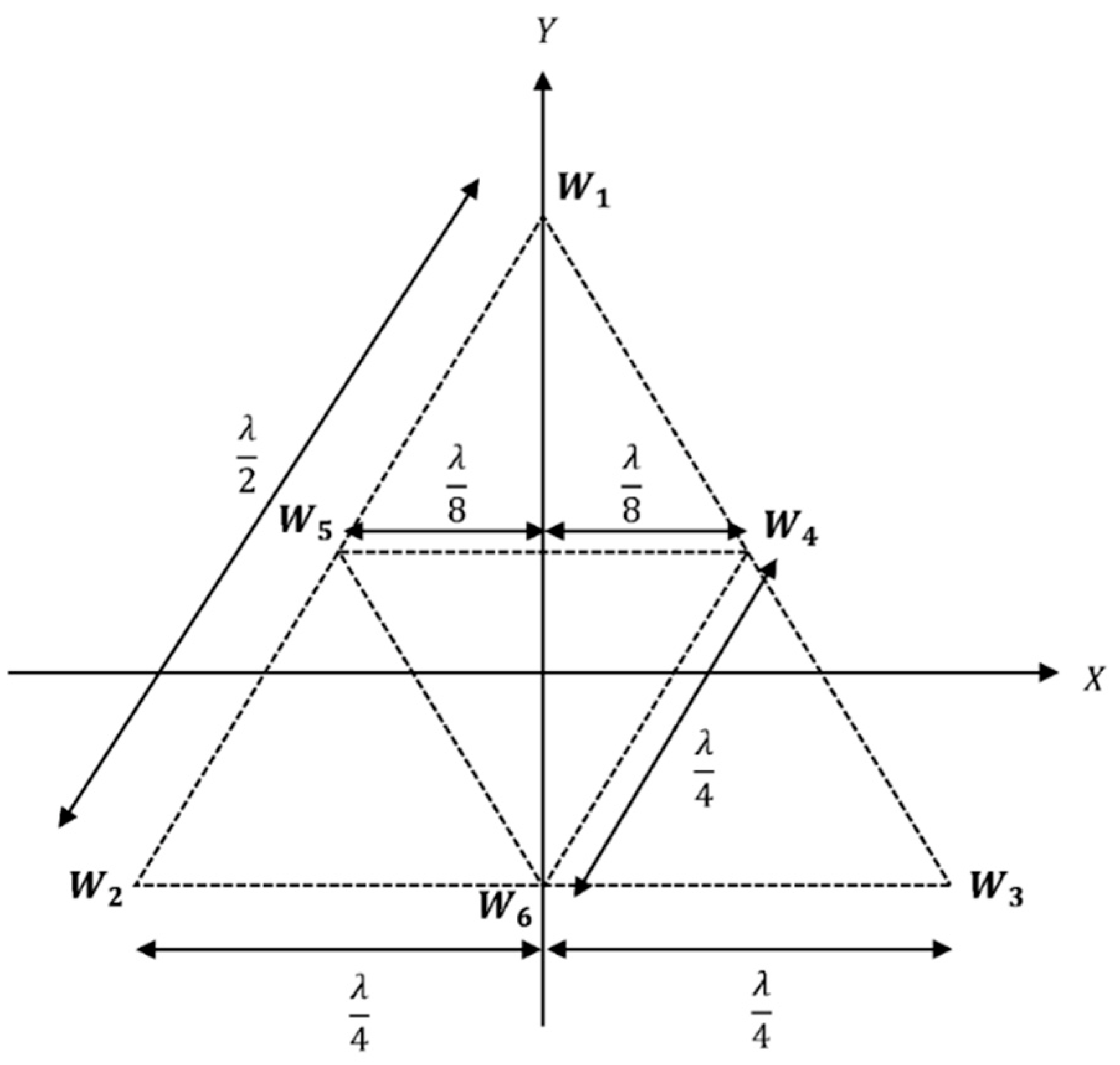
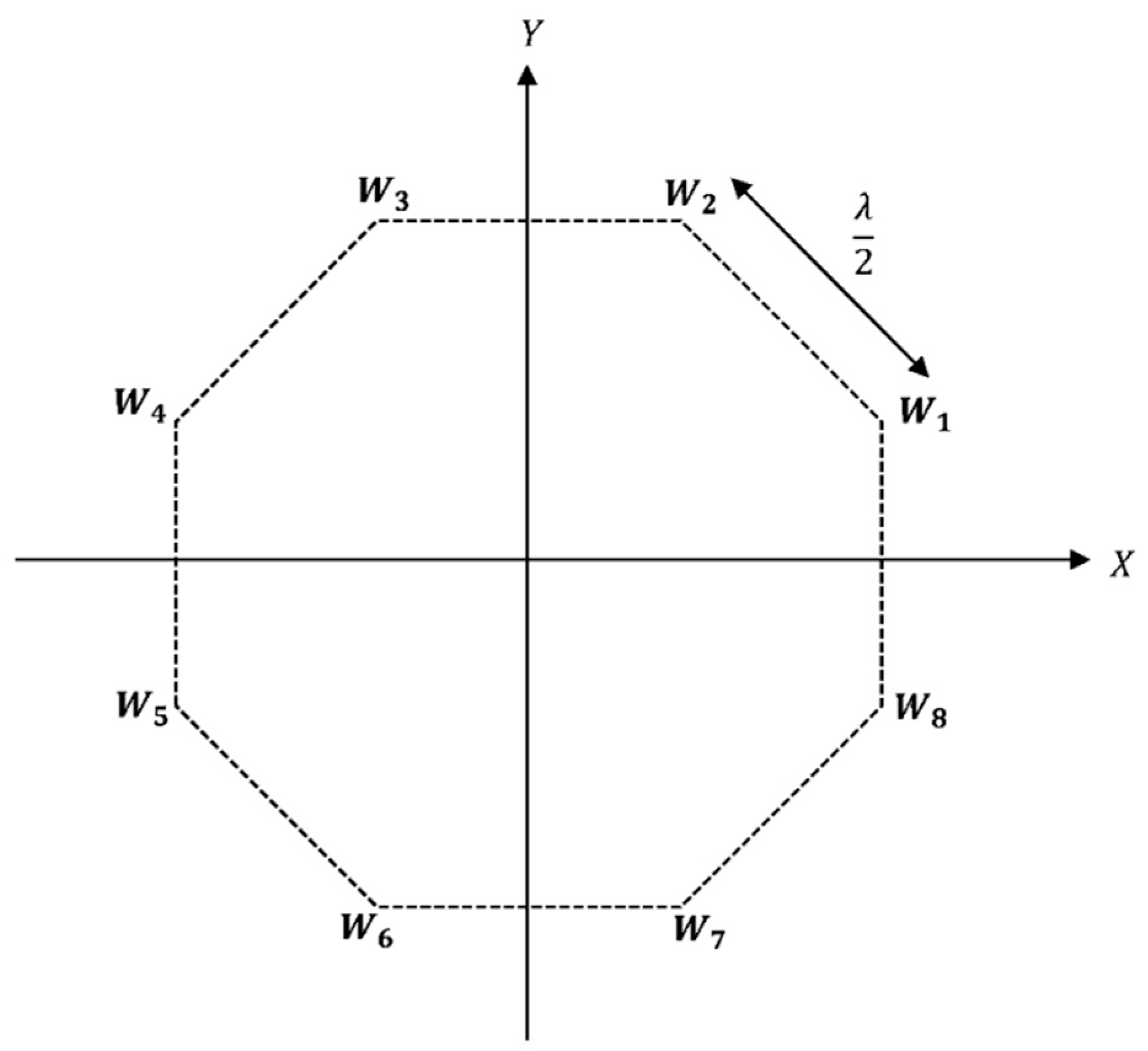
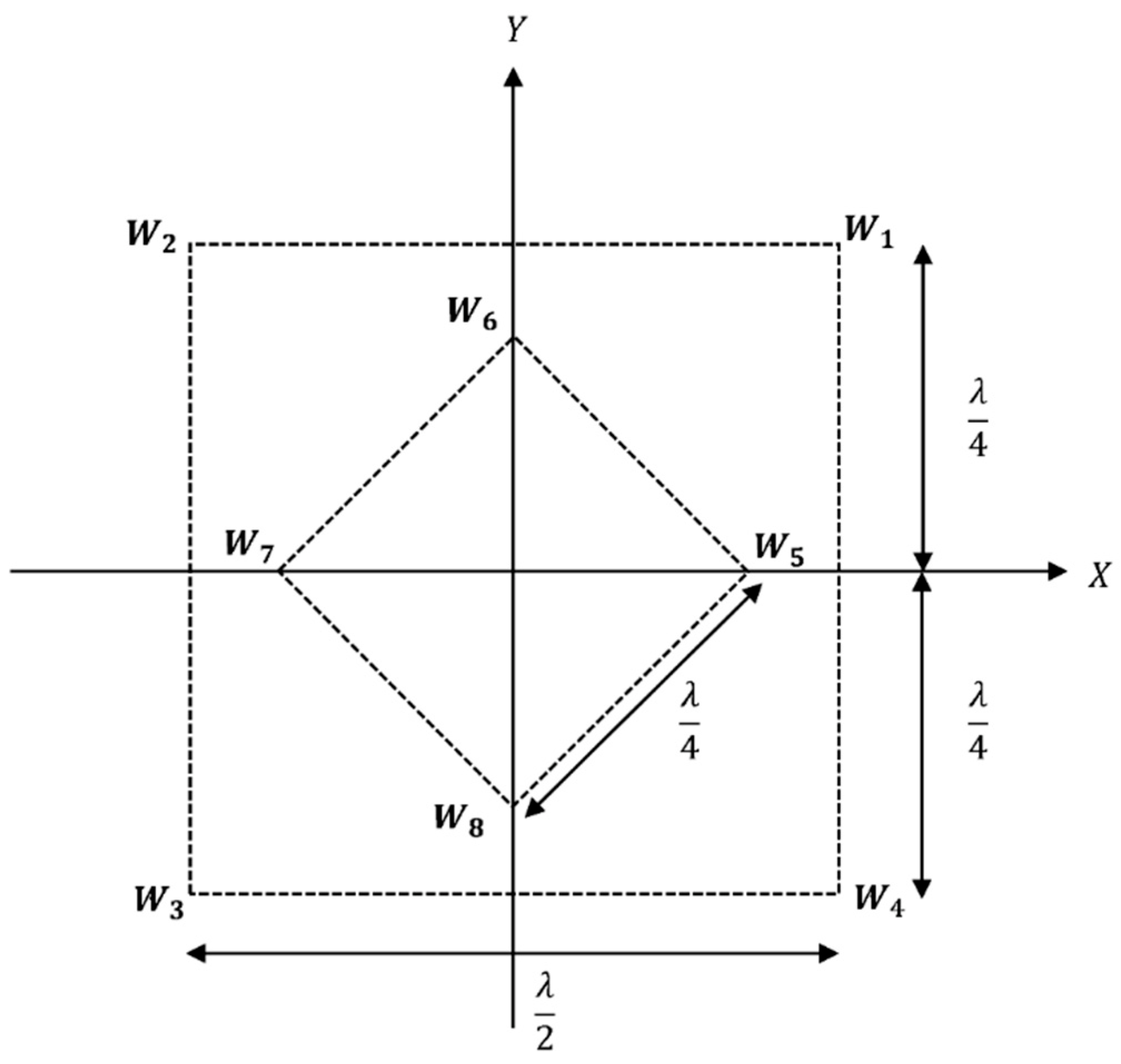
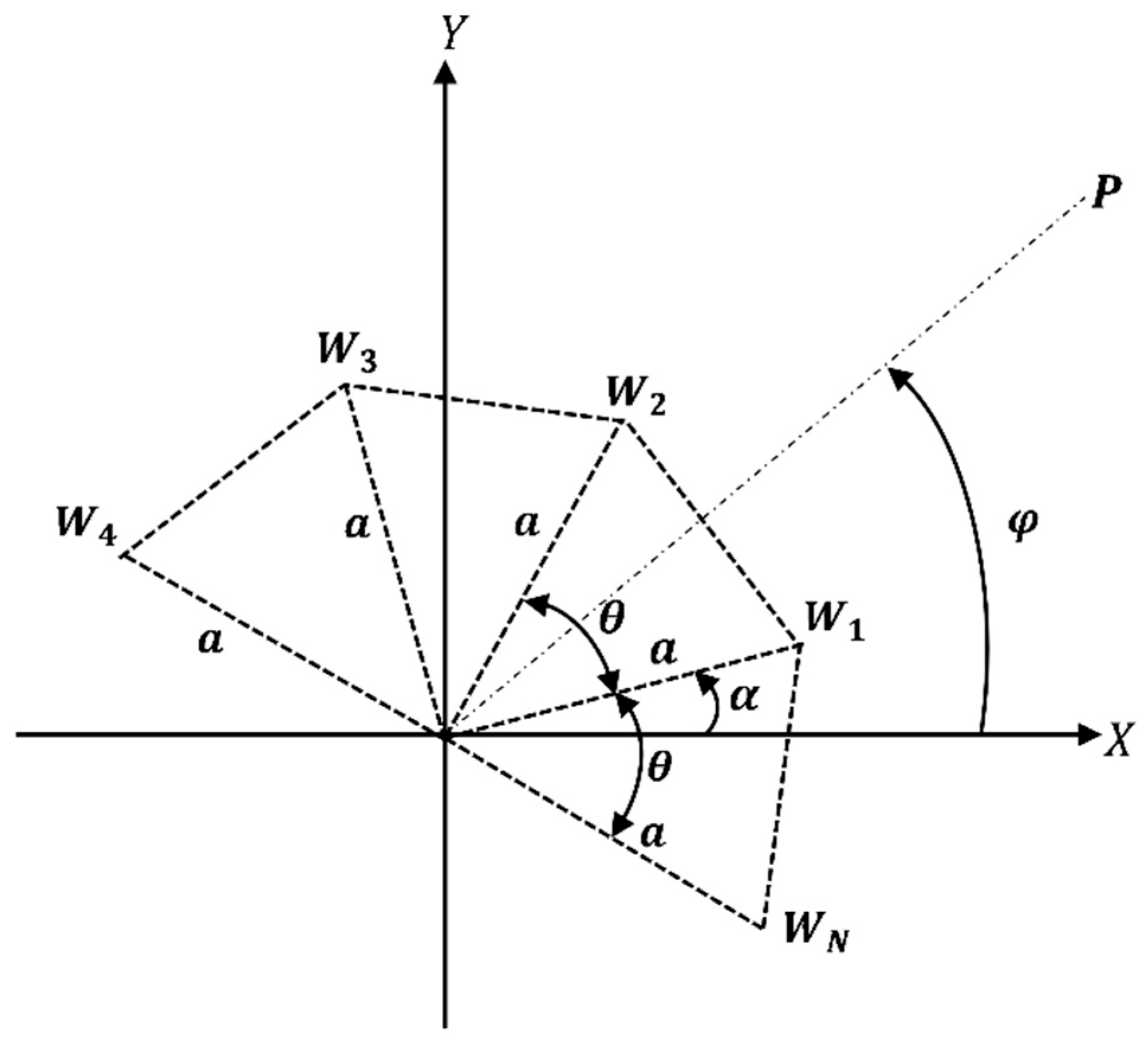
2. Antenna Array Configurations for a Single Rotatable Beam
Optimization of Phase Delay Factors
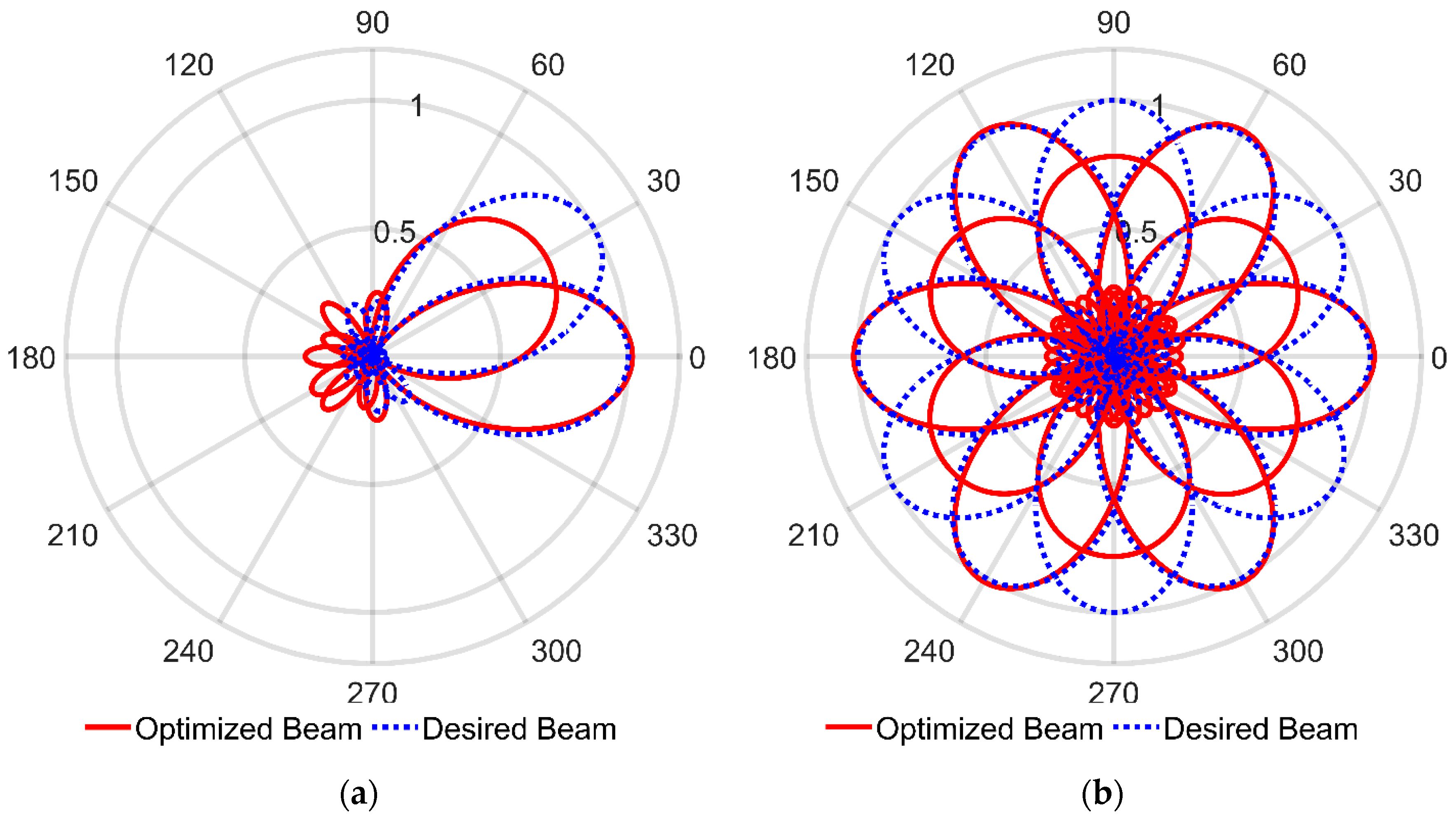
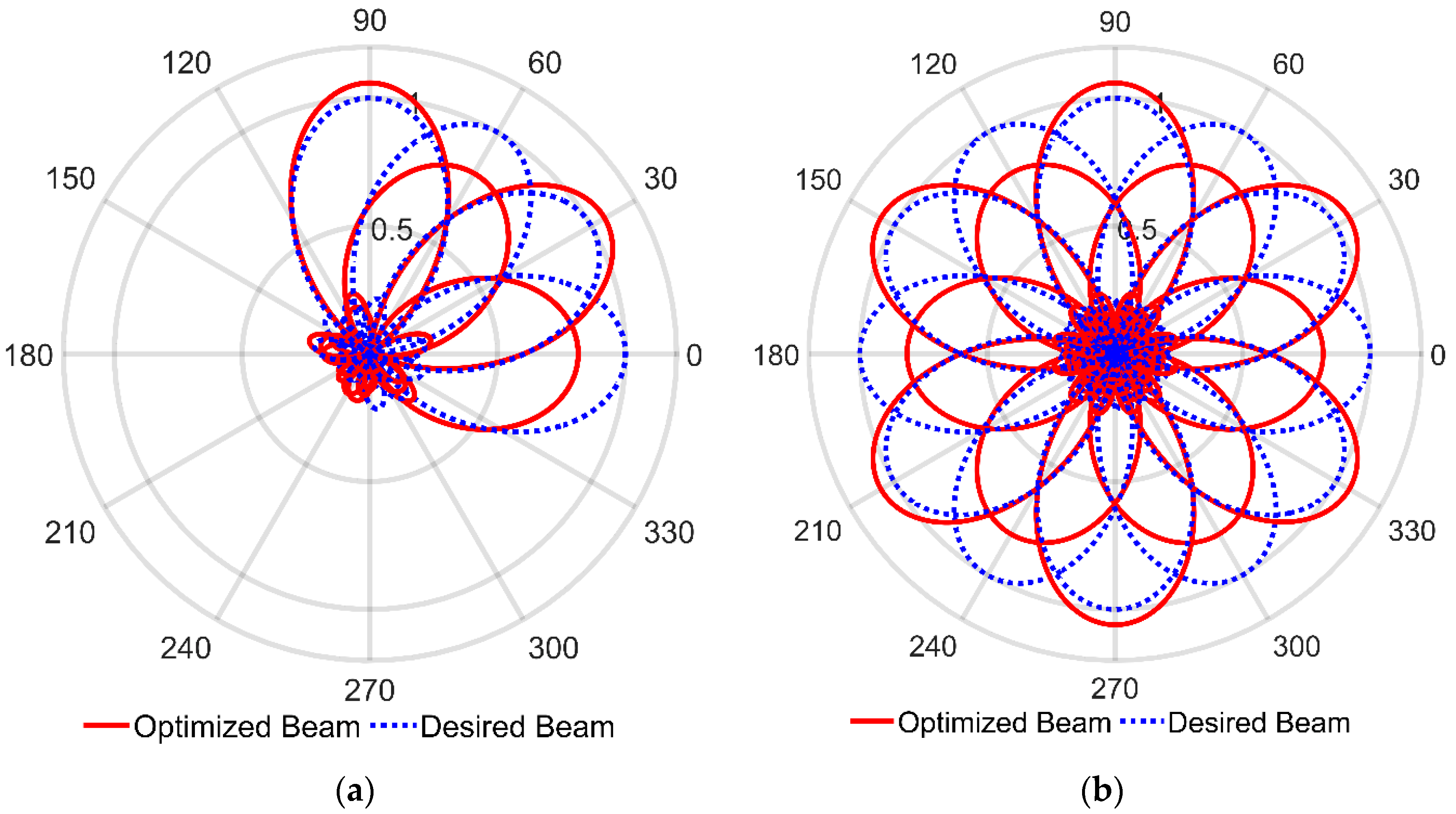
3. Numerical Evaluations
3.1. Beam Shifting at 30° Steps
3.2. Beam Shifting at 15° Steps
3.3. Beamsteering towards an Arbitrary Angle
3.4. Further Observations
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Supriya, R.; Kumar, D.S. Adaptive Algorithms in Smart Antenna Beamformation for Wireless Communication. In Proceedings of the 2016 International Conference on Communication and Signal Processing (ICCSP), Melmaruvathur, India, 6–8 April 2016; pp. 1850–1853. [Google Scholar] [CrossRef]
- Tian, H.L.; Cheadle, D. An Electronically Steerable Parasitic Array Radiator Antenna with Adaptive Beamforming Ability. In Proceedings of the 2017 International Workshop on Electromagnetics: Applications and Student Innovation Competition, London, UK, 30 May–1 June 2017; pp. 103–104. [Google Scholar] [CrossRef]
- Agiwal, M.; Roy, A.; Saxena, N. Next Generation 5G Wireless Networks: A Comprehensive Survey. IEEE Commun. Surv. Tutorials 2016, 18, 1617–1655. [Google Scholar] [CrossRef]
- Salunke, D.B.; Kawitkar, R.S. Analysis of LMS, NLMS and MUSIC Algorithms for Adaptive Array Antenna System. Int. J. Eng. Adv. Technol. (IJEAT) 2013, 2, 130–133. [Google Scholar]
- Obaid, A.; Hussain, F.; Fernando, X. Adaptive Switching for Efficient Energy Harvesting in Energy Constraint IoT Devices. In Proceedings of the 2017 IEEE 86th Vehicular Technology Conference (VTC-Fall), Toronto, ON, Canada, 24–27 September 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Obaid, A.; Fernando, X.; Jaseemuddin, M. A Mobility-Aware Cluster-Based MAC Protocol for Radio- Frequency Energy Harvesting Cognitive Wireless Sensor Networks. IET Wirel. Sens. Syst. 2021, 11, 206–218. [Google Scholar] [CrossRef]
- Kausar, A.; Mehrpouyan, H.; Sellathurai, M.; Qian, R.; Kausar, S. Energy Efficient Switched Parasitic Array Antenna for 5G Networks and IoT. In Proceedings of the 2016 Loughborough Antennas Propagation Conference (LAPC), Loughborough, UK, 14–15 November 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Muirhead, D.; Imran, M.A.; Arshad, K. A Survey of the Challenges, Opportunities and Use of Multiple Antennas in Current and Future 5G Small Cell Base Stations. IEEE Access 2016, 4, 2952–2964. [Google Scholar] [CrossRef]
- Hong, W.; Jiang, Z.H.; Yu, C.; Zhou, J.; Chen, P.; Yu, Z.; Zhang, H.; Yang, B.; Pang, X.; Jiang, M.; et al. Multibeam Antenna Technologies for 5G Wireless Communications. IEEE Trans. Antennas Propag. 2017, 65, 6231–6249. [Google Scholar] [CrossRef]
- Chataut, R.; Akl, R. Massive MIMO Systems for 5G and Beyond Networks-Overview, Recent Trends, Challenges, and Future Research Direction. Sensors 2020, 20, 2753. [Google Scholar] [CrossRef] [PubMed]
- Ardi, E.M.; Shubair, R.M.; Mualla, M.E. Adaptive Beamforming Arrays for Smart Antenna Systems: A Comprehensive Performance Study. In Proceedings of the IEEE Antennas and Propagation Society Symposium, Monterey, CA, USA, 20–25 June 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 3, pp. 2651–2654. [Google Scholar] [CrossRef]
- Singh, A.; Kumar, A.; Ranjan, A.; Kumar, A.; Kumar, A. Beam Steering in Antenna. In Proceedings of the 2017 International Conference on Innovations in Information, Embedded and Communication Systems (ICIIECS), Coimbatore, India, 17–18 March 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Hoole, P.R.P.; Pirapaharan, K.; Hoole, S.R.H. An Electromagnetic Field Based Signal Processor for Mobile Communication Position-Velocity Estimation and Digital Beam-Forming: An Overview (Asia-Pacific Symposium on Applied Electromagnetics and Mechanics (APSAEM10)). J. Jpn. Soc. Appl. Electromagn. 2011, 19, S33–S36. [Google Scholar]
- Pirapaharan, K.; Kunsei, H.; Senthilkumar, K.S.; Hoole, P.R.P.; Hoole, S.R.H. A Single Beam Smart Antenna for Wireless Communication in a Highly Reflective and Narrow Environment. In Proceedings of the 2016 International Symposium on Fundamentals of Electrical Engineering (ISFEE), Bucharest, Romania, 30 June–2 July 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Senthilkumar, K.S.; Pirapaharan, K.; Hoole, P.R.P.; Hoole, R.R.H. Single Perceptron Model for Smart Beam Forming in Array Antennas. Int. J. Electr. Comput. Eng. 2016, 6, 2300. [Google Scholar] [CrossRef]
- Uluisik, C. Antenna Systems with Beam Forming and Beam Steering Capabilities for HF Skywave Radars. Turkish J. Electr. Eng. Comput. Sci. 2010, 18, 485–498. [Google Scholar] [CrossRef]
- Bodhe, S.K.; Hogade, B.G.; Nandgaonkar, S. Beamforming Techniques for Smart Antenna Using Rectangular. Int. J. Electr. Comput. Eng. 2014, 4, 257–264. [Google Scholar] [CrossRef]
- Sun, Z.; Akyildiz, I.F. Optimal MIMO Antenna Geometry Analysis for Wireless Networks in Underground Tunnels. In Proceedings of the GLOBECOM 2009—2009 IEEE Global Telecommunications Conference, Honolulu, HI, USA, 30 November–4 December 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Kulkarni, J.; Sim, C.Y.D. Wideband CPW-Fed Oval-Shapaed Monopole Antenna for Wi-Fi 5 and Wi-Fi 6 applications. Prog. Electromagn. Res. C 2021, 107, 173–182. [Google Scholar] [CrossRef]
- Kulkarni, J.; Abdullah, G.A.; Desai, A.; Sim, C.Y.D.; Poddar, A. Design and Analysis of Wideband Flexible Self-Isolating MIMO Antennas for Sub-6 5G and WLAN Smartphone Terminals. Electronics 2021, 10, 3031. [Google Scholar] [CrossRef]
- Pirapaharan, K.; Hoole, P.R.P.; Kumsei, H.; Senthilkumar, K.S.; Hoole, S.R. A New Smart Antenna for 5/6G Wireless Systems: Narrow 360° Steerable Beam With No Reflectors. In Smart Antennas and Electromagnetic Signal Processing for Advanced Wireless Technology: With Artificial Intelligence Applications and Coding; River Publishers: Gistrup, Denmark, 2020; pp. 147–166. [Google Scholar]
- Widrow, B.; Mantey, P.E.; Griffiths, L.J.; Goode, B.B. Adaptive Antenna Systems. Proc. IEEE 1967, 55, 2143–2159. [Google Scholar] [CrossRef]
- Griffiths, L.J. A Simple Adaptive Algorithm for Real Time Processing in Antenna Arrays. Proc. IEEE 1969, 57, 1696–1704. [Google Scholar] [CrossRef]


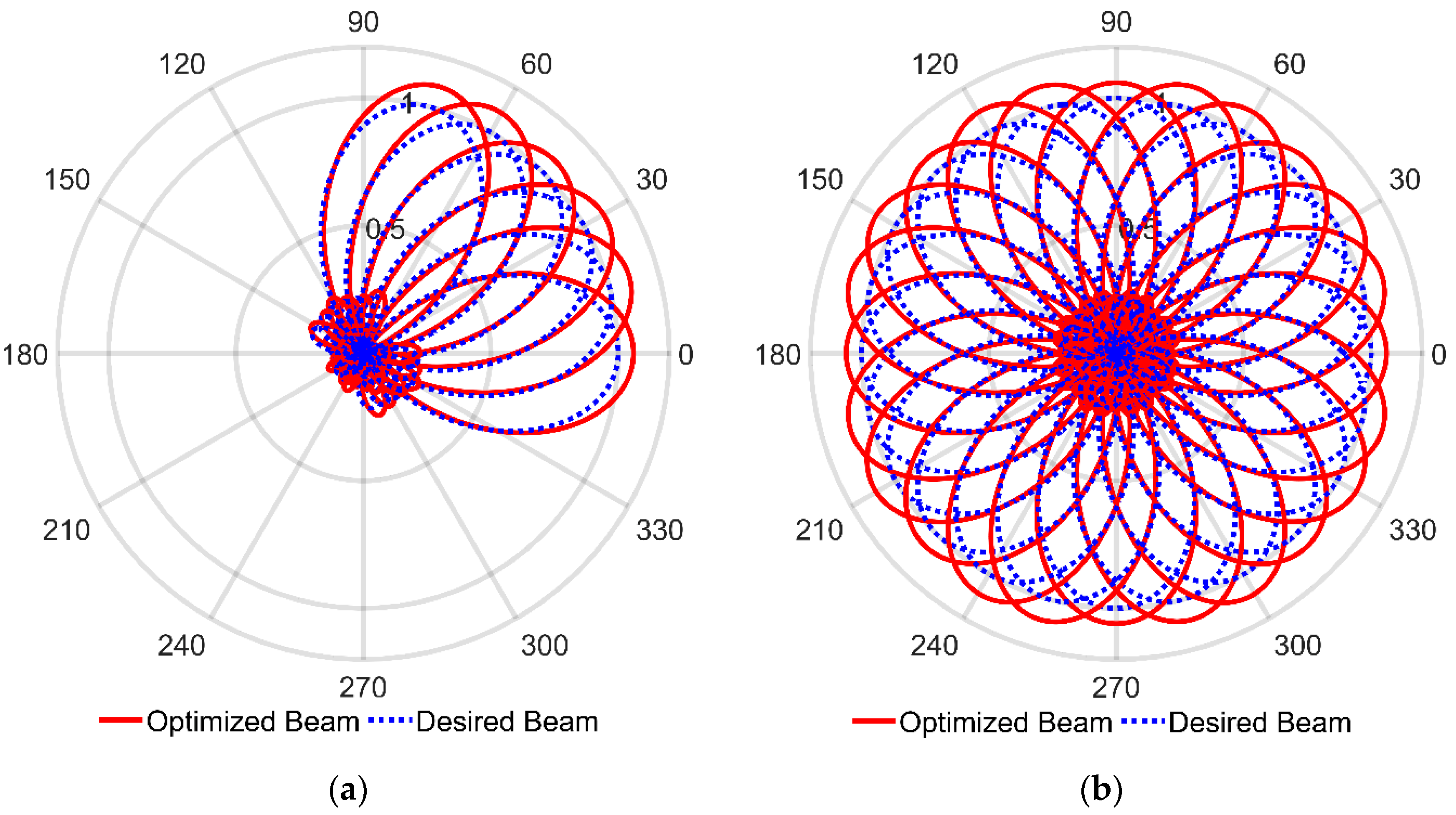
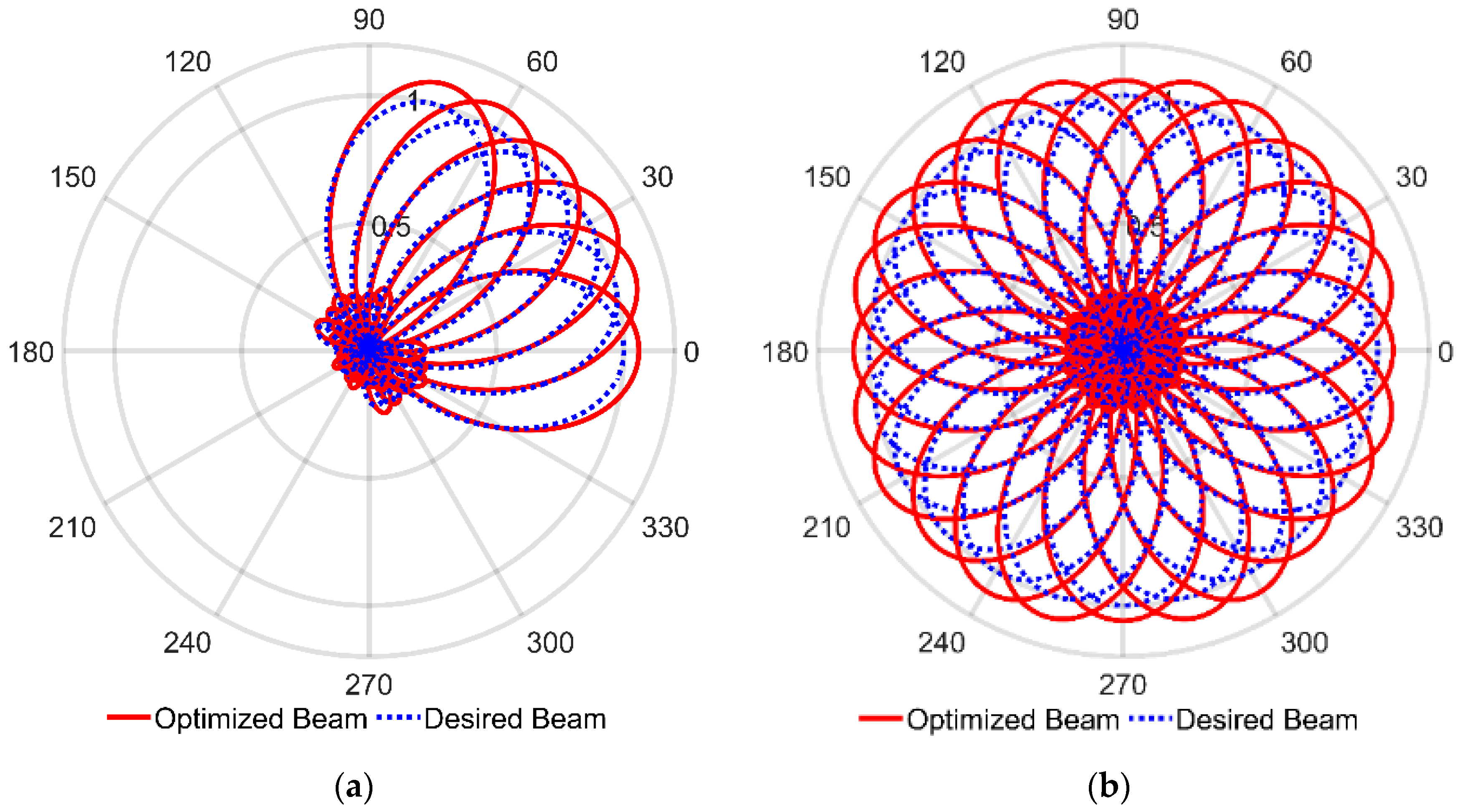

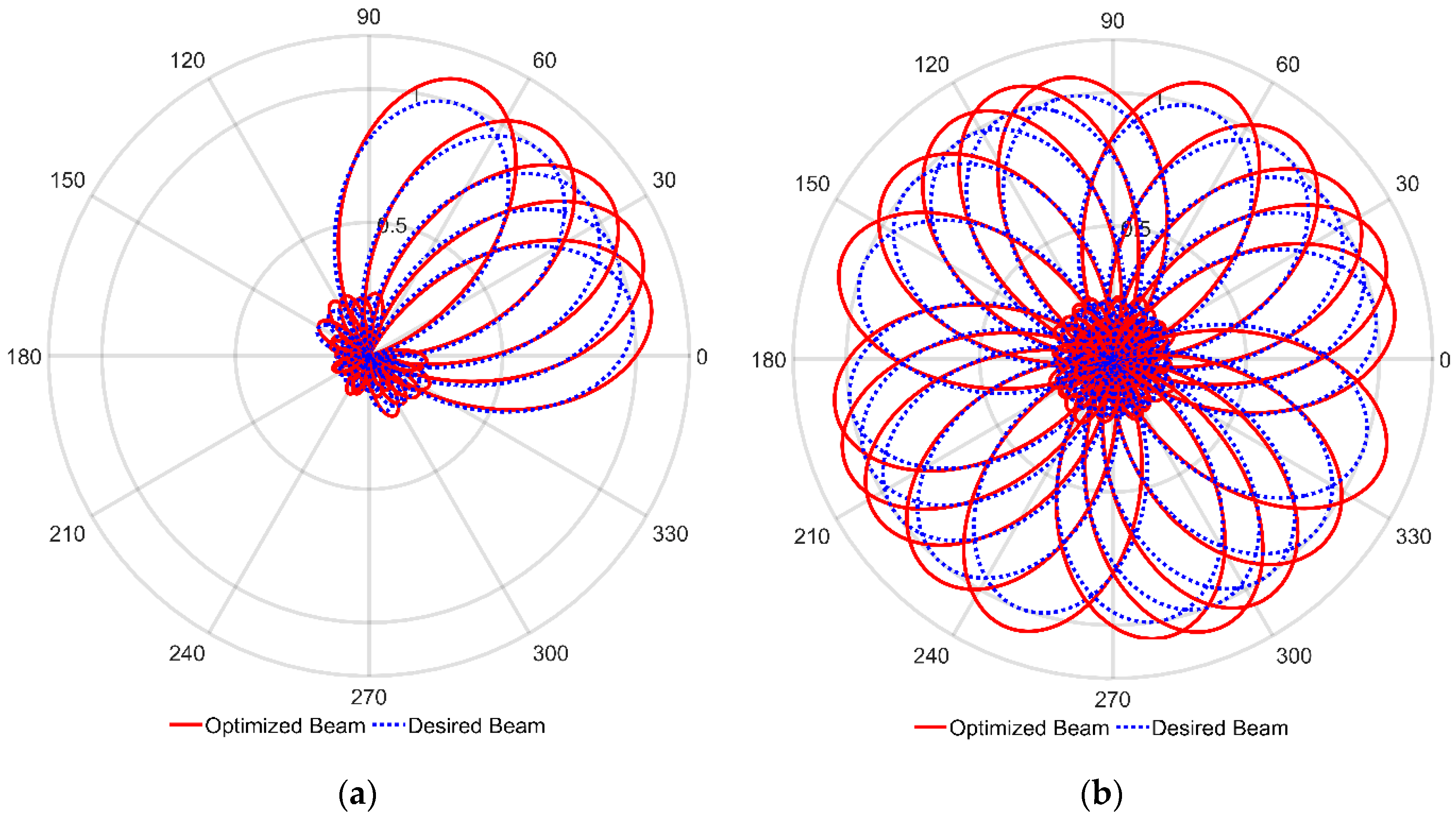
| Configurations | Optimized Angle | Maximum Directivity | Sidelobe Reduction | Single Beam Patterns |
|---|---|---|---|---|
| Equilateral Triangular | 0° | 2.88 at −0.09° | 0.38 with the sidelobe located at 138.56° |  |
| 30° | 3.09 at 29.91° | 0.73 with the sidelobe located at −150.00° | 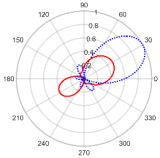 | |
| 60° | 2.89 at 59.91° | 0.41 with the sidelobe located at −76.46° |  | |
| 90° | 3.10 at 89.91° | 0.70 with the sidelobe located at −90.18° | 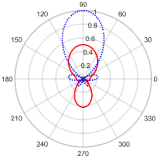 | |
| Square | 0° | 5.09 at −0.09° | 0.31 with the sidelobe located at 180.00° |  |
| 30° | 3.95 at 12.15° | 0.56 with the sidelobe located at −128.2276° | 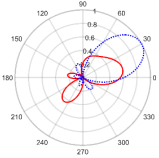 | |
| 60° | 3.95 at 77.67° | 0.56 with the sidelobe located at −141.38° | 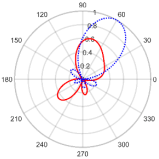 | |
| Regular Hexagonal | 0° | 6.42 at −0.09° | 0.08 with the sidelobe located at −133.02° | 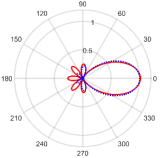 |
| 30° | 5.06 at 29.91° | 0.12 with the sidelobe located at −150.00° | 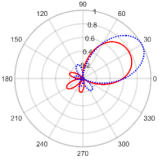 |
| Configurations | Optimized Angle | Maximum Directivity | Sidelobe Reduction | Single Beam Patterns |
|---|---|---|---|---|
| Two-Triangular | 0° | 5.23 at −0.09° | 0.05 with the sidelobe located at −107.81° | 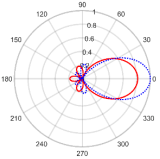 |
| 30° | 6.75 at 29.91° | 0.05 with the sidelobe located at 106.69° |  | |
| 60° | 5.23 at 59.91° | 0.06 with the sidelobe located at 168.77° | 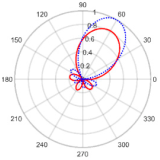 | |
| 90° | 6.75 at 89.91° | 0.05 with the sidelobe located at 13.13° | 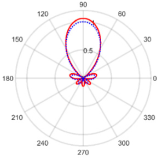 | |
| Regular Octagonal | 0° | 7.78 at −0.09° | 0.13 with the sidelobe located at 70.38° | 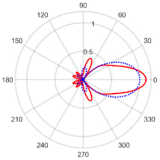 |
| 15° | 6.84 at 6.89° | 0.14 with the sidelobe located at −66.45° |  | |
| 30° | 6.85 at 38.50° | 0.14 with the sidelobe located at 111.27° |  | |
| Two-Square 1 | 0° | 6.94 at −0.09° | 0.06 with the sidelobe located at −75.1487° | 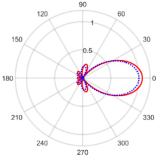 |
| 15° | 7.07 at 15.85° | 0.05 with the sidelobe located at −62.44° | 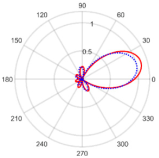 | |
| 30° | 7.10 at 29.84° | 0.04 with the sidelobe located at 107.26° | 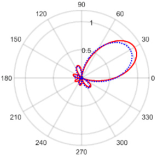 | |
| 45° | 6.92 at 44.91° | 0.06 with the sidelobe located at −30.72° | 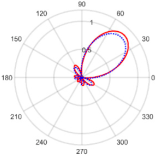 | |
| 60° | 7.08 at 60.48° | 0.05 with the sidelobe located at −17.44° |  | |
| 75° | 7.08 at 74.76° | 0.05 with the sidelobe located at 152.26° | 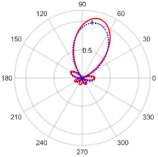 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pirapaharan, K.; Ajithkumar, N.; Sarujan, K.; Fernando, X.; Hoole, P.R.P. Smart, Fast, and Low Memory Beam-Steering Antenna Configurations for 5G and Future Wireless Systems. Electronics 2022, 11, 2658. https://doi.org/10.3390/electronics11172658
Pirapaharan K, Ajithkumar N, Sarujan K, Fernando X, Hoole PRP. Smart, Fast, and Low Memory Beam-Steering Antenna Configurations for 5G and Future Wireless Systems. Electronics. 2022; 11(17):2658. https://doi.org/10.3390/electronics11172658
Chicago/Turabian StylePirapaharan, Kandasamy, Nagananthakumaran Ajithkumar, Konesamoorthy Sarujan, Xavier Fernando, and Paul R. P. Hoole. 2022. "Smart, Fast, and Low Memory Beam-Steering Antenna Configurations for 5G and Future Wireless Systems" Electronics 11, no. 17: 2658. https://doi.org/10.3390/electronics11172658
APA StylePirapaharan, K., Ajithkumar, N., Sarujan, K., Fernando, X., & Hoole, P. R. P. (2022). Smart, Fast, and Low Memory Beam-Steering Antenna Configurations for 5G and Future Wireless Systems. Electronics, 11(17), 2658. https://doi.org/10.3390/electronics11172658







