Hardware/Software Co-Design of a Circle Detection System Based on Evolutionary Computing

Abstract

In recent years, the strategy of co-designing Hardware/Software (HW/SW) systems has been widely adopted to exploit the synergy between both approaches thanks to technological advances that have led to more powerful devices providing an increasingly better cost–benefit trade-off. This paper presents an HW/SW system for the detection of multiple circles in digital images based on a genetic algorithm. It is implemented on an Ultra96-v2 development board, which contains a Xilinx Zynq UltraScale+ MPSoC device and supports a Linux operating system that facilitates application development. The design is powered by developing an interactive computing environment by means of the Jupyter Notebook platform, in which different programming languages coexist. The specific advantages of each of these languages have been used to describe the hardware component that accelerates the evolutionary computation for circle detection (VHDL), to execute SW-HW interaction functions, as well as the pre- and post-processing of the images (ANSI-C) and to code, evaluate, and document the system execution process (Python). As a result, a computationally efficient application was obtained, with high accuracy in the detection of circles in synthetic and real images, and with a high degree of reconfigurability that provides the user with the necessary tools to incorporate it in a specific area of interest.

1. Introduction

In computer vision, the detection of circles has remained as one of the important tasks in the analysis of digital images, since human beings, in the development of their daily lives, can face multiple situations where they interact with a variety of objects characterized by their circular or spherical shape. In these everyday scenarios, this type of figure can be found as a characteristic of many natural objects (ocular iris, cells, or some fruits) or artificially created as a product of a manufacturing process (mechanical parts, traffic signs, and balls). Its digital identification is a basic requirement for optimizing and automating tasks related to inspection, tracking, counting, or classification of objects in central areas such as medicine [1], transportation [2,3,4], sports [5], or the food-processing industry [6].

Traditionally, the Circular Hough Transform (CHT) has been used to perform the task of detecting circles in digital images because it provides high accuracy and a good noise response, but the computational cost and the amount of memory required are serious drawbacks in implementing this technique in embedded systems with limited resources, such as the ones used today in many IoT devices. The simplest strategies to mitigate this handicap consist in limiting the values of the possible detected radii to a finite interval or defining angular steps wide enough to evaluate candidate circles while maintaining an acceptable level of efficacy in the detection task. These approaches, however, have not significantly improved the cost/benefit balance; which has motivated the proposal of more efficient alternatives for CHT optimization that combine reduced operations [7] or efficient memory consumption [8,9] with the advantages provided by the use of Field-Programmable Gate Arrays (FPGAs) for implementing dedicated hardware to accelerate task processing by means of design techniques based on pipelining or parallelism.

In addition to CHT, other circle detection methods have been developed based on different strategies such as random candidate location [10,11], the power of a point theorem [12], bee colony algorithms [13,14,15], and genetic algorithms (GAs) [16]. In particular, GAs appear among alternative strategies because they provide some of the most effective optimization and search algorithms within computational intelligence [17,18], as they have, among their main features, the ability to provide reliable solutions, adapt to varied problems, avoid local minima, and evaluate multiple solutions simultaneously.

The efficacy of GAs has also been boosted by their implementation in programmable devices, with their impact reflected in multiple applications. To cite just a few examples, in the area of computer vision, Teja and Bachu [19] implement a GA for motion estimation on a device of the Virtex-6 family. In transportation, Tuncer and Yildirim propose in [20] an optimal way of tracing paths of navigation of mobile robots by using a GA implemented in a device of the Virtex-5 family. Moreover, in this application area, Allaire et al. present in [21] the implementation of a GA in a Virtex-II Pro family device for the optimization of unmanned aerial vehicle routing with two outstanding characteristics: a small size that allows it to be integrated directly into the target vehicle, and the capacity to achieve real-time processing required by the nature of the problem. In the area of artificial intelligence, Dumesnil et al. [22] implemented an artificial neural network in a Spartan-6 family device that is tuned by a GA implemented as a parallel process.

Technological advances in the last decade have demonstrated the convenience of implementing embedded systems on system-on-chip (SoC) devices, as an alternative to cope with the high computational cost and high response time of GAs that are ultimately intended to be embedded in computer vision systems. These kind of devices are characterized by relatively high computational capacity, small size, and a very advantageous cost/performance balance [23,24], allowing users to jointly exploit the benefits of software and hardware implementations.

In support of embedded systems development, Xilinx has been at the forefront of providing a wide range of powerful devices and tools that allow both software developers and hardware designers to integrate hybrid designs into different platforms. Furthermore, the PYNQ (Python Productivity for Zynq) environment provided by the PYNQ project [25] allows users to take advantage of the programmable logic and processing systems that are part of the Xilinx Zynq architecture using the “Jupyter Notebook” platform, from which it is possible to describe and execute the functionality of a hybrid design using functions and libraries, coded in C or Python, that interact with overlays (hardware analogy to software libraries) implemented in the programmable logic.

This paper presents a complete embedded system that uses a GA to detect circles in digital images based on the strategy published in [16] and whose HW implementation was detailed in [26]. The system, including support for I/O peripherals, has been implemented on an Ultra96-v2 development board, which is powered by a device of the Xilinx Zynq-Ultrascale+ MPSoC family that combines Programmable Logic (PL) with a Processing System (PS) based on a quad-core ARM Cortex-53 application processor.

Taking advantage of the development board features, the proposed system has been provided with a high degree of flexibility and efficacy in the following way: First, all GA stages are implemented in hardware for their acceleration in the PL, since they perform the critical task within the runtime. Second, pre- and post-processing tasks are implemented in the software running on the PS using ANSI C language to take advantage of the execution speed of a compiled language. Finally, both the control of the I/O peripherals of the development board completing the system, and the execution control of the tasks distributed between the PS and the PL, are coded using the main language of the Jupyter Notebook (Python) to ease the analysis of the system performance by including the facility of exploring “live” and interactively each of its stages. Additionally, each stage of the system was properly documented, and multimedia resources were used to improve the analysis of its results.

To guide the reading of this document, Section 2 presents the general structure of the detection system, detailing the tasks involved and their distribution among the software and hardware components of the system. Section 3 describes the execution of the evaluation and validation protocol developed for this purpose and presents a detailed analysis of the results. Finally, Section 4 summarizes the conclusions reached from the previous analysis.

2. System Description

The complete Circle Detection System (CDS) is physically composed of the three elements shown in Figure 1: an input peripheral (webcam), a development board (Ultra96-v2), and an output peripheral (monitor). The use of the Jupyter Notebook platform for creating and sharing computational documents simplifies the development of software components for the capture and presentation of images through the IO devices. This web-based interactive platform, provided by the PYNQ environment and executed on the PS included in the programmable device of the development board, allows using a rich ecosystem of application-specific libraries written in C or Python, which are directly executed from the notebook. The PYNQ environment also provides a set of Python utility functions for the interface and control of hardware components implementing the circle detection GA on the PL of the programmable device.

To coordinate the operation of the system, one of the main features of the Jupyter Notebook platform is the possibility of defining and organizing the different tasks that compose the process so that they can be evaluated “live” and separately to facilitate debugging. To achieve this, the notebook has an element called a “code-cell”, in which one or multiple tasks can be programmed. When a code-cell is executed, its corresponding output is presented within the notebook and may include multimedia representations such as tables, diagrams, graphs, images, audio, or video. The block diagram in Figure 2 shows the distribution of the main groups of tasks that define the CDS, as well as the hierarchy of execution and the interaction between the different code-cells that define them.

The execution of the system starts by defining the configuration parameters and capturing the input image using the webcam connected to the development board. A pre-processing stage is performed on this set of inputs, where the main task is the detection of the edges of the image to generate the data structure that feeds the GA that carries out the circle detection strategy. Once the data structure is sent to the overlay that implements the GA in hardware, its internal stages process the data according to the following order: (1) the construction of the initial population formed by candidate circles (individuals), where each circle is encoded using 3 random edge pixels; (2) the assessment of the individuals’ fitness to determine their ability to correctly represent a circle within the image; (3) the selection of the fittest individuals to promote their features in future generations through their offspring; and (4) the exploration of new candidate circles resulting from the combination of the features of the selected individuals using crossover and genetic mutations. At the end of the detection process, the GA provides a set of results that are used in a post-processing stage to superimpose the detected circles on the original image and to report in files the temporal performance and efficacy of the system. Finally, the output image is displayed on-screen through the DisplayPort incorporated in the development board.

The development of the system’s internal components has been carried out through the use of different programming and description languages in such a way that, as a whole, they provide the system with an adequate balance between performance and interactivity. The Python language is suitable for the implementation of interface tasks with input and output devices, since it is a high-level language with a large collection of libraries that can be adopted for the control of peripherals and the visualization of the results of the internal processes. The C language, which is capable of providing higher performance as a compiled language, was used to implement the specific processing steps of the detection process. Finally, the VHDL language was selected to describe the functionality of the AG and facilitate its hardware implementation using the resources of the programmable device.

The design parameters presented in

Table 1. CDS design parameters.

Parameter	Value
Image dimensions	640 × 480
Image depth	24 bits
Image file format	BMP
Genes per individual	3
Population size	64
Selection method	Roulette Wheel
Crossover strategy	One-point
Number of elite individuals	1
Crossover probability	50%
Mutation probability	12.5%

were used in the development of the system. These parameters were selected based on the full software implementation of the detection strategy presented by Ayala et al. in [16] and the preliminary implementation of a hybrid and optimized version of that strategy presented by Rojas et al. in [26].

Within these parameters, the image size is of great importance since some design features such as the minimum detectable radius, or the resource consumption (bus length and memory size), are directly related to the algorithm performance (convergence speed). By setting the image size to 640 × 480 pixels, we obtain an adequate processing time, low resource consumption, and provide the system with a resolution compatible with multiple monitors or screens.

2.1. Input Data

The input data for the system come from two different sources. The first is the input peripheral through which the image capture is performed, and the second is the command interface, which allows the user to define the execution parameters for the processing stages and the GA. The used input peripheral is a Trust eLight webcam connected to a USB port on the Ultra96-v2 board. This port is linked to the PS of the Zynq-Ultrascale+ device and is used as a traditional USB host port to control the webcam. Access to the camera is provided by the OpenCV library, one of the leading Python image and video processing libraries. In OpenCV, the function cv2.Videocapture() is used to configure the dimensions of the input image according to the design parameters (640 × 480) and to capture the image. Once these processes have been validated, the input image is displayed on the notebook for visual verification by the user and then stored in BMP format in the notebook’s local directory for later access in the next stage of the process. In order to initiate the detection process, the user must also provide through the command interface the set of data required in the processing stages, defining the configuration parameters presented in

Table 2. CDS input parameters description.

Parameter	Type	Range	Description
Image_name	BMP file	-	Input file. Can be captured via webcam or uploaded from a repository.
Sigma	real	>0	Standard deviation of the Gaussian blur filter used in Canny’s method.
tlow	real	[0, 1]	Low value to use in hysteresis.
thigh	real	[0, 1]	High value to use in hysteresis.
fit	real	[0, 1]	Threshold of fitness to reach convergence.
mc	integer	>0	Number of circles to detect within the image.
gns	integer	>0	Generations to perform if the fitness threshold is not reached.
inc	integer	>0	Interval between generations to report partial detection results.
tests	integer	>0	Number of executions of the AG.
Output_file	txt file	-	Output file where results of debugging and/or temporary analysis are recorded.

.

2.2. Pre-Processing

The file format, dimensions, and depth image parameters are validated first at this stage to ensure that they meet the design requirements. An important feature of the implemented detection technique is that part of the required data structure must be generated from a single-pixel edge image. To obtain this image, the Canny edge detection algorithm is used with the previously defined sigma, tlow, and thigh parameters.

The data structure used as input to the circle detection GA is composed of the elements described in

Table 3. Data structure generated in the pre-processing stage and used as input to the circle detection GA.

Name	Type	Length	Description
BE_Img	Vector	307200	Binary representation of the edge image, where each edge pixel is assigned the value of ‘1’. Its length is constant and equal to the product of the image dimensions (640 × 480).
XY_Img	Vector	Variable	Coordinates (x,y) of the edge pixels. Its length is variable since each image has a different number of edge pixels
IPop_AG	Vector	64	Initial population of the GA. It is formed by candidate circles (individuals) representing possible solutions to the detection task.

, where vectors BE_Img, XY_Img, and IPop_AG correspond to a direct extraction of information from the edge image. The IPop_AG vector consists of 64 individuals, each of which is defined by three pixels randomly chosen from the edge image that is stored in the BE_Img vector, whose corresponding coordinates are stored in the XY_Img vector. Each individual is composed of 3 pixels since this is the number of points necessary to uniquely determine a circle, whose parameters in terms of center and radius are given by Equations (1)–(3). Each of these vectors will be stored in a RAM block arranged for this purpose in the design using the specific BRAM resources available in the PL of the programmable device.

$$x_0={\displaystyle \frac{\left|\begin{array}{cc}{x}_j^2+y_j^2-(x_i^2+y_i^2)& 2(y_j-y_i)\\ x_k^2+y_k^2-(x_i^2+y_i^2)& 2(y_k-y_i)\end{array}\right|}{4((x_j-x_i)(y_k-y_i)-(x_k-x_i)(y_j-y_i))}}$$

(1)

$$y_0={\displaystyle \frac{\left|\begin{array}{cc}2(x_j-x_i)& x_j^2+y_j^2-(x_i^2+y_i^2)\\ 2(x_k-x_i)& x_k^2+y_k^2-(x_i^2+y_i^2)\end{array}\right|}{4((x_j-x_i)(y_k-y_i)-(x_k-x_i)(y_j-y_i))}}$$

(2)

$$r=\sqrt{{(x-x_o)}^2+{(y-y_o)}^2}$$

(3)

Following the analogy with an evolutionary process, the vector containing the initial population is also designated as the “genotype space” within the genetic algorithm, and the BE_Img vector is designated as the “search space” since it contains the entire binary representation of the edge image where each edge pixel represents a generation that could be used to encode the individuals of the first generation and will be used as a reference to encode the subsequent generations.

This data structure is then complemented by the user-defined configuration parameters in Table 2 that describe the GA execution features.

To ease the interaction between the processing stages executed on the PS and the hardware realization of the GA implemented on the PL, we encapsulated as an IP module with AXI4-Lite interface. AXI4 (Advanced eXtensible Interface 4) is the fourth generation of the AMBA interface specification from ARM, adopted for Xilinx as IP interconnect standard for programmable devices from the Series-7, Zynq-7000, and UltraScale+ families. AXI4-Lite is typically used for memory-mapped communication between processors and low-throughput peripherals. In our case, the input and output ports of the GA are allocated to a series of registers that can be accessed from the PS using common read and write instructions on the respective addresses. In this way, these registers are used both to send the complete data structure and to receive the results of the GA once convergence is reached or the maximum possible number of generations is exceeded.

In addition to the reading and writing tasks to access the input and output ports of the GA, it is necessary to perform two additional tasks for the correct operation of the hardware component. One of them, directly related to the previous two, consists in defining the address window of the processor’s memory map through which the input and output registers of the IP module implemented in hardware will be accessed. The other one is responsible for loading the bitstream file generated as result of the GA synthesis and implementation processes to define the functionality of the programmable device.

These 4 tasks (load bitstream, define register window, and read and write registers) used for PS–PL communication are supported by their respective functions within the Application Programming Interface (API) developed in the C language by Brown [27] as a faster alternative to the Python drivers provided in the PYNQ environment.

2.3. GA Hardware Implementation

The Xilinx Vivado Design Suite tool set was used to develop the hardware component of the detection system. Among the facilities offered by this software, it includes the IP Integrator tool, especially suitable for developing IP-based hardware structures that combine user-designed components and IP cores provided by Xilinx. In addition, the IP-based design flow is well-suited to the development of the modular structure that the GA presents. The successive stages of the GA were implemented in the PL of the Ultra96-v2 board programmable device according to the flow chart shown in Figure 3, whose functionality is detailed in the following subsections.

2.3.1. Initial Population

As previously mentioned, the detection strategy developed in this work is based on the location of candidate circles (individuals) that are represented by coding three randomly chosen points that are part of its perimeter. This coding scheme is possible since, to mathematically represent a circle in terms of its center and radius, only any three points on its perimeter are needed, as shown in Equations (1)–(3). This set of equations is used to encode the initial population stored in vector IPop_AG using the indices corresponding to the three random points within the vector XY_img. Therefore, its implementation in hardware encompasses two tasks: the decoding of individuals and calculation of the parameters of corresponding center and radius.

To decode every individual Cn in the population, the design presented in Figure 4 is implemented. The process begins with the separation of each of the genes that make up an individual into different buses. These genes represent indexes of the XY_img vector that has been stored in the corresponding RAM. Each gene is used as a reading address, thus obtaining a triad of coordinates ((xi,yi),(xj,yj),(xk, and yk)). Considering that each triad of coordinates corresponds to pixels that have been selected randomly, there is the possibility that Equations (1) and (2) present an indeterminacy if there is collinearity between pairs of them. To avoid this problem, a validation stage is implemented to discard those individuals that present this characteristic by assigning them a null aptitude value.

2.3.2. Phenotype

Calculating the center ($x_0$, $y_0$) and radius (r) of the individuals is also known as the transformation of the individuals from the “genotype space” to the “phenotype space”. This task is performed using Equations (1)–(3) to evaluate every triad of coordinates i, j, and k that have been previously decoded. The transformation involves a large number of operations. For this reason, we designed it to avoid the implementation of multiple modules that represent the same operation and to parallelize the execution of the operations. Figure 5 shows the blocks that represent the tasks in which the implementation of this stage was distributed based on the arithmetic hierarchy.

2.3.3. Fitness-Elitism

This module allows every individual to be scored with a fitness value according to the number of pixels of the virtual circle that coincide with the real pixels of the binary vector BE_img stored in its corresponding RAM. The main consideration for the design of this block lies in the definition of a finite range of integers for the possible calculated radii. This consideration is necessary since there is the possibility of calculating radii of circles that exceed the dimensions of the image or are small enough to generate false positives with a very high fitness value. Given the dimensions of the image, a maximum radius of 320 pixels is defined to detect circles with a minimum of 50% of their perimeter inside the image and a minimum radius of 10 pixels to reach a maximum angular delta of 0.1 radians per pixel. Once the radii constrains are defined, the fitness value calculation for each individual starts by implementing Equations (4) and (5) to obtain the location of the virtual perimeter pixels ($x_v$,$y_v$).

$$x_v=x_0+r\ast cos\left(\frac{2\pi i}{N_s}\right);i=0,1,2,\dots N_s-1$$

(4)

$$y_v=y_0+r\ast sin\left(\frac{2\pi i}{N_s}\right);i=0,1,2,\dots N_s-1$$

(5)

In this equations, variable Ns is defined as the length of the circumference, so that the angular delta ($\delta \alpha$) with which the perimeter of each candidate circle will be spanned will be 1/r, as shown in Equation (6).

$$\left(\frac{2\pi i}{N_s}\right)=\left(\frac{2\pi i}{2\pi r}\right)=\left(\frac{i}{r}\right)=\left(\frac{1}{r}\right)i=>\delta \alpha =\left(\frac{1}{r}\right)$$

(6)

As the possible radii are bounded in a finite range of integers, so are angular deltas. Taking advantage of this fact, a lookup table is implemented to store all possible angular deltas. The implementation of the trigonometric functions sin() and cos() is performed by means of the Xilinx LogiCORE IP CORDIC, which is also designed to solve other types of functions such as hyperbolic functions or for conversions between rectangular and polar coordinate systems. This IP has a high degree of configurability, which allows an ideal coupling with the IPs designed by the authors, in addition to providing a level of accuracy in the results that meets the needs of the system. The implementation of these equations is completed with the subsequent multiplication by the radius and addition of the coordinate of the respective center. Finally, the calculated virtual coordinates ($x_v$,$y_v$) are mathematically adapted to be used as reading addresses of the RAM that contains the BE_img vector to implement Equation (7) [16].

$$F\left(E\right)=\frac{{\sum }_{i=0}^{N_s}E(x_v,y_v)}{N_s}$$

(7)

The E() function defines numerically whether a virtual coordinate exists (‘1’) or does not exist (‘0’) as a real border pixel within the vector. The number of matches in the entire perimeter is quantified by extending the sum to all the evaluated points. This is implemented using a counter that is increased by one each time the calculated virtual pixel coincides with an edge pixel in the $N_s$-queried addresses. By normalizing each fitness value between 0 and 1 using a divisor, it is possible to use this value to compare the individuals’ ability to detect a circle. Figure 6 shows the block diagram corresponding to the implementation of Equations (4), (5) and (7) for fitness evaluation.

2.3.4. Selection

The emulation of the natural selection process ensures that the features of individuals to solve the detection task are inherited by new generations based on the fitness. This suggests a higher probability of survival of the fittest individual without suppressing the probability of survival of the least fit. The selection strategy implemented in this design is based on the roulette wheel. In this mechanism, the probability that an individual will be selected is calculated as the ratio between its fitness and the accumulated fitness of the entire population, so, in terms of the roulette wheel analogy, the individual fitness is represented by an angular aperture over the roulette wheel circumference, where the 2$\pi$ radians of the latter represents the cumulative fitness of the population such that the angular ratio equals the probability that an individual will be selected. To accomplish this emulation, three main tasks are implemented in hardware and schematized in the block diagram presented in Figure 7: generation of a random number, accumulation of the individual fitness, and selection of the individual who will inherit its genetic characteristics to the next generation.

The generation of the random number used in each roulette wheel spin emulation is performed by means of an open-source PRNG developed by [28] that has been included in the system as an entropy source. Its low resource consumption and its ability to generate a pseudo-random number per clock cycle are perfectly suited to the system requirements. For the accumulation of the fitness, a sequential reading of the memories that store the population and fitness values is performed such that each individual and its corresponding fitness are available in the same clock cycle. This reading process is the base to carry out a progressive accumulation of the fitness. The selection process is performed based on the continuous comparison between the generated threshold and the cumulative fitness. The accumulation of the fitness will eventually exceed the pseudo-random threshold, which activates a flag that will be used as an enabler to store in a RAM memory the individual who provided its fitness to exceed the threshold. Since the threshold is random, the selected individual will be random as well. This roulette wheel spin is emulated as many times as there are individuals in the population to guarantee the same population density over time.

2.3.5. Crossover and Mutation

The population formed from the selection process is made up of individuals possessing better characteristics than their ancestors to solve the detection task. The natural selection process ends with the application of two genetic operators: crossover and mutation. The crossover allows the generation of new individuals through the exchange of features between the selected individuals, thus opening two ways to favor convergence: one by generating features that improve the fitness achieved by their ancestors, and the other by generating worse features than the original ones, which will decrease the probability of selecting the individual in the next iteration of the GA. In this design, we implemented a one-point crossover with a 50% acceptance probability, indicating that approximately half of the population will retain the features with which they were selected. By performing the exchange of features by separating the individuals at a single random point and exchanging one of its ends, the features of the ancestors are kept as complete as possible in the offspring, which also contributes positively to convergence. A multi-point crossover process would undermine the effectiveness of fitness-based selection. Mutation is applied by seeking to explore unknown areas of the search space that have not been considered in solving the detection task. We performed this operation by modifying the bits of the individuals by means of the logical XOR operation with a random mask. Since this genetic operator affects all genes of an individual, the convergence trend may be lost; therefore, a mutation acceptance probability of 10% is implemented to conserve a significant number of individuals representing the evolutionary process. Figure 8 shows the block diagram describing the implementation of both crossover and mutation operators.

2.4. Post-Processing

When GA convergence has been reached by having achieved a fitness threshold, or the established generation limit has been exceeded, the GA detection results are transmitted to the PS via the AXI4-Lite communication bus. The detection results consist of center, radius, fitness value, time to detect the elite individual, and total execution time. Once these data are available on the PS, a post-processing stage is performed in order to generate a report and a graphic validation of the process.

For graphic validation, a copy of the input image is generated and stored in the same directory as the input image. The detected circle is superimposed on this copy of the image using the software implementation of Equations (4) and (5), so that the user can act as a reference vision system to verify the location of the detected circle. For the numeric results report, a plain text file is generated to show the behavioral and temporal data.

2.5. CDS Notebook

One of the main characteristics of the Jupyter Notebook platform is that it has been designed to facilitate data analysis and a detailed description of source code by incorporating interactive components in the programming process. This means that the platform allows the documentation of a program and its interactive execution to be provided in a single file. Another characteristic is that a notebook can be accessed using a web browser, which facilitates its access and execution. Additionally, a notebook can include graphical output such as images, video, graphics or mathematical equations, among others, which enhances the presentation of results. The content in a notebook can be organized using 3 types of independent cells: code, markdown, and raw. Each of them can be modified and/or executed independently, in any order and multiple times. They differ in the fact that only code-type cells can generate output that will appear immediately below them, while the other two types of cells can only include formatted (markdown) or unformatted (raw) text.

Figure 9 shows an example of the use of markdown (left) and code (right) cells. This example describes the first step that is executed in the system, in which the markdown cell is used to detail the objectives of the task and what functions are needed to achieve those objectives, while the code-cell contains the structured use of those functions to generate the desired output. Each of the subsequent tasks that are executed in the system are documented using both types of cells (markdown-cell + code-cell) in a similar manner. As mentioned before, an output will be generated every time this code-cell is executed, and every code-cell includes a counter to ease the identification of the output with its respective input.

Although the code-cells can be executed independently, it is possible that there is a consequent dependency of the information processing as it happens in our case. Mentioning a trivial example, in this system it is not possible to execute the detection task if the input image has not been previously defined. Figure 10 presents a diagram that guides the user in the flow of information between the notebook cells.

Considering these features, a notebook has been developed to execute and document the whole set of tasks of the system presented in the flowchart of Figure 2. Its codification is briefly described below:

• Code-cell 1. Webcam configuration: The input image dimensions are configured, and the webcam is enabled to perform the capture process. To achieve this, the set() function, a member of the VideoCapture class from cv2 library, is used.
• Code-cell 2. Capture image: The image is captured and stored in the notebook’s local directory. The read() function from VideoCapture class is used to capture the image, and the imwrite() function of the cv2 library is used to store it. It is also possible to select a different image from an image repository.
• Code-cell 3. Image preview: It provides the visualization of the input image before executing any processing stage with which the user has the possibility of validating or modifying the scene in order to meet the requirements demanded by his/her application such as capture distance, positioning of the reference system, and capture angle, among others. The visualization of this image is performed by means of the matplotlib library, through the pyplot interface, using the imshow() and show() functions together.
• Code-cell 4. Circle Detection: As previously mentioned, it is currently possible to work with code from different programming languages within the same notebook. Taking advantage of this functionality, this cell runs the executable file resulting from the compilation of the code developed in ANSI C that contains both the functions to control the data transfer between PS–PL and execute the AG implemented in hardware, as well as the pre- and post-processing stages described in the previous subsection. Here, the user must provide the input parameters previously detailed in Table 2. The input image can be selected between the captured image or a local image repository. The output files generated during the execution of the detection process are stored in the local directory of the notebook. By configuring the operating parameters of this task, the user can generate different strategies to study the evolutionary process in detail.
• Code-cell 5. Numeric results: Both the numerical results and the images produced in the execution of the previous cell are presented to facilitate their analysis. By means of the function read_csv() available in the pandas library, the detection results recorded in TXT files are accessed and presented in tabular form. The information reported consists of the number of generations and number of clock cycles required to detect the circle, the total number of generations and clock cycles employed by the AG, and the fitness of the elite individual.
• Code-cell 6. Graphic trends: By accessing the numerical values, the evolution of the elite individual’s fitness is presented graphically by means of the plot() function of the pyplot interface.
• Code-cell 7. Image post-viewing (notebook): The detected circles are superimposed on the copy of the input image stored in the local directory. To read it, the imread() function of the cv2 library is used, and it is displayed inside the notebook using the imshow() and show() functions of the pyplot interface.
• Code-cell 8. Image post-viewing (monitor): The user has a second option to display the output image, so in this cell code the pynq.lib.video library is used to take advantage of the DisplayPort available on the board to display the image on an external monitor.

3. Evaluation and Validation

The notebook developed for the execution of the circle detection system embedded in the Ultra96-v2 board provides the necessary functionalities to evaluate the performance of the system and validate its response for different scenarios in which it may be required. For this evaluation and validation process, a test protocol was executed in which three statistical studies are carried out: evolution and efficacy, performance, and response to noise. Each of the studies was performed by setting the parameters from Table 2 to the values shown in

Table 4. CDS input parameter values for evaluation and validation process.

Parameter	Value
Image database	30
Sigma	1.8
tlow	0.3
thigh	0.9
fit	0.9
mc	1–5
gns	500
inc	[10, 500]
tests	1000

.

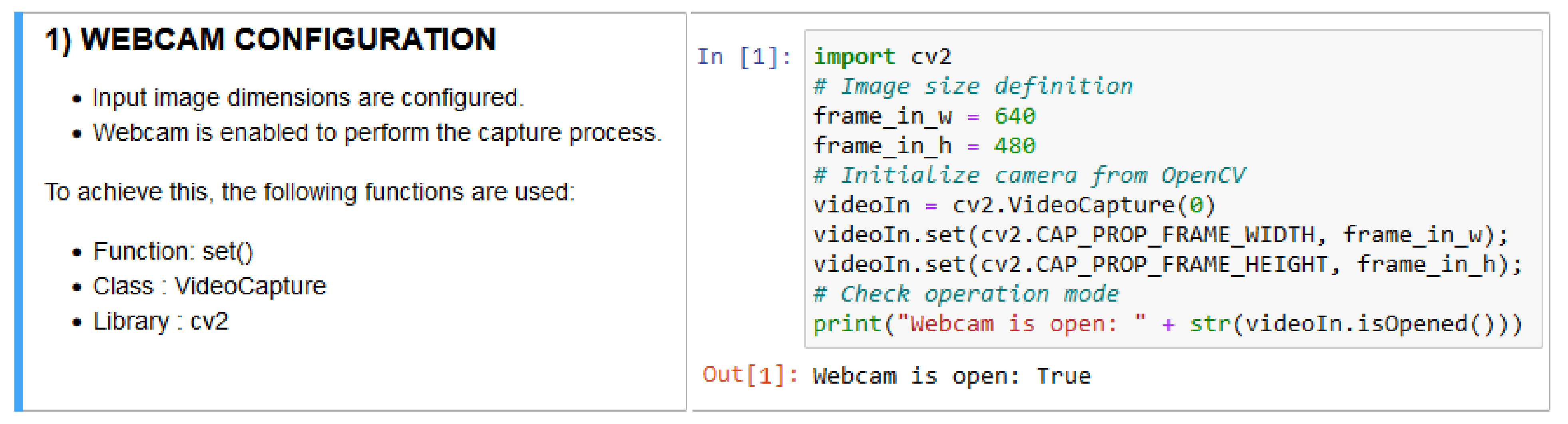
The image database is made up of three groups that differ from each other in the nature of the circles they contain. One group consists of images with circles that were traced digitally by means of an image editing software (synthetic images). The next group is composed of images of circular objects that can be found in a daily life scenario and that have a circular shape either naturally or as a consequence of their manufacturing process (real images). Finally, the last group is formed by images of hand-drawn figures (real images). In this work, a sample of 5 images per group is presented.

3.1. Evolution and Efficacy

The outcome of the implementation of a genetic algorithm is equivalent to that of the emulation of an evolutionary process. Therefore, for the whole image database, the trend corresponding to the fitness evolution of the elite individual is verified with respect to the number of emulated generations. To illustrate this process, Figure 11 presents an input image from the real-image samples (Figure 11a), the corresponding fitness evolution trend of the elite individual when emulating once the evolutionary process and sampling the fitness every 10 generations (Figure 11b), and the graphical representation of the detected circle superimposed on the input image (Figure 11c). Repeating this process for the image database leads to detecting the circles presented in Figure 12, where each row corresponds to each of the three image groups. The respective fitness evolution trend plots are presented in Figure 13 and were grouped according to the corresponding image type.

The results of the fitness evolution trend of the elite individuals presented in Figure 13 validate the correct emulation of the evolutionary process in each of the images and, at the same time, reflect the random nature of the genetic algorithm. This randomness makes it impossible to characterize the fitness trend in any case, leaving as the only predictable outcome the progressive increase in the fitness value until it reaches or exceeds its threshold or the established limit of generation.

Once the correct emulation of the evolutionary process has been verified, a statistical analysis of the detected circles is performed to determine the efficacy of the system, and for this it is necessary to distinguish between synthetic and real images. On one hand, the first row of Figure 12 shows a sample of synthetic images that were designed by the authors and, therefore, the center and radius parameters are predefined. Based on this information, it is possible to determine the detection efficacy in synthetic images by measuring the hit rate between these predefined parameters and the results of the system after performing 1000 system runs. A hit is only counted when these parameters coincide, since in the digital edition of the images the circles are traced with high precision. Another important feature of the synthetic images lies in the control of the number of figures surrounding the circle, which makes it possible to determine the relationship between the efficacy of the system and the amount of edge pixels of the image. This relationship is analyzed by progressively adding figures from an initial image (Figure 12a) and comparing the percentage of hits among the subsequent images (Figure 12b–e). Increasing the number of figures translates into a progressive increase in the search space in each image, which also represents a higher degree of difficulty to execute the detection task correctly with a fixed population size.

Considering that in this type of image a hit is counted as a match of parameters, the results in Figure 14 show that there is a directly proportional relation between the efficacy of the system and the percentage of the search space represented by the circle. It also indicates that the system has a high level of efficacy by reaching a hit percentage higher than 70% when increasing the number of figures surrounding the circle with respect to the initial figure. The analysis of this relation is complemented by the noise response study presented in Section 3.3.

On the other hand, rows 2 and 3 of Figure 12 show the samples of the two groups of real images. These groups are distinguished because, unlike the synthetic images, they were obtained from the capture of a real-world scenario, and the center and radius parameters of the circles contained in those images are unknown, making it necessary to use a different strategy than the one used in the synthetic images to analyze the efficacy of the system. Then, as an alternative, the parameters of the detected circles will be compared with a series of reference parameters obtained by an observer, acting as a reference system, who uses an image editing software to trace on each image of the database the circles that she/he detects. Additionally, the standard deviation of each parameter will be calculated in order to qualitatively analyze the results in the two groups of real images.

Table 5. Reference parameters detected by the reference system (columns 2–4), average of detected parameters (columns 5–7), and standard deviation of each one (columns 8–10).

Figure	${\mathit{x}}_{\mathbf{ref}}$	${\mathit{y}}_{\mathbf{ref}}$	${\mathit{r}}_{\mathbf{ref}}$	$\mathit{\mu }$(x)	$\mathit{\mu }$(y)	$\mathit{\mu }$(r)	$\mathit{\sigma }$(x)	$\mathit{\sigma }$(y)	$\mathit{\sigma }$(r)
Figure 12f	233	231	146	233.47	230.64	146.43	1.52	1.60	1.84
Figure 12g 1	388	234	102	388.08	234.57	102.14	0.09	0.68	0.37
Figure 12h	266	238	207	265.88	237.89	207.12	0.36	0.34	0.35
Figure 12i	389	157	99	389.01	156.97	98.98	0.11	0.16	0.16
Figure 12j	375	283	107	375.00	282.96	107.00	0.07	0.22	0.07
Figure 12k	302	175	141	301.74	175.19	140.58	1.19	0.44	3.29
Figure 12l	293	251	160	293.18	251.21	159.88	2.01	4.58	1.35
Figure 12m	316	237	167	315.98	236.66	167.20	0.49	2.74	1.22
Figure 12n	318	315	78	317.83	314.77	77.83	1.59	0.54	2.56
Figure 12o	312	237	151	312.04	237.01	151.44	0.47	1.23	2.67

¹ The study of this image is further developed to analyze the case of two concentric circles.

records the results of the real images as follows: reference parameters in columns 2–4; average of the detected parameters in columns 5–7; and standard deviation of the parameters in columns 8–10. In this table of results, we can observe that, for the group of images with machine-made circular objects (Figure 12f–j), the average values of the set of parameters are approximately equal to the reference values, and the maximum values of standard deviation are 1.52, 1.60, and 1.84 pixels for the center and radius parameters, respectively, which represents a very low level of deviation in comparison with the image dimensions (640 × 480 pixels). There is a particular case where the standard deviation of the radius value is 17.7 pixels, a case for which a detailed analysis is presented later in this section.

For the group of images with hand-drawn figures (Figure 12k–o) there is also a fairly high approximation between the reference values and the calculated averages, but the standard deviation values increase on a general basis, reaching maximum values of 2.01, 4.58, and 3.29 pixels for the center and radius parameters, respectively. The generalized increase in the standard deviation values is due to the nature of the circle embedded in the images. In the first group of real images, a high accuracy in the tracing is assumed beforehand since the objects are either manufactured by a machine or present a circular shape in a natural way while, in the second group of real images, the circles are traced by hand and, therefore, their accuracy is not at the level of circular objects, which means that the results of their detection present a wider range in the standard deviation of the whole set of their parameters.

Table 6. Hit percentage for each detected parameter based on 1, 2, and 3$\sigma$ criterion.

Figure	x			y			r
	$1\sigma$	$2\sigma$	$3\sigma$	$1\sigma$	$2\sigma$	$3\sigma$	$1\sigma$	$2\sigma$	$3\sigma$
Figure 12f	94%	95%	95%	94%	95%	95%	94%	94%	95%
Figure 12g	99%	99%	99%	98%	100%	100%	86%	86%	100%
Figure 12h	87%	87%	100%	89%	89%	100%	88%	88%	100%
Figure 12i	99%	99%	99%	97%	97%	97%	98%	98%	98%
Figure 12j	100%	100%	100%	95%	95%	95%	100%	100%	100%
Figure 12k	81%	87%	100%	80%	80%	100%	59%	100%	100%
Figure 12l	60%	100%	100%	39%	100%	100%	87%	97%	98%
Figure 12m	94%	94%	97%	63%	98%	100%	91%	92%	93%
Figure 12n	74%	100%	100%	74%	100%	100%	60%	100%	100%
Figure 12o	92%	92%	96%	84%	88%	96%	56%	100%	100%

allows the analysis of the detection system efficacy as a function of the standard deviation of the parameters obtained in each run of the GA. For this purpose, the percentage of cases is indicated in which the parameters obtained after 1000 executions of the GA are in a range of 1, 2 or 3$\sigma$ with respect to the reference parameters of the corresponding image. The results presented in this table show that the system has a high level of efficacy in the detection of circles in real images since more than 80% of hits are obtained in the 2$\sigma$ range, and more than 93% of hits are obtained in the 3$\sigma$ range.

For any image where concentric circles are present, as is the case in Figure 12g, the system has the possibility of presenting convergence results towards two circles described by the same center but different radii. In that case, the statistical values presented in Table 5 and Table 6 correspond to the inner circle, but the results that can be obtained by means of the notebook provide enough information to analyze in detail the behavior of the system in front of an image containing 2 concentric circles.

If we consider as a hit the detection of any of the two circles immersed in Figure 15a (previously labeled as Figure 12g) regardless of the radii, the efficacy result is 98%, as shown in the hit histogram in Figure 15b, but when the corresponding post-processing is carried out to obtain the statistical results, the two different radii shown in Figure 15c must be considered to identify the distribution of hits among these circles to reach the 98% mentioned earlier.

Figure 16a shows the detection results obtained by performing an analysis of hits as a function of the radius; here, it can be observed that the total number of quantized hits is distributed in 47.6% for the inner circle (r = 102) and 50.4% for the outer circle (r = 140). This difference between proportions is due to the fact that the outer perimeter is formed by a larger number of pixels than the inner one and, therefore, it has a larger proportion within the search space, which increases the possibility that an individual from the initial population orients the convergence in its favor. However, if the concentric perimeters of the edge image in Figure 15c are compared, it is observed that the perimeter of the outer circle is not complete, which indicates that the maximum fitness value for this circle should be smaller than that of the inner circle.

This last analysis is presented based on Figure 16b,c, which show the evolution of the fitness of the elite individual for a run of 1000 generations. Here, it is observed that, in spite of starting the convergence process in favor of the outer circle, the randomness of the genetic operators allowed the exploration of a specific region of the search space that reoriented the convergence towards the better-defined circle, the inner one. The statistical results in Table 5 are complemented by specifying that the average value detected for the center of the outer circle equals the coordinate (387.95, 233.64), and its radius equals 139.35 pixels, and that the standard deviations equal 0.39, 0.83, and 1.03, respectively. The statistical results in Table 6 are complemented by specifying that 100% of the hits are contained in the 1$\sigma$ range for all the parameters.

3.2. Multi-Circle Detection

Concentric circles are a specific case of the presence of multiple circles within an image. Therefore, we designed the system in such a way that the user has the possibility to perform the detection of multiple circles within the same image. This is achieved by sequentially eliminating from the search space the pixels corresponding to each detected circle and executing again the block corresponding to the programmable logic as many times as necessary. The elimination of pixels from the search space is performed by the software component and is a task that does not represent a high computational cost. Extending the detection to multiple circles, the hardware acceleration of the evolutionary process is being used to the benefit of its full potential. As an illustration of this functionality, Figure 17 shows an image of each of the previously analyzed groups where there is more than one circle in the scene.

Table 7. Reference parameters detected by the reference system for images in Figure 17 (columns 2–5), their corresponding average of detected parameters (columns 5–7), and standard deviation (columns 8–10).

Figure	Circle	${\mathit{x}}_{\mathit{ref}}$	${\mathit{y}}_{\mathit{ref}}$	${\mathit{r}}_{\mathit{ref}}$	$\mathit{\mu }$(x)	$\mathit{\mu }$(y)	$\mathit{\mu }$(r)	$\mathit{\sigma }$(x)	$\mathit{\sigma }$(y)	$\mathit{\sigma }$(r)
Figure 17d	C1	351	326	112	350.56	325.57	111.95	1.21	1.54	1.65
	C2	249	140	108	249.01	139.92	107.98	0.15	0.96	1.00
	C3	465	141	101	464.75	140.54	101.30	1.20	1.04	1.13
	C4	543	316	90	542.67	316.24	89.67	1.13	0.49	0.89
	C5	118	309	109	118.09	309.45	108.91	2.20	1.93	1.71
Figure 17e	C1	323	112	81	322.91	111.72	81.29	0.60	0.56	1.90
	C2	121	100	73	121.00	99.98	72.82	0.00	0.31	1.77
	C3	318	237	115	318.02	236.99	115.30	0.17	0.19	1.93
	C4	322	380	75	321.66	379.82	74.93	0.60	0.61	1.92
	C5	514	379	80	513.55	378.79	80.00	0.50	0.41	0.00
Figure 17f	C1	160	94	75	159.68	93.59	74.62	0.89	1.16	1.81
	C2	310	231	74	310.02	230.72	73.83	2.11	1.56	0.99
	C3	466	116	88	465.71	116.05	87.54	1.21	2.47	1.34
	C4	160	299	79	159.65	298.78	79.22	1.63	1.06	1.27
	C5	460	343	33	459.91	343.46	33.30	4.67	4.50	2.06

presents the detection results using the reference system matching strategy explained in the previous section. The results and their respective analyses from this table are coherent with those presented in Table 5.

3.3. Noise

It was previously observed that the efficacy has an inverse proportional relation with respect to the increase in the search space (progressive increase in shapes) performed on the synthetic images. This analysis is complemented by considering the possibility of processing images that have been corrupted with noise. To emulate this condition, “salt and pepper” noise is added to one image from each of the groups previously presented (Figure 12a,f,k).

The noise is added progressively in 5 levels until it reaches a ratio of 2.6% in relation to the total amount of pixels of the input image (640 × 480). According to the radius values detected for each of the circles of the 3 images under evaluation, it is observed that this amount of added noise corresponds to an increase in the search spaces of 1105%, 870%, and 901% in the Figure 18a–c, respectively.

After evaluating the efficacy for the different noise levels keeping constant the evaluation parameters presented in Table 4, we can observe that a decreasing trend (blue trends) exists in all the cases in Figure 18. As expected, this trend shows that noise affects to a lesser extent the detection task in the synthetic image since the position of the non-circle pixels is controlled by the user and, intentionally, the additional geometric shapes were located in such a way that the possibility of false positive detection is minimal. However, in the two real-image cases, there is no control of the position of the non-circle pixels and, therefore, the possibility of noise contributing to the detection of a greater number of false positives is opened. However, the user has the possibility to tune the parameters of the pre-processing stage (sigma, tlow, and thigh) to improve the results of this stage to strengthen the system’s noise response (orange trends). If only the value of sigma is tuned, we can observe that the efficacy rate can be raised to values higher than 97% for the same range of noise ratio in the synthetic image and in the real image with hand-drawn traces; if the parameter tlow is also modified to evaluate the real image with a circular object, it is possible to raise its efficacy to a 90% rate.

4. Conclusions

The HW/SW co-design of a complete embedded system based on a genetic algorithm has been presented in this paper. The system was developed using Jupyter Notebook as a tool to power its performance and to ease its scientific/industrial dissemination. The usage of this platform has provided the hybrid system with the facility of accurate documentation and interactive live control of the data flow throughout its execution process.

The combination of the different description and programming languages that coexist in the system has allowed efficient execution of the detection task by: First: implementing in the FPGA logic the most computationally expensive stage corresponding to the genetic algorithm using a hardware description language, Second, efficiently executing the SW-HW interaction and data conditioning functions by means of a compiled programming language, and Third, developing an interactive environment rich in multimedia options that facilitates the control of the system via an interpreted language.

The efficacy of the hybrid system has been statistically validated on an Ultra96-v2 board for multiple-circle detection in synthetic and real images with a wide range of scenarios of diverse characteristics. The interactive environment provides a high control level over the configuration of the different processing stages.

Although a specific notebook has been developed to illustrate this work, the platform is completely configurable by definition, giving the user the possibility of adapting the hybrid HW/SW detection system to other computer vision applications and developing their own test schemes to study the system performance in scenarios outside of the case studies presented in this paper.

As in other GA-based solutions, the main drawbacks may come from the difficulty of ensuring that convergence is achieved in a reasonable amount of time. In this sense, some possible strategies to speed up the algorithm even more, with the idea that it can be applied in vision systems with more demanding requirements, could consist of making the most of the resources of the programmable device to evolve several populations in parallel, or to use inference techniques based on soft-computing to select the initial population(s) according to a heuristic depending on the scenario or the type of images. These ideas, together with a possible extension of the GA to identify more complex elliptical figures, constitute the main lines of progression of this work.