A Survey of Trajectory Planning Techniques for Autonomous Systems
Abstract
:1. Introduction
1.1. Objective and Contents
- Consolidation of relevant work: Human drivers have an amazing ability to simultaneously perceive a vehicle’s environment while steadily performing the essential motion movements. Globally, researchers are working on replicating the maneuverable capabilities of human drivers in designing autonomous guided vehicles that are simple in design, provide safety, and are efficient) [47,48,49,50,51]. Therefore, this study strives to provide valuable insight into the land, aerial, and underwater vehicles for readers in-order to understand their utilities in the industry and research.
- Limitations and the way forward: Another major contribution of this research involved identifying the impediments associated with path optimization and obstacle avoidance using numerical and nature-inspired methods. Characteristics that do not contribute toward finding the optimal trajectory optimization for ground and aerial vehicles are identified and categorized into two categories: (i) numerical methods and nature-inspired techniques: limitations; (ii) numerical methods and nature-inspired techniques: restrictions. A complete way forward is also suggested.
1.2. Paper Organization
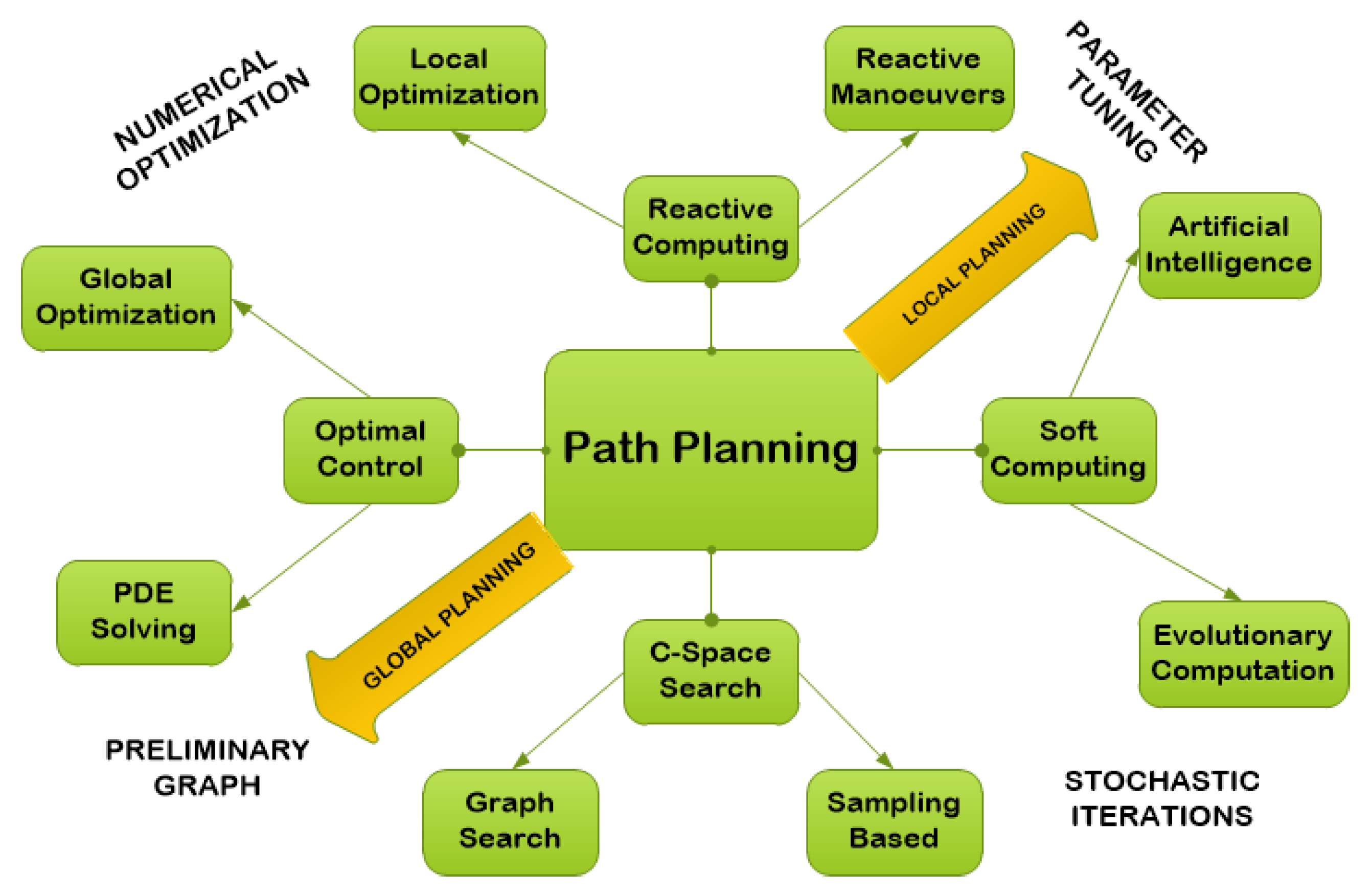
2. Trajectory Planning Fundamentals
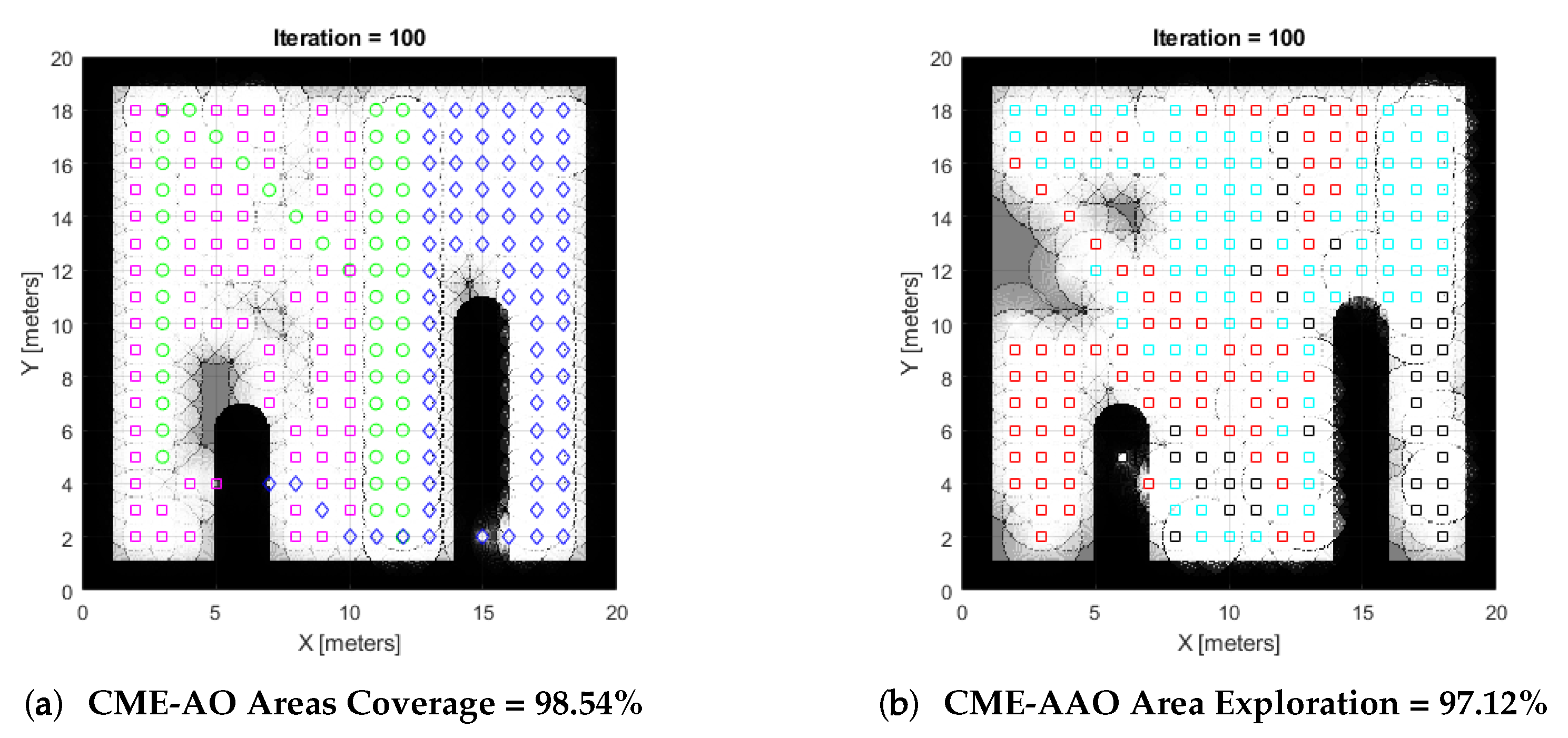
| Algorithm 1 Integrated CME-Adaptive Aquila Optimizer. |
|
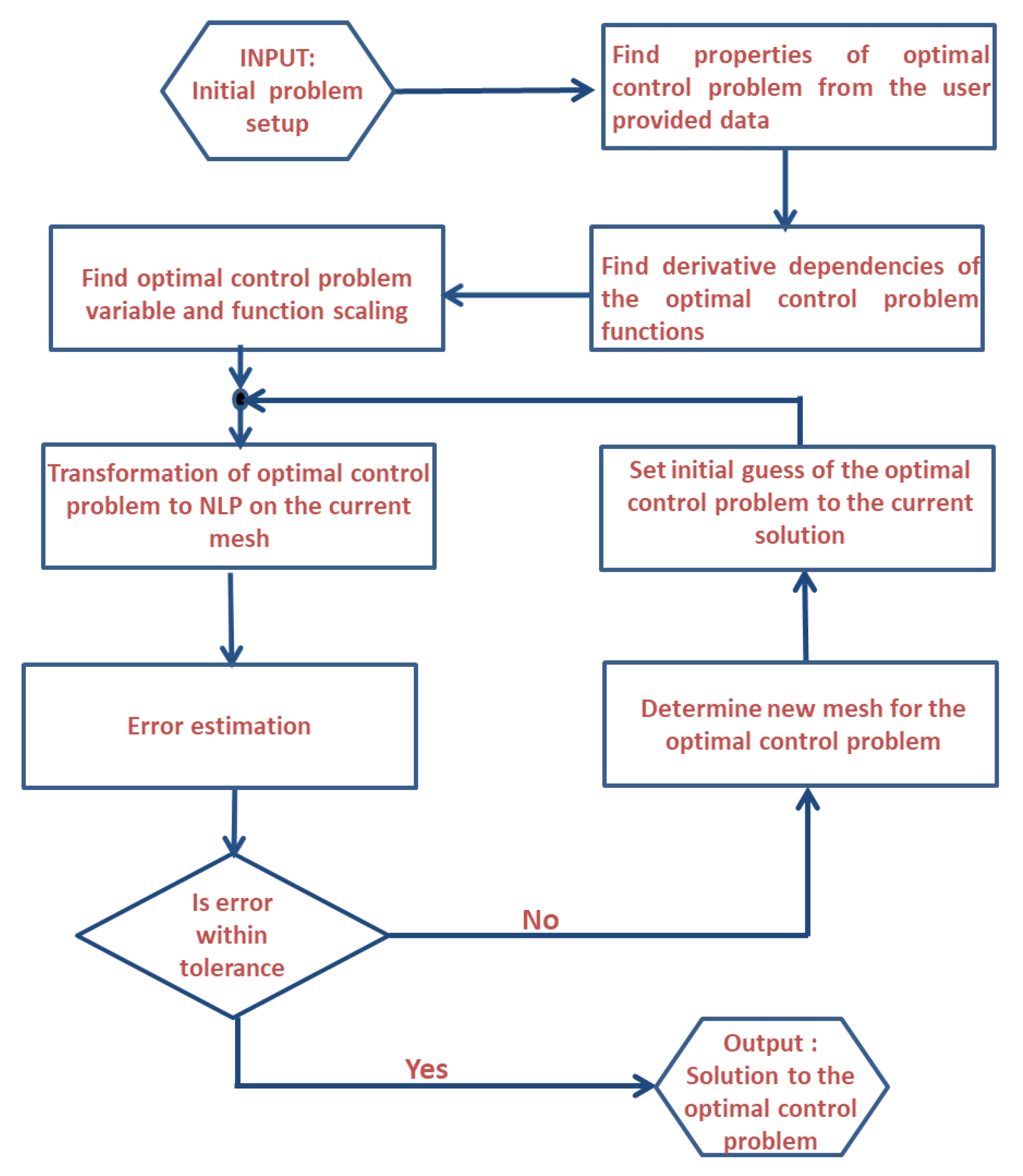
Trajectory Planning: Mathematical Framework
3. Relevant Studies
3.1. Numerical Techniques
3.1.1. Applications to Aerial Vehicles
3.1.2. Applications to Ground Vehicles
3.1.3. Application to Underwater Vehicle (AUV)
3.2. Bio-Inspired Techniques
3.2.1. Application to Aerial Vehicles
3.2.2. Application to Ground Vehicles
3.2.3. Application to Underwater Vehicles
3.3. Hybrid Techniques
3.3.1. Application to Aerial Vehicles
3.3.2. Application to Ground Vehicles
3.3.3. Underwater Vehicles
4. Challenges, Recommendations, and Future Directions
4.1. Challenges Involved in Path Planning
4.1.1. Inaccurate Results
4.1.2. Sensor Dependence
4.1.3. Dependent on Environmental Observation
4.1.4. Computational Cost
4.1.5. Insufficient Literature on Space Exploration
4.1.6. Simulated Work
4.2. Proposed Solutions
4.3. Potential Future Directions
5. Conclusions
- (1)
- Consolidation of available information. A detailed review of the trajectory planning and optimization is presented from the application points of view of ground (single and multi-robot), aerial, and underwater vehicles. Solutions along with future directions are presented at the end of the manuscript.
- (2)
- Problem formulation and generation of optimal trajectories. An explanation of how different algorithms could be integrated to build a mathematical model for planning and the formation of trajectory components were presented with a literature survey.
- (3)
- Limitations and a way forward. Though numerous works have reviewed robotics, aerial and underwater vehicle systems have been presented together with optimization techniques and numerical methods, and no single algorithm produced desired results or accurate output; therefore, a hybridization of different algorithms was used by researchers. Two optimization algorithms or two numerical methods together can be integrated, or a mix and match of techniques can be used to obtain the desired characteristics results.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| UAV | Unmanned Aerial Vehicles |
| AUV | Autonomous Underwater Vehicles |
| UGVs | Unmanned Ground Vehicles |
| SLAM | Simultaneous Localization and Mapping |
| sUAV | Small Unmanned Aerial Vehicle |
| UAAV | Unmanned Aerial-Aquatic Vehicle |
| ROS | Robot Operating System |
| UUV | Unmanned Underwater Vehicle |
| GPS | Global Positioning System |
| IMU | Inertial Measurement Unit |
| MPC | Model Predictive Control |
| IN | Inertial Navigation |
| IM | Image Processing Technique |
| RL | Reinforcement Learning |
| PSO | Particle Swarm Optimization |
| GWO | Grey Wolf Optimization |
| ANN | Artificial Neural Network |
| GA | Genetic Algorithm |
| ALO | Ant Lion Optimization |
| WOA | Whale Optimization |
| MFO | Moth Flame Optimization |
| PRM | Probabilistic Roadmap |
| CNN | Convolutional Neural Network |
| SLI | Sylvester Law of Inertia |
| UWG | Underwater Glider |
References
- Berlin, T. Spirit of Berlin: An Autonomous Car for the DARPA Urban Challenge Hardware and Software Architecture. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.108.3075&rep=rep1&type=pdf (accessed on 27 June 2022).
- Gul, F.; Mir, I.; Abualigah, L.; Sumari, P.; Forestiero, A. A Consolidated Review of Path Planning and Optimization Techniques: Technical Perspectives and Future Directions. Electronics 2021, 10, 2250. [Google Scholar] [CrossRef]
- Aguilar, W.G.; Sandoval, S.; Limaico, A.; Villegas-Pico, M.; Asimbaya, I. Path Planning Based Navigation Using LIDAR for an Ackerman Unmanned Ground Vehicle. In Proceedings of the International Conference on Intelligent Robotics and Applications, Shenyang, China, 8–11 August 2019; pp. 399–410. [Google Scholar]
- Le, A.V.; Nhan, N.H.K.; Mohan, R.E. Evolutionary algorithm-based complete coverage path planning for tetriamond tiling robots. Sensors 2020, 20, 445. [Google Scholar] [CrossRef] [PubMed]
- Thoma, J.; Paudel, D.P.; Chhatkuli, A.; Probst, T.; Gool, L.V. Mapping, localization and path planning for image-based navigation using visual features and map. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 7383–7391. [Google Scholar]
- Krell, E.; Sheta, A.; Balasubramanian, A.P.R.; King, S.A. Collision-free autonomous robot navigation in unknown environments utilizing pso for path planning. J. Artif. Intell. Soft Comput. Res. 2019, 9, 267–282. [Google Scholar] [CrossRef]
- Vis, I.F. Survey of research in the design and control of automated guided vehicle systems. Eur. J. Oper. Res. 2006, 170, 677–709. [Google Scholar] [CrossRef]
- Sanchez-Lopez, J.L.; Wang, M.; Olivares-Mendez, M.A.; Molina, M.; Voos, H. A real-time 3d path planning solution for collision-free navigation of multirotor aerial robots in dynamic environments. J. Intell. Robot. Syst. 2019, 93, 33–53. [Google Scholar] [CrossRef]
- Hussain, A.; Hussain, I.; Mir, I.; Afzal, W.; Anjum, U.; Channa, B.A. Target Parameter Estimation in Reduced Dimension STAP for Airborne Phased Array Radar. In Proceedings of the 2020 IEEE 23rd International Multitopic Conference (INMIC), Bahawalpur, Pakistan, 5–7 November 2020; pp. 1–6. [Google Scholar]
- Yi, J.H.; Lu, M.; Zhao, X.J. Quantum inspired monarch butterfly optimisation for UCAV path planning navigation problem. Int. J. Bio-Inspired Comput. 2020, 15, 75–89. [Google Scholar] [CrossRef]
- Majeed, A.; Lee, S. A new coverage flight path planning algorithm based on footprint sweep fitting for unmanned aerial vehicle navigation in urban environments. Appl. Sci. 2019, 9, 1470. [Google Scholar] [CrossRef]
- Hussain, A.; Anjum, U.; Channa, B.A.; Afzal, W.; Hussain, I.; Mir, I. Displaced Phase Center Antenna Processing For Airborne Phased Array Radar. In Proceedings of the 2021 International Bhurban Conference on Applied Sciences and Technologies (IBCAST), Islamabad, Pakistan, 12–16 January 2021; pp. 988–992. [Google Scholar]
- Forestiero, A.; Mastroianni, C.; Spezzano, G. Building a peer-to-peer information system in grids via self-organizing agents. J. Grid Comput. 2008, 6, 125–140. [Google Scholar] [CrossRef]
- Forestiero, A. Heuristic recommendation technique in Internet of Things featuring swarm intelligence approach. Expert Syst. Appl. 2022, 187, 115904. [Google Scholar] [CrossRef]
- Rath, M.K.; Deepak, B. PSO based system architecture for path planning of mobile robot in dynamic environment. In Proceedings of the 2015 Global Conference on Communication Technologies (GCCT), Thuckalay, India, 23–24 April 2015; pp. 797–801. [Google Scholar]
- Mir, I.; Eisa, S.A.; Maqsood, A. Review of dynamic soaring: Technical aspects, nonlinear modeling perspectives and future directions. Nonlinear Dyn. 2018, 94, 3117–3144. [Google Scholar] [CrossRef]
- Noor, M.A.; Noor, K.I.; Al-Said, E.; Waseem, M. Some new iterative methods for nonlinear equations. Math. Probl. Eng. 2010, 2010, 198943. [Google Scholar] [CrossRef]
- Hull, T.; Enright, W.H.; Jackson, K. Runge-Kutta Research at Toronto. Appl. Numer. Math. 1996, 22, 225–236. [Google Scholar] [CrossRef]
- Verbeke, J.; Cools, R. The Newton-Raphson method. Int. J. Math. Educ. Sci. Technol. 1995, 26, 177–193. [Google Scholar] [CrossRef]
- Wood, G.R. The bisection method in higher dimensions. Math. Program. 1992, 55, 319–337. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Meraihi, Y.; Ramdane-Cherif, A.; Acheli, D.; Mahseur, M. Dragonfly algorithm: A comprehensive review and applications. Neural Comput. Appl. 2020, 32, 16625–16646. [Google Scholar] [CrossRef]
- Abualigah, L.; Shehab, M.; Alshinwan, M.; Alabool, H. Salp swarm algorithm: A comprehensive survey. Neural Comput. Appl. 2019, 32, 1–21. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper optimisation algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef]
- Brammya, G.; Praveena, S.; Ninu Preetha, N.; Ramya, R.; Rajakumar, B.; Binu, D. Deer hunting optimization algorithm: A new nature-inspired meta-heuristic paradigm. Comput. J. 2019. [Google Scholar] [CrossRef]
- Mirjalili, S. The ant lion optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl.-Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Ma, G.; Zhang, Y.; Nee, A. A simulated annealing-based optimization algorithm for process planning. Int. J. Prod. Res. 2000, 38, 2671–2687. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The arithmetic optimization algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Gao, X.Z.; Govindasamy, V.; Xu, H.; Wang, X.; Zenger, K. Harmony search method: Theory and applications. Comput. Intell. Neurosci. 2015, 2015, 258491. [Google Scholar] [CrossRef]
- Abualigah, L.; Yousri, D.; Abd Elaziz, M.; Ewees, A.A.; Al-qaness, M.A.; Gandomi, A.H. Aquila Optimizer: A novel meta-heuristic optimization Algorithm. Comput. Ind. Eng. 2021, 157, 107250. [Google Scholar] [CrossRef]
- Jain, M.; Maurya, S.; Rani, A.; Singh, V. Owl search algorithm: A novel nature-inspired heuristic paradigm for global optimization. J. Intell. Fuzzy Syst. 2018, 34, 1573–1582. [Google Scholar] [CrossRef]
- Yiqing, L.; Xigang, Y.; Yongjian, L. An improved PSO algorithm for solving non-convex NLP/MINLP problems with equality constraints. Comput. Chem. Eng. 2007, 31, 153–162. [Google Scholar] [CrossRef]
- Huang, W.H.; Fajen, B.R.; Fink, J.R.; Warren, W.H. Visual navigation and obstacle avoidance using a steering potential function. Robot. Auton. Syst. 2006, 54, 288–299. [Google Scholar] [CrossRef]
- Gul, F.; Rahiman, W. An Integrated approach for Path Planning for Mobile Robot Using Bi-RRT. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Terengganu, Malaysia, 27–28 August 2019; Volume 697, p. 012022. [Google Scholar]
- Gul, F.; Rahiman, W.; Nazli Alhady, S.S. A comprehensive study for robot navigation techniques. Cogent Eng. 2019, 6, 1632046. [Google Scholar] [CrossRef]
- Tzafestas, S.G. Mobile robot path, motion, and task planning. Introd. Mob. Robot. Control. 2014, 429–478. [Google Scholar] [CrossRef]
- Contreras-Cruz, M.A.; Ayala-Ramirez, V.; Hernandez-Belmonte, U.H. Mobile robot path planning using artificial bee colony and evolutionary programming. Appl. Soft Comput. 2015, 30, 319–328. [Google Scholar] [CrossRef]
- Ganeshmurthy, M.; Suresh, G. Path planning algorithm for autonomous mobile robot in dynamic environment. In Proceedings of the 2015 3rd International Conference on Signal Processing, Communication and Networking (ICSCN), Chennai, India, 26–28 March 2015; pp. 1–6. [Google Scholar]
- Montiel, O.; Orozco-Rosas, U.; Sepúlveda, R. Path planning for mobile robots using Bacterial Potential Field for avoiding static and dynamic obstacles. Expert Syst. Appl. 2015, 42, 5177–5191. [Google Scholar] [CrossRef]
- Tuncer, A.; Yildirim, M. Design and implementation of a genetic algorithm IP core on an FPGA for path planning of mobile robots. Turk. J. Electr. Eng. Comput. Sci. 2016, 24, 5055–5067. [Google Scholar] [CrossRef]
- Szczepanski, R.; Bereit, A.; Tarczewski, T. Efficient Local Path Planning Algorithm Using Artificial Potential Field Supported by Augmented Reality. Energies 2021, 14, 6642. [Google Scholar] [CrossRef]
- Chaari, I.; Koubaa, A.; Bennaceur, H.; Ammar, A.; Alajlan, M.; Youssef, H. Design and performance analysis of global path planning techniques for autonomous mobile robots in grid environments. Int. J. Adv. Robot. Syst. 2017, 14, 1729881416663663. [Google Scholar] [CrossRef]
- Do, C.H.; Lin, H.Y. Differential evolution for optimizing motion planning of mobile robot. In Proceedings of the 2017 IEEE/SICE International Symposium on System Integration (SII), Taipei, Taiwan, 11–14 December 2017; pp. 399–404. [Google Scholar]
- Szczepanski, R.; Tarczewski, T. Global path planning for mobile robot based on Artificial Bee Colony and Dijkstra’s algorithms. In Proceedings of the 2021 IEEE 19th International Power Electronics and Motion Control Conference (PEMC), Gliwice, Poland, 25–29 April 2021; pp. 724–730. [Google Scholar]
- Bertozzi, M.; Broggi, A.; Fascioli, A. Vision-based intelligent vehicles: State of the art and perspectives. Robot. Auton. Syst. 2000, 32, 1–16. [Google Scholar] [CrossRef]
- Franke, U.; Gavrila, D.; Gern, A.; Görzig, S.; Janssen, R.; Paetzold, F.; Wöhler, C. From door to door—Principles and applications of computer vision for driver assistant systems. In Intelligent Vehicle Technologies; Elsevier: Amsterdam, The Netherlands, 2001; pp. 131–188. [Google Scholar]
- Dickmanns, E.D.; Behringer, R.; Dickmanns, D.; Hildebrandt, T.; Maurer, M.; Thomanek, F.; Schiehlen, J. The seeing passenger car’VaMoRs-P’. In Proceedings of the Intelligent Vehicles’ 94 Symposium, Paris, France, 24–26 October 1994; pp. 68–73. [Google Scholar]
- Nagel, H.H.; Enkelmann, W.; Struck, G. FhG-Co-Driver: From map-guided automatic driving by machine vision to a cooperative driver support. Math. Comput. Model. 1995, 22, 185–212. [Google Scholar] [CrossRef]
- Thorpe, C.; Hebert, M.H.; Kanade, T.; Shafer, S.A. Vision and navigation for the Carnegie-Mellon Navlab. IEEE Trans. Pattern Anal. Mach. Intell. 1988, 10, 362–373. [Google Scholar] [CrossRef]
- Kahveci, N.E.; Ioannou, P.A. Adaptive steering control for uncertain ship dynamics and stability analysis. Automatica 2013, 49, 685–697. [Google Scholar] [CrossRef]
- Rao, A.V. A survey of numerical methods for optimal control. Adv. Astronaut. Sci. 2009, 135, 497–528. [Google Scholar]
- Bock, H.G.; Plitt, K.J. A multiple shooting algorithm for direct solution of optimal control problems. IFAC Proc. Vol. 1984, 17, 1603–1608. [Google Scholar] [CrossRef]
- Abualigah, L.; Elaziz, M.A.; Khodadadi, N.; Forestiero, A.; Jia, H.; Gandomi, A.H. Aquila Optimizer Based PSO Swarm Intelligence for IoT Task Scheduling Application in Cloud Computing. In Integrating Meta-Heuristics and Machine Learning for Real-World Optimization Problems; Springer: Berlin/Heidelberg, Germany, 2022; pp. 481–497. [Google Scholar]
- Janet, J.A.; Luo, R.C.; Kay, M.G. The essential visibility graph: An approach to global motion planning for autonomous mobile robots. In Proceedings of the 1995 IEEE International Conference on Robotics and Automation, Nagoya, Japan, 21–27 May 1995; Volume 2, pp. 1958–1963. [Google Scholar]
- Mir, I. Dynamics, Numeric Optimization and Control of Dynamic Soaring Maneuvers for a Morphing Capable Unmanned Aerial Vehicle. Ph.D. Thesis, National University of Sciences & Technology, Islamabad, Pakistan, 2018. [Google Scholar]
- Schubert, K.F.; Rao, A.V. Minimum-Time Low-Earth Orbit to High-Earth Orbit Low-Thrust Trajectory Optimization. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Hilton Head, SC, USA, 11–15 August 2013. [Google Scholar]
- Jodeh, N.M.; Coon, T.; Masternak, T.J.; Cobb, R.; Agte, J.S. Optimal Airborne Trajectories for Data Collected from Emplaced Ground Sensor Arrays. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, National Harbor, MD, USA, 13–17 January 2014; p. 1291. [Google Scholar]
- Kim, M.K.; Tahk, M.J.; Park, B.G.; Kim, Y.Y. Terminal Velocity Maximization of Air-to-Air Missiles in Agile Turn Phase. In Proceedings of the MATEC Web of Conferences, Chongqing, China, 15–17 June 2016; EDP Sciences: Les Ulis, France, 2016; Volume 77, p. 07009. [Google Scholar]
- Zhou, W.; Zhang, C.; Li, J.; Fathy, H.K. A pseudospectral strategy for optimal power management in series hybrid electric powertrains. IEEE Trans. Veh. Technol. 2016, 65, 4813–4825. [Google Scholar] [CrossRef]
- Hong, S.M.; Seo, M.G.; Shim, S.W.; Tahk, M.J.; Lee, C.H. Sensitivity analysis on weight and trajectory optimization results for multistage guided missile. IFAC-PapersOnLine 2016, 49, 23–27. [Google Scholar] [CrossRef]
- Dahmen, T.; Saupeand, D. Optimal pacing strategy for a race of two competing cyclists. J. Sci. Cycl. 2014, 3, 12. [Google Scholar]
- Hu, X.; Perez, H.E.; Moura, S.J. Battery charge control with an electro-thermal-aging coupling. In Proceedings of the ASME 2015 Dynamic Systems and Control Conference. American Society of Mechanical Engineers, Columbus, OH, USA, 28–30 October 2015. [Google Scholar] [CrossRef]
- Kodera, M.; Ogawa, H.; Tomioka, S.; Ueda, S. Multi-objective design and trajectory optimization of space transport systems with RBCC propulsion via evolutionary algorithms and pseudospectral methods. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014; p. 0629. [Google Scholar]
- Diwale, S.S.; Lymperopoulos, I.; Jones, C.N. Optimization of an airborne wind energy system using constrained gaussian processes. In Proceedings of the Control Applications (CCA), 2014 IEEE Conference on, Dubrovnik, Croatia, 3–5 October 2014; pp. 1394–1399. [Google Scholar]
- Moon, Y.; Kwon, S. Lunar soft landing with minimum-mass propulsion system using H2O2/kerosene bipropellant rocket system. Acta Astronaut. 2014, 99, 153–157. [Google Scholar] [CrossRef]
- Kaushik, H.; Mohan, R.; Prakash, K.A. Utilization of wind shear for powering unmanned aerial vehicles in surveillance application: A numerical optimization study. Energy Procedia 2016, 90, 349–359. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H.; Sun, F. Charging time and loss optimization for LiNMC and LiFePO4 batteries based on equivalent circuit models. J. Power Sources 2013, 239, 449–457. [Google Scholar] [CrossRef]
- Wolf, S.; Bertschinger, R.; Saupe, D. Road cycling climbs made speedier by personalized pacing strategies. In Proceedings of the 4th International Congress on Sport Sciences Research and Technology Support, Porto, Portugal, 7–9 November 2016; pp. 109–114. [Google Scholar]
- Coşkun, E.c. Multistage Launch Vehicle Design with Thrust Profile and Trajectory Optimization. Ph.D. Thesis, Middle East Technical University, Çankaya/Ankara, Turkey, 2014. [Google Scholar]
- Grymin, D.J.; Farhood, M. Two-step system identification for control of small UAVs along pre-specified trajectories. In Proceedings of the American Control Conference (ACC), Portland, OR, USA, 4–6 June 2014; pp. 4404–4409. [Google Scholar]
- Lührs, B.; Niklass, M.; Froemming, C.; Grewe, V.; Gollnick, V. Cost-benefit assessment of 2d and 3d climate and weather optimized trajectories. In Proceedings of the 16th AIAA Aviation Technology, Integration, and Operations Conference, Washington, DC, USA, 13–17 June 2016; p. 3758. [Google Scholar]
- Peloni, A.; Rao, A.V.; Ceriotti, M. Automated Trajectory Optimizer for Solar Sailing (ATOSS). Aerosp. Sci. Technol. 2018, 72, 465–475. [Google Scholar] [CrossRef]
- Smith, E.; Tavernini, D.; Claret, C.; Velenis, E.; Cao, D. Optimal yaw-rate target for electric vehicle torque vectoring system. In The Dynamics of Vehicles on Roads and Tracks: Proceedings of the 24th Symposium of the International Association for Vehicle System Dynamics (IAVSD 2015), Graz, Austria, 17–21 August 2015; CRC Press: Boca Raton, FL, USA, 2016; p. 107. [Google Scholar]
- Gul, F.; Rahiman, W.; Alhady, S.N.; Ali, A.; Mir, I.; Jalil, A. Meta-heuristic approach for solving multi-objective path planning for autonomous guided robot using PSO–GWO optimization algorithm with evolutionary programming. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 7873–7890. [Google Scholar] [CrossRef]
- Owen, M.P.; Duffy, S.M.; Edwards, M.W. Unmanned aircraft sense and avoid radar: Surrogate flight testing performance evaluation. In Proceedings of the 2014 IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 0548–0551. [Google Scholar]
- Mir, I.; Maqsood, A.; Taha, H.E.; Eisa, S.A. Soaring Energetics for a Nature Inspired Unmanned Aerial Vehicle. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; p. 1622. [Google Scholar]
- Mir, I.; Akhtar, S.; Eisa, S.; Maqsood, A. Guidance and control of standoff air-to-surface carrier vehicle. Aeronaut. J. 2019, 123, 283–309. [Google Scholar] [CrossRef]
- Mohamed, S.A.; Haghbayan, M.H.; Westerlund, T.; Heikkonen, J.; Tenhunen, H.; Plosila, J. A survey on odometry for autonomous navigation systems. IEEE Access 2019, 7, 97466–97486. [Google Scholar] [CrossRef]
- Mir, I.; Maqsood, A.; Akhtar, S. Dynamic modeling & stability analysis of a generic UAV in glide phase. In Proceedings of the MATEC Web of Conferences, Beijing, China, 12–14 May 2017; EDP Sciences: Les Ulis, France, 2017; Volume 114, p. 01007. [Google Scholar]
- Bitzinger, R.A. Chapter 2: Transition and Readjustment in Second-Tier Defence Industries: Five Case Studies. Adelphi Ser. 2003, 43, 39–62. [Google Scholar] [CrossRef]
- Mir, I.; Taha, H.; Eisa, S.A.; Maqsood, A. A controllability perspective of dynamic soaring. Nonlinear Dyn. 2018, 94, 2347–2362. [Google Scholar] [CrossRef]
- Mir, I.; Maqsood, A.; Akhtar, S. Optimization of Dynamic Soaring Maneuvers for a Morphing Capable UAV. In Proceedings of the AIAA Information Systems-AIAA Infotech@ Aerospace, Grapevine, TX, USA, 9–13 January 2017; p. 0678. [Google Scholar]
- Mir, I.; Maqsood, A.; Eisa, S.A.; Taha, H.; Akhtar, S. Optimal morphing–augmented dynamic soaring maneuvers for unmanned air vehicle capable of span and sweep morphologies. Aerosp. Sci. Technol. 2018, 79, 17–36. [Google Scholar] [CrossRef]
- Hasircioglu, I.; Topcuoglu, H.R.; Ermis, M. 3-D path planning for the navigation of unmanned aerial vehicles by using evolutionary algorithms. In Proceedings of the 10th Annual Conference on Genetic and Evolutionary Computation, Atlanta, GA, USA, 12–16 July 2008; pp. 1499–1506. [Google Scholar]
- Caselli, S.; Reggiani, M.; Rocchi, R. Heuristic methods for randomized path planning in potential fields. In Proceedings of the 2001 IEEE International Symposium on Computational Intelligence in Robotics and Automation (Cat. No. 01EX515), Banff, AB, Canada, 29 July–1 August 2001; pp. 426–431. [Google Scholar]
- Saska, M.; Macas, M.; Preucil, L.; Lhotska, L. Robot path planning using particle swarm optimization of Ferguson splines. In Proceedings of the 2006 IEEE Conference on Emerging Technologies and Factory Automation, Prague, Czech Republic, 20–22 September 2006; pp. 833–839. [Google Scholar]
- Mansury, E.; Nikookar, A.; Salehi, M.E. Artificial Bee Colony optimization of ferguson splines for soccer robot path planning. In Proceedings of the 2013 First RSI/ISM International Conference on Robotics and Mechatronics (ICRoM), Tehran, Iran, 13–15 February 2013; pp. 85–89. [Google Scholar]
- Zhao, Y.J. Optimal patterns of glider dynamic soaring. Optim. Control. Appl. Methods 2004, 25, 67–89. [Google Scholar] [CrossRef]
- Zhao, Y.J.; Qi, Y.C. Minimum fuel powered dynamic soaring of unmanned aerial vehicles utilizing wind gradients. Optim. Control. Appl. Methods 2004, 25, 211–233. [Google Scholar] [CrossRef]
- Gill, P.E.; Murray, W.; Saunders, M.A.; Wright, M.H. User’s Guide for NPSOL (version 4.0): A Fortran Package for Nonlinear Programming; Technical report; Stanford Univ Ca Systems Optimization Lab: Standford, CA, USA, 1986. [Google Scholar]
- Zhang, Z.; Xie, P.; Ma, O. Bio-inspired trajectory generation for UAV perching. In Proceedings of the 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Wollongong, Australia, 9–12 July 2013; pp. 997–1002. [Google Scholar]
- Moses, A.; Rutherford, M.J.; Kontitsis, M.; Valavanis, K.P. UAV-borne X-band radar for collision avoidance. Robotica 2014, 32, 97. [Google Scholar] [CrossRef]
- Hügler, P.; Roos, F.; Schartel, M.; Geiger, M.; Waldschmidt, C. Radar taking off: New capabilities for UAVs. IEEE Microw. Mag. 2018, 19, 43–53. [Google Scholar] [CrossRef]
- Asvadi, A.; Peixoto, P.; Nunes, U. Detection and tracking of moving objects using 2.5 d motion grids. In Proceedings of the 2015 IEEE 18th International Conference on Intelligent Transportation Systems, Gran Canaria, Spain, 5–18 September 2015; pp. 788–793. [Google Scholar]
- Azim, A.; Aycard, O. Layer-based supervised classification of moving objects in outdoor dynamic environment using 3D laser scanner. In Proceedings of the 2014 IEEE Intelligent Vehicles Symposium Proceedings, Dearborn, MI, USA, 8–11 June 2014; pp. 1408–1414. [Google Scholar]
- Kim, Y.; Park, J.; Son, W.; Yoon, T. Modified turn algorithm for motion planning based on clothoid curve. Electron. Lett. 2017, 53, 1574–1576. [Google Scholar] [CrossRef]
- Zhang, K.; Sprinkle, J.; Sanfelice, R.G. A hybrid model predictive controller for path planning and path following. In Proceedings of the ACM/IEEE Sixth International Conference on Cyber-Physical Systems, Seattle, WA, USA, 14–16 April 2015; pp. 139–148. [Google Scholar]
- Sudhakara, P.; Ganapathy, V.; Sundaran, K. Optimal trajectory planning based on bidirectional spline-RRT for wheeled mobile robot. In Proceedings of the 2017 Third International Conference on Sensing, Signal Processing and Security (ICSSS), Chennai, India, 4–5 May 2017; pp. 65–68. [Google Scholar]
- Soylu, S.; Buckham, B.J.; Podhorodeski, R.P. A chattering-free sliding-mode controller for underwater vehicles with fault-tolerant infinity-norm thrust allocation. Ocean. Eng. 2008, 35, 1647–1659. [Google Scholar] [CrossRef]
- Herman, P. Numerical Test of Underwater Vehicle Dynamics Using Velocity Controller. In Proceedings of the 2019 12th International Workshop on Robot Motion and Control (RoMoCo), Poznań, Poland, 8–10 July 2019; pp. 26–31. [Google Scholar]
- Shen, C.; Shi, Y.; Buckham, B. Model predictive control for an AUV with dynamic path planning. In Proceedings of the 2015 54th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), Hangzhou, China, 28–30 July 2015; pp. 475–480. [Google Scholar]
- Liu, C.; Lee, S.; Varnhagen, S.; Tseng, H.E. Path planning for autonomous vehicles using model predictive control. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; pp. 174–179. [Google Scholar]
- Siddique, N.; Adeli, H. Nature inspired computing: An overview and some future directions. Cogn. Comput. 2015, 7, 706–714. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Guan, G.; Pu, X. The robot path planning based on improved artificial fish swarm algorithm. Math. Probl. Eng. 2016, 2016, 3297585. [Google Scholar] [CrossRef]
- Wang, H.J.; Fu, Y.; Zhao, Z.Q.; Yue, Y.J. An Improved Ant Colony Algorithm of Robot Path Planning for Obstacle Avoidance. J. Robot. 2019, 2019, 6097591. [Google Scholar] [CrossRef]
- Saffari, M.; Mahjoob, M. Bee colony algorithm for real-time optimal path planning of mobile robots. In Proceedings of the 2009 Fifth International Conference on Soft Computing, Computing with Words and Perceptions in System Analysis, Decision and Control, Famagusta, North Cyprus, 2–4 September 2009; pp. 1–4. [Google Scholar]
- Dao, T.K.; Pan, T.S.; Pan, J.S. A multi-objective optimal mobile robot path planning based on whale optimization algorithm. In Proceedings of the 2016 IEEE 13th International Conference on Signal Processing (ICSP), Chengdu, China, 6–10 November 2016; pp. 337–342. [Google Scholar]
- Tsai, P.W.; Dao, T.K. Robot path planning optimization based on multiobjective grey wolf optimizer. In Proceedings of the International Conference on Genetic and Evolutionary Computing, Fuzhou, China, 7–9 November 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 166–173. [Google Scholar]
- Guo, J.; Gao, Y.; Cui, G. The path planning for mobile robot based on bat algorithm. Int. J. Autom. Control. 2015, 9, 50–60. [Google Scholar] [CrossRef]
- Yang, X.S. Nature-Inspired Metaheuristic Algorithms; Luniver Press: Bristol, UK, 2010. [Google Scholar]
- Surmann, H.; Kanstein, A.; Goser, K. Self-organizing and genetic algorithms for an automatic design of fuzzy control and decision systems. In Proceedings of the EUFIT’93, Aachen, Germany, 7–10 September 1993. [Google Scholar]
- Payne, D.; Stern, J. Wavelength-switched passively coupled single-mode optical network. In Proceedings of the IOOC-ECOC, Venezia, Italy, 1–4 October 1985; Volume 85, p. 585. [Google Scholar]
- Karaboga, D.; Akay, B. A comparative study of artificial bee colony algorithm. Appl. Math. Comput. 2009, 214, 108–132. [Google Scholar] [CrossRef]
- Baykasoğlu, A.; Özbakır, L.; Tapkan, P. Artificial Bee Colony Algorithm and Its Application to Generalized Assignment Problem Swarm Intelligence Focus on Ant and Particle Swarm Optimization. In Swarm Intelligence: Focus on Ant and Particle Swarm Optimization; IntechOpen: London, UK, 2007. [Google Scholar]
- Kamil, R.T.; Mohamed, M.J.; Oleiwi, B.K. Path Planning of Mobile Robot Using Improved Artificial Bee Colony Algorithm. Eng. Technol. J. 2020, 38, 1384–1395. [Google Scholar] [CrossRef]
- Ismail, A.; Sheta, A.; Al-Weshah, M. A mobile robot path planning using genetic algorithm in static environment. J. Comput. Sci. 2008, 4, 341–344. [Google Scholar]
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Xin, D.; Hua-hua, C.; Wei-kang, G. Neural network and genetic algorithm based global path planning in a static environment. J. Zhejiang Univ. Sci. A 2005, 6, 549–554. [Google Scholar] [CrossRef]
- Li, J.; Deng, G.; Luo, C.; Lin, Q.; Yan, Q.; Ming, Z. A hybrid path planning method in unmanned air/ground vehicle (UAV/UGV) cooperative systems. IEEE Trans. Veh. Technol. 2016, 65, 9585–9596. [Google Scholar] [CrossRef]
- Lee, J.; Kang, B.Y.; Kim, D.W. Fast genetic algorithm for robot path planning. Electron. Lett. 2013, 49, 1449–1451. [Google Scholar] [CrossRef]
- Tian, L.; Collins, C. An effective robot trajectory planning method using a genetic algorithm. Mechatronics 2004, 14, 455–470. [Google Scholar] [CrossRef]
- Châari, I.; Koubaa, A.; Bennaceur, H.; Trigui, S.; Al-Shalfan, K. SmartPATH: A hybrid ACO-GA algorithm for robot path planning. In Proceedings of the 2012 IEEE Congress on Evolutionary Computation, Brisbane, Australia, 10–15 June 2012; pp. 1–8. [Google Scholar]
- Geisler, T.; Manikas, T.W. Autonomous robot navigation system using a novel value encoded genetic algorithm. In Proceedings of the The 2002 45th Midwest Symposium on Circuits and Systems, 2002. MWSCAS-2002, Tulsa, OK, USA, 4–7 August 2002; Volume 3, p. III. [Google Scholar]
- Han, W.G.; Baek, S.M.; Kuc, T.Y. Genetic algorithm based path planning and dynamic obstacle avoidance of mobile robots. In Proceedings of the 1997 IEEE International Conference on Systems, Man, and Cybernetics. Computational Cybernetics and Simulation, Orlando, FL, USA, 12–15 October 1997; Volume 3, pp. 2747–2751. [Google Scholar]
- Liu, K.; Zhang, M. Path planning based on simulated annealing ant colony algorithm. In Proceedings of the 2016 9th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 10–11 December 2016; Volume 2, pp. 461–466. [Google Scholar]
- Zhang, S.; Zhou, Y.; Li, Z.; Pan, W. Grey wolf optimizer for unmanned combat aerial vehicle path planning. Adv. Eng. Softw. 2016, 99, 121–136. [Google Scholar] [CrossRef]
- Hussien, A.G.; Amin, M.; Abd El Aziz, M. A comprehensive review of moth-flame optimisation: Variants, hybrids, and applications. J. Exp. Theor. Artif. Intell. 2020, 32, 1–21. [Google Scholar] [CrossRef]
- Watkins, W.A.; Schevill, W.E. Aerial observation of feeding behavior in four baleen whales: Eubalaena glacialis, Balaenoptera borealis, Megaptera novaeangliae, and Balaenoptera physalus. J. Mammal. 1979, 60, 155–163. [Google Scholar] [CrossRef]
- Goldbogen, J.A.; Friedlaender, A.S.; Calambokidis, J.; Mckenna, M.F.; Simon, M.; Nowacek, D.P. Integrative Approaches to the Study of Baleen Whale Diving Behavior, Feeding Performance, and Foraging Ecology. BioScience 2013, 63, 90–100. [Google Scholar] [CrossRef]
- Qu, C.; Gai, W.; Zhang, J.; Zhong, M. A novel hybrid grey wolf optimizer algorithm for unmanned aerial vehicle (UAV) path planning. Knowl.-Based Syst. 2020, 194, 105530. [Google Scholar] [CrossRef]
- Stark, C.R.; Pyke, L.M. Dynamic pathfinding for a swarm intelligence based UAV control model using particle swarm optimisation. Front. Appl. Math. Stat. 2021, 7, 744955. [Google Scholar]
- Saied, M.; Slim, M.; Mazeh, H.; Francis, C.; Shraim, H. Unmanned Aerial Vehicles Fleet Control via Artificial Bee Colony Algorithm. In Proceedings of the 2019 4th Conference on Control and Fault Tolerant Systems (SysTol), Casablanca, Morocco, 18–20 September 2019; pp. 80–85. [Google Scholar]
- Janglová, D. Neural networks in mobile robot motion. Int. J. Adv. Robot. Syst. 2004, 1, 2. [Google Scholar] [CrossRef]
- Gasparri, A.; Prosperi, M. A bacterial colony growth algorithm for mobile robot localization. Auton. Robot. 2008, 24, 349–364. [Google Scholar] [CrossRef]
- Abbas, N.H.; Ali, F.M. Path planning of an autonomous mobile robot using enhanced bacterial foraging optimization algorithm. Al-Khwarizmi Eng. J. 2016, 12, 26–35. [Google Scholar] [CrossRef]
- Khalil, A.E.K.; Anwar, S.; Husnain, G.; Elahi, A.; Dong, Z. A Novel Bio-Inspired Path Planning for Autonomous Underwater Vehicle for Search and Tracing of Underwater Target. In Proceedings of the 2021 International Conference on Innovative Computing (ICIC), Online, 15–16 September 2021; pp. 1–7. [Google Scholar]
- Zhu, D.; Li, W.; Yan, M.; Yang, S.X. The path planning of AUV based on DS information fusion map building and bio-inspired neural network in unknown dynamic environment. Int. J. Adv. Robot. Syst. 2014, 11, 34. [Google Scholar] [CrossRef]
- Yilmaz, N.K.; Evangelinos, C.; Lermusiaux, P.F.; Patrikalakis, N.M. Path planning of autonomous underwater vehicles for adaptive sampling using mixed integer linear programming. IEEE J. Ocean. Eng. 2008, 33, 522–537. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.; Zhao, W.; Wang, L. Vision-based target tracking and collision avoidance for two autonomous robotic fish. IEEE Trans. Ind. Electron. 2009, 56, 1401–1410. [Google Scholar]
- Zhu, D.; Huang, H.; Yang, S.X. Dynamic task assignment and path planning of multi-AUV system based on an improved self-organizing map and velocity synthesis method in three-dimensional underwater workspace. IEEE Trans. Cybern. 2013, 43, 504–514. [Google Scholar] [PubMed]
- Yuan, H.; Qu, Z. Optimal real-time collision-free motion planning for autonomous underwater vehicles in a 3D underwater space. IET Control. Theory Appl. 2009, 3, 712–721. [Google Scholar] [CrossRef]
- Haghighi, H.; Sadati, S.H.; Dehghan, S.; Karimi, J. Hybrid form of particle swarm optimization and genetic algorithm for optimal path planning in coverage mission by cooperated unmanned aerial vehicles. J. Aerosp. Technol. Manag. 2020, 12. [Google Scholar] [CrossRef]
- Arantes, M.d.S.; Arantes, J.d.S.; Toledo, C.F.M.; Williams, B.C. A hybrid multi-population genetic algorithm for UAV path planning. In Proceedings of the Genetic and Evolutionary Computation Conference 2016, Denver, CO, USA, 20–24 July 2016; pp. 853–860. [Google Scholar]
- Dhargupta, S.; Ghosh, M.; Mirjalili, S.; Sarkar, R. Selective opposition based grey wolf optimization. Expert Syst. Appl. 2020, 151, 113389. [Google Scholar] [CrossRef]
- Bouhamed, O.; Ghazzai, H.; Besbes, H.; Massoud, Y. Autonomous UAV navigation: A DDPG-based deep reinforcement learning approach. In Proceedings of the 2020 IEEE International Symposium on Circuits and Systems (ISCAS), Sevilla, Spain, 10–21 October 2020; pp. 1–5. [Google Scholar]
- Challita, U.; Saad, W.; Bettstetter, C. Interference management for cellular-connected UAVs: A deep reinforcement learning approach. IEEE Trans. Wirel. Commun. 2019, 18, 2125–2140. [Google Scholar] [CrossRef]
- Zhang, P.; Xiong, C.; Li, W.; Du, X.; Zhao, C. Path planning for mobile robot based on modified rapidly exploring random tree method and neural network. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418784221. [Google Scholar] [CrossRef]
- Gul, F.; Mir, S.; Mir, I. Coordinated Multi-Robot Exploration: Hybrid Stochastic Optimization Approach. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 1414. [Google Scholar]
- Bakdi, A.; Hentout, A.; Boutami, H.; Maoudj, A.; Hachour, O.; Bouzouia, B. Optimal path planning and execution for mobile robots using genetic algorithm and adaptive fuzzy-logic control. Robot. Auton. Syst. 2017, 89, 95–109. [Google Scholar] [CrossRef]
- Chen, W.; Rahmati, M.; Sadhu, V.; Pompili, D. Real-time Image Enhancement for Vision-based Autonomous Underwater Vehicle Navigation in Murky Waters. In Proceedings of the International Conference on Underwater Networks & Systems, Atlanta, GA, USA, 23–25 October 2019; pp. 1–8. [Google Scholar]
- Kumari, S.; Mishra, P.K.; Anand, V. Fault resilient routing based on moth flame optimization scheme for underwater wireless sensor networks. Wirel. Networks 2020, 26, 1417–1431. [Google Scholar] [CrossRef]
- Buschhaus, A.; Blank, A.; Ziegler, C.; Franke, J. Highly efficient control system enabling robot accuracy improvement. Procedia CIRP 2014, 23, 200–205. [Google Scholar] [CrossRef]
- Qiao, G.; Weiss, B.A. Accuracy degradation analysis for industrial robot systems. In Proceedings of the International Manufacturing Science and Engineering Conference, American Society of Mechanical Engineers, Los Angeles, CA, USA, 4–8 June 2017; Volume 50749, p. V003T04A006. [Google Scholar]
- Lagisetty, R.; Philip, N.; Padhi, R.; Bhat, M. Object detection and obstacle avoidance for mobile robot using stereo camera. In Proceedings of the 2013 IEEE International Conference on Control Applications (CCA), Hyderabad, India, 28–30 August 2013; pp. 605–610. [Google Scholar]
- Fulgenzi, C.; Spalanzani, A.; Laugier, C. Dynamic obstacle avoidance in uncertain environment combining PVOs and occupancy grid. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007; pp. 1610–1616. [Google Scholar]
- Michels, J.; Saxena, A.; Ng, A.Y. High speed obstacle avoidance using monocular vision and reinforcement learning. In Proceedings of the 22nd International Conference on Machine Learning, Bonn, Germany, 7–11 August 2005; pp. 593–600. [Google Scholar]
- Baldoni, P.D.; Yang, Y.; Kim, S.Y. Development of efficient obstacle avoidance for a mobile robot using fuzzy Petri nets. In Proceedings of the 2016 IEEE 17th International Conference on Information Reuse and Integration (IRI), Pittsburgh, PA, USA, 28–30 July 2016; pp. 265–269. [Google Scholar]
- Likhachev, M.; Ferguson, D. Planning long dynamically feasible maneuvers for autonomous vehicles. Int. J. Robot. Res. 2009, 28, 933–945. [Google Scholar] [CrossRef] [Green Version]
- Sánchez-Ibáñez, J.R.; Pérez-del Pulgar, C.J.; García-Cerezo, A. Path Planning for Autonomous Mobile Robots: A Review. Sensors 2021, 21, 7898. [Google Scholar] [CrossRef]
- Patle, B.; Pandey, A.; Parhi, D.; Jagadeesh, A. A review: On path planning strategies for navigation of mobile robot. Def. Technol. 2019, 15, 582–606. [Google Scholar] [CrossRef]
- King, J.; Likhachev, M. Efficient cost computation in cost map planning for non-circular robots. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 3924–3930. [Google Scholar]
- Campbell, S.; O’Mahony, N.; Carvalho, A.; Krpalkova, L.; Riordan, D.; Walsh, J. Path planning techniques for mobile robots a review. In Proceedings of the 2020 6th International Conference on Mechatronics and Robotics Engineering (ICMRE), Columbus, OH, USA, 27–29 September 2020; pp. 12–16. [Google Scholar]
- Ibrahim, M.I.; Sariff, N.; Johari, J.; Buniyamin, N. Mobile robot obstacle avoidance in various type of static environments using fuzzy logic approach. In Proceedings of the 2014 2nd International Conference on Electrical, Electronics and System Engineering (ICEESE), Kuala Lumpur, Malaysia, 9–10 December 2014; pp. 83–88. [Google Scholar]
- Ajeil, F.H.; Ibraheem, I.K.; Azar, A.T.; Humaidi, A.J. Grid-based mobile robot path planning using aging-based ant colony optimization algorithm in static and dynamic environments. Sensors 2020, 20, 1880. [Google Scholar] [CrossRef]
- Ali, H.; Gong, D.; Wang, M.; Dai, X. Path planning of mobile robot with improved ant colony algorithm and MDP to produce smooth trajectory in grid-based environment. Front. Neurorobotics 2020, 14, 44. [Google Scholar] [CrossRef]
- Seraji, H.; Howard, A. Behavior-based robot navigation on challenging terrain: A fuzzy logic approach. IEEE Trans. Robot. Autom. 2002, 18, 308–321. [Google Scholar] [CrossRef]
- Sharma, P.S.; Chitaliya, D. Obstacle avoidance using stereo vision: A survey. Int. J. Innov. Res. Comput. Commun. Eng. 2015, 3, 24–29. [Google Scholar] [CrossRef]
- Typiak, A. Use of laser rangefinder to detecting in surroundings of mobile robot the obstacles. In Proceedings of the Symposium on Automation and Robotics in Construction, Vilnius, Lithuania, 26–29 June 2008; pp. 26–29. [Google Scholar]
- Yang, J.; Chen, P.; Rong, H.J.; Chen, B. Least mean p-power extreme learning machine for obstacle avoidance of a mobile robot. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 1968–1976. [Google Scholar]
- Haykin, S.; Network, N. A comprehensive foundation. Neural Netw. 2004, 2, 41. [Google Scholar]
- Sun, B.; Han, D.; Wei, Q. Application of Rolling Window Algorithm to the Robot Path Planning. Comput. Simul. 2006, 23, 159–162. [Google Scholar]
- Syed, U.A.; Kunwar, F.; Iqbal, M. Guided Autowave Pulse Coupled Neural Network (GAPCNN) based real time path planning and an obstacle avoidance scheme for mobile robots. Robot. Auton. Syst. 2014, 62, 474–486. [Google Scholar] [CrossRef]
- Al-Mutib, K.; Abdessemed, F.; Faisal, M.; Ramdane, H.; Alsulaiman, M.; Bencherif, M. Obstacle avoidance using wall-following strategy for indoor mobile robots. In Proceedings of the 2016 2nd IEEE International Symposium on Robotics and Manufacturing Automation (ROMA), Ipoh, Malaysia, 25–27 September 2016; pp. 1–6. [Google Scholar]
- Ahmed, A.A.; Abdalla, T.Y.; Abed, A.A. Path planning of mobile robot by using modified optimized potential field method. Int. J. Comput. Appl. 2015, 113, 6–10. [Google Scholar] [CrossRef]
- Zhong, M.; Yang, Y.; Dessouky, Y.; Postolache, O. Multi-AGV scheduling for conflict-free path planning in automated container terminals. Comput. Ind. Eng. 2020, 142, 106371. [Google Scholar] [CrossRef]
- Cherroun, L.; Boumehraz, M.; Kouzou, A. Mobile Robot Path Planning Based on Optimized Fuzzy Logic Controllers. In New Developments and Advances in Robot Control; Springer: Berlin/Heidelberg, Germany, 2019; pp. 255–283. [Google Scholar]
- Chhotray, A.; Parhi, D.R. Navigational control analysis of two-wheeled self-balancing robot in an unknown terrain using back-propagation neural network integrated modified DAYANI approach. Robotica 2019, 37, 1346–1362. [Google Scholar] [CrossRef]
- Naazare, M.; Ramos, D.; Wildt, J.; Schulz, D. Application of Graph-based Path Planning for UAVs to Avoid Restricted Areas. In Proceedings of the 2019 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Wurzburg, Germany, 2–4 September 2019; pp. 139–144. [Google Scholar]
- Burchardt, H.; Salomon, R. Implementation of path planning using genetic algorithms on mobile robots. In Proceedings of the 2006 IEEE International Conference on Evolutionary Computation, Vancouver, BC, Canada, 16–21 July 2006; pp. 1831–1836. [Google Scholar]
- Su, K.; Wang, Y.; Hu, X. Robot path planning based on random coding particle swarm optimization. Int. J. Adv. Comput. Sci. Appl. 2015, 6, 58–64. [Google Scholar] [CrossRef]
- Darwish, A.H.; Joukhadar, A.; Kashkash, M. Using the Bees Algorithm for wheeled mobile robot path planning in an indoor dynamic environment. Cogent Eng. 2018, 5, 1426539. [Google Scholar] [CrossRef]
- Karaboga, D.; Gorkemli, B.; Ozturk, C.; Karaboga, N. A comprehensive survey: Artificial bee colony (ABC) algorithm and applications. Artif. Intell. Rev. 2014, 42, 21–57. [Google Scholar] [CrossRef]
- Agushaka, J.O.; Ezugwu, A.E. Advanced arithmetic optimization algorithm for solving mechanical engineering design problems. PLoS ONE 2021, 16, e0255703. [Google Scholar]
- Gul, F.; Mir, I.; Abualigah, L.; Sumari, P. Multi-Robot Space Exploration: An Augmented Arithmetic Approach. IEEE Access 2021, 9, 107738–107750. [Google Scholar] [CrossRef]
- Wu, H.S.; Zhang, F.M. Wolf pack algorithm for unconstrained global optimization. Mathematical Problems in Engineering 2014, 2014, 465082. [Google Scholar] [CrossRef]
- Mittal, N.; Singh, U.; Sohi, B.S. Modified grey wolf optimizer for global engineering optimization. Appl. Comput. Intell. Soft Comput. 2016, 2016, 7950348. [Google Scholar] [CrossRef]
- Liu, C.; Yan, X.; Liu, C.; Wu, H. The wolf colony algorithm and its application. Chin. J. Electron. 2011, 20, 212–216. [Google Scholar]
- Jalali, S.M.J.; Khosravi, A.; Kebria, P.M.; Hedjam, R.; Nahavandi, S. Autonomous robot navigation system using the evolutionary multi-verse optimizer algorithm. In Proceedings of the 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy, 6–9 October 2019; pp. 1221–1226. [Google Scholar]
- Jalali, S.M.J.; Hedjam, R.; Khosravi, A.; Heidari, A.A.; Mirjalili, S.; Nahavandi, S. Autonomous robot navigation using moth-flame-based neuroevolution. In Evolutionary Machine Learning Techniques; Springer: Berlin/Heidelberg, Germany, 2020; pp. 67–83. [Google Scholar]
- Chhillar, A.; Choudhary, A. Mobile Robot Path Planning Based Upon Updated Whale Optimization Algorithm. In Proceedings of the 2020 10th International Conference on Cloud Computing, Data Science & Engineering (Confluence), Noida, India, 29–31 January 2020; pp. 684–691. [Google Scholar]
- Wang, S.; Jia, H.; Abualigah, L.; Liu, Q.; Zheng, R. An improved hybrid aquila optimizer and harris hawks algorithm for solving industrial engineering optimization problems. Processes 2021, 9, 1551. [Google Scholar] [CrossRef]
- Mahajan, S.; Abualigah, L.; Pandit, A.K.; Altalhi, M. Hybrid Aquila optimizer with arithmetic optimization algorithm for global optimization tasks. Soft Comput. 2022, 26, 4863–4881. [Google Scholar] [CrossRef]
- Zhao, J.; Gao, Z.M. The heterogeneous Aquila optimization algorithm. Math. Biosci. Eng. MBE 2022, 19, 5867–5904. [Google Scholar] [CrossRef] [PubMed]
- Forestiero, A.; Papuzzo, G. Agents-based algorithm for a distributed information system in Internet of Things. IEEE Internet Things J. 2021, 8, 16548–16558. [Google Scholar] [CrossRef]
| Panel | Sensor | Software | Map Testing |
|---|---|---|---|
| ROSbot 2.0 [42] | - | Ros Operating System | Lab-based |
| Pioneer 3-DX [43] | Camera | Xilinx, GA-IP FPGA | Lab based |
| MATLAB (ROS system) [44] | – | ROS (SLAM) | Garage map |
| Aria P3-DX [45] | – | Saphira software | simple environment |
| Husarian ROSbot [46] | LiDAR | ROS | Lab |
| Ref | Sensors | Contribution |
|---|---|---|
| Moses et al. [94] | Radar Sensor | The authors presented the overall efficiency of radar and put forward the novel design of lightweight X-band radar sensor for UAVs. The Doppler effect caused the propulsion of the UAV, which provided safe and easy identification of the target and efficient maneuverability to avoid collisions. The authors noted that the proposed design is scalable and can be used for larger vehicles. |
| Hugler et al. [95] | Radar Sensor | The authors presented a detailed study on the advantages of radar with UAVs for detecting obstacles, such as their velocity and angular rates. They also provided the range tendency and the multi-target detection in the angular range of in azimuth. They conducted experimental work. |
| Mohamed et al. [80] | Radar Sensor | The authors highlighted the predominant features involved in radar sensors for detecting obstacles. They concluded that radar sensors have the capability to withstand weather conditions, making them suitable for outdoor applications. They can perfectly determine the sizes and shapes of obstacles while detecting them; however, the exact dimensions cannot be retrieved due to the low output resolutions of radar sensors. |
| Asvadi et al. [96] | Velodyne LiDAR | The authors presented the work of Velodyne LiDAR. A static 2D map was constructed, which was continuously compared with a previously constructed map using GPS/IMU. |
| Azim et al. [97] | Velodyne LiDAR | The researchers studied the obstacle detection and representation using OctoMap. They formulated the entire area with the Velodyne LiDAR sensor using spatial clustering and GPU for position correction. |
| Technique | Seminal Work |
|---|---|
| ANN [113,114] | Depends on self-organizing maps. |
| ABC [115,116,117] | The algorithm is used for optimization and imitates the bee colony pattern for the food search. Classified into three: (i) employed bees, (ii) onlooker bees, and (iii) scouts. |
| GA [118,119,120,121,122,123,124,125,126] | Extension of evolutionary algorithms; they depend on operators, e.g., mutation, crossover, and selection operators. |
| SA [127] | A probabilistic method employed for searching the global minima. It depends on the physical phenomena in solidifying fluids, such as metals. |
| GWO [21,128] | Depends on the hierarchical distribution of wolves. A mathematical model is obtained on how wolves hunt and prey. |
| AO [28,129] | Depends on mathematical operators, i.e addition, subtraction, multiplication, and division. Its popularity stems from its ease of use, with fewer parameters, making it straightforward to execute and adaptable to a wide range of applications. |
| WO [22,130,131] | Inspired by the hunting behavior of whales. They have an advantage because of their hunting strategies. |
| Problem Area | Improvement Areas |
|---|---|
| Noise occurrence [168] | Numerous studies have been conducted to limit and accommodate noise incidences in vehicle systems; however, this remains a difficulty. These (and other issues) significantly impede the real-time implementation of any algorithm. |
| Vision-based [169,170] | The difficulty comes from identifying joint points in the same dimension. This leads to uncertainty in recognizing points, resulting in conflicting interpretations of images. |
| ANN [171,172] | This approach has various advantages; however, it requires a large data set of the surrounding region for hidden layer tuning. The well-known backpropagation technique has its own drawbacks since it rapidly converges to local minima. |
| Algorithms | Benefits | Weakness | Implementation | Time Complexity |
|---|---|---|---|---|
| Fuzzy Logic | (a) It is easy to tune fuzzy rules according to need [177] | (a) Membership functions are difficult to implement. | Simulated world and real-time | |
| (b) Logic building is easy [178] | ||||
| (c) Can easily integrate with bio-inspired algorithms [177] | ||||
| Neural Network | (a) Real-time implementation is easy compared to fuzzy | (a) Neuron layer embedded in the network results in harder implementation [171] | Real-time and simulation | |
| (b) Control logic imitation is easy | (b) Layered structure increases the complexity [171] | |||
| (c) Backpropagation is beneficial [179] | ||||
| (d) Dataset collection is difficult in real-time [171] | ||||
| Genetic Algorithm | (a) Faster convergence rate [180] | (a) Local minima problem exists in a complex environment [181] | Simulated world | |
| (b) Easily integrable with other algorithms [180] | (b) System needs a lot of tuning [182] | |||
| (c) Easy implementation [183] | ||||
| ABC | (a) Fewer control parameters [117] | (a) Weak convergence rate [184] | Simulated world | |
| (b) Less execution time is needed [183] | ||||
| (c) Integrable with other algorithms [183] | ||||
| Arithmetic Algorithm | (a) Easy implementation [185] | (a) (Tad bit) less of a convergence rate [186] | Simulated World | |
| GWO | (a) Convergence rate is fast [187] | (a) A bit tricky in a complex environment [188] | Simulated world | |
| (b) Tuning of the parameter is easy [187] (c) Performs better when integrated with another algorithm [189] | ||||
| Moth flame | (a) Performs effectively in a complex environment [190] | (a) Suffers from premature convergence [191] | Simulated world and real-time | |
| WOA | (a) Fast convergence rate [192] | (a) Not easily implementable in a dynamic environment [109] | Simulated world and real-time | |
| Aquila Optimizer | (a) Effective at producing good solutions in a complex environment [193] | (a) Requires tuning of a lot of variables [194] | Simulated world and real-time | |
| (b) Convergence rate is faster initially | (b) Becomes a tad bit slow at latter iterations [195]. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mir, I.; Gul, F.; Mir, S.; Khan, M.A.; Saeed, N.; Abualigah, L.; Abuhaija, B.; Gandomi, A.H. A Survey of Trajectory Planning Techniques for Autonomous Systems. Electronics 2022, 11, 2801. https://doi.org/10.3390/electronics11182801
Mir I, Gul F, Mir S, Khan MA, Saeed N, Abualigah L, Abuhaija B, Gandomi AH. A Survey of Trajectory Planning Techniques for Autonomous Systems. Electronics. 2022; 11(18):2801. https://doi.org/10.3390/electronics11182801
Chicago/Turabian StyleMir, Imran, Faiza Gul, Suleman Mir, Mansoor Ahmed Khan, Nasir Saeed, Laith Abualigah, Belal Abuhaija, and Amir H. Gandomi. 2022. "A Survey of Trajectory Planning Techniques for Autonomous Systems" Electronics 11, no. 18: 2801. https://doi.org/10.3390/electronics11182801
APA StyleMir, I., Gul, F., Mir, S., Khan, M. A., Saeed, N., Abualigah, L., Abuhaija, B., & Gandomi, A. H. (2022). A Survey of Trajectory Planning Techniques for Autonomous Systems. Electronics, 11(18), 2801. https://doi.org/10.3390/electronics11182801









