Abstract
In the context of global ecological degradation and the gradual depletion of fossil energy sources, the importance of new energy power in production and development is rising year by year. In order to reduce the impact of fluctuations in wind power systems on the grid due to various reasons during grid connection, this paper proposes an improved Linear Active Disturbance Rejection Control (LADRC) combined with a neural network based grid-side inverter control method, which, based on the analysis of the characteristics of permanent magnet motors and the current situation of their use, enables the converter to show better control characteristics in terms of DC-side voltage fluctuation amplitude and recovery time during operation. Simulation results show that the controller is more robust and adaptable to the uncertainty and external disturbance changes of the converter under different operating conditions than the traditional control method. The system has good dynamic response performance.
1. Introduction
In recent years, the wind power new energy industry has developed rapidly against a background of policy support and rising demand. In terms of hardware, new records are constantly being set for wind turbine specifications, power numbers and impeller sizes; the corresponding software control strategies in terms of maximum wind energy tracking and pitch control are also constantly being improved [1,2].
The main control objective of the PMSG’s full power converter is to achieve maximum wind energy tracking while maintaining DC voltage stability, to convert the maximum amount of wind energy into electricity for transmission to the grid, and to provide some reactive power support to the grid. The current control strategy for full-power power electronic converters mainly includes vector control and direct power control. The former is theoretically early and technically mature, but there are problems of large control calculations and sensitivity to parameter changes [3,4]. Vector control usually uses the net measured current as the inner loop control target, combined with the outer loop control. The current loop control is often used by linear controllers such as proportional integral and proportional resonance [5], which use current feedback values to achieve the purpose of decoupling the two-phase rotating coordinate system control. The latter has a fast dynamic torque response and a simple control structure; however, the torque pulsation is large at low speeds and cannot achieve the effect of the former [6].
Active Disturbance Rejection Control (ADRC) technology is a new practical technology developed and proposed by researcher Han Jingqing in the process of continuous in-depth consideration of the intrinsic ideas of both classical regulation theory and modern control theory, fully absorbing the achievements of modern control theory in analyzing the structural nature of the system, carrying forward and enriching the essence of PID ideas, and developing and applying special non-linear effects. The core idea is to take the simple integral series type as the standard type, treat the part of the system dynamics different from the standard type as the total disturbance, use the expansion state observer as a means to estimate the total disturbance in real time and eliminate it, thus reducing the controlled object full of disturbance, uncertainty and non-linearity to the standard integral series type, making the design of the control system from complex to simple, from abstract to intuitive [7]. Later, after a considerable number of simulations and engineering practice by Prof. Gao’s team, a whole set of parameters of the ADRC was correlated with the controller frequency and the observer frequency, so that the number of parameters to be rectified was significantly reduced, simplifying the process of parameter rectification and making the physical meaning more prominent. The research and promotion of ADRC technology has been greatly advanced [8,9]. The LADRC consists of three main components: a Linear Tracking Differentiator (LTD), which sets up the transition process and acquires the differential signal of the process; a Linear Extended State Observer (LESO), which observes the total system disturbance; and a Linear State Error Feedback (LSEF) for generating control quantities.
Both ADRC and LADRC currently have a number of applications in wind power generation. Considering that the total disturbance of the observer can be partially compensated by the model characteristics of the controlled object, Gao et al. added the idea of model compensation to the ADRC controller to achieve better current tracking characteristics [10]. Liu et al. proposed a measurement delay compensated LADRC controller, which eliminated the unmatched disturbance compensation due to measurement delay, and its effectiveness was demonstrated after evaluation of the closed-loop current gain as well as the frequency response of disturbance rejection [11]. Yuan et al. introduced a differential signal to the LESO in the LADRC to improve the system’s ability to suppress high frequency signals [12]. Most of the current improvements to the LADRC have been made to the LESO, so this paper also chooses to adapt the LADRC controller structure starting from the LESO.
Neural networks (NNs), also known as artificial neural networks (ANNs), are simplified models designed to mimic some of the characteristics of biological neurons from the perspective of information processing, combining mathematical and physical methods, and are also a certain abstraction of the neural networks of the human brain. The general neural network is composed of several parts: neurons, network topology and learning algorithms, and is currently used in function approximation, pattern recognition, classification and data compression [13].
This paper proposes a grid-side inverter control method that combines improved LADRC with neural networks based on vector control, and optimizes the structure of LADRC by combining the principle of deviation control. It is also verified that the composite controller structure has better control quality in stabilizing the DC-side voltage and resisting external disturbances by comparing the established wind power system simulation model with the conventional LADRC.
2. Mathematical Modelling of Wind Power Systems
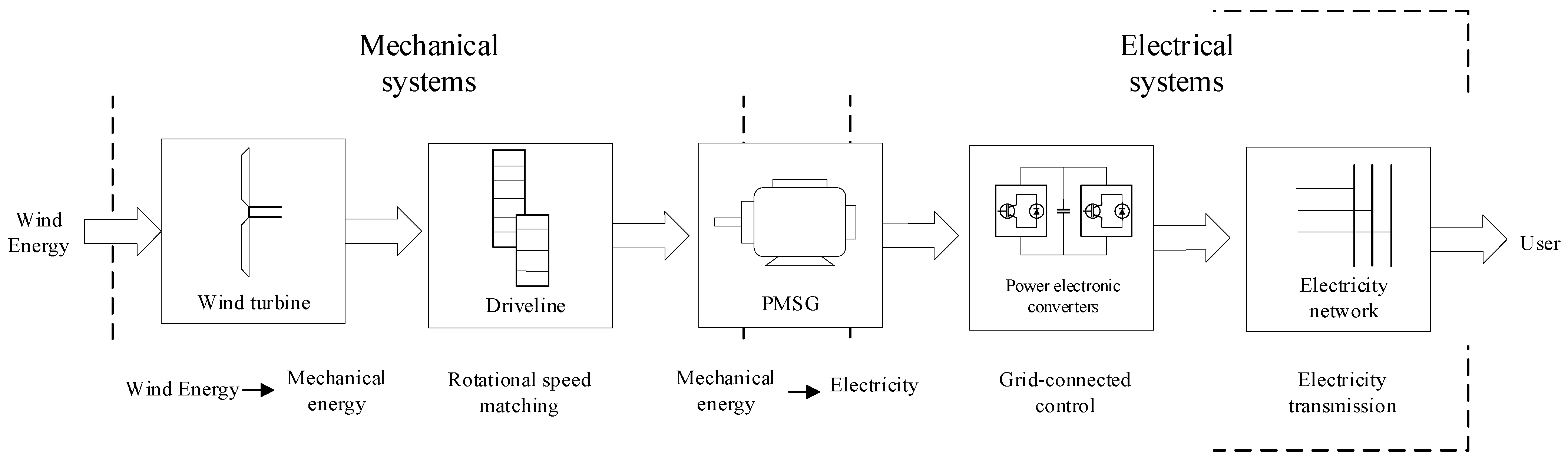
The permanent magnet synchronous wind power system consists of a wind turbine, a drive train, a PMSG, a power electronic converter and other equipment as well as a control system, the overall structure of which is shown in Figure 1. The wind turbine first captures the fluctuating wind energy and converts it into rotating mechanical energy, which is then converted into electrical energy by the generator and fed into the grid via the power electronic converter. It is worth noting that the permanent magnet synchronous wind power system does not have a gearbox and its drive train only has couplings, which greatly reduces energy losses.
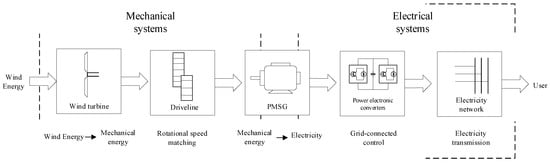
Figure 1.
Structure of a permanent magnet synchronous wind power system.
2.1. Permanent Magnet Synchronous Generator Structure and Mathematical Model
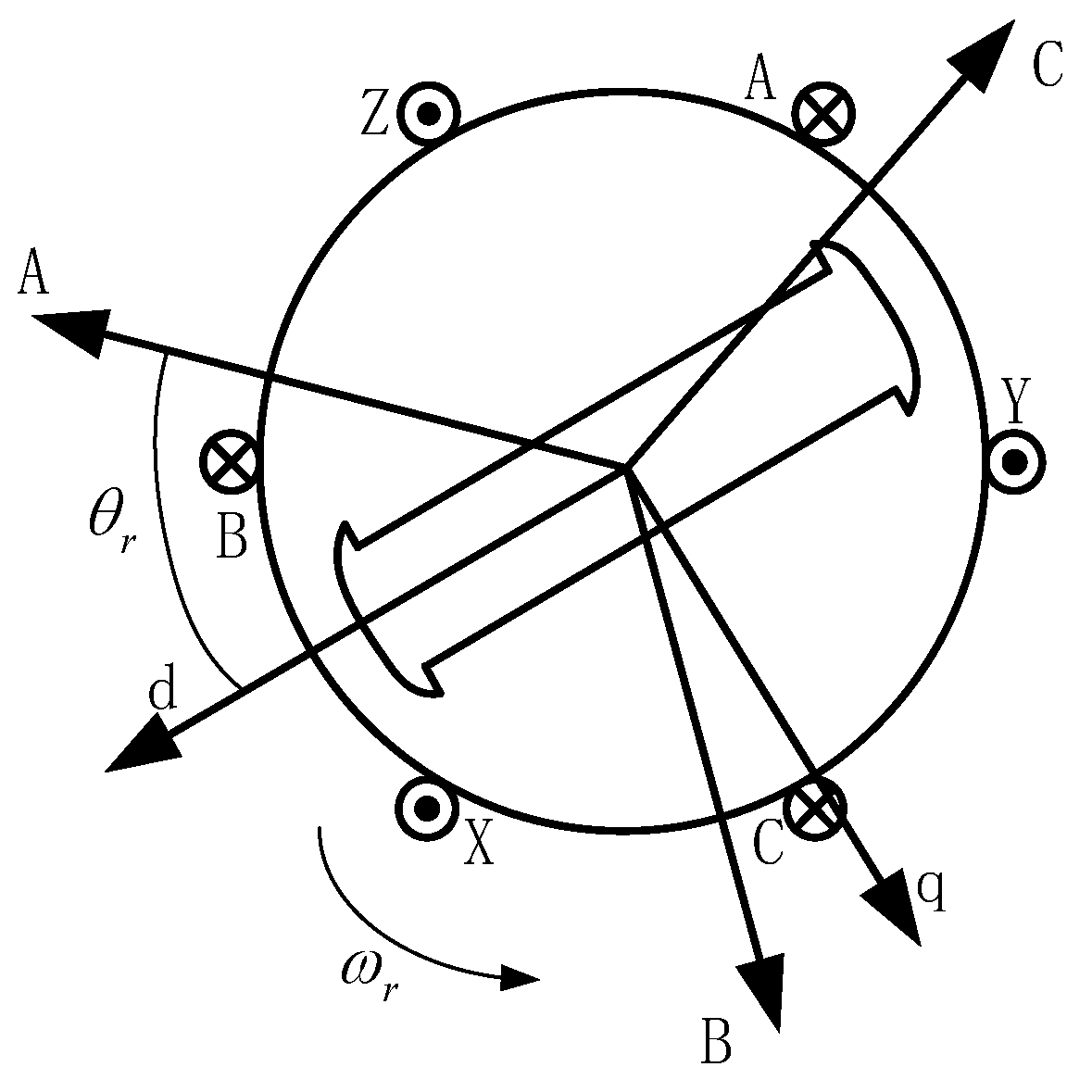
The permanent magnet synchronous generator (PMSG), the core component in a wind power system, absorbs mechanical energy and generates electrical power. The rotor section is made of permanent magnet material, eliminating the need for an excitation coil structure. The internal structure of the PMSG is complex, making it highly complex and difficult to discuss in terms of electromagnetic field modelling. The physical structure of a permanent magnet direct drive wind turbine is shown in Figure 2 [14].
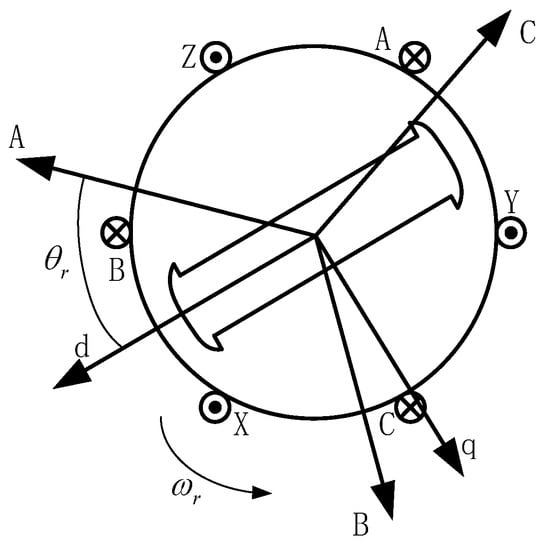
Figure 2.
Internal structure of the PMSG.
The stator winding of the PMSG is the same as that of an ordinary electrically excited synchronous motor, which is an AC three-phase symmetrical winding with a phase difference of 120°, denotes the synchronous speed, denotes the angular value of the extreme axis of the permanent magnet overrunning the A-phase winding, and the positive direction of the A-phase of the stator winding is preset as the reference direction. Because the mathematical model of PMSG in a rotating coordinate system can reduce the complexity and coupling in the motor modelling process, the mathematical models developed in this paper are all based on a two-phase rotating coordinate system [15], and the mathematical models are derived as follows under the premise of making some assumptions [16].
The voltage equation and the equation for the magnetic chain in the dq axis are obtained after transformation [17]:
where , , , , , , , are the components of each physical quantity on the sub-axis, respectively, and denotes the stator angular frequency in rad/s.
The equation for the electromagnetic torque under the dq axis is:
where denotes the number of pole pairs and denotes the magnetic chain on the rotor of the permanent magnet.
2.2. Net-Side Inverter Structure and Mathematical Model
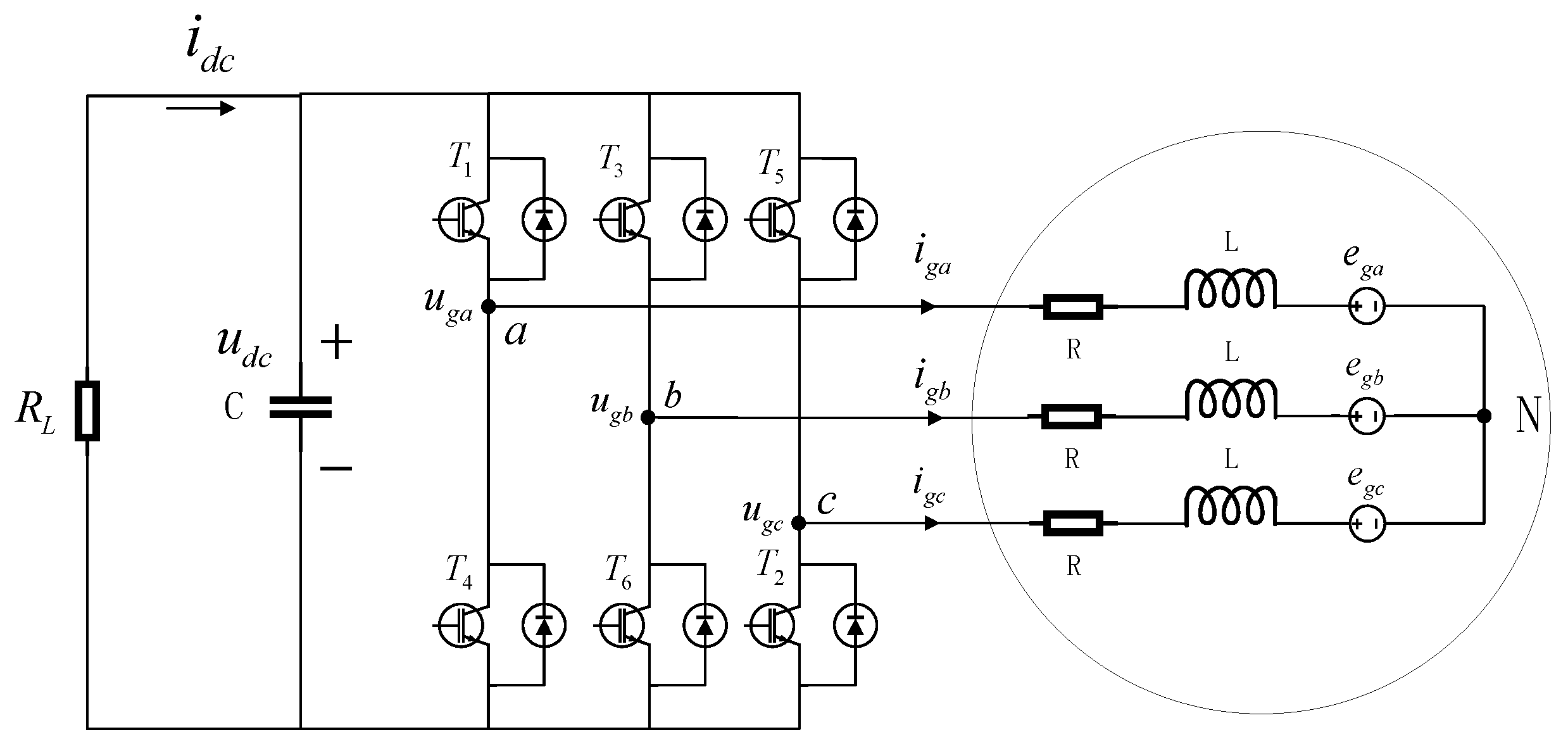
In grid-connected wind power systems, the control strategy of the grid-side inverter is key. The basic requirements are generally twofold, namely, to ensure voltage stability on the DC side and to achieve control of the grid-connected current. Figure 3 shows the topology of the network-side voltage source PWM inverter. In the figure, , , denote the three-phase grid electric potential, is the filtering resistor, is the filtering inductor, , , is the three-phase voltage output from the inverter, , , is the three-phase current, is the dc bus current, is the dc capacitance, is the dc bus voltage, denotes the adjustable resistor, represents the insulated gate bipolar transistor (IGBT).
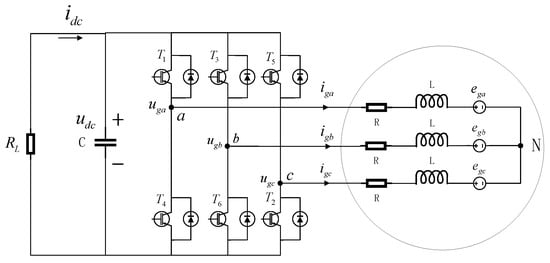
Figure 3.
Topology of the network-side inverter.
After the Clark and Park transformations, the voltage and current equations in the coordinate system are similarly derived as [18,19]:
where denotes the synchronous rotational angular velocity and denotes the switching function introduced to satisfy the conduction rule of the three-phase inverter circuit, described as follows.
Due to the conduction rules of the three-phase inverter circuit, i.e., the same phase (the same half of the bridge) alternates between the upper and lower arms, i.e., the upper and lower arms of the same phase do not conduct at the same time, otherwise they would short-circuit the power supply on the DC side, with three bridge arms conducting at the same time and the other three cutting off at any one moment. Therefore, the switching function is introduced to each bridge arm to produce the effect, satisfies:
2.3. DC Link Modelling
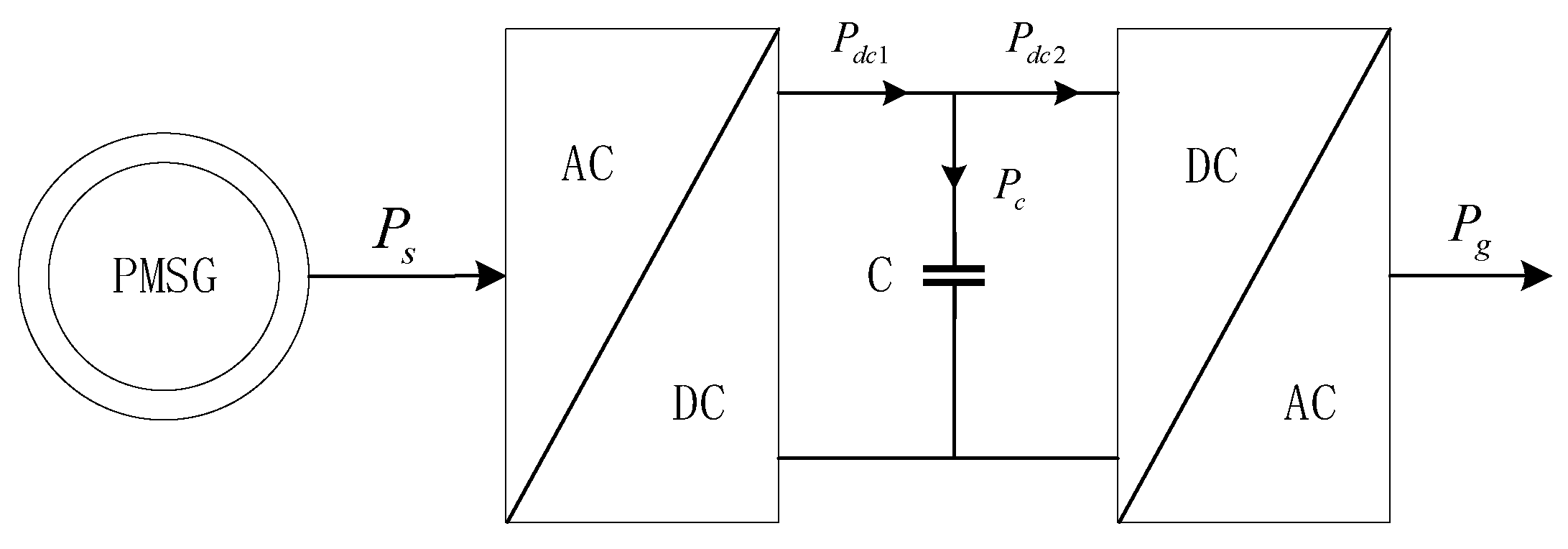
The two sides of the converter are connected by a DC bus, which acts as a bridge in the middle and plays a role in stabilizing the voltage on the DC side, filtering undesirable waveforms and the transition of energy flow so that both sides reach a dynamic balance. The power (energy) flow diagram is shown in Figure 4, where is the total power received by the converter from the generator, is the output power of the machine-side converter, is the active power flowing through the capacitor, is the input power or DC output power on the network side and is the output power of the network-side inverter.
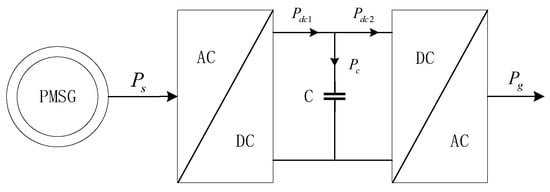
Figure 4.
Schematic diagram of power flow.
In the DC bus capacitor, the stored energy is:
Then the active power flowing through the busbar capacitor is:
Assume that the components in the diagram are ideal components and that the system power losses are negligible. Then, from another point of view, the active power flowing through the busbar capacitor can also be expressed as:
It can be seen that the energy transfer between the two converters on the machine side and the network side is only stable and free of other losses if , i.e., the active power flowing through the bus capacitors, is guaranteed. This can only be achieved by controlling the grid-side DC bus voltage so that it is as stable as possible at a nominal value, reducing the impact on the overall system stability.
3. LADRC-Based Wind Power System Controller Design
3.1. Improved LADRC Design Based on the Principle of Deviation Control
A conventional external loop control model for the LADRC inverter voltage based on the mathematical model derived in Section 2 is:
where and are the observed estimates of the DC bus voltage and the observed estimates of its differential . is the estimate of the total disturbance from the extended state observer. is the observer gain matrix, consisting of the observer bandwidth . The observer gain matrix of a traditional LADRC takes and is the controller bandwidth.
The analysis shows that the deviation of the traditional LADRC can effectively regulate the derivative of the observation , but it is not optimal for regulating the derivatives of and . In other words, the deviation does not describe well the error between the observed and actual values of the latter two state variables, so new deviations need to be found to regulate and thus redesign the dilated state observer [20,21]. From Equation (9) and the error equation it follows that:
Further collated as:
It follows that when the derivative of is adjusted using the deviation , the deviation between and can be expressed as . Thus, based on the above deviation control principle, an improved LESO can be constructed as follows.
The individual state variables and their derivatives are continuously derivable during the operation of LESO, so that the derivatives of each order of can be calculated, thus further simplifying the dilated state observer part of Equation (12).
The new observer gain coefficient matrix is obtained by configuring the poles of the new dilated state observer at , where denotes the observer bandwidth.
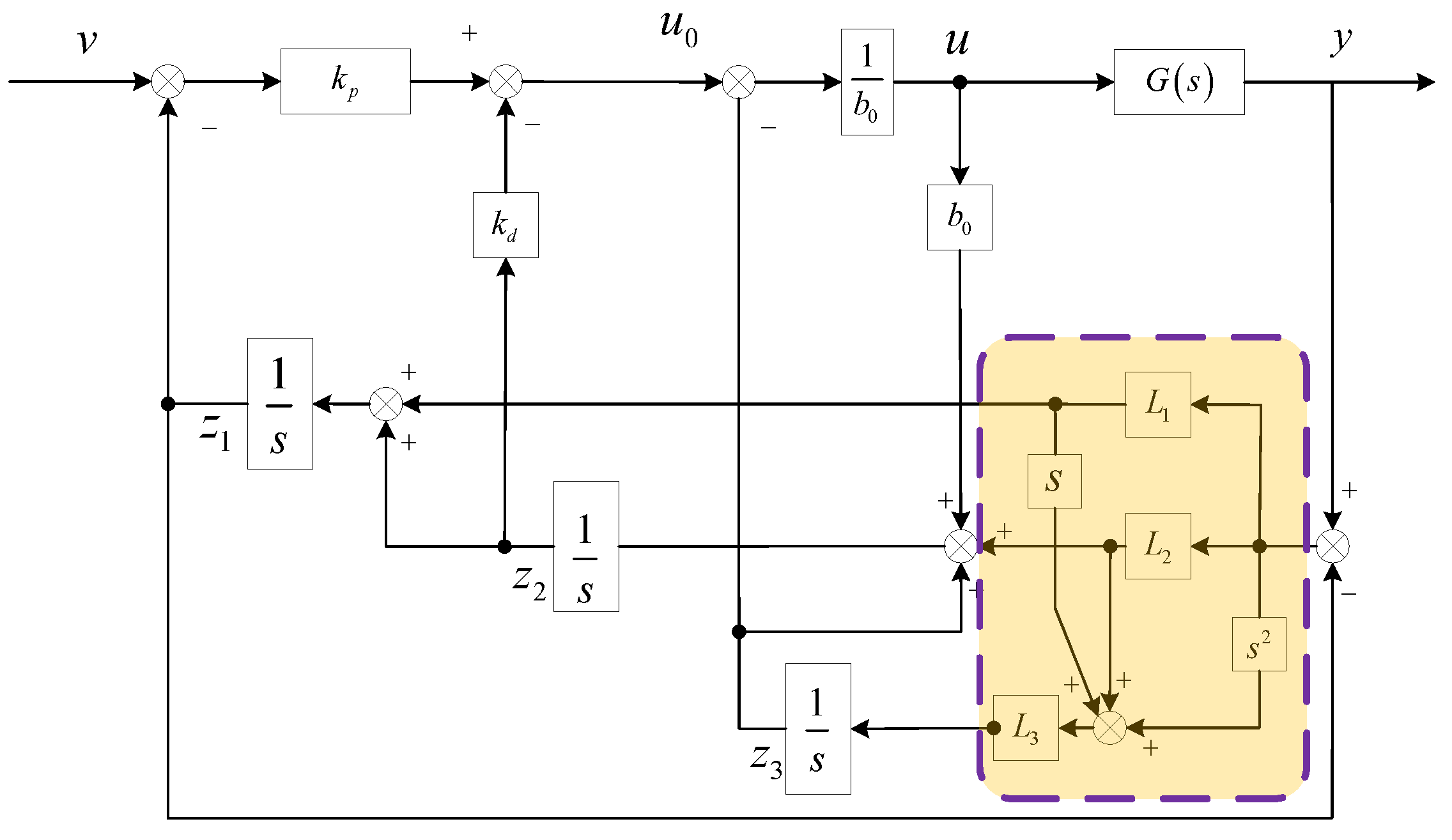
The final control system block diagram for the modified LADRC consisting of the modified LESO, the linear feedback control law (LSEF), and the disturbance compensation link is shown in Figure 5.
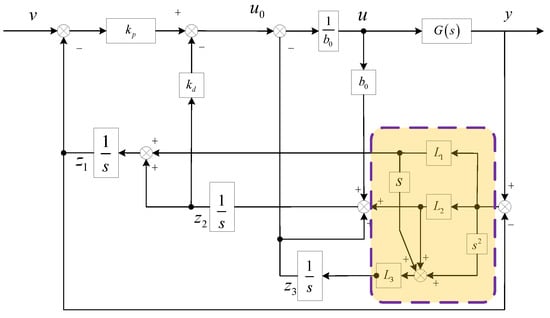
Figure 5.
Block diagram of the improved LADRC control structure.
Combining Equations (9) and (12), the transfer functions of the three LESO variables , and in relation to the inputs can be derived as follows.
The simplification leads to the following:
Of which: ,
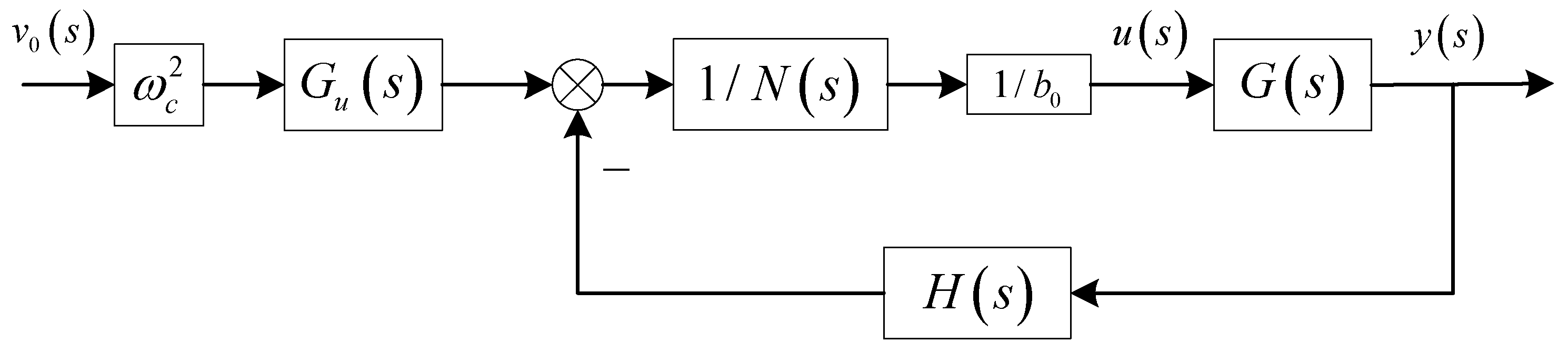
The transformation of the control structure of the modified LADRC can be drawn according to Equation (15) as shown in Figure 6.
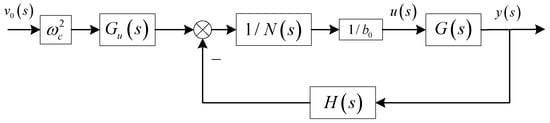
Figure 6.
Conversion diagram of the improved LADRC control structure.
3.2. Composite Controller Design Combined with Neural Networks
Although the improved LADRC or LADRC itself already has certain advantages over traditional control methods for the control of the system, the estimation theory of the dilated state observer shows that its role is to estimate the real-time motion of the object in order to complete the compensation of the model and the external disturbance, and when the parameters of the dilated state observer are set to vary over a wide range, the control effect is generally inferior to that of a system with smaller variations.
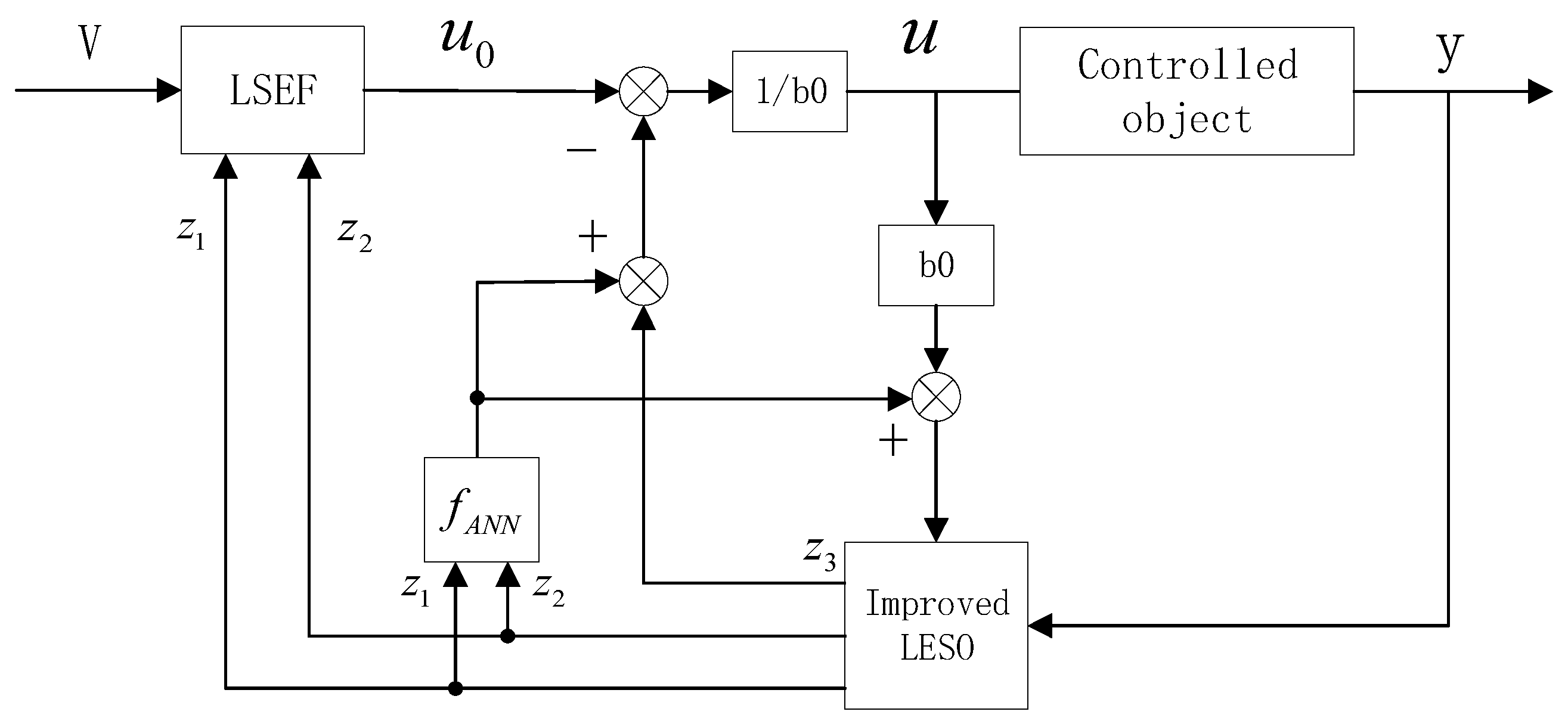
This section is intended to compensate for a part of the characteristics of the controlled object by using the property that artificial neural networks of a certain structure can arbitrarily approximate a linear function. The specific theoretical idea is to assume a known part of the mathematical model as , where is the known part of the system and is the unknown part of the system. By incorporating into a linearly expanding state observer, the object of the observer’s estimation becomes only , not the whole , reducing the observer’s workload. The neural network is embedded into the linear self-rejecting control algorithm, using the estimated output and of LESO as the input to the neural network and as the desired output of the neural network, so that the range of variation of the system is reduced, thus improving the adaptability and control quality of the controller [22,23]. The control structure diagram of the neural network embedded into the linear self-resistant controller is shown in Figure 7 below.
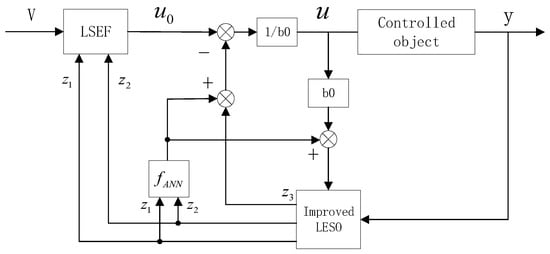
Figure 7.
Block diagram of ANN-LADRC control structure.
The ANN-LADRC control system model combining a linear state error feedback control law and a disturbance compensation link is expressed as:
The restructured controller model takes the estimated output of LESO, and , as inputs to the neural network and as the desired output of the neural network, so that the improved LADRC controller can access the known part of the system, , and thus improve the control quality.
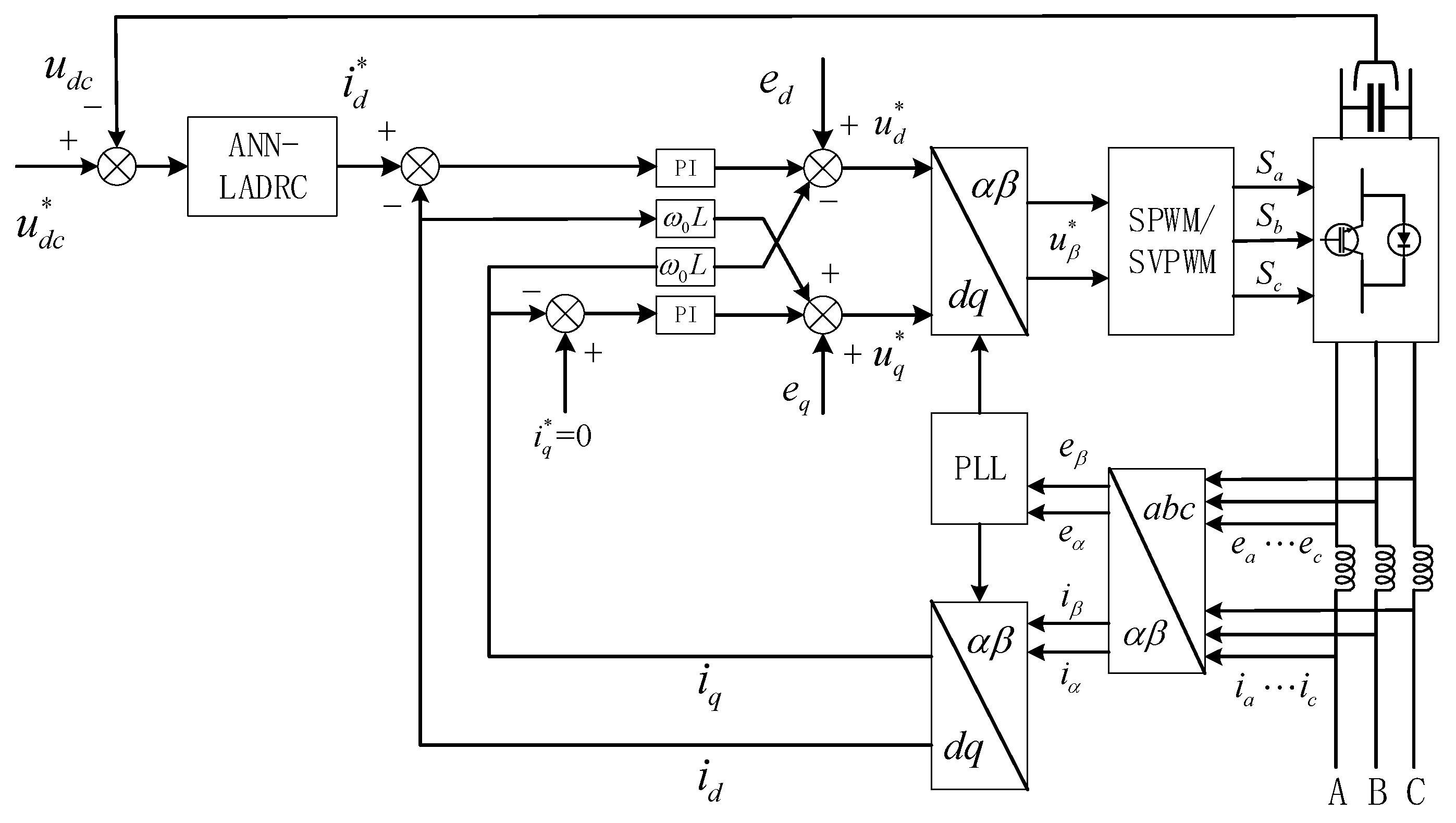
The specific operation to obtain the known part is described as follows: a set of parameters is called out using the original controller so that the system can meet the control requirements under the regulation of the parameters, after which the values of and are extracted from the linearly expanding state observer and saved; the network structure of a certain neural network and the training termination conditions are given with and as inputs and as the desired output, and the BP algorithm is used for training. Finally, the trained function is embedded into the controller structure and the control effect is observed. As the BP algorithm for feedforward neural networks is slow to converge and generally takes a long time, and the initial weights are chosen randomly and do not necessarily converge to the ideal weights, the neural network here is trained offline. The overall control block diagram of the system is shown in Figure 8 below.
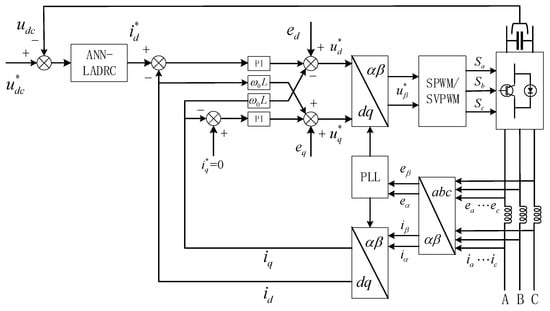
Figure 8.
Overall control block diagram of the network-side inverter. The superscript * indicates the reference value.
4. Analysis of Simulation Results
In this section, simulation results of the conventional LADRC and the improved ANN-LADRC controller models are built and applied to the DC bus voltage control of a 20 kW permanent magnet direct-drive wind power system built [24,25], respectively, by setting different fault conditions such as voltage rise and fall, in order to verify the effectiveness of the proposed improved approach in terms of wind power system applications. The controller parameters are: the observer bandwidth is 700, the controller bandwidth is and the controller gain is .
In this article, three different fault conditions are tested, i.e., a 50% drop in voltage balance, a 50% drop in voltage unbalance and a 30% rise in voltage balance, all of which are caused by voltage fluctuations on the customer side of the grid, whether natural or man-made. These three fault conditions are also the most common conditions faced by the grid in practice, so the three most frequent fault conditions are chosen in this paper to test the control effect of the controller. In the simulation, the step response is set directly to the grid voltage to simulate the fluctuations in the grid in real production, when the fault starts, when it ends and how deep the fluctuations are.
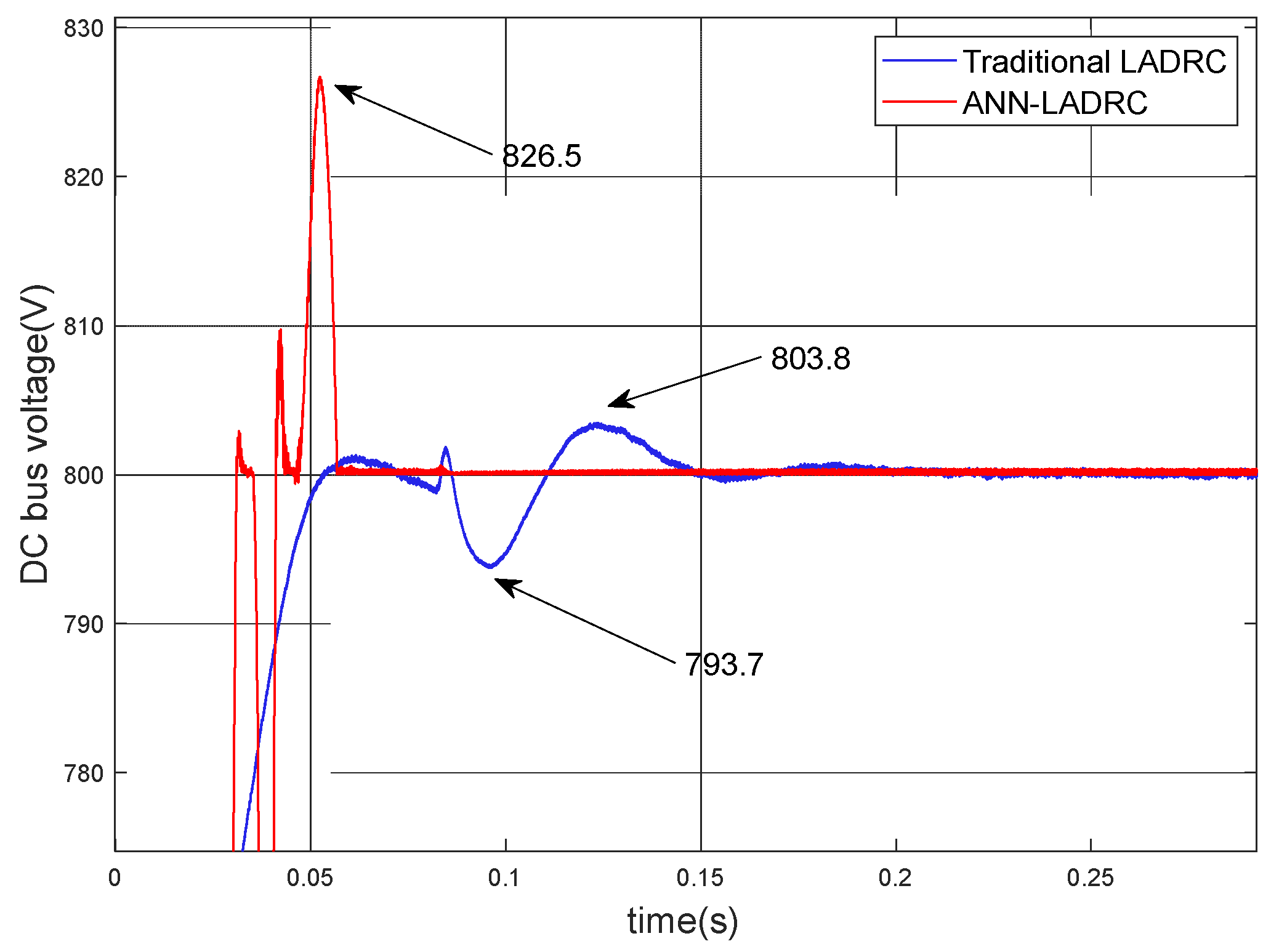
The control effect of the initial stage is shown in Figure 9. At this stage, the control method proposed in this paper does not show too much superiority compared to the control effect of the conventional LADRC, and even the overshoot appears to increase compared to the conventional LADRC. It can be seen from the graph that the final steady state values achieved by both control methods are only slightly improved, but the time required for the ANN-LADRC to reach steady state is significantly reduced, which is an improvement in the time required to get the system to smooth operation as soon as possible.
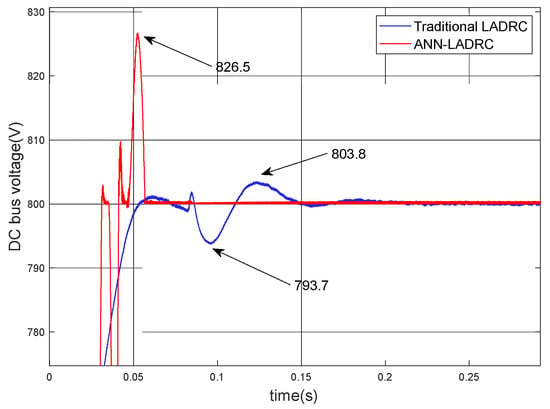
Figure 9.
Initial control bus voltage waveform.
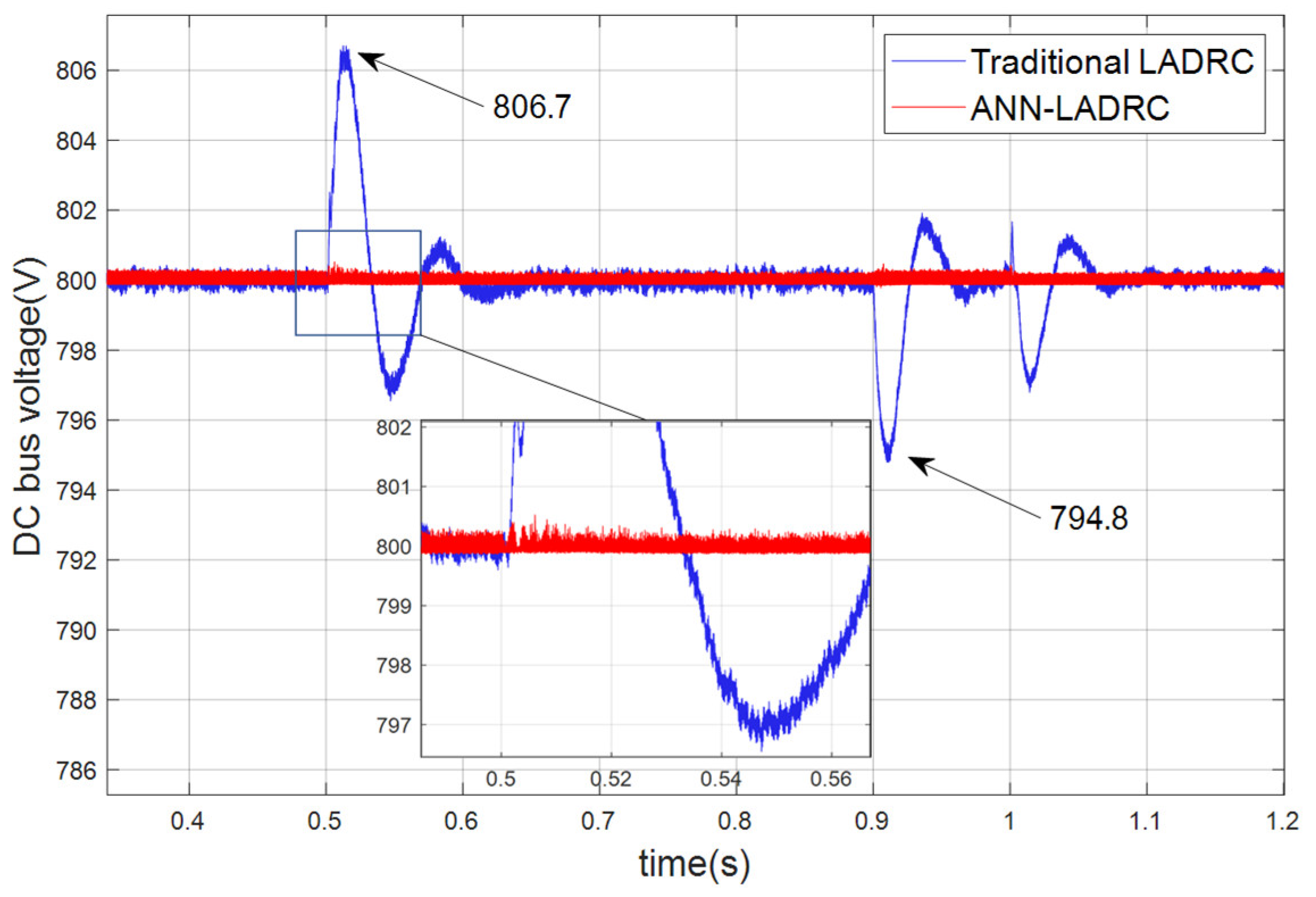
The voltage pattern of the DC bus when a voltage balance dip occurs in the grid, i.e., a low voltage crossing, is shown in Figure 10. Balanced dips mean that each single phase of the three-phase voltage produces a dip of the same magnitude, where the fault is set to start at 0.5 s, last 0.4 s and then end at 0.9 s, with a voltage dip depth of 50%. As can be seen from the graph, the ANN-LADRC produces almost no significant fluctuations compared to the conventional LADRC overshoot of a maximum value of 806.7, with the latter fluctuations remaining largely below 800.8 as can be seen in the partial magnification. In addition, in terms of repair time, the control effect of ANN-LADRC is more obvious, compared to the conventional LADRC repair time of about 150 ms; ANN-LADRC only took about 25 ms to return to its original state.
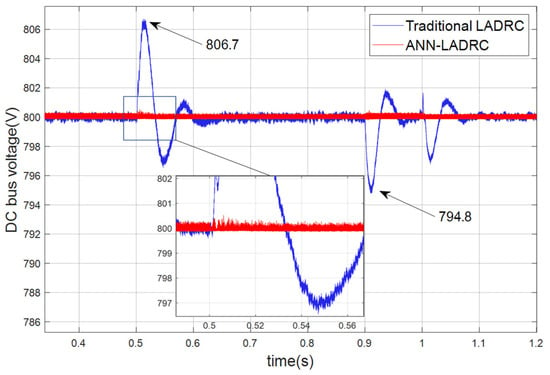
Figure 10.
Net-side voltage balance dip 50% bus voltage waveform.
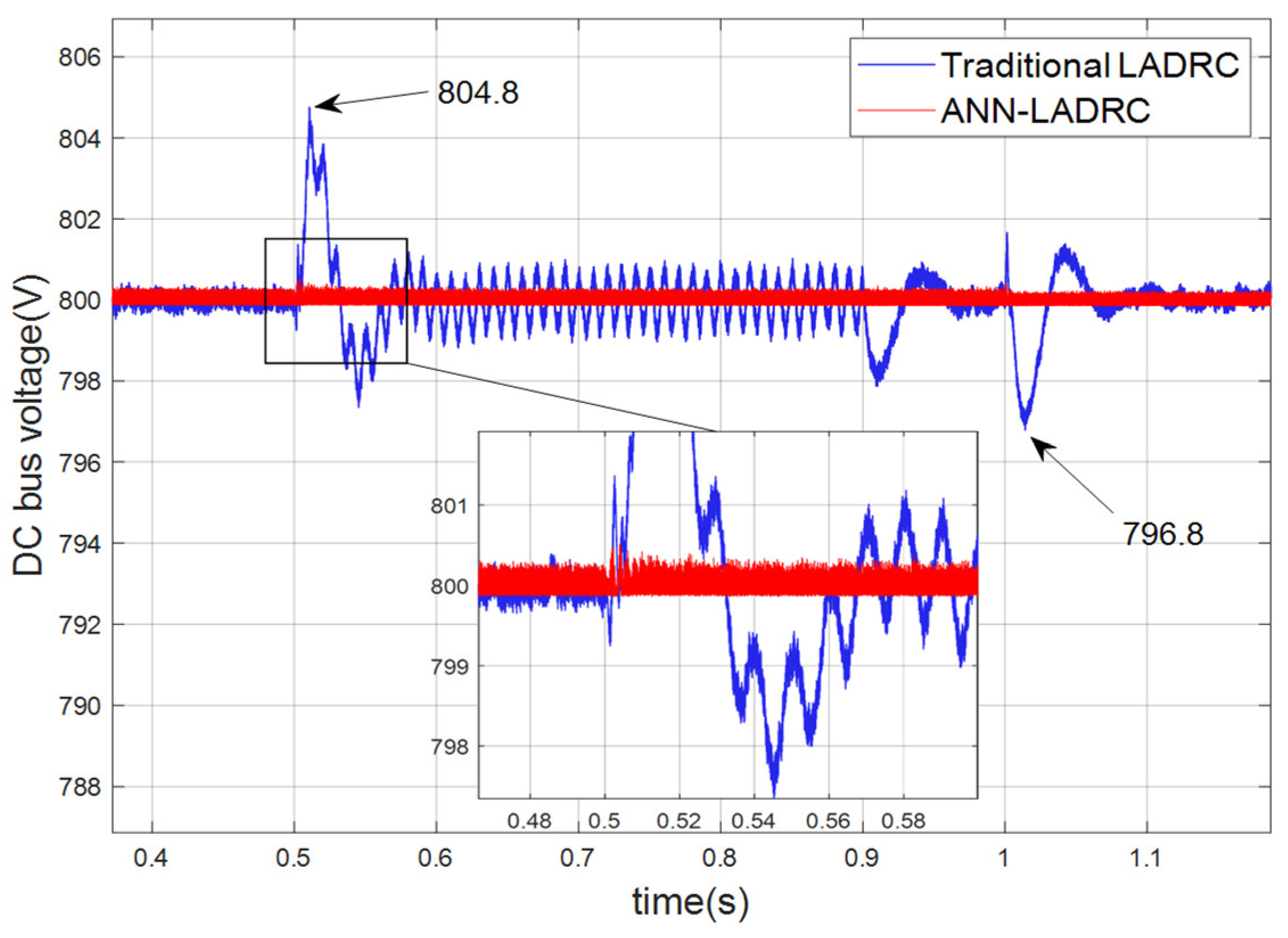
The DC bus voltage pattern when a voltage unbalance dip occurs in the grid is shown in Figure 11. An unbalanced dip means that one or two of the three phase voltages dip, while the other two or one phase voltage remains unchanged, again setting the fault occurrence to start at 0.5 s and last 0.4 s before ending at 0.9 s with a voltage dip depth of 50%. As can be seen from the graph, both control methods achieve steady state during the voltage dip fault, but both produce varying degrees of increase in steady state amplitude, although the ANN-LADRC fluctuations still have a significant advantage over the traditional LADRC plus or minus 1.2 amplitude fluctuations. Similarly, the new control method offers significant improvements in both the regulation amplitude and the regulation time at the beginning and end of the phase subjected to a voltage change shock.
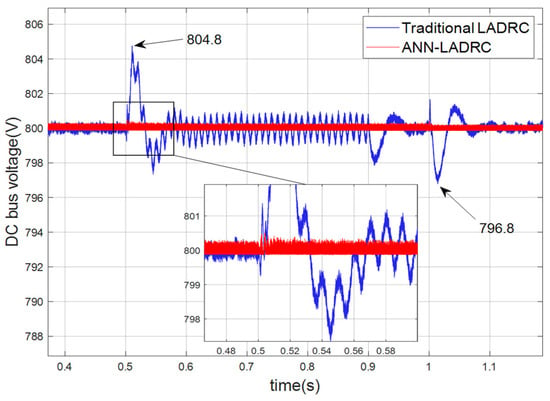
Figure 11.
Net-side voltage unbalance dip 50% bus voltage waveform.
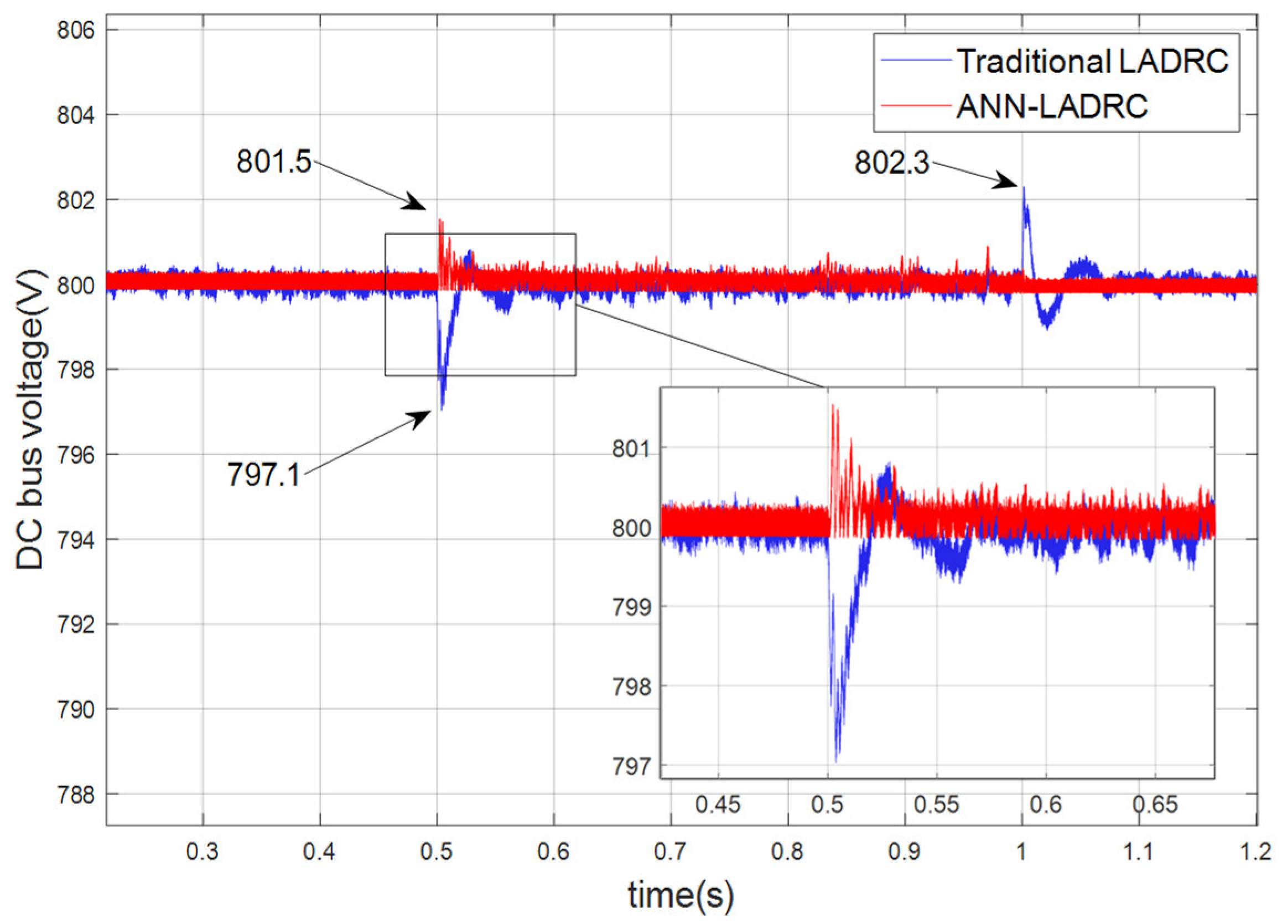
The DC bus voltage pattern when a voltage rise occurs in the grid is shown in Figure 12, where the fault is set to start at 0.5 s and last for 0.5 s before ending at 1 s, with a voltage rise of 30%. As can be seen from the Figure 12, the improvement in the control effect of ANN-LADRC under these conditions is not very significant compared to conventional, and only the amplitude control effect at the beginning and end of the shock is relatively significantly improved. During the duration of the fault, the bus voltage under the control of both methods produces slight amplitude fluctuations and drifts.
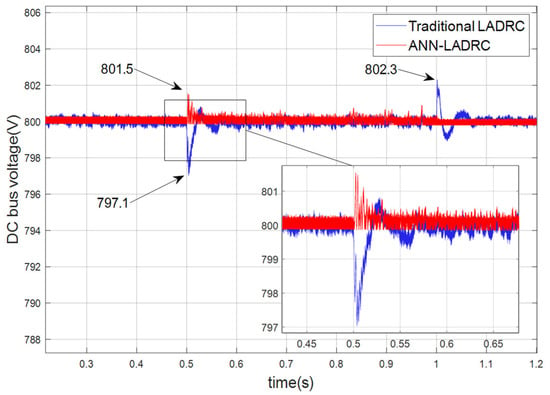
Figure 12.
Waveform diagram of bus voltage with 30% increase in network-side voltage.
Combining the above simulation data, tables of the characteristics of the offset and recovery time of the DC bus voltage under different controllers were designed, respectively, as shown in the Table 1 and Table 2 below. A positive value in the line “Effectiveness enhancement” indicates an increase, while a negative value indicates a decrease.

Table 1.
DC bus voltage offset with different controllers.

Table 2.
DC bus voltage repair time with different controllers.
Combining the above simulation results and the data tables, the improved ANN-LADRC controller has a 420.6% increase in overshoot during the initialization phase of the system compared to the conventional LADRC controller, when analyzed in terms of the maximum offset of the DC bus voltage. A review of the literature suggests that this fluctuation may originate from the system internal disturbance brought about by the neural network function embedded in the conventional LADRC structure. In themselves, the estimates of the dilated state observer in LADRC are theoretically supposed to be incorporated directly into the linear error feedback control law, whereas the embedded neural network function requires two estimates of the input state observer and predicts an output value to be passed into the linear error feedback control law, thus possibly creating a perturbation to the system at the beginning of its operation. However, when the neural network function enters a steady state after initialization, i.e., when it is able to make smooth predictions, the system quickly returns to a steady state again. The ANN-LADRC controller shows a significant advantage over the other three fault conditions set out in the paper, with maximum offsets reduced by 89.4%, 87% and 48.3%, respectively, compared to conventional LADRC. Workers in the joint venture have shown that in actual grid-connected production of wind power, where the system has a large amplitude margin at initialization, the indicator of greater concern is the controller’s ability to cope with fluctuations brought about by internal and external disturbances in the system once it has started working. In other words, the ANN-LADRC makes a moderate sacrifice of what the system hardware can bear in exchange for achieving better control at the more demanding metrics, a solution that is of some significance in practical work production.
From the perspective of DC bus voltage restoration time, both for the initialization of the system and the three subsequent fault conditions, the ANN-LADRC shows better control compared to the conventional LADRC; they are reduced by 71%, 86.7%, 61.5% and 69.6%, respectively. For the high overshoot in system initialization, ANN-LADRC can restore it to its rated value in a very short time to avoid a continuous shock to the hardware system, and also reflects that the newly-designed composite controller can restore the system to a steady state in a shorter time in the face of fault disturbances, thus reducing production interruptions caused by shocks to the system’s hardware due to faults.
In summary, the composite controller ANN-LADRC is far better than the traditional LADRC in all control performance, except for the large overshoot generated during system initialization, and the magnitude margin during system hardware initialization in production is relatively large, so the composite ANN-LADRC controller designed in this paper meets the needs of actual production and has some practical significance for wind power grid-connected projects.
5. Conclusions
The inverter control strategy is a key technology in the overall wind power system. An excellent control strategy in the inverter control process is more likely to stimulate the evolving advanced power electronics semiconductor manufacturing technology. This paper focuses on the research into and implementation of a network-side inverter control strategy based on a combination of vector control, LADRC algorithm, and neural network algorithm, and our main achievements are as follows.
- Based on the analysis of the wind power system model and the characteristics of the LADRC, mathematical models of the PMSG, the grid-side inverter and the DC link were derived. A model of a 20 kW permanent magnet direct-drive wind power system was built in the simulation software and different fault conditions environments were simulated to prepare for the verification of the system performance under different control strategies.
- A wind power inverter control system based on a neural network self-rejecting controller was developed by combining the LADRC controller improved by deviation control with a neural network algorithm. A conventional LADRC and a modified ANN-LADRC controller model were built and applied to the built wind power system model for testing. The simulation results show that the self-rejecting controller incorporating the neural network has a better control quality of the bus voltage due to the reduced observer workload by compensating for the partially unknown model. The controller is more adaptive and robust to uncertainties and external disturbances in permanent magnet direct-drive wind power systems. The controller algorithm is simple and the system has a stronger dynamic response performance.
Author Contributions
Conceptualization, J.S.; methodology, J.S. and T.W.; software, J.R., T.W. and M.L.; validation, J.S. and H.J.; formal analysis, J.S.; investigation, J.S., M.L. and H.J.; resources, H.J., M.L. and J.R.; data curation, J.S. and J.R.; writing—original draft preparation, J.S.; writing—review and editing, T.W.; visualization, J.S. and J.R.; supervision, T.W.; project administration, T.W.; funding acquisition, T.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We appreciate our reviewers and editors for their precious time.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Qu, S.Y. Research on the key issues of wind power generation technology. China Plant Eng. 2019, 8, 196–197. (In Chinese) [Google Scholar]
- Guan, J.P.; Xu, Y.H. A Review of Research on the Application of Power Electronic Transformers in Wind Power Systems. Adv. Technol. Electr. Eng. Energy 2019, 38, 88–96. (In Chinese) [Google Scholar]
- Yin, M.; Xu, Y.; Shen, C.; Liu, J.; Dong, Z.Y.; Zou, Y. Turbine stability-constrained available wind power of variable speed wind turbines for active power control. IEEE Trans. Power Syst. 2016, 32, 2487–2488. [Google Scholar] [CrossRef]
- Yang, J.F.; Hu, Y.H. Optimal direct torque control for permanent magnet synchronous motors. Chin. J. Electr. Eng. 2011, 31, 109–115. (In Chinese) [Google Scholar]
- Yuan, L.; Guo, Q. Parameters Designed Method and Control Strategy of Three-phase LCC Grid-connected Inverter. Power Electron. 2018, 52, 101–103. (In Chinese) [Google Scholar]
- Li, C.Y.; Wang, W.C. Improvement of control strategy for network-side converters. Technol. Innov. Appl. 2018, 29, 19–20. (In Chinese) [Google Scholar]
- Han, J.Q. Self-Disturbance Control Technology: Control Technology to Estimate and Compensate for Uncertainties; Defense Industry Press: Beijing, China, 2008. (In Chinese) [Google Scholar]
- Zheng, Z.; Geng, H.; Yang, G. High Voltage Ride-through Control Strategy of Grid-connected Inverter for Renewable Energy Systems. Proc. CSEE 2015, 35, 1463–1472. (In Chinese) [Google Scholar]
- Wang, H.J.; Zhao, D.H.; Zhao, H.; Yue, Y.J. Control strategy study of grid-connected inverter in direct-driven type wind power system. Chin. J. Power Sources 2015, 39, 1289–1292. (In Chinese) [Google Scholar]
- Gao, Y.; Huo, X.; Ma, K.; Zhao, H. Modified model-compensation ADRC controller and its application in PMSM current loop. Int. J. Model. Identif. Control 2020, 35, 140–150. [Google Scholar] [CrossRef]
- Liu, C.; Luo, G.; Chen, Z.; Tu, W. Measurement delay compensated LADRC based current controller design for PMSM drives with a simple parameter tuning method. Isa Trans. 2020, 101, 482–492. [Google Scholar] [CrossRef] [PubMed]
- Yuan, C.; Zhou, X.; Ma, Y.; Gao, Z.; Zhou, Y.; Wang, C. Improved Application of Third-Order LADRC in Wind Power Inverter. Energies 2020, 13, 4412. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Nguyen, T.D. Calculation of parameters for altering the ship’s course at sea using Artificial Neural Network (ANN). IOP Conf. Ser. Mater. Sci. Eng. 2020, 862, 32097. [Google Scholar] [CrossRef]
- Li, B. Research on Maximum Power Tracking Control Algorithm for Permanent Magnet Synchronous Wind Power Generation System. Master’s Thesis, South China University of Technology, Guangzhou, China, 2017. (In Chinese). [Google Scholar]
- Xie, Z.; Zhang, X.; Yang, S.Y.; Song, H.H.; Qu, T.Y. High Voltage Ride-through Control Strategy of Doubly Fed Induction Wind Generators Based on Virtual Impedance. Proc. CSEE 2012, 32, 16–23. (In Chinese) [Google Scholar]
- Yuan, X. A set of multilevel modular medium-voltage high power converters for 10-MW wind turbines. IEEE Trans. Sustain. Energy 2014, 5, 524–534. [Google Scholar] [CrossRef]
- Wang, X.; Sun, D.; Zhu, Z.Q. Resonant-based backstepping direct power control strategy for DFIG under both balanced and unbalanced grid conditions. IEEE Trans. Ind. Appl. 2017, 53, 4821–4830. [Google Scholar] [CrossRef]
- Wang, D. Research on Control Strategies for Grid-Connected Conberter System of Direct-Driben Wind Turbine. Master’s Thesis, North China Electric Power University, Beijing, China, 2016. (In Chinese). [Google Scholar]
- Li, S. Research on Conberter Control Technonlogy of Permanent Magnet Direct Drive Wind Power Generation System. Master’s Thesis, Jiangsu University, Jiangsu, China, 2020. (In Chinese). [Google Scholar]
- Sun, D.S.; Zhang, Y. J Improvement and observation accuracy analysis of linear extended state observer. J. Natl. Univ. Def. Technol. 2017, 39, 111–117. (In Chinese) [Google Scholar]
- Gao, Z.Q. On the foundation of active distuibance rejection control. Control Theory Appl. 2013, 30, 1498–1510. (In Chinese) [Google Scholar]
- Zhang, J. Application of ADRC Based on BP in Blackbody Temperature Control System. Master’s Thesis, Tianjin University of Technology, Tianjin, China, 2018. (In Chinese). [Google Scholar]
- Yang, Q.L.; Hao, X.H.; Zhang, H.P. Research on Brushless DC Motor Controller Based on Neural Network Self-Anti-Disturbance Control. Sci. Technol. Eng. 2008, 8, 6478–6481. (In Chinese) [Google Scholar]
- Feng, Y. Modeling and Simulation of direct driven permanent magnet wind power generation system based on MATLAB/simulink. Electron. Test 2020, 58–59. (In Chinese) [Google Scholar] [CrossRef]
- Liang, J.W.; Liu, X.P.; Yang, Y. Design and Simulation of a 2 kW Dirct-Driven Permanent Magnet Synchronous Wind Generator. Small Spec. Electr. Mach. 2011, 39, 13–14. (In Chinese) [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).