Rapid Harmonic Detection Scheme Based on Expanded Input Observer
Abstract
:1. Introduction
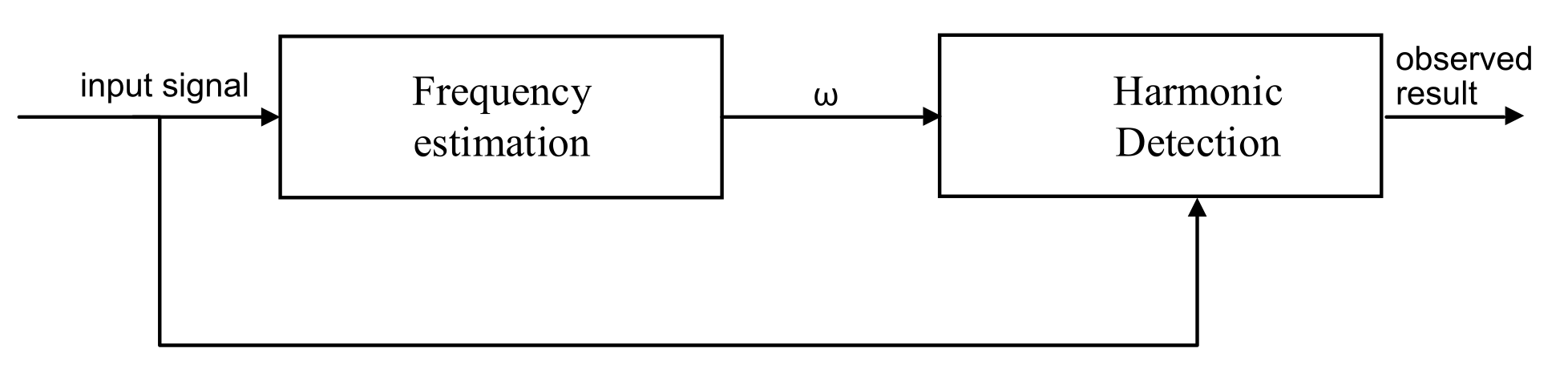
2. Harmonic Detection
2.1. Design Method for Input Observer
2.2. Frequency Estimation Model
3. Simulation Results
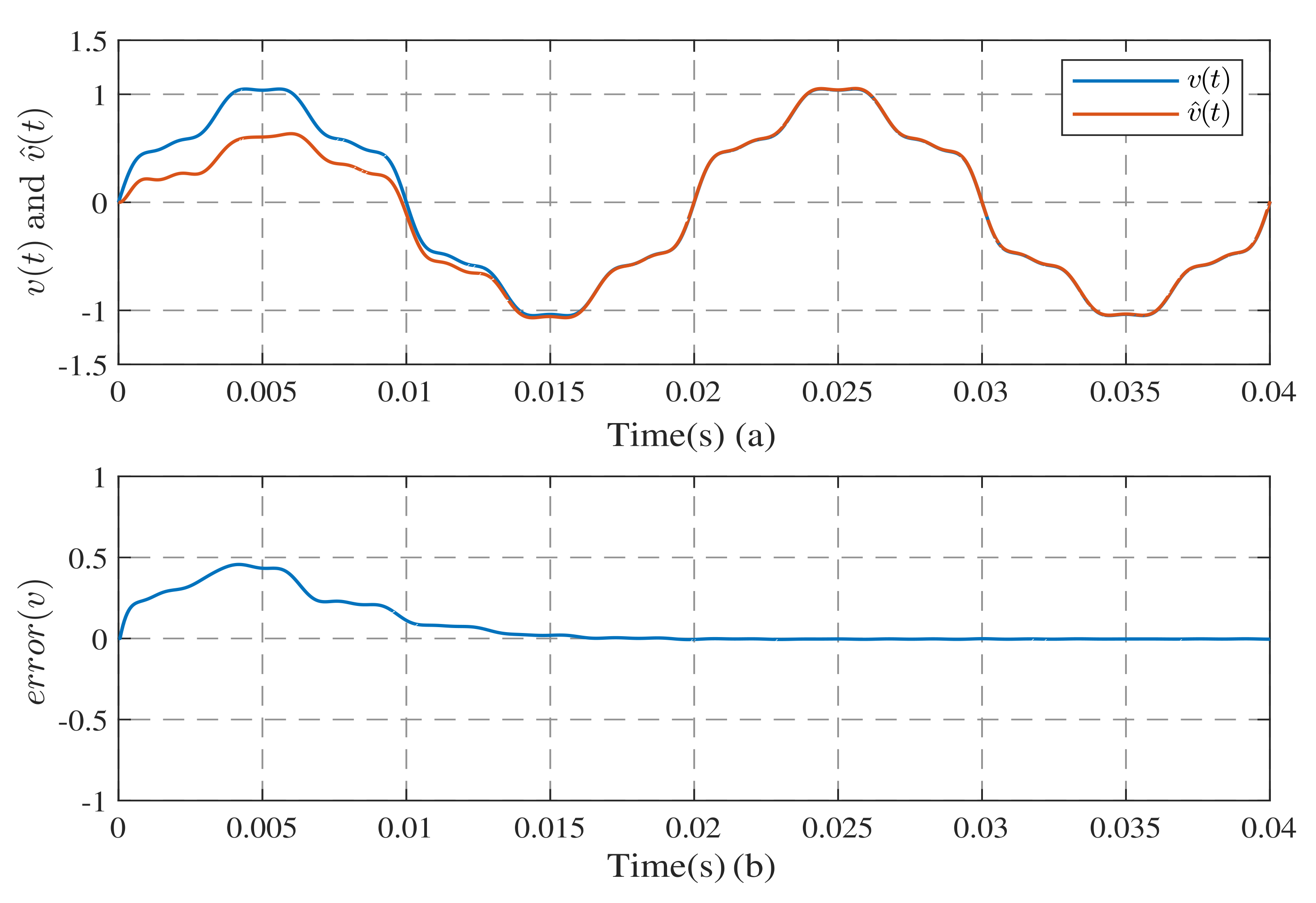
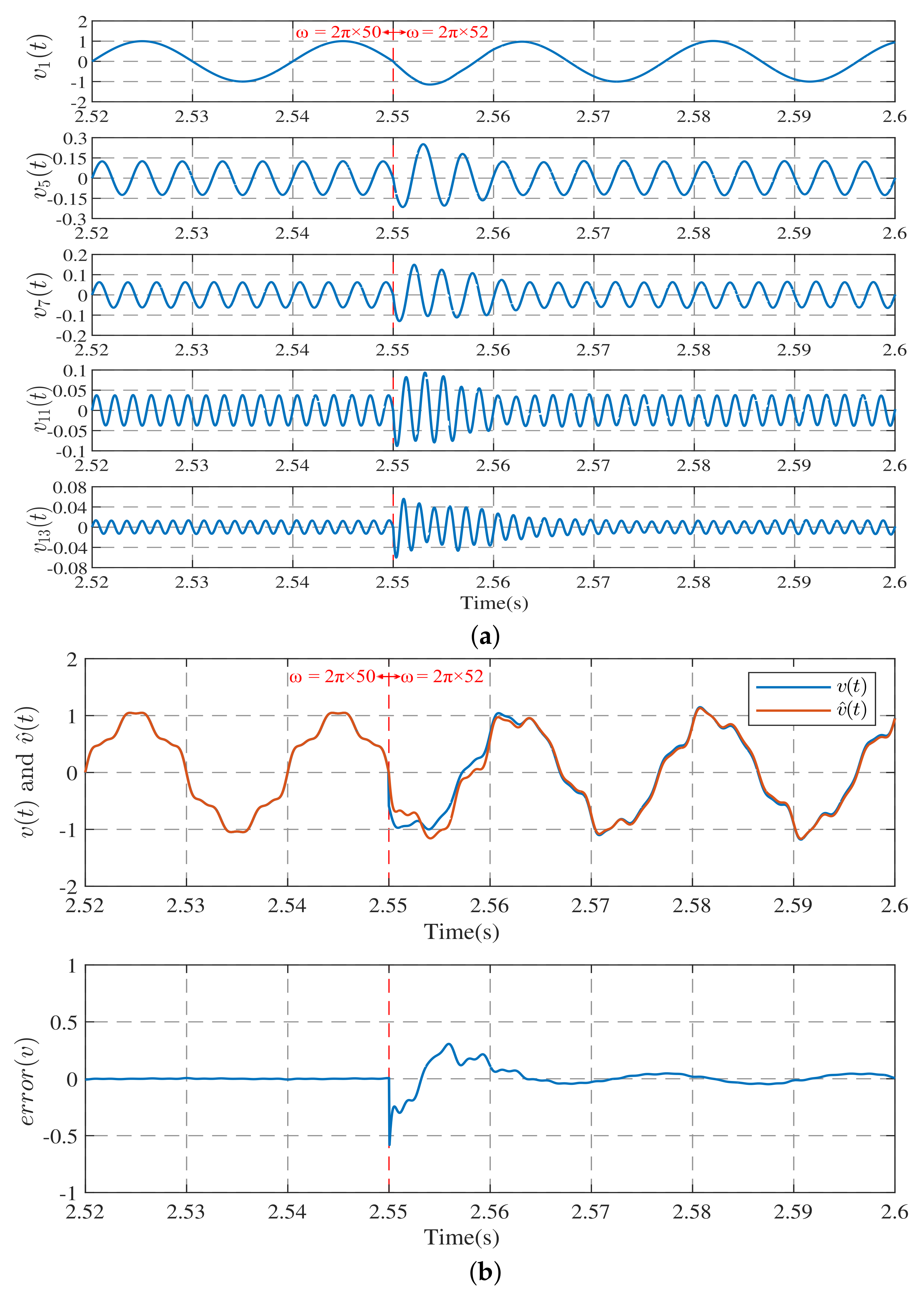
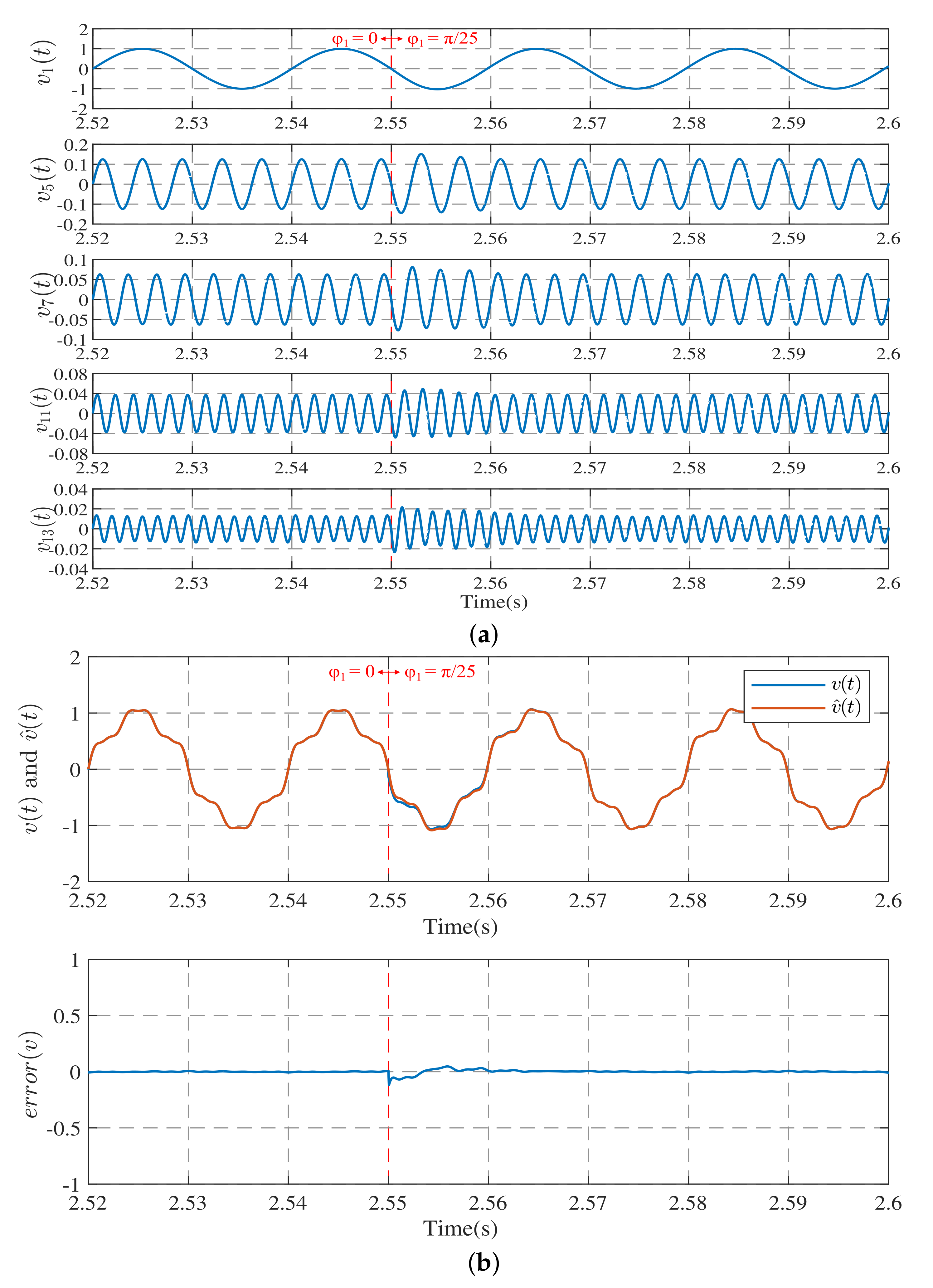
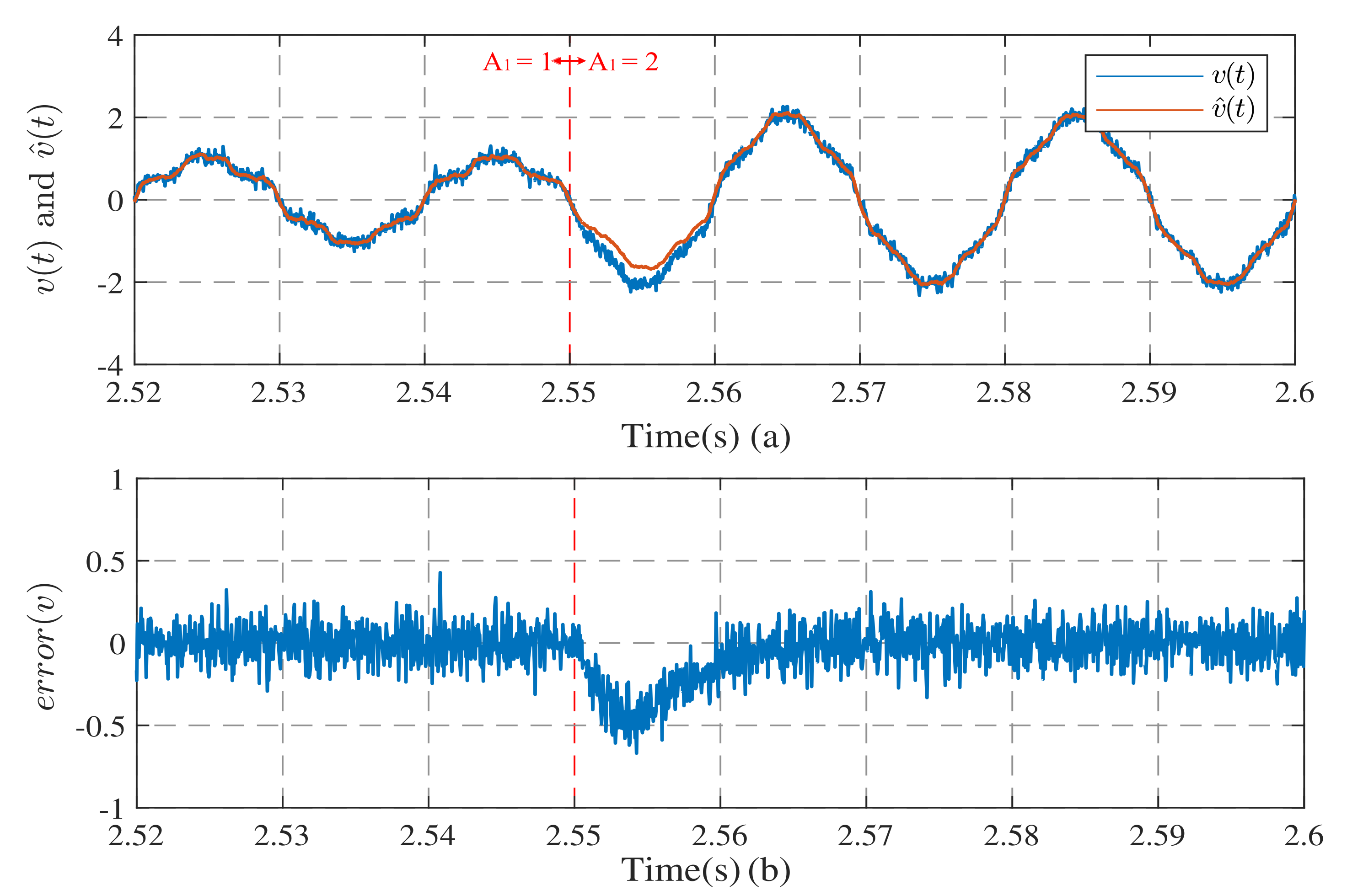
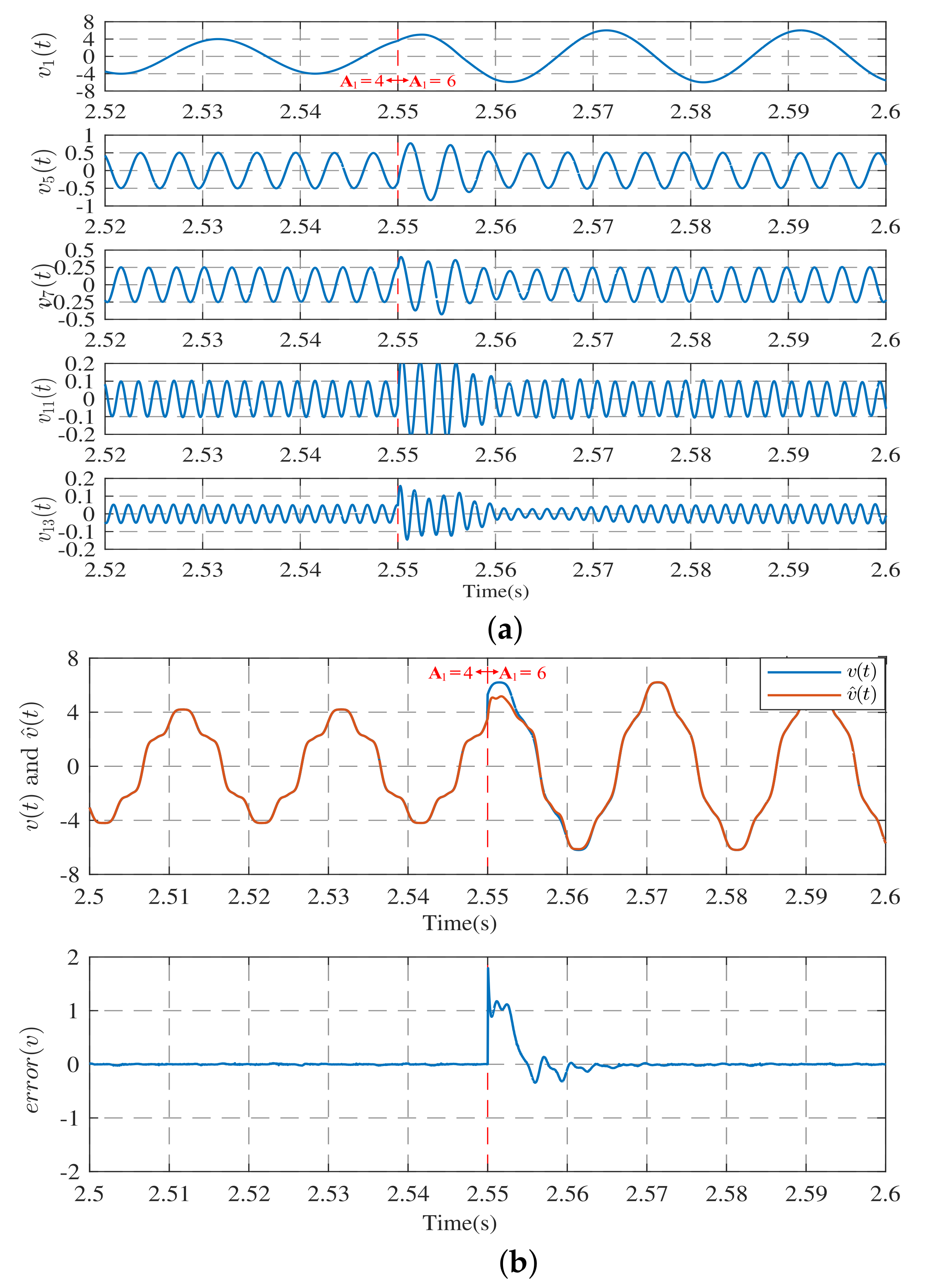
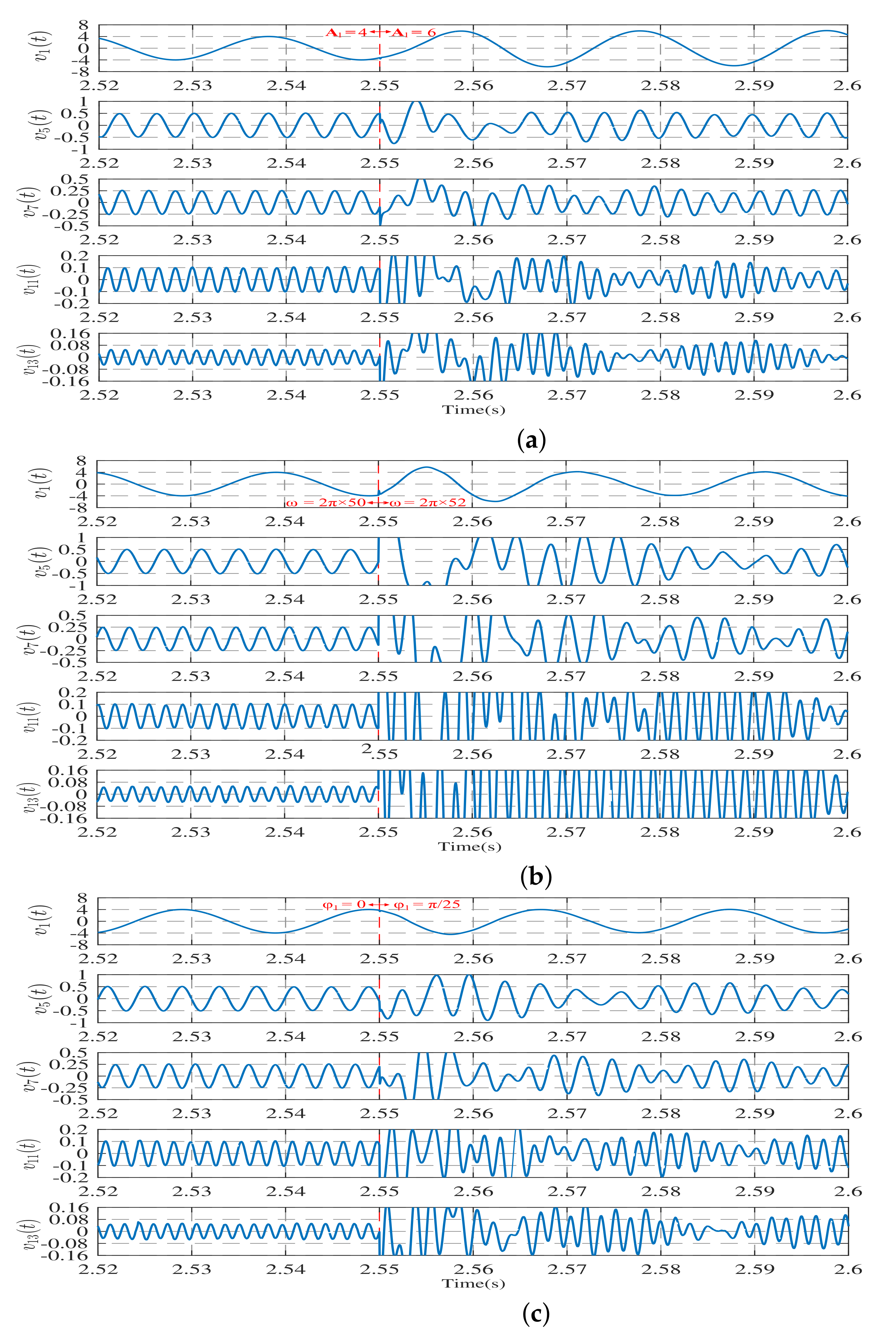
3.1. Simulation of Harmonic Observation Models
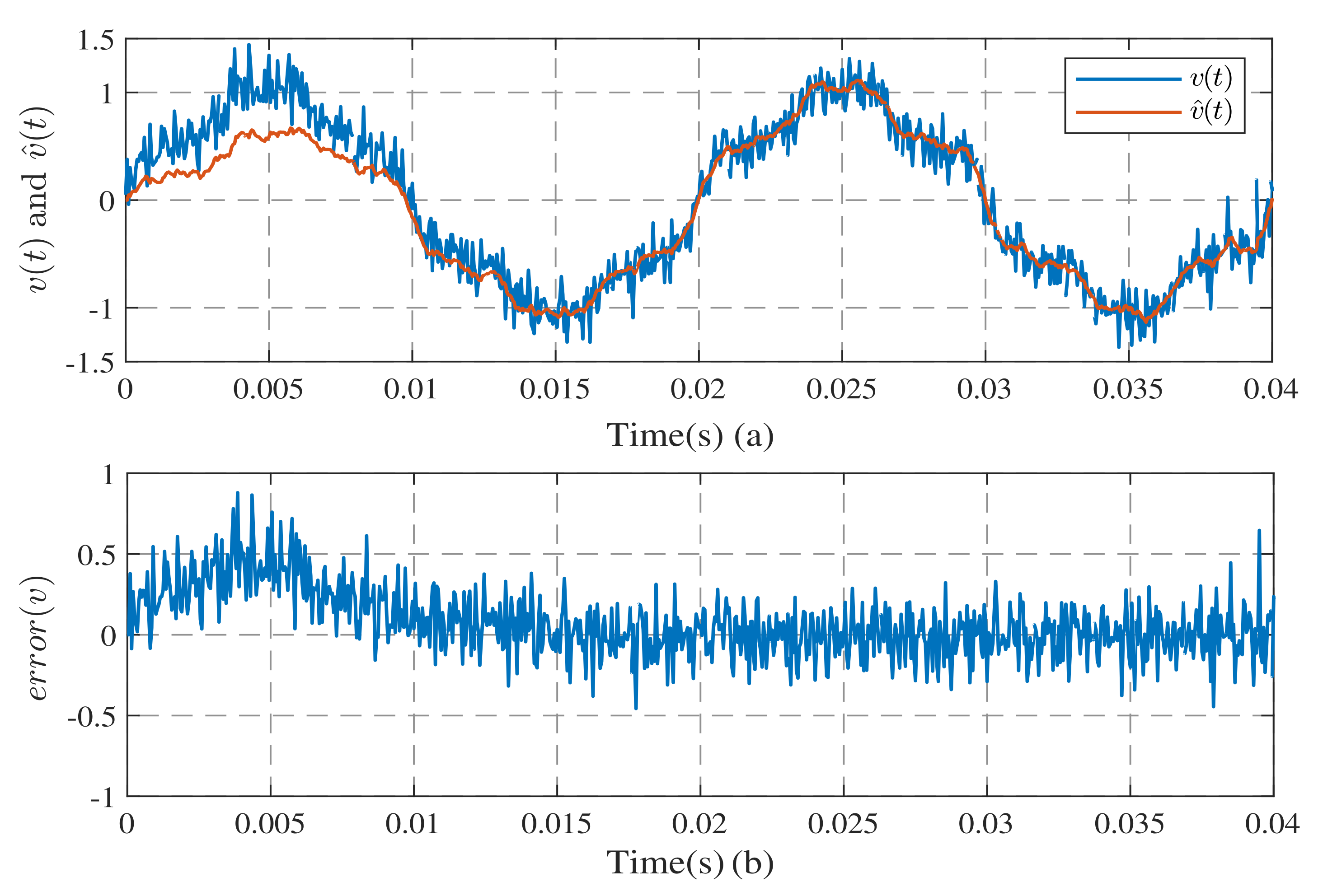
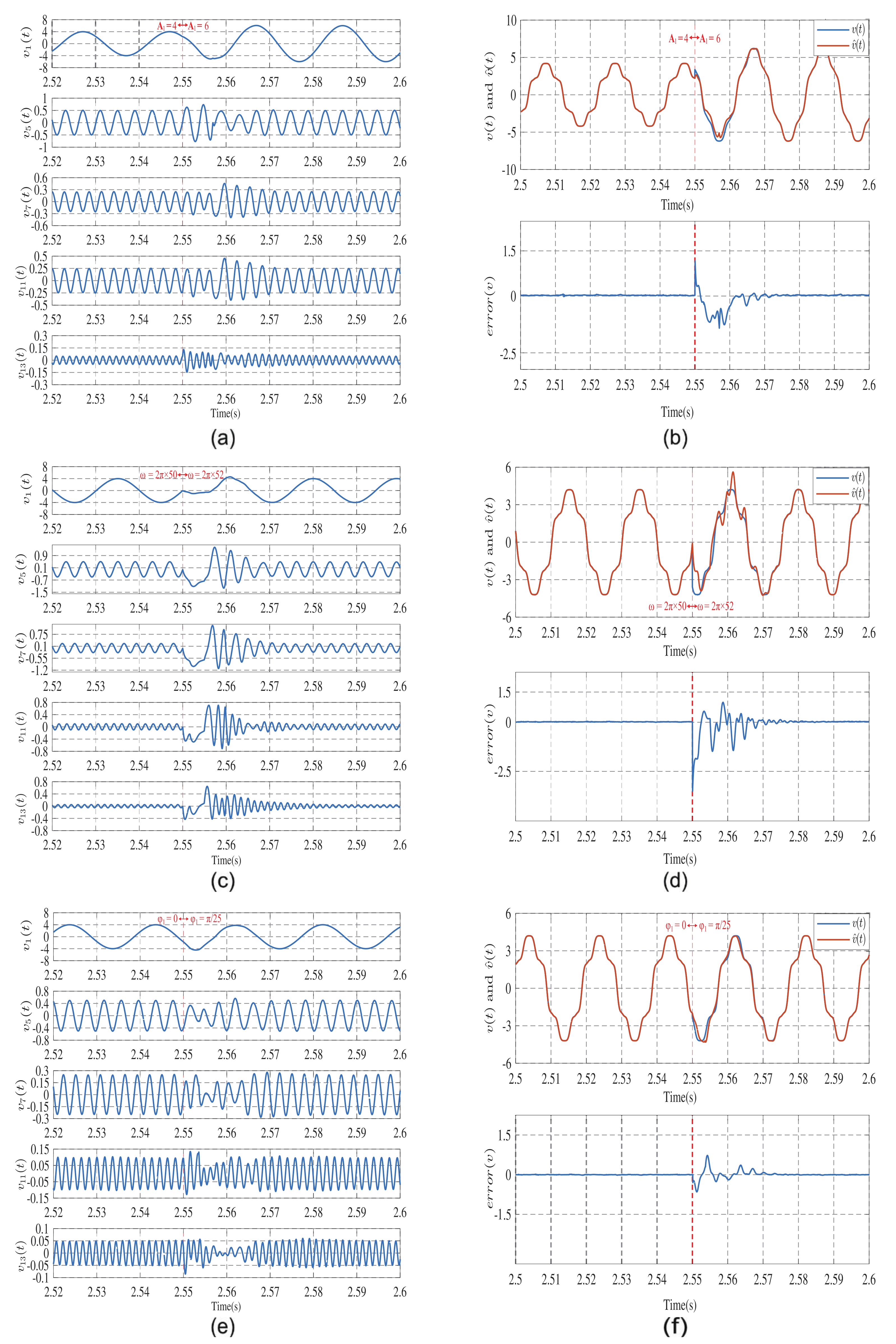
3.2. Simulation of the Harmonic Observation System with Frequency Estimation
3.3. Comparison with Other Methods
3.3.1. Comparison with FFT
3.3.2. Comparison with 3CS Frequency Estimation Method
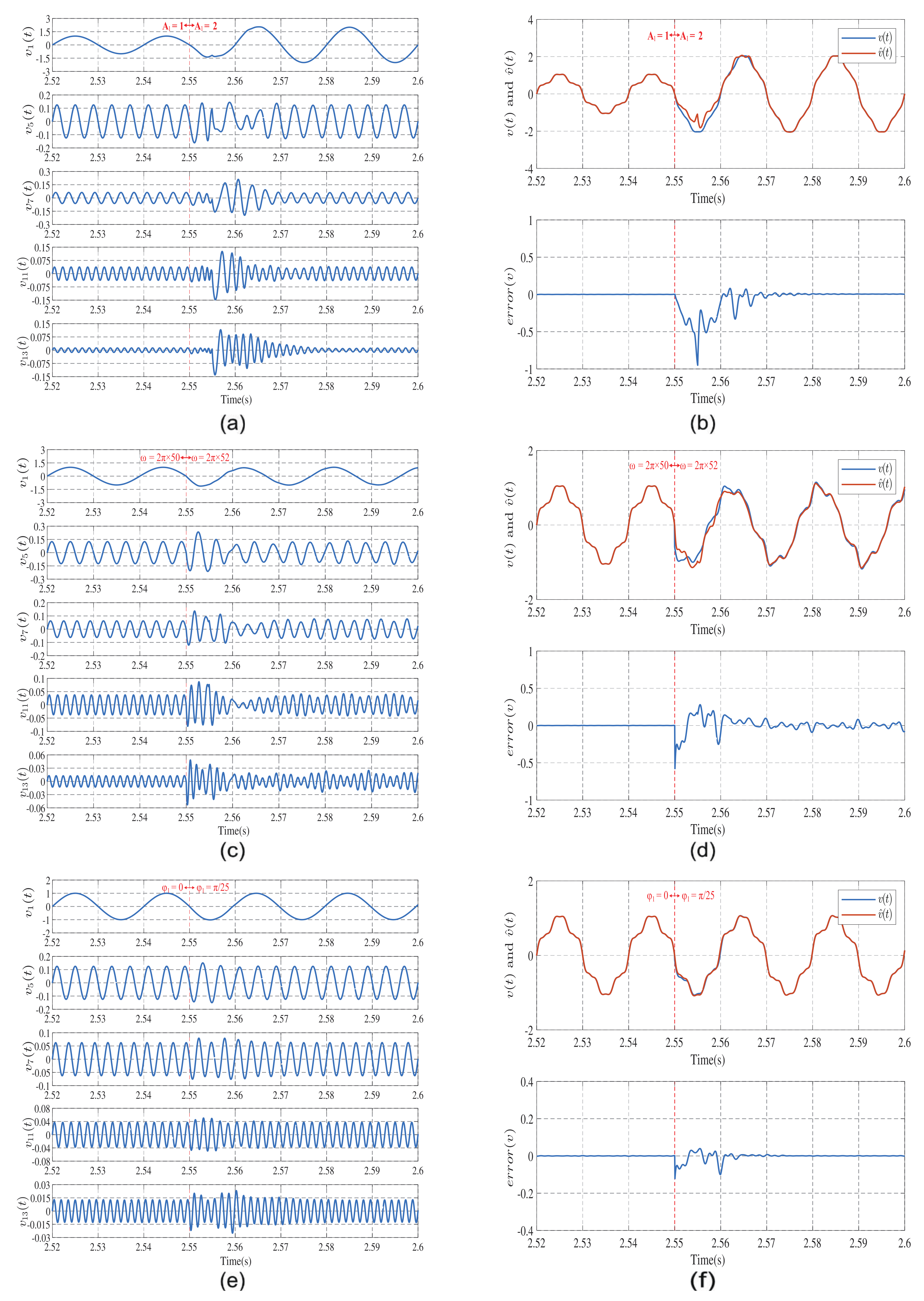
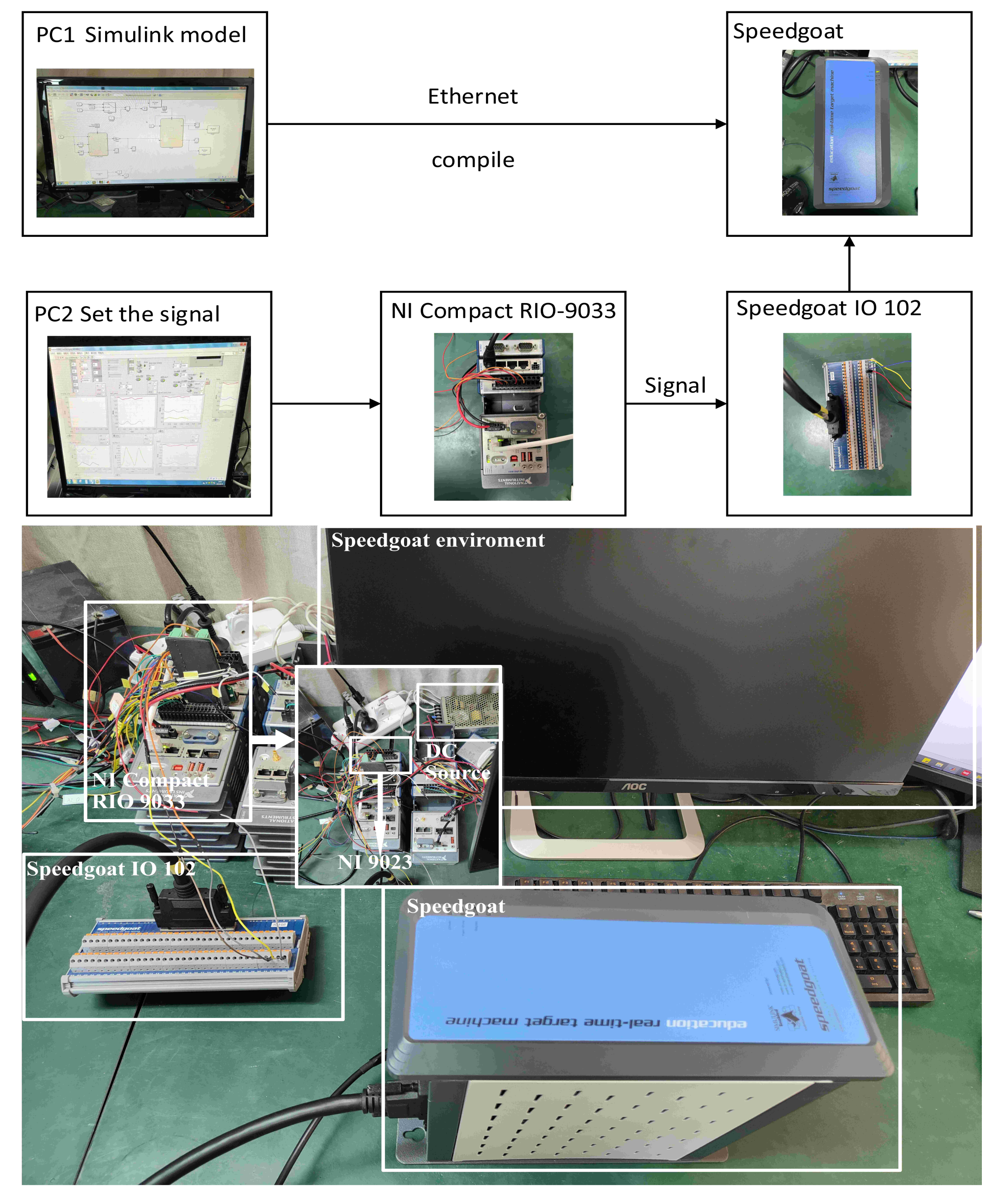
4. Experiment
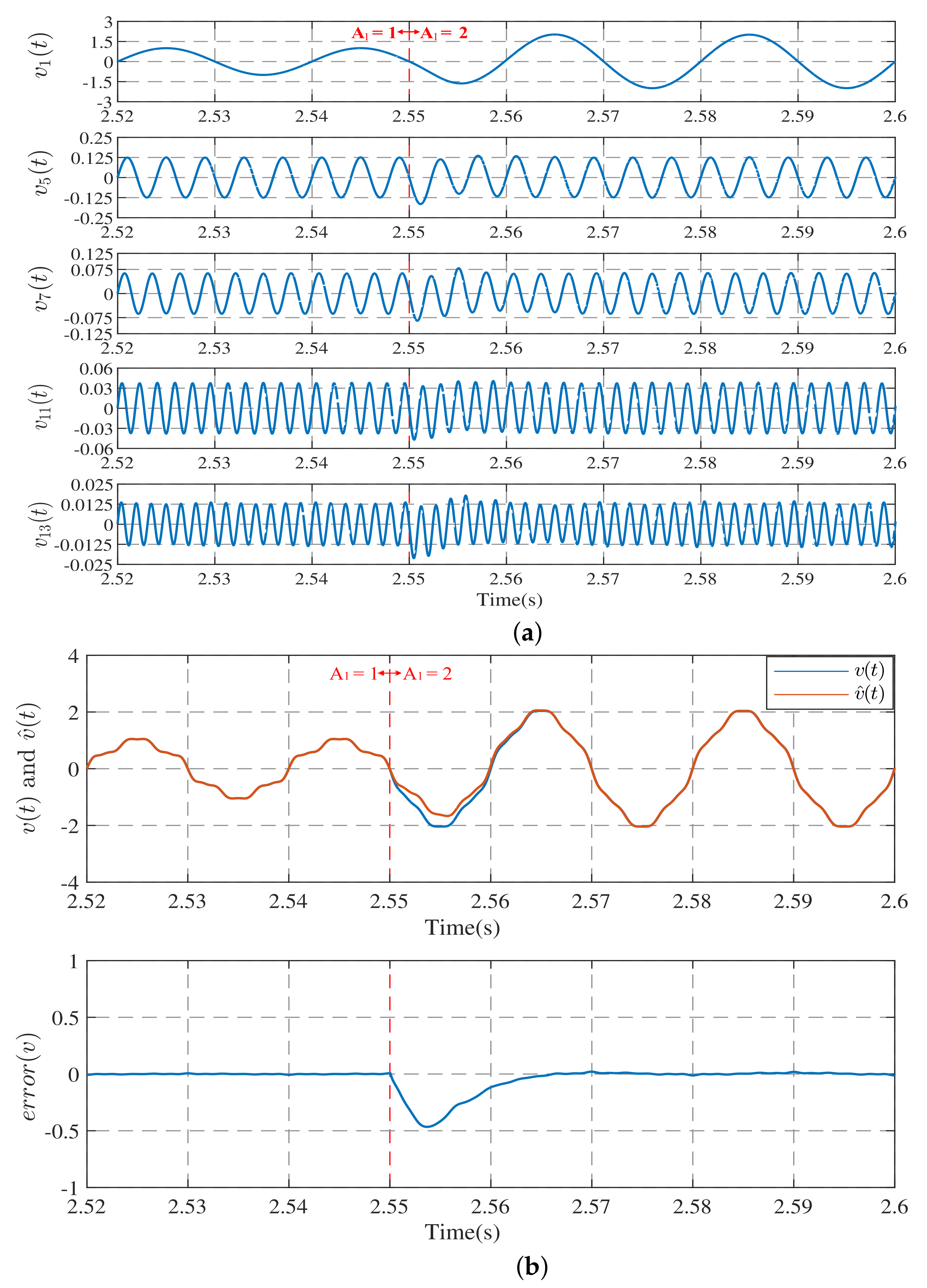
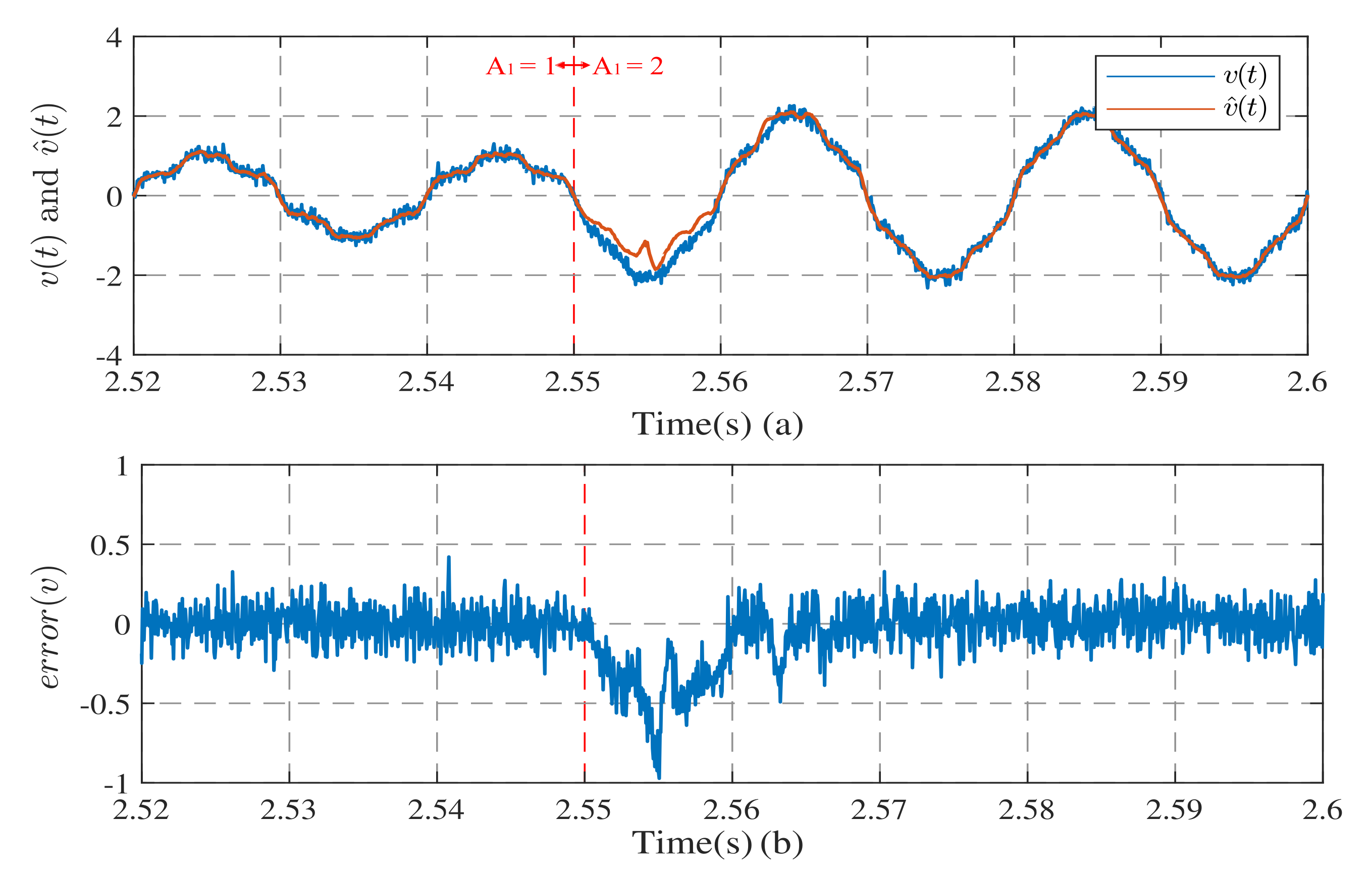
4.1. Experiment on a Harmonic Observation System with Frequency Estimation
4.2. Comparison with Other Methods
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| SOGI | Second-Order Generalized Integration |
| RCP | Rapid Control Prototype |
| FFT | Fast Fourier Transform |
| WT | Wavelet transform |
| DFT | Discrete Fourier Transform |
| KF | Kalman filter |
| DC | Direct Current |
| LMS | Least Mean Square |
| RMS | Root Mean Square |
| SNR | Signal–Noise Ratio |
| 3CS | Thee-Consecutive-Sample |
References
- Ujile, A.; Ding, Z. A dynamic approach to identification of multiple harmonic sources in power distribution systems. Int. J. Electr. Power Energy Syst. 2016, 81, 175–183. [Google Scholar] [CrossRef]
- Shi, J.; Liu, Z. Harmonic Detection Technology for Power Grids Based on Adaptive Ensemble Empirical Mode Decomposition. IEEE Access 2021, 9, 21218–21226. [Google Scholar] [CrossRef]
- Shi, H.; Li, Y.; Jiang, Z.; Zhang, J. Comprehensive power quality evaluation method of microgrid with dynamic weighting based on CRITIC. Meas. Control. 2021, 54, 1097–1104. [Google Scholar] [CrossRef]
- Jain, S.K.; Singh, S.N. Harmonics estimation in emerging power system: Key issues and challenges. Electr. Power Syst. Res. 2011, 81, 1754–1766. [Google Scholar] [CrossRef]
- Eskandarian, N.; Beromi, Y.A.; Farhangi, S. Improvement of dynamic behavior of shunt active power filter using fuzzy instantaneous power theory. J. Power Electron. 2014, 14, 1303–1313. [Google Scholar] [CrossRef]
- Wang, P.; Lu, J.; Shi, L.; Zhang, Y.; Tong, Z.; Wang, N. Method for extracting current envelope for broken rotor bar fault detection of induction motors at time-varying loads. IET Electr. Power Appl. 2019, 14, 1067–1077. [Google Scholar] [CrossRef]
- Akhil Vinayak, B.; Anjali Anand, K.; Jagadanand, G. Wavelet-based real-time stator fault detection of inverter-fed induction motor. IET Electr. Power Appl. 2020, 14, 82–90. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Y.; Zhang, H. Harmonic Detection Method Based on Windowed Double-Spectrum Interpolation FFT. In Proceedings of the 2019 International Conference on Robots & Intelligent System (ICRIS), IEEE, Haikou, China, 15–16 June 2019; pp. 74280–74290. [Google Scholar] [CrossRef]
- Xuming, W.A.N.G.; Kejun, L.E.I.; Yang, X.; Li, M.; Wang, X. Harmonic Analysis Based on Blackman-Harris Self-Multiplication Window. In Proceedings of the 2020 5th Asia Conference on Power and Electrical Engineering (ACPEE), IEEE, Chengdu, China, 4–7 June 2020; pp. 2165–2169. [Google Scholar] [CrossRef]
- Li, C.; An, Q. Harmonic Detection Algorithm Based on Kaiser Window. In Proceedings of the 2020 IEEE Conference on Telecommunications, Optics and Computer Science (TOCS), IEEE, Shenyang, China, 11–13 December 2020; pp. 60–63. [Google Scholar] [CrossRef]
- Wen, H.; Zhang, J.; Yao, W.; Tang, L. LFFT-Based Amplitude Estimation of Power Distribution Systems Signal Distorted by Harmonics and Noise. IEEE Trans. Ind. Inform. 2017, 14, 447–1455. [Google Scholar] [CrossRef]
- Yan, H.; Yin, B.; Gao, M. Harmonic Detection in Electric Power System Using Wavelet Transform and Particle Swarm Optimization. In Proceedings of the 2018 IEEE 4th Information Technology and Mechatronics Engineering Conference (ITOEC), IEEE, Chongqing, China, 14–16 December 2018; pp. 701–704. [Google Scholar] [CrossRef]
- Wang, X.-L.; Wang, W.-B. Harmonic signal extraction from noisy chaotic interference based on synchrosqueezed wavelet transform. Chin. Phys. B 2015, 24, 080203. [Google Scholar] [CrossRef]
- Zhou, X.S.; Chen, G.Z.; Ma, Y.J. A Survey on Detecting Methods for Harmonic of power system. Adv. Mater. Res. 2013, 614, 907–910. [Google Scholar] [CrossRef]
- Sun, S.-G.; Wang, J.-Q.; Shi, S.-Q. Study on real-time detection of harmonics and reactive currents in single phase circuit. Electr. Meas. Instrum. 2008, 45, 4–7. [Google Scholar]
- Guo, J.; Jiang, C.; Guan, C.; Zhang, T.; Pu, J. Modeling and Simulation of Power Grid Voltage Harmonic Detection Method Based on Adaptive Kalman Filter. In Proceedings of the 2021 33rd Chinese Control and Decision Conference (CCDC), Kunming, China, 22–24 May 2021; pp. 6166–6172. [Google Scholar] [CrossRef]
- Cherif, H.; Benakcha, A.; Laib, I.; Chehaidia, S.E.; Menacer, A.; Soudan, B.; Olabi, A.G. Early detection and localization of stator inter-turn faults based on discrete wavelet energy ratio and neural networks in induction motor. Energy 2020, 212, 118684. [Google Scholar] [CrossRef]
- Ibrahim, W.A.; Morcos, M.M. Artificial intelligence and advanced mathematical tools for power quality applications: A survey. IEEE Trans. Power Deliv. 2002, 17, 668–673. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhen, Z.; Cui, J.; Wang, Y. Harmonic Detection for Harmonic/Inter-Harmonic Based on Improved Glowworm Swarm Optimization and Neural Network. IEEJ Trans. Electr. Electron. Eng. 2020, 15, 1769–1779. [Google Scholar] [CrossRef]
- Selvajyothi, K.; Janakiraman, P.A. Extraction of harmonics using composite observers. IEEE Trans. Power Deliv. 2007, 23, 31–40. [Google Scholar] [CrossRef]
- Li, P.; Jin, W.; Li, R.; Guan, M. Harmonics detection via input observer with grid frequency fluctuation. Int. J. Electr. Power Energy Syst. 2020, 115, 105461. [Google Scholar] [CrossRef]
- Xu, M.; Sang, Z.; Li, X.; You, Y.; Dai, D. An Observer-Based Harmonic Extraction Method with Front SOGI. Machines 2022, 10, 95. [Google Scholar] [CrossRef]
- Wen, X.Y.; Wang, Z.; Zhang, W. K; Sun, J.G. Research on harmonic extraction method based on pairwise observer. Control. Decis. Mak. 2022, 2022, 1–6. [Google Scholar]
- Xu, B.Q.; Li, G.B.A. Study on the Improved Harmonic Current Detecting Method Based on ip—iqCalculating Modes. Adv. Mater. Res. 2012, 433, 6144–6150. [Google Scholar] [CrossRef]
- Xu, Y.; Du, Y.; Cheng, S. A method of de-noise and harmonics detection in power system based on periodicity analysis. MAPAN 2018, 33, 169–177. [Google Scholar] [CrossRef]
- Wang, G.; Wang, X.; Zhao, C. An Iterative Hybrid Harmonics Detection Method Based on Discrete Wavelet Transform and Bartlett–Hann Window. Appl. Sci. 2020, 10, 3922. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, X.; Qi, C. Estimation of electrical harmonic parameters by using the Interpolated FFT algorithm based on Blackman window. J. Zhejiang Univ. Sci. Ed. 2006, 33, 650. [Google Scholar]
- Yilmaz, A.S.; Alkan, A.; Asyali, M.H. Applications of parametric spectral estimation methods on detection of power system harmonics. Electr. Power Syst. Res. 2008, 78, 683–693. [Google Scholar] [CrossRef]
- Yang, J.; Yang, G.; Gao, J.-H. A power harmonic detection method based on Wavelet Neural Network. In Proceedings of the 2009 International Conference on Machine Learning and Cybernetics, Baoding, China, 12–15 July 2009; Volume 6, pp. 3645–3649. [Google Scholar] [CrossRef]
- Sykora, T.; Brettschneider, Z.; Svec, J.; Tlusty, J.; Valouch, V. The Possibility of 3rd Harmonic Filtration. In Proceedings of the 4th International Scientific Symposium on Electric Power Engineering, Stara Lesna, Slovakia, 9–21 September 2007; pp. 494–500. [Google Scholar]
- Roncero-Sanchez, P.; del Toro Garcia, X.; Torres, A.P.; Feliu, V. Robust Frequency-Estimation Method for Distorted and Imbalanced Three-Phase Systems Using Discrete Filters. IEEE Trans. Power Electron. 2011, 26, 1089–1101. [Google Scholar] [CrossRef]




| SNR(db) | Error Mean | RMS-Error |
|---|---|---|
| 24.06 | −2.158 × | 4.843 × |
| 21.05 | −3.249 × | 6.696 × |
| 19.29 | −4.087 × | 8.137 × |
| 18.04 | −4.793 × | 9.359 × |
| 17.07 | −5.415 × | 1.044 × |
| SNR(db) | Error Mean | RMS-Error |
|---|---|---|
| 24.06 | −2.147 × | 4.852 × |
| 21.05 | −3.237 × | 6.703 × |
| 19.29 | −4.073 × | 8.143 × |
| 18.04 | −4.778 × | 9.364 × |
| 17.07 | −5.399 × | 1.044 × |
| No. | Set Values | FFT | Obverser | Relative Error |
|---|---|---|---|---|
| 1 | 100 | 100 | 100 | 0.000% |
| 5 | 12.5 | 12.532 | 12.532 | 0.252% |
| 7 | 6.25 | 6.2413 | 6.2391 | −0.175% |
| 11 | 3.75 | 3.7590 | 3.7521 | 0.056% |
| 13 | 1.25 | 1.2475 | 1.2430 | −0.563% |
| SNR(db) | Error Mean of 3CS | RMS-Error of 3CS |
|---|---|---|
| 24.06 | 1.331 × | 4.933 × |
| 21.05 | 1.266 × | 6.795 × |
| 19.29 | 2.657 × | 8.241 × |
| 18.04 | 3.234 × | 9.459 × |
| 17.07 | 2.819 × | 1.054 × |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Z.; Xu, M.; Li, P.; Wang, Q. Rapid Harmonic Detection Scheme Based on Expanded Input Observer. Electronics 2022, 11, 2860. https://doi.org/10.3390/electronics11182860
Zhu Z, Xu M, Li P, Wang Q. Rapid Harmonic Detection Scheme Based on Expanded Input Observer. Electronics. 2022; 11(18):2860. https://doi.org/10.3390/electronics11182860
Chicago/Turabian StyleZhu, Zuoping, Maoguang Xu, Po Li, and Qiuyu Wang. 2022. "Rapid Harmonic Detection Scheme Based on Expanded Input Observer" Electronics 11, no. 18: 2860. https://doi.org/10.3390/electronics11182860
APA StyleZhu, Z., Xu, M., Li, P., & Wang, Q. (2022). Rapid Harmonic Detection Scheme Based on Expanded Input Observer. Electronics, 11(18), 2860. https://doi.org/10.3390/electronics11182860







