Extended State Observer Based-Backstepping Control for Virtual Synchronous Generator
Abstract
:1. Introduction
- On the basis of the previous investigations, the basic mathematical model of VSG is established according to the extent of the situation.
- With the addition of compensating signals, a nonlinear BSC based on ESO is constructed for the virtual synchronous generator system, enabling system stability in off-grid mode, grid-tied mode, and transition operation.
- ESO is developed to estimate unknown disturbances and ensure tracking of dynamic system errors based on the external disturbances in the system model, allowing the microgrid to operate similarly to the actual operation.
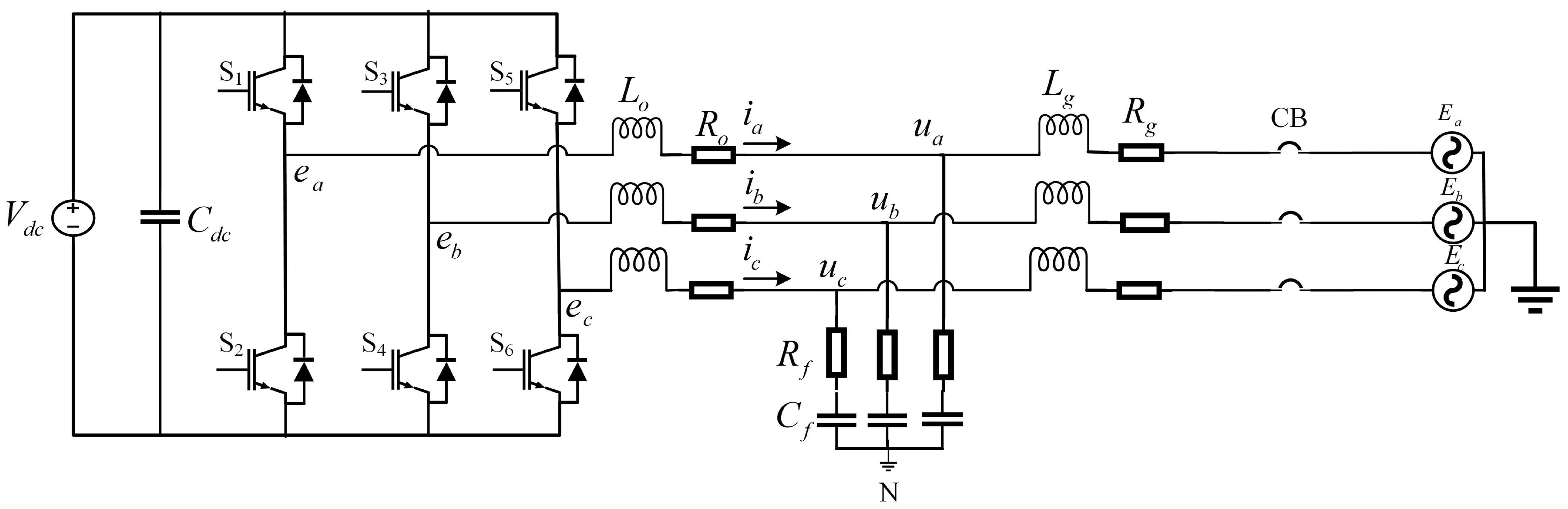
2. System Structure and Modeling
2.1. Mathematical Model of Synchronous Generator
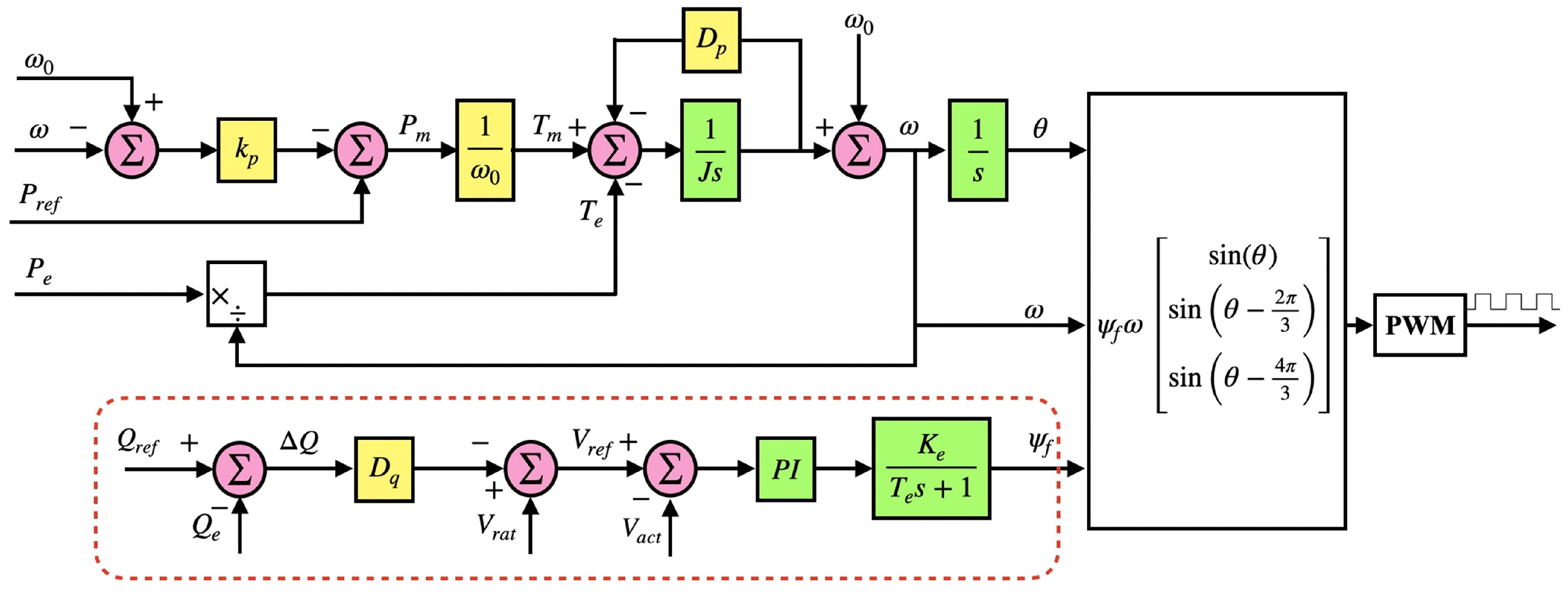
2.2. VSG Proposed Structure
- To mimic the synchronous generator’s flux weakness caused by the DC voltage applied to the rotor’s excitation circuit and the inductance of the rotor coil, which causes the stator to delay.
- A low-pass filter with a time constant can remove and filter high-frequency components of the output signals, which helps with the design of the backstepping controller based on ESO.
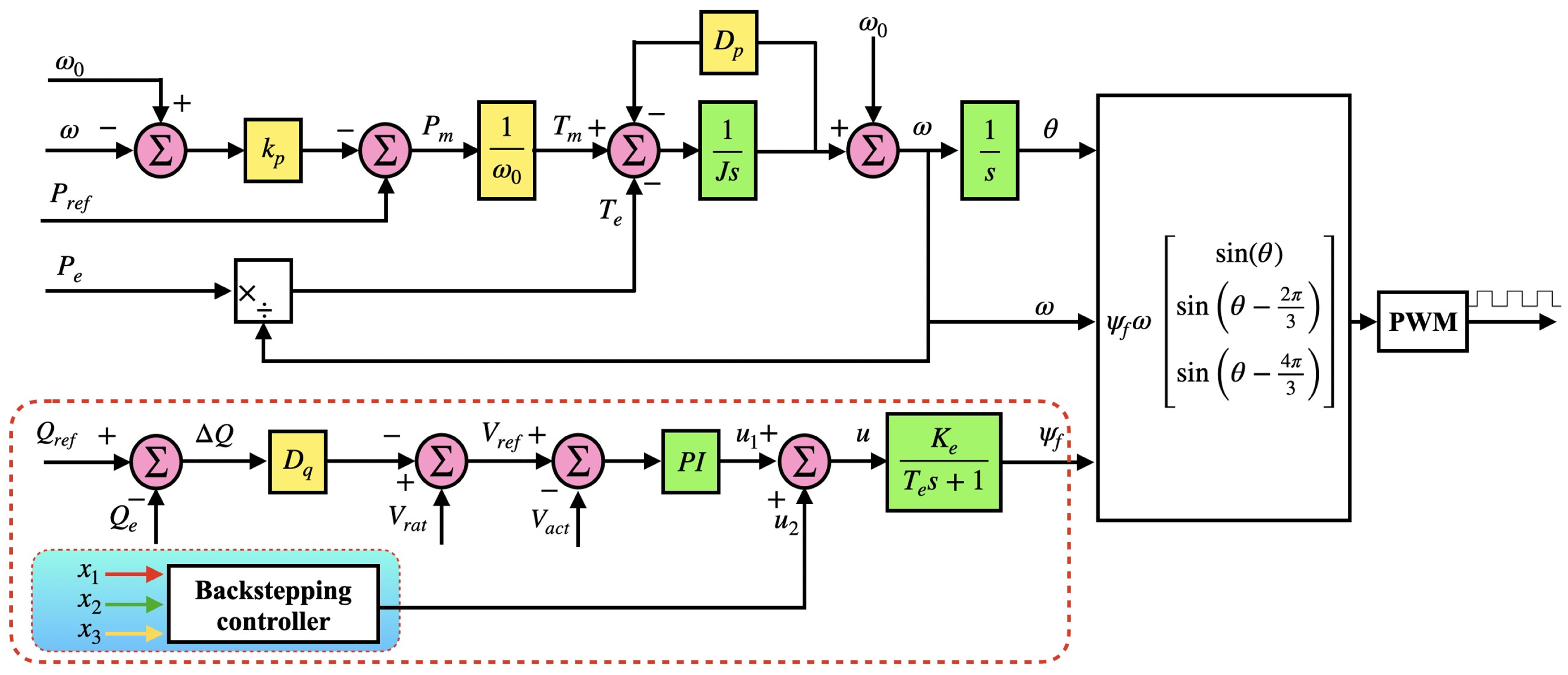
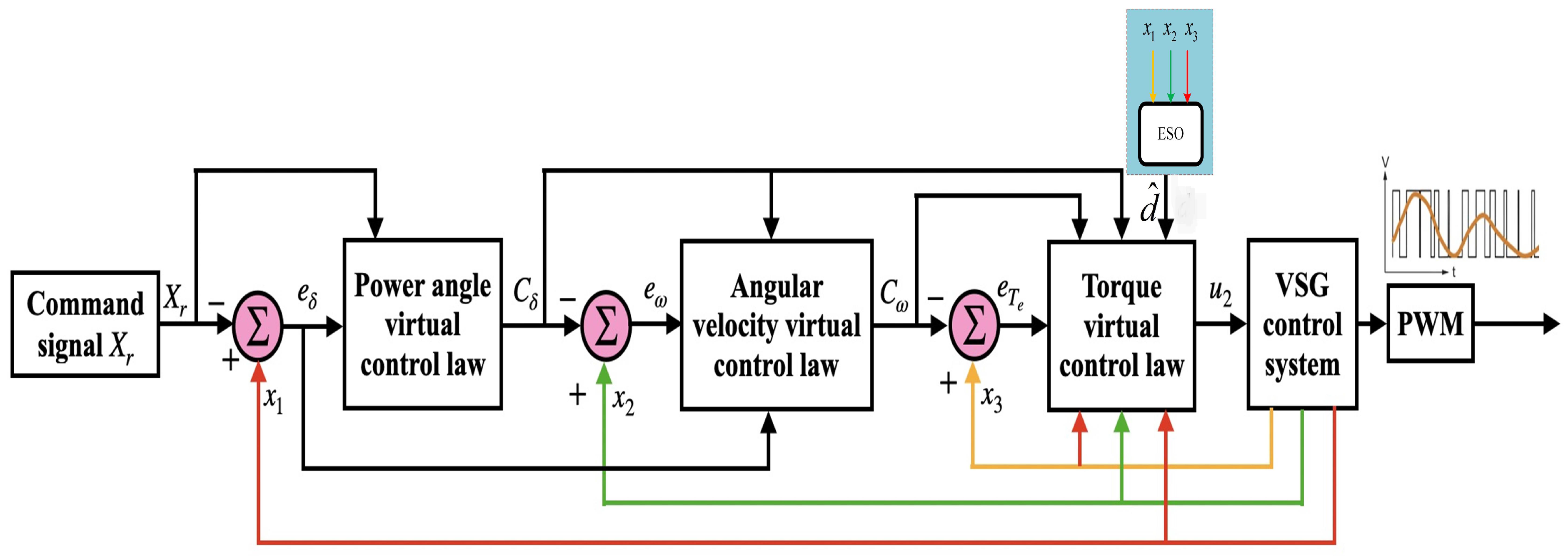
3. Proposed Control Method
3.1. Voltage Control Strategy
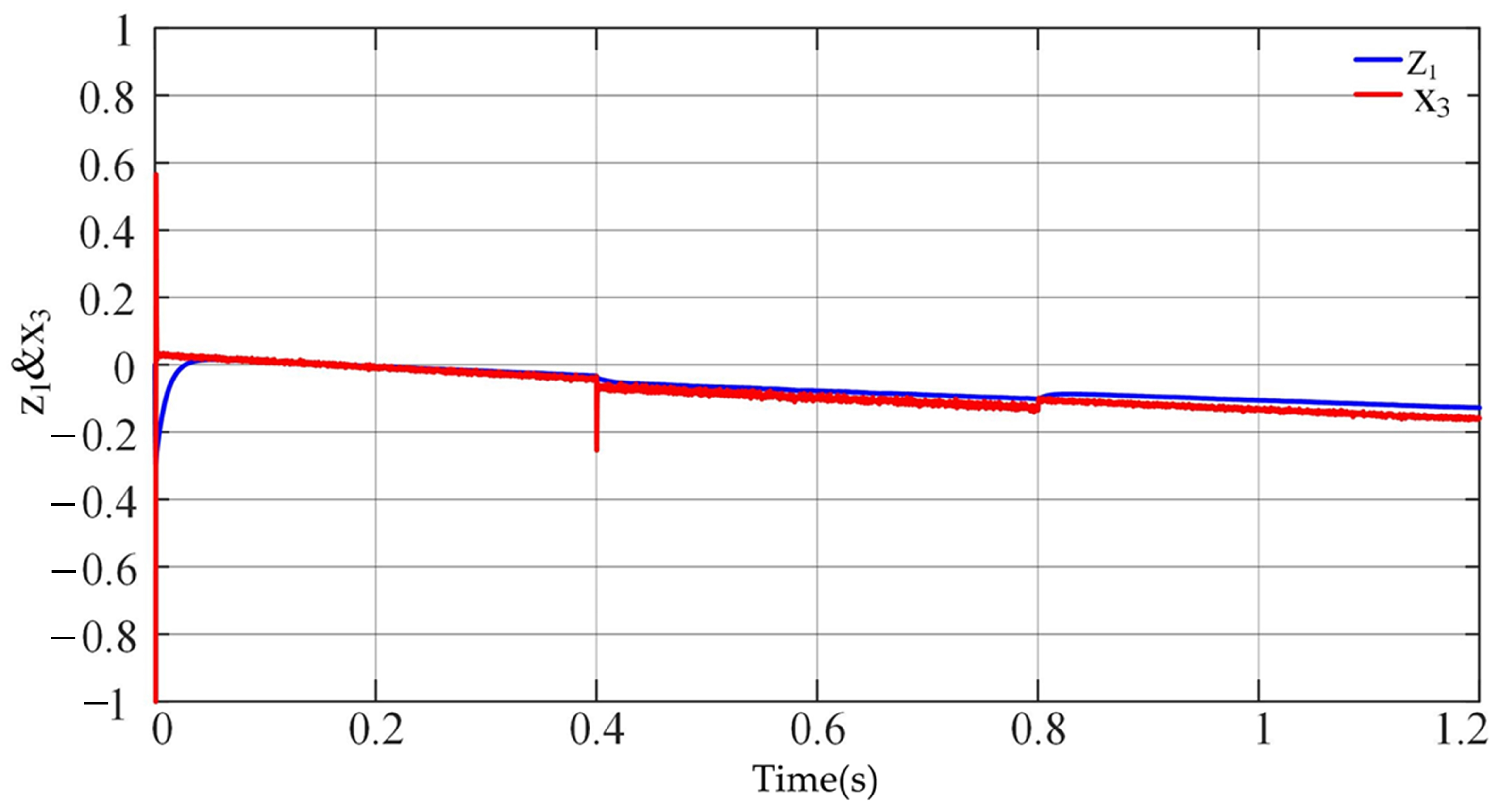
3.2. ESO Observer
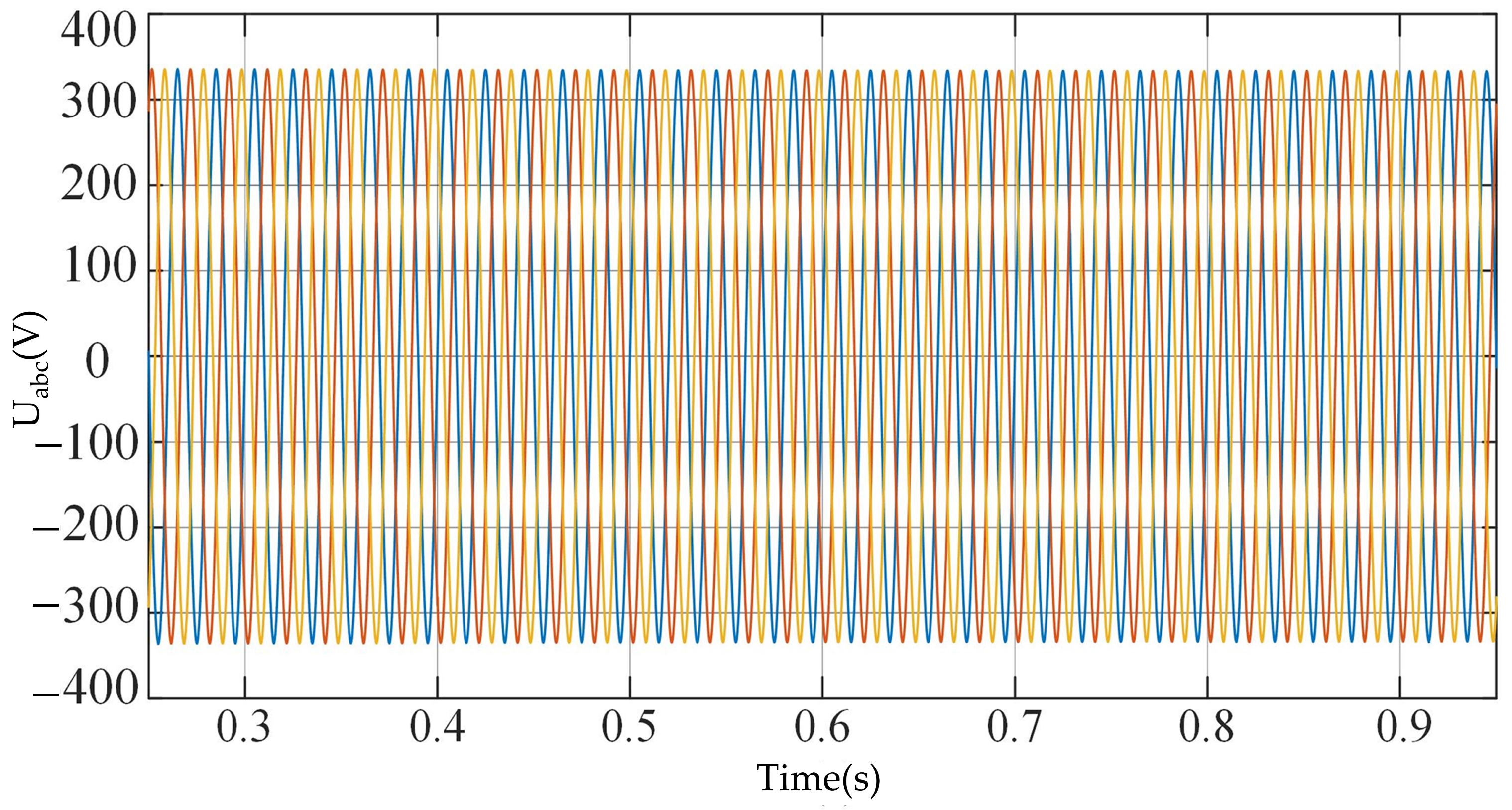
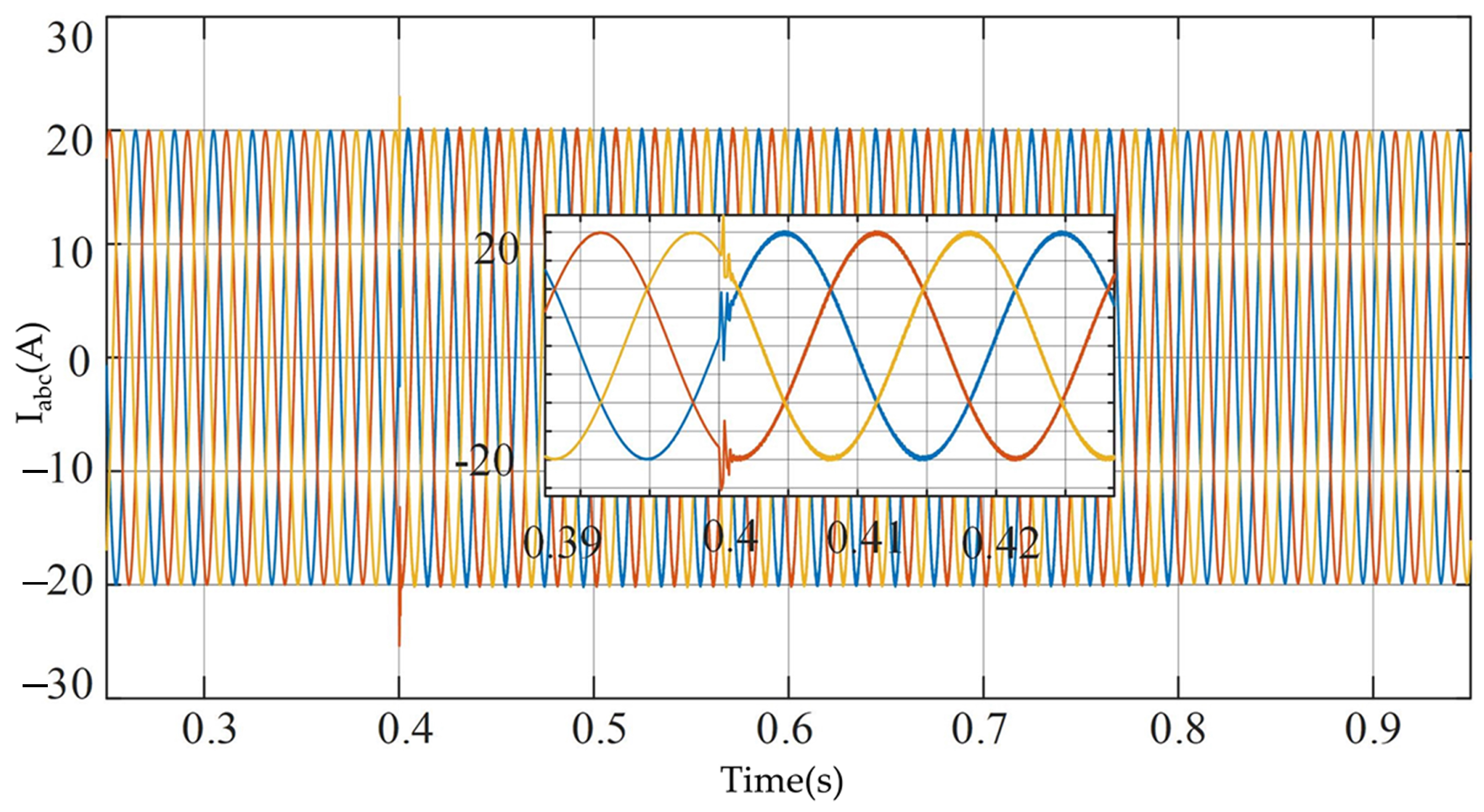
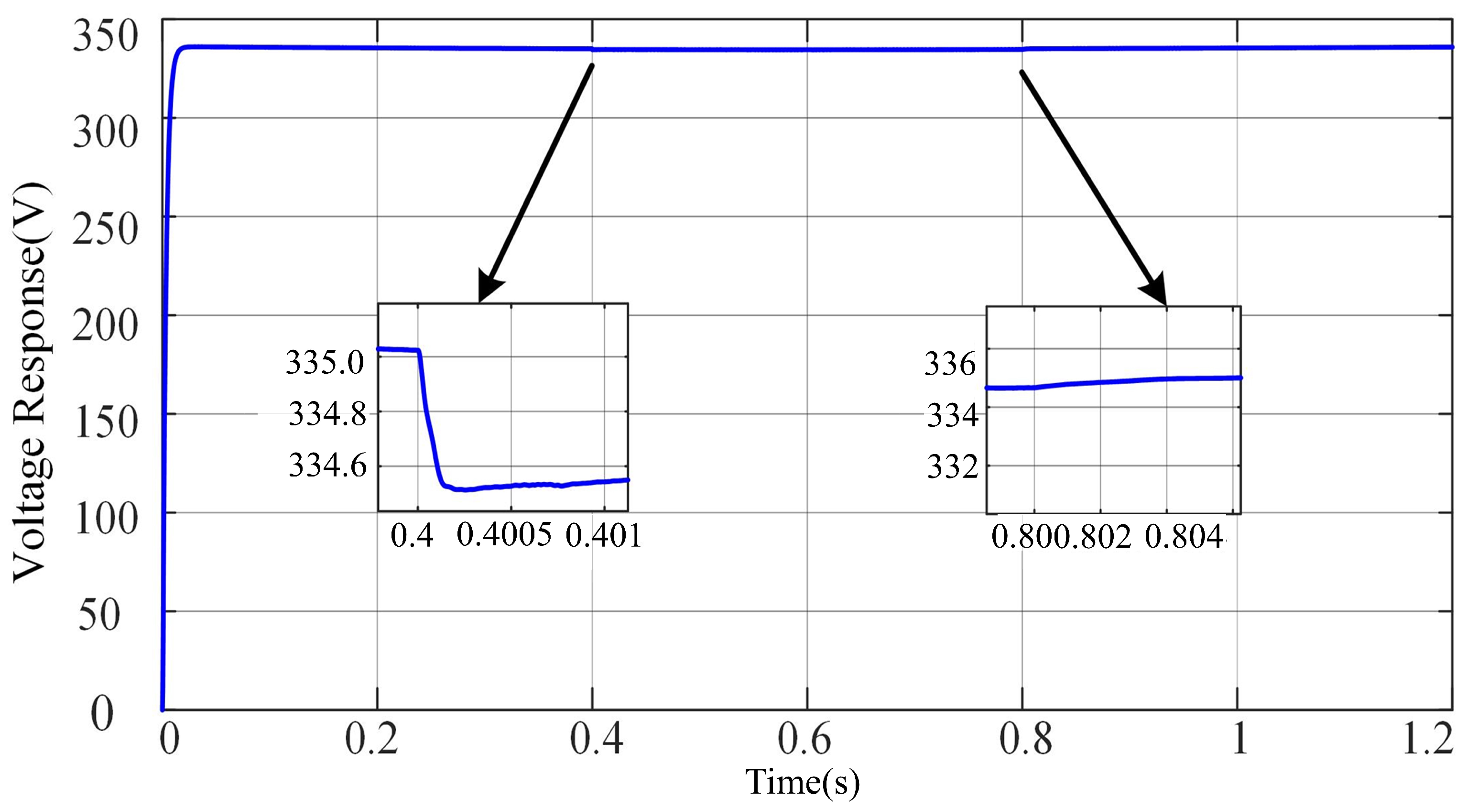
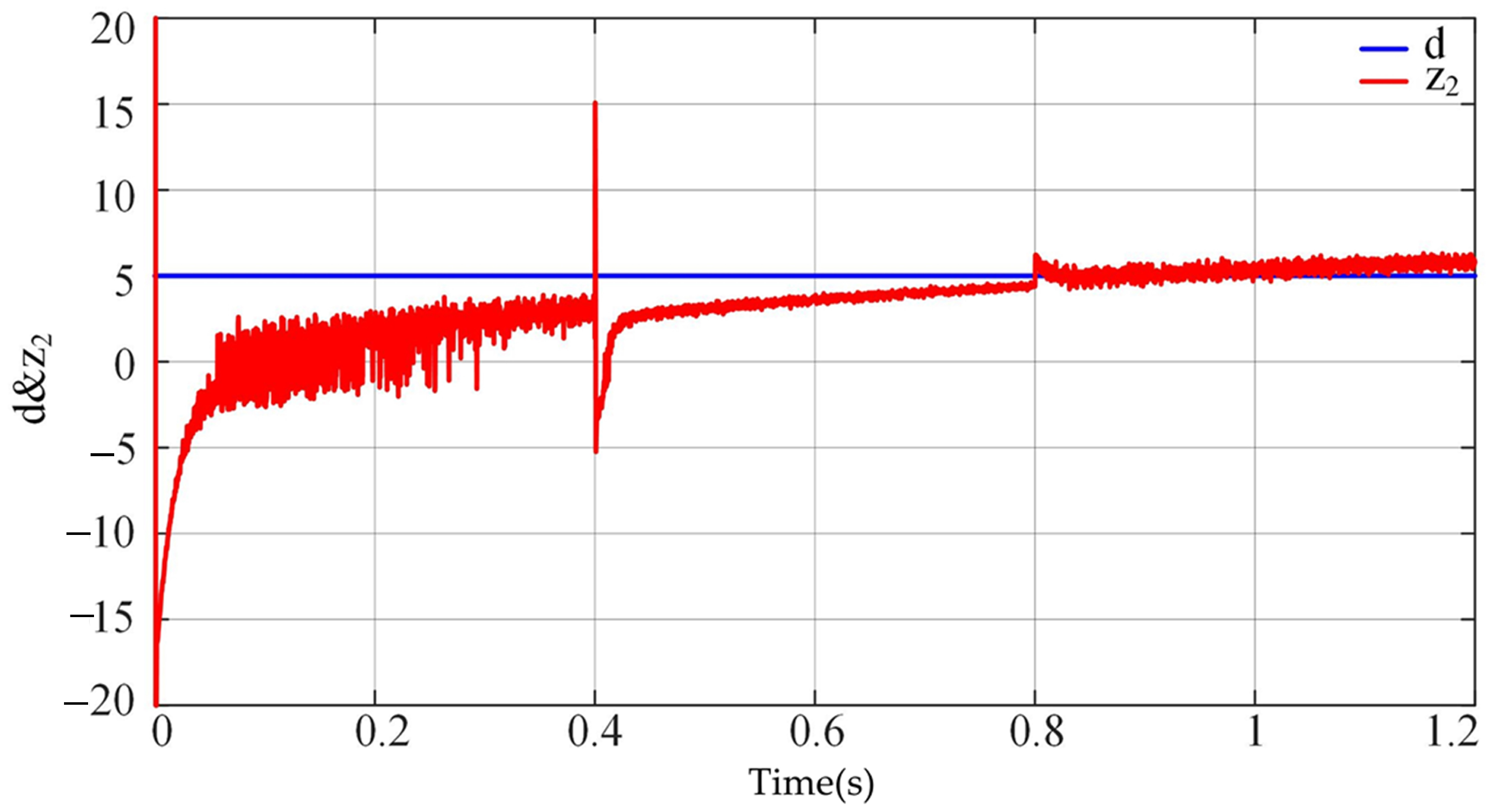
4. Simulation Results
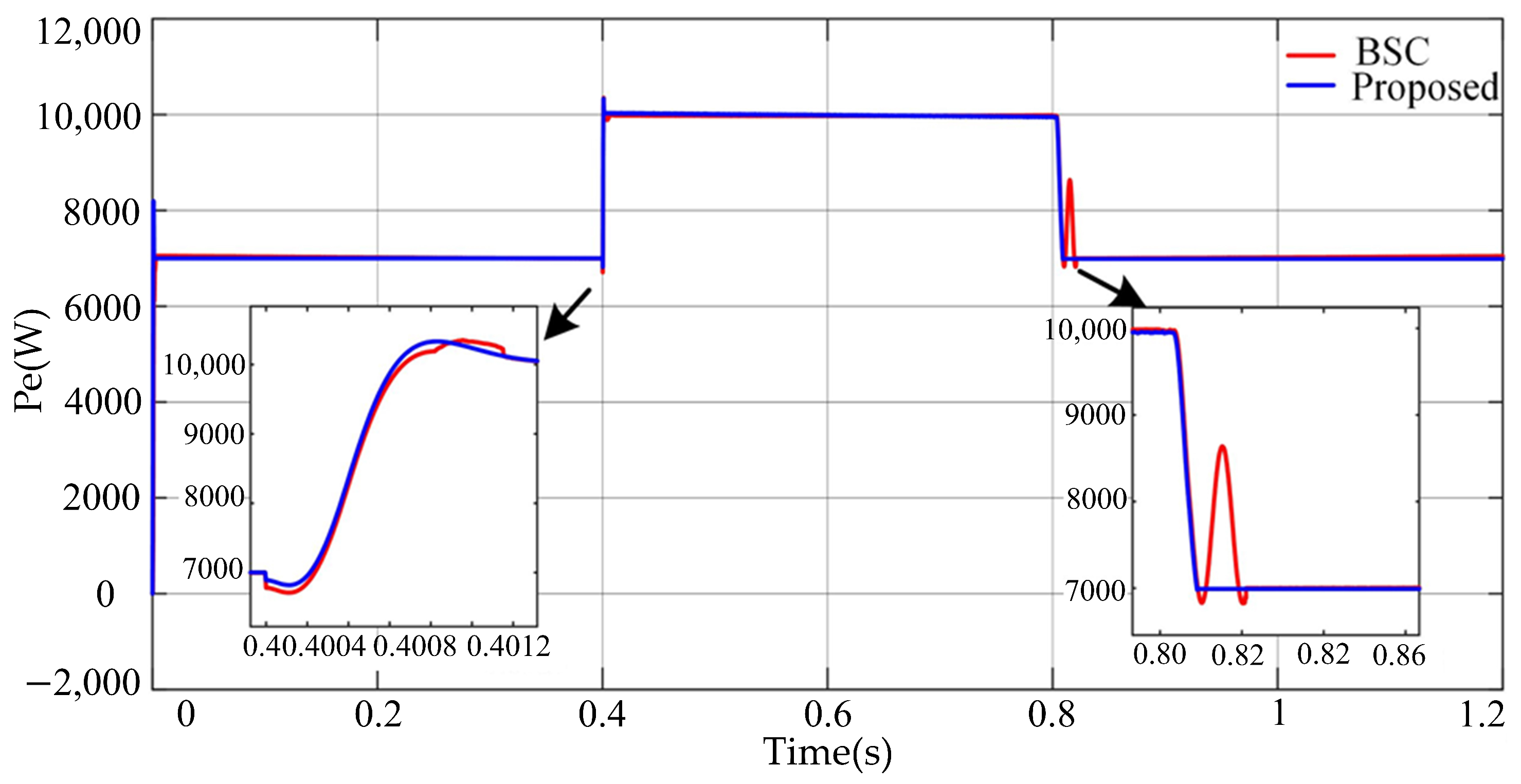
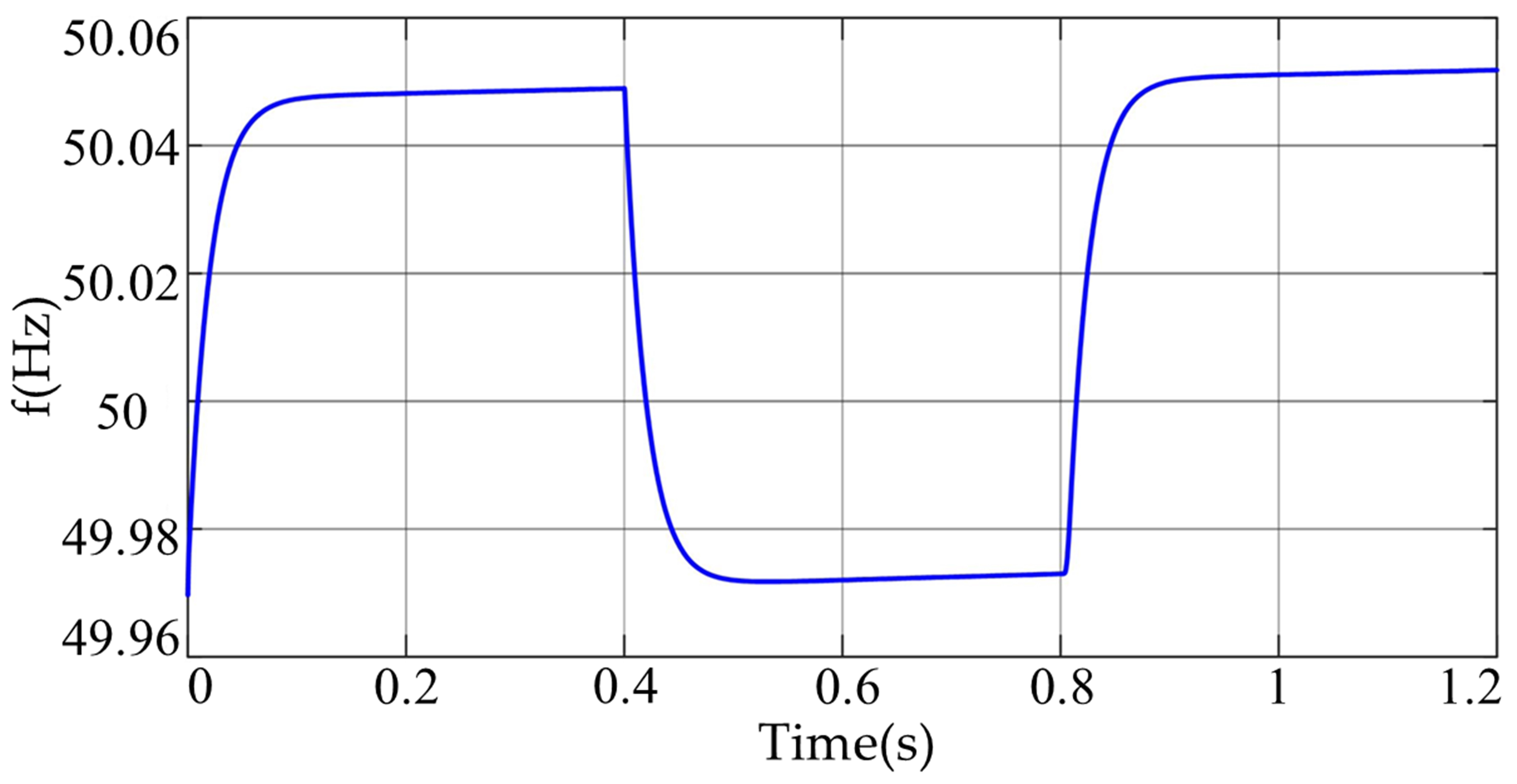
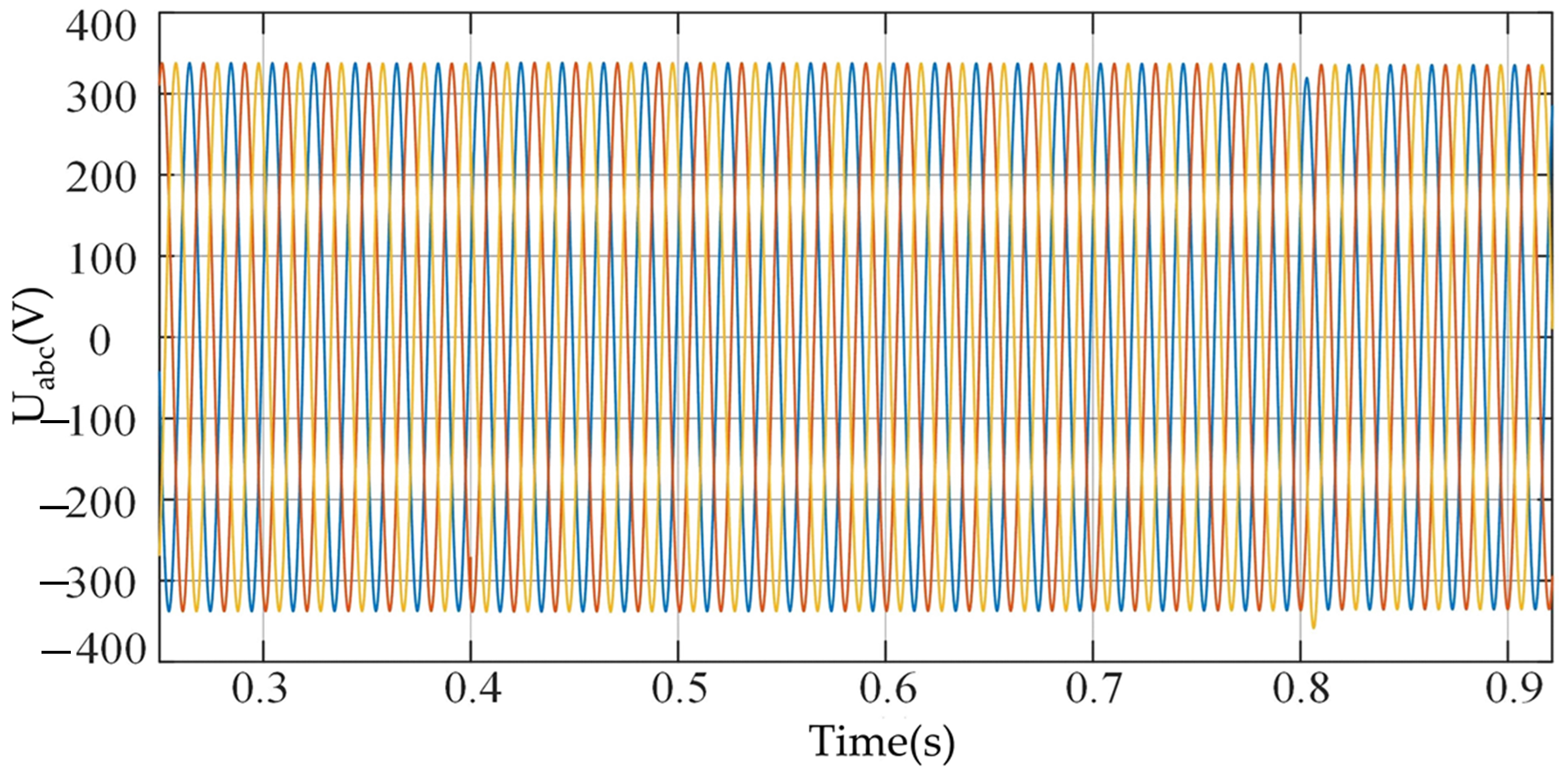
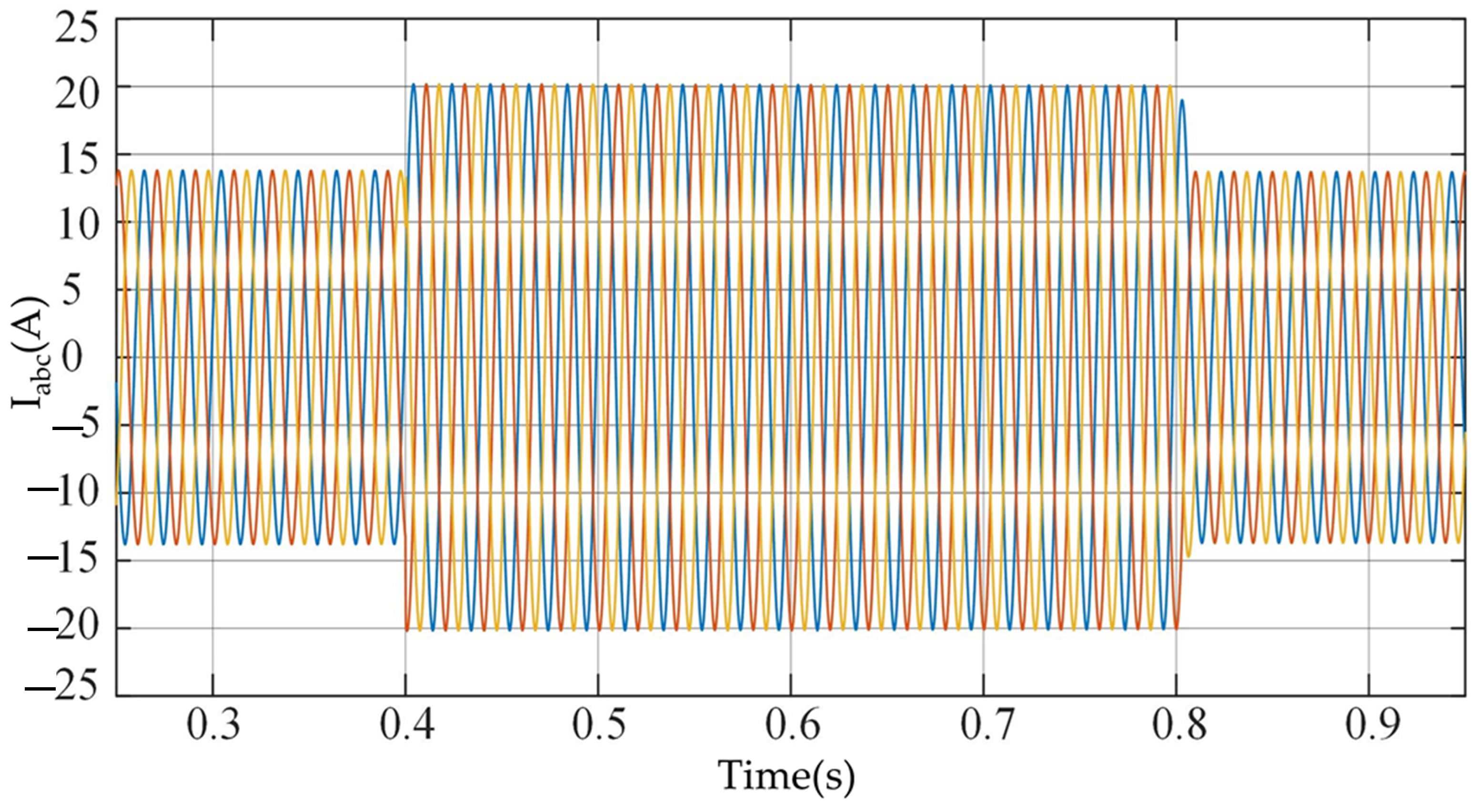
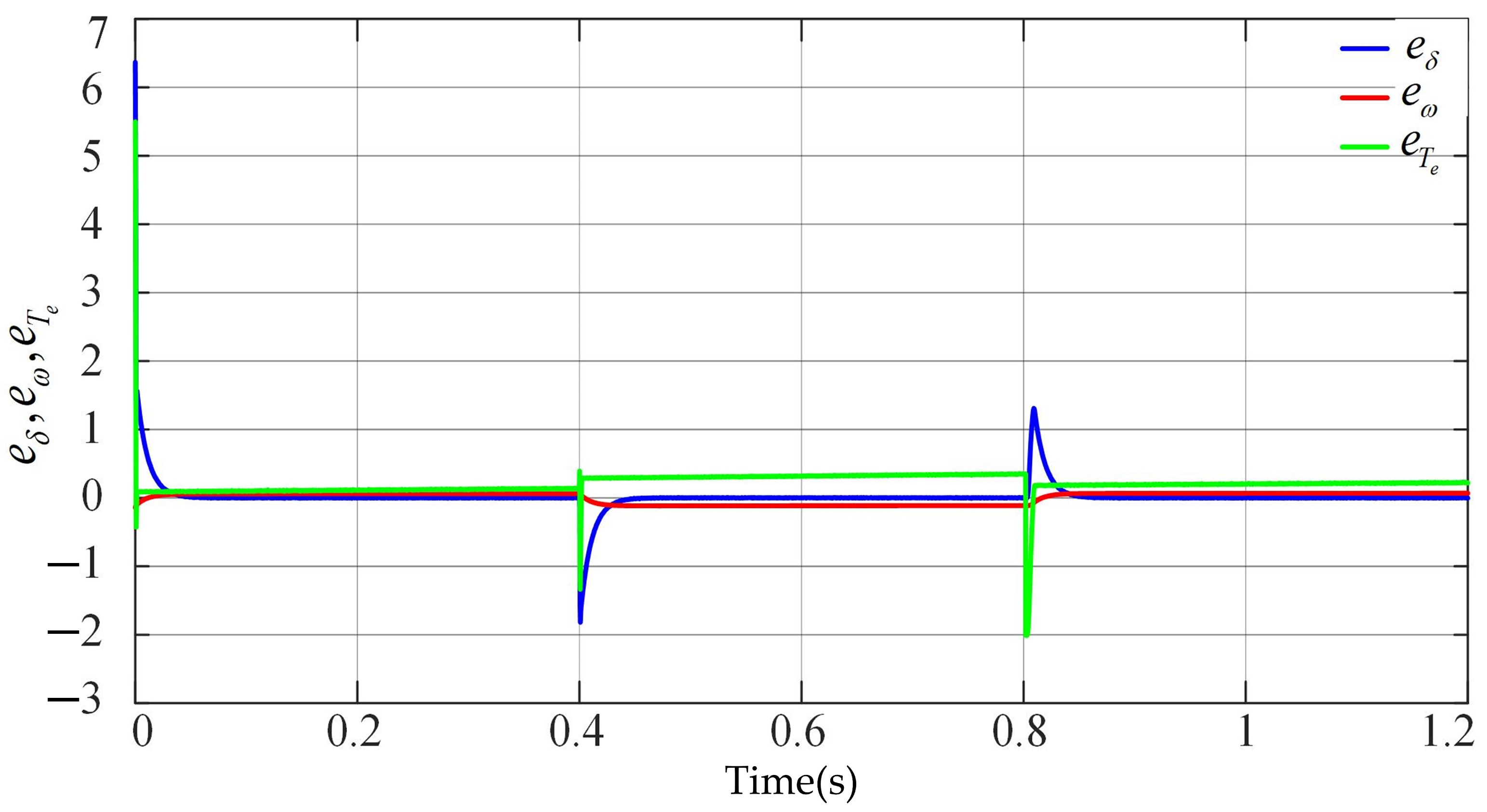
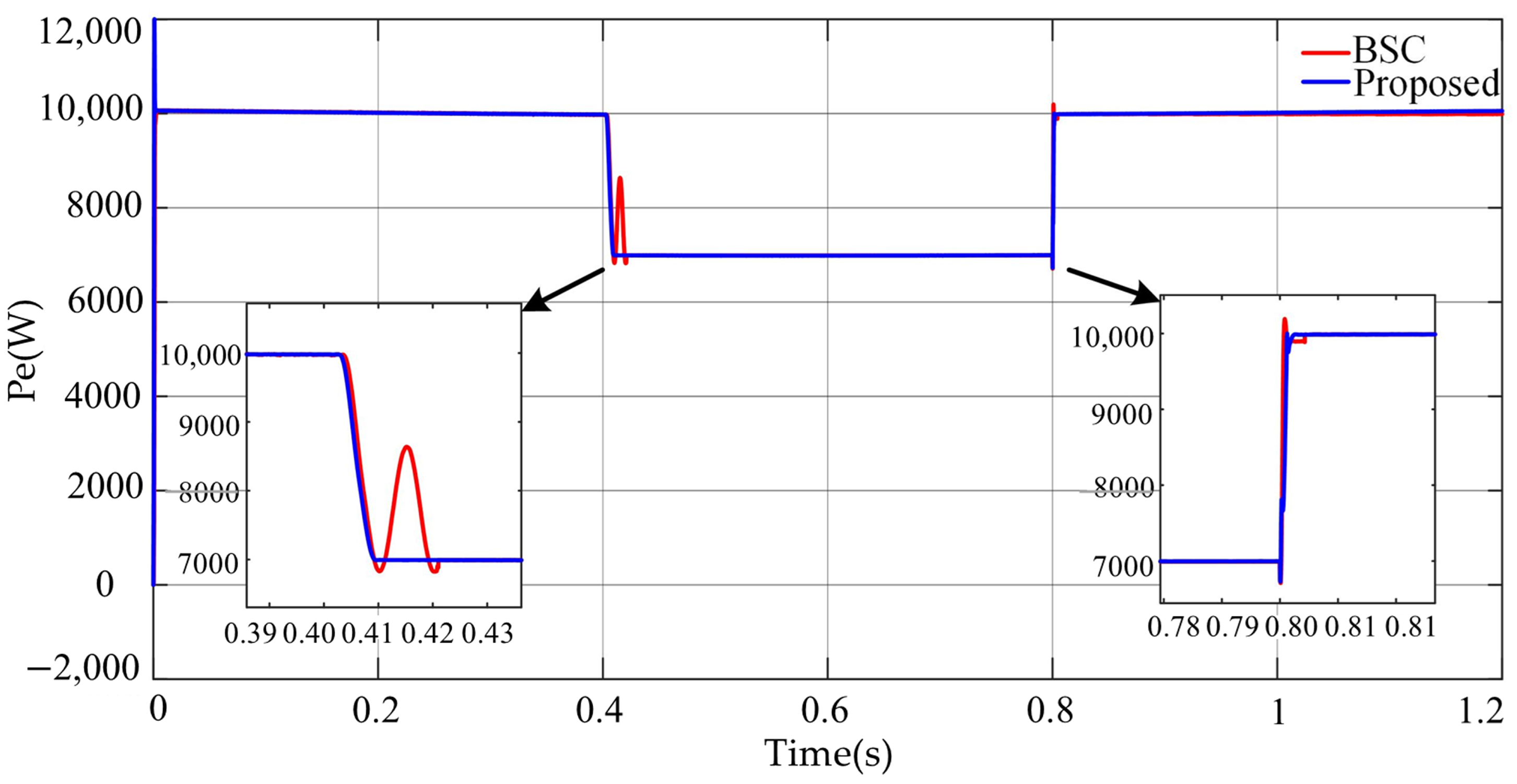
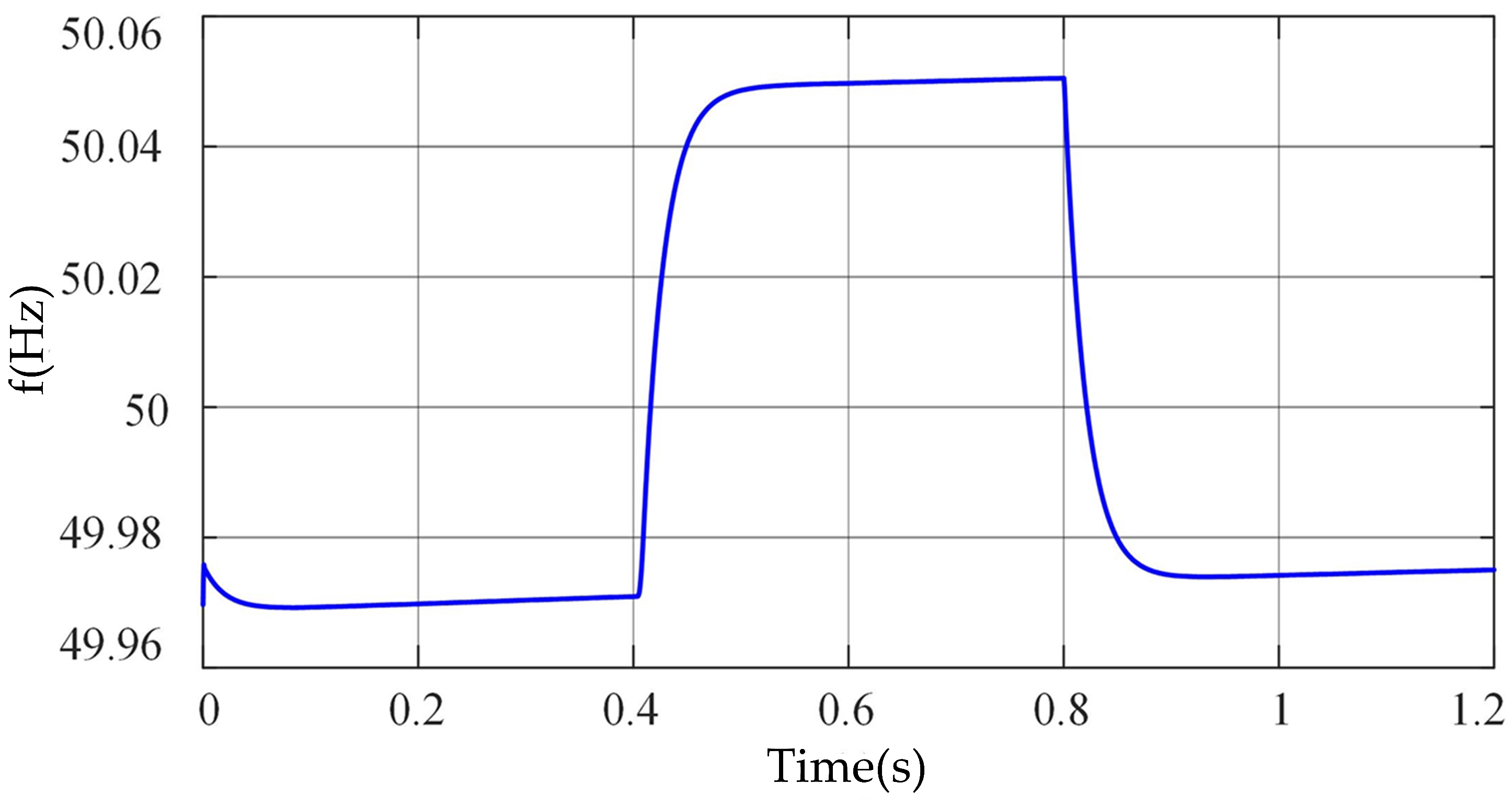
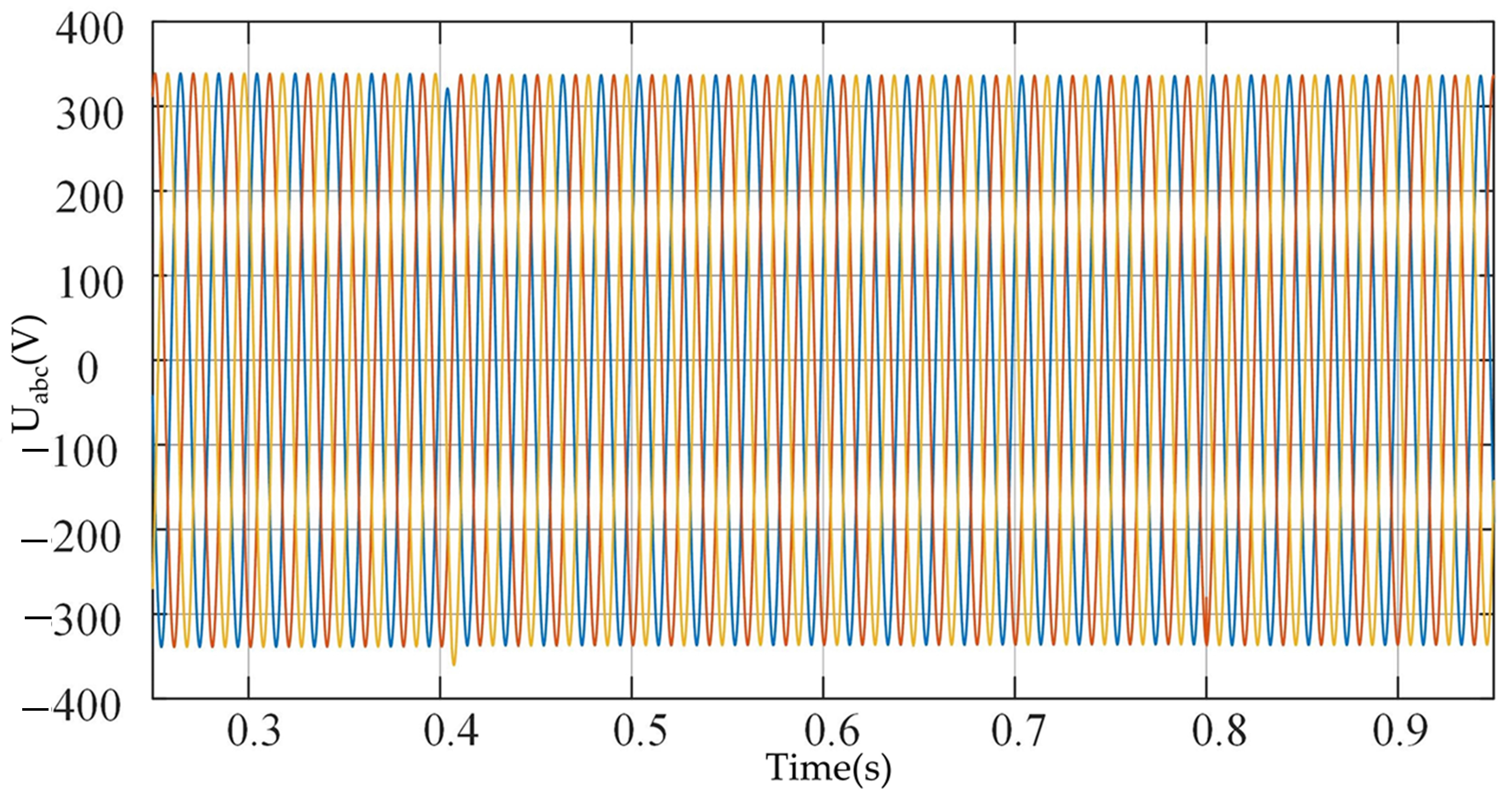
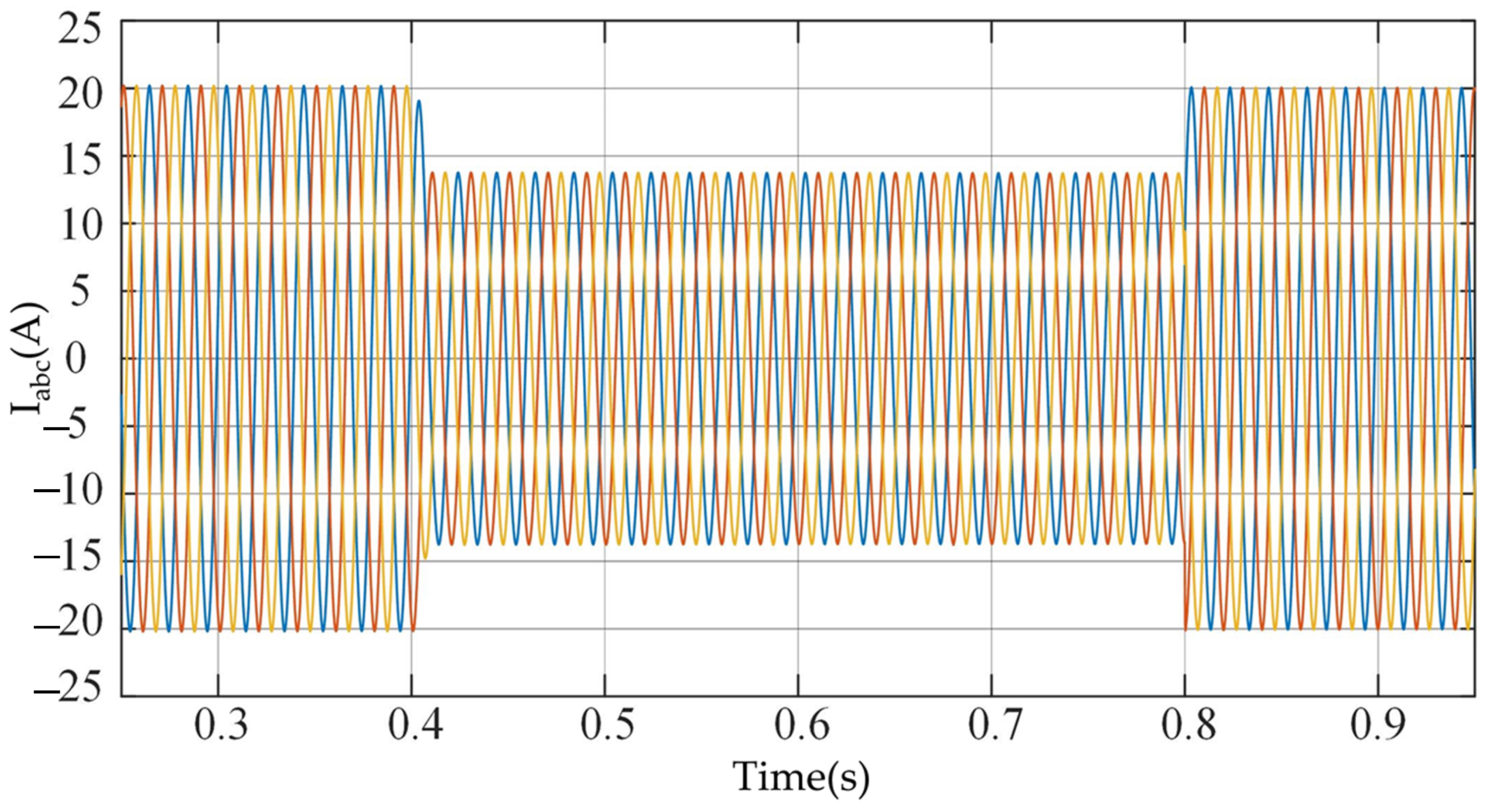
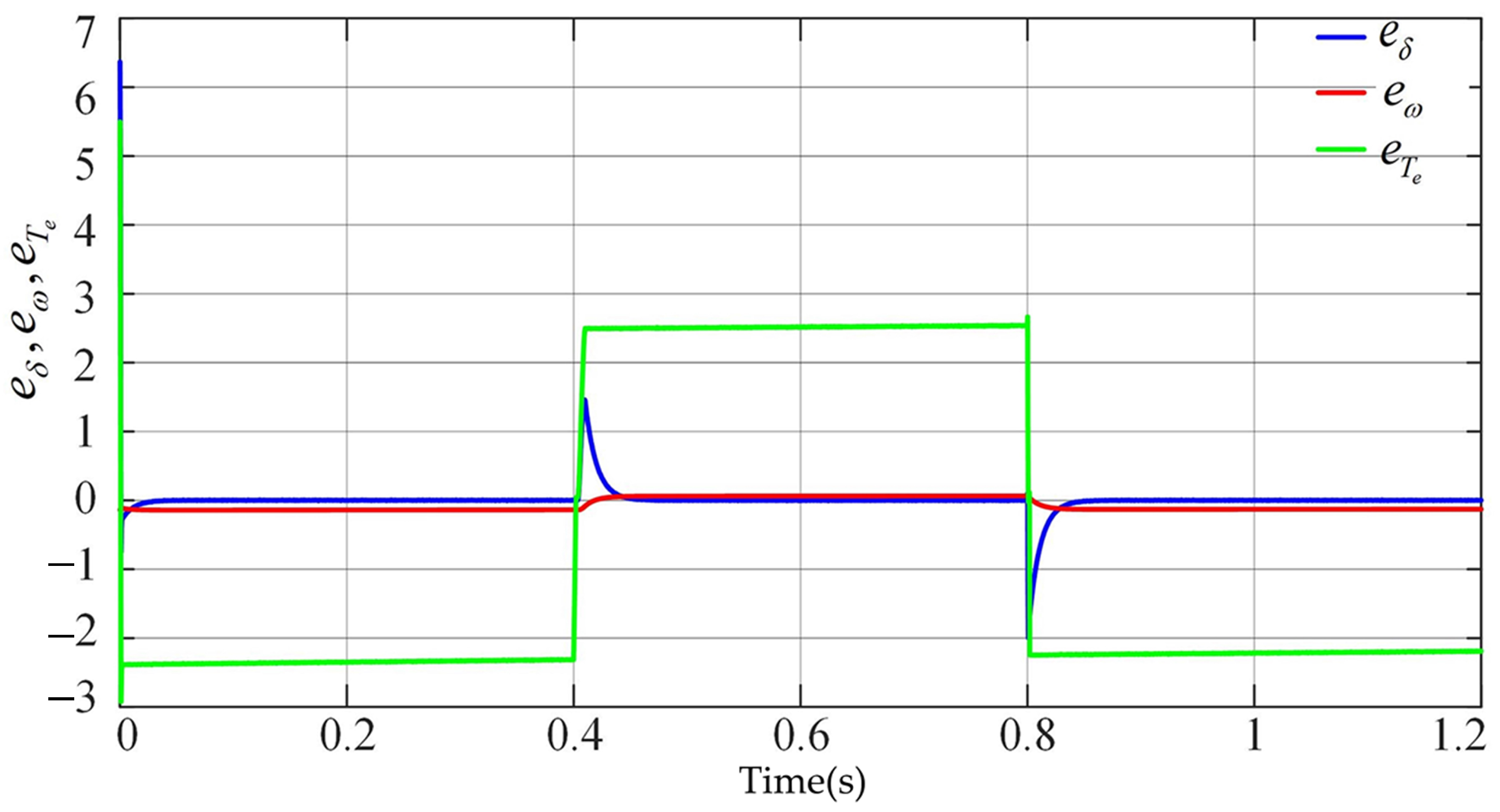
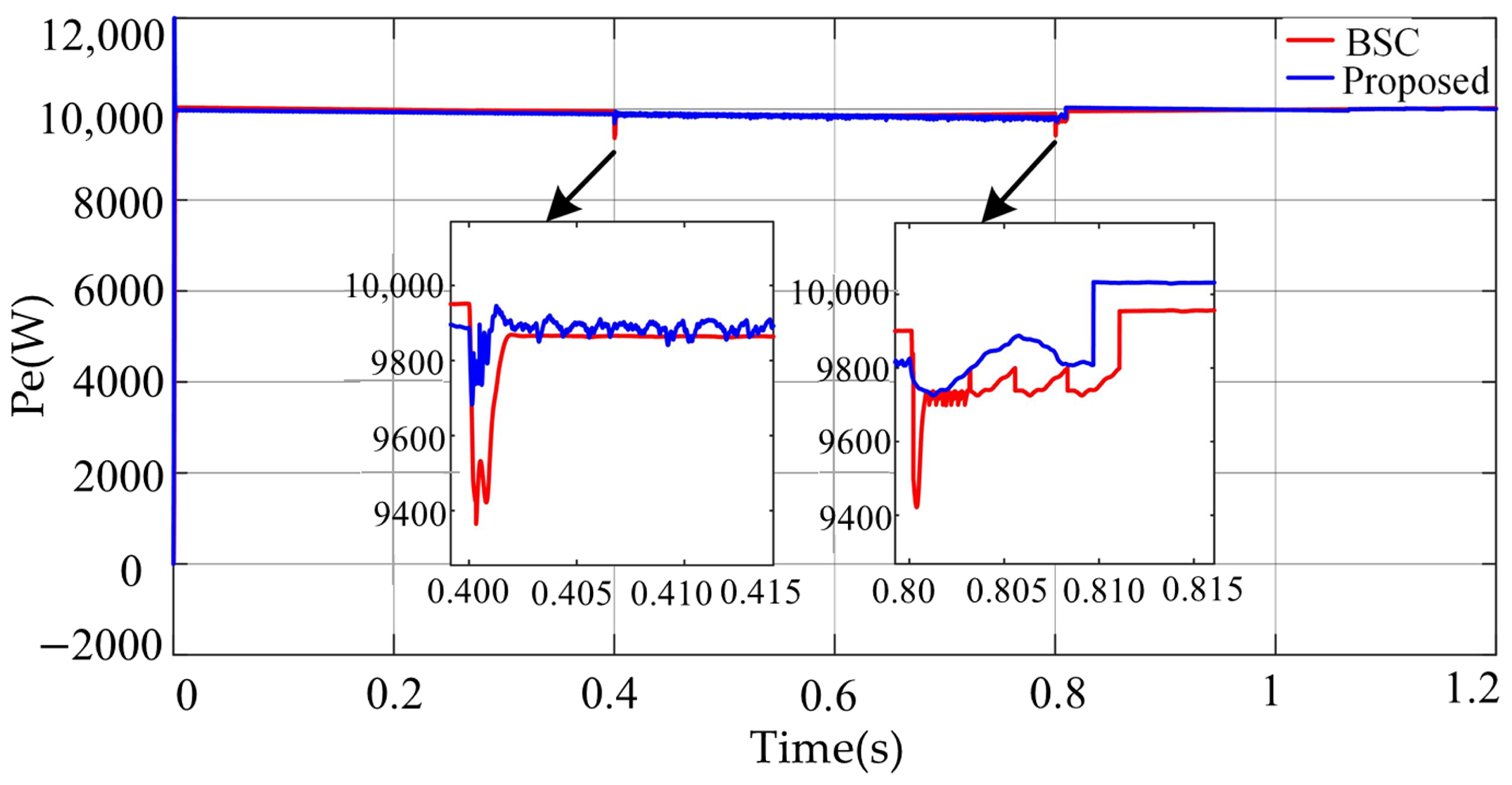
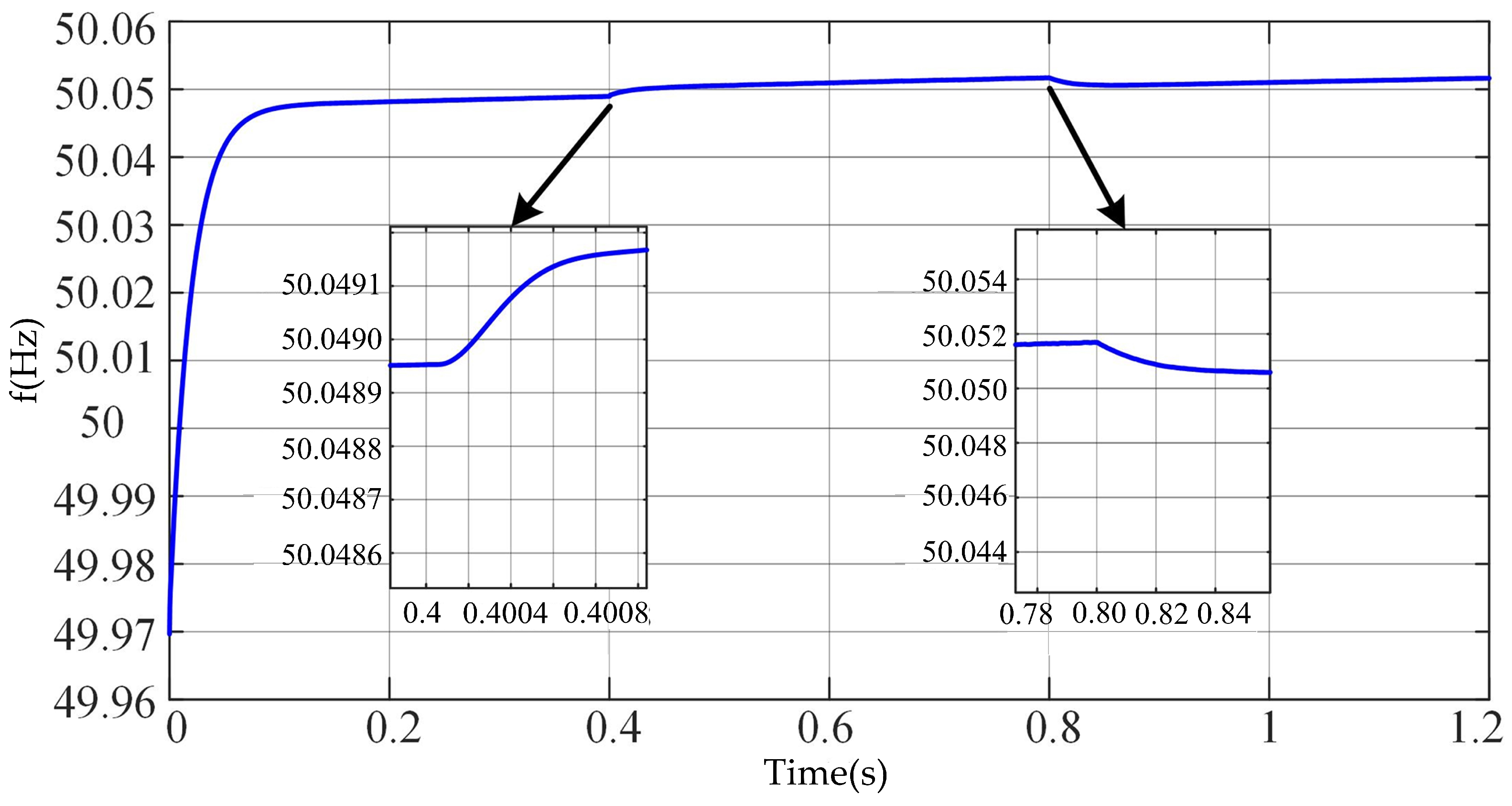
4.1. Load Variation Disturbances
4.1.1. Case-1
4.1.2. Case-2
4.2. Transition Process
5. Discussion
5.1. Load Variation Disturbances
5.1.1. Case-1
5.1.2. Case-2
5.2. Transition Process
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ATSMC | Adaptive Terminal Sliding Mode Control |
| OPIC | Optimized Proportional-Integral Controller |
| ISMBC | Integral Sliding Mode Backstepping Control |
| ACBC | Adaptive Command-Filter Backstepping Control |
| ATSMBSC | Adaptive Terminal Sliding Mode Backstepping Control |
| FIS | Fuzzy Inference System |
Appendix A
References
- Magdy, G.; Bakeer, A.; Nour, M.; Petlenkov, E. A new virtual synchronous generator design based on the SMES system for frequency stability of low-inertia power grids. Energies 2020, 13, 5641. [Google Scholar] [CrossRef]
- Abdalla, M.A.A.; Min, W.; Mohammed, O.A.A. Two-stage energy management strategy of EV and PV integrated smart home to minimize electricity cost and flatten power load profile. Energies 2020, 13, 6387. [Google Scholar] [CrossRef]
- Nogami, S.; Yokoyama, A.; Daibu, T.; Hono, Y. Virtual synchronous generator model control of PV for improving transient stability and damping in a large-scale power system. Electr. Eng. Jpn. 2019, 208, 21–28. [Google Scholar] [CrossRef]
- Badal, F.R.; Das, P.; Sarker, S.K.; Das, S.K. A survey on control issues in renewable energy integration and microgrid. Prot. Control Mod. Power Syst. 2019, 4, 8. [Google Scholar] [CrossRef]
- Kamel, R.M.; Chaouachi, A.; Nagasaka, K. Detailed analysis of microgrid stability during islanding mode under different load conditions. Engineering 2011, 3, 508. [Google Scholar] [CrossRef]
- Zeng, Y.; Qian, J.; Yu, F.; Mei, H.; Yu, S. Damping Formation Mechanism and Damping Injection of Virtual Synchronous Generator Based on Generalized Hamiltonian Theory. Energies 2021, 14, 7082. [Google Scholar] [CrossRef]
- Chen, M.; Zhou, D.; Blaabjerg, F. Modelling, implementation, and assessment of virtual synchronous generator in power systems. J. Mod. Power Syst. Clean Energy 2020, 8, 399–411. [Google Scholar] [CrossRef]
- Yang, C.; Yang, F.; Xu, D.; Huang, X.; Zhang, D. Adaptive command-filtered backstepping control for virtual synchronous generators. Energies 2019, 12, 2681. [Google Scholar] [CrossRef]
- Rehman, H.U.; Yan, X.; Abdelbaky, M.A.; Jan, M.U.; Iqbal, S. An advanced virtual synchronous generatorcontrol technique for frequency regulation of grid-connected PV system. Int. J. Electr. Power Energy Syst. 2021, 125, 106440. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, Q.; Guo, Z.; Zhang, H.; Li, M.; Li, F. Coordinated control strategy for a PV-storage grid-connected system based on a virtual synchronous generator. Glob. Energy Interconnect. 2020, 3, 51–59. [Google Scholar] [CrossRef]
- Bevrani, H.; Ise, T.; Miura, Y. Virtual synchronous generators: A survey and new perspectives. Int. J. Electr. Power Energy Syst. 2014, 54, 244–254. [Google Scholar] [CrossRef]
- Alipoor, J.; Miura, Y.; Ise, T. Stability assessment and optimization methods for a microgrid with multiple VSG units. IEEE Trans. Smart Grid 2016, 9, 1462–1471. [Google Scholar] [CrossRef]
- Liu, J.; Miura, Y.; Ise, T. A novel oscillation damping method of virtual synchronous generator control without PLL using pole placement. In Proceedings of the 2018 IEEE International Power Electronics Conference, Niigata, Japan, 20–24 May 2018. [Google Scholar]
- Yu, Y.J.; Cao, L.K.; Zhao, X. A novel control strategy of virtual synchronous generator in island microgrids. Syst. Sci. Control Eng. 2018, 6, 136–145. [Google Scholar] [CrossRef]
- Mohamed, M.M.; El Zoghby, H.M.; Sharaf, S.M.; Mosa, M.A. Optimal virtual synchronous generator control of battery/supercapacitor hybrid energy storage system for frequency response enhancement of photovoltaic/diesel microgrid. J. Energy Storage 2022, 51, 104317. [Google Scholar] [CrossRef]
- Zhou, B.; Meng, L.; Yang, D.; Ma, Z.; Xu, G. A Novel VSG-Based Accurate Voltage Control and Reactive Power Sharing Method for Islanded Microgrids. Sustainability 2019, 11, 6666. [Google Scholar] [CrossRef]
- Lalitha, M.P.; Anupama, S.; Faizal, K.M. Fuzzy logic controller for parallel inverters in microgrids using virtual synchronous generator control. In Proceedings of the IEEE International Conference on Energy, Communication, Data Analytics and Soft Computing (ICECDS), Chennai, India, 1–2 August 2017. [Google Scholar]
- Li, W.; Xie, J.; Zhang, M.; Guo, C. Adaptive damping control strategy of virtual synchronous generator based on fuzzy control. In Proceedings of the IOP Conference Series, Zamosc, Poland, 25–27 November 2021. [Google Scholar]
- Karimi, A.; Khayat, Y.; Naderi, M.; Dragicevic, T.; Mirzaei, R.; Blaabjerg, F.; Bevrani, H. Inertia response improvement in AC microgrids: A fuzzy-based virtual synchronous generator control. IEEE Trans. Power Electron. 2019, 35, 4321–4331. [Google Scholar] [CrossRef]
- Karimi, A.; Jafarian, Y.; Bevrani, H.; Mirzaei, R. Frequency response improvement in microgrids:afuzz-based virtual synchronous generator approach. Int. J. Ind. Electron. Control Optim. 2020, 3, 147–158. [Google Scholar]
- Kerdphol, T.; Watanabe, M.; Hongesombut, K.; Mitani, Y. Self-adaptive virtual inertia control-based fuzzy logic to improve frequency stability of microgrid with high renewable penetration. IEEE Access 2019, 7, 76071–76083. [Google Scholar] [CrossRef]
- Zhang, L.; Zheng, H.; Wan, T.; Shi, D.; Lyu, L.; Cai, G. An integrated control algorithm of power distribution for islanded microgrid based on improved virtual synchronous generator. IET Renew. Power Gener. 2021, 15, 2674–2685. [Google Scholar] [CrossRef]
- Lin, S.; Lin, L.; Wen, B. A Voltage Control Strategy of VSG Based on Self-Adaptive Inertia Coefficient and Droop Coefficient. Math. Probl. Eng. 2021, 2021, 5567826. [Google Scholar] [CrossRef]
- Zhang, G.; Yang, J.; Wang, H.; Cui, J. Presynchronous Grid-Connection Strategy of Virtual Synchronous Generator Based on Virtual Impedance. Math. Probl. Eng. 2020, 2020, 3690564. [Google Scholar] [CrossRef]
- Liu, J.; Miura, Y.; Ise, T. Fixed-parameter damping methods of virtual synchronous generator control using state feedback. IEEE Access 2019, 7, 99177–99190. [Google Scholar] [CrossRef]
- Li, J.; Wen, B.; Wang, H. Adaptive virtual inertia control strategy of VSG for microgrid based on improved bang-bang control strategy. IEEE Access 2019, 7, 39509–39514. [Google Scholar] [CrossRef]
- Li, L.; Li, H.; Tseng, M.L.; Feng, H.; Chiu, A.S. Renewable energy system on frequency stability control strategy using virtual synchronous generator. Symmetry 2020, 12, 1697. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, Y.; Dong, J.; Mao, X.; Chen, J.; Wen, B.; Zhang, Z. A Novel Pre-Synchronization Control for Grid Connection of Virtual Synchronous Generator. Elektron. Ir Elektrotechnika 2020, 26, 25–31. [Google Scholar] [CrossRef]
- Lan, Y.H. Backstepping control with disturbance observer for permanent magnet synchronous motor. J. Control Sci. Eng. 2018, 2018, 4938389. [Google Scholar] [CrossRef]
- Teng, Q.; Xu, D.; Yang, W.; Li, J.; Shi, P. Neural network-based integral sliding mode backstepping control for virtual synchronous generators. Energy Rep. 2021, 7, 1–9. [Google Scholar] [CrossRef]
- Dou, Z.; Tang, L.; Sun, Y.; Zhang, C.; Yang, W.; Xu, D. Prescribed Performance-Based Adaptive Terminal Sliding Mode Control for Virtual Synchronous Generators. Math. Probl. Eng. 2022, 2022, 5742759. [Google Scholar] [CrossRef]
- Deng, G.; Cheng, L.; Yang, B. Adaptive optimizing control for nonlinear synchronous generator system with uncertain disturbance. Complexity 2019, 2019, 7604320. [Google Scholar] [CrossRef]
- Wang, R.; Liu, X.; Huang, Y. Synchronous Generator Excitation System for a Ship Based on Active Disturbance Rejection Control. Math. Probl. Eng. 2021, 2021, 6638370. [Google Scholar]
- Zhang, Y.; Zhu, J.; Dong, X.; Zhao, P.; Ge, P.; Zhang, X. A control strategy for smooth power tracking of a grid-connected virtual synchronous generator based on linear active disturbance rejection control. Energies 2019, 12, 3024. [Google Scholar] [CrossRef]
- Liu, J.; He, J.; Iu, H.H.C. Realization of Low-Voltage and High-Current Rectifier Module Control System Based on Nonlinear Feed-Forward PID Control. Electronics 2021, 10, 2138. [Google Scholar] [CrossRef]
- Zhang, Z.; Guo, Y.; Song, X. Improved Nonlinear Extended State Observer-Based Sliding-Mode Rotary Control for the Rotation System of a Hydraulic Roofbolter. Entropy 2021, 24, 41. [Google Scholar] [CrossRef] [PubMed]
- Xue-song, Z.; Chao, L.; You-jie, M.; Ji, L.; Yang, Y. The Simulation Study of Auto Disturbance Rejection Controller Based on S-Function. In Proceedings of the 2011 Third International Conference on Measuring Technology and Mechatronics Automation, Shangshai, China, 6–7 January 2011. [Google Scholar]
- Shuai, T.; Weijun, W.; Shu, L.; Longbo, M.; Wenqiang, W. Research on Control Technology of Distributed Power Generation Virtual Synchronous Generator. In Proceedings of the IOP Conference Series on Earth and Environmental Science (EES), Chongqing, China, 20–22 February 2021. [Google Scholar]
- Abbaker, A.O.; Wang, H.; Tian, Y. Voltage control of solid oxide fuel cell power plant based on intelligent proportional integral-adaptive sliding mode control with anti-windup compensator. Trans. Inst. Meas. Control 2020, 42, 116–130. [Google Scholar] [CrossRef]
- Edan, R.F.; Mahdi, A.J.; Wahab, T.M.A. Optimized proportional-integral controller for a photovoltaic-virtual synchronous generator system. Int. J. Power Electron. Drive Syst. 2022, 13, 509. [Google Scholar] [CrossRef]
- Sun, Y.; Xu, D.; Yang, W.; Bi, K.; Yan, W. Adaptive Terminal Sliding Mode Backstepping Control for Virtual Synchronous Generators. In Proceedings of the IEEE 9th Data Driven Control and Learning Systems Conference, Liuzhou, China, 20–22 November 2020. [Google Scholar]
- Zhang, L.; Zheng, H.; Cai, G.; Zhang, Z.; Wang, X.; Koh, L.H. Power-frequency oscillation suppression algorithm for AC microgrid with multiple virtual synchronous generators based on fuzzy inference system. IET Renew. Power Gener. 2022, 16, 1589–1601. [Google Scholar] [CrossRef]



| Parameter | Value | Description |
|---|---|---|
| 800 V | DC-link voltage | |
| 400 V | Line-ground voltage | |
| 0.065 | Grid resistance | |
| 0.001 mH | Grid inductance | |
| 5 | Output resistance | |
| 0.5 mH | Output inductance | |
| 10 f | Filter capacitor | |
| 2 | Filter damping resistor | |
| 10 kHz | Switching frequency |
| Parameter | Value | Description |
|---|---|---|
| 10 kW | Rated active power | |
| J | 0.5 kg·m | Moment of inertia |
| D | 20 | Damping coefficient |
| 314 rad/s | Nominal angular frequency | |
| , | 0.0001, 0.001 | Frequency and voltage droop gain |
| , | 1, 0.1 | LPF time constant and gain |
| , | 2, 2000 | PI controller parameters |
| Strategy | Validation | Microgrid Case | Advantages | Disadvantages |
|---|---|---|---|---|
| Proposed method | MATLAB/ Simulink | -Islanded -Grid connected | -Simple. -Good dynamics response to power step and transition process. -External disturbance is considered. | -Inrush current at the moment of connection. -Absence of experimental test. |
| ATSMC [31] | MATLAB/ Simulink | -Grid connected | -Good tracking performance. -Small frequency deviation during transition process. | -Complicated with many design parameters. -Power deviation during grid connection. |
| OPIC [40] | MATLAB/ Simulink | -Grid connected | -Small RoCoF response to change of system frequency. -Short adjust time. | -Large voltage deviation under sudden load change. |
| ISMBC [30] | MATLAB/ Simulink | -Grid connected | -Simple. -Good tracking performance. -Includes external disturbances. | -Power deviation during grid connection. |
| ACBC [8] | MATLAB/ Simulink | -Islanded -Grid connected | -Includes multi-VSG. -Smooth transition process. -Short adjust time. | -Complicated. -Power deviation during demand change. |
| ATSMBSC [41] | MATLAB/ Simulink | -Grid connected | -Simple. -Good dynamics when changes to islanded mode. -Less power adjust time | -Voltage transients during grid connection. -Large power deviation during grid connection. |
| FIS [42] | Simulink/ Experiment | -Islanded -Grid connected | -Simple. -Includes multi-VSG. -Short adjust time. | -Poor dynamic response to load disturbance. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haroon, S.I.A.; Qian, J.; Zeng, Y.; Zou, Y.; Tian, D. Extended State Observer Based-Backstepping Control for Virtual Synchronous Generator. Electronics 2022, 11, 2988. https://doi.org/10.3390/electronics11192988
Haroon SIA, Qian J, Zeng Y, Zou Y, Tian D. Extended State Observer Based-Backstepping Control for Virtual Synchronous Generator. Electronics. 2022; 11(19):2988. https://doi.org/10.3390/electronics11192988
Chicago/Turabian StyleHaroon, Shamseldeen Ismail Abdallah, Jing Qian, Yun Zeng, Yidong Zou, and Danning Tian. 2022. "Extended State Observer Based-Backstepping Control for Virtual Synchronous Generator" Electronics 11, no. 19: 2988. https://doi.org/10.3390/electronics11192988
APA StyleHaroon, S. I. A., Qian, J., Zeng, Y., Zou, Y., & Tian, D. (2022). Extended State Observer Based-Backstepping Control for Virtual Synchronous Generator. Electronics, 11(19), 2988. https://doi.org/10.3390/electronics11192988






