Bi-Level Fuzzy Expectation-Based Dynamic Anti-Missile Weapon Target Allocation in Rolling Horizons
Abstract
:1. Introduction
- An analysis of uncertainty factors is performed. The disruptions caused by multiple uncertainties, such as combat environment, interference from enemy targets, and limited detection equipment, affect the final results of weapon target allocation to varying extents. In this paper, the following uncertainties are mainly considered: the uncertainty of target-type identification results and the destruction probabilities of our weapons are taken as fuzzy variables. Then, the fuzzy expectation model is adopted to construct an uncertainty model, and the reprogramming strategy of marginal benefits is used to solve dynamic uncertainties, such as the emergence of new targets and the disappearance of old targets.
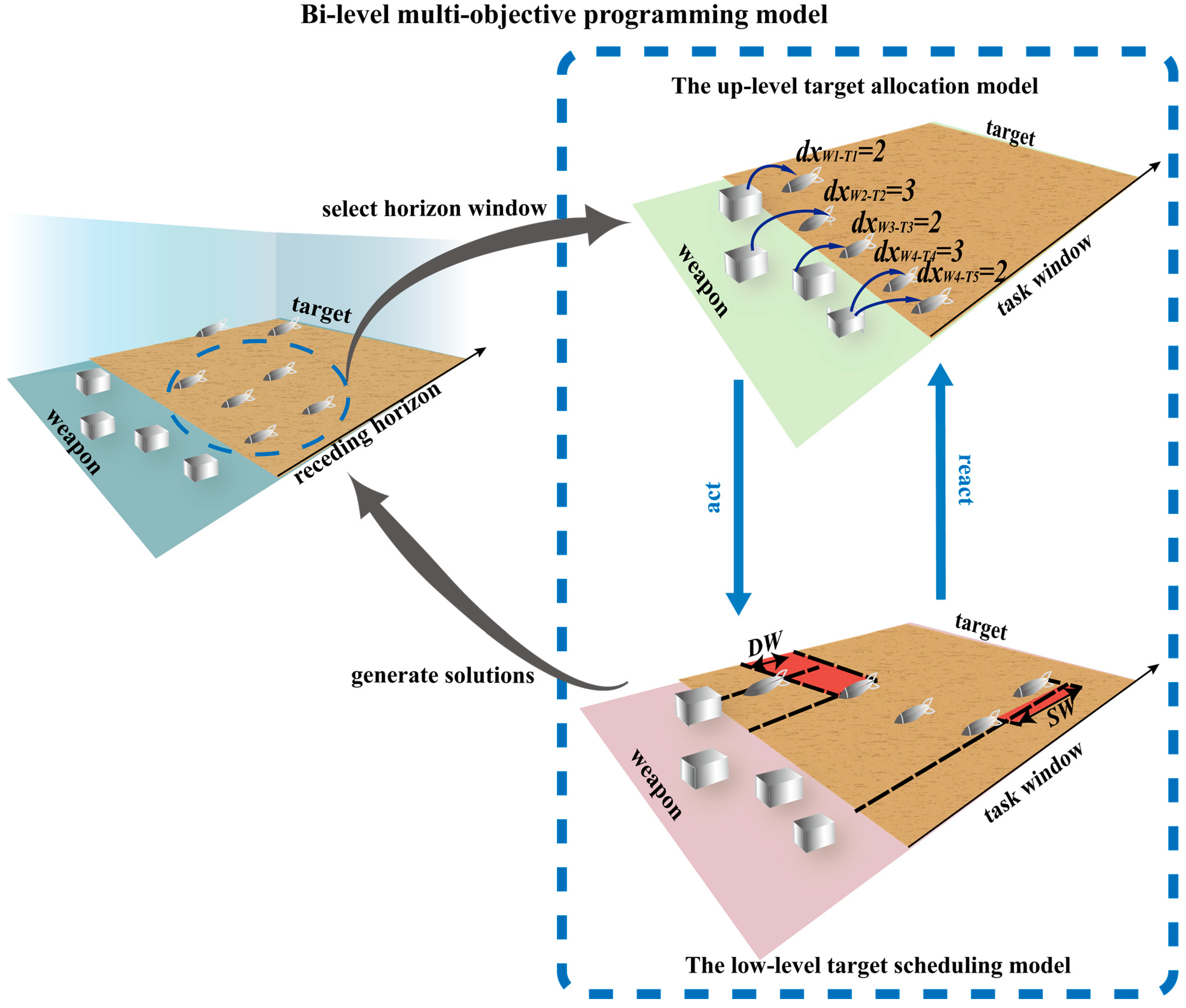
- A bi-level dynamic weapon target allocation model is proposed. We propose a bi-level dynamic weapon target allocation model in this paper under a rolling horizon framework. For the upper-level objectives, the weapon target allocation problem (WTA) is considered on the basis of synergistic effectiveness, while for the lower-level objectives, the firepower-scheduling problem (FSP) is considered. This reflects the coupling and constraint relationships between multiple combat targets, which makes the model more closely related to combat needs.
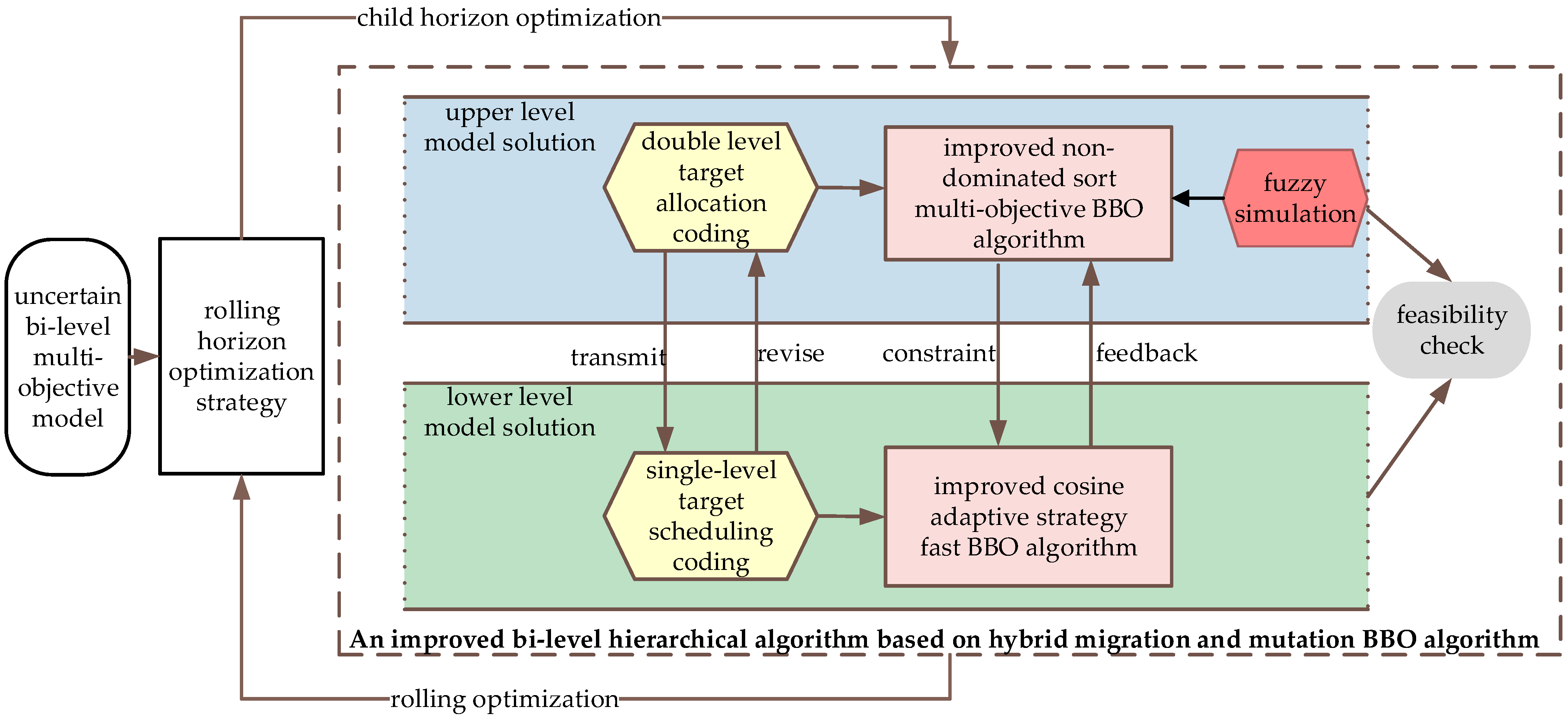
- An improved bi-level recursive BBO algorithm is proposed on the basis of hybrid migration and variation for solving the model. Given a certain degree of complexity of the bi-level model, it is necessary to develop new intelligent algorithms for the corresponding solution. In this paper, the BBO algorithm is adapted for the multi-objective bi-level programming model. In addition, an improved BBO algorithm is proposed separately to solve the multi-objective bi-level programming model in an efficient way.
2. Problem and Model
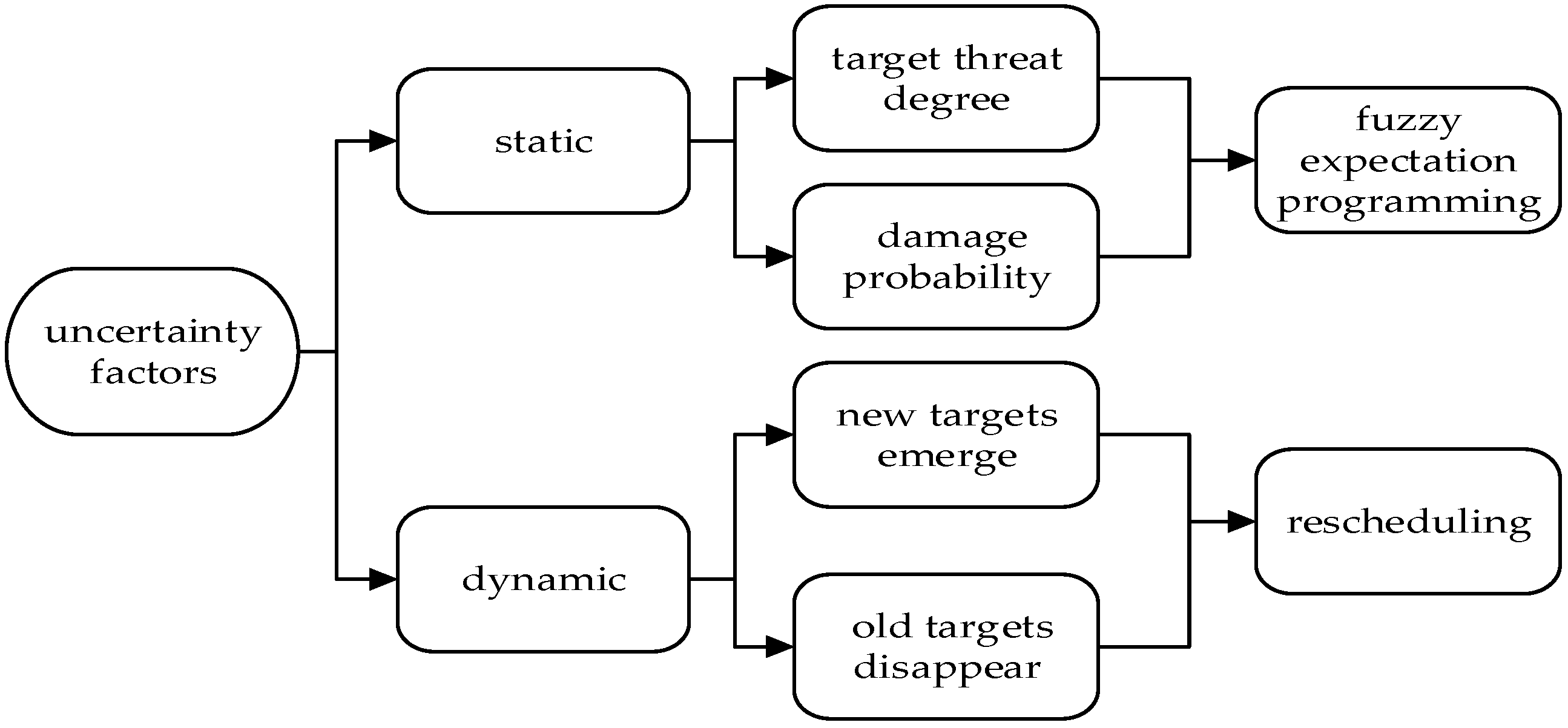
2.1. Uncertainty Factor Analysis
- Static uncertainty: This type of uncertainty does not vary with time, which can be caused by the limitations of the sensor detection capability and the penetration characteristics of incoming targets so that the measured data and the acquired battlefield information are uncertain, and the degree of uncertainty is difficult to measure.
- Since this uncertainty is characterized by ambiguity and mainly affects the relevant parameters in the model, the following two static uncertainties were considered.
- (1)
- Target threat degree: The target threat degree is affected by kinematic information, such as the speed and altitude of missiles, and is related to the degree of real-time and the accuracy of information obtained. If a target has a higher threat level to our target, priority is given to shoot it in order to obtain a greater effect of destruction and protection of our assets. The target threat level under information-based conditions requires not only state information, such as the target’s speed, altitude, and heading angle, but also tactical information, such as target type, maneuver behavior, and game strategy, and thus has a strong uncertainty characteristic.
- (2)
- Damage probability: Due to the high cost of weapons and equipment, the probability of destruction can only be derived from simulation and historical data, which has obvious uncertainty characteristics in the complex anti-missile environment.
- 2.
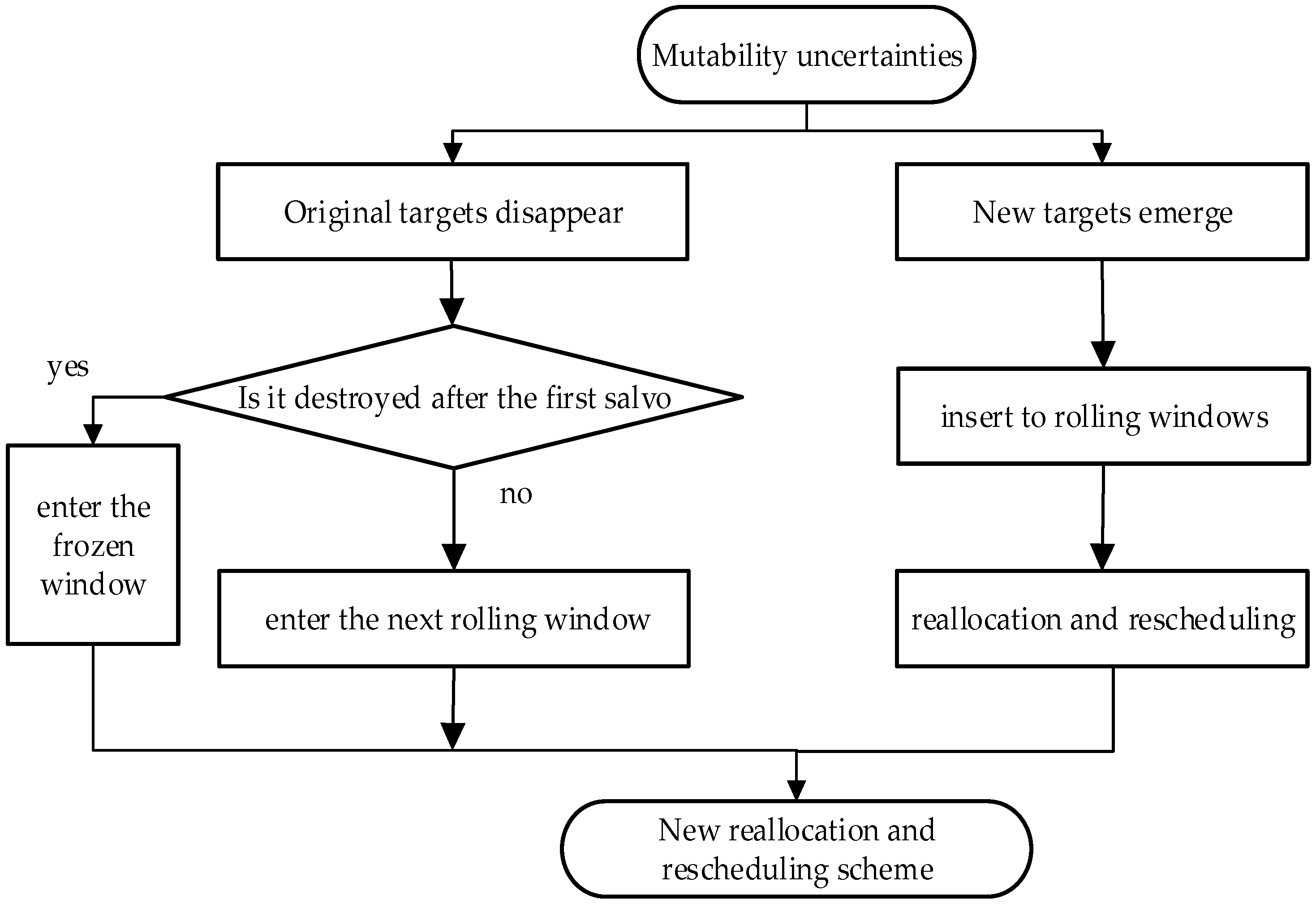
- Dynamic uncertainties: Dynamic uncertainties change with time, and their changes often have a great impact on the overall anti-missile process model by changing the characteristic and structure, such as the type and model of the targets, the trajectory of the motion state, the results of true and false identification, the sudden change in the target information, etc. The time and scale of their occurrence are unknown relative to the decision-making moments. In this paper, we considered two cases of dynamic uncertainties, i.e., the emergence of new targets and the disappearance of old targets.
- The enemy maneuvering situation was not considered.
- The time consumption of wave transfer and ammunition replenishment was not considered.
- We assumed that the target ballistic prediction and the predicted target time window were accurate enough.
- Each incoming target was assigned at least one firepower.
- Each weapon was equipped with multiple firepowers, with a maximum of one fire at a time against each target, and the total number of fires assigned could not exceed the limit on the number of fires for that weapon.
- A target was considered to be successfully intercepted when the cumulative probability of firepower damage to the target reached the lower limit of severe damage.
- There were several different interception strategies for intercepting incoming targets, including firing a single interceptor; firing multiple interceptors in unison; “shoot-observe-shoot” and other various strategies; and a combination of different interception strategies.
2.2. Bi-Level Dynamic Weapon Target Allocation Model Construction
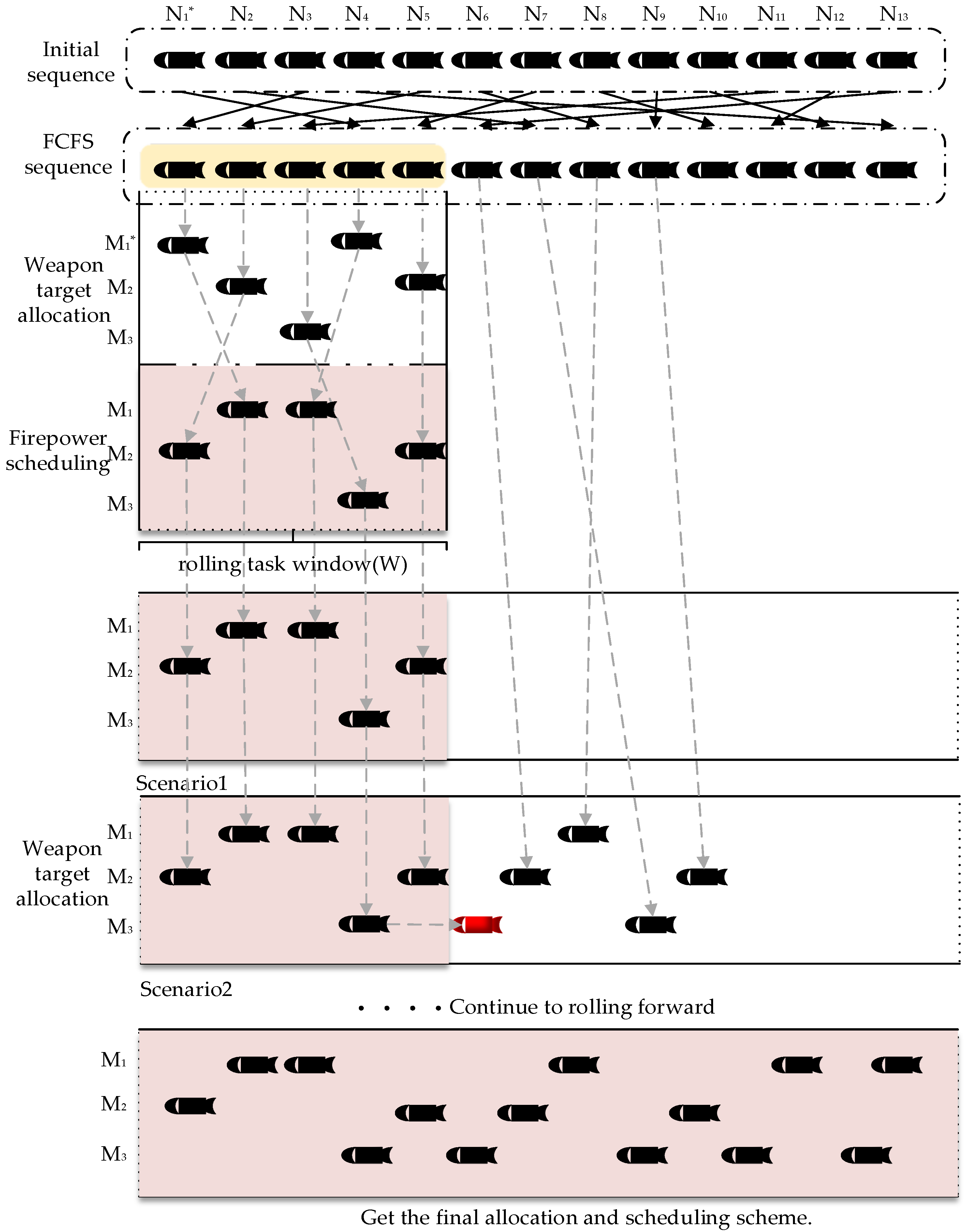
2.2.1. Rolling Horizon Optimization Strategy
2.2.2. Upper-Level Multi-Objective Weapon Target Allocation Function
- Objective function F1:
- 2.
- Objective function F2:
- 3.
- The constraints:
2.2.3. Lower-Level Firepower Collaborative Scheduling Function
2.2.4. Reprogramming Strategy Based on Marginal Benefits
3. Improved Bi-Level Recursive BBO Algorithm Based on Hybrid Migration and Variation
3.1. Upper-Level INSBBO Algorithm
3.1.1. Upper-Level Algorithm Coding
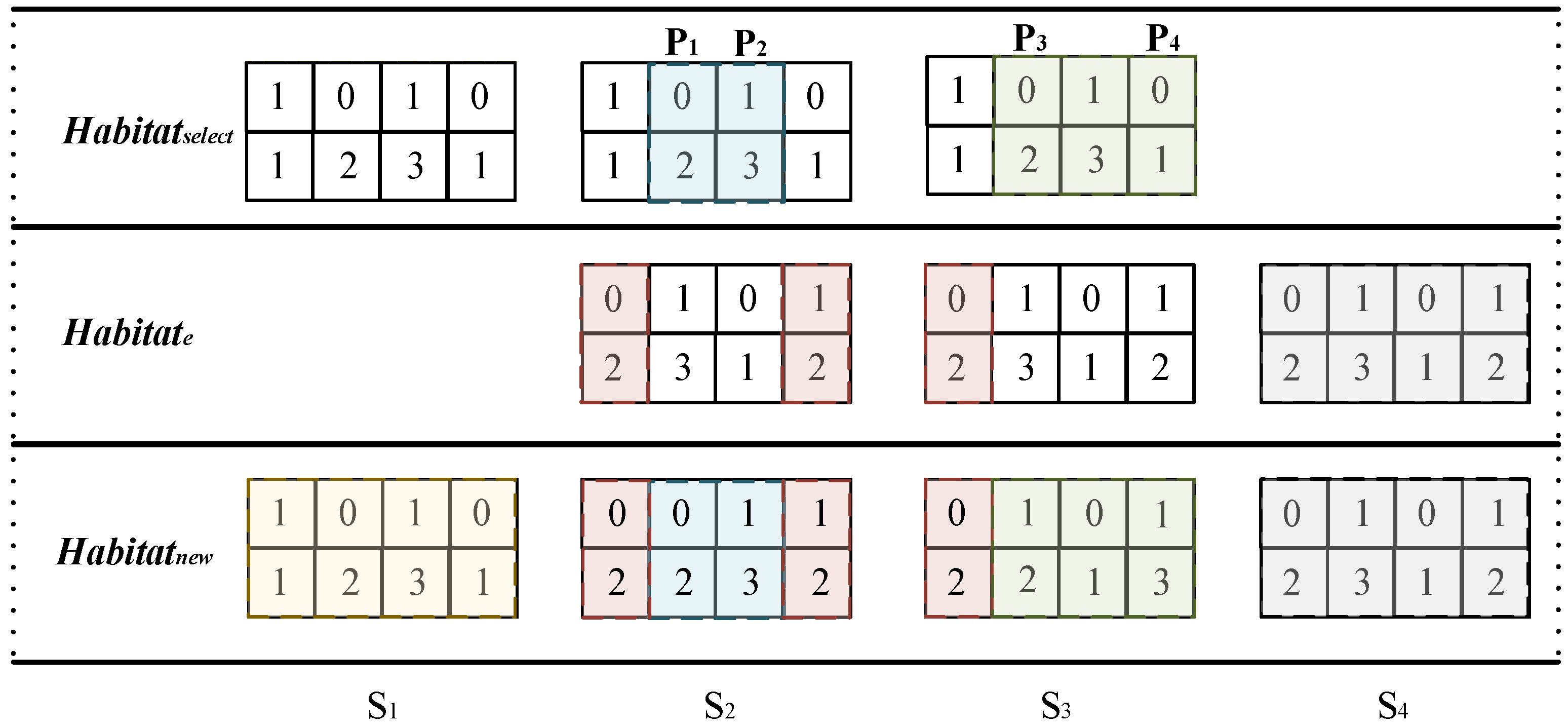
3.1.2. Hybrid Migration Operator
3.1.3. Hybrid Variation Operator
3.1.4. Hybrid Variation Operator
3.1.5. Mixed Elite Mechanism
3.2. Lower IBBO-Solving Algorithm
3.2.1. Algorithm Coding
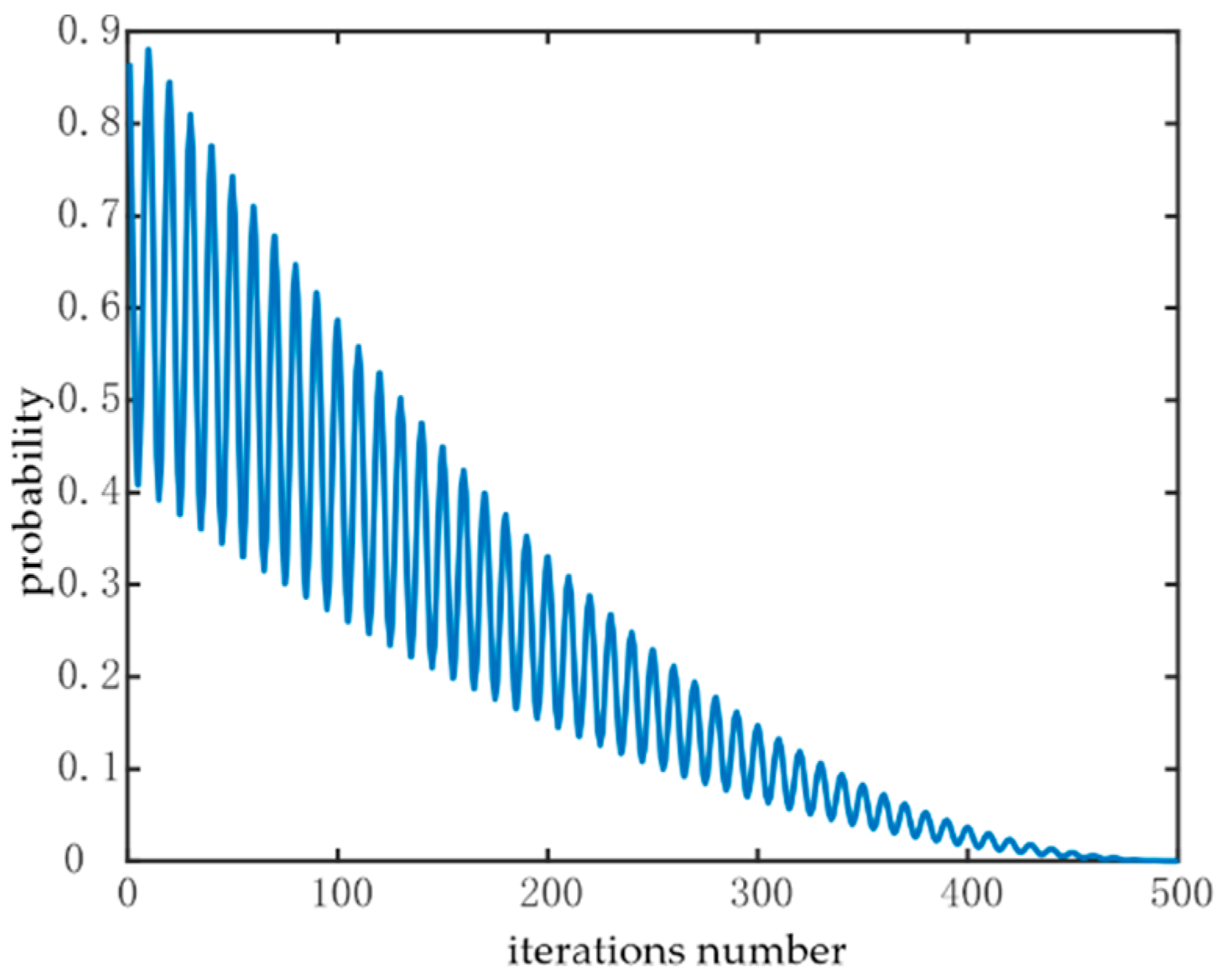
3.2.2. Cosine Adaptive Migration Pressure Selection Mechanism
3.3. Improved Bi-Level Recursive BBO Algorithm Based on Hybrid Migration and Variation
4. Experiment and Analysis
4.1. Parameter Analysis
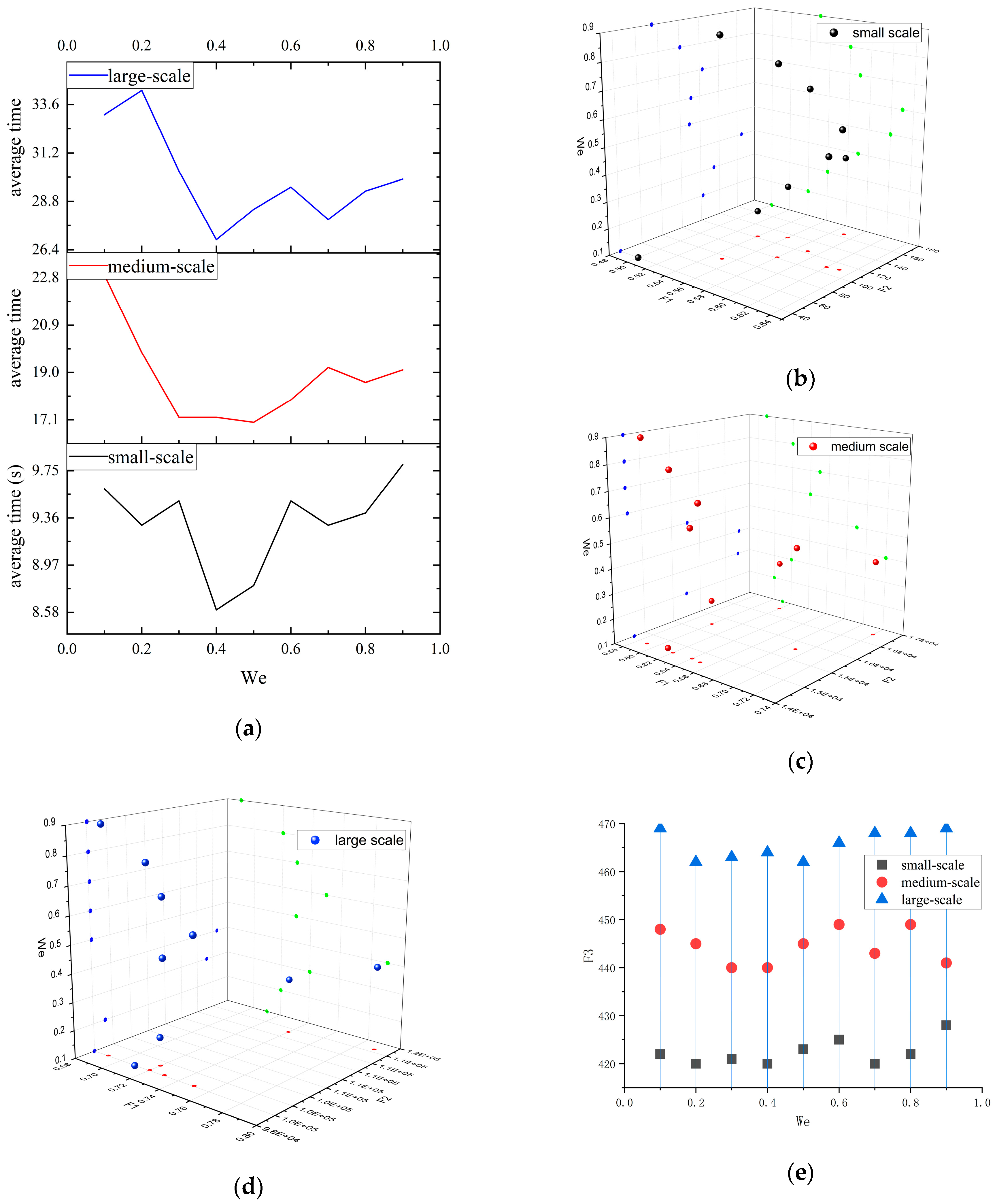
4.1.1. Rolling Horizon Window and Anti-Missile Fire Collaboration Problem Scale Study
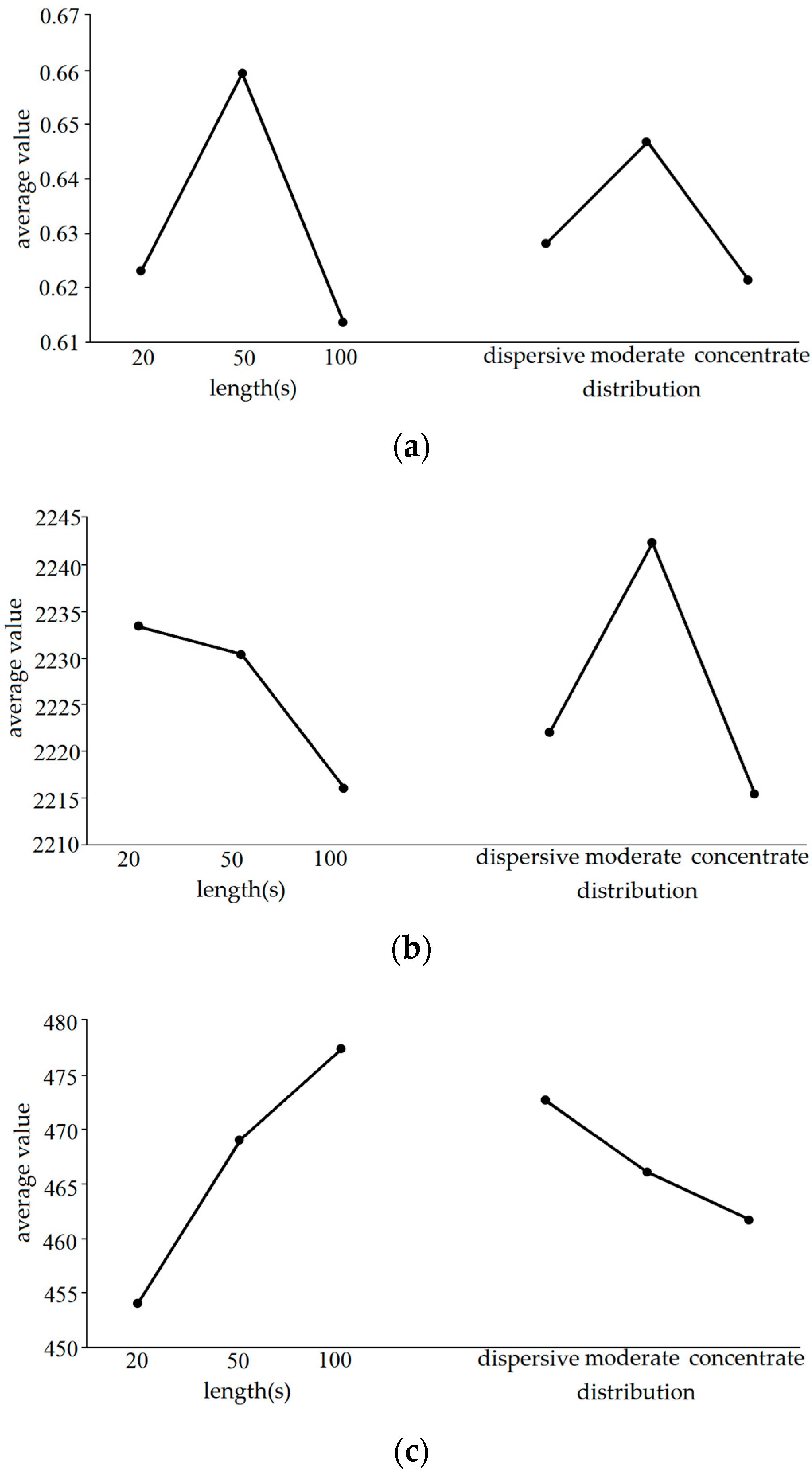
4.1.2. Study on the Length and Distribution of Interceptable Time Window
4.2. Analysis of Scenes
4.2.1. Simulation Experimental Hypothesis
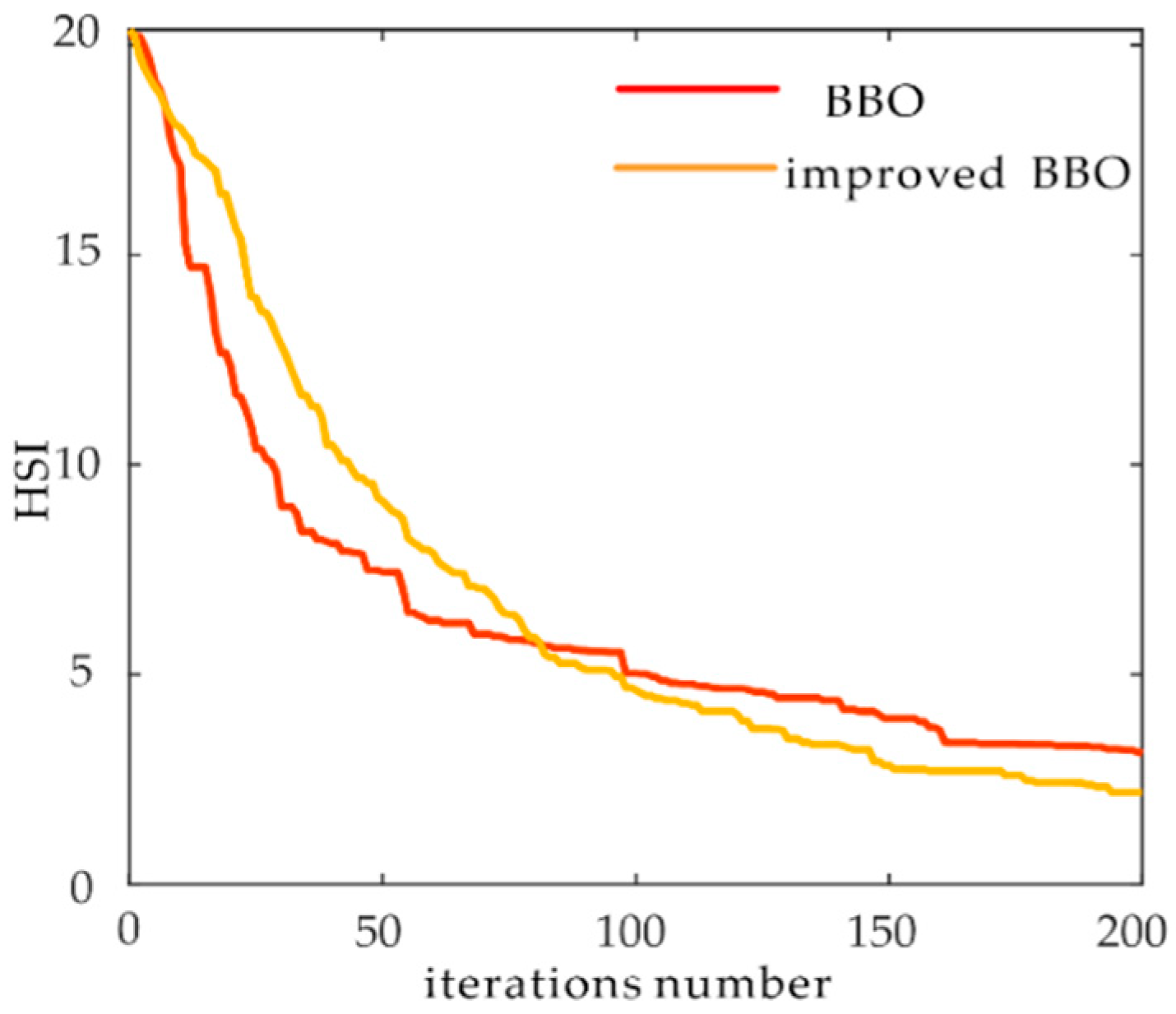
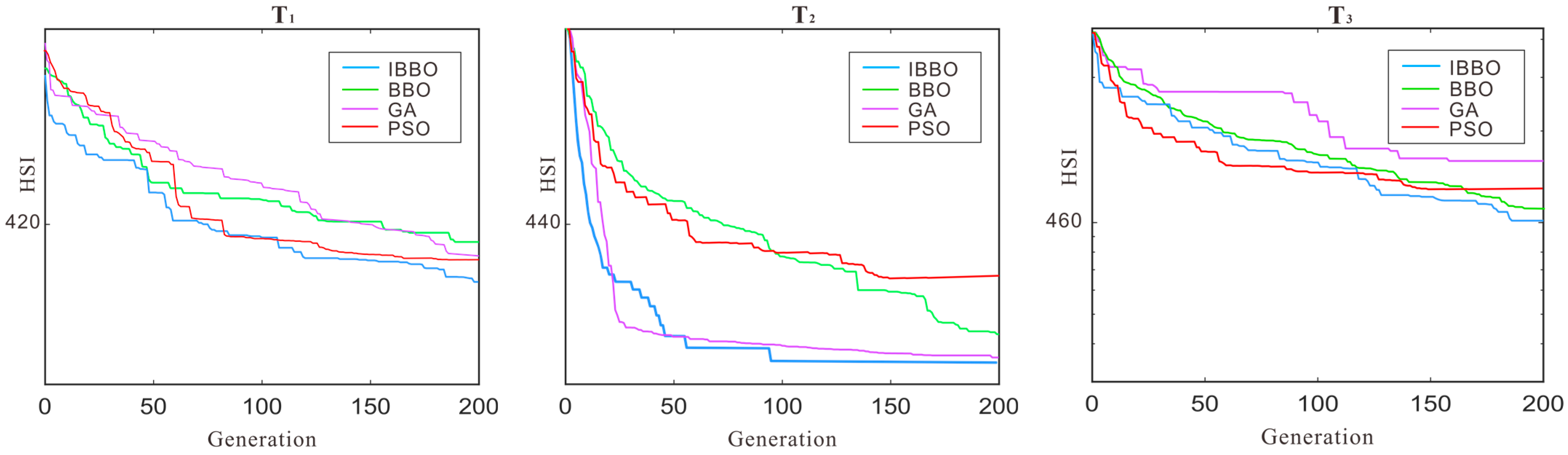
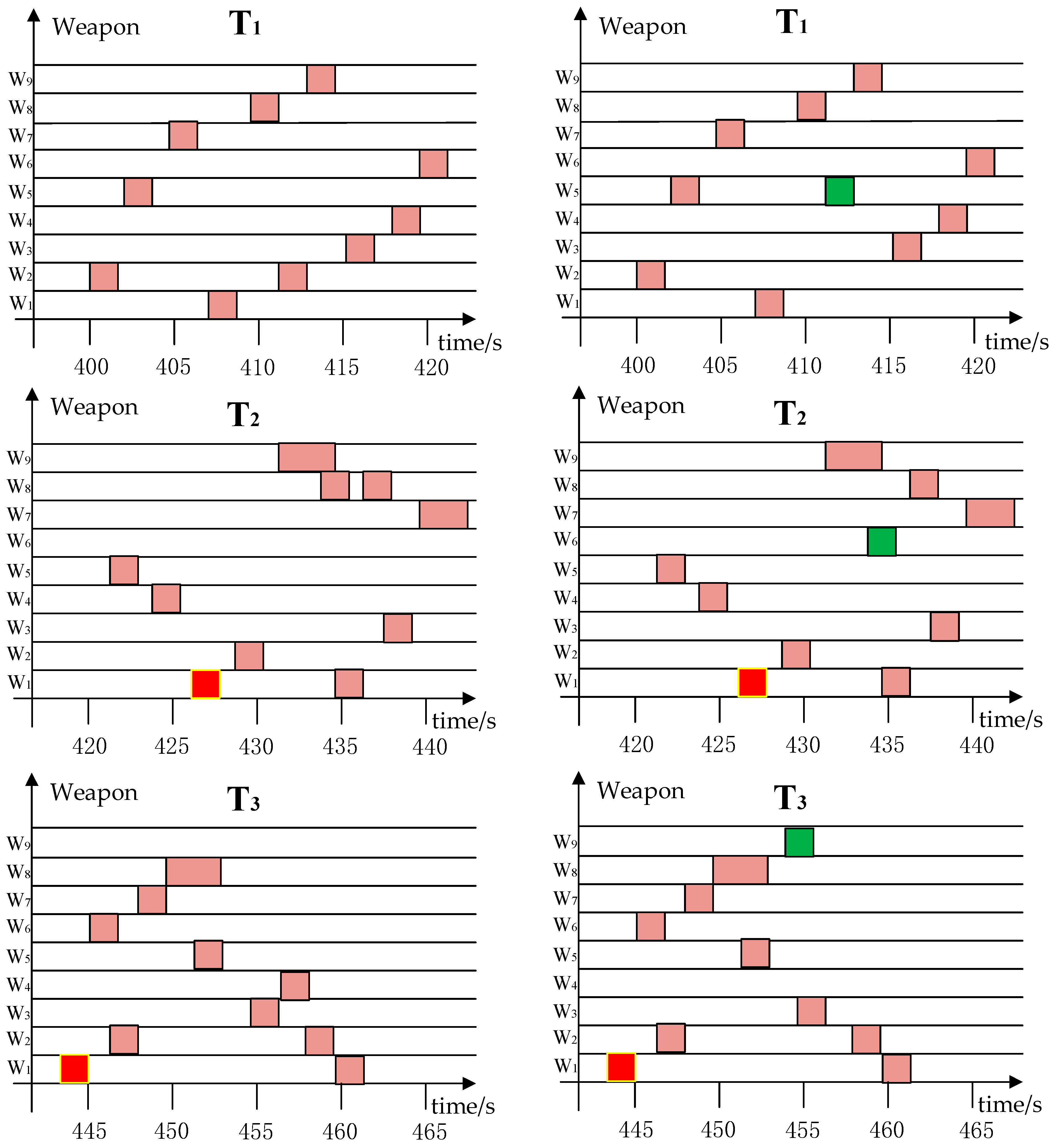
4.2.2. Simulation Experiment Results and Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Manne, A.S. A target-assignment problem. Oper. Res. 1958, 6, 346–351. [Google Scholar] [CrossRef]
- Shang, G.; Zaiyue, Z.; Xiaoru, Z. Immune genetic algorithm for weapon-target assignment problem. Intell. Inf. Technol. Appl. 2007, 7, 145–148. [Google Scholar]
- Bogdanowic, Z. A new efficient algorithm for optimal assignment of smart weapons to targets. Comput. Math. Appl. 2009, 58, 1965–1969. [Google Scholar] [CrossRef]
- Wang, M.; Fan, Y. Intelligent solving algorithm for effects-based firepower allocation model of conventional missiles. Syst. Eng. Electron. 2017, 39, 2509–2514. [Google Scholar]
- Lee, M.Z. Constrained weapon–target assignment: Enhanced very large scale neighborhood search algorithm. IEEE Trans. Syst. Man Cybern. 2010, 40, 198–204. [Google Scholar] [CrossRef]
- Volle, K.; Rogers, J. Weapon–target assignment algorithm for simul-taneous and sequenced arrival. J. Guid. Control Dyn. 2018, 41, 2361–2373. [Google Scholar] [CrossRef]
- Zhang, K.; Zhou, D.Y.; Yang, Z. Constrained multi-objective weapon target assignment for area targets by efficient evolutionary algorithm. IEEE Access 2019, 7, 176339–176360. [Google Scholar] [CrossRef]
- Khosla, D. Hybrid genetic approach for the dynamic programming for missile defense interceptor fire control. Eur. J. Oper. Res. 2016, 242, 1–14. [Google Scholar]
- Davis, M.T.; Robbins, M.J.; Lunday, B.J. Approximate dynamic programming for missile defense interceptor fire control. Eur. J. Oper. Res. 2016, 259, 873–886. [Google Scholar] [CrossRef]
- Fan, C.L.; Xin, Q.H.; Fu, Q. Modeling and realization of dynamic firepower allocation problem based on fuzzy chance constrained bi-level programming. Syst. Eng. Theory Pract. 2016, 5, 1318–1330. [Google Scholar]
- Kwon, O.; Lee, K.; Park, S. Targeting and scheduling problem for field artillery. Comput. Ind. Eng. 1997, 33, 693–702. [Google Scholar] [CrossRef]
- Cha, Y.H.; Kim, Y.D. Fire scheduling for planned artillery attack operations under time-dependent destruction probabilities. Omega 2010, 38, 383–392. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, Y.F.; Zhen, Z.Y. Multi-weapon multi-target assignment based on hybrid genetic algorithm in uncertain environment. International. J. Adv. Robot. Syst. 2020, 17, 17–24. [Google Scholar]
- Xu, H.; Xing, Q.H.; Wang, W. WTA for air and missile defense based on fuzzy multi-objective programming. Syst. Eng. Electron. 2018, 40, 563–570. [Google Scholar]
- Wang, S.Q. Application Study of Variable Fuzzy Fet Multi-Attribute Decision Making Theory on Large-Formation Air Defense Decision Making. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2011. [Google Scholar]
- Pan, Q.; Zhou, D.; Tang, Y. A novel antagonistic weapon-target assignment model considering uncertainty and its solution using decomposition co-Evolution algorithm. IEEE Access 2019, 6, 1–12. [Google Scholar] [CrossRef]
- Xu, W.; Chen, C.; Ding, S. A bi-objective dynamic collaborative task assignment under uncertainty using modified MOEA/D with heuristic initialization. Expert Syst. Appl. 2020, 140, 1–24. [Google Scholar] [CrossRef]
- Li, J.; Xin, B.; Panos, M. Solving bi-objective uncertain stochastic resource allocation problems by the CVaR-based risk measure and decomposition-based multi-objective evolutionary algorithms. Ann. Oper. Res. 2021, 296, 639–666. [Google Scholar] [CrossRef]
- Zhao, T.; Cao, H.; Dian, S. A Self-organized method for a hierarchical fuzzy logic system based on a fuzzy autoencoder. IEEE Trans. Fuzzy Syst. 2022, 1, 1–21. [Google Scholar] [CrossRef]
- Wang, W.; Liu, X.L.; Wang, J. Method of area antiaircraft weapon target assignment for the warship formation under informationized conditions. Syst. Eng.-Theory Pract. 2015, 35, 1011–1018. [Google Scholar]
- Chang, T.; Kong, D.; Hao, N. Solving the dynamic weapon target assignment problem by an improved artificial bee colony algorithm with heuristic factor initialization. Appl. Soft Comput. 2018, 70, 845–863. [Google Scholar] [CrossRef]
- Li, L.; Liu, F.; Long, G. Modified particle swarm optimization for BMDS interceptor resource planning. Appl. Intell. 2016, 44, 471–488. [Google Scholar] [CrossRef]
- Feng, C.; Yao, P.; Jing, X.N. Weapon-target assignment based on improved quantum-inspired immune clonal multi-objective optimization algorithm. Comput. Eng. Sci. 2017, 37, 2314–2319. [Google Scholar]
- Chu, X.G.; Ma, Z.W.; Chen, X.J. Look-ahead margin-greedy constructive algorithm for the multi-objective optimizationof the weapon target assignment problem. Syst. Eng. Electron. 2019, 41, 2252–2259. [Google Scholar]
- Wu, W.H.; Guo, X.F.; Zhou, S.Y. Improved differential evolution algorithm for solving weapon-target assignment problem. Syst. Eng. Electron. 2021, 43, 1012–1021. [Google Scholar]
- Xin, B.; Wang, Y.; Chen, J. An efficient marginal-return-based constructive heuristic to solve the sensor-weapon-target assignment problem. IEEE Trans. Syst. Man Cybern. Syst. 2018, 1, 1–12. [Google Scholar] [CrossRef]
- Simon, D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Rifai, A.P.; Nguyen, H.T.; Aoyama, H. Non-dominated sorting biogeography-based optimization for bi-objective reentrant flexible manufacturing system scheduling. Appl. Soft Comput. 2018, 62, 187–202. [Google Scholar] [CrossRef]
- Kalyanam, K.; Casbeer, D.; Pachter, M. Monotone optimal threshold feedback policy for sequential weapon target assignment. J. Aerosp. Inf. Syst. 2017, 14, 68–72. [Google Scholar] [CrossRef]
- Karasakal, O. Air defense missile-target allocation models for a naval task group. Comput. Oper. Res. 2008, 35, 1759–1770. [Google Scholar] [CrossRef]
- Liu, B.; Liu, Y.K. Expected value of fuzzy variable and fuzzy expected value models. IEEE Trans. Fuzzy Syst. 2002, 10, 445–450. [Google Scholar]





| Symbol Description | |
|---|---|
| Parameter | Meaning |
| s | the index of rolling horizons, |
| the number of available weapons of rolling horizon s | |
| the number of targets of rolling horizon s | |
| the weapons collection of rolling horizon s; | |
| the incoming target collection of rolling horizon s; | |
| the destruction probability of rolling horizon s; denotes the destruction probability of weapon I against target j of rolling horizon s | |
| the target threat degree of rolling horizon s; denotes the threat degree of target j of rolling horizon s | |
| the moment when weapon i strikes target j of rolling horizon s; | |
| ; denotes weapon i allocated to target j of rolling horizon s | |
| the earliest interceptable moment of target j | |
| the latest interceptable moment of target j | |
| the maximum number of targets contained in rolling horizon s; | |
| number of elite solutions obtained after iteration | |
| the maximum number of firepower of weapon i | |
| the boundary value of severe destruction probability | |
| , , | the penalty factors, respectively, are large positive integers |
| the time interval between the first and second flushes in the same firepower lane | |
| the time intervals needing to be met between firepower from different weapons | |
| Level 1 | Level 2 | Level 3 | |
|---|---|---|---|
| distribution of interceptable time window | concentrated | moderate | dispersive |
| length of of interceptable time window | short (20 s) | moderate (50 s) | long (100 s) |
| Objective Function | Average Time | |
|---|---|---|
| upper level | INSBBO | 12.7821 |
| NSBBO | 13.482 | |
| NSGA-Ⅱ | 14.231 | |
| MOPSO | 11.642 | |
| lower level | IBBO | 4.27 |
| BBO | 4.31 | |
| GA | 5.34 | |
| PSO | 4.98 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Fan, C.; Liu, S.; Xing, H.; Qi, C. Bi-Level Fuzzy Expectation-Based Dynamic Anti-Missile Weapon Target Allocation in Rolling Horizons. Electronics 2022, 11, 3035. https://doi.org/10.3390/electronics11193035
Zhu X, Fan C, Liu S, Xing H, Qi C. Bi-Level Fuzzy Expectation-Based Dynamic Anti-Missile Weapon Target Allocation in Rolling Horizons. Electronics. 2022; 11(19):3035. https://doi.org/10.3390/electronics11193035
Chicago/Turabian StyleZhu, Xiaowen, Chengli Fan, Shengli Liu, Huaixi Xing, and Cheng Qi. 2022. "Bi-Level Fuzzy Expectation-Based Dynamic Anti-Missile Weapon Target Allocation in Rolling Horizons" Electronics 11, no. 19: 3035. https://doi.org/10.3390/electronics11193035
APA StyleZhu, X., Fan, C., Liu, S., Xing, H., & Qi, C. (2022). Bi-Level Fuzzy Expectation-Based Dynamic Anti-Missile Weapon Target Allocation in Rolling Horizons. Electronics, 11(19), 3035. https://doi.org/10.3390/electronics11193035






