Low-Frequency Noise Modeling of 4H-SiC Metal-Oxide-Semiconductor Field-Effect Transistors
Abstract
:1. Introduction
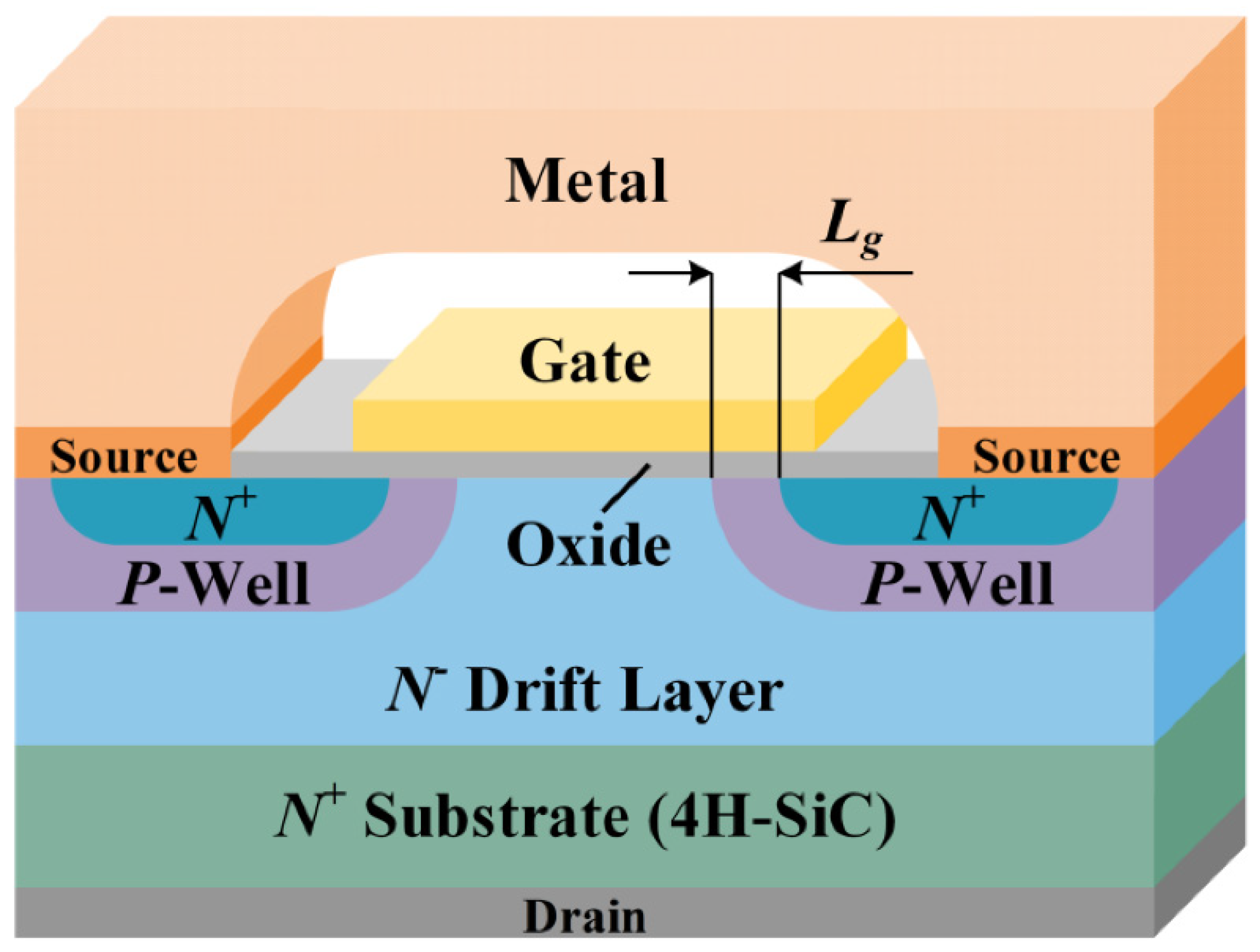
2. Derivation of Noise Model
3. Calculation of Trap State Density
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| LFN | Low-Frequency Noise |
| SiC | Silicon Carbide |
| MOSFETs | Metal-Oxide-Semiconductor Field-Effect Transistors |
| c-Si | Monocrystalline Silicon |
| Poly-Si | Polycrystalline Silicon |
| TFTs | Thin-Film Transistors |
| PSD | Power Spectral Density |
| VDM | Vertical Double Implant |
References
- Rumyantsev, S.L.; Shur, M.S.; Levinshtein, M.E.; Ivanov, P.A.; Palmour, J.W.; Das, M.K.; Hull, B.A. Low frequency noise in 4 H-SiC metal oxide semiconductor field effect transistors. J. Appl. Phys. 2008, 104, 094505. [Google Scholar] [CrossRef]
- Elasser, A.; Chow, T.P. Silicon carbide benefits and advantages for power electronics circuits and systems. Proc. IEEE 2002, 90, 969–986. [Google Scholar] [CrossRef]
- Ino, K.; Miura, M.; Nakano, Y.; Aketa, M.; Kawamoto, N. SiC Power Device Evolution Opening a New Era in Power Electronics. In Proceedings of the 2019 IEEE International Conference on Electron Devices and Solid-State Circuits (EDSSC), Xi’an, China, 12–14 June 2019; pp. 1–3. [Google Scholar] [CrossRef]
- Lv, C.; Hu, C.; Luo, J.; Liu, S.; Qiao, Y.; Zhang, Z.; Song, J.; Shi, Y.; Cai, J.; Watanabe, A. Recent advances in graphene-based humidity sensors. Nanomaterials 2019, 9, 422. [Google Scholar] [CrossRef] [PubMed]
- Dastgeer, G.; Shahzad, Z.M.; Chae, H.; Kim, Y.H.; Ko, B.M.; Eom, J. Bipolar Junction Transistor Exhibiting Excellent Output Characteristics with a Prompt Response against the Selective Protein. Adv. Funct. Mater. 2022, 32, 2204781. [Google Scholar] [CrossRef]
- Chen, H.; He, L. The spatial and energy distribution of oxide trap responsible for 1/f noise in 4H-SiC MOSFETs. J. Phys. Commun. 2021, 5, 035002. [Google Scholar] [CrossRef]
- Bolotnikov, A.; Losee, P.; Matocha, K.; Glaser, J.; Nasadoski, J.; Wang, L.; Elasser, A.; Arthur, S.; Stum, Z.; Sandvik, P.; et al. 3.3kV SiC MOSFETs designed for low on-resistance and fast switching. In Proceedings of the 2012 24th International Symposium on Power Semiconductor Devices and ICs, Bruges, Belgium, 3–7 June 2012; pp. 389–392. [Google Scholar] [CrossRef]
- Zhang, C.X.; Shen, X.; Zhang, E.X.; Fleetwood, D.M.; Schrimpf, R.D.; Francis, S.A.; Roy, T.; Dhar, S.; Ryu, S.H.; Pantelides, S.T. Temperature dependence and postirradiation annealing response of the 1/f noise of 4H-SiC MOSFETs. IEEE Trans. Electron Devices 2013, 60, 2361–2367. [Google Scholar] [CrossRef]
- Yang, X.; Chen, Y.Q.; Hou, B.; Xu, X.; Wang, J.; Huang, Y.; Chen, Q.; Zhou, C. Degradation behavior and defect analysis for SiC power MOSFETs based on low-frequency noise under repetitive power-cycling stress. IEEE Trans. Electron Devices 2020, 68, 666–671. [Google Scholar] [CrossRef]
- Wang, J.L.; Chen, Y.Q.; Feng, J.T.; Xu, X.B.; En, Y.F.; Hou, B.; Gao, R.; Chen, Y.; Huang, Y.; Geng, K.W. Trap analysis based on low-frequency noise for SiC power MOSFETs under repetitive short-circuit stress. IEEE J. Electron Devices Soc. 2020, 8, 145–151. [Google Scholar] [CrossRef]
- Simoen, E.; Claeys, C. On the flicker noise in submicron silicon MOSFETs. Solid State Electron. 1999, 43, 865–882. [Google Scholar] [CrossRef]
- Fleetwood, D.M. 1/f Noise and Defects in Microelectronic Materials and Devices. IEEE Trans. Nucl. Sci. 2015, 62, 1462–1486. [Google Scholar] [CrossRef]
- Van Der Wel, A.P.; Klumperink, E.A.M.; Kolhatkar, J.S.; Hoekstra, E.; Snoeij, M.F.; Salm, C.; Wallinga, H.; Nauta, B. Low-Frequency Noise Phenomena in Switched MOSFETs. IEEE J. Solid-State Circuits 2007, 42, 540–550. [Google Scholar] [CrossRef]
- Chobola, Z. Noise as a tool for non-destructive testing of single-crystal silicon solar cells. Microelectron. Reliab. 2001, 41, 1947–1952. [Google Scholar] [CrossRef]
- Vandamme, L.K.J. Noise as a diagnostic tool for quality and reliability of electronic devices. IEEE Trans. Electron Devices 1994, 41, 2176–2187. [Google Scholar] [CrossRef]
- McWhorter, A.L.; Kingston, R.H. Semiconductor Surface Physics; University of Pennsylvania: Philadelphia, PA, USA, 1957; p. 207. [Google Scholar]
- Hooge, F.N. 1/f noise sources. IEEE Trans. Electron Devices 1994, 41, 1926–1935. [Google Scholar] [CrossRef]
- Rumyantsev, S.L.; Shur, M.S.; Levinshtein, M.E.; Ivanov, P.A.; Palmour, J.W.; Agarwal, A.K.; Dhar, S. Si-like low-frequency noise characteristics of 4H-SiC MOSFETs. Semicond. Sci. Technol. 2011, 26, 085015. [Google Scholar] [CrossRef]
- Dimitriadis, C.A.; Kamarinos, G.; Brini, J. Model of low frequency noise in polycrystalline silicon thin-film transistors. IEEE Electron Device Lett. 2001, 22, 381–383. [Google Scholar] [CrossRef]
- Deng, W.; Liang, P.; Wei, C. Low frequency noise modeling of polycrystalline silicon thin-film transistors. Eur. Phys. J. Appl. Phys. 2009, 48, 10303. [Google Scholar] [CrossRef]
- Fung, T.C.; Baek, G.; Kanicki, J. Low frequency noise in long channel amorphous In–Ga–Zn–O thin film transistors. J. Appl. Phys. 2010, 108, 074518. [Google Scholar] [CrossRef] [Green Version]
- Theodorou, C.G.; Tsormpatzoglou, A.; Dimitriadis, C.A.; Khan, S.A.; Hatalis, M.K.; Jomaah, J.; Ghibaudo, G. Origin of low-frequency noise in the low drain current range of bottom-gate amorphous IGZO thin-film transistors. IEEE Electron Device Lett. 2011, 32, 898–900. [Google Scholar] [CrossRef]
- Ghibaudo, G.; Roux, O.; Nguyen, D.C.; Balestra, F.; Brini, J. Improved analysis of low frequency noise in field-effect MOS transistors. Phys. Stat. Sol. 1991, 124, 571–581. [Google Scholar] [CrossRef]
- Rhayem, J.; Rigaud, D.; Valenza, M.; Szydlo, N.; Lebrun, H. 1/f noise in amorphous silicon thin film transistors: Effect of scaling down. Solid State Electron. 1999, 43, 713–721. [Google Scholar] [CrossRef]
- Iñiguez, B.; Xu, Z.; Fjeldly, T.A.; Shur, M.S. Unified model for short-channel poly-Si TFTs. Solid State Electron. 1999, 43, 1821–1831. [Google Scholar] [CrossRef]
- Jacunski, M.D.; Shur, M.S.; Owusu, A.A.; Ytterdal, T.; Hack, M.; Iniguez, B. A short-channel DC SPICE model for polysilicon thin-film transistors including temperature effects. IEEE Trans. Electron Devices 1999, 46, 1146–1158. [Google Scholar] [CrossRef]
- Park, J.C.; Kim, S.W.; Kim, C.J.; Kim, S.; Kim, D.H.; Cho, I.T.; Kwon, H.I. Low-frequency noise in amorphous indium-gallium-zinc oxide thin-film transistors from subthreshold to saturation. Appl. Phys. Lett. 2010, 97, 122104. [Google Scholar] [CrossRef]
- Fang, J.; Deng, W.; Ma, X.; Huang, J.; Wu, W. A surface-potential-based DC model of amorphous oxide semiconductor TFTs including degeneration. IEEE Electron Device Lett. 2016, 38, 183–186. [Google Scholar] [CrossRef]
- Deng, W.; Zheng, X.; Chen, R.; Liu, Y. Subthreshold characteristics of polysilicon TFTs. Solid State Electron. 2008, 52, 695–703. [Google Scholar] [CrossRef]
- Ghittorelli, M.; Torricelli, F.; Kovács-Vajna, Z.M. Analytical physical-based drain-current model of amorphous InGaZnO TFTs accounting for both non-degenerate and degenerate conduction. IEEE Electron Device Lett. 2015, 36, 1340–1343. [Google Scholar] [CrossRef]
- Wei, X.; Deng, W.; Fang, J.; Ma, X.; Huang, J. Determination of bulk and interface density of states in metal oxide semiconductor thin-film transistors by using capacitance–voltage characteristics. Eur. Phys. J.-Appl. Phys. 2017, 80, 10103. [Google Scholar] [CrossRef]
- Lebedev, A.A.; Levinshtein, M.E.; Ivanov, P.A.; Kozlovski, V.V.; Strel’chuk, A.M.; Shabunina, E.I.; Fursin, L. Effect of Irradiation with 15-MeV Protons on Low Frequency Noise in Power SiC MOSFETs. Semiconductors 2019, 53, 1568–1572. [Google Scholar] [CrossRef]
- Choi, H.S.; Jeon, S.; Kim, H.; Shin, J.; Kim, C.; Chung, U.I. Verification of Interface state properties of a-InGaZnO thin-film transistors with SiNx and SiO2 gate dielectrics by low-frequency noise measurements. IEEE Electron Device Lett. 2011, 32, 1083–1085. [Google Scholar] [CrossRef]
- Jeong, C.Y.; Park, I.J.; Cho, I.T.; Lee, J.H.; Cho, E.S.; Ryu, M.K.; Park, S.H.K.; Song, S.H.; Kwon, H.I. Investigation of the Low-Frequency Noise Behavior and Its Correlation with the Subgap Density of States and Bias-Induced Instabilities in Amorphous InGaZnO Thin-Film Transistors with Various Oxygen Flow Rates. Jpn. J. Appl. Phys. 2012, 51, 100206. [Google Scholar] [CrossRef]


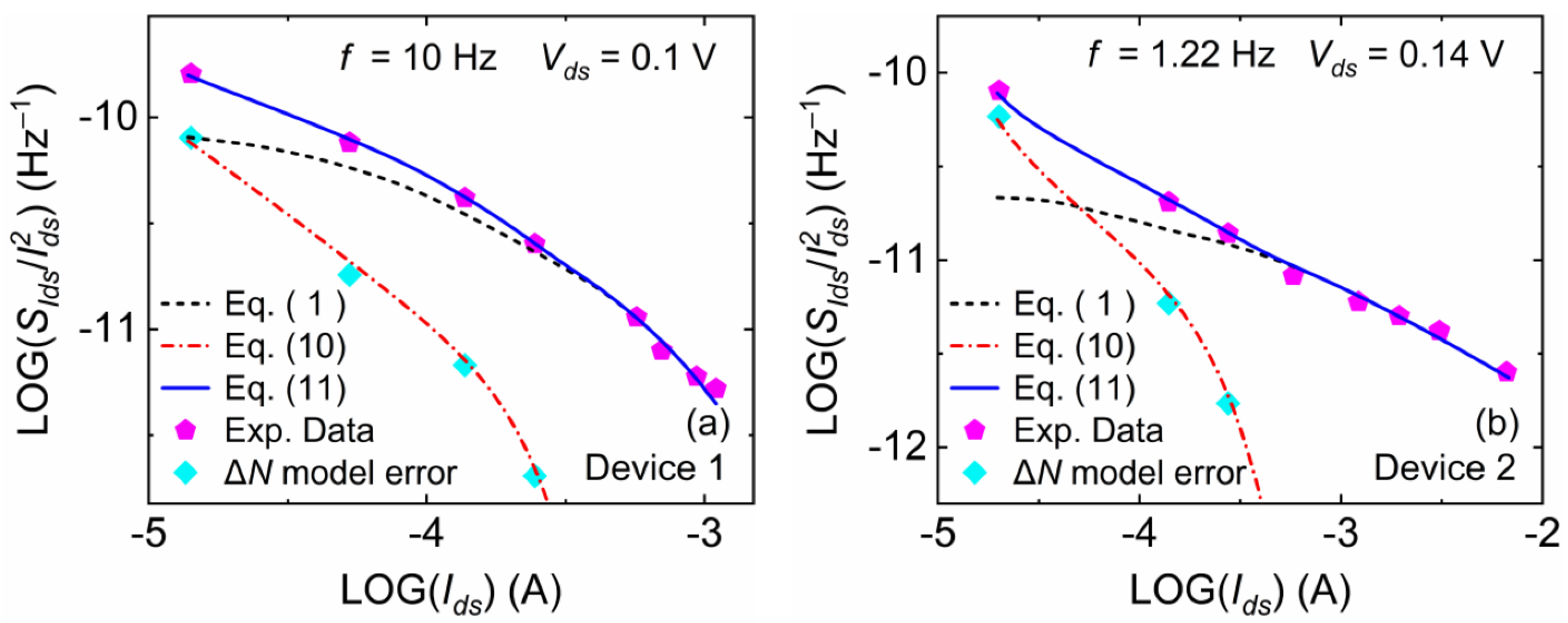
| Parameters | Figure 4a (Device 1) | Figure 4b (Device 2) |
|---|---|---|
| SVfb (V2/Hz) | 4 × 10−11 | 1.15 × 10−12 |
| Vds (V) | 0.1 | 0.14 |
| T (K) | 298 | 298 |
| η | 3.5 | 11.35 |
| μeff (cm2/Vs) | 3.3 | 0.5 |
| Vth (V) | 5 | 2 |
| Cox (F/cm2) | 2 × 10−8 | 1 × 10−8 |
| εSiC (F/cm) | 8.6 × 10−13 | 8.6 × 10−13 |
| f (Hz) | 10 | 1.22 |
| αH | 2.86 × 10−4 | 1.95 × 10−4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Ye, W.; Xiong, X.; Deng, W. Low-Frequency Noise Modeling of 4H-SiC Metal-Oxide-Semiconductor Field-Effect Transistors. Electronics 2022, 11, 3050. https://doi.org/10.3390/electronics11193050
Liu Y, Ye W, Xiong X, Deng W. Low-Frequency Noise Modeling of 4H-SiC Metal-Oxide-Semiconductor Field-Effect Transistors. Electronics. 2022; 11(19):3050. https://doi.org/10.3390/electronics11193050
Chicago/Turabian StyleLiu, Yuan, Weijie Ye, Xiaoming Xiong, and Wanling Deng. 2022. "Low-Frequency Noise Modeling of 4H-SiC Metal-Oxide-Semiconductor Field-Effect Transistors" Electronics 11, no. 19: 3050. https://doi.org/10.3390/electronics11193050
APA StyleLiu, Y., Ye, W., Xiong, X., & Deng, W. (2022). Low-Frequency Noise Modeling of 4H-SiC Metal-Oxide-Semiconductor Field-Effect Transistors. Electronics, 11(19), 3050. https://doi.org/10.3390/electronics11193050






