Research on BeiDou B1C Signal Abnormal Monitoring Algorithm Based on Machine Learning
Abstract
:1. Introduction
2. BeiDou B1C Signal Characteristics and Its Threat Model
2.1. BDS B1C Signal Structure
2.2. Threat Model and Distortion Type of BeiDou B1C Signal
- Threat Model A (TM-A): This type of threat is expressed as the advance or delay of the falling edge of each unit code (TC) block relative to the normal falling edge (Δ).
- Threat Model B (TM-B): This type of threat is expressed as a 2-order step ringing response of the code block, and fd is the oscillation frequency in MHZ. σ is the damping coefficient in monap per second (MNp/s).
- Threat Model C (TM-C): This type of threat is represented as a combination of digital distortion and analog distortion.
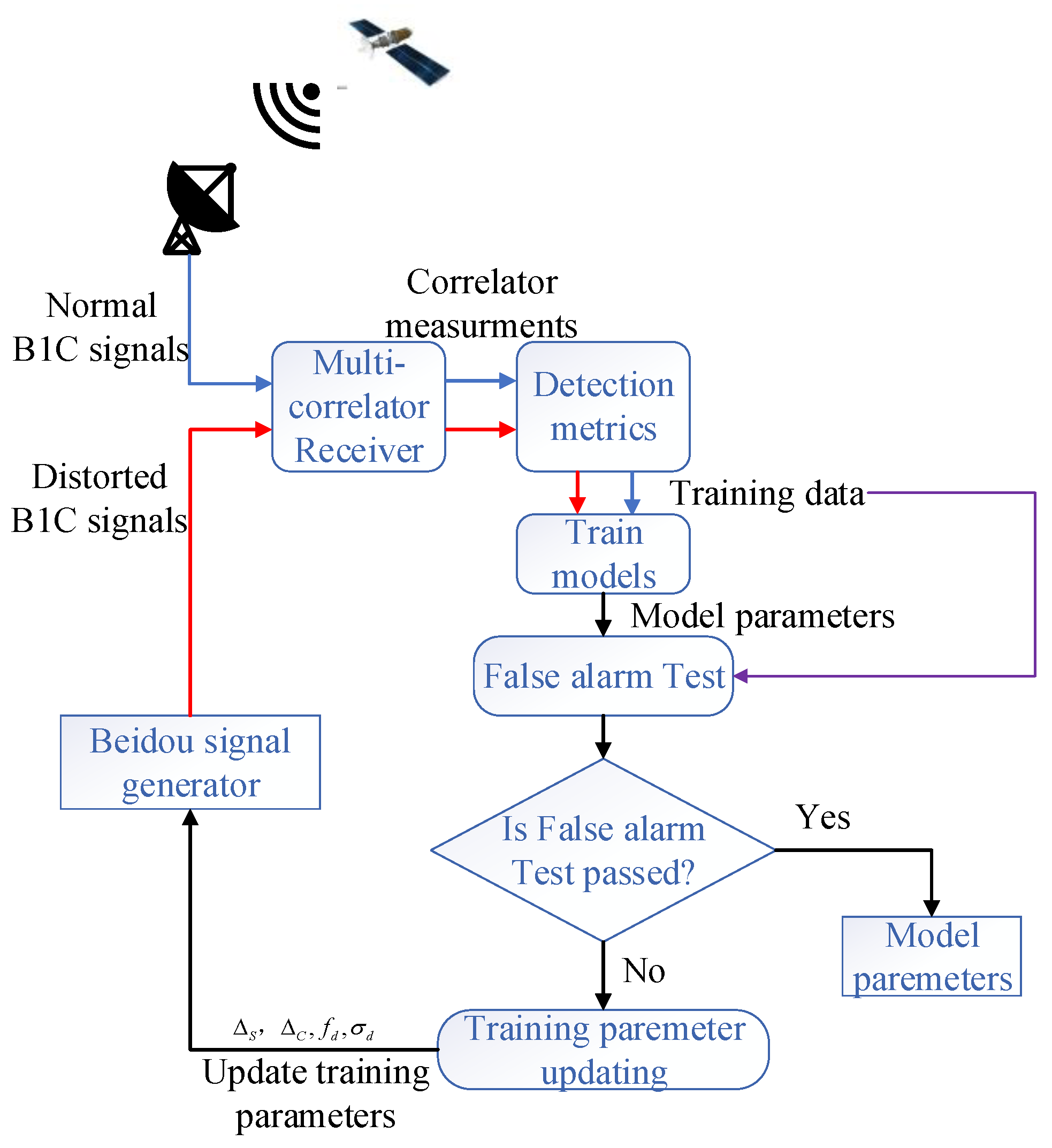
3. QDA-Based Multi-Correlator Method
3.1. Offline Training
3.2. Online Monitoring
4. Experimental Results
4.1. Experimental Configuration
4.2. Classification Results of Three Distortions
4.3. Classification Accuracy of Different Feature Vectors
4.4. Comparison with Traditional Methods
4.5. Real Signal Evaluation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mitelman, A.; Phelts, R. A real-time signal quality monitor for GPS augmentation systems. In Proceedings of the 13th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 2000), Salt Lake City, UT, USA, 19–22 September 2000. [Google Scholar]
- Pagot, J.; Thevenon, P. Threat models design for new GNSS signals. In Proceedings of the 2016 International Technical Meeting of The Institute of Navigation, Monterey, CA, USA, 25–28 January 2016. [Google Scholar]
- Sun, C.; Zhao, H. A Novel Digital Threat Model and Effect Analysis on Modernized BeiDou Signals. In Proceedings of the 2016 International Technical Meeting of The Institute of Navigation, Monterey, CA, USA, 25–28 January 2016. [Google Scholar]
- Pagot, J.; Julien, O. Signal Quality Monitoring for New GNSS Signals. Navigation 2018, 65, 83–97. [Google Scholar] [CrossRef]
- He, C.; Guo, J. A newevil waveforms evaluating method for new BDS navigation signals. GPS Solut. 2018, 22, 1–13. [Google Scholar] [CrossRef]
- Sun, C.; Cheong, J. GNSS Spoofing Detection by Means of Signal Quality Monitoring (SQM) Metric Combinations. IEEE Access 2018, 6, 66428–66441. [Google Scholar] [CrossRef]
- Ali, K.; Manfredini, E. Vestigial signal defense through signal quality monitoring techniques based on joint use of two metrics. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium—PLANS 2014, Monterey, CA, USA, 5–8 May 2014. [Google Scholar]
- Phelts, R. Multicorrelator Techniques for Robust Mitigation of Threatsto GPS Signal Quality. Ph.D. Dissertation, Stanford University, Stanford, CA, USA, 2001. [Google Scholar]
- International Civil Aviation Organization. Aeronautical Telecommunications. Int. Stand. Recomm. Pract. 2006, 1, 55–61. [Google Scholar]
- Fontanella, D.; Paonni, M. A Novel Evil Waveforms Threat Model for New Generation GNSS Signals-Theoretical Analysis and Performance. In Proceedings of the ESA Workshop on Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing (NAVITEC), Noordwijk, The Netherlands, 8–10 December 2010. [Google Scholar]
- Sun, C.; Zhao, H. A frequency domain-based detection technique for digital distortion on GNSS signals. In Proceedings of the Institute of Navication GNSSC, Oregon, Portland, 12 September 2016. [Google Scholar]
- Sun, C.; Zhao, H. The IFFT-based SQM method against digital distortion in GNSS signals. GPS Solut. 2018, 21, 1457–1468. [Google Scholar] [CrossRef]
- Wei, K.; Cui, X. A Research on Modeling and Monitoring of New BDS B1C Signal Distortions in the Context of BeiDou Satellite Based Augmentation System. In Proceedings of the Institute of Navigation International Technical Meeting 2020, San Diego, CA, USA, 21–24 January 2020. [Google Scholar]










| Parameter | Value |
|---|---|
| Tracking technique | E-L(BOC(1,1) local replica) |
| Correlator spacing | 0.5 TC |
| Front-end bandwidth | 16 MHz |
| Sampling frequency | 40 MHz |
| ADC resolution | 4 Bits |
| Coherent integration time | 10 ms |
| Parameter | Value | ||
|---|---|---|---|
| M (In Chip Unit, TC) | n1 (Amount) | n2 (Amount) | |
| 0.02 | 10 | 10 | |
| 0.02 | 8 | 8 | |
| 0.02 | 6 | 6 | |
| 0.02 | 4 | 4 | |
| 0.03 | 4 | 4 | |
| 0.04 | 3 | 3 | |
| Test Data Set | Satellite | ||
|---|---|---|---|
| BDS-M2 | BDS-M3 | BDS-M5 | |
| Group 1 | 0.0024% | 0.0042% | 0.0031% |
| Group 2 | 0.0007% | 0.0015% | 0.0013% |
| Group 3 | 0.0003% | 0.0009% | 0.0008% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Yu, B.; Yi, Q.; Zhao, J.; Yang, J.; Guo, C. Research on BeiDou B1C Signal Abnormal Monitoring Algorithm Based on Machine Learning. Electronics 2022, 11, 3201. https://doi.org/10.3390/electronics11193201
Liu L, Yu B, Yi Q, Zhao J, Yang J, Guo C. Research on BeiDou B1C Signal Abnormal Monitoring Algorithm Based on Machine Learning. Electronics. 2022; 11(19):3201. https://doi.org/10.3390/electronics11193201
Chicago/Turabian StyleLiu, Liang, Baoguo Yu, Qingwu Yi, Jingbo Zhao, Jianglei Yang, and Chengjun Guo. 2022. "Research on BeiDou B1C Signal Abnormal Monitoring Algorithm Based on Machine Learning" Electronics 11, no. 19: 3201. https://doi.org/10.3390/electronics11193201
APA StyleLiu, L., Yu, B., Yi, Q., Zhao, J., Yang, J., & Guo, C. (2022). Research on BeiDou B1C Signal Abnormal Monitoring Algorithm Based on Machine Learning. Electronics, 11(19), 3201. https://doi.org/10.3390/electronics11193201






