Hybrid Full Adders: Optimized Design, Critical Review and Comparison in the Energy-Delay Space

Abstract

In this paper, we design and compare seven meaningful hybrid one-bit full adders topologies that are optimized in terms of energy-delay trade-offs to operate in multibit ripple carry adders. The goal is to provide the designer with a simple and powerful approach for choosing the best topology for a given power budget, speed performance, or any combination of both. The design and comparison deal with 4-bit and 8-bit ripple carry adders and exploit the derivation of the energy-efficient curves in the energy-delay space. To do so, first we define the procedures to obtain energy consumption and propagation delay by simulating a ripple carry adder designed at a transistor level. Then, we introduce a design methodology to optimize a ripple carry adder by minimizing some significant figures-of-merit in terms of energy-delay trade-offs. The comparison of the energy-efficient curves allows us to make a simple and effective comparison as well as to identify the best one-bit full adder topologies.

1. Introduction

The one bit full adder (OBFA) is a key element for performing calculation operations, as it is the main circuit to implement a n-bit adder, the basic arithmetic circuit of every digital system [1,2]. Hence, the choice of a specific transistor-level topology of OBFA and its corresponding design must be pursued with particular attention and care. Indeed, in a digital system, the OBFA determines the performance of the parts dedicated to the execution of arithmetic operations, thus strongly affecting the overall performance of the system in terms of speed and energy consumption.

Among the numerous topologies adopted to implement an OBFA, two general design strategies can be identified. The natural (and more trivial) way makes use of only one logic style [1,2]. In contrast, the hybrid strategy considers different logic styles that are shared and combined together to gain performance benefits [3,4].

Compared to conventional approaches based on a single logic style, hybrid topologies seem to be particularly interesting. For example, in OBFAs the benefits of transmission gate [1] or transmission function [5] logic styles can be nullified by their intrinsic lack of driving capability, a drawback that can be solved merging a second different logic style. For this reason, in recent years, the hybrid approach has gained greater interest as demonstrated by the several topologies proposed in the literature [3,4,6,7,8,9,10].

Considering the assortment of OBFAs, further extended with the introduction of hybrid structures, the comparison of different topologies at the transistor-level becomes a typical, but not trivial, target. In this scenario, the lack of effective comparison criteria makes it difficult for the designer to select the best topology for a given power budget, speed performance or any combination of both. Some comparison approaches were proposed initially in [11,12,13] and, more recently, in [3,4,6,7,8,9,10,14,15,16,17,18], where new topologies were also presented. All these approaches compared the OBFA topologies with regard to speed, energy consumption, power-delay product, or a mixture of other equivalent factors. In general, the comparison considered only a couple of design points instead of inspecting the whole energy-delay space (EDS).

Over the past two decades, the EDS has become the primary domain for comparing digital circuits and systems fairly. Indeed, exploiting the generalized figure of merit (FOM), $E^i{D}^j$, introduced in [19,20,21,22,23], we can fully understand the energy-delay trade-offs of a digital circuit. The generalized FOM can also be used to compare different basic arithmetic circuits or blocks in terms of energy-delay properties but, in the case of full adders, it was only used in [24] and [25]. In the first article, the comparison was conducted on an architectural level, since different structures of n-bit full adders were analyzed. In the second work, the comparison considered different OBFA topologies at the transistor-level and, with the exception of two hybrid circuits, it focused on traditional and more consolidated structures. Therefore, a clear and reliable comparison of a meaningful set of hybrid OBFAs in the entire EDS is still missing.

In this paper, we compare the most promising and meaningful hybrid OBFA in the whole EDS. The goal is to provide the designer with a simple and powerful approach for choosing the best topology for a given power budget, speed performance or any combination of both. The comparison also includes the last recent topologies and concerns the following hybrid structures:

• Low-Power (LP) full adder [26];
• New Hybrid Pass Static CMOS (NHPSC) full adder [4];
• Hybrid full adder with 22 Transistors (HFA-22T) [18];
• Hybrid full adder with Buffer and 26 Transistors (HFA-B-26T) [18];
• high-speed hybrid full adder design-2 (HSHFA-D2) [9];
• high-speed hybrid full adder design-4 (HSHFA-D4) [9];
• scalable low-power hybrid full adder (SLPHFA) [10].

In addition, the conventional mirror CMOS (CMC) full adder is also included in the comparison so as to have a well-known and consolidated topology as a reference structure.

The comparison exploits the design methodology presented in [25], where the transistors of OBFAs were sized by minimizing the generalized FOM, $E^i{D}^j$, for some specific values of i and j. The procedure allowed one to build the energy-efficient curve (EEC) that was subsequently used to compare different structures. Unlike [25], where the design methodology and the comparison considered the single OBFA cell, in this case the design (and the transistor sizing) is focused on multibit ripple carry adders consisting of the hybrid OBFAs mentioned above.

The paper is structured as follows. Section 2 outlines how the EEC can be used to compare digital circuits. Section 3 briefly describes the considered OBFA topologies. Section 4 reports the adopted simulation strategies. Section 5 illustrates the optimized design strategy through the energy-efficient curve determination. Section 6 summarizes the OBFA comparison. Finally, Section 7 reports conclusions and final remarks.

2. Overview on the Energy-Delay Space

The product of energy and delay ($ED$) measures the trade-off between speed and dissipation and is a well-known figure of merit (FOM) typically used in the analysis and design of digital circuits and systems. A more generalized approach was proposed in the early 2000s where the general parameter, $E^i{D}^j$ (or the interchangeable $E{D}^{\eta }$, with $\eta =j/i$), was introduced in [19] to account for any speed-dissipation trade-off. For this parameter, the cases of minimum energy dissipation and minimum delay are represented by $j/i=0$ ($\eta =0$) and $j/i=\infty$ ($\eta =\infty$), respectively. In the same paper, assuming a defined power supply of the circuit or system under consideration, the energy efficient curve (EEC) is also introduced.

The EEC is composed of the points where the circuit or system has the minimum delay for a given energy consumption or, equivalently, the minimum energy consumption for a given delay. It is apparent that any design point above the EEC is inefficient because either, at the same delay, an unnecessary higher energy dissipation is wasted or, at the same energy, a higher delay is present.

As shown in [20], the EEC can be modeled by:

$$\left(\frac{E}{E_0}-1\right)\left(\frac{D}{D_0}-1\right)=1,$$

(1)

where $E_0$ and $D_0$ are the asymptotes that represent the two theoretical minimum for the energy and the delay, respectively. When plotted in the Energy-Delay Space (EDS), the EEC follows the hyperbolic function shown in Figure 1. Of course, real circuits may diverge from (1) and, to model realistic cases, the parameter $\gamma$ ($0<\gamma \le 1$) was introduced in [21,22] to correct relationship (1) into:

$$\left(\frac{E}{E_0}-1\right)\left(\frac{D}{D_0}-1\right)=\gamma .$$

(2)

It can be demonstrated that the EEC is composed of the points that minimize the generic FOM, $E^i{D}^j$, as parameters i and j vary [20,24]. In other words, all optimal transistor sizing that minimize $E^i{D}^j$ lie on the EEC.

The EEC represents a useful and simple tool for comparing similar digital circuits, whether they are transistor-level topologies or system architectures. Consider for example the two EECs shown in Figure 2, which refer to two different digital circuits, namely A (red) and B (blue). Assume also that the two circuits are designed in the points, $P_0$ and $Q_0$, shown in the figure. Limiting the comparison to these two points only, we can conclude that circuit A performs better than B in terms of delay and, on the other side, that circuit B is better than A in terms of dissipation.

Focusing the attention on the two EECs that describe their respective circuits with regard to energy-delay trade-offs, it becomes evident that, with respect to circuit A designed in point $P_0$, circuit B can be designed at the same speed but with a lower energy consumption (point $Q_1$) or with a lower delay at the same energy consumption (point $Q_2$). Conversely, with respect to circuit B designed in point $Q_0$, circuit A can be designed with a lower delay at the same energy consumption (point $P_1$) or at the same delay but with a lower energy consumption (point $P_2$). More generally, the two EECs in Figure 2 divide the EDS in two regions. If speed is the main specification, circuit B can be designed to perform better than A. On the other hand, if power dissipation is the main goal, circuit A can be designed to perform better than B. The best solution is achieved by considering the design points that lie in the two solid lines that belong to both circuits and by discarding the design points in the dashed lines.

3. OBFA Topologies

The OBFA structures that will be compared in the following are briefly discussed in this section. All of them receive three input bits, A, B and $C_{\mathrm{i}}$ (i.e., the bits to be summed and the Carry Input from the previous stage), and generate two output bits, the Sum and the Carry Output, defined by

$$\begin{array}{cc}\hfill S& =A\oplus B\oplus C_{\mathrm{i}}\hfill \end{array}$$

(3a)

$$\begin{array}{cc}\hfill C_{\mathrm{o}}& =\left(A+B\right)C_{\mathrm{i}}+AB\hfill \end{array}$$

(3b)

being $X\oplus Y=X\overline{Y}+\overline{X}Y$ the xor operator.

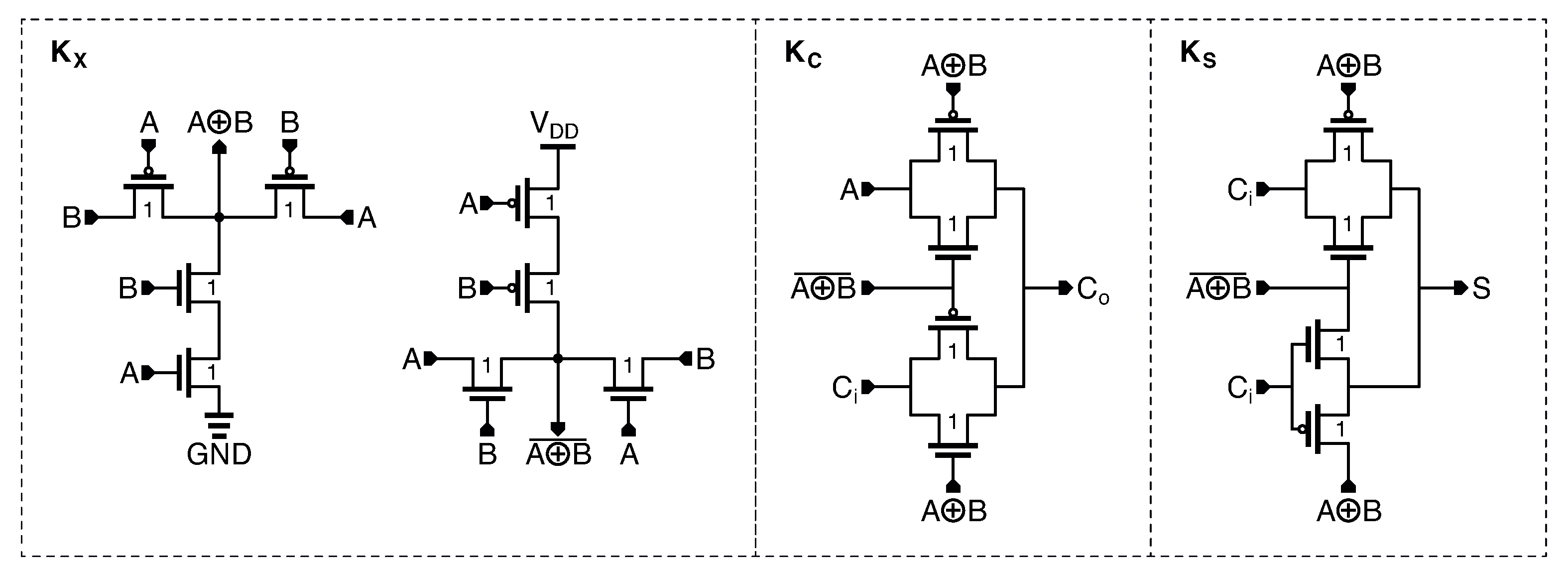
The low-power (LP) full adder is shown in Figure 3. It is one of the first hybrid topologies and was presented in [26]. It is based on the low power xor and xnor gates, introduced in [27], that produce the intermediate Propagate signals, $P=A\oplus B$ and $\overline{P}=\overline{A\oplus B}$. Then, the two outputs are generated by:

$$\begin{array}{cc}\hfill S& =\left(A\oplus B\right)\overline{C_{\mathrm{i}}}+\left(\overline{A\oplus B}\right)C_{\mathrm{i}}\hfill \end{array}$$

(4a)

$$\begin{array}{cc}\hfill C_{\mathrm{o}}& =\left(A\oplus B\right)C_{\mathrm{i}}+\left(\overline{A\oplus B}\right)A,\hfill \end{array}$$

(4b)

which are formally equivalent to (3). The current drawn from the power line is very small as only two transistors are directly connected to $V_{\mathrm{DD}}$ and GND. This greatly reduces the power dissipation. However, the current flowing through the input terminals must be taken into account as it represents the main contribution to the energy consumption of the cell. The LP full adder belongs to the group of OBFA with no driving capability, as its outputs are not decoupled from the inputs of the next cell. This poses a serious drawback in the propagation of the Carry signal in n-bit adders. In fact, as analyzed in [13], when this type of cells is cascaded to compose an n-bit adder, the overall propagation delay of the carry signal becomes proportional to $n^2$, a value that can be prohibitive when a large number of bits have to be summed.

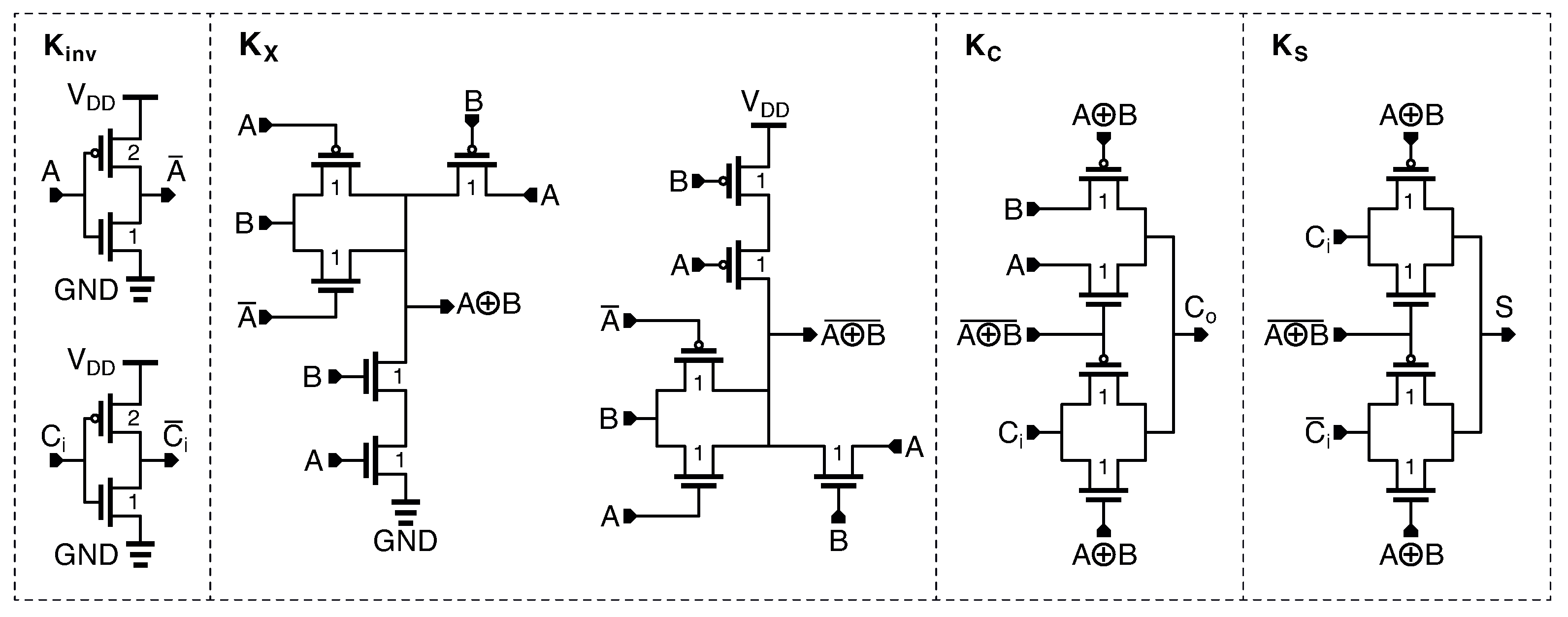
The new hybrid pass static CMOS (NHPSC) full adder is shown in Figure 4 and was proposed in [4]. The cell is a mixture of pass-transistor, transmission-gate, and standard CMOS logic. As CMOS inverters decouple the NHPSC full adder cell from the subsequent stages, it belongs to the group of OBFA with driving capability. In the original paper, it turned out to be the best over other topologies, so it was included in our comparison.

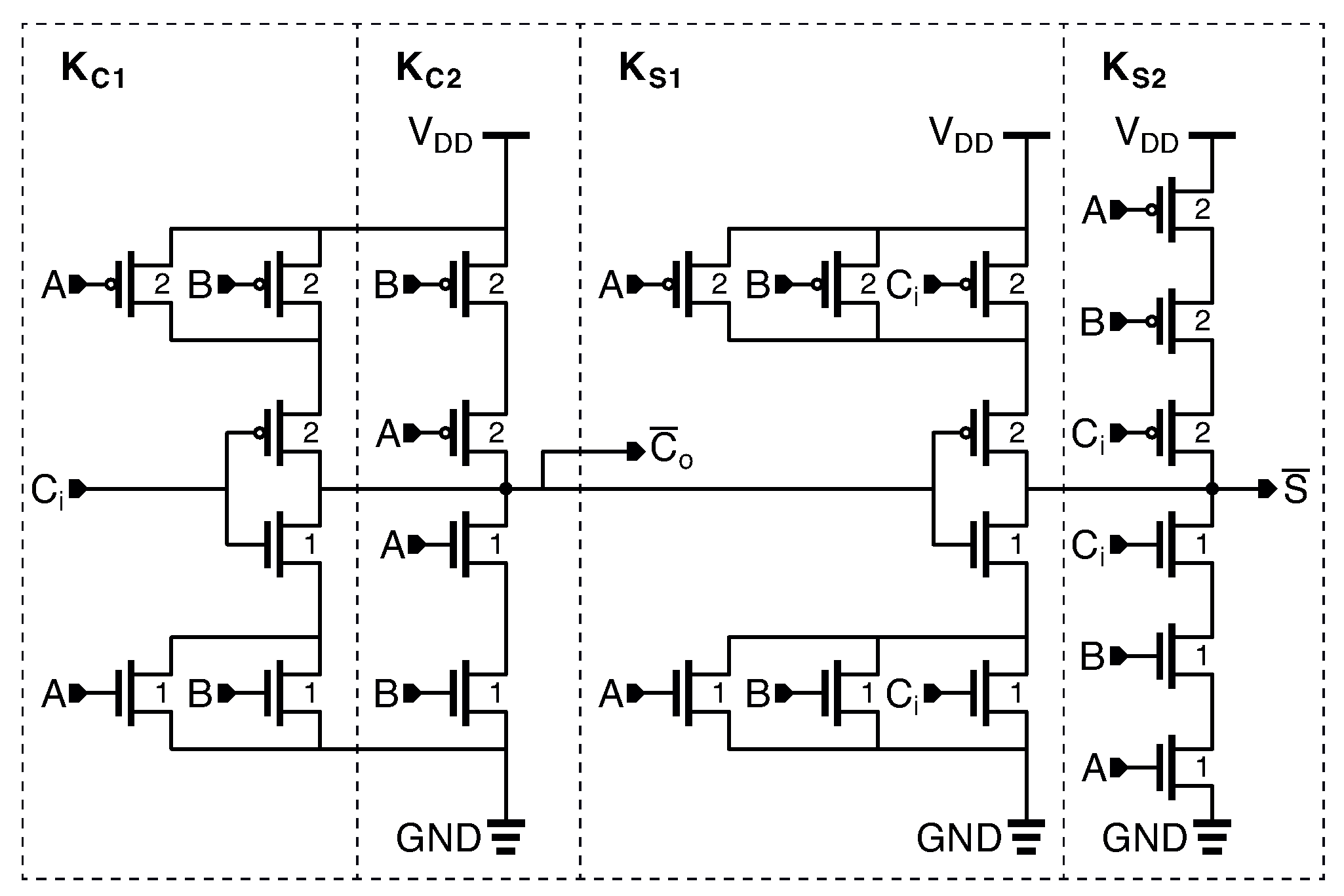
The hybrid full adder with 22 transistors (HFA-22T) and the hybrid full adder with buffer and 26 transistors (HFA-B-26T) are depicted in Figure 5 and Figure 6, respectively, and were both introduced in [18]. They exploited a new simultaneous XOR-XNOR circuit, that avoid glitches in the output nodes of the full adder. After introducing the XOR-XNOR circuit, the original paper presented also six new full adder topologies. Among these we have chosen for the comparison the HFA-22T cell, which is the most promising topology with no driving capability, and the HFA-B-26T cell, which is the most promising topology with driving capability.

The high-speed hybrid full adder design-2 (HSHFA-D2), shown in Figure 7, and the high-speed hybrid full adder design-4 (HSHFA-D4), shown in Figure 8 was presented in [9] in a group of four new full adders. In this case, the FAs are also based on a new high-speed, low-power 10-T XOR–XNOR circuit, which provided full simultaneous swing outputs and improved delay performance. Among the four topologies presented in the original paper, we have chosen for the comparison the HSHFA-D2 cell, that is the most promising topology with driving capability, and the HSHFA-D4 cell, which is the most promising topology with no driving capability.

The scalable low-power hybrid full adder (SLPHFA), shown in Figure 9, was presented in [10]. Differently from other topologies, the carry generation section is made up of a new AND-OR module with transmission gates and complementary pass transistor logic and does not use an intermediate propagate signal. The sum section exploits two XOR modules implemented using transmission gates and pass transistors. The circuit has no driving capability.

As we mentioned in the introduction, we included the conventional mirror CMOS (CMC) full adder in the comparison so as to have a well-known and consolidated topology as a reference structure. The CMC topology is shown in Figure 10. In this circuit, the Sum output is produced by exploiting the relationship $S=AB{C}_{\mathrm{i}}+\overline{C_{\mathrm{o}}}(A+B+C_{\mathrm{i}})$ [2]. It still remains one of the most used full adder topologies and is easily available in industrial libraries of standard cells.

Since the CMC cell produces the complemented signals, $\overline{S}$ and $\overline{C_{\mathrm{o}}}$, multibit adders are implemented as depicted in Figure 11, where the carry path does not require any signal inversion. This implementation exploits the properties of the sum function [2]:

$$\begin{array}{cc}\hfill \overline{S}& =S(\overline{A},\overline{B},\overline{C_{\mathrm{i}}})\hfill \end{array}$$

(5a)

$$\begin{array}{cc}\hfill \overline{C_{\mathrm{o}}}& =C_{\mathrm{o}}(\overline{A},\overline{B},\overline{C_{\mathrm{i}}}).\hfill \end{array}$$

(5b)

4. Comparison Strategy and Simulations

To extract the features of the OBFAs, we examined multi-bit ripple-carry adders (RCAs) and, in particular, we focused the comparison considering 4-bit and 8-bit structures. However, this is not a limitation since the same approach can be applied to any multi-bit RCA.

The multibit RCA, whose basic cell is the OBFA, is designed in a 28-nm FD-SOI CMOS technology from STMicroelectronics and, to simplify our investigation, we used regular threshold transistors only ($V_T\sim 350$ mV). The process allows a minimum channel size of $W_{\min }/L_{\min }=80\mathrm{nm}/30\mathrm{nm}$ with a nominal supply voltage of 1 V.

Each OBFA cell is described through suitable design parameters whose values are chosen with the help of the Cadence optimization tool (i.e., ADE Assembler). The design parameter values are constrained in limited ranges that are explored by the optimization tool through transient simulations of the entire multi-bit RCA. The target of the optimization process is to minimize a FOM defined with regard to delay and energy of the multi-bit RCA. As a consequence, by defining some suitable FOMs in terms of propagation delay and energy dissipation per clock cycle, the optimization tool can sweep the EDS and is able to find the EEC of the multi-bit RCA.

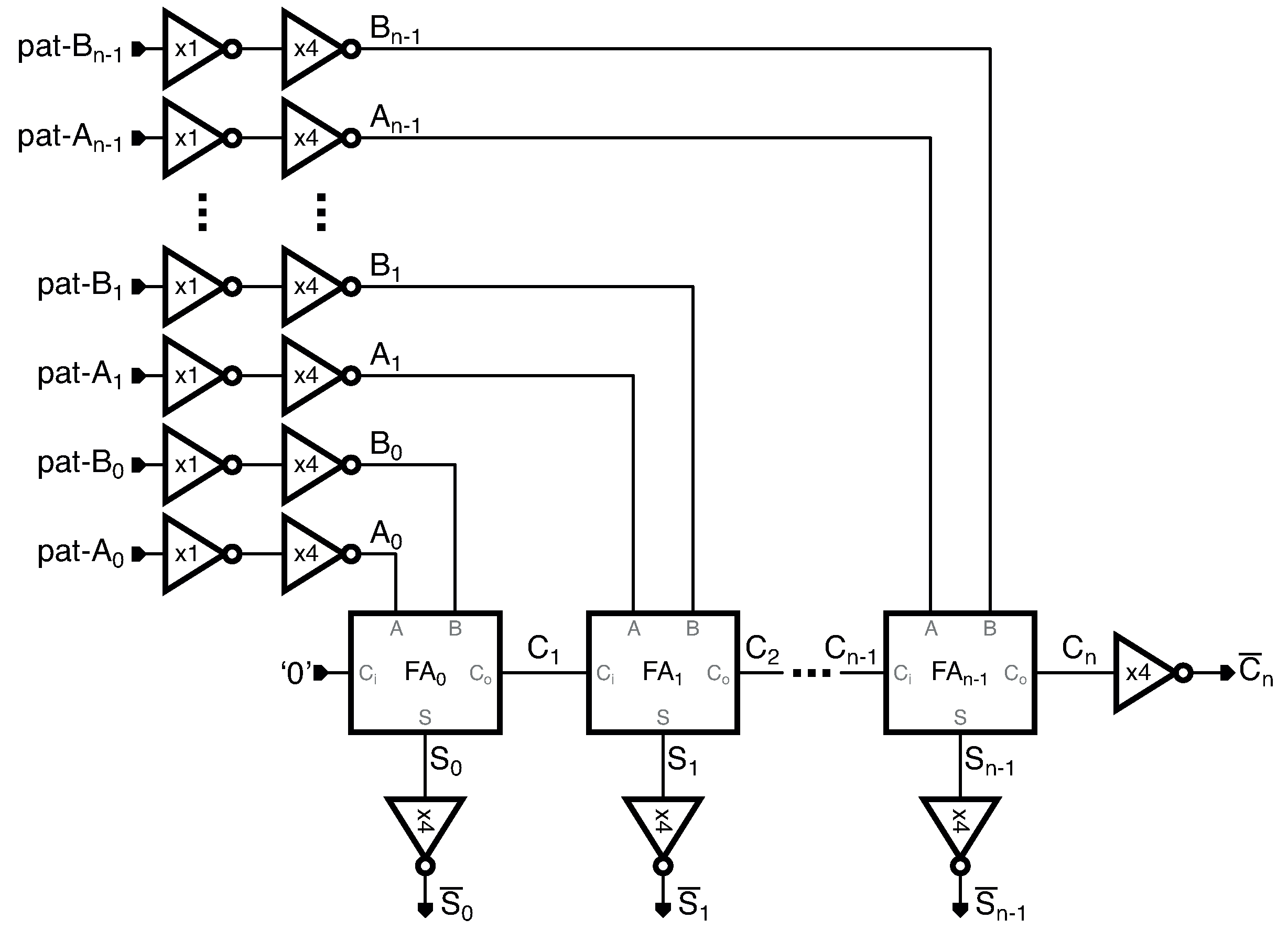
The schematic of the test-bench used for transient simulations is shown in Figure 12 where the n-bit RCA is realized by connecting the carry output of the ($j-1$)-th cell to the carry input of the j-th cell [2]. In the following, to simplify the notation, $C_j$ refers to the carry input of the j-th cell.

4.1. Carry Propagation Delay

In RCAs, the main speed limitation is determined by the carry signal that propagates through the cells of the multi-bit structure. Therefore, we are interested in measuring the interval of time between the simultaneous application of the input signals ($A_j,B_j$ in Figure 12) and the carry output of the last cell ($C_n$ in Figure 12). This interval of time is measured between 50% of input transition to the corresponding 50% of output transition and defines the Carry Propagation Delay (CPD). Obviously, we are interested in measuring the worst CPD that occurs when all the cells of the RCA propagate the carry signal.

With the exception of the first cell, FA${}_0$, the worst CPD is to be found among those input combinations that make the carry of every cell toggle only on the basis of the carry of the previous one. This happens when the propagate signal of such cells is high, that is for $P_j=A_j\oplus B_j=1$ or, in other words, when

$$A_j=\overline{B_j}(\forall j=1,2,\dots ,n-1).$$

(6)

Under the constraint set by (6), let us define ${\tau }_A$ as the propagation delay of the carry in the generic j-th cell when $A_j=1$ and ${\tau }_B$ as the propagation delay when $A_j=0$. If ${\tau }_A>{\tau }_B$ it is simple to show that the worst propagation delay between the first and the last carry output (i.e., between $C_1$ and $C_n$ in Figure 12) is observed when $A_j=1$ for any $j=1,2,\dots ,n-1$. Conversely, if ${\tau }_B>{\tau }_A$ the worst delay is observed when $A_j=0$ for any $j=1,2,\dots ,n-1$. It is evident that both conditions are to be explored.

In addition, two cases of carry propagation can be distinguished. In the first case, all carry signals start from zero and, when the cell FA${}_0$ sets $C_1=1$, all subsequent carry signals propagate to one. In the second case, all carry signals start from one and, when the cell FA${}_0$ sets $C_1=0$, all subsequent carry signals propagate to zero. Since $C_1=A_0{B}_0$, the first case occurs when the product $A_0{B}_0$ toggles from ‘0’ to ‘1’ while the second case when the product $A_0{B}_0$ toggles from ‘1’ to ‘0’.

Based on the discussion above, the worst CPD can be found by examining the four transitions reported in

Table 1. Transitions for determining the worst carry propagation delay.

	${\mathit{A}}_{\mathit{j}}=1;{\mathit{B}}_{\mathit{j}}=0$	${\mathit{A}}_{\mathit{j}}=0;{\mathit{B}}_{\mathit{j}}=1$
	$(j=1,2,\dots ,n-1)$	$(j=1,2,\dots ,n-1)$
	T1	T2
$A_0{B}_0=0\to 1$	$\mathbf{A}=00\dots 0\to 11\dots 1$	$\mathbf{A}=00\dots 0\to 00\dots 1$
	$\mathbf{B}=00\dots 0\to 00\dots 1$	$\mathbf{B}=00\dots 0\to 11\dots 1$
	T3	T4
$A_0{B}_0=1\to 0$	$\mathbf{A}=11\dots 1\to 11\dots 1$	$\mathbf{A}=00\dots 1\to 00\dots 0$
	$\mathbf{B}=00\dots 1\to 00\dots 0$	$\mathbf{B}=11\dots 1\to 11\dots 1$

, denoted as T1, T2, T3 and T4.

The test-bench in Figure 12 uses digital (ideal) patterns, pat-A${}_j$ and pat-B${}_j$, as input signals. The ideal patterns are shaped by two cascaded inverters (FO1 and FO4) to provide realistic inputs, $A_j$ and $B_j$, to the multi-bit RCA. The ideal patterns are sketched in Figure 13. First 6-bit sequences provide the four transitions defined in Table 1 and are used for the evaluation of the CPD. Subsequent bitstreams are randomly generated and, as detailed in the next subsection, are used to estimate the energy consumption.

In the evaluation of the propagation delay we consider $\overline{C_n}$ as the output signal. This is because, when the RCA is made up of OBFAs with no driving capability, the last carry, $C_n$, is not perfectly shaped and the identification of the 50% of output transition may fail. Reading the output after an inverter gate allows us to read a correct output signal at the price of a negligible added delay. Moreover, since the carry propagation depends on the product $A_0{B}_0$, one of these two waveforms is used as the input signal. Specifically, in transitions T1 and T3 we use $B_0$ and in transitions T2 and T4 we consider $A_0$.

Hence, the worst CPD is evaluated by:

$$\mathrm{CPD}=max\left[\mathrm{del}{(\overline{C_n},B_0)}_{\mathrm{T}1},\mathrm{del}{(\overline{C_n},A_0)}_{\mathrm{T}2},\mathrm{del}{(\overline{C_n},B_0)}_{\mathrm{T}3},\mathrm{del}{(\overline{C_n},A_0)}_{\mathrm{T}4}\right],$$

(7)

where $\mathrm{del}{(Y,X)}_{\mathrm{T}}$ represents the operator that evaluate the propagation delay between two digital signals, Y and X, at transition T.

4.2. Energy Consumption

The energy consumption accounts for the average energy dissipated in the multi-bit RCA per clock cycle. It is computed by simulating the circuit in Figure 12 using random bitstreams for the digital patterns, pat-A${}_j$ and pat-B${}_j$. Random bitstreams are generated using the Matlab code in Figure 13. Each bitstream sequence stems from a specific seed (set by the rng function) so that the patterns are reproducible and can be used as a reference for future tests. From Matlab, the patterns stored in the A and B matrices are saved into a text file that is easily read by Cadence Virtuoso for transient simulations.

The following simulation setup is used to evaluate the energy dissipation per clock cycle, E. We simulate the multi-bit RCA over the time window, $T_W$, driving it with the above mentioned digital bitstreams of length $L_S$ (i.e., the variable streamLength in the Matlab code). The switching frequency, $f_s$, establishes the interval between two consecutive transitions ($T_s=1/f_s$) and is small enough to allow the signals to settle properly. Obviously, the simulation window is related to $L_S$ and $f_s$ by:

$$T_W=\frac{L_S}{f_s}.$$

(8)

For any power supply and input terminal, q, we record the overall power that enters the multi-bit RCA as $p_q\left(t\right)=v_q\left(t\right)i_q\left(t\right)$ and evaluate the corresponding average value:

$$\langle p_q\left(t\right)\rangle =\frac{1}{T_W}{\int }_0^{T_W}{v}_q\left(t\right)i_q\left(t\right)\mathrm{d}t.$$

(9)

Multiplying (9) by the switching period, $T_s=1/f_s$, we obtain the energy dissipated across terminal q per clock cycle:

$$E_q=\frac{\langle p_q\left(t\right)\rangle }{f_s}=\frac{1}{L_S}{\int }_0^{T_W}{v}_q\left(t\right)i_q\left(t\right)\mathrm{d}t.$$

(10)

Finally, summing all the terminal contributions together, yields:

$$E=\frac{1}{f_s}\sum _q\langle p_q\left(t\right)\rangle ,$$

(11)

which represents the desired energy consumption per clock cycle.

In our specific case, we set a 1-GHz switching frequency and a bitstream length, $L_S$, of 128. As shown in Figure 13, the simulation patterns also include the 6-bit headers for the CPD evaluation. However, they were cut off for evaluating the energy consumption.

4.3. Normalization

To compare different digital structures independently of the technology adopted, we normalize energy and delay to specific reference quantities [25]. As the reference delay, $D_0$, we define the average propagation delay exhibited by a symmetrical FO4 not gate loaded by a symmetrical FO16 inverter and driven by a minimum-size one. This is the delay of a gate in a tapered FO4 chain buffer. The reference energy, $E_0$, is that dissipated in an unloaded and minimum-size symmetrical inverter (i.e., $W_p=2W_n=2W_{\min }$, $L=L_{\min }$ and $C_L=0$ F) during one clock cycle. The reference values in our 28-nm FD-SOI CMOS technology result in:

$$\begin{array}{cc}\hfill E_0& =183.4\times {10}^{-18}\mathrm{J}\hfill \end{array}$$

(12a)

$$\begin{array}{cc}\hfill D_0& =13.5\times {10}^{-12}\mathrm{s}.\hfill \end{array}$$

(12b)

5. Determination of the Energy-Efficient Curves

For any OBFAs described in Section 3, we designed 4-bit and 8-bit RCAs in the Cadence environment. The designs were conducted by determining the EECs using the definitions of energy and delay in Section 4.

Each OBFA is partitioned into individual sections and each section is identified by a distinct parameter (i.e., $K_{C1}$, $K_{C2}$, …) that sets the relative transistor size in the section with respect to the minimum value allowed by the process, $W_{\min }/L_{\min }$. In any section, transistors are also marked with a multiplication factor that accounts for their relative sizes in that section. So, for example, referring to the section denoted by $K_{\mathrm{inv}}$ in Figure 4, the size of PMOS transistors is $2\times K_{\mathrm{inv}}\times W_{\min }/L_{\min }$, while the size of NMOS transistors is $1\times K_{\mathrm{inv}}\times W_{\min }/L_{\min }$. This multiplication factor allows us to specify the ratio between PMOS and NMOS transistors in the same section.

Once the RCA is set out, the points of the EEC are determined by searching for those parameters that minimize a set of corresponding FOMs defined in the form $E^i{D}^j$. Specifically, the procedure regards seven FOMs that correspond to as many design points, namely $D_{\min }$, $E{D}^3$, $E{D}^2$, $ED$, $E^{2}D$, $E^{3}D$ and $E_{\min }$. The minimization process of the FOMs is executed by means of the Cadence Virtuoso optimization tool. The tool can minimize a target function by adjusting specific parameters of the OBFA (i.e., $K_{C1}$, $K_{C2}$, …) defined in suitable design intervals.

The LP full adder, depicted in Figure 3, consists of three sections which correspond to three parameters that can be explored by the optimization tool. However, since the propagation delay of the Sum signal does not impact on the CPD (that represents the main speed limitation of a multi-bit RCA), we can set $K_S=1$ as this does not affect the propagation delay but reduce the energy dissipation of the RCA. As a consequence, the optimization process regards $K_X$ and $K_C$, only, defined between 1 and 10 with a 0.5-step.

Table 2. 4-bit RCAs: EEC design points (FOMs), normalized delay, normalized energy and relative design parameters.

OBFA	FOM	$\mathbf{D}/{\mathbf{D}}_0$	$\mathbf{E}/{\mathbf{E}}_0$	${\mathbf{K}}_{\mathbf{inv}}$	${\mathbf{K}}_{\mathbf{X}|\mathbf{X}1}$	${\mathbf{K}}_{\mathbf{X}2}$	${\mathbf{K}}_{\mathbf{C}|\mathbf{C}1}$	${\mathbf{K}}_{\mathbf{C}2}$	${\mathbf{K}}_{\mathbf{C}\mathbf{inv}}$
LP	$D_{\min }$	4.04	29.7		5.0		6.0
	$E{D}^3$	4.15	24.6		3.5		4.0
	$E{D}^2$	4.24	23.1		3.0		3.5
	$ED$	4.56	20.6		2.5		2.5
	$E^{2}D$	5.64	17.6		1.5		1.5
	$E^{3}D$	7.16	16.1		1.0		1.0
	$E_{\min }$	7.16	16.1		1.0		1.0
	$D_{\min }$	7.28	73.5	6.5	5.5	2.0	7.0	2.0	5.5
	$E{D}^3$	7.58	56.7	5.0	3.5	1.0	5.0	2.0	3.5
	$E{D}^2$	8.05	45.3	3.0	2.0	1.0	3.5	1.0	2.5
NHPSC	$ED$	8.52	41.8	2.5	1.5	1.0	3.0	1.0	2.0
	$E^{2}D$	9.82	36.9	1.5	1.5	1.0	2.0	1.0	1.5
	$E^{3}D$	11.7	34.1	1.0	1.5	1.0	1.5	1.0	1.0
	$E_{\min }$	12.2	33.6	1.0	1.5	1.0	1.0	1.0	1.0
	$D_{\min }$	4.44	36.0	1.5	3.5		7.5
	$E{D}^3$	4.61	28.9	1.0	2.0		7.0
	$E{D}^2$	4.61	28.9	1.0	2.0		6.5
HFA-22T	$ED$	4.81	27.1	1.0	1.5		4.5
	$E^{2}D$	5.75	23.4	1.0	1.0		2.5
	$E^{3}D$	6.30	22.5	1.0	1.0		2.0
	$E_{\min }$	9.09	20.7	1.0	1.0		1.0
	$D_{\min }$	7.55	74.7	8.0	2.0		7.5		6.0
	$E{D}^3$	8.44	41.9	3.5	1.0		2.5		2.5
	$E{D}^2$	8.44	41.9	3.5	1.0		2.5		2.5
HFA-B-26T	$ED$	9.59	33.9	1.0	1.0		1.5		1.5
	$E^{2}D$	10.9	30.7	1.5	1.0		1.0		1.0
	$E^{3}D$	11.8	29.7	1.0	1.0		1.0		1.0
	$E_{\min }$	11.8	29.7	1.0	1.0		1.0		1.0
	$D_{\min }$	7.33	79.6	8.5	2.5		8.0		6.0
	$E{D}^3$	7.81	49.4	4.5	1.0		3.5		3.0
	$E{D}^2$	8.16	43.7	3.5	1.0		2.5		2.5
HSHFA-D2	$ED$	9.32	35.7	2.0	1.0		1.5		1.5
	$E^{2}D$	10.6	32.4	1.5	1.0		1.0		1.0
	$E^{3}D$	11.5	31.3	1.0	1.0		1.0		1.0
	$E_{\min }$	11.5	31.3	1.0	1.0		1.0		1.0
	$D_{\min }$	4.65	33.4		3.0		5.0
	$E{D}^3$	4.78	27.9		1.5		4.0
	$E{D}^2$	4.78	27.9		1.5		4.0
HSHFA-D4	$ED$	5.19	24.8		1.0		3.0
	$E^{2}D$	5.89	22.6		1.0		2.0
	$E^{3}D$	6.67	21.5		1.0		1.5
	$E_{\min }$	8.23	20.5		1.0		1.0
	$D_{\min }$	8.48	48.7	3.0			8.5	3.5
	$E{D}^3$	8.87	36.3	2.0			4.5	2.5
	$E{D}^2$	9.00	35.1	2.0			4.0	2.5
SLPHFA	$ED$	10.0	30.0	1.5			2.5	2.0
	$E^{2}D$	12.5	25.1	1.0			1.5	1.0
	$E^{3}D$	13.9	23.8	1.0			1.0	1.0
	$E_{\min }$	13.9	23.8	1.0			1.0	1.0
	$D_{\min }$	5.84	54.3				10.0	8.0
	$E{D}^3$	6.11	39.9				6.0	4.5
	$E{D}^2$	6.31	36.7				5.0	4.0
CMC	$ED$	7.25	29.9				3.0	2.5
	$E^{2}D$	8.56	26.4				2.0	1.5
	$E^{3}D$	9.57	25.2				1.5	1.5
	$E_{\min }$	12.1	23.6				1.0	1.0

and

Table 3. 8-bit RCAs: EEC design points (FOMs), normalized delay, normalized energy and relative design parameters.

OBFA	FOM	$\mathbf{D}/{\mathbf{D}}_0$	$\mathbf{E}/{\mathbf{E}}_0$	${\mathbf{K}}_{\mathbf{inv}}$	${\mathbf{K}}_{\mathbf{X}|\mathbf{X}1}$	${\mathbf{K}}_{\mathbf{X}2}$	${\mathbf{K}}_{\mathbf{C}|\mathbf{C}1}$	${\mathbf{K}}_{\mathbf{C}2}$	${\mathbf{K}}_{\mathbf{C}\mathbf{inv}}$
	$D_{\min }$	14.4	51.7		6.5		3.0
	$E{D}^3$	14.8	42.7		3.0		2.5
	$E{D}^2$	15.3	39.5		2.5		2.0
LP	$ED$	16.3	36.3		2.0		1.5
	$E^{2}D$	16.6	35.6		1.5		1.5
	$E^{3}D$	21.3	32.3		1.0		1.0
	$E_{\min }$	21.3	32.3		1.0		1.0
	$D_{\min }$	13.9	137	5.5	5.0	1.0	4.5	1.0	4.5
	$E{D}^3$	14.4	116	4.5	3.0	1.0	4.5	1.0	3.0
	$E{D}^2$	14.8	108	3.5	2.5	1.0	4.5	1.0	3.0
NHPSC	$ED$	17.4	85.2	2.0	2.0	1.0	2.5	1.0	2.0
	$E^{2}D$	20.3	76.1	1.5	1.5	1.0	1.5	1.0	1.5
	$E^{3}D$	24.5	69.9	1.0	1.5	1.0	1.0	1.0	1.0
	$E_{\min }$	24.5	69.9	1.0	1.5	1.0	1.0	1.0	1.0
	$D_{\min }$	15.6	56.9	1.0	3.0		3.5
	$E{D}^3$	15.7	49.4	1.0	1.5		3.0
	$E{D}^2$	16.1	46.0	1.0	1.0		2.5
HFA-22T	$ED$	16.1	46.0	1.0	1.0		2.5
	$E^{2}D$	17.4	44.2	1.0	1.0		2.0
	$E^{3}D$	17.4	44.2	1.0	1.0		2.0
	$E_{\min }$	27.5	41.0	1.0	1.0		1.0
	$D_{\min }$	14.5	173	7.5	7.0		7.0		6.0
	$E{D}^3$	14.9	107	5.0	1.0		3.5		3.5
	$E{D}^2$	16.1	86.4	3.0	1.0		2.5		2.5
HFA-B-26T	$ED$	18.4	71.9	2.0	1.0		1.5		1.5
	$E^{2}D$	21.2	64.9	1.5	1.0		1.0		1.0
	$E^{3}D$	23.0	62.6	1.0	1.0		1.0		1.0
	$E_{\min }$	23.0	62.6	1.0	1.0		1.0		1.0
	$D_{\min }$	13.9	201	10.0	1.5		10.5		8.0
	$E{D}^3$	15.0	114	5.0	1.0		4.0		3.5
	$E{D}^2$	16.5	90.5	3.0	1.0		2.5		2.5
HSHFA-D2	$ED$	18.7	75.7	2.0	1.0		1.5		1.5
	$E^{2}D$	21.4	68.4	1.5	1.0		1.0		1.0
	$E^{3}D$	23.2	66.0	1.0	1.0		1.0		1.0
	$E_{\min }$	23.2	66.0	1.0	1.0		1.0		1.0
	$D_{\min }$	15.3	64.1		4.0		3.5
	$E{D}^3$	15.7	49.5		1.5		3.0
	$E{D}^2$	16.2	45.4		1.0		2.5
HSHFA-D4	$ED$	16.8	43.4		1.0		2.0
	$E^{2}D$	18.1	41.5		1.0		1.5
	$E^{3}D$	18.1	41.5		1.0		1.5
	$E_{\min }$	22.5	39.6		1.0		1.0
	$D_{\min }$	16.3	124	3.0			13.0	4.0
	$E{D}^3$	17.2	85.3	2.0			6.0	3.0
	$E{D}^2$	17.7	78.4	2.0			5.0	2.5
SLPHFA	$ED$	19.8	65.5	1.5			3.0	2.0
	$E^{2}D$	26.4	52.6	1.0			1.5	1.0
	$E^{3}D$	29.3	50.3	1.0			1.0	1.0
	$E_{\min }$	29.3	50.3	1.0			1.0	1.0
	$D_{\min }$	10.5	120				12.0	6.5
	$E{D}^3$	11.1	82.9				6.5	3.5
	$E{D}^2$	11.5	76.2				5.5	3.0
CMC	$ED$	13.1	63.2				3.5	2.0
	$E^{2}D$	16.2	54.2				2.0	1.5
	$E^{3}D$	18.7	51.1				1.5	1.0
	$E_{\min }$	23.7	48.5				1.0	1.0

show the data returned by the minimization process for the 4-bit and the 8-bit RCA, respectively. The first two columns identify the OBFA topology and the design points, in terms of FOMs, minimized by the optimization process. The next two columns show the normalized CPD, $D/D_0$, and the normalized energy per clock cycle, $E/E_0$. The remaining columns report the design parameters that were explored by the optimization tool. The data of the two tables will be used in the following to trace the EECs of the analyzed structures; therefore, the relative discussion will be conducted on subsequent figures.

The NHPSC full adder, shown in Figure 4, is made up of seven sections. Parameter $K_{\mathrm{inv}}$ defines the section that deals with the inversion of input signals. The section dedicated to the xor/xnor operation is identified by $K_{X1}$ and $K_{X2}$. The Carry section is identified by $K_{C1}$, $K_{C2}$ and $K_{C\mathrm{inv}}$. Finally, $K_S$ identifies the Sum section. We set $K_S=1$ and explore the EDS with the remaining parameters to find the EEC. Parameters $K_{\mathrm{inv}}$, $K_{X1}$, $K_{C1}$ and $K_{C\mathrm{inv}}$ range from 1 to 10 while $K_{X2}$ and $K_{C2}$ range in from 1 to 3, all with a 0.5-step. The results of the minimization process are reported in Table 2 and Table 3.

The HFA-22T and the HFA-B-26T full adders are depicted in Figure 5 and Figure 6 and are partitioned into four and five sections, respectively. In both circuits $K_{\mathrm{inv}}$ identifies the section that deals with the inversion of input signals. Parameters $K_X$, $K_C$ and $K_S$ identify the xor/xnor section, the Carry section and the Sum section, respectively. The HFA-B-26T full adder includes a driving stage in the Carry section, identified by $K_{C\mathrm{inv}}$. In both circuits we set $K_S=1$, and explore the EDS to find the EECs. For the HFA-22T full adder, $K_{\mathrm{inv}}$ and $K_X$ range from 1 to 5 while $K_C$ range from 1 to 10, both with a 0.5-step. For the HFA-B-26T full adder, $K_{\mathrm{inv}}$, $K_X$, $K_C$ and $K_{C\mathrm{inv}}$ range from 1 to 10 with a 0.5-step. The minimization process is summarized in Table 2 and Table 3.

The HSHFA-D2 and the HSHFA-D4 full adders are depicted in Figure 7 and Figure 8 and are partitioned into five and three sections, respectively. In both circuits $K_X$, $K_C$ and $K_S$ identify the xor/xnor section, the Carry section and the Sum section, respectively. In the HSHFA-D2 full adder, $K_{\mathrm{inv}}$ identifies the section that inverts input signals and $K_{C\mathrm{inv}}$ identifies the driving stage in the Carry section. Setting $K_S=1$, we explore the EDS to find the EECs. For the HSHFA-D2 full adder, $K_{\mathrm{inv}}$, $K_C$ and $K_{C\mathrm{inv}}$ range from 1 to 15 while $K_X$ ranges from 1 to 5, all with a 0.5-step. For the HSHFA-D4 full adder, $K_X$ and $K_C$ range from 1 to 10 with a 0.5-step. The minimization process results are reported in Table 2 and Table 3.

The SLPHFA full adder, shown in Figure 9, is partitioned into five sections. Section $K_{\mathrm{inv}}$ deals with the inversion of input signals, sections $K_{C1}$ and $K_{C2}$ are dedicated to the Carry, section $K_X$ to the xor operation and $K_S$ to the Sum. We $K_S=1$ and, since the xor section is used to generate the Sum signal only, we can also set $K_X=1$ without affecting the CPD of the RCA. The EDS is explored by ranging $K_{\mathrm{inv}}$ and $K_{C2}$ from 1 to 5, and $K_{C1}$ from 1 to 15, all with a 0.5-step. Table 2 and Table 3 report the results of the minimization process.

The CMC full adder, shown in Figure 10, is partitioned into four sections. Parameters $K_{S1}$ and $K_{S2}$ were set to 1 so that the minimization process concerned the parameters related to the carry section, only. $K_{C1}$ and $K_{C2}$ were defined 1 to 15 and from 1 to 10, respectively, both with a step of 0.5. Table 2 and Table 3 show the results of the minimization process.

An example of the optimization process performed by the Cadence Virtuoso simulation environment is shown in Figure 14 for the two RCAs built with the HFA-B-26T One-Bit full adder cell. The graph shows two energy-efficient curves, for a 4-bit and an 8-bit RCA. The optimization tool looks for seven design points by minimizing the corresponding FOM defined in terms of $E^i{D}^j$. Gray dots in the figure are the design points scanned by the minimization algorithm. Blue dots are the optimal design points found by the minimization algorithm, as reported in Table 2 and Table 3. Similar plots are obtained for all the remaining seven OBFA topologies but were not included because they do not provide any additional information.

6. Comparison

The data collected in Table 2 and Table 3 allow us to make an effective comparison among the various RCAs implemented with different OBFAs.

Figure 15 shows the EECs of the 4-bit RCAs implemented with the OBFAs analyzed in the previous sections. In the figure, filled symbols (squares, circles, triangles) are used to identify OBFAs with driving capability while OBFAs without driving capability are identified by empty symbols. The figure is extremely powerful since, it allows the designer to choose the best topology at a glance in terms of energy-delay trade-offs. Moreover, it makes clear which OBFAs should be avoided.

The figure reveals that, among the hybrid solutions, the OBFAs with driving capability (NHPSC, HFA-B-26T and HSHFA-D2) and the recent SLPHFA have similar EECs and do not provide any advantage in terms of Energy-Delay trade-offs. In fact, with respect to other solutions, the corresponding 4-bit RCAs are slower and dissipate a higher amount of energy. The CMC has better performance and is the best among the OBFAs with driving capabilities. The HFA-22T, the HSHFA-D4 and, particularly, the LP OBFA are the best choice in terms of energy-delay trade-offs for any value of energy and delay.

Figure 16 shows the EECs of the 8-bit RCAs implemented with the various OBFAs. In this case, filled symbols (squares, circles, triangles) identify OBFAs with driving capability while empty symbols identify those without driving capability. As expected, with respect to the 4-bit case, energy consumption and delay increase by increasing the number of bits of the RCA, n.

In the 8-bit case, among the hybrid topologies, the OBFAs with driving capability (NHPSC, HFA-B-26T and HSHFA-D2) and the recent SLPHFA are confirmed to have the worst behavior in the energy-delay space while the HFA-22T, the HSHFA-D4 and the LP OBFA behave better since they achieve same speed performance at the cost of a lower dissipation. However, as predicted in [13], the delays of these three latter topologies, increase with $n^2$ so that, if n is high and speed is of primary concern, the traditional CMC OBFA still remains the best solution over any hybrid topology in the range $[D_{\min },ED]$. Conversely, the LP OBFA confirms its superior performance if the energy is the main constraint to be minimized.

Finally, for the eight OBFAs analyzed, Figure 17 reports the 4-bit and the 8-bit EECs normalized to the number of bits, n. The figure confirms the behavior forecasted in [13] for the topologies without driving capability. In OBFAs with driving capability (CMC, NHPSC, HFA-B-26T and HSHFA-D2) and in the SLPHFA the 4-bit and 8-bit EECs normalized to the number of bits remain almost unchanged since both energy and delay increase proportionally to n. In HFA-22T, HSHFA-D4 and LP OBFAs the delay increases with $n^2$ so that the 8-bit EEC is right shifted with respect to the corresponding 4-bit curve. It is worth noting that, even if the SLPHFA has no driving capability, it behaves as an OBFA with driving capability. This is because the input carry signal drives only transistor gates and the path between $C_i$ and $C_o$ is not modeled with an $RC$ network.

7. Conclusions

We designed and compared seven meaningful topologies of hybrid OBFAs that were optimized in terms of energy-delay trade-offs to operate in multibit RCAs. The design and comparison dealt with 4-bit and 8-bit RCAs and exploited the derivation of the EECs in the EDS. The well-known and consolidated CMC full adder was also included in the comparison as a reference structure.

Since the derivation of the EEC implies the determination of energy consumption and propagation delay, we defined the procedures for getting them through circuit simulations. Then, we presented a design methodology to optimize an RCA by minimizing some significant FOMs (e.g., $E^i{D}^j$). Specifically, we partitioned each OBFA of the RCA into a few sections, each identified by an individual parameter that stood for the relative transistor sizes in the section with respect to the minimum size of the technology process, $W_{\min }/L_{\min }$. The numerical optimizer of the circuit simulator was used to minimize the FOMs and find out the EEC of the RCA.

All the EECs were plotted in two different graphs for the 4-bit case and the 8-bit one. This allowed us to make a simple and effective comparison as well as to identify the best OBFA topologies. For the 4-bit case, the comparison revealed that HFA-22T, HSHFA-D4 and LP OBFAs are the best solutions among the other hybrid topologies and also compared to the traditional CMC full adder. For the 8-bit case, the comparison showed that, with respect to other hybrid topologies, HFA-22T, HSHFA-D4 and LP OBFAs behave better since they achieve the same speed performance at the cost of a lower dissipation. However, if n is large and speed is of primary concern, the traditional CMC OBFA still remains the best solution over any hybrid topology analyzed.