Power Quality Disturbance Recognition Using Empirical Wavelet Transform and Feature Selection
Abstract
:1. Introduction
- (1)
- Compared with EMD, the EWT is more suitable and robust to a segmented PQD signal, especially in the selection of decomposed parameter optimization.
- (2)
- Based on experiment results, the permutation entropy and ReliefF algorithm are vital for feature selection, which help to filter the significant components, eliminating redundant features.
- (3)
- The proposed algorithm observes the characteristics of the PQD signal from a multiresolution perspective and improves the robustness and the precision of the classifier model.
2. Related Work
3. Theoretical Background
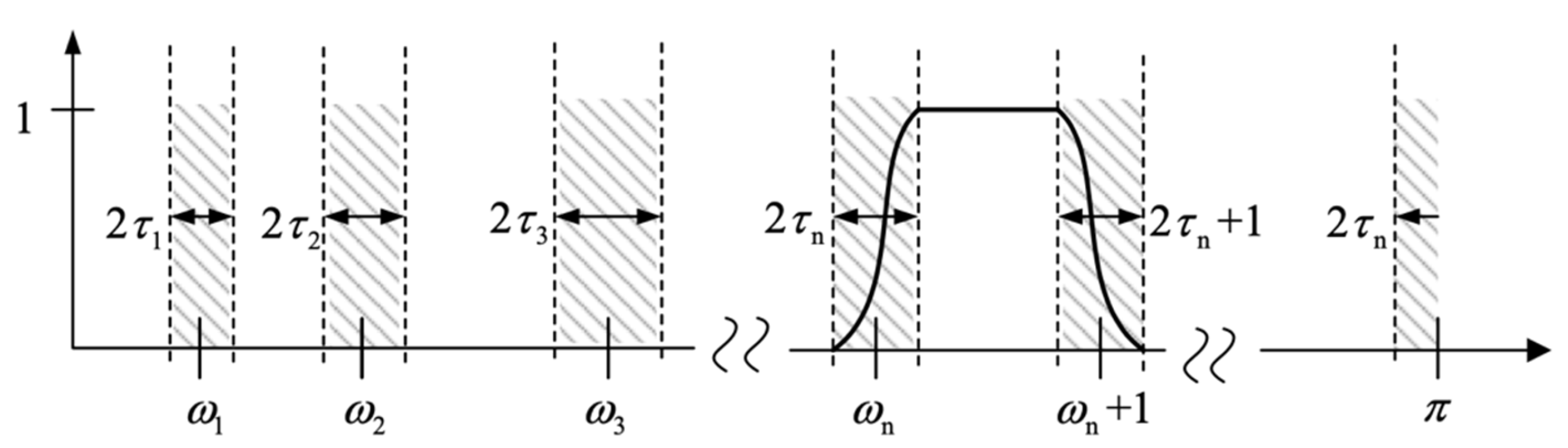
3.1. Basic Theory of Empirical Wavelet Transform
3.2. Permutation Entropy
3.3. ReliefF-Based Feature Selection Method
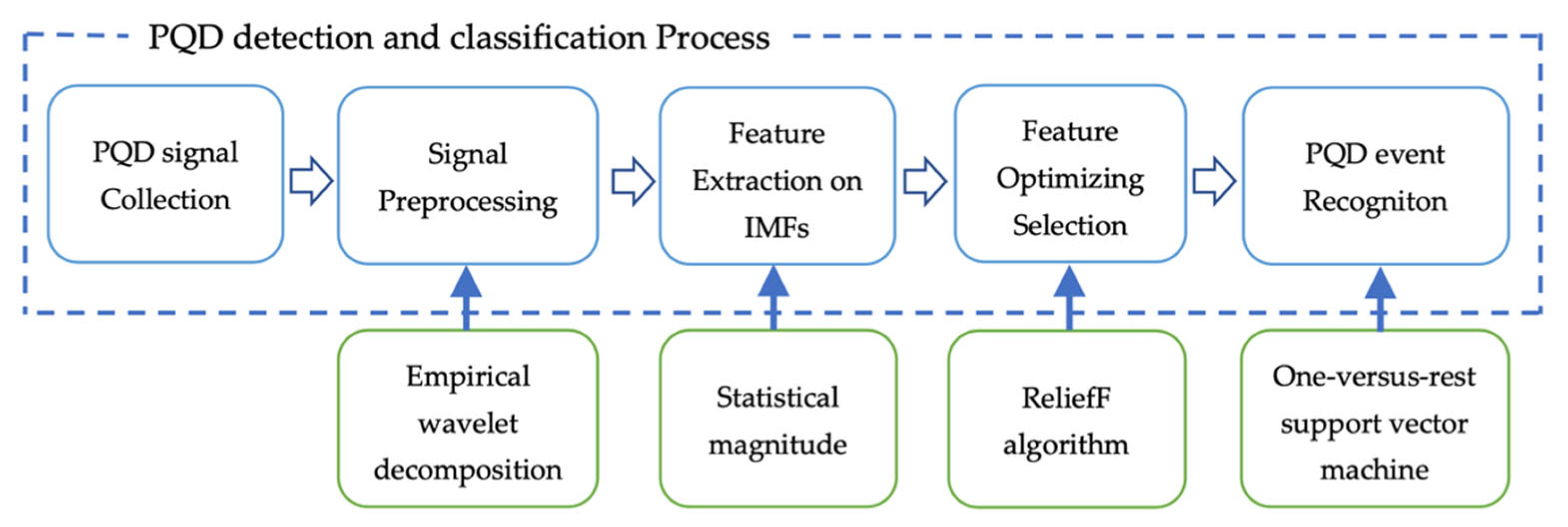
4. Proposed Method
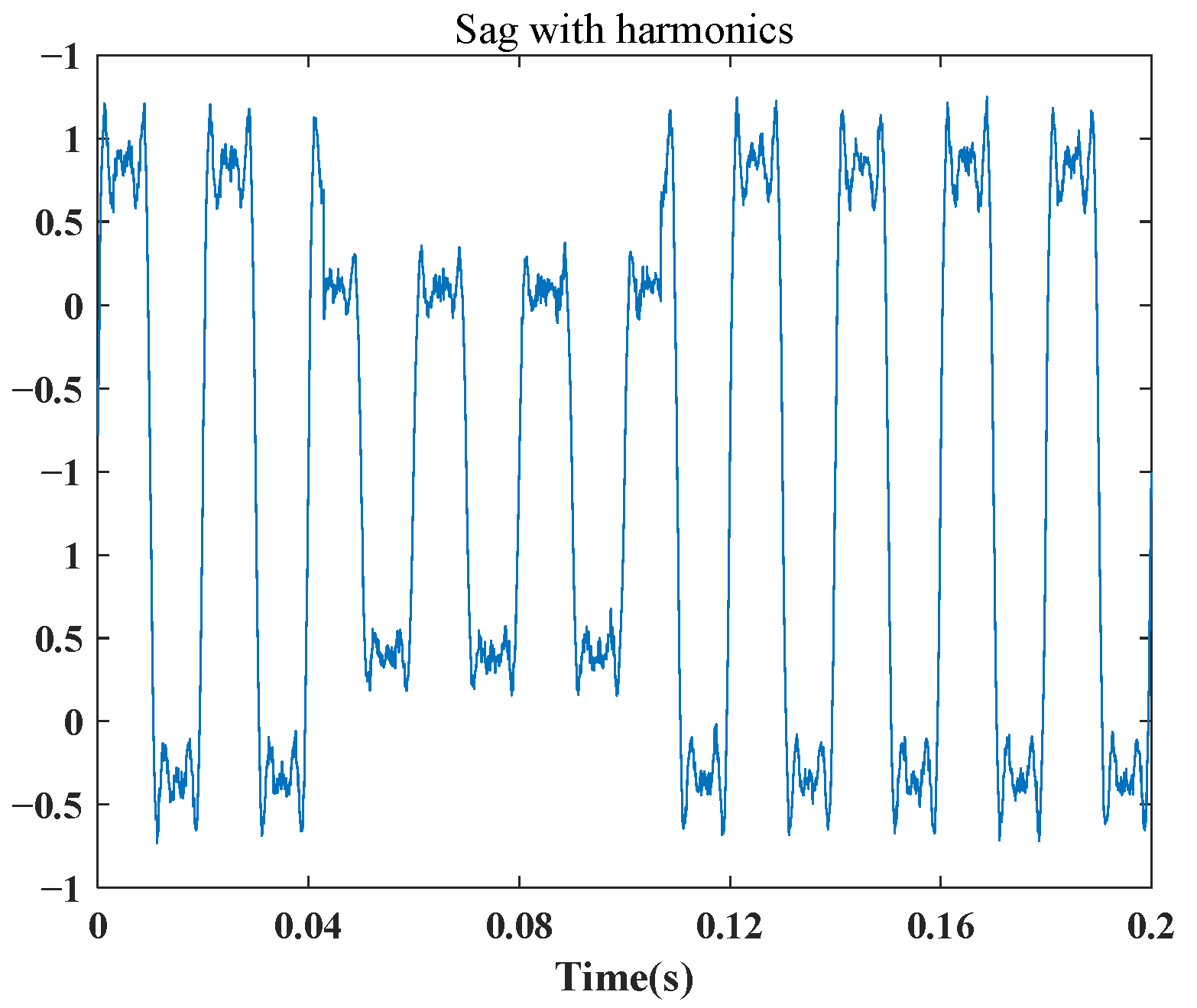
4.1. PQD Signal Simulation
4.2. EWT Signal Segmentation
4.3. Feature Extraction and Selection
4.4. Multiclass Pattern Recognition
5. Experimental Results and Discussion
5.1. Experimental Setup
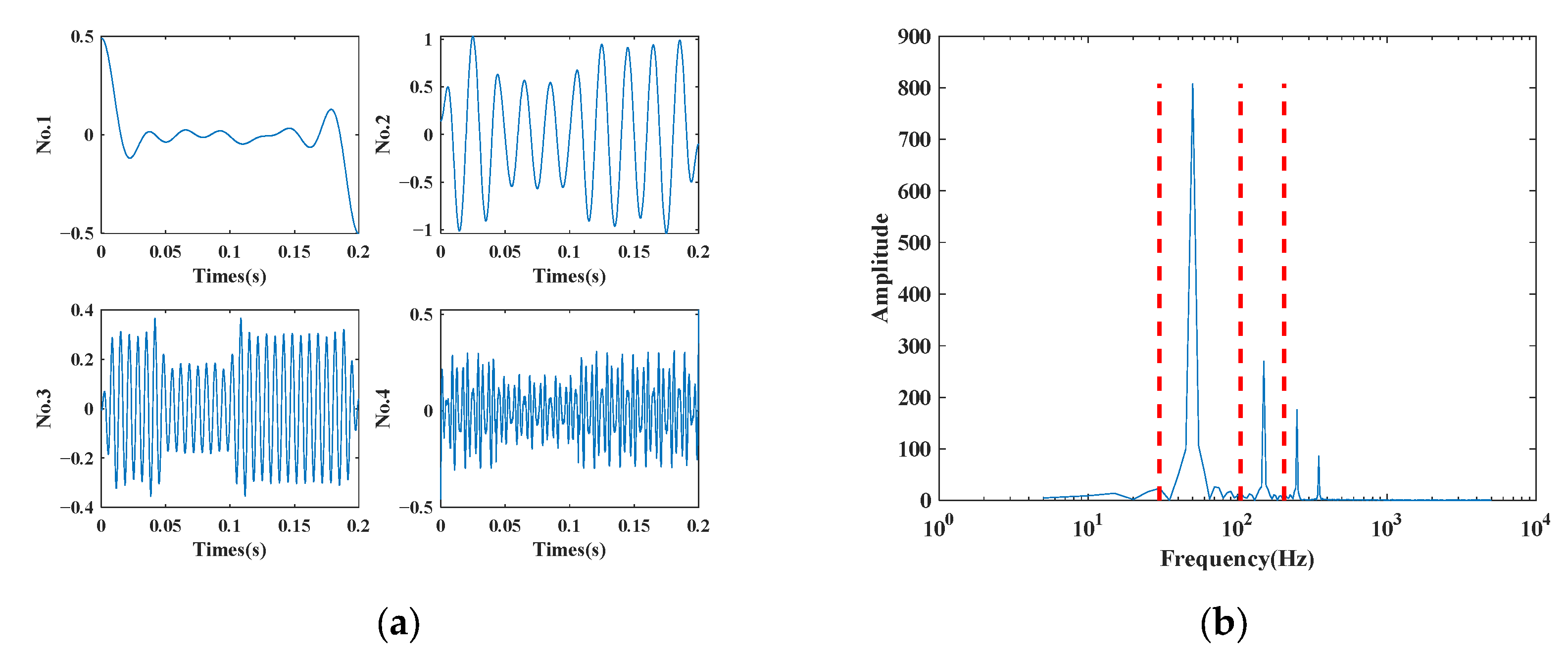
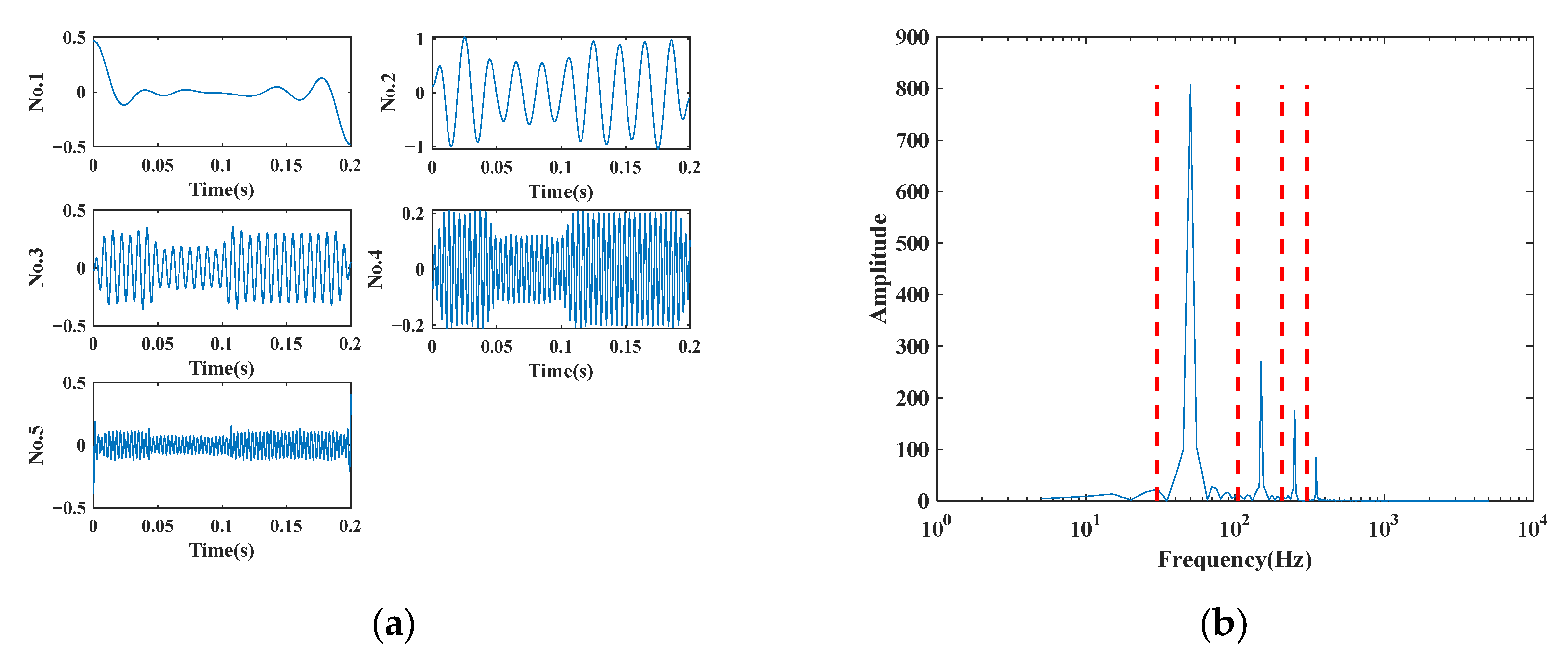
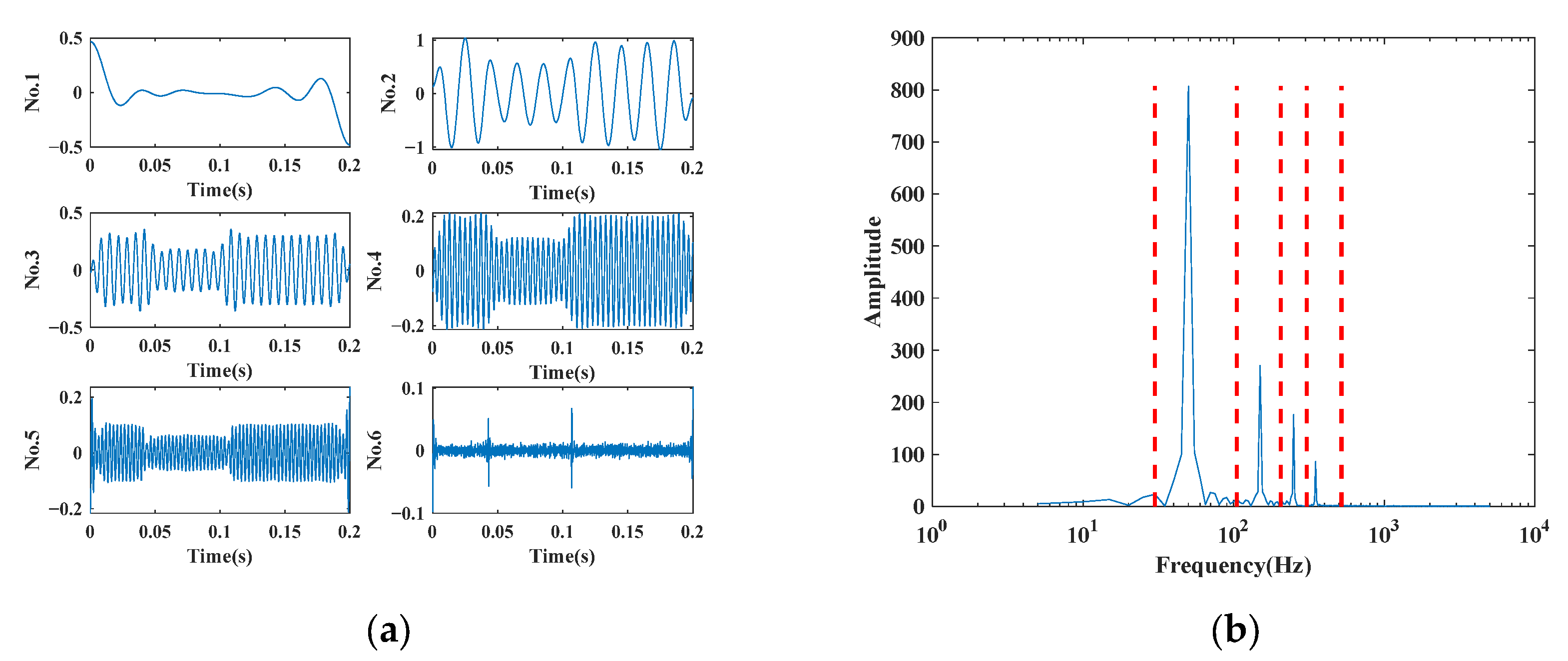
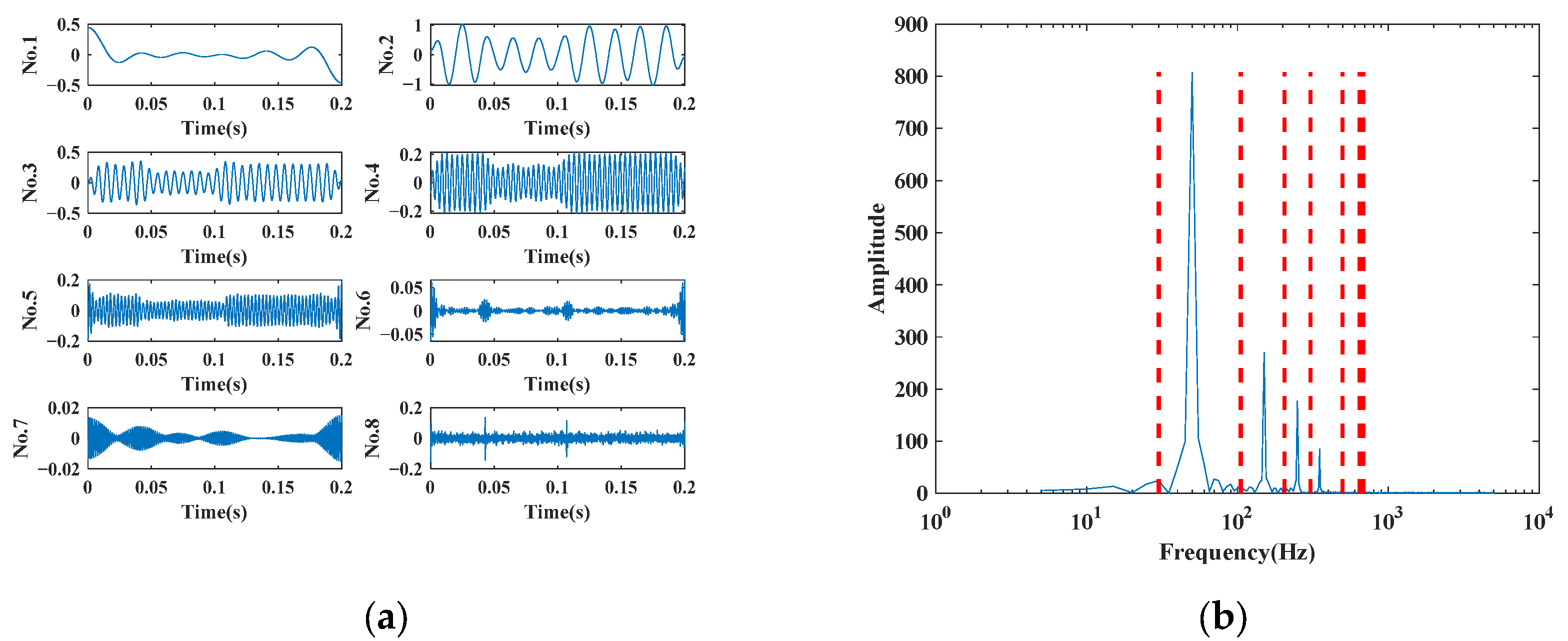
5.2. EWT Decomposition
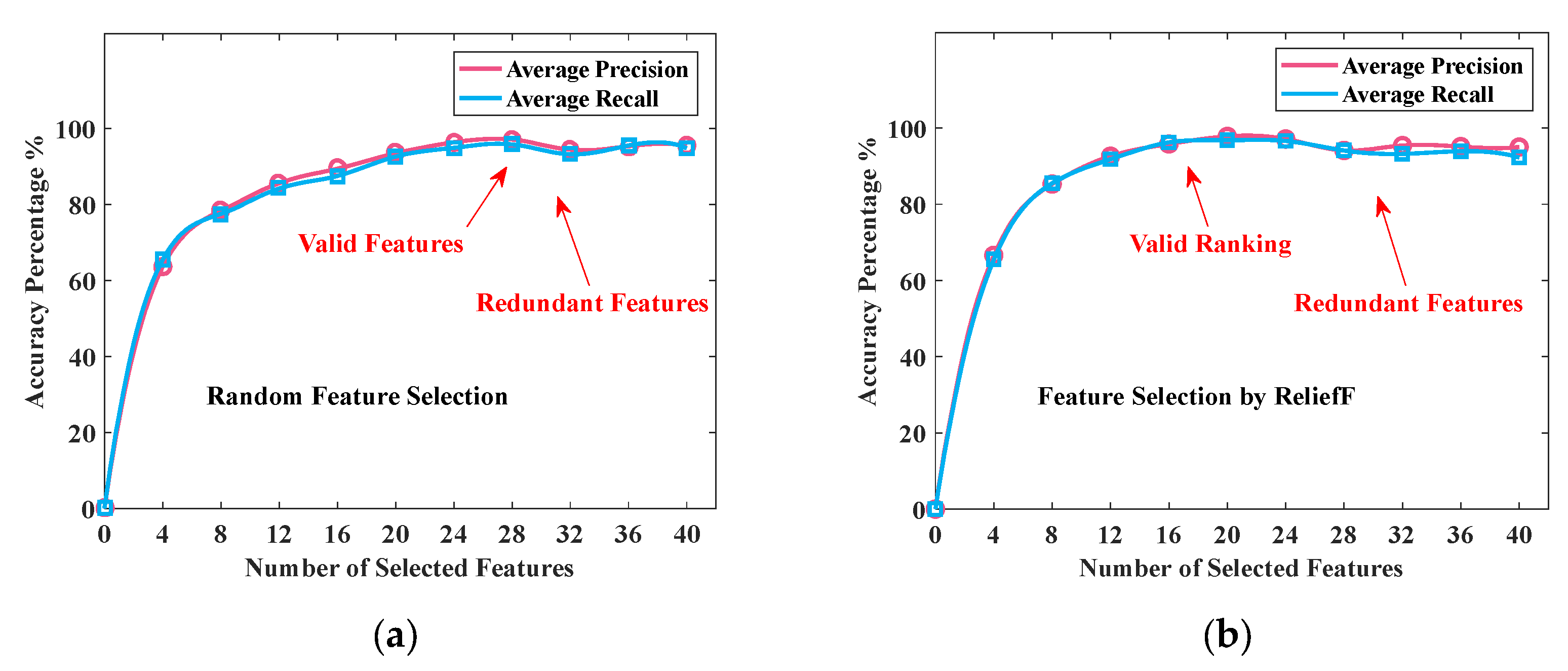
5.3. ReliefF Feature Selection
5.4. Performance with Real Experiments
5.5. Performance with Noisy Data
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PQD | Power Quality Disturbances |
| SVM | Support Vector Machine |
| FT | Fourier Transform |
| STFT | Short-time Fourier transform |
| WPT | Wavelet Packet Transform |
| EMD | Empirical Mode Decomposition |
| IMF | Intrinsic Mode Functions |
| EWT | Empirical Wavelet Transform |
| RMS | Root-Mean-Square value |
| DT | Decision Tree |
| SVM | Support Vector Machine |
| ANN | Artificial Neural Network |
| SNR | Signal-to-Noise Ratio |
| OVR | One-Versus-Rest |
| RBF | Radial Basis Function |
References
- Xiao, F.; Ai, Q. Data-Driven Multi-Hidden Markov Model-Based Power Quality Disturbance Prediction That Incorporates Weather Conditions. IEEE Trans. Power Syst. 2019, 34, 402–412. [Google Scholar] [CrossRef]
- Xiao, F.; Lu, T.; Ai, Q.; Wang, X.; Chen, X.; Fang, S.; Wu, Q. Design and Implementation of a Data-Driven Approach to Visualizing Power Quality. IEEE Trans. Smart Grid 2020, 11, 4366–4379. [Google Scholar] [CrossRef]
- Jena, M.K.; Panigrahi, B.K.; Samantaray, S.R. A New Approach to Power System Disturbance Assessment Using Wide-Area Postdisturbance Records. IEEE Trans. Ind. Inform. 2018, 14, 1253–1261. [Google Scholar] [CrossRef]
- Liang, C.; Teng, Z.; Li, J.; Yao, W.; Hu, S.; Yang, Y.; He, Q. A Kaiser Window-Based S-Transform for Time-Frequency Analysis of Power Quality Signals. IEEE Trans. Ind. Inform. 2021, 18, 965–975. [Google Scholar] [CrossRef]
- Gu, T.Y.; Gao, Y.P.; Wu, C.; Lin, C.H.; Fan, Q.; Xu, M.M. Power quality disturbance detection based on improved wavelet threshold function and singular value decomposition. Electr. Meas. Instrum. 2020, 57, 111–118. [Google Scholar]
- Solis-Munoz, F.J.; Elvira-Ortiz, D.A.; Jaen-Cuellar, A.Y.; Romero-Troncoso, R.; Osornio-Rios, R.A. A Novel Methodology for Power Quality Disturbances Detection and Classification in Industrial Facilities. J. Sci. Ind. Res. 2020, 79, 819–823. [Google Scholar]
- Mahela, O.P.; Khan, B.; Alhelou, H.H.; Tanwar, S. Assessment of power quality in the utility grid integrated with wind energy generation. IET Power Electron. 2020, 13, 2917–2925. [Google Scholar] [CrossRef]
- He, S.; Li, K.; Zhang, M. A Real-Time Power Quality Disturbances Classification Using Hybrid Method Based on S-Transform and Dynamics. IEEE Trans. Instrum. Meas. 2013, 62, 2465–2475. [Google Scholar] [CrossRef]
- Abdelsalam, A.A.; Hassanin, A.M.; Hasanien, H.M. Categorisation of power quality problems using long short-term memory networks. IET Gener. Transm. Distrib. 2021, 15, 1626–1639. [Google Scholar] [CrossRef]
- Om Prakash, M.; Abdul Gafoor, S. Power quality recognition in distribution system with solar energy penetration using S-transform and Fuzzy C-means clustering. Renew. Energy 2017, 106, 37–51. [Google Scholar]
- Yu, Y.; Zhao, W.; Li, S.; Huang, S. A Two-Stage Wavelet Decomposition Method for Instantaneous Power Quality Indices Estimation Considering Interharmonics and Transient Disturbances. IEEE Trans. Instrum. Meas. 2021, 70, 1–13. [Google Scholar] [CrossRef]
- Choe, S.; Yoo, J. Wavelet Packet Transform Modulus-Based Feature Detection of Stochastic Power Quality Disturbance Signals. Appl. Sci. 2021, 11, 2825. [Google Scholar] [CrossRef]
- Manjula, M.; Mishra, S.; Sarma, A. Empirical mode decomposition with Hilbert transform for classification of voltage sag causes using probabilistic neural network. Int. J. Electr. Power Energy Syst. 2013, 44, 597–603. [Google Scholar] [CrossRef]
- Singh, R.H.; Mohanty, S.R.; Kishor, N.; Thakur, K.A. Real-Time Implementation of Signal Processing Techniques for Dis-turbances Detection. Electr. Power Syst. Res. 2019, 66, 3550–3560. [Google Scholar]
- Gilles, J. Empirical wavelet transform. IEEE Trans. Signal. Process. 2013, 61, 3999–4010. [Google Scholar] [CrossRef]
- Kamble, S.; Thote, P.; Rathore, C.; Marothiya, A. Estimation of various PQ indices at point of common coupling using empirical wavelet transform. IET Sci. Meas. Technol. 2019, 13, 862–873. [Google Scholar] [CrossRef]
- Thirumala, K.; Umarikar, A.C.; Jain, T. Estimation of Single-Phase and Three-Phase Power-Quality Indices Using Empirical Wavelet Transform. IEEE Trans. Power Deliv. 2014, 30, 445–454. [Google Scholar] [CrossRef]
- Fu, L.; Zhu, T.; Pan, G.B.; Chen, S.H.; Zhong, Q.; Wei, Y.D. Power Quality Disturbance Recognition Using VMD-Based Feature Extraction and Heuristic Feature Selection. Appl. Sci. 2019, 9, 4901. [Google Scholar] [CrossRef] [Green Version]
- Chaudhary, P.; Rizwan, M. Voltage regulation mitigation techniques in distribution system with high PV penetration: A review. Renew. Sustain. Energy Rev. 2018, 82, 3279–3287. [Google Scholar] [CrossRef]
- Naderian, S.; Salemnia, A. Method for classification of PQ events based on discrete Gabor transform with FIR window and T2FK-based SVM and its experimental verification. IET Gener. Transm. Distrib. 2017, 11, 133–141. [Google Scholar] [CrossRef]
- Liu, Z.; Cui, Y.; Li, W. A Classification Method for Complex Power Quality Disturbances Using EEMD and Rank Wavelet SVM. IEEE Trans. Smart Grid 2015, 6, 1678–1685. [Google Scholar] [CrossRef]
- Achlerkar, P.D.; Samantaray, S.; Manikandan, M.S. Variational Mode Decomposition and Decision Tree Based Detection and Classification of Power Quality Disturbances in Grid-Connected Distributed Generation System. IEEE Trans. Smart Grid 2016, 9, 3122–3132. [Google Scholar] [CrossRef]
- Xi, Y.; Li, Z.; Tang, X.; Zeng, X. Classification of power quality disturbances based on KF-ML-aided S-transform and multilayers feedforward neural networks. IET Gener. Transm. Distrib. 2020, 14, 4010–4020. [Google Scholar] [CrossRef]
- Fu, L.; Wei, Y.; Fang, S.; Zhou, X.; Lou, J. Condition Monitoring for Roller Bearings of Wind Turbines Based on Health Evaluation under Variable Operating States. Energies 2017, 10, 1564. [Google Scholar] [CrossRef] [Green Version]
- Xie, S.; Li, K.; Xiao, M.; Zhang, L.; Li, W. Key Quality Indicators Prediction for Web Browsing with Embedded Filter Feature Selection. Appl. Sci. 2020, 10, 2141. [Google Scholar] [CrossRef] [Green Version]
- IEEE. 1159-1995 IEEE Recommended Practice for Monitoring Electric Power Quality. 1995, pp. 1–80. Available online: https://webstore.ansi.org/standards/ieee/11591995 (accessed on 1 December 2021).
- Khokhar, S.; Zin, A.A.M.; Memon, A.P.; Mokhtar, A.S. A new optimal feature selection algorithm for classification of power quality disturbances using discrete wavelet transform and probabilistic neural network. Measurements 2017, 95, 246–259. [Google Scholar] [CrossRef]
- Fu, L.; Zhu, T.; Zhu, K.; Yang, Y. Condition Monitoring for the Roller Bearings of Wind Turbines under Variable Working Conditions Based on the Fisher Score and Permutation Entropy. Energies 2019, 12, 3085. [Google Scholar] [CrossRef] [Green Version]
- Thirumala, K.; Pal, S.; Jain, T.; Umarikar, A.C. A classification method for multiple power quality disturbances using EWT based adaptive filtering and multiclass SVM. Neurocomputing 2019, 334, 265–274. [Google Scholar] [CrossRef]
- Zhu, T.; Qu, Z.; Xu, H.; Zhang, J.; Shao, Z.; Chen, Y.; Prabhakar, S.; Yang, J. RiskCog: Unobtrusive Real-Time User Authentication on Mobile Devices in the Wild. IEEE Trans. Mob. Comput. 2020, 19, 466–483. [Google Scholar] [CrossRef]
- Zhu, T.; Fu, L.; Liu, Q.; Lin, Z.; Chen, Y.; Chen, T. One Cycle Attack: Fool Sensor-Based Personal Gait Authentication with Clustering. IEEE Trans. Inf. Forensics Secur. 2021, 16, 553–568. [Google Scholar] [CrossRef]
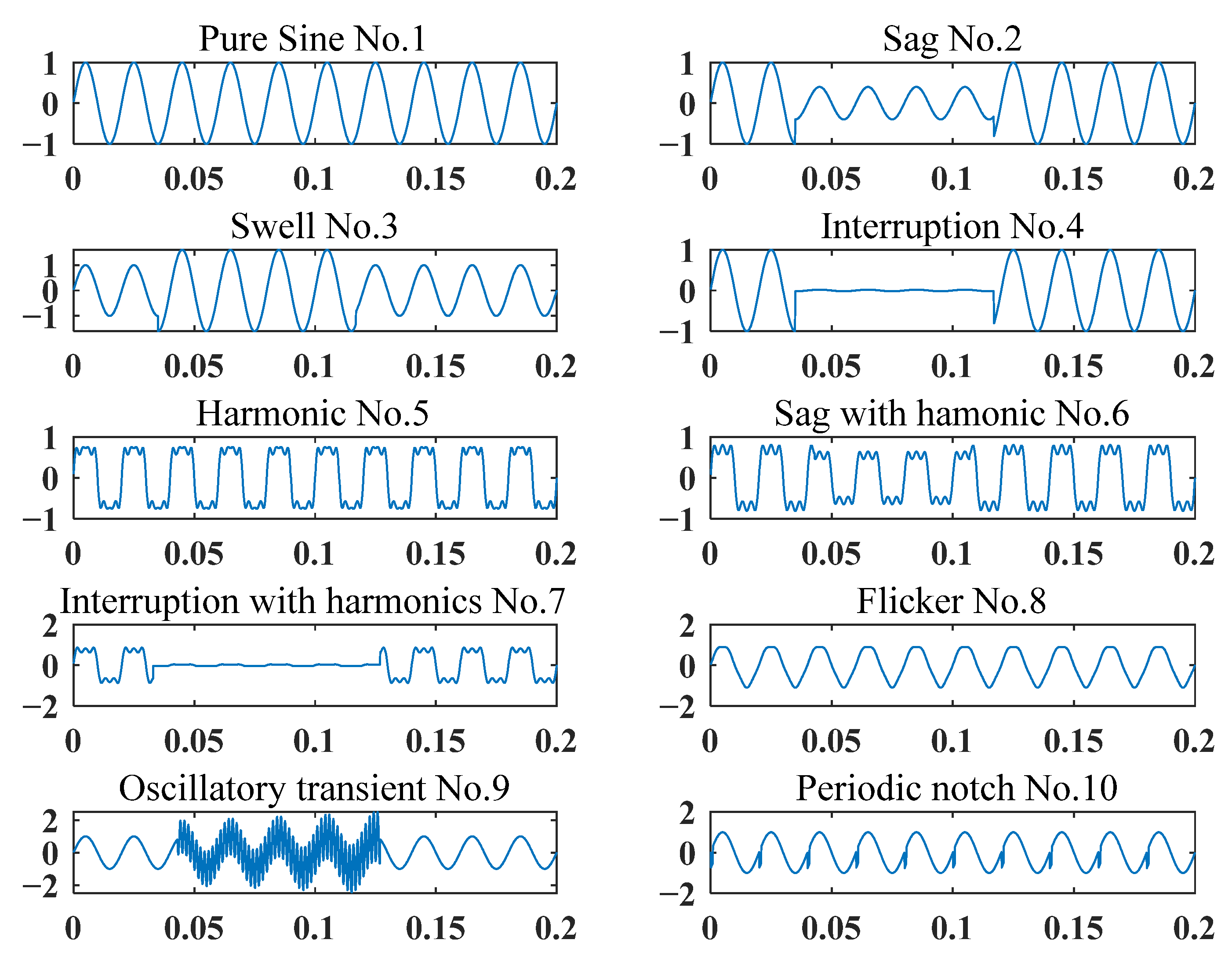

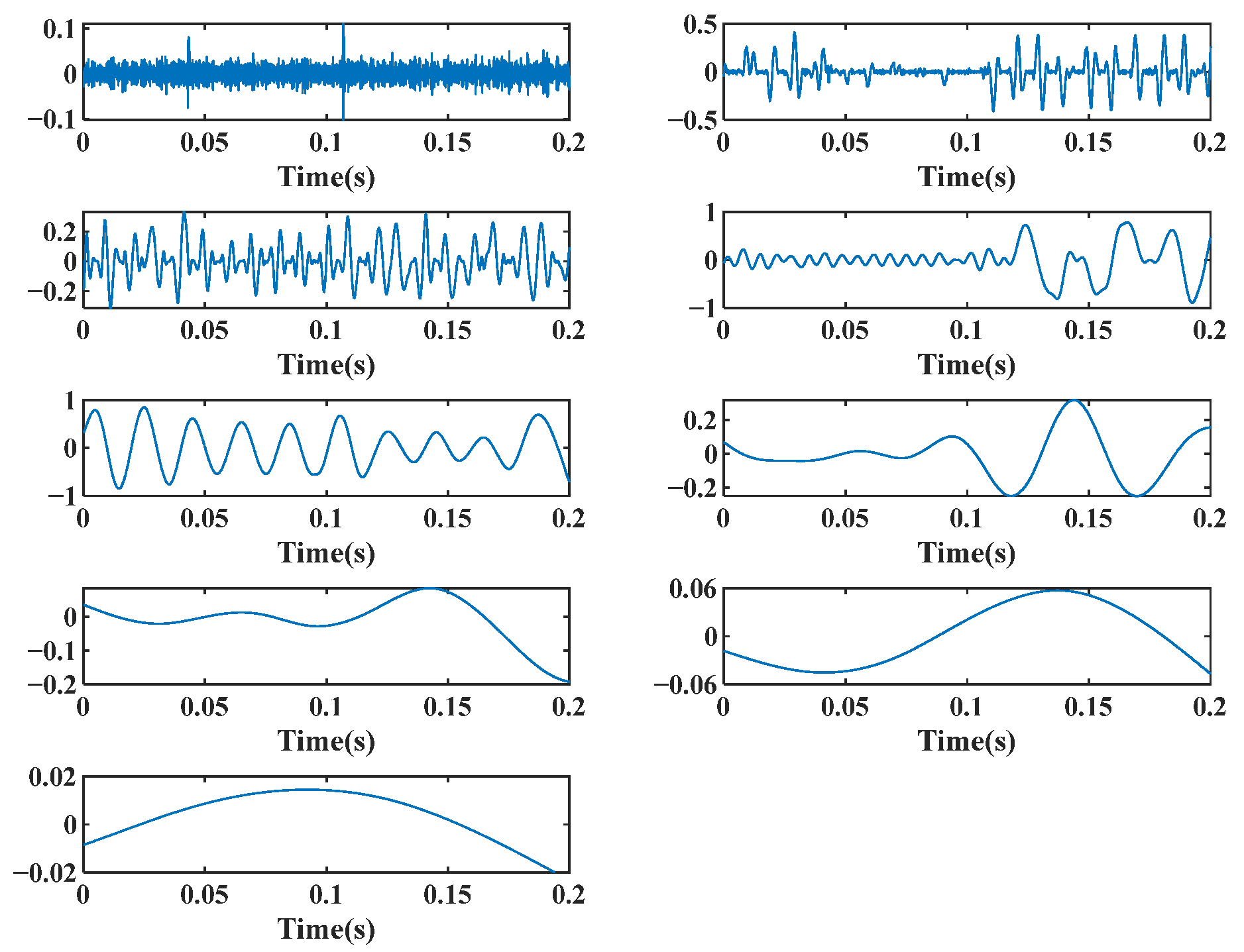
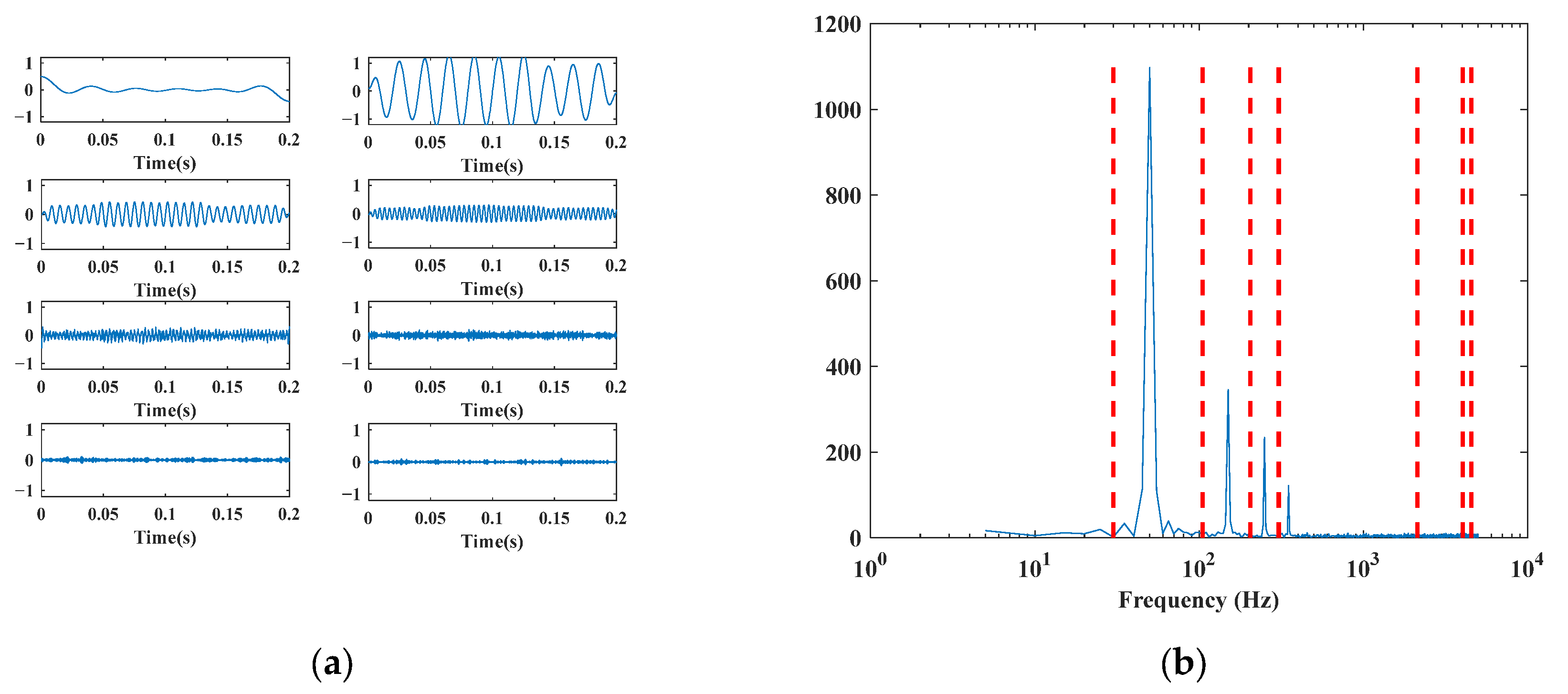
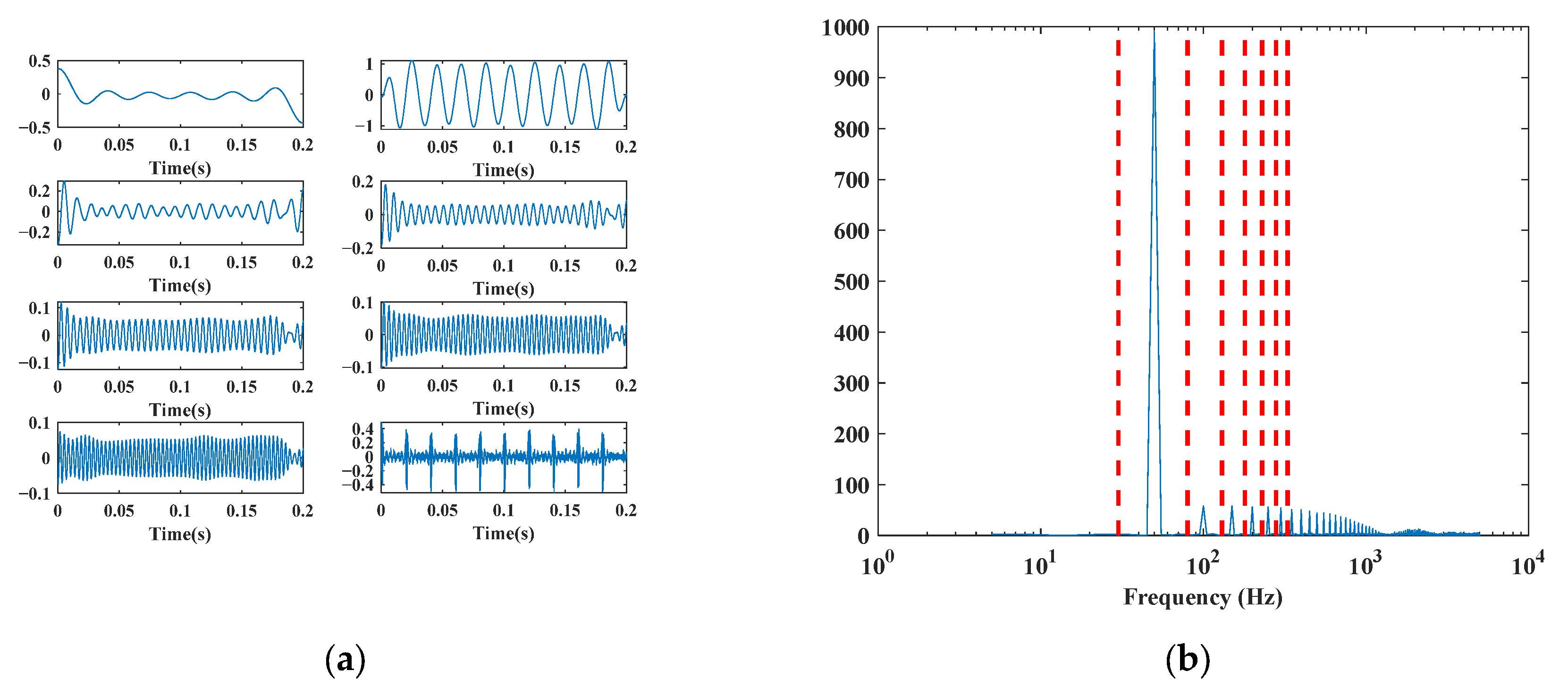

| Label | PQD Type | Mathematical Model | Parameters |
|---|---|---|---|
| C1 | Pure Sine | ||
| C2 | Sag | ||
| C3 | Swell | ||
| C4 | Interrupt | ||
| C5 | Harmonics | ||
| C6 | Sag with harmonics | ||
| C7 | Interrupt with harmonics | ||
| C8 | Flicker | ||
| C9 | Oscillatory transient | ||
| C10 | Periodic notch |
| No. | Statistical Feature | Expression |
|---|---|---|
| 1 | RMS | |
| 2 | Average | |
| 3 | Standard Deviation | |
| 4 | Variance | |
| 5 | Range | |
| 6 | Kurtosis | |
| 7 | Skewness | |
| 8 | Average Deviation | |
| 9 | Permutation Entropy |
| Assigned Class | True Class | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | |
| C1 | 423 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| C2 | 0 | 435 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| C3 | 1 | 0 | 406 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| C4 | 0 | 3 | 0 | 411 | 0 | 0 | 0 | 0 | 0 | 0 |
| C5 | 0 | 0 | 0 | 0 | 428 | 0 | 0 | 0 | 0 | 0 |
| C6 | 0 | 0 | 0 | 0 | 0 | 403 | 0 | 0 | 0 | 0 |
| C7 | 0 | 0 | 0 | 0 | 0 | 0 | 415 | 0 | 0 | 0 |
| C8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 437 | 0 | 0 |
| C9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 429 | 0 |
| C10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 422 |
| Recognized Class | Signal-to-Noise Ratio | ||
|---|---|---|---|
| 15 dB | 25 dB | 35 dB | |
| C1 | 95.2% | 99.2% | 100% |
| C2 | 100% | 100% | 100% |
| C3 | 98.2% | 100% | 100% |
| C4 | 100% | 100% | 100% |
| C5 | 95.2% | 96.8% | 98.0% |
| C6 | 96.4% | 98.2% | 100% |
| C7 | 93.8% | 97.4% | 98.2% |
| C8 | 98.2% | 98.8% | 100% |
| C9 | 100% | 100% | 100% |
| C10 | 97.6% | 98.2% | 99.2% |
| Overall | 97.41% | 98.86% | 99.54% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Li, Z.; Pan, G.; Xu, F. Power Quality Disturbance Recognition Using Empirical Wavelet Transform and Feature Selection. Electronics 2022, 11, 174. https://doi.org/10.3390/electronics11020174
Chen S, Li Z, Pan G, Xu F. Power Quality Disturbance Recognition Using Empirical Wavelet Transform and Feature Selection. Electronics. 2022; 11(2):174. https://doi.org/10.3390/electronics11020174
Chicago/Turabian StyleChen, Sihan, Ziche Li, Guobing Pan, and Fang Xu. 2022. "Power Quality Disturbance Recognition Using Empirical Wavelet Transform and Feature Selection" Electronics 11, no. 2: 174. https://doi.org/10.3390/electronics11020174
APA StyleChen, S., Li, Z., Pan, G., & Xu, F. (2022). Power Quality Disturbance Recognition Using Empirical Wavelet Transform and Feature Selection. Electronics, 11(2), 174. https://doi.org/10.3390/electronics11020174






