Global Optimization in Robust Fractional Control of Uncertain Fractional Order Systems: A Thermal Application Using the STM32 Microcontroller

Abstract

In this paper, we suggest an improvement to our previously undertaken approach. Briefly, this approach consisted of applying the robust fractional predictive control (RFPC) for a class of constrained fractional systems implementing the min–max optimization technique. The RFPC controller requires resolution of a non-convex min–max optimization problem. The resolution of this problem, however, can only conduce to local solutions. The reason is simple: the objective function to be optimized is non-convex due to the presence of uncertainties. In the present work, we propose a global optimization-based RFPC controller for an uncertain fractional order system. A determinist global optimization method, namely, generalized geometric programming (GGP), is proposed to solve this problem for the uncertain fractional order system. The GGP method consists of converting a non-convex problem into a convex one via the application of variable changes. The technique of the convexification of this method is applied in line with the objective function to be optimized. Consequently, we obtained a new convex criterion and a convex problem. From an experimental point of view, we applied the proposed RFPC to a real thermal system using an STM32 microcontroller in order to control our thermal system.

1. Introduction

The notion of fractional (non-integer) computation was expounded by Riemann and Liouville at the turn of the nineteenth century. Their goal was to expand non-integer order operators by employing the non-integer orders. A century later, Grünwald–Letnikov introduced the discrete concept of fractional equations [1].

Fractional systems have been widely used in many areas (including physics, chemistry, and biology) whenever the phenomena governing dynamics obey an equation with partial derivatives of diffusion [2,3,4]. This diffusion phenomenon shows, through a classical mono-dimensional theory, a fractional behavior on the order of 0.5. Therefore, the application of fractional operators in the modeling of diffusive systems appears obvious. Fractional tools also appear in automation and robotics, especially in their use in modeling, identification, control, and robust control [5]. In the nineties, Alain Oustaloup proposed the fractional order technique as a solution for controlling dynamic systems [6,7]. In 1999, Podlubny has also developed the non-integer PID regulator [1]. The evolution of fractional control continues to draw the attention of several researchers as well as industrialists [8,9,10,11,12,13,14,15,16].

As for predictive control (PC), it is regarded as one of the most advanced regulator methods. This is because it is the only control approach that enables us to take into account, explicitly and systematically, all forms of restrictions when designing and executing the control. PC also enables the control of a large class of systems [17], among which is the fractional systems [18,19,20,21]. The philosophy of predictive control draws on the use of an internal model of the real process in order to determine the optimal control obtained through minimizing a performance criterion. In fact, the degree of precision of the model describing the real system has a great impact on the predictive control’s performances. To better explain the system behavior in a practical manner, it is necessary to consider the parameter uncertainties. Following the integration of uncertainties, the control problem is to design correctors that are robust, in other words, insensitive to these uncertainties. This explains the use of the robust predictive control (RPC). The strategy adopted by this controller in the presence of uncertainties is to treat the worst-case scenario when determining the best optimal control [22]. The integration of uncertainties in the model generally results in a non-convex problem. Therefore, the control law will be local, which can lead to a poor performance of the closed-loop process. In the case of integer systems (classical system), many researchers have used global optimization techniques to determine the optimal control law that represents the overall solution of the optimization problem [23,24,25,26,27,28,29,30]. Among these techniques, we mention specifically the generalized geometric programming, hereafter abbreviated as GGP. This approach consists of converting a non-convex problem into a convex one via the application of variable changes. Several works have proved that it has a set of advantages compared to classical optimization algorithms [31,32,33].

Recently, a number of researchers have worked on the implementation of robust predictive control techniques for a non-integer order process. In [34], the authors developed a robust non-integer controller based on a predictive controller of a chaotic process. Sopasakis et al. [35] used the tube-based MPC method to implement the robust predictive control on a non-integer order discrete time process. Ardashir et al. [36] explained an RPC related on a fuzzy model to control fractional chaotic systems with time delay. Esfahani [37] also developed an RPC for a discrete-time switched linear process using the linear non-integer transformation. However, the aforementioned authors used local methods in their respective works to determine the optimal control.

This paper proposes a global optimization-based RFPC controller. The Grünwald–Letnikov’s (G-L) approach was employed here as a non-integer internal model to predict the future dynamic behavior of the process. The RFPC controller requires resolution of a non-convex min–max optimization problem due to the presence of the uncertainties. The GGP method is employed to solve this problem and, thus, to find the global optimum.

The structure of this paper is as follows: Section 2 explains the Grünwald–Letnikov (G-L) approach used to model the non-integer order systems. In addition, the various steps involved in determining the RFPC control law are also described in detail. Section 3 presents the global optimization approach used in the present work and explains the implementation of the GGP strategy in the algorithm of the RFPC controller. The experimental results acquired using a real system based on an STM32 microcontroller are presented in Section 4.

2. Background and Problem Formulation

2.1. Modeling of a Fractional Order System

The non-integer order calculation is a generalization of the non-integer fundamental operator, ${}_{t_0}D_t^{\alpha }$, which is represented as follows:

$${}_{t_0}D_t^{\alpha }=\{\begin{array}{ll} \frac{d^{\alpha }}{d{t}^{\alpha }}& \alpha >0\\ 1& \alpha =0\\ {\displaystyle \underset{t0}{\overset{t}{\int }}{(d\tau )}^{\alpha }}& \alpha \text{<}0\end{array}$$

(1)

There are several mathematical definitions of the fractional calculation. These definitions do not necessarily provide the same outcomes, but they are equivalent for several functions [38]. The most known method of fractional control synthesis is the G–L method [39], which figures as follows:

$${}_{t_0}D_t^{\alpha }g(t)=\underset{h\to 0}{\lim }\frac{1}{h^{\alpha }}{\displaystyle \sum _{i=0}^{\left(t-t_0\right)/h}{(-1)}^i}\left(\begin{array}{l}\alpha \\ i\end{array}\right)g(t-ih)$$

(2)

where “h” is the sampling period.

For infinitely tiny “h”, the order “a” of a function “g(t)” is approximated in [40].

$${}_{t_0}D_t^{\alpha }g(t)=\frac{1}{h^{\alpha }}{\displaystyle \sum _{i=0}^{\left(t-t_0\right)/h}{(-1)}^i\left(\begin{array}{l}\alpha \\ i\end{array}\right)g(t-ih)}$$

(3)

This equation’s simulation necessitates the computation of a sum of increasing size over time. Using the short memory approach, this sum can be lowered [2]. Thus, relation (3) can be rephrased to:

$${}_{t_0}D_t^{\alpha }g(t)=\frac{1}{h^{\alpha }}{\displaystyle \sum _{i=0}^N{(-1)}^i\left(\begin{array}{l}\alpha \\ i\end{array}\right)g(t-ih)}$$

(4)

A non-integer order process can be given by this relation:

$${\displaystyle \sum _{l=0}^L{a}_l{D}_t^{{}^{{\alpha }_{a_l}}}y(t)}={\displaystyle \sum _{m=0}^M{b}_m{D}_t^{{\alpha }_{b_m}}u(t)}$$

(5)

in which $\left(a_l,b_m\right)\in R^2, \mathrm{and} \left({\alpha }_{al},{\alpha }_{bm}\right)\in R_{+}^2$.

To provide an appropriate description of this fractional order process, we need to take into consideration the uncertainty parameters $a_l \mathrm{and} b_m$. $a_l\in \left[{\underset{\_}{a}}_l , {\overline{a}}_l\right]{ \mathrm{and} b}_m\in \left[{\underset{\_}{b}}_m , {\overline{b}}_m\right]$.

Each fractional operator in the non-integer differential Equation (5) is replaced by its approximation (4), which allows to obtain [41]:

$$y(k)=\frac{1}{{\displaystyle \sum _{l=0}^L\frac{a_l}{h^{{\alpha }_{a_l}}}}}{\displaystyle \sum _{m=0}^M\frac{b_m}{h^{{\alpha }_{b_m}}}{\displaystyle \sum _{i=0}^N{\left(-1\right)}^i\left(\begin{array}{l}{\alpha }_{b_m}\\ i\end{array}\right)u(k-i)}}-\frac{1}{{\displaystyle \sum _{l=0}^L\frac{a_l}{h^{{\alpha }_{a_l}}}}}{\displaystyle \sum _{l=0}^L\frac{a_l}{h^{{\alpha }_{a_l}}}{\displaystyle \sum _{i=1}^N{\left(-1\right)}^i\left(\begin{array}{l}{\alpha }_{a_l}\\ i\end{array}\right)y(k-i)}}$$

(6)

2.2. RFPC Design

In the following section, we define the procedure used to obtain the optimum control law for RFPC of uncertain non-integer order systems. Hence, the Grünwald–Letnikov approach expressed by Equation (6) was used. Subsequently, and in keeping with the overall meaning, we define y(k) as a function of u(k − 1). Thus, Equation (6) was rephrased as [8]:

$$\Delta y(k)=\frac{1}{{\displaystyle \sum _{l=0}^L\frac{a_l}{h^{{\alpha }_{a_l}}}}}\left({\displaystyle \sum _{m=0}^M\frac{b_m}{h^{{\alpha }_{b_m}}}{\displaystyle \sum _{i=0}^N{\left(-1\right)}^i\left(\begin{array}{l}{\alpha }_{b_m}\\ i\end{array}\right)\Delta u(k-1-i)}}\right)-\frac{1}{{\displaystyle \sum _{l=0}^L\frac{a_l}{h^{{\alpha }_{a_l}}}}}\left({\displaystyle \sum _{l=0}^L\frac{a_l}{h^{{\alpha }_{a_l}}}{\displaystyle \sum _{i=1}^N{\left(-1\right)}^i\left(\begin{array}{l}{\alpha }_{a_l}\\ i\end{array}\right)\Delta y(k-i)}}\right)$$

(7)

where by $\Delta =1-q^{-1}$.

Equation (7) produced the output of the fractional process in $k+1$:

$$\begin{array}{l}y(k+1)=y(k)+\left(\frac{1}{{\displaystyle \sum _{l=0}^L\frac{a_l}{h^{{\alpha }_{a_l}}}}}{\displaystyle \sum _{m=0}^M\frac{b_m}{h^{{\alpha }_{b_m}}}}\right)\Delta u(k)+\frac{1}{{\displaystyle \sum _{l=0}^L\frac{a_l}{h^{{\alpha }_{a_l}}}}}\left({\displaystyle \sum _{m=0}^M\frac{b_m}{h^{{\alpha }_{b_m}}}{\displaystyle \sum _{i=1}^N{\left(-1\right)}^i\left(\begin{array}{l}{\alpha }_{b_m}\\ i\end{array}\right)\Delta u(k-i)}}\right)\\ -\frac{1}{{\displaystyle \sum _{l=0}^L\frac{a_l}{h^{{\alpha }_{a_l}}}}}\left({\displaystyle \sum _{l=0}^L\frac{a_l}{h^{{\alpha }_{a_l}}}{\displaystyle \sum _{i=1}^N{\left(-1\right)}^i\left(\begin{array}{l}{\alpha }_{a_l}\\ i\end{array}\right)\Delta y(k+1-i)}}\right)\end{array}$$

(8)

This equation can be restated as follows:

$$y(k+1)={\beta }_1\Delta u(k)+y_l(k+1)$$

(9)

where ${\beta }_1=\left(\frac{1}{{\displaystyle \sum _{l=0}^L\frac{a_l}{h^{{\alpha }_{a_l}}}}}{\displaystyle \sum _{m=0}^M\frac{b_m}{h^{{\alpha }_{b_m}}}}\right)$ and $y_l(k+1)$ is the free response of the process:

$$y_l(k+1)=y(k)+\frac{1}{{\displaystyle \sum _{l=0}^L\frac{a_l}{h^{{\alpha }_{a_l}}}}}\left({\displaystyle \sum _{m=0}^M\frac{b_m}{h^{{\alpha }_{b_m}}}{\displaystyle \sum _{i=1}^N{\left(-1\right)}^i\left(\begin{array}{l}{\alpha }_{b_m}\\ i\end{array}\right)\Delta u(k-i)}}\right)-\frac{1}{{\displaystyle \sum _{l=0}^L\frac{a_l}{h^{{\alpha }_{a_l}}}}}\left({\displaystyle \sum _{l=0}^L\frac{a_l}{h^{{\alpha }_{a_l}}}{\displaystyle \sum _{i=1}^N{\left(-1\right)}^i\left(\begin{array}{l}{\alpha }_{a_l}\\ i\end{array}\right)\Delta y(k+1-i)}}\right)$$

(10)

Thus, the equation of the predictor j-step y(k + j) can be determined by repeated recursion, which figures as [8]:

$$y(k+j)={\displaystyle \sum _{i=1}^j{\beta }_{j-i+1}\Delta u(k+i-1)}+y_l(k+j)$$

(11)

Predictive control involves the minimization of the performance criterion. This is given by:

$$J={\displaystyle \sum _{j=1}^{N_2}{(y(k+j)-w(k+j))}^2+\lambda {\displaystyle \sum _{i=0}^{N_1-1}\Delta u{(k+i)}^2}}$$

(12)

where by y(k + j) is expressed by the relation (11) and w(k + j) is the reference signal.

The output signal which extends along the prediction horizon N₂ is defined as:

$$Y=G\Delta U+Y_l$$

(13)

where by:

$$\begin{array}{l}Y={\left[y(k+1),\dots ,y(k+N_2\right]}^T\\ \Delta U={\left[\Delta u(k),\dots ,\Delta u(k+N_1-1)\right]}^T\\ Y_l={\left[y_l(k+1),\dots ,y_l(k+N_2)\right]}^T\end{array}$$

(14)

The G matrix features as:

$$G=\left[\begin{array}{llll}{\beta }_1 & 0 & \cdots & 0\\ {\beta }_2& {\beta }_1& \cdots & 0\\ ⋮& ⋮& \cdots & ⋮\\ {\beta }_{N_2} & {\beta }_{N_2-1}& \cdots & {\beta }_{N_2-N_1+1}\end{array}\right]$$

(15)

The objective function of Relation (12) is given as:

$$J={(Y-W)}^T(Y-W)+\lambda \Delta U^T\Delta U$$

(16)

in which is the reference signal on the prediction horizon:

$$W=\left[w(k+1),\dots w(k+N_2)\right]$$

(17)

2.3. Problem Statement

In connection with the uncertain fractional system, the control law of the RFPC controller is found through the worst-case technique. Therefore, the robust control law proves to be based on the solution suggested to the min–max problem [42], which is formulated as:

$$\underset{\Delta U\in \Omega }{{\displaystyle \min }}\hspace{1em}\underset{(a_l, b_m)\in \Psi }{{\displaystyle \max }} J(\Omega ,\Psi )$$

(18)

subject to:

$$\begin{array}{l} {\underset{\_}{a}}_l\le a_l\le {\overline{a}}_l , \mathrm{l}=0,\dots ,L\\ {\underset{\_}{b}}_m\le b_m\le {\underset{\_}{b}}_m, \mathrm{m}=0,\dots ,M\end{array}$$

(19)

and

$$\begin{array}{l}{u}_{\min }\le u(k+j-1)\le u_{\max }, j=1,\dots ,N_1\\ \Delta u_{\min }\le \Delta u(k+j-1)\le \Delta u_{\max }, j=1,\dots ,N_1\end{array}$$

(20)

$\Omega$ is the set of limits of the control sequence, and $\Psi$ is the set of parameter uncertainties.

$$\begin{array}{l}\Psi =\left\{a_l, b_m/a_l\in \left[{\underset{\_}{a}}_l , {\overline{a}}_l\right]{ \mathrm{and} \mathrm{b}}_m\in \left[{\underset{\_}{b}}_m , {\overline{b}}_m\right]\right\},\\ l\in \left[0 , L\right] \mathrm{and} \mathrm{m}\in \left[0 , M\right]\end{array}$$

(21)

The difference among all robust predictive control strategies is the type of model chosen for real processes. Certainly, in many types of models, for example, when the models are represented by fractional order operations and are subject to structured uncertainties, as in our case, the robust predictive control of these models is much more complex. This could be accounted for by the non-convexity of the criterion with respect to the uncertainties and control increments. Subsequently, the min–max problem cannot be solved by classical optimization methods. Indeed, the GGP-method-based FRPC controller (FRPC-GGP) is proposed for uncertain non-integer order systems in order to solve this problem.

3. GGP Method

In this paper, the GGP is the global method that as chosen to determine the global control law for the uncertain non-integer processes. It is founded on the polynomial form of the non-convex criterion. The major idea is that by applying some variable-change techniques, such as power and exponential transformations, the initially non-convex optimization problem is translated into a convex one.

3.1. Convexification Strategy of the GGP Method

The mathematical equation of a GGP problem with free variables is given by the following equations [43]:

$$\min {\displaystyle \sum _{q=1}^{T_0}{c}_q{z}_q}$$

(22)

subject to

$$\begin{array}{l}{\displaystyle \sum _{p=1}^{T_v}{h}_{vp}{z}_{vp}\le l_v,v=1,\dots ,V,}\\ z_q=x_1^{{\alpha }_{q1}}{x}_2^{{\alpha }_{q2}}\dots x_n^{{\alpha }_{qn}},q=1,\dots T_0, \\ z_{vp}=x_1^{{\beta }_{vp1}}{x}_2^{{\alpha }_{vp2}}\dots x_n^{{\alpha }_{vpn}}\\ \underset{\_}{x_i}\le x\le \overline{x_i}\end{array}$$

The convexification rules of the GGP method are usually applied only to positive variables. In several problems, the definition domain of $x_i$ can be negative. This is not a restriction. Indeed, a simple translation of the variables makes us take into account negative variables: $x_i=y{x^{\prime }}_i+z$.

where $y=\frac{\overline{x_i}-\underset{\_}{x_i}}{\overline{{x^{\prime }}_i}-\underset{\_}{{x^{\prime }}_i}}$ and $z=\frac{\underset{\_}{x_i}\overline{{x^{\prime }}_i}-\overline{x_i}\underset{\_}{{x^{\prime }}_i}}{\overline{{x^{\prime }}_i}-\underset{\_}{{x^{\prime }}_i}}$.

Before illustrating the convexification strategies of the GGP approach of a non-convex function, we need to introduce several definitions, propositions, theorems, and properties relating to convexity.

Definition 1

[43]. A function $g(X)$ is monomial if it is written in this form:

$$g(X)=r{\displaystyle \prod _{j=1}^n{x}_j^{\delta j}} , \mathrm{X}=(x_1,\dots ,x_n),{ \mathrm{x}}_j, \mathrm{r}, {\delta }_j\in R,\forall j,$$

The determinant of the $D(X)$ matrix is represented as:

$$\det D(X)={(-r)}^n\left({\displaystyle \prod _{j=1}^n{\delta }_j{x}_j^{n{\delta }_j-2}}\right)\left(1-{\displaystyle \sum _{j=1}^n{\delta }_j}\right)$$

where $D(X)$ is the hessian matrix of $g(X)$.

Remark 1

[43]. $\det D(X)\ge 0$ if $x_j\ge 0$ ,${\delta }_j\ge 0$ , and$r\ge 0$;

Remark 2

[43]. $\det H(X)\ge 0$ if $x_j\ge 0$, ${\delta }_j\ge 0$, $r\le 0$, and $\left(1-{\displaystyle \sum _{j=1}^n{\delta }_j}\right)\ge 0$.

Using the previous remarks, we obtain the following suggestions:

Suggestion 1

[43]. A function $g(X)=r{\displaystyle \prod _{j=1}^n{x}_j^{\delta j}}$ is convex if ${\delta }_j\le 0$, $r\ge 0$, and $x_j\ge 0$;

Suggestion 2

[43]. A function $g(X)=r{\displaystyle \prod _{j=1}^n{x}_j^{\delta j}}$ is convex for ${\delta }_i\ge 0$

$$x_j\ge 0, r\le 0, \mathrm{and} \left(1-{\displaystyle \sum _{j=1}^n{\delta }_j}\right)\ge 0.$$

The crucial idea in the convexification strategy for the GGP approach is to transform every non-convex variable of problem (22) into a convex one.

For example, we study a function, which figures as:

$$g(k_1,k_2,\dots ,k_n)=r{k}_1^{d_1}{k}_2^{d_2}\dots k_n^{d_n}$$

(23)

Indeed, the convexification of this equation relies on the values of

$$r \mathrm{and} d_j (\mathrm{for} \mathrm{j}=1,\dots ,n)$$

-

Positive term$\left(r>0\right)$: if $d_j\ge 0$, new terms $z_j$ are inserted by $k_j=\exp (z_j)$. Therefore, relation (23) can be expressed as:

$$r{k}_1^{d_1}{k}_2^{d_2}\dots k_n^{d_n}=r\exp (d_1{z}_1+d_2{z}_2+\dots +d_n{z}_n)$$

-

Negative term$\left(r<0\right)$: if $d_j<0$ or $\left(1-{\displaystyle \sum _{j=1}^n{\delta }_j}\right)\ge 0$, then new terms $z_j$ are added, with $x_j=z_j^{1/c}$, $j=1,\dots ,n \mathrm{and} c={\displaystyle \sum _{j=1}^n\delta j}$.

Therefore, Function (23) can be expressed as $r{x}_1^{d_1}{x}_2^{d_2}\dots x_n^{d_n}=r{z}_1^{1/c}{z}_2^{1/c}\dots z_n^{1/c}$, which is convex by proposition 2.

Based on the convexification technique given above, the non-convex problem is changed into a convex one. After the transformation of the min–max problem (18), we can use a classical optimization approach to resolve it. Hence, the global solution is reached.

3.2. RFPC-GGP Algorithm

In this paragraph, we will explain the application of the GGP strategy into the RFPC controller’s algorithm. Equation (18) can be represented as:

$$\underset{\Delta U\in \Omega }{{\displaystyle \min }}{J}^{*}(\Omega )$$

(24)

where by

$$J^{*}(\Omega )=\underset{(a_l, b_m)\in \Psi }{{\displaystyle \max }} J(\Omega ,\Psi )$$

(25)

It is useful to remember that the main purpose of the RFPC-GGP algorithm is to render the objective function a convex one. Consequently, the convexification strategy of this optimization method, by means of the set of rules given above, is applied to the criterion J. This results in a fractional but convex problem that can be solved by the predefined fmincon in the MATLAB software. This procedure is summarized by an algorithm, which figures as follows:

• Step 1: Determining the limits of the uncertain parameters and the controller parameters;
• Step 2: Applying the convexification strategy on criterion J;
• Step 3: Determining the optimal values $a_l \mathrm{and} b_m$ by solving the Equation (25);
• Step 4: Using the parameters $a_l \mathrm{and} b_m$ determined in step 3, solve Equation (24) and obtain the global optimal values of the future control increments, by having recourse to a conventional optimization method;
• Step 5: Implementing the global optimal control;
• Step 6: Return to Step (3), taking into account the new parameters.

4. Experiment Results

In this part, the method suggested in this work was implemented in a real thermal process (Figure 1 and Figure 2) [44,45,46].

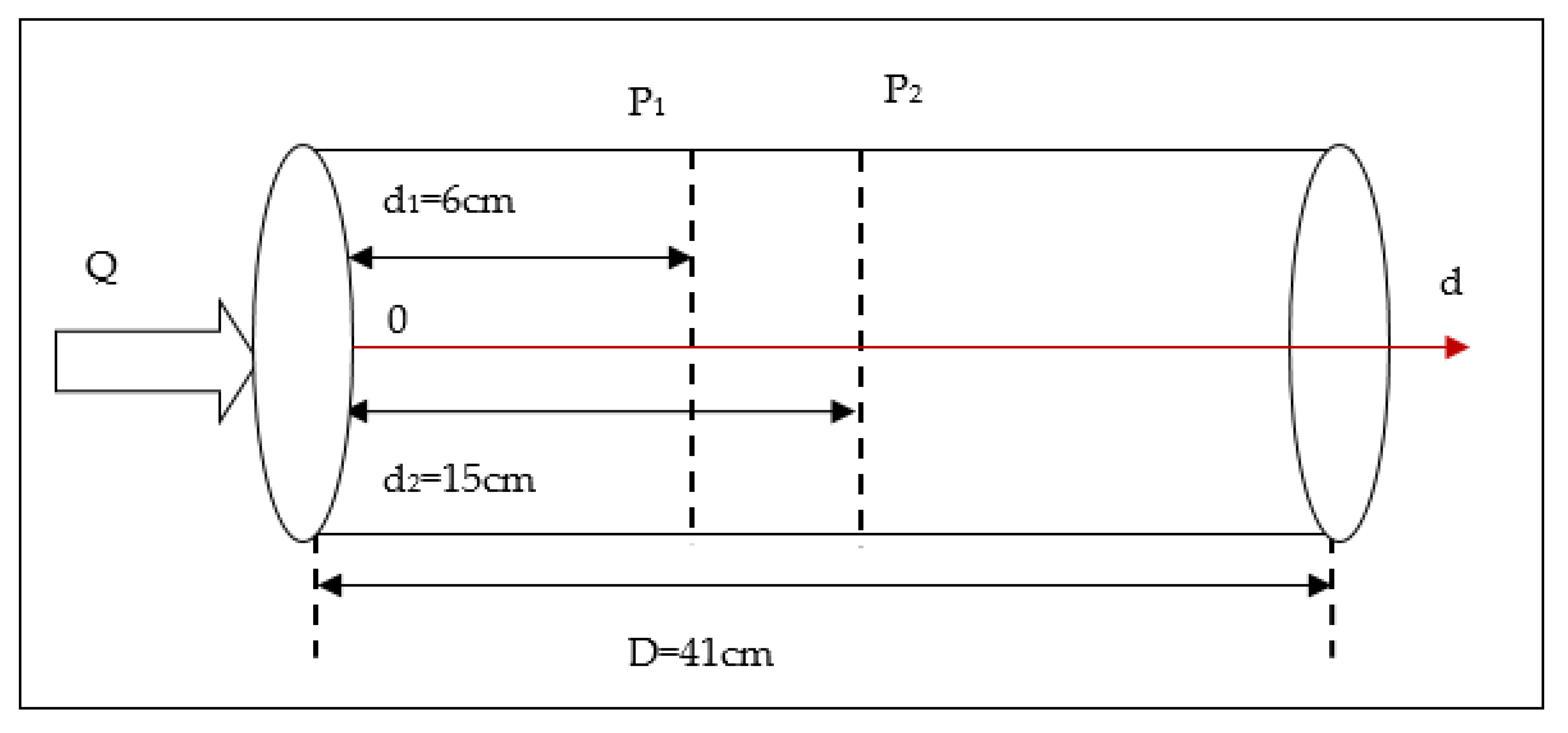
4.1. Thermal Process Identification

The bar of the real thermal process was thermally insulated and exposed to a heating resistor to generate unidirectional heat transfer flux. This process input was a flux (Q) generated by a heat resistor and linked by a data-card of the type USB-6009. The power interface that separates the acquisition board and the heating resistor was a dimmer board (PWM converter). The output sequence for our system was the bar temperature. The sensor’s signal was amplified to obtain a voltage of the output ranging from 0 to 5 v.

The goal was to keep the temperature at the specified setpoint at two places, P₂ and P₂, at a distance of d₁ = 6 cm and d₂ = 15 cm from the heating resistor, respectively (Figure 3).

In order to determine the real non-integer order model of this process, a given sequence, was applied to the heating resistor. Then, the temperature measured was saved. We determined the two non-integer models of our system H₁(s) and H₂(s) for the two points P₂ and P₂, respectively, on basis of the experimental data and utilizing the SRIVCF fractional model identification method [47].

$$H_1(s)=\frac{1.82}{37.14s^{1.5}+90.5s+11.19s^{0.5}+1}{e}^{-25s}$$

(26)

$$H_2(s)=\frac{1.4}{216.69s^{1.5}+188.42s+3.08s^{0.5}+1}{e}^{-55s}$$

(27)

We used a different input sequence to the heating resistor to validate the two fractional models. In addition, we measured the corresponding temperatures for the two points P₁ and P₂. From this experimental data, we found that the model’s responses were very close to the measured temperatures.

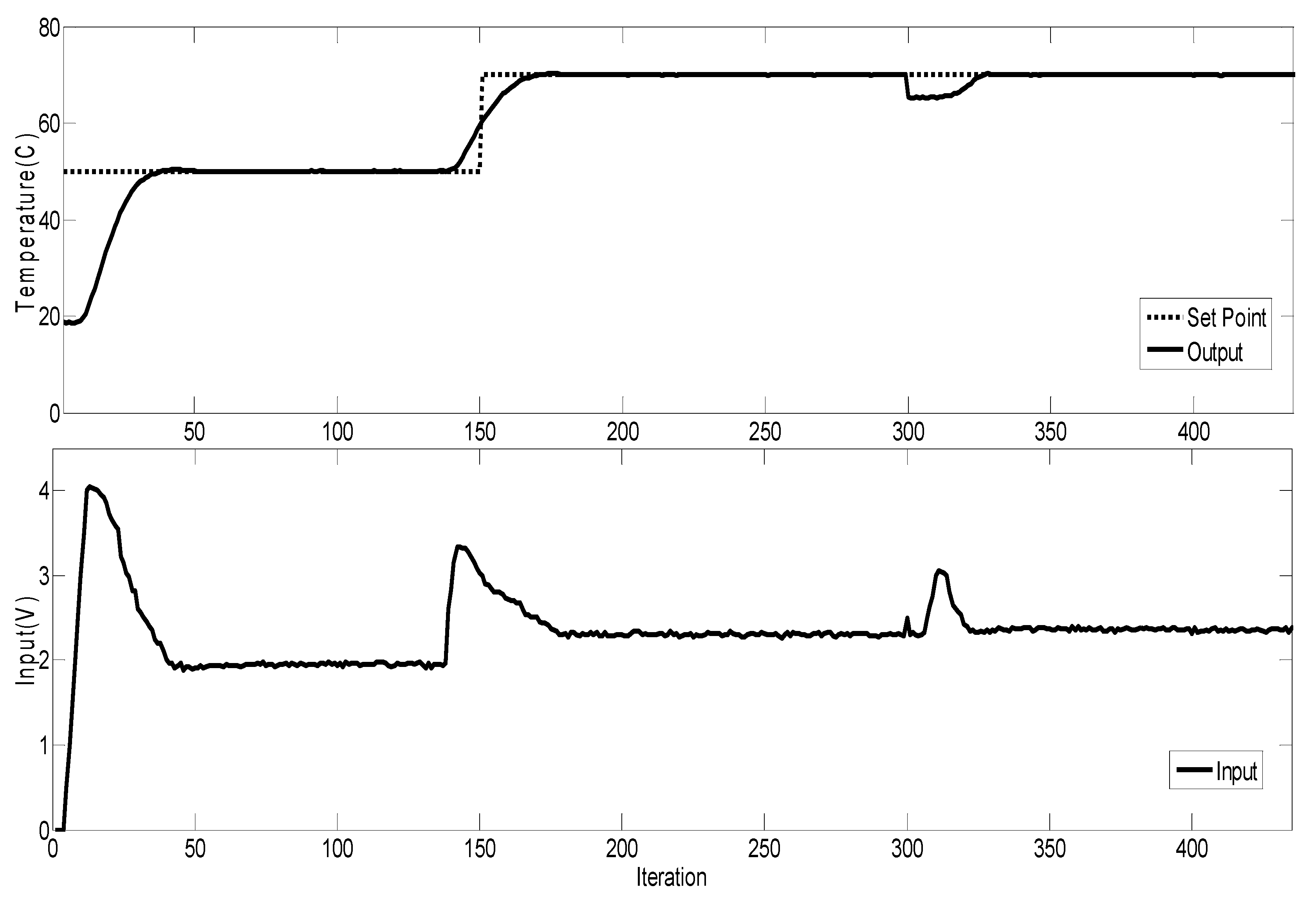
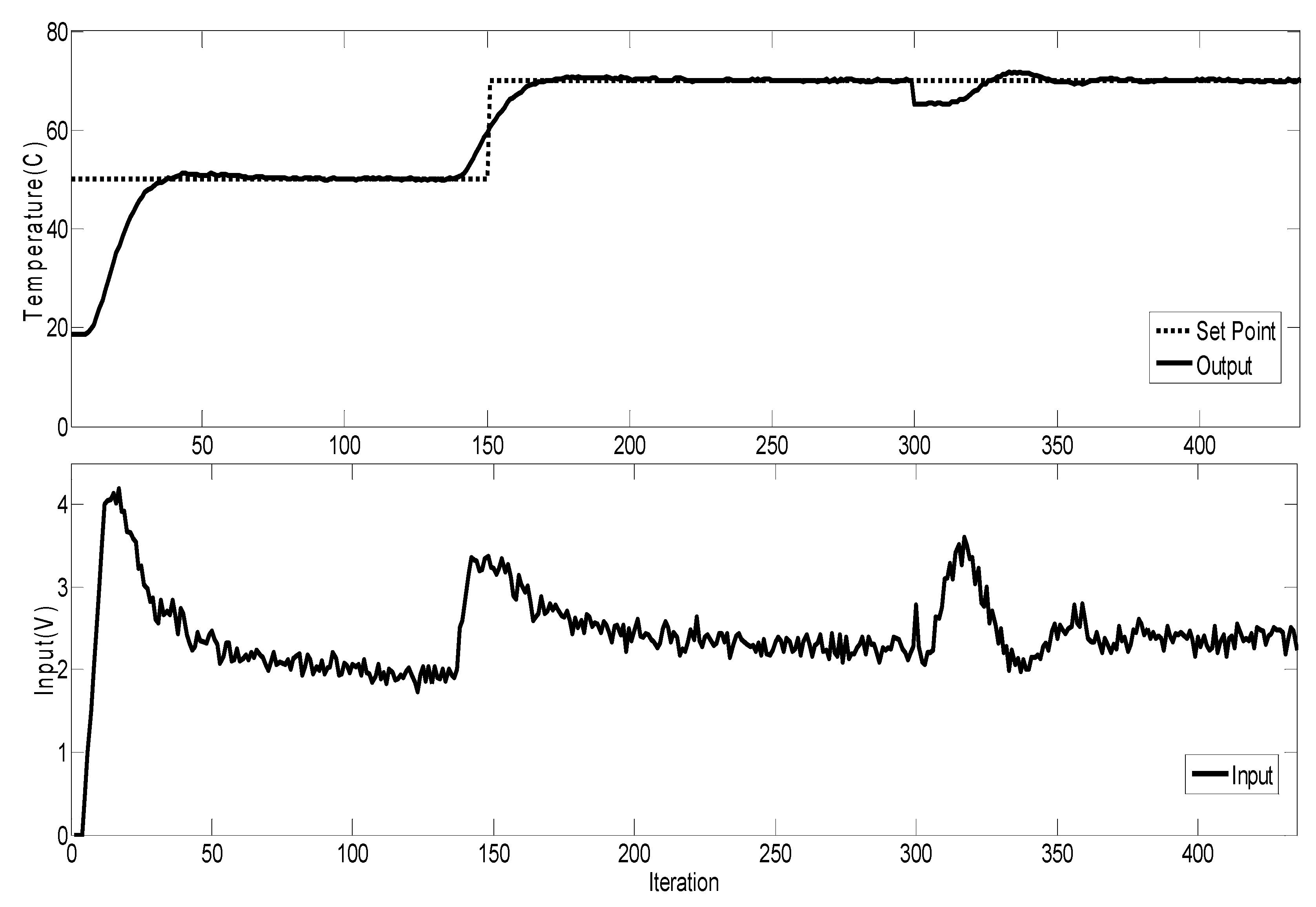
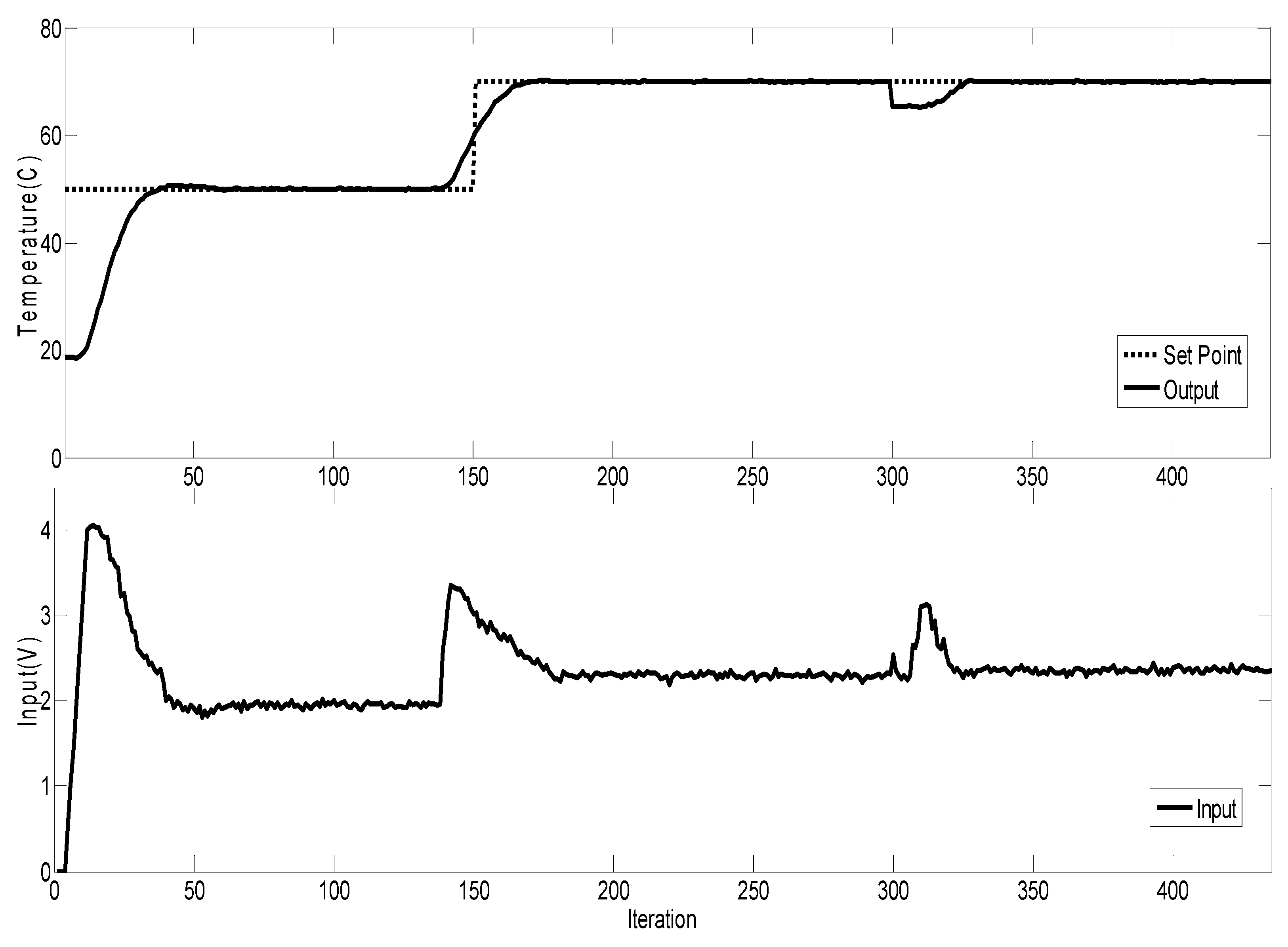
4.2. Controller Application

In this section, the task was to implement the proposed RFPC-GGP controller of the thermal system. Our purpose was to control the metallic rod temperature with respect to the dynamic process change, caused by the sensor position change at the sample time 300.

The synthesis of the RFPC-GGP controller requires the use of an uncertain non-integer order model. Thus, from the two models expressed by the Equations (26) and (27) and by making use of the maximum delay, we obtained an uncertain fractional transfer function defined by:

$$G(s)=\frac{b_0}{a_2{s}^{1.5}+a_{1}s+a_0{s}^{0.5}+1}{e}^{-55s}$$

(28)

where:

$$\begin{array}{l}{b}_0\in \left[1.4, 1.82\right]\\ a_2\in [37.14, 216.69]\\ a_1\in [90.5, 188.42]\\ a_0\in [3.08, 11.19]\end{array}$$

The technique of the convexification of the GGP method given in Section 3 was applied in line with criterion “J”. Consequently, we obtained a new convex criterion and a convex problem.

The robust fractional controller we proposed is intended with the following parameters:

$$N_1=1,{ \mathrm{N}}_2=15 \mathrm{and} \lambda =1$$

Figure 4 shows that the outputs (i.e., temperatures) and the inputs (i.e., thermal flux) evolved when the proposed RFPC-GGP controller was implemented in the thermal system. On the basis of these results, one could conclude that the outputs followed the desired reference. In addition, the thermal flux provided a small variation and respected the constraints. Thus, this proposed RFPC-GGP controller exhibited good performances despite the changing thermal process dynamics caused by the sensor position changes at iteration 300.

For further assessment of the proposed RFPC-GGP controller, a comparison test was used to determine if there were significant similarities or differences between this controller and the two other controllers: the first was the RFPC controller, which was obtained via the local optimization method; the second was the genetic algorithm-based RFPC controller (RFPC-GA). All predictive controllers were designed using the same parameters.

Figure 5 shows the evolutions of the temperatures and the thermal flux when the RFPC controller with the local optimization was applied to the thermal process. It also shows that the output sequence followed the set point with slight fluctuations.

The RFPC-GA controller was designed using the “GA” toolbox in MATLAB, which is represented as follows:

• Codification: the real coding was used because the objective function to be optimized was real;
• Fitness function: it is considered by the performance criterion to be optimized;
• The size of the population was fixed at 40 individuals;
• Stopping conditions: the algorithm stopped when the number of generations reached 100 or if there was no improvement in the performance criterion for 50 successive generations.

The behavior of the response produced by the RFPC-GA controller is shown in Figure 6. These results reveal two facts: the output signal followed the set point and the optimal control yielded by the proposed RFPC-GGP controller was smoother than the one produced by the RFPC-GA controller.

In the actual test, the average (M) and the variance (V) of the control signal were calculated, respectively, by $M=\frac{1}{N}{\displaystyle \sum _{k=1}^{N}u(k)}$ and $V=\frac{1}{N}{\displaystyle \sum _{k=1}^{N}u{(k)}^2}.$

Table 1. Average and variance of the control sequence.

Control	Average	Variance
Entry 1 RFPC-GGP	2.3225	5.6032
Entry 2 RFPC-GA	2.3246	5.6175
RFPC (local optimization)	2.4151	6.08

shows the results in terms of the average and the variance for the three RFPC controllers. On the basis of these results, we also deduced that the optimal control produced through the RFPC controller, which was based on global optimization algorithms, presented the least control variance compared to the control law determined by means of the RFPC that was determined by a local optimization method. Moreover, the optimal control determined by the proposed RFPC-GGP was smoother than the one found by the RFPC-GA.

4.3. RFPC Using STM32 Microcontroller

Embedded computing applications are invading the industrial environment as well as our daily life. Over the last few decades, the continuously increasing needs for technicality have led to the integration of very strong automation in all industrial products. STM32 microcontrollers are based on the ARM^® Cortex^®-M processor and provide greater freedom for MCU users [48]. These devices are an ideal choice for the implementation of complex controls as in our case for fractional predictive control. In the present work, we chose the high-performance STM32F746IGT6 microcontroller to implement the RFPC proposed controller. This microcontroller was characterized by low power consumption, low price, and a wide range of peripherals. The STM32 Keil kit based on a JTAG programming interface was used. Since converting “m” (MATLAB) files to “C” files decreases program runtime performance, we chose to program directly in the Keil language (C/C++).

The analog control was injected into the real system. Subsequently, the output voltage of the real system which is in the interval of 0–1 V is processed after an analogue filter to make it in an interval of 0–3.3 V, since the voltage range supported by the STM32 input–output ports is 0–3.3 V. This analog output is sent to the STM32 that converts it using ADC to a digital value and sends it to the Keil compiler (Figure 7).

Figure 8 shows that the temperatures and the thermal flux evolve when the proposed RFPC-GGP controller using the STM32 microcontroller. On the basis of these results, we can deduce the efficiency of the algorithm proposed using the STM32 microcontroller in terms of good tracking and zero static error.

5. Conclusions

In this work, we presented the design of an RFPC controller for the uncertain non-integer order process. Parameters uncertainties are used to take into consideration the uncertain of the non-integer process that results in solving a non-convex min–max problem. Therefore, the GGP-method-based RFPC-GGP controller was proposed for the non-integer process with structured uncertainties in order to solve this problem. The GGP method, which is a global deterministic optimization method, consisted of converting a non-convex problem into a convex one via the application of variable changes. Consequently, we obtained a new convex criterion and a convex problem. The practical experiments on a fractional thermal system indicated that the proposed RFPC-GGP controller produced good performances, unlike the RFPC controller obtained through the local optimization method and the RFPC-GA controller. In addition, the implementation of the proposed controller on thermal system using the STM32 microcontroller exhibited good performance despite the changing of the thermal process dynamic. In our future works, this may lead to the application of the RFPC-GGP controller to other systems, for example, multi-input multi-output (MIMO) uncertain non-integer systems.