Global Optimization in Robust Fractional Control of Uncertain Fractional Order Systems: A Thermal Application Using the STM32 Microcontroller
Abstract
:1. Introduction
2. Background and Problem Formulation
2.1. Modeling of a Fractional Order System
2.2. RFPC Design
2.3. Problem Statement
3. GGP Method
3.1. Convexification Strategy of the GGP Method
- -
- Positive term: if , new terms are inserted by . Therefore, relation (23) can be expressed as:
- -
- Negative term: if or , then new terms are added, with , .
3.2. RFPC-GGP Algorithm
- Step 1: Determining the limits of the uncertain parameters and the controller parameters;
- Step 2: Applying the convexification strategy on criterion J;
- Step 3: Determining the optimal values by solving the Equation (25);
- Step 4: Using the parameters determined in step 3, solve Equation (24) and obtain the global optimal values of the future control increments, by having recourse to a conventional optimization method;
- Step 5: Implementing the global optimal control;
- Step 6: Return to Step (3), taking into account the new parameters.
4. Experiment Results
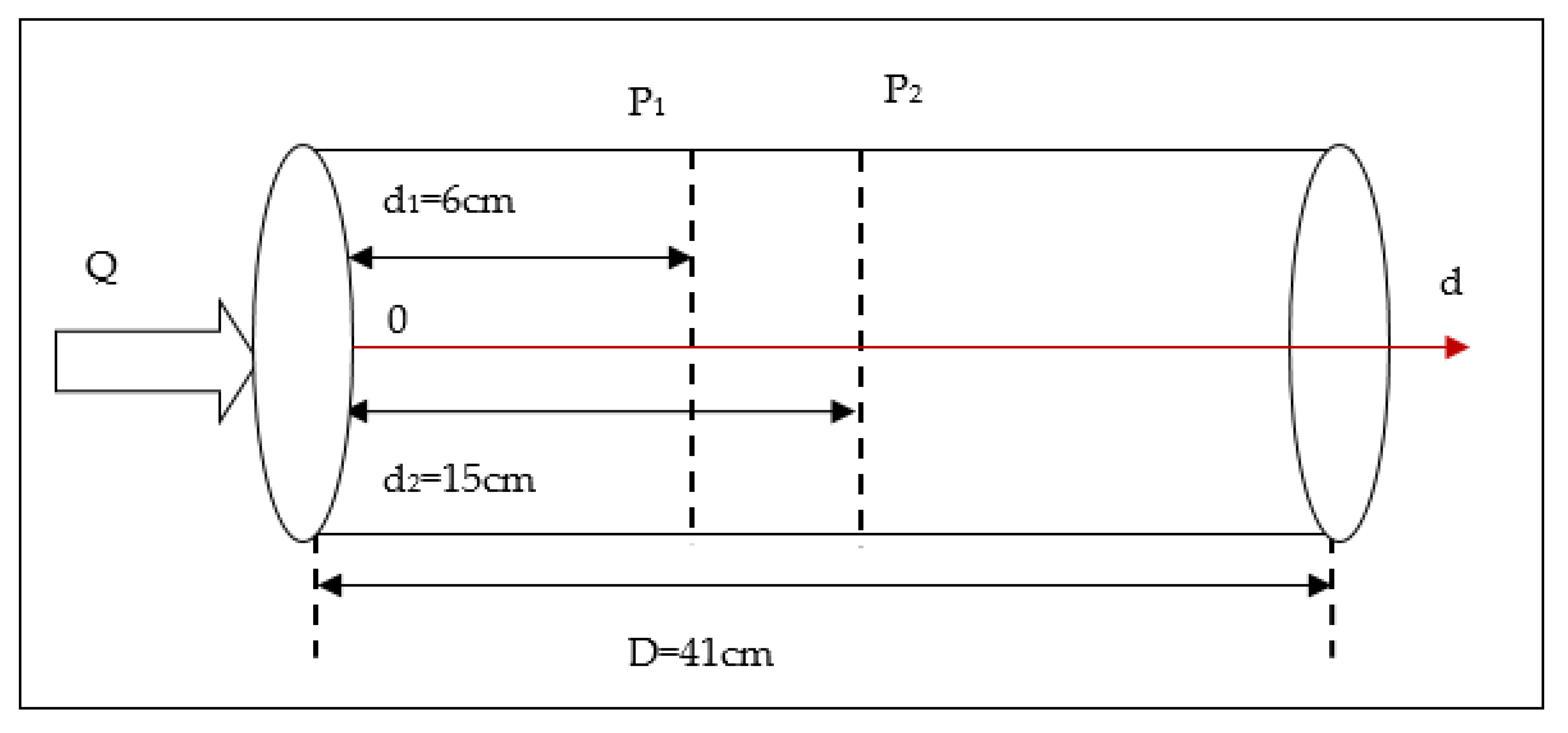
4.1. Thermal Process Identification
4.2. Controller Application
- Codification: the real coding was used because the objective function to be optimized was real;
- Fitness function: it is considered by the performance criterion to be optimized;
- The size of the population was fixed at 40 individuals;
- Stopping conditions: the algorithm stopped when the number of generations reached 100 or if there was no improvement in the performance criterion for 50 successive generations.
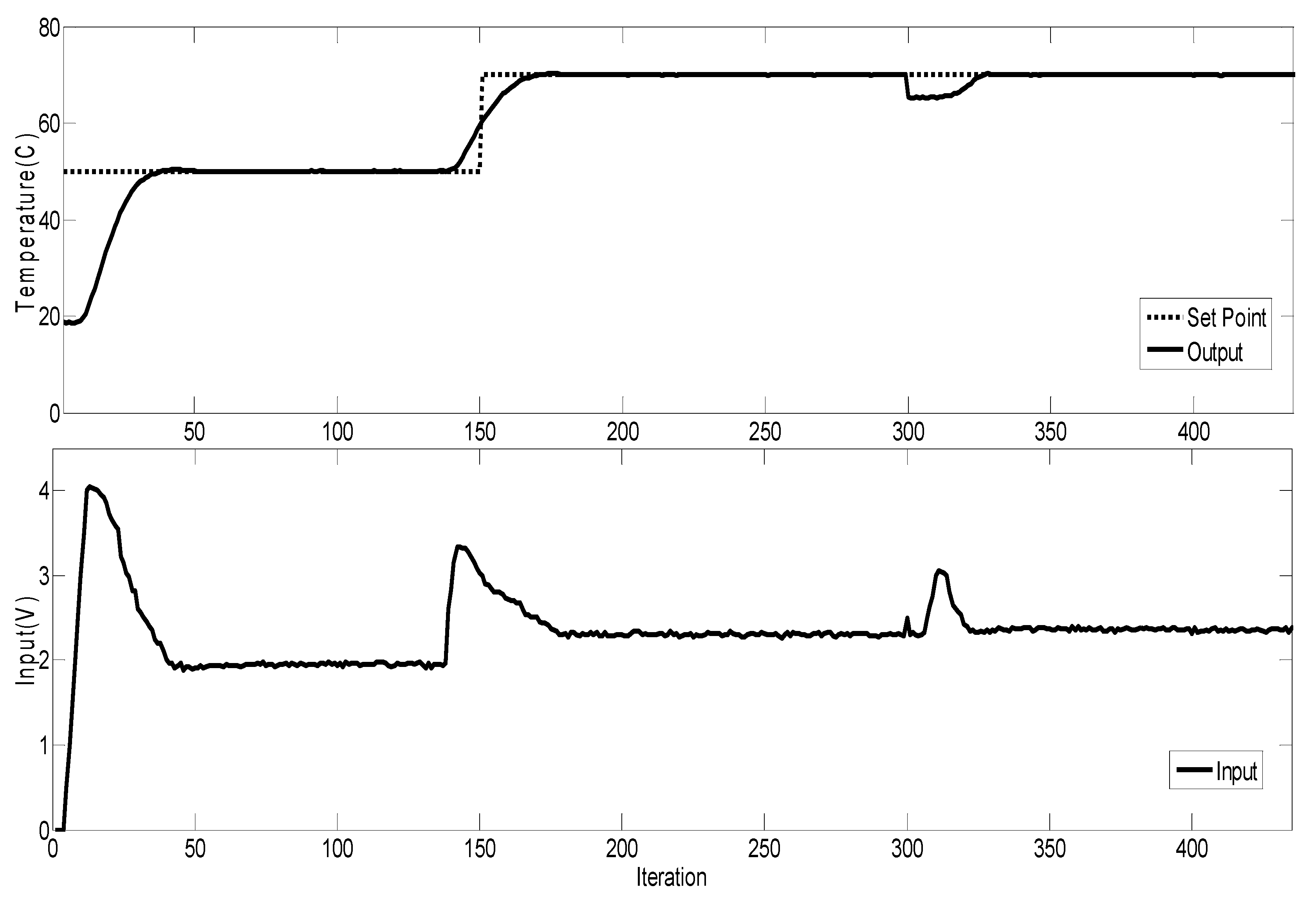
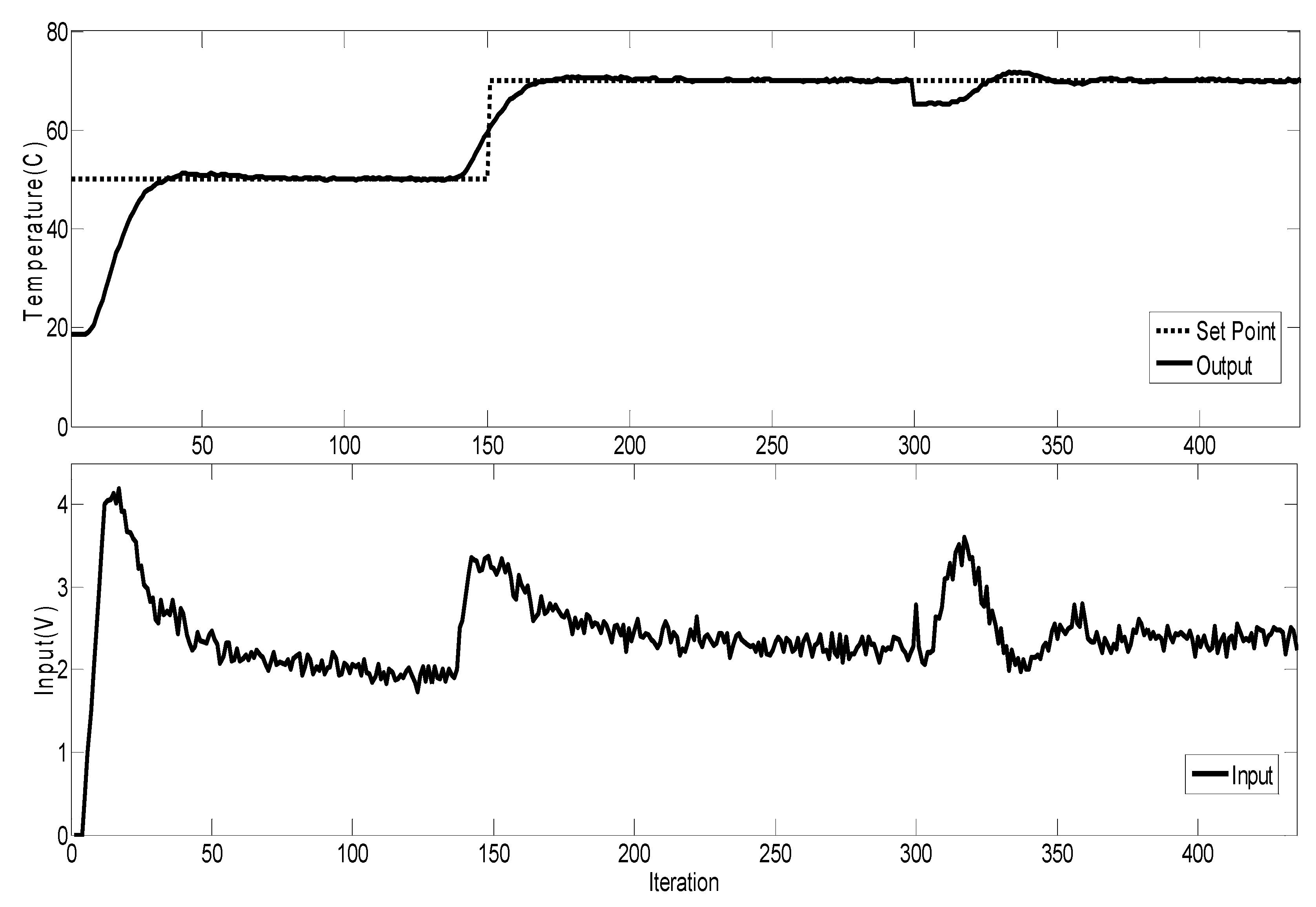
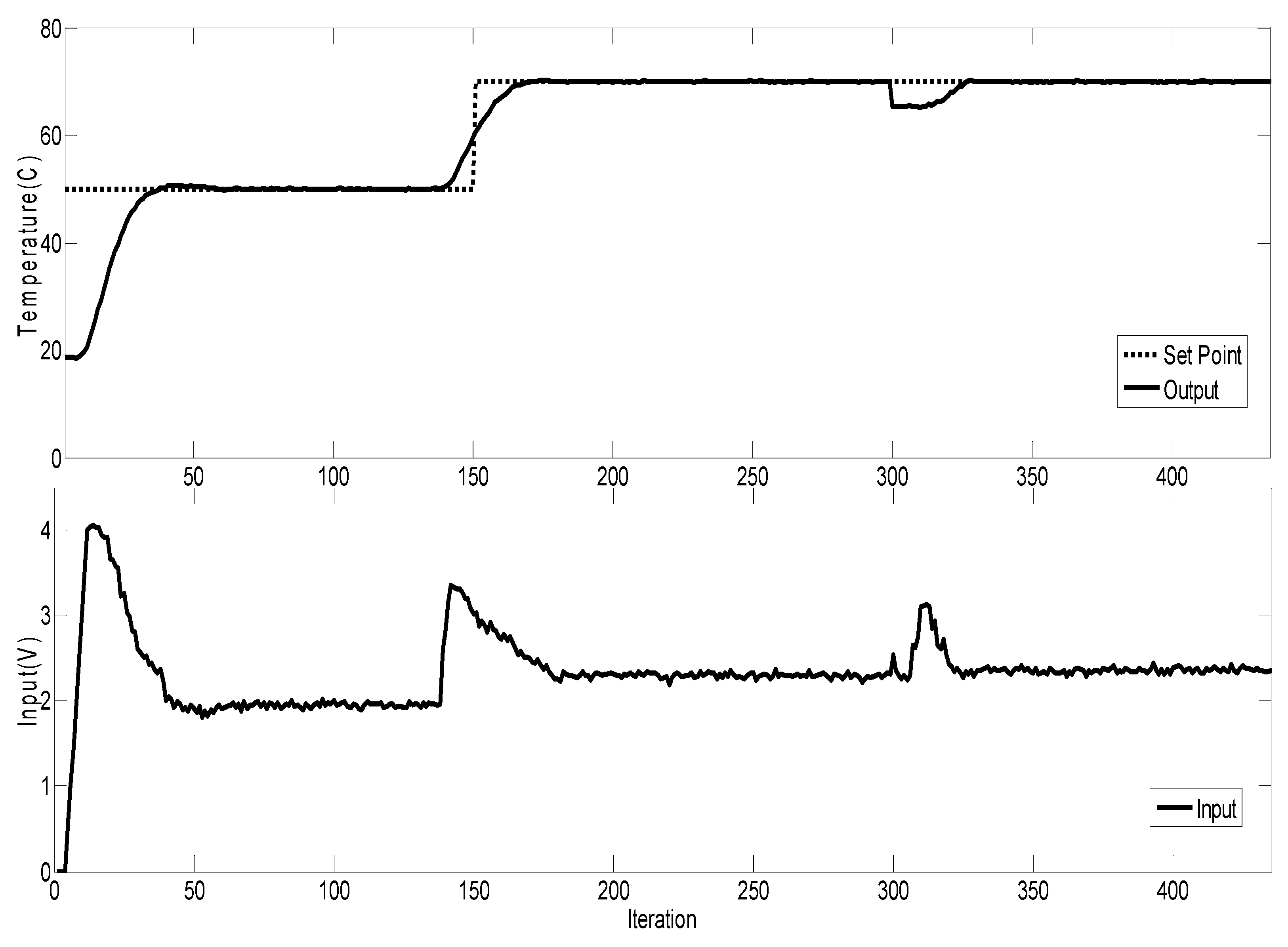
4.3. RFPC Using STM32 Microcontroller
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Podlubny, I. Fractional Differential Equations; Academie Press: New York, NY, USA, 1999. [Google Scholar]
- Bagley, R.; Calico, R. Fractional order state equations for the control of viscoelastically damped structures. J. Guid. Control Dyn. 1991, 14, 304–311. [Google Scholar] [CrossRef]
- Mainardi, F.; Raberto, M.; Gorenflo, R.; Scalas, E. Fractional calculus and continuous-time finance II: The waiting-time distribution. Phys. A Stat. Mech. Appl. 2000, 287, 468–481. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Tian, Q.; Chen, L.; Yang, J. Simulation of a viscoelastic flexible multibody system using absolute nodal coordinate and fractional derivative methods. Multibody Syst. Dyn. 2009, 21, 281–303. [Google Scholar] [CrossRef]
- Shantanu, D. Functional Fractional Calculs for System Identification and Controls; Springer: Berlin, Germany, 2008. [Google Scholar]
- Oustaloup, A. From fractality to non-integer derivation through recursivity, a property common to these two concepts: A fundamental idea from a new process control strategy. In Proceedings of the 12th IMACS World Conf., Paris, France, 18–22 July 1988; pp. 203–208. [Google Scholar]
- Oustaloup, A. La Commande CRONE (Commande Robuste d’Ordre Non Entier); Hermès: Paris, France, 1991. [Google Scholar]
- Rhouma, A.; Bouani, F. Robust model predictive control of uncertain fractional systems: A thermal application. IET Control Theory Appl. 2014, 8, 1986–1994. [Google Scholar] [CrossRef]
- Raynaud, H.F.; Zergainoh, A. State-space representation for fractional order controllers. Automatica 2000, 36, 1017–1102. [Google Scholar] [CrossRef]
- Baris, B.A.; Abdullah, A.; Celaleddin, Y. Auto-tuning of PID controller according to fractional-order reference model approximation for DC rotor control. Mechatronics 2013, 23, 789–797. [Google Scholar]
- Dastjerdi, A.A.; Vinagre, B.M.; Chenc, Y.; HosseinNiaa, S.H. Linear fractional order controllers; A survey in the frequency domain. Annu. Rev. Control. 2019, 47, 51–70. [Google Scholar] [CrossRef]
- Goyal, V.; Mishra, P.; Deolia, V.K. A Robust Fractional Order Parallel Control Structure for Flow Control using a Pneumatic Control Valve with Nonlinear and Uncertain Dynamics. Arab. J. Sci. Eng. 2019, 14, 2597–2611. [Google Scholar] [CrossRef]
- Chen, K.; Tang, R.; Li, C.; Lu, J. Fractional order PIλ controller synthesis for steam turbine speed governing systems. ISA Trans. 2018, 77, 49–57. [Google Scholar] [CrossRef]
- Shabnam, P.; Peyman, B. Parallel cascade control of dead time processes via fractional order controllers based on Smith predictor. ISA Trans. 2020, 98, 186–197. [Google Scholar]
- Bahram, Y.; Mehdi, H. Constrained Control of Semilinear Fractional-Order Systems: Application in Drug Delivery Systems. In Proceedings of the Conference on Control Technology and Applications (CCTA) 2020, Montréal, QC, Canada, 9–11 August 2020. [Google Scholar]
- Pantelis, S.; Sarimveis, H. Stabilising Model Predictive Control for Discrete-time Fractional-order Systems. Automatica 2016, 75, 24–31. [Google Scholar]
- Fukushima, H.; Kim, T.; Sugie, T. Adaptive model predictive control for a class of constrained linear systems based on comparison model. Automatica 2007, 43, 301–308. [Google Scholar] [CrossRef]
- Stefan, D. Model-Plant Mismatch in Fractional Order Model Predictive Control. Theor. Dev. Appl. Non-Integer Order Syst. 2015, 357, 281–291. [Google Scholar]
- Boudjehem, D.; Boudjehem, B. A Fractional Model Predictive Control for Fractional Order Systems. In Fractional Dynamics and Control; Springer Nature: Cham, Switzerland, 2011; pp. 59–71. [Google Scholar]
- Qin, Z.; Qibing, J.; Ridong, Z. Design of fractional order predictive functional control for fractional industrial processes. Chemom. Intell. Lab. Syst. 2016, 152, 34–41. [Google Scholar]
- Rhouma, A.; Hafsi, S.; Bouani, F. Practical application of fractional order controllers to a delay thermal system. Comput. Syst. Sci. Eng. 2019, 34, 305–313. [Google Scholar] [CrossRef]
- Camacho, E.F.; Bordons, C. Model Predictive Control; Springer: Berlin, Germany, 2004. [Google Scholar]
- Thamallah, A.; Sakly, A.; M’Sahli, F. A new constrained PSO for fuzzy predictive control of Quadruple-Tank process. Measurement 2019, 136, 93–104. [Google Scholar] [CrossRef]
- Bouzouita, B.; Bouani, F.; Ksouri, M. Solving non convex min-max predictive controller. In Proceedings of the Information, Decision and Control Conference, New Orleans, LA, USA, 12–14 December 2007. [Google Scholar]
- Lijun, C.; Shangfeng, D.; Yaofeng, H.; Meihui, L.; Dan, X. Robust model predictive control for greenhouse temperature based on particle swarm optimization. Inf. Processing Agric. 2018, 5, 329–338. [Google Scholar]
- Kouramas, K.I.; Panos, C.; Faísca, N.P.; Pistikopoulos, E.N. An algorithm for robust explicit/multi-parametric model predictive control. Automatica 2013, 49, 381–389. [Google Scholar] [CrossRef]
- Kouramas, K.I.; Panos, C.; Faísca, N.P.; Pistikopoulos, E.N. Explicit/multi-parametric model predictive control (MPC) of linear discrete-time systems by dynamic and multi-parametric programming. Automatica 2011, 47, 1638–1645. [Google Scholar] [CrossRef]
- Na, M.G.; Hwang, I.J. Design of a PWR power controller using model predictive control optimized by a genetic algorithm. Nucl. Eng. Technol. 2006, 38, 81–92. [Google Scholar]
- Rejane, B.A.; Antonio, A.R.C. Filtered predictive control design using multi-objective optimization based on genetic algorithm for handling offset in chemical processes. Chem. Eng. Res. Des. 2017, 117, 265–273. [Google Scholar]
- TayyebTaher, M.; Esmaeilzadeh, S.M. Model predictive control of attitude maneuver of a geostationary flexible satellite based on genetic algorithm. Adv. Space Res. 2017, 60, 57–64. [Google Scholar] [CrossRef]
- Bouzouita, B.; Bouani, F.; Wertz, V.; Ksouri, M. Implementation of SISO Robust Predictive Control to a Three TanksSystem. In Proceedings of the IEEE International Conference on Control Applications, San Antonio, TX, USA, 3–5 September 2008. [Google Scholar]
- Kherigi, A.; Bouani, F.; Ksouri, M. A GGP approach to solve non convex min-max predictive controller for a class of constrained MIMO systems described by state-space models. Int. J. Control Autom. Syst. 2011, 9, 452–460. [Google Scholar] [CrossRef]
- BenHariz, M.; Bouani, F. Robust Fixed Low-Order Controller for Uncertain Decoupled MIMO Systems. J. Dyn. Syst. Meas. Control 2018, 140, 02100. [Google Scholar]
- Boudjehem, D.; Boudjehem, B. Robust Fractional Order Controller for Chaotic Systems. IFAC-PapersOnLine 2016, 49, 175–179. [Google Scholar] [CrossRef]
- Sopasakisy, P.; Ntouskas, S.; Sarimveis, H. Robust model predictive control for discrete-time fractional-ordersystems. In Proceedings of the 23rd Mediterranean Conference on Control and Automation (MED), Torremolinos, Spain, 16–19 June 2015. [Google Scholar]
- Ardashir, M.; Sehraneh, G.; Okyay, K.; Sohrab, K.M. Robust predictive synchronization of uncertain fractional-order time-delayed chaotic systems. Soft Comput. 2019, 23, 6883–6898. [Google Scholar]
- Esfahani, P.S.; Pieper, J.K. Robust model predictive control for switched linear systems. ISA Trans. 2019, 89, 1–11. [Google Scholar] [CrossRef]
- Tavazoei, M.S. A note on fractional-order derivatives of periodic functions. Automatica 2010, 46, 945–948. [Google Scholar] [CrossRef]
- Hajiloo, A.; Nariman-zadeh, N.; Moeini, A. Pareto optimal robust design of fractional-order PID controllers for systems with probabilistic uncertainties. Mechatronics 2012, 22, 788–801. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculs and Fractional Differential Equation; John Wiley and Son: New York, NY, USA, 1993. [Google Scholar]
- Oustaloup, A.; Olivier, C.; Ludovic, L. Representation et Identification Par Modèle Non Entier; Lavoisier: Paris, France, 2005. [Google Scholar]
- Ramirez, D.; Alamo, T.; Camacho, E. Efficient implementation of constrained min-max model predictive control with bounded uncertainties. In Proceedings of the 41th IEEE Conference on Decision and Control, Las Vegas, NV, USA, 10–13 December 2002. [Google Scholar]
- Tsai, J.F.; Lin, M.H.; Hu, Y.C. On generalized geometric programming problems with non positive variables. Eur. J. Oper. Res. 2007, 178, 10–19. [Google Scholar] [CrossRef]
- Battaglia, J.L.; Cois, O.; Puigsegur, L.; Oustaloup, A. Solving an inverse heat conduction problem using a non-integer identified model. Int. J. Heat Mass. Transf. 2001, 44, 2671–2680. [Google Scholar] [CrossRef]
- Rhouma, A.; Bouani, F.; Bouzouita, B.; Ksouri, M. Model predictive control of fractional order systems. J. Comput. Nonlinear Dyn. 2014, 9, 031011. [Google Scholar] [CrossRef]
- Rhouma, A.; Hafsi, S.; Laabidi, k. Fractional PI Stabilization of Delay Systems: Application to a Thermal System. J. Appl. Nonlinear Dyn. 2019, 8, 509–518. [Google Scholar] [CrossRef]
- Malti, R.; Victor, S.; Oustaloup, A.; Garnier, H. An optimal instrumental variable method for continuous-time fractional model identification. In Proceedings of the 17th IFAC World Congress, Seoul, Korea, 6–11 July 2008; pp. 14379–14384. [Google Scholar]
- Krzysztof, O.; Maciej, R.; Jakub, Z. The Frequency and Real-Time Properties of the Microcontroller Implementation of Fractional-Order PID Controller. Electronics 2021, 10, 524. [Google Scholar]




| Control | Average | Variance |
|---|---|---|
| Entry 1 RFPC-GGP | 2.3225 | 5.6032 |
| Entry 2 RFPC-GA | 2.3246 | 5.6175 |
| RFPC (local optimization) | 2.4151 | 6.08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rhouma, A.; Hafsi, S.; Bouani, F. Global Optimization in Robust Fractional Control of Uncertain Fractional Order Systems: A Thermal Application Using the STM32 Microcontroller. Electronics 2022, 11, 268. https://doi.org/10.3390/electronics11020268
Rhouma A, Hafsi S, Bouani F. Global Optimization in Robust Fractional Control of Uncertain Fractional Order Systems: A Thermal Application Using the STM32 Microcontroller. Electronics. 2022; 11(2):268. https://doi.org/10.3390/electronics11020268
Chicago/Turabian StyleRhouma, Aymen, Sami Hafsi, and Faouzi Bouani. 2022. "Global Optimization in Robust Fractional Control of Uncertain Fractional Order Systems: A Thermal Application Using the STM32 Microcontroller" Electronics 11, no. 2: 268. https://doi.org/10.3390/electronics11020268
APA StyleRhouma, A., Hafsi, S., & Bouani, F. (2022). Global Optimization in Robust Fractional Control of Uncertain Fractional Order Systems: A Thermal Application Using the STM32 Microcontroller. Electronics, 11(2), 268. https://doi.org/10.3390/electronics11020268






