FedZaCt: Federated Learning with Z Average and Cross-Teaching on Image Segmentation

Abstract

In Federated Learning (FL), data communication among clients is denied. However, it is difficult to learn from the decentralized client data, which is under-sampled, especially for segmentation tasks that need to extract enough contextual semantic information. Existing FL studies always average client models to one global model in segmentation tasks while neglecting the diverse knowledge extracted by the models. To maintain and utilize the diverse knowledge, we propose a novel training paradigm called Federated Learning with Z-average and Cross-teaching (FedZaCt) to deal with segmentation tasks. From the model parameters’ aspect, the Z-average method constructs individual client models, which maintain diverse knowledge from multiple client data. From the model distillation aspect, the Cross-teaching method transfers the other client models’ knowledge to supervise the local client model. In particular, FedZaCt does not have the global model during the training process. After training, all client models are aggregated into the global model by averaging all client model parameters. The proposed methods are applied to two medical image segmentation datasets including our private aortic dataset and a public HAM10000 dataset. Experimental results demonstrate that our methods can achieve higher Intersection over Union values and Dice scores.

1. Introduction

Automatically recognizing structures in a medical image is an important process for screening or diagnosing disease. Though segmentation models based on deep learning methods [1,2] have shown promising performances [3,4], large amounts of data are always required to train robust models. As privacy concerns increase, collecting data, especially medical image data from multiple institutions, is difficult. To collaboratively learn from distributed data stored on multiple clients, Federated Learning (FL) [5,6,7,8] aggregates models in the Central server trained on multiple clients with promising privacy preservation. During the FL process, though all the data samples are kept locally and not exchanged, the distribution knowledge about the client data is extracted by the client models. To cover the distribution of all client data, we believe that model communication [9] among clients is necessary to enhance the FL model.

In existing FL methods, the model communication mainly focuses on two usual aspects including the model parameters [10,11] and the model distillation. Due to the simple and reliable implementation, the parameter-averaged method named Federated Averaging (FedAvg) [10] is popular. In FedAvg, the Central server averages the model parameters of all client servers and transfers the synchronized model to clients for locally continued training. Unlike the Ensemble Learning (EL) [12,13], which always combines many weak learners to vote on the final results, FL always obtains one global model ultimately and uses the global model to acquire the final results. However, weak learners in EL actually learn diverse knowledge from sample data, which contributes to the high performance. It is necessary to design a new FL method to fully use the diverse knowledge of the client data.

The distillation-based method attempts to use the teaching method to train the global model, where the client models teach the global model to learn the client data knowledge. The common operation [14] uses the locally computed logits to build global models. Though some methods [15] distill the public data to preserve privacy, introducing extra data is an unnecessary burden. Recently, new teaching methods [16,17] using multi-teacher models have been proposed to improve the domain adaptation performance. Learning from the diverse knowledge of multi-teacher models trained on different domains, the student model learns more information about multiple domains. Actually, the teacher models may become better by learning from each other, which has not been introduced to FL. In addition, most distillation-based methods are used in classification tasks. For segmentation tasks, the parameter-averaged methods are always adopted. However, all these studies try to train a global model representing all client models during the training process. Meanwhile, traditional FL approaches train client models to fit the local data distribution and limit models to only learn semantic information from the local data. This crucial problem restricts the model communication effects of client models to limit FL’s global performance. Therefore, an effective and privacy-preserving model communication method for utilizing knowledge is essential for training robust FL models.

In this study, we design a new Federated learning training paradigm that promotes model communication from model parameters and distillation. This paradigm is called Federated Learning with Z-average and Cross-teaching (FLZaCt). For one thing, FLZaCt disables the global model during the training process while producing the individual client models to maintain diverse knowledge extracted from multiple client data. Additionally, local client models learn from the local data distribution and the other clients’ data distribution. The proposed paradigm enables each client to access other clients’ model knowledge rather than the dataset to preserve privacy. The local client model knowledge can represent the local data distribution and transmit the distribution information to the other clients.

In this way, FLZaCt captures the local client data distribution and benefits from the cross-client knowledge. Effective communication contributes to high FL model performance because of high knowledge utilization. This paradigm is conducted on our private and public datasets, which outperforms the traditional FedAvg paradigm in extensive experiments.

Our main contributions are summarized as follows:

1.

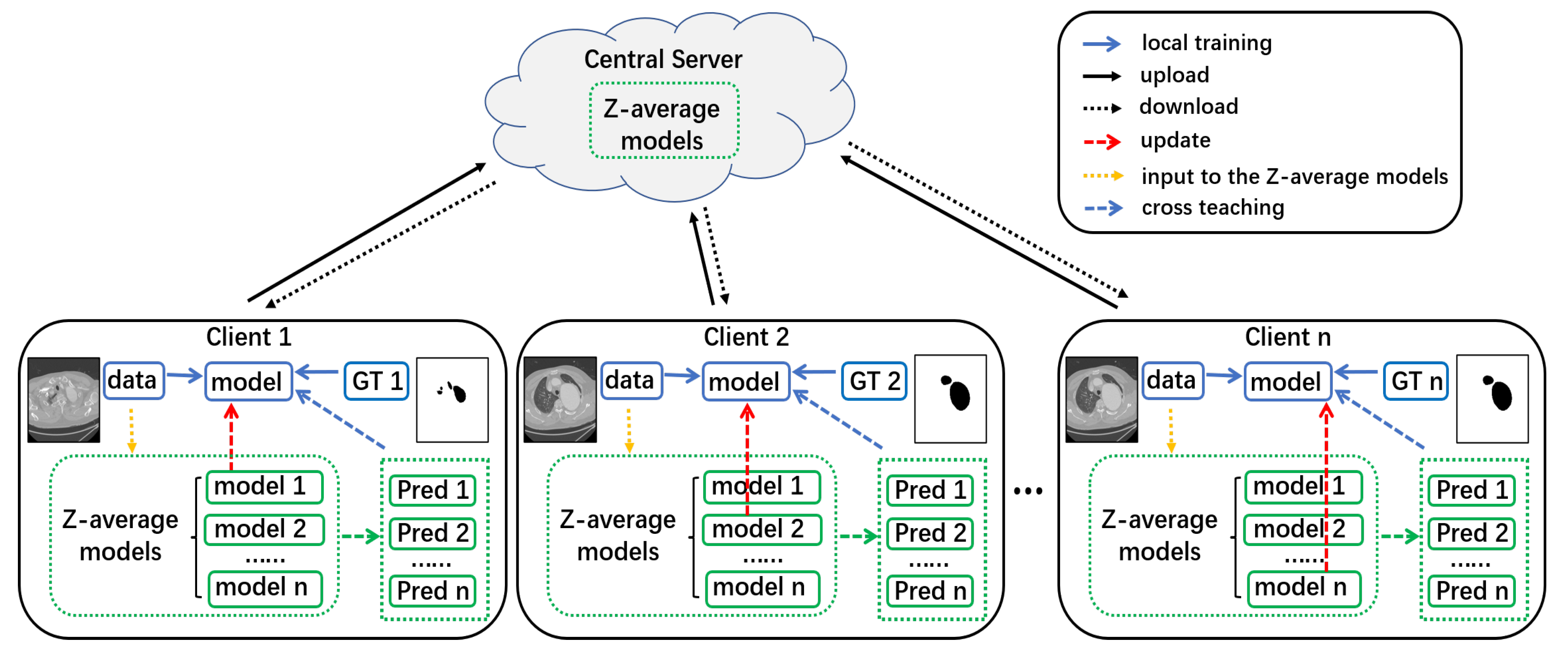
In a medical image segmentation scenario, a novel Federated learning training paradigm called Federated Learning with Z-average and Cross-teaching (FLZaCt) is proposed to improve the knowledge communication effects among client models trained by the client under-sampled data, which protects the privacy and does not need extra data.

2.

We present a new parameter-based communication method called the Z-average to construct differentiated multiple client models that maintain diverse knowledge about the semantic information.

3.

We introduce a new distillation-based communication method called Cross-teaching that optimizes the local client model to learn more semantic information using the local ground truth and the other client models’ knowledge.

4.

Extensive segmentation experiments demonstrate that our methods achieve superior performance over traditional methods with evaluations on our private aortic segmentation dataset and a public HAM10000 segmentation dataset.

2. Related Work

2.1. Federated Learning

As a promising privacy-preserving method, FL aims to train models from decentralized data scattered on various clients. After locally training on the client data, client models will be aggregated to a global model shared with all clients for continued local training. The training round, including the local training and the global updating, is repeated several times until the stopping condition is met. Without sharing local data among clients, most FL methods regard the client model as representing the client data distribution. From the view of the model parameters, the Federated Averaging method (FedAvg) [10] is generally adopted, where a global model can be learned after every training round. It is well known that FedAvg is effective for aggregating all client models and is extensively applied in many works [18,19,20]. To alleviate the challenge of a non-i.i.d. data distribution in multiple clients [21], some studies proposed extensions of FedAvg such as FedProx [22] and MOON [23] to reduce the bias. From the view of the model distillation, many data-dependent distillation methods [14] rely on the extra auxiliary dataset to train the global model. Recently, the data-free method [15] has been proposed to tackle the heterogeneity problem. These methods design new schemes to tackle the client drift in classification problems.

However, few FL ideas are studied in segmentation tasks. Segmentation models have different network architectures that need enough context information. Though the study [24] tried implementing FL systems for segmenting brain tumors, the adopted strategy still proves the effectiveness of Federated averaging parameters. For privacy-preserving medical image segmentation, the FedAvg remains the preferred algorithm [25] regardless of low communication efficiency due to ignoring the diverse model knowledge. Unlike FedAvg, our study explores a new FL paradigm to promote the information communication efficiency by fully using the differentiation among multiple under-sampled datasets.

2.2. Semantic Segmentation

Semantic segmentation has attracted extensive attention in image processing as a typical computer vision task. Most segmentation models are based on an encoder–decoder [26] structure to capture useful segmentation features. Unet [27] and DeeplabV3+ [28] are two current models widely utilized in many studies [29,30]. To contain enough context features, the convolution segmentation models usually use progressive down-sample and up-sample stages to obtain the low-level spatial information and the high-level position information. Benefiting from the skip connections, Unet, based on the encoder–decoder architecture, makes full use of the high-level and low-level feature maps to aggregate multi-level deep features, which can generate better results. This structure concurrently learns low-level details and high-level semantics without extra parameters. This feature fusing idea is proven to be effective according to its tremendous success. Additionally, a series of Deeplab models [31,32] adopts the dilated (or atrous) convolution [33] to obtain a larger reception field and wider context semantic features. What is more, Deeplab uses ASPP [34] to further learn multi-scale information. Large amounts of extensions of Unet and Deeplab have been proposed such as Bayesian UNet [35] and DeeplabV3+. Different combinations of skip connections are conducted to aggregate full-scale feature maps such as Unet++ [36]. What is more, the STDC model [37] is a popular one for the real-time segmentation.

Various deep segmentation models have addressed many clinical medical image processes [3,4]. In the segmentation of brain images [38,39] and MRI sequence images [40,41], deep learning methods successfully segment the target area. Reference [42] used Unet to segment the fetal heart structures for the first time. Reference [30] also used DeeplabV3+ to segment aortic vessels and compare the difference among several backbones. These well-known segmentation models can be directly applied in training FL segmentation models. In this paper, we focus on the FL training paradigm and conduct experiments mainly adopting the Unet, DeepLabv3+, and STDC model.

3. Methods

3.1. Overview

The traditional FedAvg method is the baseline method and is described as Equation (1).

$$FedAvg\left(w\right)=\frac{n_i}{N}\sum _{i=1}^n{w}_i,$$

(1)

where $w_i$ represents the client model parameters, $n_i$ represents the data number of client i, and N represents the total data number of all clients, as shown in Equation (2).

$$N=\sum _{i=1}^n{n}_i.$$

(2)

In the FedAvg process, the Central server aggregates all client models to one global model, which is then shared with clients to update the local models.

The main procedure and the corresponding framework of this study are shown in Algorithm 1 and Figure 1. Firstly, we conducted the client models by locally training to calculate the Z-average metric, whose details are shown in Section 3.2. Then, in the Federated training process, the dotted lines of the proposed method are shown in Figure 1. The corresponding descriptions are shown in Algorithm 1. After initializing the client models and five local training epochs, all the client models are uploaded to the global server, where n client models are aggregated to the Z-average models. Different from the common FL paradigm, the Z-average models have n models, not one global model. Moreover, each client downloads all the Z-average models instead of the corresponding one. Next, the client updates the corresponding local model. In the Cross-teaching epoch, the local data are input in the client model, as well as the Z-average models. The Z-average models retain the diverse knowledge and provide the fundament for the Cross-teaching method. Not only the local ground truth, but all the predictions of the Z-average models are regarded as the supervision to optimize the local model.

Algorithm 1 The process of FedZaCt.

1: procedureZ-average metric( ) 2:     for each $i\in \{1...N\}$ do 3:         local training: client model $M_i$ 4:     end for 5:     cross-client inference: $ce{m}_{i,j}$ 6:     Z transformation: $Zce{m}_{i,j}$ 7:     Z-average metric: $Z_{j,i}$ 8:     setting diagonal value: $Z_{i,i}=0.5,\forall i\in \{1...N\}$ return Z 9: end procedure 10: procedureLocal training( ) 11:     for each $i\in \{1...N\}$ do 12:         for $epoch\in \{1...5\}$ do 13:            local training: client model $M_i$←$\{x_i,y_i\}$ 14:         end for 15:     end for 16: end procedure 17: procedureCross-teaching( ) 18:     for each $i\in \{1...N\}$ do 19:         one Cross-teaching epoch: $M_i$←$\{x_i,y_i$, Z-average models} 20:     end for 21: end procedure 22: procedureFederated training 23:     for each $i\in \{1...N\}$ do 24:         client model $M_i$ loads the same initial model 25:     end for 26:     for each training round $t\in \{1...T\}$ do 27:         local training 28:         client models are uploaded to the Central server 29:         the Central server conducts Z-average models 30:         all clients download the Z-average models 31:         client i updates the corresponding model $M_i$ 32:         Cross-teaching 33:     end for 34: return$M_i$ 35: end procedure

3.2. Z-Average

Supposing we have n clients, n client models should be aggregated to one global model in the common FL paradigm, while in this study, we used the Z-average method to aggregate n client models to the Z-average models that own n models and still maintain diverse knowledge. The Z-average method constructs multiple aggregation models from the parameter-based communication aspect to retain diverse knowledge. More details are as follows. Firstly, we trained the models for each client individually without exchanging any information among the clients. This process is only a local training, not a Federated learning process. The local training model $M_i$ learns from the data distribution in client i. After enough local client training, we conducted the cross-client inference to obtain the cross-evaluation metric $cem$, where $ce{m}_{i,j}$ represents the evaluation of model $M_j$ on client i. For each evaluation vector in client i, the $ce{m}_i$ are normalized as $Zce{m}_i$ by Z-score transformation. The equation is defined as:

$$Zce{m}_{i,j}=Abs(ce{m}_{i,j}-mean\left(ce{m}_i\right))/std\left(ce{m}_i\right),$$

(3)

where $mean\left(ce{m}_i\right)$ represents the mean value of $ce{m}_i$, $Abs(.)$ represents the absolute value, and $std\left(ce{m}_i\right)$ represents the standard deviation value of $ce{m}_i$.

Then, we set the average value of $Zce{m}_{i,j}$ and $Zce{m}_{j,i}$ as the $Z_{i,j}$ and $Z_{j,i}$ values of the Z-average metric. This average method is shown in Equation (4).

$$Z_{i,j}=Z_{i,j}=0.5\ast (Zce{m}_{i,j}+Zce{m}_{j,i}).$$

(4)

Finally, the diagonal values of the Z-average metric, which are regarded as hyperparameters, are set as 0.5 to aggregate more information from other client models.

After calculating the Z-average metric, the FL training process begins. Every five local training epochs later, for n clients, we aggregate all client models to conduct Z-average models that have n models by means of the Z-average metric. The parameters of $M_j$ are calculated as Equation (5).

$$ZAvg(w,j)=\frac{n_i}{n}\sum _{i=1}^n{Z}_{i,j}\ast w_i.$$

(5)

During the FL training process of this study, the client models are different from each other, which means $M_i$ learns all the client data distribution and retains a unique individual representation. Every five local training epochs, the client models are uploaded to the global server to be aggregated as the Z-average models, which will be downloaded to all clients.

3.3. Cross-Teaching

From the distillation-based communication aspect, we propose a data-free Federated distillation method. This Cross-teaching method attempts to use the Z-average models to train local client models. After downloading the Z-average models, each client updates the corresponding local model. In the next local training epoch, all the client models, including the local client model and the other client models, provide guidance information for the local model optimization. Because the model knowledge represents the trained data distribution, not only is the ground truth worth learning, but the diverse knowledge from Z-average models is essential for supervising the local model. For each batch, the Z-average models generate predictions, which are also regarded as the targets corresponding to the sampled data. We optimized the local model parameters by the local ground truth and the predictions from the Z-average models together. This Cross-teaching process is implemented by designing the loss function, shown in Equation (6).

$$\mathcal{L}(x_i,y_i,w_i,w)={\mathcal{L}}_{ce}(f(x_i,w_i),y_i)+{\mathcal{L}}_{cross}(x_i,w,w_i),$$

(6)

where $x_i$ represents the input image for the models, $y_i$ represents the local ground truth corresponding to $x_i$, $w_i$ represents the parameters of the local client model $M_i$, w represents the parameters of the Z-average models, $f(.)$ represents the prediction of the segmentation model, $\mathcal{L}$ represents the total loss, ${\mathcal{L}}_{ce}$ represents the loss between the prediction of $w_i$ and $y_i$, and ${\mathcal{L}}_{cross}$ represents the loss between the prediction of $w_i$ and the prediction of w.

$${\mathcal{L}}_{cross}(x_i,w,w_i)=\frac{1}{n}\sum _{j=1}^n{\mathcal{L}}_{ce}(f(x_i,w_i),Binary\left(f(x_i,w_j)\right)),$$

(7)

where $Binary(.)$ represents the binary value of the prediction of $w_j$ and is used as the target information.

$${\mathcal{L}}_{ce}(\widehat{y},y)=ylog\widehat{y},$$

(8)

where y represents the ground truth and $\widehat{y}$ represents the prediction value.

After the Cross-teaching epoch, the client model will train with local data and the local ground truth only for five epochs. The local training epoch number and Cross-teaching epoch number are hyperparameters. Then, the client models are uploaded to the global server for aggregating the Z-average models. This training round repeats until the stop condition is met.

4. Experiments

4.1. Dataset

In this study, we chose two datasets, including a private aortic dataset and the public HAM10000 dataset [43] to perform the experiments. Based on these two datasets, the reported results are consistent, though different segmentation models are adopted showing our methods’ generality. We conducted comparison experiments to prove the effectiveness of our method and ablation studies to observe more details.

4.1.1. The Private Aortic Dataset

This private aortic dataset comes from An Zhen hospital. This study has the approval of the Ethics Committee of Beijing Anzhen Hospital Affiliated with the Capital University of Medical Sciences. The data were collected in accordance with the tenets of the Declaration of Helsinki from studies that had research ethics committee approval.

The data were annotated by junior doctors and then reviewed by senior doctors. The target area was the aortic vessel area. In total, 108 persons, including 25,117 images, were annotated. The dataset was split into the training set (87 persons) and the test set (21 persons). The training set included 20,020 images, which was divided into four clients. Clients 1, 2, 3, and 4 have 20, 26, 19, and 22 persons, obtaining 5060, 5059, 4926, and 4975 images, respectively. The test set had 21 persons and includes 5097 images. All client datasets and the test dataset did not have an intersection with each other.

4.1.2. The Public HAM10000 Dataset

As a public dataset, the HAM10000 dataset [43] has 10,015 dermatoscopic images, which aims to diagnose pigmented skin lesions automatically. The training set, including 8012 images, was divided into four clients. Each client had 2003 images. The test set also had 2003 images. All these images had their corresponding ground truth.

4.2. Experiment Implementations

Each client adopted the same training configuration, which contained the model structure, the loss function, the optimizer, and the learning rate. To show the generality, we chose three typical model structures, Unet, DeepLabV3+, and STDC, as the base structures. As a segmentation task, cross-entropy loss is commonly used. The Adam optimizer was applied, and the learning rate was set to 0.0001.

When beginning to train the FL models, all client models load the same initial model to reduce the model perturbation.

After five local training epochs, the Central server aggregates all client models by the Z-average metric and transfers the Z-average models to the clients. Then, each client updates its local model and trains by Cross-teaching for one epoch. Next, the client model is only trained with the ground truth for five epochs. One training round contains five local training epochs and one Cross-teaching epoch. The whole training process has 15 training rounds, including 80 epochs. In the inference stage, all client models are averaged equally in the inference stage to conduct one global model as the FL model.

In particular, the experiments were conducted on Unet, DeepLabV3+, and STDC. Unet adopts four down-sample and four up-sample stages, which use the DenseNet block. Each DenseNet block contains four convolution layers and one concatenation operation. DeepLabV3+ adopts ResNet18 as the backbone. STDC adopts STDCNet813 as the backbone.

4.3. Evaluation Metrics

We chose the commonly used Intersection over Union (IoU), Dice score (Dice), Precision (Prec), and Recall as the basic quantitative evaluation methods in the segmentation tasks. The IoU and Dice score are defined in Equations (9) and (10).

$$IoU=\frac{X\ast Y}{X+Y-X\ast Y},$$

(9)

$$Dice=2\ast \frac{X\ast Y}{X+Y},$$

(10)

where X and Y represent the prediction and the target metric, respectively.

In this study, we conducted ten repeated experiments and calculated the mean values of the IoU, Dice, Prec, and Recall in repeated experiments to report the evaluation results. Higher scores represent better performance, which means a higher similar degree between the prediction and the ground truth.

5. Results and Discussion

To reveal the effectiveness of the proposed methods, we observed the performance of both the private aortic dataset and the public HAM10000 dataset. These two datasets are similar tasks that segment one foreground object and the background. In this section, the mean evaluation values of ten repeated experiments show the comparison of different training methods. To clearly show the performance of our method, the experiments were not only conducted in the Federated training scheme, but also the Central training scheme. To fairly compare the methods in the communication cost, we conducted experiments by communicating models every epoch. It is noted that “Central” means the Central training method with collecting all data, “FedAvg1” means that the models communicate every epoch, and “FedAvg” means that models communicate every six epochs. “FedAvg+Ct” means the combination of the FedAvg and the Cross-teaching method; “Fed+Za” means adopting the Z-average method instead of the FedAvg method to train the FL models; “FedZaCt” means the combination of “Fed+Za” and the Cross-teaching method,. In FedAvg, FedAvg+Ct, Fed+Za, and FedZaCt, models communicate every six epochs. Based on these training methods, we ran the experiments using private and public datasets to observe the results.

5.1. Results

Shown in

Table 1. Mean evaluation values of ten repeated experiments on the private aortic dataset.

Scheme	Paradigm	Unet				DeepLabV3+				STDC
		IoU	Dice	Rrec	Recall	IoU	Dice	Rrec	Recall	IoU	Dice	Rrec	Recall
Central	-	80.30	88.36	92.76	87.22	78.54	87.06	89.11	86.33	72.16	82.21	88.68	80.80
Federated	FedAvg1	80.26	88.99	92.87	86.72	78.63	87.17	89.33	86.64	72.52	82.13	88.37	79.98
	FedAvg	80.78	88.73	92.39	85.78	78.20	86.78	90.22	85.31	72.77	82.31	88.15	80.70
	FedAvg+Ct	81.51	89.28	91.55	88.21	78.94	87.39	90.28	86.13	72.84	82.41	88.69	80.41
	Fed+Za	81.24	88.91	93.18	86.51	79.34	87.66	89.91	86.89	73.34	82.77	89.15	80.50
	FedZaCt (Ours)	82.10	89.62	92.20	88.24	79.67	87.89	89.57	87.63	73.75	83.10	89.22	80.91

are the results on the private aortic dataset. Compared to the models from the Central training, one baseline method, models adopting Federated training generally achieve higher scores. In the Federated scheme, Fed+Za and Ct are the proposed methods that both performed better than FedAvg. Furthermore, the combination of Fed+Za and Ct obtained the best results significantly, which improved the IoU, as well as the Dice scores dramatically compared to FedAvg. The proposed approaches successfully outperformed the traditional method FedAvg and the Central training method. Based on Unet, our achieved IoU scores were 1.32% and 1.80% higher than FedAvg and Central. From the communication cost aspect, the proposed method was less expensive and achieved better scores than FedAvg1.

The results of the public HAM10000 dataset are reported in

Table 2. Mean evaluation values of ten repeated experiments on the public HAM10000 dataset.

Scheme	Paradigm	Unet		DeepLabV3+
		IoU	Dice	IoU	Dice
Central	-	85.52	92.29	86.15	92.51
Federated	FedAvg	84.69	91.78	85.74	92.31
	FedAvg+Ct	85.22	92.10	85.72	92.10
	Fed+Za	85.57	92.38	86.20	92.56
	FedZaCt (Ours)	85.65	92.40	86.38	92.67

. In contrast to the results on the private dataset, the Central training on the public dataset had higher scores than FedAvg. However, it is noticeable that, based on Unet, the Fed+Za and Ct methods achieved better performance than FedAvg. In addition, based on Unet and DeepLabV3+, the combination method performed best as usual, with scores higher than the Central training and the other Federated methods. Based on Unet, our achieved IoU scores were 0.96% and 0.13% higher than FedAvg and Central. Though the improved evaluation values on this public dataset were not as high as the values on the private dataset, it is consistent that our methods can achieve superior performance over the other methods on both datasets.

5.2. Ablation Study

To assess the importance of our methods, more details on Unet were compared among the Federated methods. In

Table 3. Ablation results in the Federated paradigms. Based on Unet, the mean IoU values of ten repeated experiments on the private aortic dataset.

Paradigm	client1	client2	client3	client4	Aggregation
FedAvg	71.03 ± 7.73	72.55 ± 7.05	72.01 ± 3.62	79.64 ± 0.78	80.78 ± 0.83
FedAvg+Ct	76.13 ± 4.30	74.12 ± 2.68	75.48 ± 1.94	79.11 ± 1.03	81.51 ± 0.39
Fed+Za	81.60 ± 0.70	79.42 ± 0.80	79.68 ± 0.89	78.40 ± 1.32	81.24 ± 1.74
FedZaCt (Ours)	81.04 ± 1.03	79.22 ± 0.64	79.72 ± 0.84	78.69 ± 0.53	82.10 ± 0.22

, there are client models results that were before the latest aggregating. “Aggregation” means that these four models were aggregated into one Federated model by averaging all parameters.

5.2.1. The Differentiation among Multi-under-Sampled Datasets

According to the results on the two datasets, different client models had different performances, especially in the FedAvg paradigm. After the latest local training on the private dataset, the performance difference in models represents the difference of the client dataset distribution. With the FedAvg paradigm on the private dataset, the highest and lowest scores were 79.64% and 71.03%, which reveals the significant distribution difference among client datasets. It is noted that, with our method, the difference range was narrowed with the highest score 81.04% and the lowest score 78.69%. What is more, the client models generally achieved higher scores with our method rather than FedAvg. These phenomena were consistent on the public dataset. This result reflects that our method guides client models to learn more about the global distribution. Besides, the aggregation models performed better than the client models, which shows that the client datasets are under-sampled.

5.2.2. The Performance of the Z-Average Method

From the parameter-based view, to design models with diverse knowledge, the Z-average method was introduced to enrich the representation of the models. To show the effectiveness of Za, we observed that the scores of Fed+Za and FedZaCt were better than those of FedAvg and FedAvg+Ct, respectively. The methods with Za generally obtained high performance in all clients. When adopting Za, not only the aggregation models, but all the client models commonly achieved high scores. Though not all client models had the same improvement on both datasets, the aggregation models had conclusively higher results than the models without Za.

5.2.3. The Performance of the Cross-Teaching Method

In this experiment, we studied the effect of the Cross-teaching method, which aims to enrich the knowledge of the models. From the distillation-based view, the Cross-teaching method takes advantage of diverse knowledge to optimize the model training. To show the effectiveness of Ct, we observed that the scores of FedAvg+Ct and FedZaCt were better than those of FedAvg and Fed+Za, respectively. Compared to the methods without Ct, the methods with Ct were able to achieve reliably better scores, not only on all client models, but also on the aggregation models. Despite the little fluctuation in some clients, the aggregation models with Ct had stable improvements.

In particular, the aggregation models generally performed better than the client models. This phenomenon reveals that the clients did not have enough data to cover the whole distribution and under-sampling really existed in each client. To alleviate the over-fitting of the client models, communication is necessary for a robust FL model. Our proposed communication methods, including the model parameters and distillation aspects, contributed to better segmentation results.

5.3. Discussion

Deep learning models are extensively applied to automatically process medical images. However, the privacy issue limits medical image processing. FL is a promising privacy-preserving training scheme as a typical method without collecting all data together. Instead of sharing data among clients, exchanging of the model information is secure for protecting the privacy, while training robust models from multiple client datasets. Due to the under-sampling problem, each client model is over-fit within the local data, resulting in under-fitting the true distribution. To tackle this problem, we proposed a novel training paradigm named Federated Learning with Z-average and Cross-teaching (FLZaCt), which trains models to learn diverse model representation and from multiple client datasets. This paradigm provides a novel and fundamental idea for learning from decentralized data. Extensive experiments conducted on the private aortic dataset and the public HAM10000 dataset demonstrated the proposed approach’s superiority.

Our study applied the proposed paradigm to a Federated learning scene with four clients and one Central server. Each client owns the subset of the whole dataset and has no intersection with the other clients. Experiments were conducted on two datasets. In Table 1 and Table 2, it is found that, on the private and the public dataset, the performance details were different. On the private dataset, Central may obtain models adopting Unet with lower evaluation scores than FedAvg. However, on the public dataset, Central obtained models adopting Unet or DeepLabV3+ with higher evaluation scores than FedAvg. In addition, Unet was more suitable for the aortic segmentation, while DeepLabV3+ was more suitable for the HAM10000 dataset. Though some inconsistent details may be due to the model structure difference, it is convincing that the proposed approach FedZaCt outperformed the other Federated schemes and exceeded the Central. Our paradigm consists of the Z-average method and the Cross-teaching method. These two methods both contribute to improving the information exchange among client data. As the combination of Za and Ct, FedZaCt, whose effectiveness was proven by adequate experimental results, uses the Za method to develop individual models and the Ct method to facilitate information communication among individual models. Ablation studies proved that our proposed approach stably improved the performance of the FL models.

Comparing FedAvg1 with our proposed methods, we found it necessary to construct diverse models to learn diverse knowledge. In FedAvg1, it requires two communication times per epoch, including one uploading and one downloading. In FedZaCt, it requires uploading 1 model and downloading 4 models every 6 training epochs. In terms of the communication cost, FedZaCt is less expensive than FedAvg1. Actually speaking, the Central training method reached the limit of the frequency of model communication, which means the model communicates every iteration. The experimental results showed that FedZaCt achieved better scores than FedZaCt and Central. As a consequence, diverse knowledge is helpful for better model performance.

In Table 3, there is a distinct difference among multiple client datasets. Our proposed method practically promoted the performance of the client models, as well as the aggregation models. The aggregation models generally had higher scores than the client models. Communication among clients increased the evaluation scores by reducing the over-fitting in under-sampled data. The proposed approach successfully improved the communication efficiency by employing more robust FL models. Though the improved degree in the public HAM10000 dataset was low, we believe this is because the task is simpler than the private dataset. The comparisons of the qualitative examples on two datasets are shown in Figure 2 and Figure 3.

5.4. Limitation and Future Work

One limitation of this study is the Z-average models. To obtain the Z-average metric, we conducted local training on local client data before FL training, which increased the time cost. How to conduct averaged models needs more careful consideration. It is expected that a less time-consuming method will be introduced. In addition, the suitable diagonal value is worth exploring. Another limitation is the Cross-teaching method. All the Z-average models must be downloaded to all clients, which increases the bandwidth cost. It may be troublesome for models with a large scale of parameters. When the client number increases, the communication cost due to downloading the Z-average models will limit the application of our proposed methods. In the future, how to adjust the communication frequency or propose new methods to construct diverse models may be explored.

6. Conclusions

In this work, we proposed a novel and fundamental Federated training paradigm, which aims to improve the communication efficiency among under-sampled client datasets with privacy preservation. The effectiveness of this paradigm was demonstrated on two typical model structures, including Unet and DeepLabV3+, which were experimented on two medical image segmentation datasets. This paradigm enables the client models to learn from other client data distributions without leaking privacy and extra data. In particular, the proposed paradigm is extendable to other segmentation model structures, which has great potential for improving the results of the FL segmentation models. It is believed that more clinical tasks will adopt this paradigm, and the paradigm will bring more opportunities to deep learning models in the future.