A Large Scale Evolutionary Algorithm Based on Determinantal Point Processes for Large Scale Multi-Objective Optimization Problems

Abstract

Global optimization challenges are frequent in scientific and engineering areas where loads of evolutionary computation methods i.e., differential evolution (DE) and particle-swarm optimization (PSO) are employed to handle these problems. However, the performance of these algorithms declines due to expansion in the problem dimension. The evolutionary algorithms are obstructed to congregate with the Pareto front rapidly while using the large-scale optimization algorithm. This work intends a large-scale multi-objective evolutionary optimization scheme aided by the determinantal point process (LSMOEA-DPPs) to handle this problem. The proposed DPP model introduces a mechanism consisting of a kernel matrix and a probability model to achieve convergence and population variety in high dimensional relationship balance to keep the population diverse. We have also employed elitist non-dominated sorting for environmental selection. Moreover, the projected algorithm also demonstrates and distinguishes four cutting-edge algorithms, each with two and three objectives, respectively, and up to 2500 decision variables. The experimental results show that LSMOEA-DPPs outperform four cutting-edge multi-objective evolutionary algorithms by a large margin.

1. Introduction

In recent decades, large-scale evolutionary optimization algorithms have played a significant role in engineering and science as they often surface in many real-world optimization problems (MOPs). These algorithms are categorized in four categories [1,2] decomposition-based MOEAs [3,4,5,6,7,8], performance-based MOEAs [9,10,11,12,13,14,15,16,17,18], Pareto-based MOEAs [19,20], and finally, the multi-objective algorithms which do not fall in any of the prescribed categories [21,22,23,24]. The performance and scalability of multi-objective evolutionary algorithms (MOEAs) have earned the attention of researchers; however, the attention has restricted the performance and scalability in the decision space. Large-scale optimization issues, which have an increased dimension and a large number of decision variables, have caused several multi-objective optimization issues to become increasingly complex [25].

The efficiency of many existing traditional multi-objective algorithms consistently degraded due to increase in the depth of the decision space, also known as the “curse of dimensionality” [26,27,28,29,30,31,32]. The investigation of large-scale multi-objective optimization problems (LSMOP) is still immature [33,34,35,36,37,38,39,40,41], as only four approaches have been identified [26,33,34,35,36,37,38,39,40,41]. MOEAs are implemented using decision variable clustering that has been suggested in Ma et al. [38]. The authors of [38] have proposed a multi-objective algorithm employed using decision variable (MOEA/DVA) analysis and which further divides the decision variables into three categories depending on their values for convergence and diversity. By more clearly partitioning the decision variables, adding various selections, and proposing various search strategies for various groups, Zhang et al. [26] extended the concept of MOEA/DVA [38] and developed an evolutionary algorithm for large-scale many-objective optimization (LMEA). Large-scale choice factors have been suggested to be divided into two groups by Liu et al. [42], namely, variables associated with convergence and variables linked to variety. Furthermore, using an interdependence analysis for optimization, principal components analysis (PCA) has been used to lower the dimension of the convergence-related variables that would be divided into various subproblems. Additionally, Chen et al. divided the variables into clusters related to convergence and variety and suggested optimizing the subproblems concurrently [37] and sequentially [43], respectively. However, it should be emphasized that such algorithms frequently require many fitness assessments to obtain sufficiently accurate clustering on decision variables. To speed up the search for the global optimum, Tian et al. [34] introduced a modified competitive swarm optimizer for large-scale multi-objective problems called LMOCSO. To create an offspring population, Zhang et al. [18] created an information feedback model (IFM) using the data from the population’s prior placements.

MOEAs are built on the cooperative co-evolution (CC) paradigm. To resolve enormous many-objective problems, Antonio and Coello used the cooperative co-evolution framework and a distinct evolution algorithm (GDE3). They further added that MOEA/D and co-evolutionary techniques might be used for decomposition in both decisions and objective spaces [41]. For large-scale multi-objective issues, Li et al. cooperative’s co-evolutionary algorithm grouping technique is also put out by the authors of [39]. The transformation-based MOEA faces numerous issues; thus, the authors of [36] have applied a problem transformation method to condense the search space and act as a genetic algorithm for any population-based multi-objective algorithms. The dimension reduction approach was then put into practice by He et al. [44] by optimizing several weight factors and multiple decision space orientations. The most recent suggestion to enhance the functionality of the WOF framework [45] was proposed by He et al. [44]. They recommended using random dynamic grouping rather than ordered grouping. While the current large-scale optimization algorithms exhibit promising results, each group of methods has drawbacks, which are considered in this study. To identify interactive decision variables, cooperative co-evolution and clustering approaches based on multi-objective evolutionary algorithms require categorizing decision variables that cost a more significant number of objective values to identify interactive decision variables. This further reduces how well CC framework-based MOEAs perform on the wrong groups. It is not necessarily true that groupings of choice variables may be distinguished. To solve large-scale interactive choice variables, grouping procedures like linear grouping, ordered grouping, random grouping, and others that do not require extra objective assessments to discover interactive decision variables, are not appropriate.

The problem transformation-based MOEAs are quite competitive while improving the capability of convergence in large-scale optimization susceptible to local optima [45,46]. Additionally, the grouping strategy greatly limits the versatility of the method described in [45]. In light of the considerations mentioned earlier, it is clear how crucial it is to apply a multi-objective evolutionary technique to focus its search in the right way to find several great and promising solutions for complex optimization issues. The large-scale evolutionary multi-objective algorithm, or LMOEA-DPP for short, is proposed in this study as a solution to this problem. On several large-scale multi-objective issues ranging from 500 to 2000 decision variables, large-scale multi-objective evolutionary algorithms with determinantal point processes (LSMOEA-DPP) perform well. Using the kernel matrix in the population and decision space, LMOEA-DPP quantitatively analyses and evaluates each solution’s probable search direction and distribution. The kernel matrix is further divided into similarity and quality components to reflect population diversity and convergence. We have applied the DPP to choose solutions with convergence based on the decomposition of the kernel matrix and larger diversity. Further, we have implemented corner selection [47] to enhance kernel matrix’s functionality. The following are the major contributions of this study.

1

The balance between convergence and variety has been achieved by the reproduction process followed by the environmental selection process. A crossover with current parent individuals is performed using guiding solutions in the first reproduction, followed by a second reproduction with no guiding solutions involved in developing offspring individuals.

2

We have used a kernel matrix to adapt to various LSMOEA-DPP. The kernel matrix defines the similarity measure as the angle’s cosine value among two solutions that measures solution quality using the L2 norm of an objective vector. By default, the MOP is divided into a collection of reference vectors, and each subproblem is chosen using both angle base and Euclidean distance.

3

This study also suggests using a kernel matrix that searches for non-dominated solutions set to combine DPP selection with LSMOPs to choose a subset of the population.

The remainder of this paper has been structured as follows. The background information is elaborated in Section 2. The essential structure and specifics of the suggested LMOEA-DPP algorithm are described in Section 3. After discussing the experimental conditions and comparing the outcomes, Section 4 presents the test problems utilized in our studies and a performance indicator to measure the performance of resulting non-dominated solutions. Finally, Section 5 lays out the findings and lists the subsequent works.

2. Background

Since they provide distributions of fermion systems at thermal equilibrium, determinantal point processes are initially recognized as a class by the authors of [48], who named it fermion processes. According to the Pauli exclusion principle, there is no antibunching effect between two fermions. A DPP provides a detailed definition of this repulsion. The standard combinatorial and probabilistic features of DPPs have been well-understood thanks to the recent rush of interest they have received in the math and engineering communities. The determinantal has been widely used as a standard since it was initially used by Borodin and Olshanski [49].

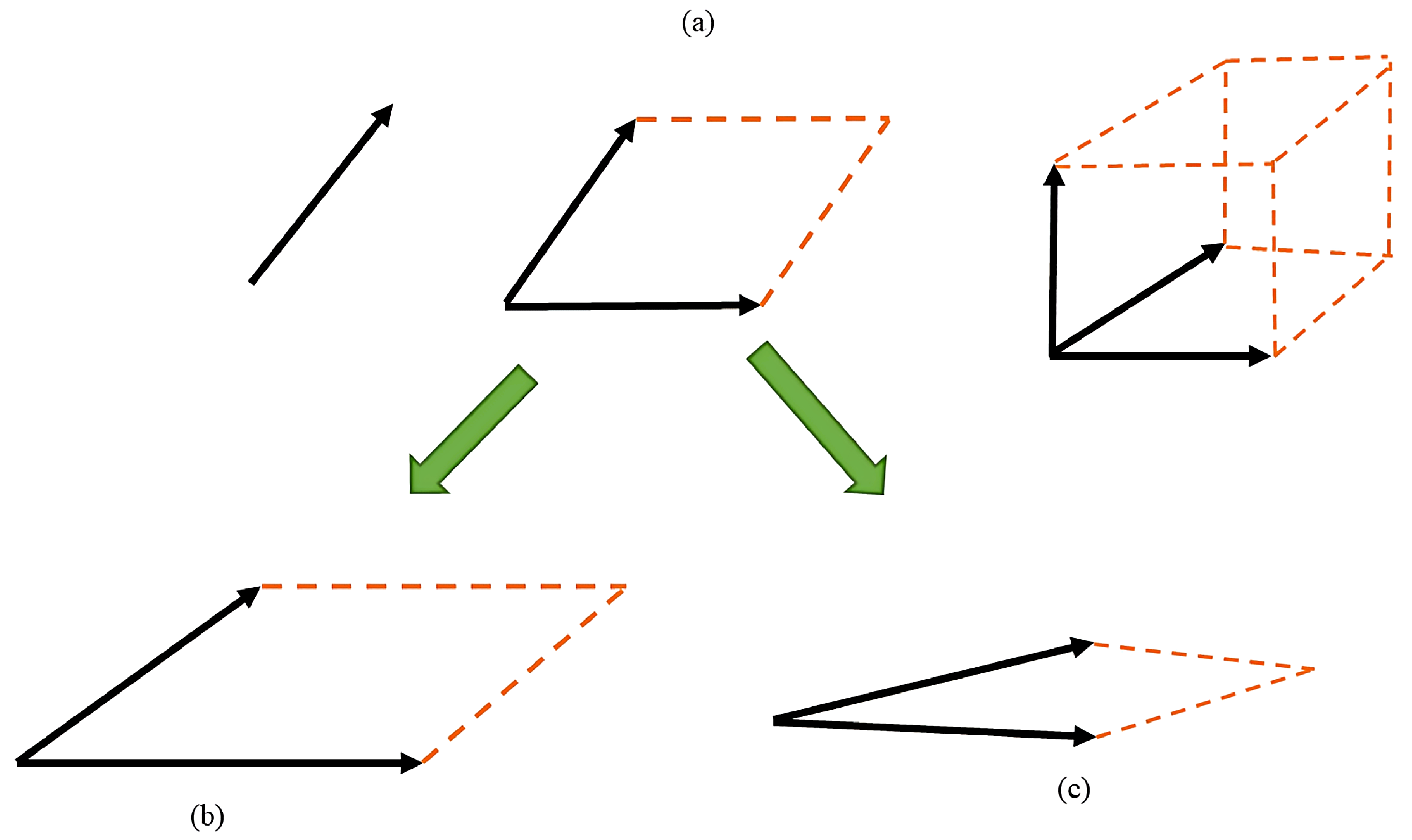
2.1. The Determinantal Point Process (DPP)

DPP has been used to select subset tasks i.e., text summarization, graph sampling, and product recommendation. The point process is taken as a probabilistic measurement of Y instantiating of set Y, as illustrated in (1). We have assumed that the discrete-finite point-processes, i.e., $\mathbf{Y}=\left\{1\cdots M\right\}$ [50].

$$p_L(Y=\mathbf{Y})=\frac{det({\mathbf{L}}_Y)}{det(\mathbf{L}+1)}$$

(1)

where $M\times M$ semi definite represents $\mathbf{L}$ kernel matrix has been indexed with $\left\{1\cdots M\right\}$, I shows the $M\times M$ identity matrix while $det(.)$ signifies the determinant. ${\mathbf{L}}_y$ shows a kernel matrix L with indices limited by entries indexed in a subset ‘Y’ [50]. If instantiation cardinality Y to K has been limited as k-DPPs, a conditional DPP that models only sets of cardinality k and DPPs that can be further represented as (2):

$$p_L^k\left(Y=\mathbf{Y}\right)=\frac{det\left({\mathbf{L}}_y\right)}{{\sum }_{|Y^{{}^{\prime }}|-k}det\left({\mathbf{L}}_{y^{\prime }}\right)}$$

(2)

To deduce expense of computing $p_L^k\left(Y\right)$, that needs $0\left(M^k\right)$ steps, the authors of [51] have proposed the following method. Initially, the kernel matrix L has been eigen decomposed $L={\sum }_{i-1}^M{\lambda }_i{v}_i{v}_i^T$ with the group of an eigen-vectors V and eigen-values $\lambda$. If $\mathbf{J}$ forms a set of k eigenvectors, then J is an instantiation of $\mathbf{J}$, while the probability of J can be modeled as (3)

$$Pr(J=\mathbf{J})=\frac{{\prod }_{i\in J{\lambda }_i}}{{\sum }_{\left|J\right|-k}{\prod }_{m\in J\lambda m}}$$

(3)

The denominator allows all possible instantiations J of J where $Pr$ represents the probability while $P_L(Y=\mathbf{Y})$ represents the measure of probability. In [51], it is illustrated that, while sampling is carried out from DPPs, the probability of an element n form Y is given by

$$Pr\left(n\right)=\frac{1}{V}\sum _{v\in V}{\left(V^T{e}_n\right)}^2$$

(4)

with $e_n$ the $n^{th}$ unit vector $e_n=\left(0,\cdots ,1\cdots ,0\right)$ with element 0 other than the index element n one.

2.2. DPPs Geometry

Let B is a $D\times M$ matrix that $L=B^{\top }B$. (B is always equivalent to $D<M$) while L is a positive semi-definite.) It illustrates B column by $B_n$ for $n=1,2,\cdots ,M$

$$P_L\left(Y\right)\propto det\left(L_Y\right)=Vo{l}^2({\left\{B_n\right\}}_n\in Y),$$

(5)

where the right hand side shows the squared $\left|Y\right|$-dimensional volume of parallel piped span through B’s column respective to the elements of Y.

In this study, the columns of B are seen as feature vectors that describe the components of Y. The probability offered through DPP to set the Y has been related to volume encompassed with associated feature vectors. Furthermore, kernel L computes similarity by applying the dot products of feature vectors that can be seen in Figure 1. It also allows for crucial DPP testing features. Larger volumes and orthogonal feature vectors make diverse sets more likely. Degenerate parallel-piped is defined by items with parallel vectors. Alternatively, large magnitude feature vectors emerge due to their multiplication in the spanned volumes for sets including them.

2.3. Corner Solution

In LSMOPs, most of the solutions become non-dominated after few generations [52], which often leads to the algorithm losing selection power. To rectify this problem, quality modification of the definition solution is done with help from corner solutions [47]. The solution has been considered a corner solution if one solution is found while decreasing N and K objectives. However, [53] revealed that the corner solutions are always difficult to find for $k>1$. Hence, the proposition of approximation schemes to the corner solutions are presented in Section 3.

3. Proposed Innovative Global Optimization Algorithm

A multi objective minimization problem (without loss of generality) a can be structured as (6),

$$\begin{array}{cc}\hfill & Minf\left(x\right)=(f_1\left(x\right),f_2\left(x\right),\cdots ,f_m\left(x\right))\hfill \\ & S.t.x\in {\mathbb{R}}^D\hfill \end{array}$$

(6)

where objectives are represented by m and the detection vector can be represented by $x=\left(x_1,x_2,\cdots ,x_D\right)$, in which D is the decision space. We have considered 2- and 3-objective problems with many decision variables that range from hundreds to thousands [50]. The decision factors grow exponentially as the search space expands, which worsens search performance, especially the capacity of optimization algorithms to converge. To overcome and resolve this issue, we provide a determinantal point process strategy paired with a twofold reproduction strategy to boost convergence, as well as a new, enhanced environmental selection approach to boost variety. Two contrasting environmental selection procedures are provided to increase variety while conserving the diversity of the population, and this must be taken into account. In contrast to [50], where the promising solutions are simply employed for population initialization, we can see from Figure 1 that guiding solutions are included into each generation’s reproduction process. We shall go into more depth about LSMOEA-DPPs below. First, the overall framework of LSMOEA-DPP is given. Next, we go into further depth about how the kernel matrix was calculated. The environmental selection process and other crucial elements of the LSMOEA-DPP are then covered in detail one by one. The flowchart of the proposed LSMOEA-general DPPs structure, which consists of three main parts—environmental choices, identification of guiding solutions, and guided double production—is shown in Figure 2.

3.1. Framework of the LSMOEA-DPP

The Pseudo code of LSMOEA-DPP is shown in Algorithm 1. The M random solutions are used to fill in initial population P followed by which extraction of corner solution archive (CSA) P. In steps 3 qnd 4, the ideal point $z^{*}$ and nadir point $z^{nad}$ are initialized based on the value of $P4$ where $Z_n^{*}$ and $Z^{nad}$ are computed by (7) and (8).

$$\begin{array}{c}\hfill Z^{*}={\left(Z_1^{*},Z_2^{*},\cdots ,Z_m^{*}\right)}^T\\ \hfill Z_n^{*}=\min \left(\left\{\left(f_n\left(x\right)\right)|x\in P\right\}\right)\\ \hfill Z^{nad}={\left(Z_2^{nad},Z_2^{nad},\cdots ,Z_m^{nad}\right)}^T\\ \hfill Z_n^{nad}=\max \left(\left\{\left(f_n\left(x\right)\right)|x\in P\right\}\right)\end{array}$$

(7)

$Z_n^{*}$ and $Z_n^{nad}$ normalize objective values $f_n\left(x\right)$, as illustrated in (7). This is a merit as different scales are being followed as objective functions may have widely diverse scales.

$$f_n\left(x\right)=\frac{f_n\left(x\right)-z_n^{*}}{z_n^{nad}-z_n^{*}}$$

(8)

The following steps are iterated until function evaluations pass a fixed limit (80,000 considered for this study). Moreover, 2M solutions are chosen as a mating pool during every iteration. While, 2M solutions are chosen as mating pool $P^{\prime }$ during each iteration. Moreover, we have used polynomial mutation [54] and simulated binary crossover (SBX) [55] to generate population C of candidates. The ideal point $z^{*}$ is updated by (7) after environmental selection $z^{nad}$ can updated as (8).

Algorithm 1: Proposed LSMOEA-DPP Framework.

Input: M (The Size of Population)

1 P← Initialization of population (M)

2 $CSA\leftarrow P$

3 $z^{*}\leftarrow InitializeIdealPoint\left(P\right)$

4 $z^{nad}\leftarrow InitializeNadirPoint\left(P\right)$

5 while total function evaluations >= 80,000 do

3.2. Mating Pool

To enable the production of high-quality results, the generation of the mating pooling $P^{\prime }$ is done by element selection from union of CSA and P. thus; the convergence ($con\left(x\right)$) is of the $x=p$ solution according to (9).

$$con\left(x\right)=\frac{1}{{\sum }_{n=1}^m{\left(f_n\left(x\right)\right)}^2}$$

(9)

As shown in Algorithm 2, a solution x has been randomly selected from the union PUCSA. If $con\left(y\right)$ of the solution $y=arg{min}_{y\in P}\left\{cos(x,y)\right\}$ is larger than $con\left(x\right)$ and the randomly generated number is lower than a certain threshold $\delta (x,y),y$ is added to $P^{\prime }$. Otherwise, x is added to $P^{\prime }$. The threshold $\delta (x,y)$ is executed according to (10)

$$\begin{array}{c}\hfill \delta (x,y)=\frac{cos(x,y)-mincos}{maxcos-mincos}\\ \hfill maxcos=\underset{p,q\in \cup CSA,p\ne q}{max}\left\{cos(p,q)\right\}\\ \hfill mincos=\underset{p,q\in P\cup CSA,p\ne q}{min}\left\{cos(p,q)\right\}\end{array}$$

(10)

While children must be produced, two random parents are chosen from the mating pool $P^{\prime }$.

Algorithm 2: Mating Pool filling.

Input: P (The size of Population)

1 Normalization $(P\cup CSA,z^{nad},z^{*})$

2 $P^{{}^{\prime }}\leftarrow \varphi$

3 for $n=1$do

3.3. Complementary Environmental Selection

In the first scenario, non-dominated solutions are chosen from the C and P pair. If there are more significant non-dominated solutions than N, then the kernel matrix L has been performed, and P is further improved through DPPs selection. Further, the suggested technique uses guiding solutions that replicate LMOEA-DPP to hasten convergence. The MOEA is necessary to keep convergence and variety in a healthy balance. The determinantal point process and complementary environmental selection technique are added in LMOEA-DPP, which are discussed in the following paragraphs, to further overcome and satisfy the criteria.

Each member of the parent population $Pt$ is first picked to do the crossover along with a randomly chosen solution, resulting in $\left|P_t\right|$ solutions, which also signify population size. Environment selection is first applied to the solution to produce an transitional parent population, $Pt$, followed by use of a mutation operator to produce an transitional offspring population, $O_t^{{}^{\prime }}·P_t$, which has been joined with $O_t^{{}^{\prime }}$, and $S_G$ representing guiding solution set. After environmental selection, reproduction is done by carrying out crossover on the mutation and intermediate parent population $P_t$ to create $O_t$, which signifies the offspring, and last but not least to parent population $P_{t+1}$. The next generation is attained by carrying out similar environment selection on combined population modeled as $C_t^{{}^{\prime }}=P_t^{{}^{\prime }}\cup O_t$.

The environment selection technique used is displayed in Algorithm 3. As seen in Algorithm 3, environmental selection makes use of decomposition-based techniques (lines 10–12). For decomposition-based selection, the objective values of every member of the combined population $C_t$ are normalised and allocated to closest reference-vector. If total number of reference vectors allocated to one solution is more than a predetermined threshold, $N_{\in }$, decomposition-based environmental selection is employed. Alternately, the various predetermined and flexible reference directions used in the elitist nondominated sorting method provided in NSGA-II have been used to select environment. The population variety can be preserved because the environmental selection employed in this study prevents the number of chosen offspring from being too small. The strategy of decomposition selection has been executed with respect to the consummation measure given in (11):

$${\mathsf{\Psi }}_n=\frac{cos{\theta }_{n,j}}{d_n}$$

(11)

where $cos{\theta }_{n,j},=\frac{F\left(x_n\right)·W_j}{\parallel F\left(X_n\right)\parallel ·\parallel W_j\parallel }$ shows the cosine value of ${\theta }_{n,j}$ among individual n and it has been associated reference-vector represented by $w_j$,whereas $d_i$ represents the Euclidean distance amongst n individual and ideal point in objective space. This is followed by crowding distance for all solutions having the same number in the front. A truncation selection has been performed to select M optimal solutions. In order to show the convergence and variety of the population, the kernel matrix L is described, whereas (2) is used to compute the elements $Lxy$.

$$L_{xy}=q\left(x\right)s(x,y)q\left(y\right)$$

(12)

where $x,y\in P,q\left(x\right)$ shows the solution x quality and $S(x,y)$ is the similarity between x and $yS(x,y)$ defined in (13).

$$S(x,y)=exp(-cos(x,y))$$

(13)

where $cos(x,y)$ has been mentioned as cosine of angles between x and y solutions. Moreover, the quality $q\left(x\right)$ for solutions x has been computed on the basis of its convergence as modeled in (14) and (15).

$$q\left(x\right)=\left\{\begin{array}{cc}co{n}_1\left(x\right)x\in outsidespace& \\ 2*ma{x}_{p\in P}\left(co{n}_1\left(p\right)\right)x\in insidespace\end{array}\right.$$

(14)

$$co{n}_1\left(x\right)=\frac{con\left(x\right)}{{max}_{p\in P}\left(con\left(p\right)\right)}$$

(15)

The outer and inner spaces show regions of the goal space, where $con1$ is the normalised convergence. Here, x belongs to inner space if $\sqrt{{\sum }_{I-1}^M}{f}_n{\left(x\right)}^2\le t$ and x to outer space, contrarily. The threshold t has been set to $t=max\left\{\sqrt{{\sum }_{n-1}^M{f}_n{\left(x\right)}^2|x\in CSA}\right\}$.

Algorithm 3: Environmental Selection.

Input: $C_t^{{}^{\prime }}$ in initial selection and $C_t$ in 2nd selection

Selection;

$\mathbf{W}$: Sets of the reference vectors V;

M: Initial population size for LSMOEA-DPPs;

$M_{\in }$: Threshold to find respective method in Environmental selection.

Output: $P_{t+1}$: Population for following generation

1 Objective value Normalization in combined population;

2 Allocation of particular individuals in population to the nearest reference vectors   from $\mathbf{W}$;

3 if# of reference vector allocated to each individual !< $N_{\in }$

then

Corner Solution Archive (CSA) differentiates the outside space and inside space. The approximation method has been used to initiate CSA. Moreover, we have explained a corner solution in both situations $k=1$: to compute objective solutions $n=1,2,\cdots ,M$ regarding the value of k, and the solution has been classified in ascending order of objective value $f_i$. Thus, we have received M sorted lists and added the first $\lceil \frac{N}{3M}\rceil$ of each list into CSA. $1<k<M$: with consideration of $k=M-1$, an approximation method has been implemented to attain CSA. With any objective $i=1,2,\cdots ,M$, solutions are sorted in ascending criteria of $\sqrt{{\sum }_{j-1,j\ne i}^M{\left(f_j\left(x\right)\right)}^2}$ and attain M sorted lists. The initial solutions of each list are selected in the CSA. With the above two situations, we obtain $\left|CSA\right|=\lceil \frac{N}{3M}\rceil \times M+\lceil \frac{2N}{3M}\rceil \times M\approx N$. That is to say each objective contributes $\lceil \frac{N}{M}\rceil$ solutions to the CSA.

Further, the Kernel matrix has been computed after computing cosine angle among each solutions pair in the population. Additionally, the qualities of all solutions accommodate $q\left(x\right)$ quality of all solutions x and row vector q. Following that, a quality matrix, Q, is created by multiplying $q^T$ by q. In order to modify and produce L, L is multiplied by Q decisively in an element-by-element order. ⊗ displays the element-wise product of 2 matrices of similar size, as is the case in the second final step of Algorithm 4.

Algorithm 4: The Kernel Matrix Computation.

Input: P (the size of population), CSA

1 for the solution $x\in P$do

9 $Q={\mathfrak{q}}^{\mathfrak{T}}·q$

10 $L=Q\otimes L$

Output: L

Moreover, the DPP Selection (DPPs-Selection) details are presented in Algorithm 5. $M\times M$ Kernel Matrix (L) has been eigen decomposed to attain Eigenvector set $V={\left\{v_r\right\}}_{r-1}^M$ and the Eigenvalue set $\lambda ={\left\{{\lambda }_r\right\}}_{r-1}^M$. Hence, ${\left\{v_r\right\}}_{r-1}^M$ has been truncated by keeping k largest eigenvectors and sorted in descending order of eigenvalues, while each loop iteration has been an element index with ${\sum }_{v\in V}{\left(v^T{e}_n\right)}^2$ that can be further added to the index set S. In this phase, the dimension of $e_n=(0,0,\cdots ,1,\cdots ,0,0)$ shows the $n^{th}$ standard unit vector in ${\mathbb{R}}^M$. In the next stage, V has been replaced with orthonormal basis for the subspace of V orthogonal to $e_n$. Towards the end, the S (index set) of the chosen elements has been returned. Fundamentally, the selection of DPPs has been completed in two different phases: firstly, the selection of eigenvectors k of L that have highest corresponding $\lambda$; second is the selection of indices elements with ${\sum }_{\mathfrak{v}\in \mathfrak{V}}{\left(v^{{}^T{e}_n}\right)}^{{}^2}$ one by one.

Algorithm 5: The selection of DPPs.

Input: L (The Kerne_Matrix), size of Subset = k

1 $\left({\left\{v_r\right\}}_{r-1}^M,\left\{v_r^{M_{r-1}}\right\}\right)$ whereas $\left(L\right)$ = Eigen decomposition

2 $V\leftarrow$ Choose eigenvectors (k ) from ${\left\{v_r\right\}}_{r-1}^M$ in reference to max k eigen-values   ${\left\{{\lambda }_r\right\}}_{r-1}^M$

3 $S\leftarrow \varphi$

4 while $\left|V\right|>0$ do

4. Experiment Settings and Result Analysis

A series of empirical tests on nine benchmark problems, referred to as LSMOP1–9 [56], with 500, 1000, 2000, and 2500 decision variables are done to examine the performance of the proposed technique.

Table 1. LSMOP Characteristic Problems Test.

Problems		Characteristics
	Modelity	Shape	Separability
LSMOP-1	Unimodal Modelity	Linear shape	Full separability
LSMOP-2	Mixed Modelity	Linear shape	Partial separability
LSMOP-3	Multi-modal Modelity	Linear shape	Mixed separability
LSMOP-4	Mixed Modelity	Linear shape	Mixed separability
LSMOP-5	Unimodal Modelity	Convex shape	Full separability
LSMOP-6	Mixed Modelity	Convex shape	Partially separability
LSMOP-7	Multimodal Modelity	Convex shape	Mixed separability
LSMOP-8	Mixed Modelity	Convex	Mixed separability
LSMOP-9	Mixed Modelity	Disconnected	Full separability

lists the characteristics of the nine exam issues. The inverted generational distance (IGD), which can account for both accuracy and diversity of a solution set in approximating the actual Pareto front [57,58], is a commonly used performance indicator that is used to evaluate the quality of the solution sets obtained by the algorithms. Given that solutions set P, the IGD has been modeled as (16).

$$IGD(P,P^{*})=\frac{{\sum }_{x^{*}\in p^{*}}d(x^{*},P)}{|P^{*}|}$$

(16)

where $d(x^{*},P)$ is the smallest Euclidean distance between a reference solution $x^{*}$ in $P^{*}$ and all solutions P, where $P^{*}$ is a collection of uniformly distributed reference points. The size of P. $P^{*}$ is $P^{*}$. It should be mentioned that the quality of the produced optimum solutions improves with decreasing IGD values.

Following an empirical study of the contributions made by various components of LSMOEA-DPP, the remainder of the section covers the environment in which the experiments were conducted. On nine two, the approach is compared to four state-of-the-art methods, and 20 and 0.9 are used to create three-dimensional LSMOPs with up to 2500 decision factors. Table 1 shows the characteristics test of LSMOP [56].

4.1. Experimental Setup

All compared algorithms in this study are run 20 times (on each test instance), independently, in which the maximum number of objective evaluations (FEmax) is set at 80,000. Moreover, each algorithm calculates the IGD value of solution set realized by all algorithms, respectively. On the Pareto front of each test problem, 10,000 uniformly distributed reference points are sampled as in [21]. Furthermore, a Wilcoxon rank sum test [59] has been applied by using Bonferroni correction at a 0.5 to evaluate if the attained solution set performance by any of two algorithms has been statistically dissimilar from the other [60,61]. The symbols ‘−’, ‘+’ and ‘=’ illustrate that the results attained by implementing the proposed LSMOEA-DPP are optimal, worse than, and/or comparable to, respectively.

To solve the complex multi-objective issue, the proposed approach uses a genetic algorithm (GA). Herein, the starting population size is chosen as N = 153 and the reproduction operators include polynomial mutation and simulated binary crossover (SBX). Moreover, crossover probability ($p_c$) and distribution index (${\eta }_c$) are set at 0.9 and 20 for SBX, respectively. The mutation probability $p_m$ and distribution index ${\eta }_m$ for PM are set at 1/D and 20, respectively, while D has been considered as total number of decision variables. Next, the total solutions generated (randomly) are 30 along the search direction. Lastly, the threshold $N_{\in }$ = 2N/3 to find the selection strategy applied during environmental selections. We have used similar parameter settings for all algorithms compared in this study (as used in their original literature). Therefore, to optimize the original problem and each transformed problem, the maximum number of objective evaluations are set at 800 and 400, respectively.

4.2. Analysis of the Experimental Results

In this section, experiments are performed on nine different LSMOP test problems given in Table 1 for 500, 1000, 2000, and 2500 dimensions to demonstrate the effectiveness and efficiency of LSMOEA-DPP on LSMOP1–9 with two and three objectives, respectively.

Table 2. Literature Review Comparative Analysis.

Reference No	Optimization Techniques Used	Accuracy	Complexity Level
[2]	Performance Metrics Ensemble	Fair	Very complex
[25]	Global Optimization	Low	Average
[26]	Decision Variable clustering & Non-dominated Sorting	High	Average
[28]	Multiple-strategy learning particle swarm optimization & Two-stage searching mechanism	High	Less Complex
[29]	Particle Swarm Optimization, Segment Predominant learning Optimization	High	Average
[62]	Decision variable grouping, Decision space reduction, & Novel Search strategies.	High	Very Complex

shows the literature review comparative analysis of the primary essential references regarding the technique used, their accuracy, and their complexity level to solve large-scale multi-objective problems. From Table 2, most of the references have a high accuracy rate for solving optimization problems, but this comes with an average complexity level to very complex.

As can be seen, Refs. [25,29] have high accuracy with an average complexity level. Ref. [28] with multi-strategy learning particle swarm optimization search mechanism is the only one that achieves high accuracy and sustains less complexity. Therefore, this helps select the best method for solving large-scale optimization problems.

Table 3. The Statistical result (Median and Median Absolute Deviation) obtained by LSMOEA-DPP and four compared algorithms on 500, 1000, 2000, and 2500 on 2-Objective LSMOP1–9 problems.

Problem	M	D	MOEADVA	LMOCSO	LSMOF	MOEAD	LSMOEADPP
LSMOP1	2	500	1.4062e-1 (5.42e-3) +	1.3372e+0 (1.00e-1) −	5.9889e-1 (5.47e-2) =	6.3180e-1 (1.18e-1) −	6.0395e-1 (4.18e-2)
		1000	4.2611e-2 (3.28e-4) +	1.5183e+0 (5.45e-2) −	6.3999e-1 (2.14e-2) −	6.7100e+0 (6.04e-1) −	6.2794e-1 (4.75e-2)
		2000	1.2933e-2 (3.66e-4) +	1.5644e+0 (2.75e-2) −	6.5257e-1 (2.21e-2) =	6.9393e+0 (8.28e-1) −	6.4003e-1 (2.67e-2)
		2500	9.2551e-3 (2.88e-4) −	1.5796e+0 (3.45e-2) −	6.5101e-1 (1.85e-2) −	4.2072e+0 (3.79e-1) −	9.0791e-3 (3.07e-4)
LSMOP2	2	500	6.2621e-2 (3.30e-4) −	4.5700e-2 (5.84e-4) −	1.9279e-2 (4.86e-4) −	7.0899e-2 (1.14e-3) −	1.9264e-2 (4.00e-4)
		1000	3.2863e-2 (1.66e-4) −	2.5307e-2 (3.95e-4) −	1.1443e-2 (1.84e-4) −	3.8924e-2 (2.10e-3) −	1.0443e-2 (4.51e-4)
		2000	1.7924e-2 (2.31e-4) −	1.4030e-2 (2.81e-4) −	8.5405e-3 (3.47e-4) −	2.0717e-2 (1.51e-4) −	1.0332e-2 (2.69e-4)
		2500	1.4934e-2 (3.85e-4) −	1.1676e-2 (2.46e-4) −	9.5457e-3 (3.15e-4) −	1.6455e-2 (8.94e-5) −	1.1486e-2 (4.12e-4)
LSMOP3	2	500	3.4226e+0 (4.93e-1) −	2.2194e+1 (3.83e+0) −	1.5714e+0 (3.77e-3) −	2.7099e+1 (7.66e+0) −	1.5654e+0 (8.68e-4)
		1000	1.7959e+0 (5.07e-2) −	2.4727e+1 (6.10e+0) −	1.5785e+0 (4.92e-3) −	2.8951e+1 (6.71e+0) −	1.5738e+0 (3.68e-4)
		2000	1.0804e+0 (1.40e-2) −	2.8148e+1 (1.43e+0) −	1.5773e+0 (1.44e-4) −	3.0802e+1 (7.20e+0) −	1.0723e+0 (1.00e-4)
		2500	9.2935e-1 (9.71e-3) =	2.8682e+1 (4.76e+0) −	1.5779e+0 (1.17e-4) −	2.2149e+1 (7.33e+0) −	9.2916e-1 (1.14e-2)
LSMOP4	2	500	4.8246e-2 (7.39e-4) −	9.0366e-2 (1.35e-3) −	5.0425e-2 (1.75e-3) −	1.2402e-1 (3.68e-3) −	4.0538e-2 (2.59e-4)
		1000	1.4908e-2 (2.93e-4) −	5.2411e-2 (4.75e-4) −	2.7831e-2 (6.40e-4) −	7.3170e-2 (2.05e-3) −	1.3411e-2 (9.96e-4)
		2000	6.1755e-3 (3.56e-4) −	2.9962e-2 (2.16e-4) −	1.6726e-2 (3.52e-4) −	4.0805e-2 (5.30e-4) −	1.5175e-2 (3.65e-4)
		2500	5.3751e-3 (3.54e-4) −	2.5071e-2 (2.15e-4) −	1.6530e-2 (7.54e-4) −	3.0987e-2 (9.21e-4) −	5.2445e-3 (4.85e-4)
LSMOP5	2	500	3.9520e-1 (1.36e-2) +	2.8686e+0 (1.16e-1) −	7.4195e-1 (2.71e-4) −	1.1375e+1 (1.38e+0) −	7.4209e-1 (0.00e+0)
		1000	1.2228e-1 (2.89e-3) +	3.2203e+0 (1.68e-1) −	7.4192e-1 (1.58e-4) −	1.4864e+1 (1.59e+0) −	7.4209e-1 (0.00e+0)
		2000	3.4879e-2 (6.22e-4) +	3.2752e+0 (1.38e-1) −	7.4209e-1 (0.00e+0) =	1.5428e+1 (1.41e+0) −	7.4209e-1 (0.00e+0)
		2500	2.3334e-2 (3.04e-4) −	3.3334e+0 (1.23e-1) −	7.4209e-1 (0.00e+0) −	9.3920e+0 (1.11e+0) −	2.3166e-2 (4.56e-4)
LSMOP6	2	500	2.6772e+0 (3.50e+0) −	7.9260e-1 (8.17e-3) −	7.0468e-1 (1.89e-1) −	8.0800e-1 (8.71e-3) −	3.2039e-1 (5.23e-4)
		1000	1.8657e+0 (2.76e+0) −	7.7045e-1 (2.64e-3) −	6.8490e-1 (7.28e-4) −	7.7428e-1 (1.60e+0) −	3.1252e-1 (2.94e-4)
		2000	7.0940e-1 (7.15e-1) −	7.5721e-1 (6.56e-4) −	3.0883e-1 (1.25e-4) −	7.5703e-1 (9.28e-1) −	3.0879e-1 (1.18e-4)
		2500	7.3782e-1 (2.08e+0) −	7.5399e-1 (7.38e-4) −	3.0768e-1 (1.30e-4)+	7.5374e-1 (5.09e-4) −	6.2937e-1 (8.57e-1)
LSMOP7	2	500	8.0192e+1 (6.66e+0) −	5.7964e+2 (1.06e+2) −	1.5078e+0 (9.78e-4) −	1.6902e+4 (4.51e+3) −	1.5021e+0 (1.50e-3)
		1000	2.5410e+1 (1.09e+0) −	9.4475e+2 (1.57e+2) −	1.5137e+0 (7.44e-4) −	3.1051e+4 (6.39e+3) −	1.5103e+0 (3.34e-4)
		2000	1.0549e+1 (2.39e-1) +	1.1627e+3 (9.92e+1) −	1.5146e+0 (7.26e-4) −	3.6112e+4 (4.40e+3) −	1.5139e+0 (5.03e-4)
		2500	8.4641e+0 (2.36e-1) =	1.7786e+3 (2.25e+2) −	1.5170e+0 (9.95e-4) +	4.9477e+4 (9.55e+3) −	8.5032e+0 (1.25e-1)
LSMOP8	2	500	2.5023e-1 (7.95e-3) +	1.8967e+0 (1.25e-1) −	7.4188e-1 (2.39e-4) −	7.5571e+0 (1.44e+0) −	7.4209e-1 (0.00e+0)
		1000	7.3660e-2 (8.03e-4) −	2.2786e+0 (1.60e-1) −	7.4199e-1 (1.94e-4) −	9.8467e+0 (6.17e-1) −	7.2562e-1 (0.00e+0)
		2000	2.0770e-2 (3.35e-4) +	2.5568e+0 (1.39e-1) −	7.4209e-1 (0.00e+0) =	1.0405e+1 (6.63e-1) −	7.4209e-1 (0.00e+0)
		2500	1.4240e-2 (5.56e-4) +	2.5419e+0 (2.24e-1) −	7.4209e-1 (0.00e+0) −	7.2183e+0 (8.03e-1) −	1.4004e-2 (3.19e-4)
LSMOP9	2	500	4.5782e-1 (4.04e-2) +	8.7112e-1 (1.77e-1) −	8.0882e-1 (7.01e-4) −	2.7666e+1 (3.48e+0) −	8.1004e-1 (9.09e-4)
		1000	1.1718e-1 (4.95e-3) +	2.8625e+0 (6.42e-1) −	8.0576e-1 (1.19e-3) −	3.9097e+1 (3.99e+0) −	8.0695e-1 (2.28e-3)
		2000	3.4876e-2 (2.41e-3) +	5.1625e+0 (2.44e+0) −	8.0614e-1 (4.23e-3) =	4.4518e+1 (2.45e+0) −	8.0468e-1 (1.69e-3)
		2500	2.4722e-2 (1.32e-3) =	5.8595e+0 (1.52e+0) −	8.0475e-1 (2.79e-3) −	2.9026e+1 (2.63e+0) −	2.4707e-2 (2.31e-3)
+/−/=			13/20/3	0/36/0	2/29/5	0/36/0	23/13/0

and

Table 4. The Statistical result (Median and Median Absolute Deviation) obtained by LSMOEA-DPP and five compared algorithms on 500, 1000, 2000, and 2500 on 3-Objective LSMOP1–9 problems.

Problem	M	D	MOEADVA	LMOCSO	LSMOF	MOEAD	LSMOEADPP
LSMOP1	3	500	l1.5310e-1 (2.65e-3) +	1.3713e+0 (8.01e-2) −	5.7538e-1 (7.57e-3) =	2.3318e+0 (3.84e-1) −	5.7851e-1 (9.26e-3)
		1000	6.4418e-2 (1.89e-3) +	1.4725e+0 (1.04e-1) −	6.1096e-1 (1.99e-2) =	4.3365e+0 (6.68e-1) −	6.1067e-1 (1.38e-2)
		2000	4.7363e-2 (3.23e-3) +	1.5188e+0 (1.15e-1) −	6.4203e-1 (8.19e-3) =	6.3107e+0 (5.36e-1) −	6.3813e-1 (1.67e-2)
		2500	4.6129e-2 (3.72e-3) =	1.5771e+0 (1.55e-1) −	6.5703e-1 (1.77e-2) −	6.7976e+0 (6.07e-1) −	4.5164e-2 (2.41e-3)
LSMOP2	3	500	6.2848e-2 (3.37e-3) +	5.1848e-2 (6.53e-4) −	7.8036e-2 (3.42e-3) =	5.9839e-2 (2.48e-4) +	5.0355e-2 (2.94e-3)
		1000	4.9740e-2 (3.08e-3) +	4.0786e-2 (3.87e-4) −	6.0797e-2 (4.56e-3) −	4.3205e-2 (7.26e-5) +	4.0133e-2 (3.82e-3)
		2000	4.4343e-2 (2.79e-3) +	3.5473e-2 (1.85e-4) −	5.3458e-2 (2.66e-3) −	3.6078e-2 (5.36e-5) +	3.5363e-2 (4.04e-3)
		2500	4.5370e-2 (2.70e-3) =	3.4513e-2 (1.02e-4) +	5.0689e-2 (4.09e-3) −	3.4834e-2 (5.53e-5) +	3.3790e-2 (1.93e-3)
LSMOP3	3	500	2.5037e+0 (2.09e-1) −	1.2837e+1 (2.72e+0) −	8.6058e-1 (5.02e-4) =	3.8781e+0 (2.96e+0) −	8.6051e-1 (3.10e-3)
		1000	1.3333e+0 (5.76e-2) −	1.3629e+1 (2.15e+0) −	8.6070e-1 (1.10e-4) =	8.1081e+0 (3.39e+0) −	8.6066e-1 (1.41e-4)
		2000	7.9497e-1 (2.16e-2) −	1.3567e+1 (1.77e+0) −	8.6068e-1 (6.40e-5) =	1.2424e+1 (5.81e+0) −	6.8190e-1 (1.00e-4)
		2500	6.7546e-1 (1.11e-2) =	1.3329e+1 (1.87e+0) −	8.6072e-1 (1.02e-4) −	1.4873e+1 (3.28e+0) −	6.7537e-1 (1.54e-2)
LSMOP4	3	500	7.8148e-2 (2.64e-3) −	1.5152e-1 (2.02e-3) +	2.0536e-1 (6.26e-3) −	1.7483e-1 (3.78e-3) +	1.0144e-1 (6.63e-3)
		1000	5.1546e-2 (4.07e-3) +	9.3167e-2 (8.04e-4) +	1.3274e-1 (3.59e-3) =	1.0617e-1 (1.89e-3) +	1.3313e-1 (4.43e-3)
		2000	4.5686e-2 (3.88e-3) +	5.9310e-2 (3.22e-4) +	8.6618e-2 (2.88e-3) =	6.5718e-2 (4.79e-4) +	4.4963e-2 (2.94e-3)
		2500	4.4946e-2 (4.04e-3) −	5.2303e-2 (3.45e-4) −	7.5992e-2 (4.24e-3) −	5.7264e-2 (3.02e-4) −	4.3519e-2 (2.66e-3)
LSMOP5	3	500	4.1845e-1 (9.47e-3) +	2.8865e+0 (2.51e-1) −	5.4082e-1 (7.45e-2) =	2.5322e+0 (8.39e-1) −	1.8371e-1 (7.20e-2)
		1000	1.5005e-1 (3.61e-3) +	3.1521e+0 (1.92e-1) −	5.5421e-1 (9.51e-2) =	5.8966e+0 (1.26e+0) −	6.5262e-1 (1.37e-1)
		2000	7.2052e-2 (1.90e-3) +	3.1823e+0 (2.35e-1) −	5.9659e-1 (1.28e-1) =	8.1210e+0 (1.33e+0) −	3.1643e-1 (1.34e-1)
		2500	6.4266e-2 (3.43e-3) =	3.3278e+0 (1.92e-1) −	5.6857e-1 (1.02e-1) −	9.2162e+0 (7.11e-1) −	6.3560e-2 (3.13e-3)
LSMOP6	3	500	3.5414e+1 (5.39e+0) −	2.2022e+2 (1.16e+2) −	7.3389e-1 (1.50e-2) =	3.3559e+0 (1.01e+0) −	7.2039e-1 (2.58e-2)
		1000	1.2411e+1 (1.99e+0) −	4.0659e+2 (1.55e+2) −	7.4758e-1 (2.00e-2) =	1.1591e+1 (1.11e+1) −	7.4498e-1 (1.95e-2)
		2000	6.5737e+0 (6.95e-1) −	5.4063e+2 (1.04e+2) −	7.6323e-1 (2.73e-2) =	1.2397e+3 (6.24e+2) −	7.5841e-1 (1.88e-2)
		2500	5.6462e+0 (1.61e-1) =	5.4280e+2 (1.25e+2) −	7.5989e-1 (2.93e-2) +	2.8405e+3 (1.45e+3) −	5.8823e+0 (6.06e-1)
LSMOP7	3	500	1.2543e+0 (1.19e+0) −	1.1624e+0 (6.81e-2) −	8.9177e-1 (1.25e-2) +	1.0184e+0 (8.44e-2) −	8.7629e-1 (1.25e-2)
		1000	8.5598e-1 (2.24e-1) =	1.0611e+0 (3.14e-2) −	8.6669e-1 (3.76e-2) =	8.8881e-1 (1.39e-1) =	8.4505e-1 (5.03e-2)
		2000	6.1633e-1 (3.66e-2) =	1.0035e+0 (9.59e-3) −	8.5274e-1 (4.79e-2) −	7.8850e-1 (2.45e-1) −	6.1519e-1 (4.57e-2)
		2500	5.9231e-1 (2.84e-2) =	9.8762e-1 (1.01e-2) −	8.4802e-1 (4.90e-2) −	7.5047e-1 (1.76e-1) −	5.8876e-1 (2.44e-2)
LSMOP8	3	500	2.3658e-1 (5.80e-3) +	6.0305e-1 (3.04e-2) −	3.6026e-1 (8.19e-2) =	6.6628e-1 (3.01e-2) −	3.5960e-1 (1.11e-1)
		1000	9.8081e-2 (5.67e-3) +	5.8513e-1 (2.81e-2) −	3.9857e-1 (1.13e-1) =	6.3332e-1 (1.20e-2) −	3.7484e-1 (9.38e-2)
		2000	6.1872e-2 (4.50e-3) =	5.8700e-1 (3.84e-2) −	4.1896e-1 (9.96e-2) −	6.2516e-1 (9.28e-3) −	3.39805e-2 (2.57e-3)
		2500	5.9496e-2 (5.05e-3) =	5.7760e-1 (2.55e-2) −	3.6153e-1 (1.13e-1) −	6.2011e-1 (2.33e-3) −	5.9082e-2 (2.53e-3)
LSMOP9	3	500	7.9373e-1 (5.20e-2) +	2.0633e+0 (2.11e+0) −	1.5379e+0 (0.00e+0) =	5.7809e-1 (8.90e-2) +	1.5379e+0 (0.00e+0)
		1000	2.5031e-1 (1.76e-2) +	5.5351e+1 (3.46e+1) −	1.5379e+0 (3.93e-1) =	4.2654e+0 (1.92e+0) −	1.3415e+0 (3.93e-1)
		2000	1.1166e-1 (1.16e-2) =	7.7855e+1 (2.88e+1) −	1.1770e+0 (3.93e-1) −	3.7867e+1 (3.32e+0) −	1.1013e-1 (7.73e-3)
		2500	1.0570e-1 (1.06e-2) =	9.1425e+1 (4.19e+1) −	1.1537e+0 (2.21e-1) −	5.2886e+1 (3.70e+0) −	1.0438e-1 (1.42e-2)
+/−/=			0/1/8	1/8/0	1/8/0	1/8/0	28/9/0

show the statistics to compare the algorithms on 2- and 3-objective LSMOP1–9 (problems) with up to 2500 decision variables. It can be observed from Table 3 and Table 4 that LMOCSO employs the latest learning strategy that performs better as compared to MOEA/DVA, which uses the decision variable clustering. Moreover, the proposed LSMOEA-DPP improved results on 23 (from 36) 2-objective problems and 28 (from 36) 3-objective problems, respectively. It can be observed that, in Table 4, LSMOEA-DPP can achieve competitive performance when decision variables are more significant than 500.

In comparison to MOEAD, LSMOEA-DPP under-performs on five (2-objective) LSMOP test problems and nine (3-objective) LSMOP test problems, respectively, with around 2500 dimensions. LSMOEA-DPP outperformed MOEAD on 23 (from 36) 2-objective problems and 28 (from 36) 3-objective problems, respectively. The results of IGD values realized by comparing algorithms on 2- and 3-objective LSMPO 1-9 problems with up to 2500 decision variables as shown in Table 3 and Table 4. Regarding the results obtained, we can conclude that the proposed LSMOEA-DPP attains improved results as compared to MOEA/DVA, LMOCSO, LSMOF, and MOEAD.

On 3-objective LSMOP1–9 test problems with 2500 dimensions, the boxplots of the IGD values derived by MOEA/DVA, LMOCSO, LSMOF, MOEAD, and the proposed LSMOEA-DPP are shown in Figure 3, Figure 4 and Figure 5. Table 3 summarizes the median values for each method. Figure 3, Figure 4 and Figure 5 show that the LSMOEA-DPP achieved the best median outcomes among the five algorithms when applied to the LSMOP1–9 models with 2500 decision variables. Additionally, we can observe from Figure 3, Figure 4 and Figure 5 that the LSMOEA-DPPs performance are robust on the nine 2400-dimensional LSMOPs since the interquartile ranges of the IGD values it obtained are relatively modest.

From Figure 3, Figure 4 and Figure 5, we can observe that the LSMOEA-DPP maintains the best satisfactory median outcomes followed by MOEADVA, LSMOF, LMOCSO, and MOEAD across all the nine LSMOP problems sets with 2500 decision variables.

5. Conclusions

This study proposed the LSMOEA-DPP scheme to improve the convergence performance of evolutionary algorithm while solving large-scale multi-objective issues. The findings in this work validate that the proposed algorithm is appropriate to solve a variety of LSMOPs. A DPPs-Selection method has been used to select the environment. Moreover, the kernel matrix has been defined to adapt different LSMOPs. The findings demonstrate that the suggested approach performs rather well on 2- and 3-objective LSMOPs with up to 2500 dimensions while compared with the existing state-of-the-art methods. The proposal also works well to enhance the number of decision factors, as can be observed primarily. Since the performance of the proposed approach depends on how well the distribution of the reference vectors matches the Pareto front shape for the issue to be solved, it is not immune to the frequent weakness of decomposition while being extremely competitive. To obtain a more reliable environmental selection throughout the optimization, as a future research perspective, we can work to create methods to modify the reference vectors by keeping a suitable degree. We can develop new DPP techniques to boost population diversity and algorithm’s search performance on LSMOPs.