Detection Performance Evaluation for Marine Wireless Sensor Networks
Abstract
:1. Introduction
2. Background
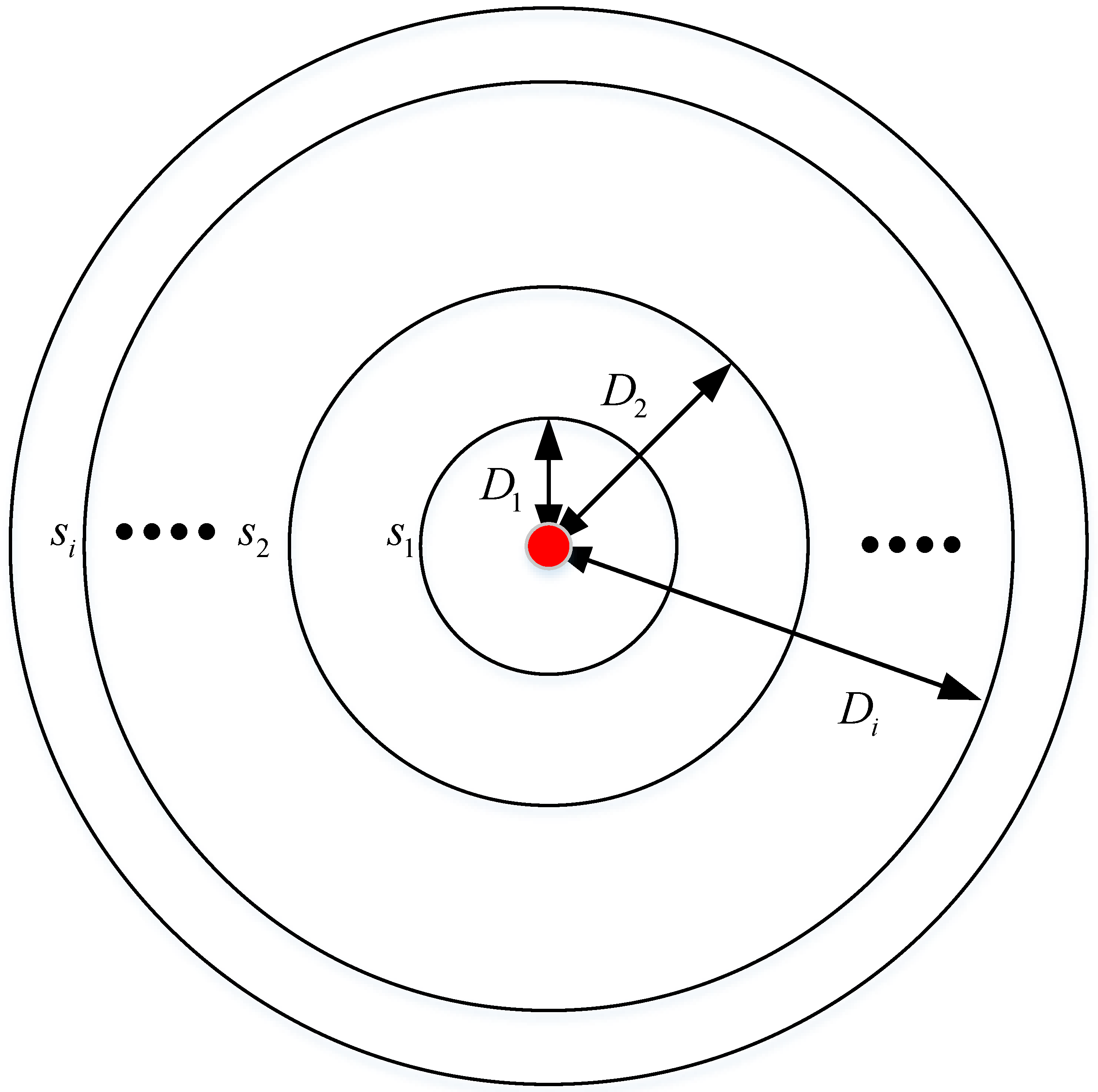
3. Methodology
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MWSNs | marine wireless sensor networks |
| CFAR | constant false alarm rate |
| PPP | Poisson point process |
| CI | covariance intersection |
References
- Luo, H.; Wang, X.; Xu, Z.; Liu, C.; Pan, J.S. A software-defined multi-modal wireless sensor network for ocean monitoring. Int. J. Distrib. Sens. Netw. 2022, 18, 1–19. [Google Scholar] [CrossRef]
- Zhou, C.; Gu, Y.; Fan, X.; Shi, Z.; Mao, G.; Zhang, Y.D. Direction-Of-Arrival estimation for coprime array via virtual array interpolation. IEEE Trans. Signal Process. 2018, 66, 5956–5971. [Google Scholar] [CrossRef]
- Wu, H.; Xian, J.; Mei, X.; Zhang, Y.; Wang, J.; Cao, J.; Mohapatra, P. Efficient target detection in maritime search and rescue wireless sensor net-work using data fusion. Comput. Commun. 2018, 136, 53–62. [Google Scholar] [CrossRef]
- Shi, C.; Ding, L.; Wang, F.; SalouASSDs, S.; Zhou, J. Joint target assignment and resource optimization framework for multitarget tracking in phased array radar network. IEEE Syst. J. 2021, 15, 4379–4390. [Google Scholar] [CrossRef]
- Fattah, S.; Gani, A.; Ahmedy, I.; Idris, M.Y.I.; Targio Hashem, I.A. A survey on underwater wireless sensor networks: Requirements, taxonomy, recent advances, and open research challenges. Sensors 2020, 20, 5393. [Google Scholar] [CrossRef]
- Diamant, R.; Lampe, L. Low probability of detection for underwater acoustic communication: A review. IEEE Access 2018, 6, 19099–19112. [Google Scholar] [CrossRef]
- Benavides, M.T.; Fodrie, F.J.; Johnston, D.W. Shark detection probability from aerial drone surveys within a temperate estuary. J. Unmanned Veh. Syst. 2019, 8, 44–56. [Google Scholar] [CrossRef]
- Yang, C.; Shi, Z.; Zhang, H.; Wu, J.; Shi, X. Multiple attacks detection in cyber-Physical systems using random finite set theory. IEEE Trans. Cybern. 2020, 50, 4066–4075. [Google Scholar] [CrossRef]
- Foglia, G.; Hao, C.P.; Farnina, A.; Giunta, G.; Orlando, D.; Hou, C. Adaptive detection of point-like targets in partially homogeneous clutter with symmetric spectrum. IEEE Trans. Aerosp. Electron. Systems. 2017, 53, 2110–2119. [Google Scholar] [CrossRef]
- Hao, C.P.; Orlando, D.; Foglia, G.; Giunta, G. Knowledge-Based adaptive detection: Joint exploitation of clutter and system symmetry properties. IEEE Signal Process. Lett. 2016, 23, 1489–1493. [Google Scholar] [CrossRef]
- Richmond, C.D. Performance of the adaptive sidelobe blanker detection algorithm in homogeneous environments. IEEE Trans. Signal Process. 2000, 48, 1235–1247. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, S.; Liu, W.; Zheng, J.; Liu, H.; Li, J. Tunable adaptive detection in colocated MIMO radar. IEEE Trans. Signal Process. 2018, 66, 1080–1092. [Google Scholar] [CrossRef]
- Mahler, R. CPHD and PHD filters for unknown backgrounds, II: Multitarget filtering in dynamic clutter. Proc. SPIE 2009, 7330, 262–268. [Google Scholar]
- Mahler, R.; Elfallah, A. CPHD and PHD filters for unknown backgrounds, III: Tractable multitarget filtering in dynamic clutter. Proc. SPIE 2010, 7698, 177–188. [Google Scholar]
- Ristic, B.; Vo, B.T.; Vo, B.N.; Farina, A. A tutorial on Bernoulli filters: Theory, implementation and applications. IEEE Trans. Signal Process. 2013, 61, 3406–3430. [Google Scholar] [CrossRef]
- Mahler, R.P.S.; Vo, B.T.; Vo, B.N. CPHD filtering with unknown clutter rate and detection profile. IEEE Trans. Signal Process. 2011, 59, 3497–3513. [Google Scholar] [CrossRef]
- Beard, M.; Vo, B.T.; Vo, B.N. Multitarget filtering with unknown clutter density using a bootstrap GMCPHD filter. IEEE Signal Process. Lett. 2013, 20, 323–326. [Google Scholar] [CrossRef]
- Punchihewa, Y.G.; Vo, B.T.; Vo, B.N.; Kim, D.Y. Multiple object tracking in unknown backgrounds with labeled random finite sets. IEEE Trans. Signal Process. 2018, 66, 3040–3055. [Google Scholar] [CrossRef] [Green Version]
- Lian, F.; Han, C.; Liu, W. Estimating unknown clutter intensity for PHD filter. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 2066–2078. [Google Scholar] [CrossRef]
- Correa, J.; Adams, M. Estimating detection statistics within a Bayes-Closed multi-Object filter. In Proceedings of the 19th International Conference on Information Fusion (FUSION), Heidelberg, Germany, 5–8 July 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 811–819. [Google Scholar]
- Dhillon, H.S.; Ganti, R.K.; Baccelli, F.; Andrews, J.G. Modeling and analysis of ktier downlink heterogeneous cellular networks. IEEE J. Sel. Areas Commun. 2012, 30, 550–560. [Google Scholar] [CrossRef] [Green Version]
- Streit, R.L. Poisson Point Processes: Imaging, Tracking and Sensing; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Haenggi, M. On Distances in uniformly random networks. IEEE Trans. Inf. Theory. 2005, 51, 3584–3586. [Google Scholar] [CrossRef]
- Fraiha, S.G.C.; Rodrigues, J.C.; Barbosa, R.N.S.; Gomes, H.S.; Cavalcante, G.P.S. An empirical model for propagation-Loss prediction in indoor mobile communications using the pade approximant. Microw. Opt. Technol. Lett. 2005, 48, 255–261. [Google Scholar] [CrossRef]
- Richards, M.A. Fundamentals of Radar Signal Processing; Tata McGraw-Hill Education: New York, NY, USA, 2005. [Google Scholar]
- Julier, S.; Uhlmann, J. A non-Divergent estimation algorithm in the presence of unknown correlations. In Proceedings of the 1997 American Control Conference, Albuquerque, NM, USA, 4–6 June 1997; IEEE: Piscataway, NJ, USA, 2002; pp. 2369–2373. [Google Scholar]
- Deng, Z.; Peng, Z.; Qi, W.; Liu, J.; Gao, Y. Sequential covariance intersection fusion Kalman filter. Inf. Sci. 2012, 189, 293–309. [Google Scholar] [CrossRef]
- Hurley, M.B. An information theoretic justification for covariance intersection and its generalization. In Proceedings of the IEEE International Conference on Information Fusion, Annapolis, MD, USA, 8–11 July 2002; IEEE: Piscataway, NJ, USA, 2002. [Google Scholar]
- Hu, J.; Xie, L.; Zhang, C. Diffusion Kalman Filtering Based on Covariance Intersection. IEEE Trans. Signal Process. 2011, 60, 12471–12476. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, X.; Song, S.H. Outage probability and finite-SNR DMT analysis for IRS-aided MIMO systems: How large IRSs need to be? IEEE J. Sel. Top. Signal Process. 2022, 16, 1070–1085. [Google Scholar] [CrossRef]
- Shnidman, D.A. Determination of required SNR values [radar detection]. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 1059–1064. [Google Scholar] [CrossRef]
- Wang, H.; Zeng, Y. SNR scaling laws for radio sensing with extremely large-scale MIMO. In Proceedings of the IEEE International Conference on Communications Workshops (ICC Workshops), Seoul, Korea, 16–20 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 121–126. [Google Scholar]



| Notations | Meanings |
|---|---|
| emitted energy of a target | |
| loss coefficient | |
| distance of -th sensor to a target | |
| detection probability | |
| false alarm rate | |
| space dimension | |
| signal-to-noise ratio | |
| Poisson intensity | |
| noise power |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Q.; Liu, Y.; Mao, R.; Yang, C. Detection Performance Evaluation for Marine Wireless Sensor Networks. Electronics 2022, 11, 3367. https://doi.org/10.3390/electronics11203367
Hu Q, Liu Y, Mao R, Yang C. Detection Performance Evaluation for Marine Wireless Sensor Networks. Electronics. 2022; 11(20):3367. https://doi.org/10.3390/electronics11203367
Chicago/Turabian StyleHu, Qi, Yaobo Liu, Ruoxin Mao, and Chaoqun Yang. 2022. "Detection Performance Evaluation for Marine Wireless Sensor Networks" Electronics 11, no. 20: 3367. https://doi.org/10.3390/electronics11203367
APA StyleHu, Q., Liu, Y., Mao, R., & Yang, C. (2022). Detection Performance Evaluation for Marine Wireless Sensor Networks. Electronics, 11(20), 3367. https://doi.org/10.3390/electronics11203367






