Abstract
Some typical security algorithms such as SHA, MD4, MD5, etc. have been cracked in recent years. However, these algorithms have some shortcomings. Therefore, the traditional one-dimensional-mapping coupled lattice is improved by using the idea of polymorphism in this paper, and a polymorphic mapping–coupled map lattice with information entropy is developed for encrypting color images. Firstly, we extend a diffusion matrix with the original 4 × 4 matrix into an n × n matrix. Then, the Huffman idea is employed to propose a new pixel-level substitution method, which is applied to replace the grey degree value. We employ the idea of polymorphism and select f(x) in the spatiotemporal chaotic system. The pseudo-random sequence is more diversified and the sequence is homogenized. Finally, three plaintext color images of , “Lena”, “Peppers” and “Mandrill”, are selected in order to prove the effectiveness of the proposed algorithm. The experimental results show that the proposed algorithm has a large key space, better sensitivity to keys and plaintext images, and a better encryption effect.
1. Introduction
In recent years, with the popularity of computers, multimedia messages have been transported through the network, causing more attention to be paid to information security. The hash algorithm is a traditional method used to encrypt passwords. When a password is created in clear text, it is run through a hash algorithm to produce the password text stored in the file system. The U.S. standard of a hash function is SHA-1 (Secure Hash Algorithm 1) with 160 bits of output length [1]. It is difficult to be sure of the security of a hash function with 160 bits of output length, and it was cracked in 2017. Additionally, other hash algorithms such as MD5 (Message-Digest Algorithm 5), MD4, and RIPEMD (RACE Integrity Primitives Evaluation Message Digest) have also been cracked [2]. Recently, encryption algorithms with higher security have become a research hotspot. Chaos encryption is a relatively new encryption idea developed in recent years, and spatiotemporal chaos is the best among them. Chaos in nonlinear science refers to a deterministic but unpredictable motion state [3,4,5,6]. Chaos has the characteristics of sensitivity to initial conditions, pseudo-randomness, and ergodicity, which makes chaos closely related to cryptography. In recent years, the security, complexity, and speed of image encryption algorithms based on chaos theory have become a research hotspot [7,8,9,10,11,12,13,14,15]. In addition, some algorithms are also proposed for image processing, image encryption, model optimization, function solutions, fault diagnosis, data security, etc. [16,17,18,19,20,21,22,23,24,25,26,27,28].
The spatiotemporal chaos model derives from the classical natural fluid-mechanics model, and the spatiotemporal chaos model has many advantages. For example, the effect of the pseudo-random sequence generated by the coupled lattice is better than the low-dimensional chaotic model, and the coupled lattice’s iterative efficiency is better than that of the low-dimensional chaotic model. However, it is found in this study that the local chaotic mapping in the previous method of coupled lattice mapping only chooses a kind of chaotic mapping, and in order to avoid the periodic window and other problems, the local chaotic mapping parameter range is also smaller. In 2004, a new encryption theory, the idea of the Polymorphic Cipher (PMC), was proposed by Roelgen, and the sequence cipher was able to generate a new dynamic [29]. Because polymorphic cryptography belongs to the self-compiled class of encryption algorithms, when an attacker attacks the system [30,31,32], the parameters produced by the attacker can be started from the compiler. Because most self-compiled systems are composed of unidirectional functions and are unreadable, they can be reassembled according to attack parameters and unidirectional functions. They can resist differential attacks and brute force attacks. Therefore, based on the idea of polymorphism proposed by Roelgen, this paper increases the local chaotic map to 4, and achieves the goal of polymorphism. Experiments show that the polymorphic coupled lattice map generates better pseudo-random sequences. The keystream generator is the key to the sequence cipher.
On the other hand, there are two typical links in the chaotic cryptosystem, namely scrambling and diffusion. The combination of scrambling and diffusion improves the security of cryptosystems [30,32], but there are still some drawbacks, and some cryptosystems that conform to this rule have been cracked. The main reason is that the chaotic dynamic performance is not fully considered when designing the algorithm. Coupled mapping lattice (CML)-based spatiotemporal chaotic systems are applied to chaotic cryptography to overcome these shortcomings. Coupled lattices have better chaotic dynamics, including more parameters, larger key spaces, and longer periods. Some encryption algorithms based on coupled lattices are not related to plaintext images [33,34,35]. The output ciphertext image relies only on the key, which has been shown to be insecure and not resistant to chosen plaintext/ciphertext attacks [36]. In this paper, we use the idea of polymorphism to improve the traditional one-dimensional-mapping coupled lattice, and construct a selective chaotic map. It can make one-dimensional coupled map lattices produce various pseudo-random sequences based on different chaotic maps. Additionally, the key space is larger than the traditional one-dimensional coupled map lattices. Moreover, the uneven distribution of chaotic sequences in one-dimensional coupled lattices is rearranged to produce homogeneous sequences, and the encryption effect is better.
The experimental results and security analysis showed that the algorithm based on the CML with polymorphic mapping can achieve the goal of polymorphism, improve the traditional one-dimensional-mapping coupled lattice, and construct a selective chaotic map.
The structure of this paper is as follows. In Section 2, we briefly discuss some basic knowledge of polymorphic spatiotemporal chaotic systems and random ergodicity, including extension of the T diffusion matrix, the polymorphic CML, and the replacement of the pixel value. In Section 3, the algorithm proposed in this paper is described in detail, including key generation, and the encryption and decryption processes of the algorithm. Section 4 shows the experimental results. A detailed security analysis of the algorithm is given in Section 5. Finally, the characteristics and shortcomings of the algorithm are summarized.
2. Polymorphic Spatiotemporal Chaotic Systems and Random Ergodicity
2.1. Extension of T Diffusion Matrix
The reversible matrix is only in a format in Ref. [37], but the diffusion effect is significant in matrix . Therefore, this paper extends the matrix to the effect, and the effect of the original matrix is the same. Furthermore, when the matrix is extended to a new reversible diffusion matrix, it maintains the reversible property and good diffusion effect of the original matrix.
Suppose is the clear matrix, and the diffusion formula is
is a plaintext matrix after diffusion.
The original matrix is
where is an arbitrary value for the control variable.
After extension matrix :
where is the size of the number of rows generated. can take any value for the control variable, which guarantees the invertibility of the matrix. To ensure the effectiveness of the implementation, a format of and above is recommended.
2.2. Polymorphic CML
Only one kind of chaotic mapping is selected in the one-dimensional coupled image lattice; the result is very good, but the chaotic sequence is not uniform, and the number of iterations needs to be abandoned. Moreover, if the parameter selection of the chaotic map is not good, it will easily lead to the phenomenon of the periodic window. So, this paper multiplies the pseudorandom sequence and the matrix mentioned in the previous paper, and diffuses a coupled image lattice to the uniform state because of the reversible property of the matrix . So, in this paper, we add four chaotic maps to the traditional chaotic map.
A coupled image lattice is a simple model that can describe the complex dynamics of closed systems and is defined as Equation (4).
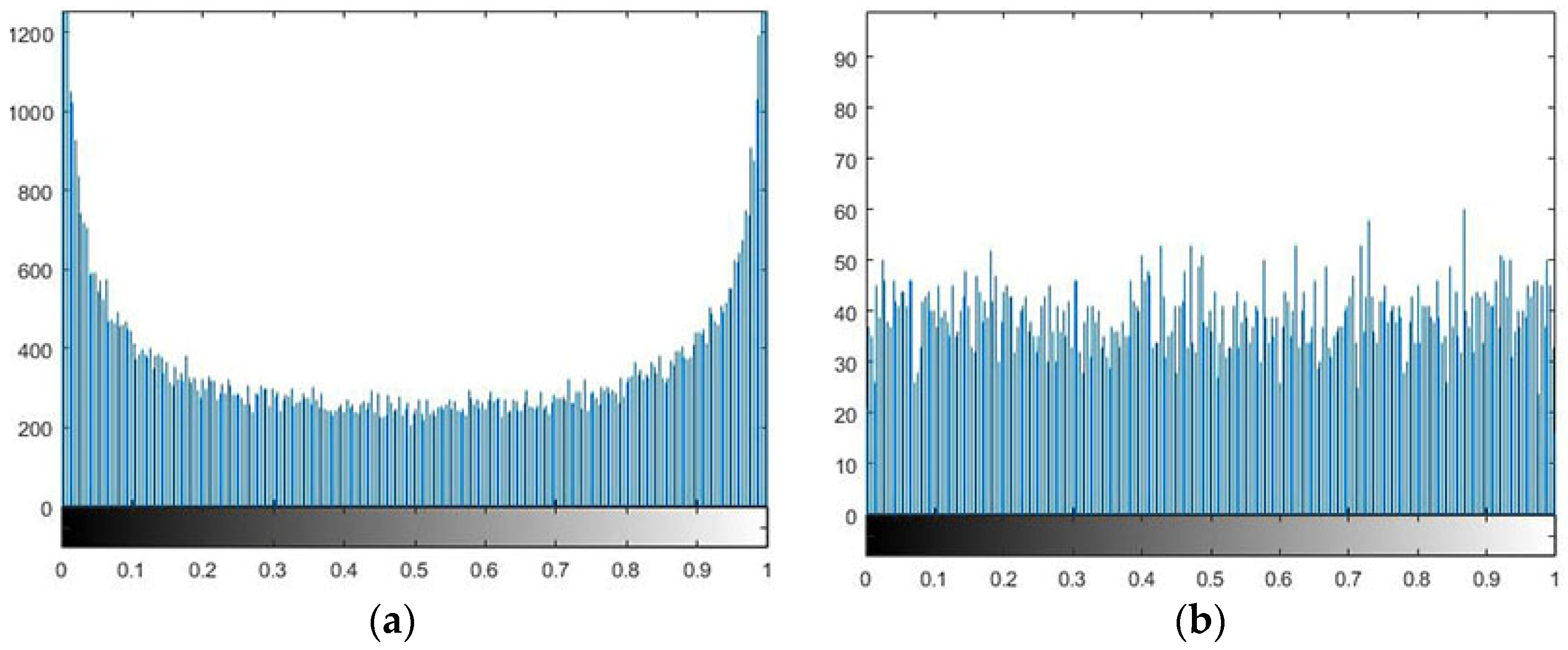
when , represents the size of the lattice. In this paper, when the CML system is used at the pixel level, it is set to 10; represents the evolution time, is the coupling coefficient, and the edge conditions are satisfied. and and are used as keys. When is a chaotic map, the dynamical characteristics of the system are also chaotic. In the course of the study, and , and 10 grids were selected and iterated 10,000 times. There was a phenomenon of two-level differentiation. When different coefficients were selected, the histogram data showed different degrees of two-level differentiation. As shown in Figure 1.
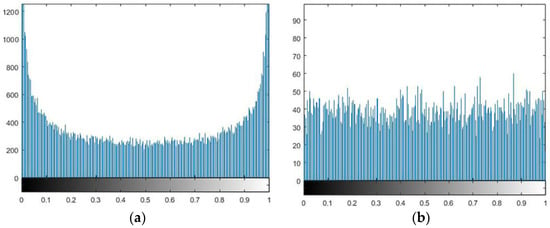
Figure 1.
Pseudorandom sequence distribution. (a) The original CML chaotic sequence is distributed. (b) After the T matrix is completed, the CML chaotic sequence is distributed.
Chaotic maps are used to generate chaotic sequences, which are random sequences generated by simple deterministic systems. Therefore, using the idea of polymorphism, let choose between them to increase the diversity of random sequences and increase the security of the algorithm. The chaotic map is defined as
The chaotic mappings and their corresponding parameter ranges are shown in Table 1. In this paper, when designing , we use a simple chaotic map to design 15 alternative mappings that can increase the change in the pseudo-random sequence. When represents all the chaotic maps, it is all selected and discarded as the state of .

Table 1.
Chaotic mappings and parameter ranges.
2.3. Use of the Probability Replacement of the Pixel Value
Suppose that for a plaintext image of size , is the number of rows and is the number of columns. If we divide them evenly into parts, calculate the frequency of every pixel value in every small image and sort them, and then, use the generated pixel values to replace the others, the pixel values can be replaced [38]. Additionally, because the pixel value is 8 bit, the higher pixel values have more information than the originals. When filling 0 to expand the digit, we need to fill 0 on the left side [39,40,41]. However, considering the complexity of key management, we recommend as follows:
Step 1: Judge the parity property of the image; if it is an odd number, chooses 1; if it is even, chooses 2; the number of part n should satisfy
Step 2: Calculate the frequency of the pixel value in every plaintext image, and construct a Huffman tree based on the frequency of the pixel value by using the Huffman encoding rule.
Step 3: Because the obtained Huffman code does not satisfy 8 bits, it needs to be extended. Because the information of high pixel values is more than that of low pixel values, it needs to fill in 0 on the left when the number 0 is extended, but not on the right side. The effects are shown in Figure 2 and Figure 3.

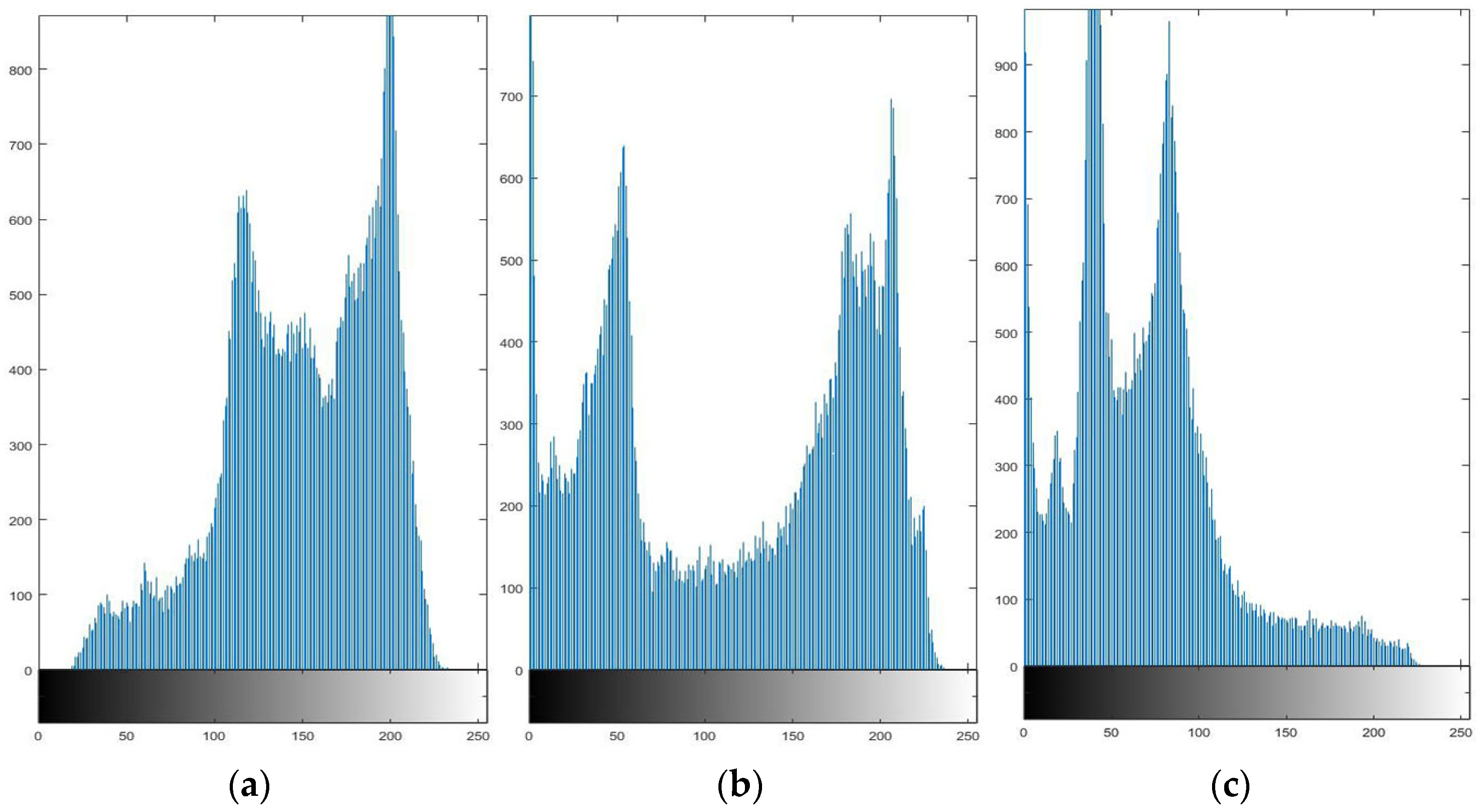
Figure 2.
RGB-channel image of Lena: (a) original plaintext, R-channel image; (b) original plaintext, G-channel image; (c) plaintext, B-channel image.

Figure 3.
RGB-channel image after the replacement of Lena pixel value: (a) replacement, after R-channel image; (b) replacement, G-channel image; (c) replacement, B-channel image.
3. Image Encryption Algorithm Based on CML with Polymorphic Mapping
3.1. Key Generation
The key parts of the cryptosystem include the control parameter of the CML system; the initial values and ; the selected ; the initial parameters of the chaotic mapping ; the ; and the RSA 1024-bit keys in the diffusion matrix .
3.2. Encryption Algorithm Process
For a plaintext image of size , the encryption process is as follows:
Step 1: Given the initial key, the SHA-256 algorithm is used to transform the sequence into binary encoding. After the sequence , the first 8 bits is selected, the first 4 bits are judged and the latter 4 bits are selected.
Step 2: According to the initial key, is obtained, is selected to obtain the selection sequence of , and the specific is selected.
Step 3: From the key , the sequence is transformed into the CML’s initial parameter and coupling coefficient. is any value and the coupling coefficient is calculated by Equation (7).
Step 4: The initial values generated by and are replaced by pixel values. The formula is as follows.
Step 5: Disposal. The scrambling processing is performed using the function . If is the vector to be sorted, , where is the sorted vector , and is the index of each item in corresponding to vector .
Step 6: The , of the diffusion matrix is selected from the rule of probability substitution.
Step 7: The two value sequences are determined; the formula is as follows:
Step 8: The bit-OR operation is performed at the end of this pixel level encryption process.
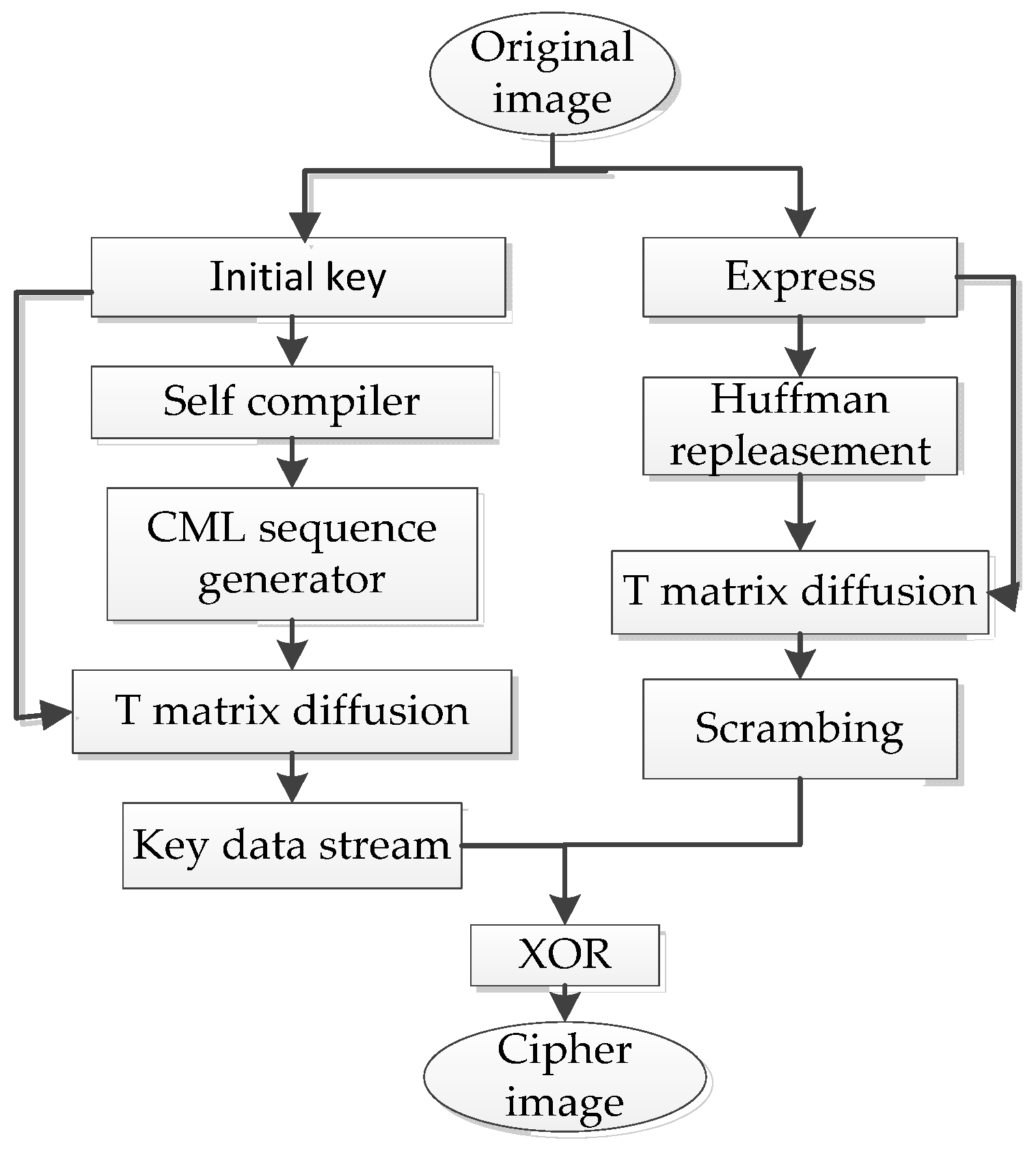
Figure 4 describes the process of the encryption algorithm.
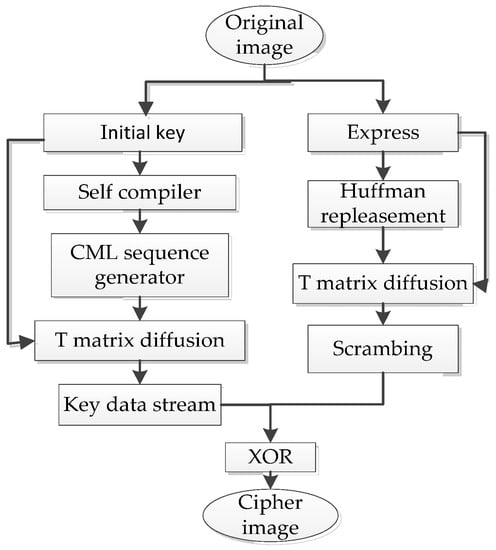
Figure 4.
Flowchart of the image encryption algorithm based on CML with polymorphic mapping.
3.3. Decryption Process of Algorithm
The Huffman code used in the encryption process is irreversible. In the process of encryption, the probability of each pixel value in the image is completely destroyed. So, in the process of decryption, the Huffman code is processed separately. This paper uses the traditional RSA scheme to deal with the problem. The other steps are the inverse of the encryption process [42,43].
4. Experimental Results
Here, we choose three plaintext color images of , “Lena”, “Peppers” and “Mandrill”, to simulate the algorithm in this paper. We choose the initial key (hash, diffusion matrix) to verify the effect, and the selected matrix size is sequences, where ; the local parameters are related to the initial key. The experimental results are the same as the expected experimental results. All three plaintext images of can be encrypted, and intuitively, no clear plaintext information appears in the image. Figure 5, Figure 6 and Figure 7 are the simulation results.

Figure 5.
Lena encryption process. (a) Original image Lena; (b) encrypted image Lena; (c) decrypted image Lena.

Figure 6.
Mandrill encryption process. (a) Original image Mandrill; (b) encrypted image Mandrill; (c) decrypted image Mandrill.

Figure 7.
Peppers encryption process. (a) Original image Peppers; (b) encrypted image Peppers; (c) decrypted image Peppers.
5. Security Analysis
In this section, we will conduct a theoretical analysis and numerical simulations of a violent attack, statistical attack, differential attack, chosen plaintext attack, etc., and compare the results with Refs. [31,32,44].
5.1. Key-Space Analysis
A large enough key space can resist violent attacks and improve the security of encryption algorithms. The key space includes all keys used in the scrambling and diffusion processes. Valid keys for this algorithm are as follows:
The initial key is:
Since the initial key used in this paper is generated by the hash function of the SHA-256 algorithm, there are a total of 256 bits, and there are 256 cases of probability replacement of the pixel values in this paper, as well as the part of the diffusion matrix and the public key, plus the secret 1024 bits in the RSA algorithm. So, if the computing precision of the computer is , the algorithm key space designed in this paper is , far greater than that of the password system; thus, this algorithm can resist the a violent attack.
5.2. Statistical Analysis
Image histogram analysis and adjacent-pixel correlation are two very important statistical properties of image encryption algorithms, and can reflect the algorithm’s ability to resist statistical attacks.
5.2.1. Histogram Analysis
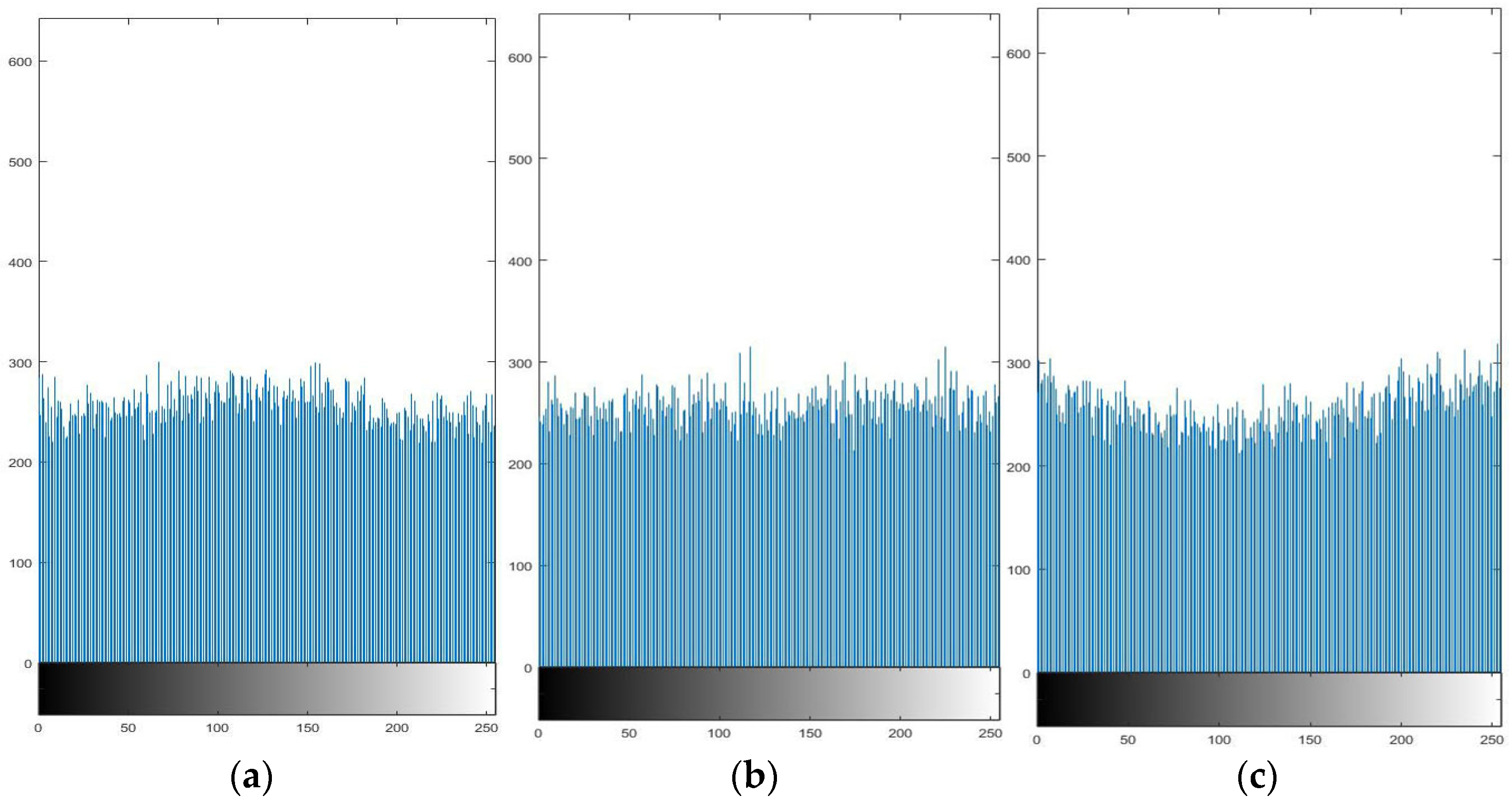
Figure 8 and Figure 9 give the histograms of the RGB channels of the plaintext and ciphertext images of “Lena”. Comparing their histograms, it can be found that the histogram distribution of encrypted plaintext images is more uniform than before encryption. Therefore, an image encrypted by this algorithm makes a statistical analysis attack difficult.
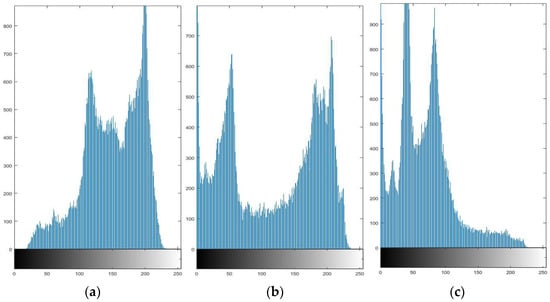
Figure 8.
RGB histogram of Lena. (a) Lena R-channel pixel histogram; (b) Lena G-channel pixel histogram; (c) Lena B-channel pixel histogram.
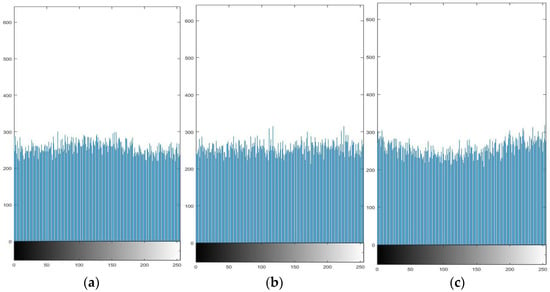
Figure 9.
RGB histogram of Lena after encryption. (a) encrypted, Lena’s R-channel pixel histogram; (b) encrypted, G-channel pixel histogram; (c) encrypted, B-channel pixel histogram.
5.2.2. Adjacent Pixel Correlation
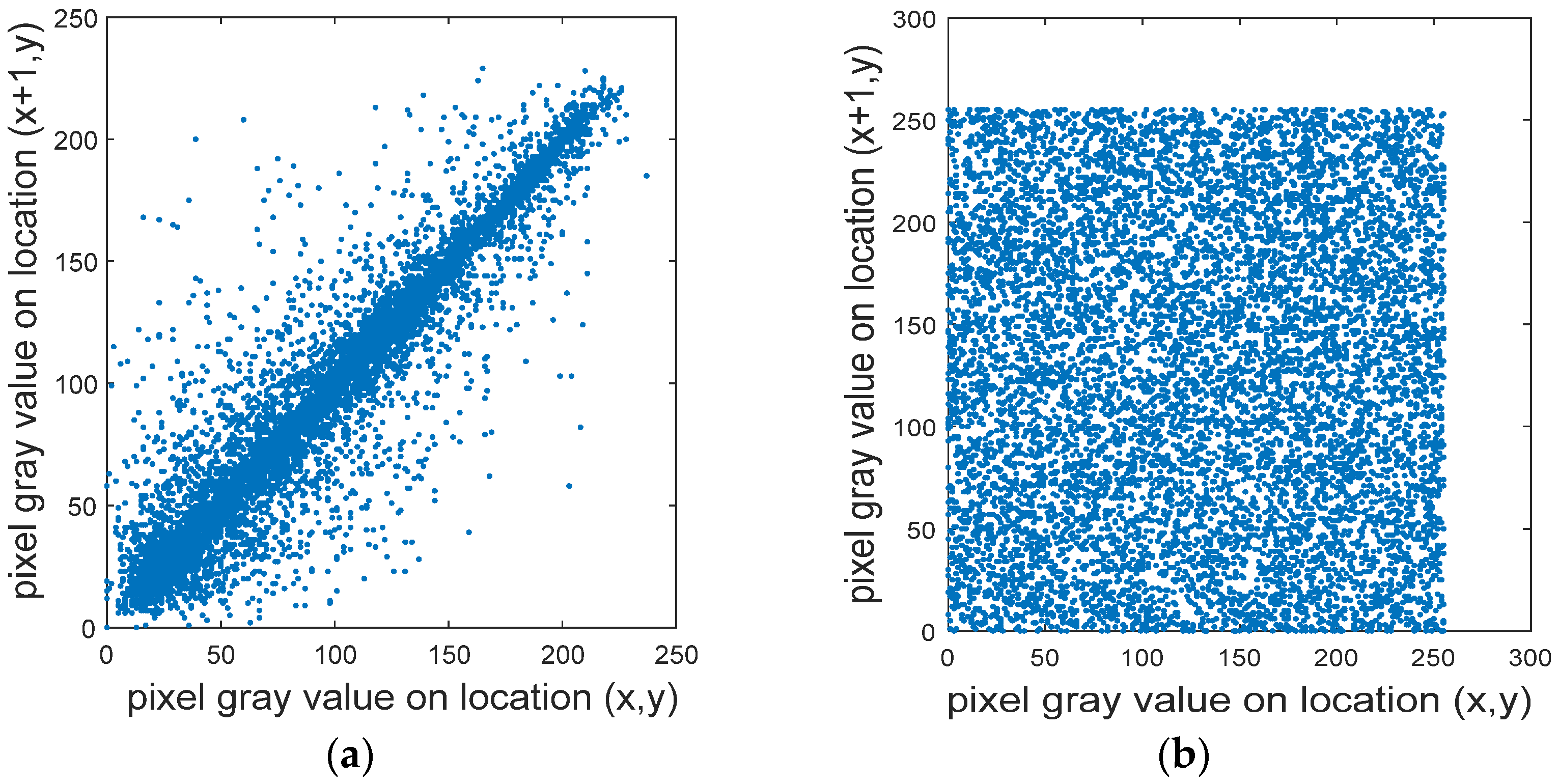
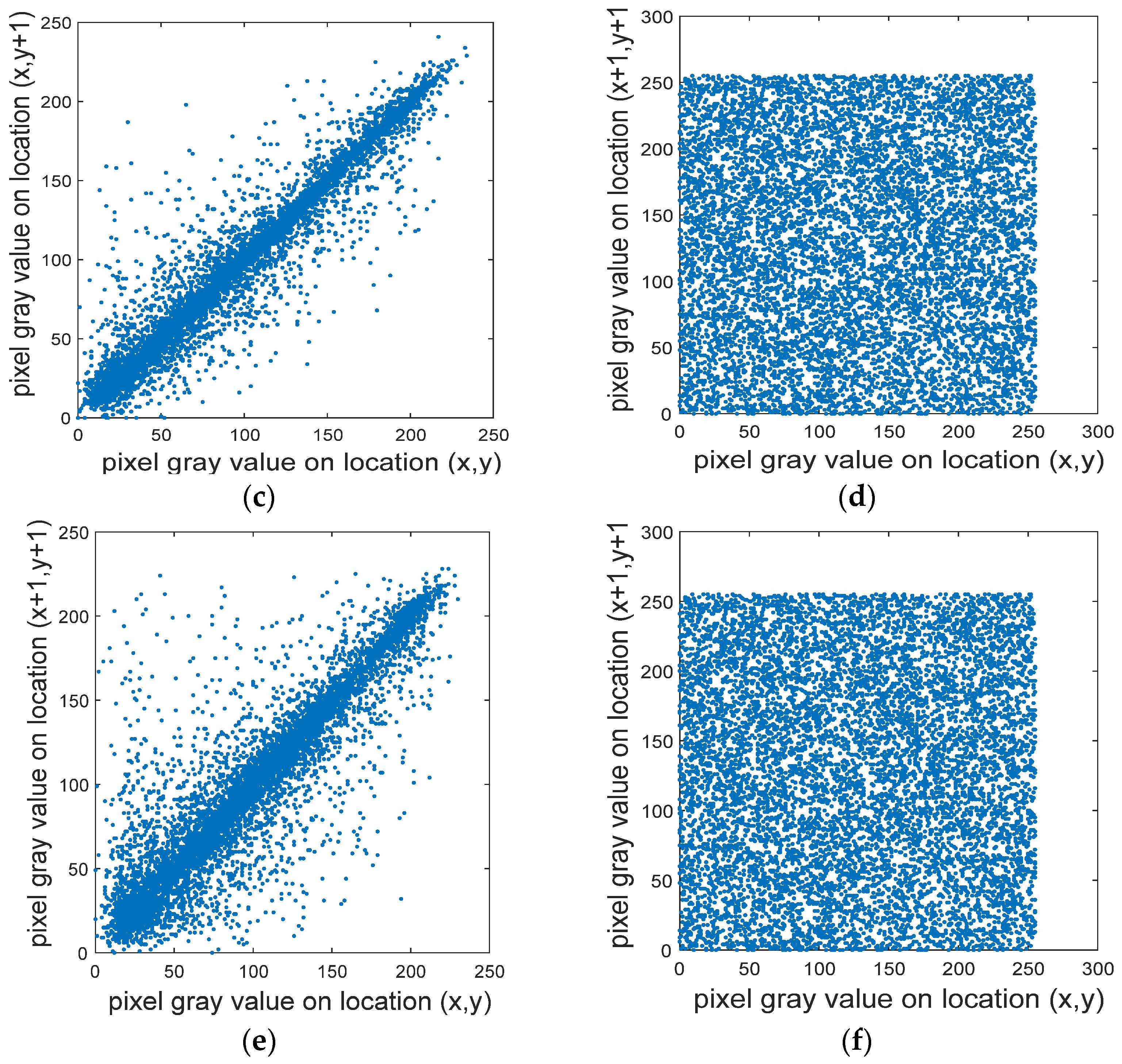
To resist statistical attacks, the correlation between adjacent pixels must be effectively reduced [31,32,44]. Using Equation (10) to calculate the correlation between the adjacent pixels of the plaintext and the ciphertext images, we randomly select 10,000 pairs of pixels in the plaintext and the ciphertext images of the “Lena” R channel, as shown in Figure 10. The correlations between the adjacent pixels of the horizontal, vertical, and diagonal lines of these pixels are also tested, as shown in Table 2.
when,
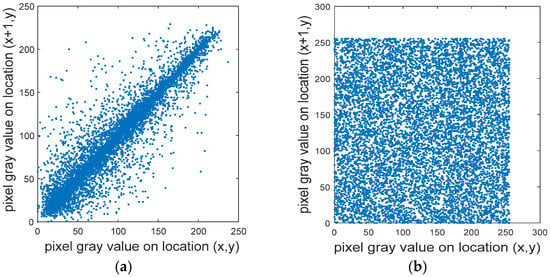
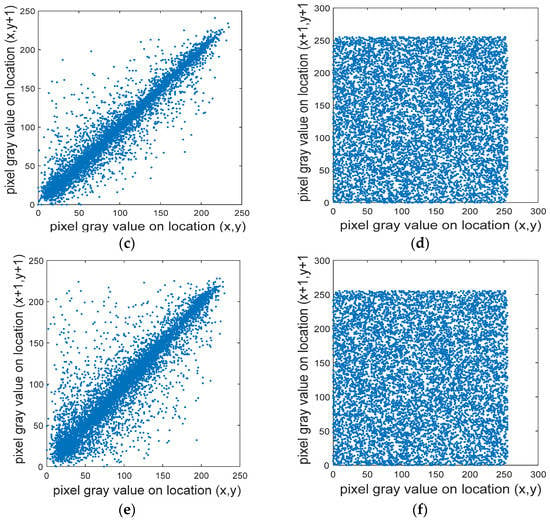
Figure 10.
The level of adjacent-pixel correlation. (a) Lena plaintext; (b) Lena ciphertext horizontal correlation; (c) Lena plaintext vertical correlation; (d) Lena clear text vertical correlation; (e) Lena plaintext diagonal correlation; (f) Lena plaintext diagonal correlation.

Table 2.
Correlation between adjacent pixels of plaintext and ciphertext images.
5.2.3. Information Entropy
Entropy is an index used to measure uncertainty [31,32,44], that is, the probability of discrete random events. The more chaotic the system is, the higher the information entropy, and vice versa. The value can be calculated by Equation (12).
Here is the probability that occurs. The information entropy of the encrypted ciphertext image should be closer to 8. The results in Table 3 show that the encrypted information of the ciphertext image is not easy to leak, and it can better resist statistical attacks.

Table 3.
Information entropy of clear and ciphertext images.
5.2.4. Resistance to Differential Attacks
A differential attack analyzes the data of the image based on the ciphertext before modification and after modification, and obtains the key by making small changes to the text. Here, the number-of-pixels change rate (NPCR) and the unified mean change intensity (UACI) are calculated [31,45]. The larger the value of NPCR, the more sensitive the encryption algorithm is to changes in the original plaintext. The larger the UACI value, the greater of the average change intensity. The number-of-pixels change rate is calculated as follows:
where and denote the width and height of the image, respectively. Additionally, and denote two ciphertext images after the original plaintext is changed by one pixel. If , then ; otherwise, . The experimental results in Table 4 show that, in general, NPCR is close to 99.6049% and UACI is close to 33.4635% [32,46]. The results show the advantages of the algorithm in resisting differential attacks.

Table 4.
NPCR and UACI values for ciphertext images.
5.2.5. Robustness Analysis
We use a noise attack and block attack to test the robustness of the algorithm [32,44]. Compared with other common noise types, salt-and-pepper noise has a greater direct impact on the ciphertext image. Therefore, this experiment considers the effect on the plaintext image after adding salt-and-pepper noise to the algorithm. We add different strengths of salt-and-pepper noise to the plaintext and use the same key for encryption and decryption. Figure 11 shows the encrypted image with three noise values of 0.02, 0.12, and 0.2, respectively.

Figure 11.
Noise experiment adding noise intensity of (a) 0.02, (b) 0.12, and (c) 0.2 after the encrypted image, and (d–f) is their corresponding decryption image.
5.2.6. Sensitivity Analysis
The main part of this article contains the initial key part, the parameter in the matrix , and the cryptographic part of the RSA algorithm. The RSA algorithm is a traditional encryption method, so it has not been tested in sensitivity tests. This paper only changed the initial key
and the , parameters in the matrix , and the , of the replacement of the pixel values under the premise that the RSA was not cracked. The experimental results in Figure 12 show that the encryption scheme of the CML color image based on the polymorphism principle designed in this paper has good sensitivity to keys.

Figure 12.
Sensitivity experiment. (a) Changes the hash value; (b) changes the of the matrix and decrypts the image of the ,; (c) changes the decryption image of the Huffman replacement rule; and (d) the correct key decryption.
5.2.7. Complexity Analysis
The time-consuming nature of the calculation of floating-point data in an encryption algorithm was considered in this section. In generating the chaotic sequence using the CML system, iterations of floating-point data were performed. When using the matrix to perform the diffusion of pixel values, the corresponding computational complexity was operations of floating-point data. It is less efficient when using Matlab R2016b to calculate and select CML sequences, but it can still meet the needs of real cryptosystems. This article mainly considers the security of the image encryption algorithm, so this does not violate the original intention of this article.
The running environment of this algorithm is 8.00 GB RAM, Intel(R) Core(TM) Intel(R) Xeon(R) CPU at 2.67 GHz, the operating system is Windows 8, and the simulation software is Matlab R2016b. We know that Matlab is an excellent piece of simulation software, but its efficiency is low; the algorithm’s running speed and programming language, CPU, memory size, operating system, etc. have certain purposes. It is less efficient when using Matlab to calculate and select CML sequences, but it can still meet the needs of real cryptosystems. The purpose of this article is to propose a more secure image encryption algorithm, so this is not contrary to the original intention of this article.
6. Conclusions
A new polymorphic coupled map lattice based on information entropy is developed for encrypting color images in this paper. Firstly, we extend a diffusion matrix with the original 4 × 4 matrix into an n × n matrix. Then, the Huffman idea is employed to propose a new pixel-level substitution method, which is applied to replace the grey degree value. We employ the idea of polymorphism and select f(x) in the spatiotemporal chaotic system. The pseudo-random sequence is more diversified and the sequence is homogenized. Three plaintext color images of , “Lena”, “Peppers” and “Mandrill”, are selected in order to prove the effectiveness of the proposed algorithm. The results show the advantages of the algorithm in resisting differential attacks. An encrypted image with three noise values of 0.02, 0.12, and 0.2 is obtained. The security of the image encryption algorithm does not violate our original intention. Therefore, the results of brute-force attacks, statistical attacks, and plaintext attacks show that the algorithm has good security. In addition, in our study, the mixed model gradually replaced the single CML model, and showed better results in resisting various typical attacks [47]. Therefore, the hybrid model of the genetic algorithm and CML will be further studied.
Author Contributions
Conceptualization, P.H. and D.L.; methodology, P.H. and Y.W.; software, Y.W. and D.L.; validation, D.L.; formal analysis, P.H.; investigation, P.H. and H.Z.; resources, D.L. and H.Z.; data curation, D.L.; writing—original draft preparation, P.H.; writing—review and editing, W.D.; visualization, W.D.; supervision, D.L.; project administration, W.D.; funding acquisition, W.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under grant number 61771087, and the Research Foundation for the Civil Aviation University of China under grant numbers 3122022PT02 and 2020KYQD123.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Stinson, D. Cryptography: Theory and Practice, 2nd ed.; CRC Press Public House of Electronic Industry: Boca Raton, FL, USA, 2002. [Google Scholar]
- Long, S. A comparative analysis of the application of hashing encryption algorithms for MD5, SHA-1, and SHA-512. J. Phys. Conf. Ser. 2019, 1314, 012210. [Google Scholar] [CrossRef]
- Wang X, Y.; Zhang, H.L. A novel image encryption algorithm based on genetic recombination and hyper-chaotic systems. Nonlinear Dyn. 2016, 83, 333–346. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, M. An image encryption algorithm based on new chaos and diffusion values of a truth table. Inf. Sci. 2021, 579, 128–149. [Google Scholar] [CrossRef]
- Li, Z.; Peng, C.; Tan, W.; Li, L. A novel chaos-based color image encryption scheme using bit-level permutation. Symmetry 2020, 12, 1497. [Google Scholar] [CrossRef]
- Zarebnia, M.; Parvaz, R. Image encryption algorithm by fractional based chaotic system and framelet transform. Chaos Solitons Fractals 2021, 152, 111402. [Google Scholar] [CrossRef]
- Wu, D.; Wu, C. Research on the time-dependent split delivery green vehicle routing problem for fresh agricultural products with multiple time windows. Agriculture 2022, 12, 793. [Google Scholar] [CrossRef]
- Li, X.; Zhao, H.; Yu, L.; Chen, H.; Deng, W.; Deng, W. Feature extraction using parameterized multisynchrosqueezing transform. IEEE Sens. J. 2022, 2, 14263–14272. [Google Scholar] [CrossRef]
- Zhou, X.B.; Ma, H.J.; Gu, J.G.; Chen, H.L.; Deng, W. Parameter adaptation-based ant colony optimization with dynamic hybrid mechanism. Eng. Appl. Artif. Intell. 2022, 114, 105139. [Google Scholar] [CrossRef]
- Li, T.Y.; Shi, J.Y.; Deng, W.; Hu, Z.D. Pyramid particle swarm optimization with novel strategies of competition and cooperation. Appl. Soft Comput. 2022, 121, 108731. [Google Scholar] [CrossRef]
- Chen, H.Y.; Miao, F.; Chen, Y.J.; Xiong, Y.J.; Chen, T. A hyperspectral image classification method using multifeature vectors and optimized KELM. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2781–2795. [Google Scholar] [CrossRef]
- Yao, R.; Guo, C.; Deng, W.; Zhao, H.M. A novel mathematical morphology spectrum entropy based on scale-adaptive techniques. ISA Trans. 2022, 126, 691–702. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.M.; Liu, J.; Chen, H.Y.; Chen, J.; Li, Y.; Xu, J.J.; Deng, W. Intelligent diagnosis using continuous wavelet transform and gauss convolutional deep belief network. IEEE Trans. Reliab. 2022, 1–11. [Google Scholar] [CrossRef]
- Wei, Y.Y.; Zhou, Y.Q.; Luo, Q.F.; Deng, W. Optimal reactive power dispatch using an improved slime Mould algorithm. Energy Rep. 2021, 7, 8742–8759. [Google Scholar] [CrossRef]
- Deng, W.; Ni, H.C.; Liu, Y.; Chen, H.L.; Zhao, H.M. An adaptive differential evolution algorithm based on belief space and generalized opposition-based learning for resource allocation. Appl. Soft Comput. 2022, 127, 109419. [Google Scholar] [CrossRef]
- Chen, H.Y.; Fang, M.; Xu, S. Hyperspectral remote sensing image classification with CNN based on quantum genetic-optimized sparse representation. IEEE ACCESS 2020, 8, 99900–99909. [Google Scholar] [CrossRef]
- Deng, W.; Zhang, L.; Zhou, X.; Zhou, Y.; Sun, Y.; Zhu, W.; Chen, H.; Deng, W.; Chen, H.; Zhao, H. Multi-strategy particle swarm and ant colony hybrid optimization for airport taxiway planning problem. Inf. Sci. 2022, 612, 576–593. [Google Scholar] [CrossRef]
- Song, Y.; Cai, X.; Zhou, X.; Zhang, B.; Chen, H.; Li, Y.; Deng, W.; Deng, W. Dynamic hybrid mechanism-based differential evolution algorithm and its application. Expert Syst. Appl. 2023, 213, 118834. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, W.G.; Liao, Y.; Song, Z.; Shi, J.; Jiang, X.; Shen, C.; Zhu, Z. Bearing fault diagnosis via generalized logarithm sparse regularization. Mech. Syst. Signal Process. 2022, 167, 108576. [Google Scholar] [CrossRef]
- Li, N.; Huang, W.G.; Guo, W.J.; Gao, G.Q.; Zhu, Z. Multiple enhanced sparse decomposition for gearbox compound fault diagnosis. IEEE Trans. Instrum. Meas. 2020, 69, 770–781. [Google Scholar] [CrossRef]
- Xu, G.; Bai, H.; Xing, J.; Luo, T.; Xiong, N.N. SG-PBFT: A secure and highly efficient distributed blockchain PBFT consensus algorithm for intelligent Internet of vehicles. J. Parallel Distrib. Comput. 2022, 164, 1–11. [Google Scholar] [CrossRef]
- Zheng, J.J.; Yuan, Y.; Zou, L.; Deng, W.; Guo, C.; Zhao, H. Study on a novel fault diagnosis method based on VMD and BLM. Symmetry 2019, 11, 747. [Google Scholar] [CrossRef]
- Wu, X.; Wang, Z.C.; Wu, T.H.; Bao, X.G. Solving the family traveling salesperson problem in the adleman–lipton model based on DNA computing. IEEE Trans. NanoBioscience 2021, 21, 75–85. [Google Scholar] [CrossRef] [PubMed]
- Cao, H.; Shao, H.; Zhong, X.; Deng, Q.; Yang, X.; Xuan, J. Unsupervised domain-share CNN for machine fault transfer diagnosis from steady speeds to time-varying speeds. J. Manuf. Syst. 2022, 62, 186–198. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, J.; Yang, X.; Ling, Y. Optimal reactive power dispatch using water wave optimization algorithm. Oper. Res. 2020, 20, 2537–2553. [Google Scholar] [CrossRef]
- Xu, G.; Dong, W.; Xing, J.; Lei, W.; Liu, J. Delay-CJ: A novel cryptojacking covert attack method based on delayed strategy and its detection. Digit. Commun. Netw. 2022; in press. [Google Scholar] [CrossRef]
- Li, X.; Shao, H.; Lu, S.; Xiang, J.; Cai, B. Highly-efficient fault diagnosis of rotating machinery under time-varying speeds using LSISMM and small infrared thermal images. IEEE Trans. Syst. Man Cybern. Syst. 2022, 30, 135–142. [Google Scholar] [CrossRef]
- Ren, Z.; Han, X.; Yu, X.; Skjetne, R.; Johan, B.; Leira, S.; Zhu, M. Data-driven simultaneous identification of the 6DOF dynamic model and wave load for a ship in waves. Mech. Syst. Signal Process. 2023, 184, 109422. [Google Scholar] [CrossRef]
- Roellgen, C.B. Polymorphic cipher theory. 2004. Available online: http://www.ciphers.de/products/polymorphic_cipher_theory.html (accessed on 12 September 2022).
- Mackowski, D.W.; Mishchenko, M.I. Calculation of the T matrix and the scattering matrix for ensembles of spheres. J. Opt. Soc. Am. A 1996, 13, 2266–2278. [Google Scholar] [CrossRef]
- Behnia, S.; Akhshani, A.; Mahmodi, H.; Akhavan, A.J.C.S. A novel algorithm for image encryption based on mixture of chaotic maps. Chaos soliton& fract. 2008, 35, 408–419. [Google Scholar]
- Hussain, I.; Shah, T.; Gondal, M.A. Image encryption algorithm based on PGL(2,GF(28)) S-boxes and TD-ERCS chaotic sequence. Nonlinear Dynam. 2012, 70, 181–187. [Google Scholar] [CrossRef]
- Hussain, I.; Shah, T.; Gondal, M.A. An efficient image encryption algorithm based on S8 S-box transformation and NCA map. Opt. Commun. 2012, 285, 4887–4890. [Google Scholar] [CrossRef]
- Zhu, Z.L.; Zhang, W.; Wong, K.W.; Yu, H. A chaos-based symmetric image encryption scheme using a bit-level permutation. Inf. Sci. Int. J. 2011, 181, 1171–1186. [Google Scholar] [CrossRef]
- Hussain, I.; Gondal, M.A. An extended image encryption using chaotic coupled map and S-box transformation. Nonlinear Dynam. 2014, 76, 1355–1363. [Google Scholar] [CrossRef]
- Baptista, M.S. Cryptography with chaos. Phys. Lett. A 1998, 240, 50–54. [Google Scholar] [CrossRef]
- Jain, A.; Rajpal, N. A robust image encryption algorithm resistant to attacks using DNA and chaotic logistic maps. Multimed. Tools Appl. 2016, 75, 5455–5472. [Google Scholar] [CrossRef]
- Rehman, A.U.; Liao, X.; Kulsoom, A.; Abbas, S. Selective encryption for gray images based on chaos and DNA complementary rules. Multimed. Tools Appl. 2015, 74, 4655–4677. [Google Scholar] [CrossRef]
- Huang, X.; Ye, G. An image encryption algorithm based on hyper-chaos and DNA sequence. Multimed. Tools Appl. 2014, 72, 57–70. [Google Scholar] [CrossRef]
- Bakhshandeh, A.; Eslami, Z. An authenticated image encryption scheme based on chaotic maps and memory cellular automata. Opt. Lasers Eng. 2013, 51, 665–673. [Google Scholar] [CrossRef]
- Xu, L.; Li, Z.; Li, J.; Hua, W. A novel bit-level image encryption algorithm based on chaotic maps. Opt. Lasers Eng. 2016, 78, 17–25. [Google Scholar] [CrossRef]
- Zhang, Q.; Guo, L.; Wei, X. Image encryption using DNA addition combining with chaotic maps. Math. Comput. Model. 2010, 52, 2028–2035. [Google Scholar] [CrossRef]
- Liu, H.; Wang, X.Y.; Kadir, A. Image encryption using DNA complementary rule and chaotic maps. Appl. Soft Comput. 2012, 12, 1457–1466. [Google Scholar] [CrossRef]
- Rhouma, R.; Belghith, S. Cryptanalysis of a spatiotemporal chaotic image/video cryptosystem. Phys. Lett. A 2008, 372, 5790–5794. [Google Scholar] [CrossRef]
- Akhshani, A.; Behnia, S.; Akhavan, A.; AbuHassana, H.; Hassana, H. A novel scheme for image encryption based on 2D piecewise chaotic maps. Opt. Commun. 2010, 283, 3259–3266. [Google Scholar] [CrossRef]
- Hussain, I.; Shah, T.; Gondal, M.A. Image encryption algorithm based on total shuffling scheme and chaotic S-box transformation. J. Vib. Control. 2014, 20, 2133–2136. [Google Scholar] [CrossRef]
- Nematzadeh, H.; Enayatifar, R.; Motameni, H. Medical image encryption using a hybrid model of modified genetic algorithm and coupled map lattices. Opt. Lasers Eng. 2018, 110, 24–32. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).