Multiscale Brain Network Models and Their Applications in Neuropsychiatric Diseases

Abstract

With the rapid development of advanced neuroimaging techniques, understanding the brain in terms of structural and functional connectomes has become one of the frontier topics in neuroscience. Different from traditional descriptive brain network models, which focused on single neuroimaging modal and temporal scales, multiscale brain network models consisting of mesoscopic neuronal activity and macroscopic functional dynamics can provide a mechanistic understanding for brain disorders. Here, we review the foundation of multiscale brain network models and their applications in neuropsychiatric diseases. We first describe some basic elements of a multiscale brain network model, including network connections, dynamics of regional neuronal populations, and model fittings to different metrics of fMRI. Secondly, we draw comparisons between multiscale brain network models and other large-scale brain models. Additionally, then we survey the related applications of multiscale brain network models in understanding underlying mechanisms of some brain disorders, such as Parkinson’s disease, Alzheimer’s disease, and Schizophrenia. Finally, we discuss the limitations of current multiscale brain network models and future potential directions for model development. We argue that multiscale brain network models are more comprehensive than traditional single modal brain networks and would be a powerful tool to explore neuronal mechanisms underlying different brain disorders measured by neuroimaging.

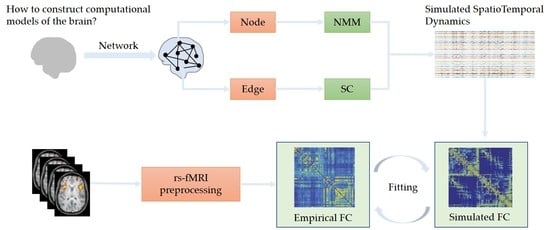
1. Introduction

The causes of many brain disorders are extremely complicated and still under debate. It is very difficult to identify the potential mechanisms underlying the symptoms of brain disorders only through experimental studies. Consequently, the demands toward the development of mathematical and computational models are increasing. Computational models can be used precisely for replicating experimental results and testing clinical hypotheses and are indispensable in neuroscience [1].

The human brain is the most complex network and consists of billions of interconnected neurons; brain functions (e.g., cognitive, memory, perception et al.) are achieved through interactions of neurons across multi-temporal and spatial scales. Thus, modeling of the brain ranges between microscale (single neurons), mesoscale (a group of neurons), and macroscale (large-scale brain network). For example, models of single neurons include the classical Hodgkin-Huxley model and its simplified variants as FitzHugh-Nagumo, Morris-Lecar Models et al. [2,3,4,5]. Models of neuronal populations differ in their complexity, one example rests on detailed biophysical properties, such as Terman and Rubin developed a conductance-based computational network model of the basal ganglia based on the physical anatomy of the brain [6]. Due to its physiological plausibility, the basal ganglia network has been used in many studies to explore the emergence of correlated oscillatory activity in the subthalamic circuit after the destruction of dopaminergic neurons or the optimization of deep brain stimulation in Parkinson’s disease [7,8,9,10]. These kinds of models provide rational analyses of complex behaviors but are constrained by their high-dimension properties that cause network dynamics to be intractable [11]. To overcome this problem, another modeling method using averaged values of neuronal activities is presented to describe the activity of collective neural behavior, such as the mean membrane potential or the firing rate of populations. These simplified models include the Fokker-Planck equation, neural mass model, Wilson-Cowan model, Jansen-Rit model, and Kuramoto oscillator et al. [12,13,14,15]. In the macroscale, early research suggested that certain brain functions were associated with specific brain regions, while a growing body of evidence indicates that brain functions emerge from interactions between spatially distributed areas of large-scale networks. Whole-brain network models may lead to a better understanding of brain functions and dysfunctions [16,17]. Previous whole-brain models focused on topological properties of networks extracted from only single modality and have been promoted by network neuroscience as well as graph theory [18,19]. These descriptive models are quite useful in identifying the differences between normal and pathological brain networks and have been used as a powerful tool to identify biomarkers for classifying and predicting brain disorders. However, they failed to explain the origins of the differences from a dynamic point of view. Motivated by the hierarchical structure of the brain, multiscale brain network models (BNMs) combining nonlinear dynamical theory with network neuroscience have attracted more attention.

Multiscale BNMs typically use the structural connectivity (SC) derived from diffusion-weighted MRIs or T1-weighted MRIs as network edges and mathematical equations simulating collective behaviors of neuronal populations as network nodes. Then, the population dynamics of each node coordinate with one another through SC is fitted to functional dynamics extracted from EEG, MEG, or fMRI to obtain plausible model parameters. Within this framework, multiscale BNMs can not only be used to estimate the relationship between structural and functional connectivity over time or synthetical disease states, but can also be used to infer microscopic neuronal underpinning supporting macroscopic brain dynamics. These models have a tremendous potential to provide mechanistic explanations and exploit feasible biomarkers for understanding and predicting brain disorders. While currently there is no golden standard for how to construct an optimal multiscale BNM, the specific model should be task dependent and built prudently. A deeper understanding of the methodological considerations for implementing a multiscale BNM may be helpful when confronting specific tasks. Thus, in this paper, we aim to provide a deeper understanding of multiscale BNMs by introducing methodological considerations in the modeling pipeline and comparing with other large-scale brain models. Specifically, during the process of modeling, model fitting to empirical data is a critical step toward understanding mechanisms underlying empirical observations. Thus, we introduce in detail machine learning methods in model fitting. We also collect information for applications of multiscale BNMs in brain disorders including Parkinson’s disease, Alzheimer’s disease, and Schizophrenia to provide reference to the literature. Finally, we highlight the current challenges in modeling multiscale BNMs and discuss the future direction of multiscale BNMs in revealing neuronal dynamic mechanisms underlying brain functional dynamics.

2. Methods for Implementing Multiscale BNMs

Multiscale BNMs are based on the theory of network neuroscience, which offers a mathematical framework to describe brain structure and function. Within this framework, each regional brain dynamics is modeled by biologically inspired mathematical equations, and connections between these regions are often estimated from diffusion-weighted MRIs or T1-weighted MRIs. With the rapid development of advanced neuroimaging techniques, in most cases, validation of the BNMs is achieved by comparing the model output with the empirical resting-state fMRI in terms of functional connectivity (FC). In recent years, increasing studies suggests that dynamical FC may be more suitable for capturing higher-order dynamics in neuroimaging data [20,21]. The representation of model fitting also moves from averaged FC to dynamical FC, even to direct fMRI time-series. In the following, the modeling pipeline for implementing a multiscale BNM is summarized in detail including estimating structural network connections, choosing models for simulating node dynamics, and fitting models to different metrics of fMRI.

2.1. Estimation of Structural Network Connections

The anatomical (structural) connectivity of the brain is a physical foundation for supporting complex brain functional dynamics and it plays an important role in determining how networks transfer information between distinct brain regions [22]. Basically, the SC is quantified through different methods in nonhuman primates and the human cortex [23,24,25,26,27], but both function through the choice of a brain parcellation and the inferring of connections to link nodes.

2.1.1. Brain Parcellation

The choice of a brain parcellation scheme is used to define brain regions-of-interest (ROIs ornode). Current ROIs (nodes) are typically derived either through a sophisticated processing pipeline or through a pre-defined atlas, such as an AAL (Automated Anatomical Labeling) atlas, Hagmann atlas, Desikan-Killiany (DK) atlas et al., to divide the image data into distinct regions. Typically, the AAL atlas divides the brain into 116 regions, while the Desikan-Killiany atlas or Hagmann atlas divide the brain into 66 regions. Although these atlases are used a lot, few of them are considered carefully on their appropriateness [28,29]. Brain parcellation is a methodologically challenging and active research field, there is currently no consensus regarding which brain parcellation schemes are optimal for defining the ROIs [30,31,32]. More detail about atlas classification and evolution can be found in [33]. As a parcellation scheme may strongly impact the topological properties of brain networks, it should be chosen carefully.

2.1.2. Inferring of Connections

Connections or edges can be estimated on diffusion-weighted MRIs (DWI), diffusion tensor imaging (DTI), or T1-weighted MRIs through a professional software package. For DWIs/DTI, the edges are estimated from the number, density, or diffusion properties of white matter tracts. While for T1-weighted MRIs, the edges represent the cortical thickness, gray matter volume, or surface area. No matter which method, the SC is often represented by a 2D adjacency matrix and has no direction [34]. There is another way to solve the directional problem of edges by estimating the effective connectivity [35,36,37].

In models, the elements of the SC matrix can be binary or weighted. Typically, a binary connection is obtained by selecting a threshold such that any edge smaller than the threshold is set to zero or otherwise set to one. Weighted connections may represent size, density, or coherence of anatomical connections. Now, weighted connections are increasingly adopted due to their plausible biological information, but there are many challenges to extract topological measures from them. One can refer to [38] for more information about the challenges of and opportunities in mapping SC with diffusion-weighted MRIs.

2.2. Selection of Node Dynamics

Each node in multiscale BNMs simulates a parceled brain region that consists of thousands of neurons and its dynamics are modeled using differential equations that specify the temporal evolution of the population activity [32]. Forrester et al. indicated that local node dynamics can have important effects on large-scale brain states [39]. For instance, some studies suggest that simulated FC is strongly resembling SC when regional activity is close to a phase transition [40] and that FC is strongly in agreement with SC when regional activity is near Hopf bifurcations [41]. Models of nodes differ in their level of detail and correspondence of their parameters to neurophysiology and can basically be divided into biophysical neural mass models or simplified abstract models. Some commonly used models to simulate node dynamics are given in Figure 1.

2.2.1. Computational Models of Node Dynamics

• Biophysical neural mass models

Many disease-related states result from neurobiological alterations. To reveal and reveal underlying mechanisms, it is advantageous for node models to capture greater biophysical fidelity, interpretable parameters, and dynamical regimes in correspondence with in vivo neural activity [37]. The simulation of each node as a large group of spiking neurons is computationally expensive, thus several early studies of BNMs used a reduced excitable neural system, such as the conductance-based neuronal model [42,43] and the FitzHugh-Nagumo neuronal model [44]. The other way to model node dynamics is by adopting neural mass models (NMMs), which are obtained by modeling the response of the neuronal system to its inputs. NMMs can track aggregate activities of synaptic activity and firing rates in populations of spiking neurons, which makes them computationally tractable and matched to the coarse spatiotemporal resolution of neuroimaging modalities [16,37,45]. The biophysically constrained dynamics and recurrent connection strengths between excitatory pyramidal neurons and inhibitory interneurons are incorporated in NMMs which make them suitable for linking synaptic-level disruptions to emergent system-level neural activity [46,47]. Empirically informed NMMs include the Wilson-Cowan and Jansen-Rit models [48,49]. In these models, the biophysically constrained dynamics and recurrent connections between excitatory pyramidal neurons and inhibitory interneurons cause them to be amenable in linking synaptic-level disruptions to emergent system-level neural activities. For instance, these models can be used to infer the effects of excitatory-inhibitory balances or neuronal oscillations to large-scale brain dynamics. Although biophysical models provide interpretable physiological meaning, they are stuck by their complex mathematical equations. Take the typical Jansen-Rit model for example, each of the neuronal populations in the Jansen-Rit model is denoted by two state variables: the average membrane potential y(t) and average firing rate x(t). The average membrane potential can be transformed into the average firing rate using a nonlinear pre-synaptic function σ(y) [17]:

$$\sigma \left(y\left(t\right)\right)=\frac{2e_0}{1+e^{r\left(v_0-y\left(t\right)\right)}}$$

(1)

where the e₀ means half of the maximum firing rate, v₀ indicates potential when half of the maximum firing rate is achieved, and r denotes the slope of the pre-synaptic function at v_0. The membrane potentials are modeled by a convolution operation with an alpha kernel and can be expressed via a second-order differential linear transformation [17]:

$$\ddot{y}\left(t\right)=Aax\left(t\right)-2a\dot{y}\left(t\right)-a^{2}y\left(t\right)$$

(2)

where $x(t)$ means the output of Equation (1), i.e., average firing rate. A presents the average excitatory synaptic gain, and a indicates the time constant of excitatory post-synaptic-potential (PSP). For simplification, a second-order differential equation can be rewritten equivalently as [17]:

$$\begin{array}{l}\dot{y}(t)=z(t)\\ \dot{z}(t)=Aax(t)-2az(t)-a^{2}y(t)\end{array}$$

(3)

as the Jansen-Rit model characterizes the dynamics of three populations, y₀ denotes the average membrane potential of the pyramidal cells and y₁, y₂ indicates the excitatory and inhibitory interneurons, respectively. Then, the dynamic interactions between those three populations of the Jansen-Rit model can be expressed using six coupled ordinary differential equations that are composed of the two operators defined in Equation (3) [17]:

$$\begin{array}{l}{\dot{y}}_0(t)=y_3(t)\\ {\dot{y}}_3(t)=Aa\left[\sigma (y_1(t)-y_2(t))\right]-2a{y}_3(t)-a^2{y}_0(t)\\ {\dot{y}}_1(t)=y_4(t)\\ {\dot{y}}_4(t)=Aa\left[p(t)+C_2\sigma (C_1{y}_0(t))\right]-2a{y}_4(t)-a^2{y}_1(t)\\ {\dot{y}}_2(t)=y_5(t)\\ {\dot{y}}_5(t)=Bb\left[C_4\sigma (C_3{y}_0(t))\right]-2b{y}_5(t)-b^2{y}_2(t)\end{array}$$

(4)

where B is the average inhibitory synaptic gain, b indicates the time constant of inhibitory PSP, C_n indicates the average number of synaptic contacts, and p(t) means excitatory input noise (mean Gaussian white noise).

• Simplified abstract models

The parameters of abstract models do not have a plausible biophysical meaning, neither does their dimensionality. Commonly used abstract models include phase oscillators, limit-cycle oscillators [50,51], and normal form Hopf bifurcation models or Andronov-Hopf bifurcation models [52,53,54,55]. The choice of simplified models depends on research interest. To elaborate, models of oscillators are usually used to simulate synchronous brain interactions on the basis of SC as well as reveal the effects of anatomical connection on functional dynamics [56]. A typical oscillator is the Kuramoto model, which uses a single-phase variable to characterize node dynamics that evolve according to a natural frequency as well as a sinusoidal interaction term [57]. Meanwhile, bifurcation models are often adopted to describe the transition from asynchronous to synchronous behavior or vice versa and investigate varied brain states according to a bifurcation parameter [58]. The commonly used bifurcation model is the Stuart Landau equations; without coupling, the node dynamics can be modeled by the Stuart Landau equations as [58]:

$$\frac{d{z}_j}{dt}=\left(a+i\omega \right)z_j-z_j{\left|z_j\right|}^2$$

(5)

where z_j is a complex-valued variable and w is the intrinsic oscillation frequency of node j.

2.2.2. Heterogeneity between Node Dynamics

At present, most BNMs treat nodes as homogeneous and simulate all node dynamics with identical parameters. However, previous areal parcellations were based on regional variations in cytoarchitecture and myeloarchitecture [59], which suggested that nodes should be heterogeneous. There are studies showing how that incorporating the heterogeneity of local node dynamics may improve the similarity between simulations and empirical data. For example, Deco et al. assigned multiple natural frequencies to nodes to make a BNM that better conforms to empirical rsMEG networks [60]. Demirtas et al. developed a large-scale cortical circuit model incorporating hierarchical heterogeneity of local microcircuit properties to be fitted into multimodal human neuroimaging data [61].

2.2.3. Dynamical System Theory of Node Dynamics

Complex large-scale brain dynamics are rooted in the intrinsic dynamical properties of neuronal populations, here we enumerate several principles of nodes dynamics that support large-scale spatiotemporal activity. Nodes are usually simulated by an averaged firing rate or membrane potential, which are named states of nodes in dynamical system regimes. The states of all nodes span a high-dimensional phase space where each combination of the system’s states is denoted as a point and points in the entire time interval constitute trajectories of the system. In terms of the different properties of trajectories in steady states, the system can be depicted in different dynamical regimes. Some critical regimes and nonlinear dynamics are stated in the following:

• Multistability: In some systems, two or more stable states coexist for the same parameter. Such a system is called a multistable system. The multistability of node dynamics can be used to explain the slow fluctuations underlying dynamical FC. Specifically, if there are only two stable states (a fixed-point and a limit cycle), the system can be assumed to be bistable.
• Metastability: In a metastability regime, no stable states exist. Additionally, the system moves along only intermittently stable state sequences.
• Bifurcation: The system changes from a stable state to another and this qualitative change is caused by a parameter of the system. In terms of the stability property after bifurcation, bifurcation can be classified as supercritical when stable objects appear and as subcritical when unstable objects emerge after bifurcation.
• Fixed-point: It refers to a steady state in a system or a stable equilibrium.
• Limit-cycle: It is a simple closed orbit, which means the system is periodically oscillating.

2.3. Model Fitting

The choice of node dynamics and estimation of connections constitute the skeleton of BNMs and further steps are required to validate the specific BNMs to find optimal working parameters. Validation of multiscale BNMs can relate the observed brain activity to the dynamical repertoire of the computational model, which leads to a better mechanistic interpretation of the observations. For example, Schirner et al. inferred multiscale neurophysiological mechanisms underlying neuroimaging signals by using the hybrid brain network model to simulate a resting-state fMRI [62]. Won et al. studied the emergence of metastable dynamics in functional brain organization via spontaneous fMRI signals and BNMs [63].

Typically, if a BNM is used to simulate an EEG, then biophysically informed forward models are required to realize the mapping from currents in the folded cortex to fluctuating extradural EEG potentials. Likewise, if the BNM is used to model an fMRI, the hemodynamic response functions are used to filter time series to simulate BOLD signals. Studies indicated that a resting-state fMRI can yield new perspectives when investigating large cohorts and patient populations as well as establishing data-sharing in the field of neuroimaging. Thus, the application of BNMs to resting-state fMRI data has become a very active area. The fitting of BNMs to empirical fMRI data is a process for identifying optimal working points or model parameters. Studies show that by choosing proper parameters, the maximal correspondence between simulated and empirical data can emerge when the model is close to a critical point at which the system may undergo a bifurcation [30]. A typical parameter of BNMs is the global coupling strength, which plays a critical role in shaping network dynamics [64]. A global decrease in the coupling strength may impact the dynamical working point of the model, as presented in [48], and the best fit of empirical resting FC matrices is obtained when the BNM is in a subcritical working point.

In the context of BNMs, the neural activity of each node can generate time-series that are maximally fitted to the empirical fMRI BOLD signals and the maximum fitness can be measured by minimizing the dissimilarity between the model-driven metrics and metrics extracted based on the empirical BOLD signals. Commonly used measures of interest include time-averaged FC, dynamic FC, and direct fMRI BOLD time-series that will be stated in detail in the following. Some other measures also have proven their effectiveness, such as whole-brain modularity, instantaneous phase, and macroscopic coherence et al. [65].

2.3.1. Time-Averaged Functional Connectivity

Time-averaged FC (static FC) is the simplest metric to characterize the coordination between simulated and empirical fMRI data. FC is the statistical correlation between different brain regions in the entire time interval and may be symmetrical (e.g., Pearson’s correlation coefficient) or asymmetrical (e.g., partial correlation coefficient) [21]. The degree of agreement between simulated and empirical FC is often measured by the Euclidean distance [53,66]. Additionally, a pipeline for fitting time-averaged FC is given in Figure 2. In the process of model fitting, the grid search is the most common method to choose optimal model parameters. Recently, Wischnewski et al. have assessed the performance of four optimization schemes: Nelder-Mead Algorithm, Particle Swarm Optimization, Covariance Matrix Adaptation Evolution Strategy, and Bayesian Optimization, and proposed the Covariance Matrix Adaptation Evolution Strategy as well as Bayesian Optimization as efficient alternatives to a high-dimensional grid search [67].

Recent results show that model fitting is dependent on types and states of models. For oscillatory models, the best fit between simulated and empirical time-averaged FC is observed at the dynamic working point where metastability is maximized [44,68,69]. For asynchronous models, the simulated FC best matches the empirically observed FC when the system is at the operating point where multistability is around a spontaneous state [19,42,70].

2.3.2. Dynamic Functional Connectivity

Many works have highlighted the nonstationarities that depict time-dependent FC dynamics. Analysis of FC data has moved beyond time-averaged to dynamic methods that assume the coordination of brain activity changes over time [20,71,72]. Dynamic FC reflects time variations of correlations between pairs of brain regions and is characterized by the ongoing switching of network patterns [73,74]. The Kolmogorov–Smirnov distance is often used to quantify the difference between simulated dynamic FC and empirical dynamical FC [65,75].

The sliding window method is the most used technique to compute correlations between time-varying FC [73,76], as given in Figure 3. We also noticed that the method of sliding windows has some limitations as the observed neural processes are highly dependent on the pre-defined temporal width of the window and the length of the step. A long window will limit the visibility of the fast timescale and a short window length will provide insufficient data for a reliable network estimation. Thus, some studies used the hidden Markov model (HMM) to describe brain activity as a dynamic sequence of discrete brain states [77], then the BNM fitting can be achieved by comparing brain states identified by HMM.

2.3.3. Direct fMRI BOLD Time-Series

It is obvious that fitting simulated signals directly to an empirical fMRI time-series is useful in developing more realistic simulations of whole-brain activity. Neural activity in each node of the BNMs can generate simulated BOLD signals using the Balloon-Windkessel hemodynamic model, enabling direct comparison with the fMRI time-series [78,79]. Schirner et al. used exhaustive searches to tune three global parameters to produce the highest fit between the empirical region-average fMRI time-series and corresponding simulated time series [62]. In high-dimensional models, the grid search is time-consuming. Naturally, some intelligent algorithms are presented to improve model fitting.

BNMs have done well in fitting the time-averaged FC, but they are variable at reproducing transient dynamic properties that occur at shorter timescales because BNMs are not synchronized with actual measurements. Then, Kashyap et al. presented a brain network autoencoder framework in which the BNM is in conjunction with a long short-term memory neural network (LSTM). As given in Figure 4, the measures are input into the LSTM to be constrained to a smaller space defined by BNM, and the next time point is reconstructed through a BNM forward equation. Then, the mismatch between the reconstructed next time point and the empirical signal is fed into the machine learning system to fit the model to an fMRI time-series [80].

The above machine learning architecture allowed the BNM to generate more realistic brain data compared with the traditional BNM, but it also brought unknowns into the dynamics and caused it to be impossible to evaluate the BNM independently. Later, Kashyap et al. presented an alternative deep learning method named the Neural Ordinary Differential Equations (ODE), which is similar to the method given in Figure 3 [81,82]. The Neural ODE method uses a sequence of observations and a given dynamical system to estimate the initial conditions of the BNM so that the BNM’s simulated dynamics are synchronized closely to the potential trajectory relative to the observed data. These deep learning methods unquestionably provide an alternative way of model fitting between BNMs and empirical data, yet they also have some limitations, such as the large amounts of computational complexity and lack of robustness. Thus, more time-efficient and robust algorithms are preferred.

3. Comparison between Multiscale BNMs and Other BNMs

3.1. Comparison between Multiscale BNMs and Descriptive BNMs

3.1.1. Descriptive BNMs

The human brain is an intricated nonlinear system where many different connections exist. In a microscopic view, the connections indicate synaptic couplings between neurons. Additionally, in a macroscopic view, the connections indicate anatomical connectivity or interactions between distinct brain regions. These different scales and modalities connections support complex cognitive functions of the brain. Early studies focused on finding the key interconnected features of the brain and identifying the differences of those features between people with different cognitive functions. SC and FC were the primary descriptive tools to represent brain networks. SC networks extracted from structural MRI data depict the physical connections between brain regions and FC networks computed by correlation between time-series of paired brain regions characterize the temporal coincidence of spatially distributed regions. As a variant of FC, EC can also be used to describe the brain network. For the analysis of descriptive brain networks, a mathematical tool named graph theory is introduced to brain networks and consequently boots the rapid development of network neuroscience. In the graph theory regime, metrics such as degree distribution, clustering coefficient, path-length, hub, and community are typically used to distinguish people with different ages, disease states, or under the effects of different drugs. The detailed definitions of these metrics can be found in [83,84,85].

3.1.2. Comparison

Graph theory-based descriptive networks provide invaluable help in identifying people with cognitive differences, but they also have some limitations such as they are constructed from single modality data and cannot link SC with FC directly. Meanwhile, they have a lack of time description and cannot capture the dynamical properties of the brain, while multiscale BNMs are capable of integrating multimodal data from structures and functional neuroimaging and exploiting the relationship between SC and FC directly. Furthermore, multiscale BNMs use dynamics of neuronal population to model the network node and bridge the gap between neuronal activity such as the averaged firing rate or membrane potential with macroscopic brain dynamics such as FC or dynamical FC. Comparing with descriptive network models, multiscale BNMs can capture the temporal dynamics and multiscale properties of the brain and can be used to reveal the neuronal mechanisms underlying brain functional dynamics through nonlinear dynamical theory. The detailed comparison between multiscale BNMs and descriptive BNM can be found in

Table 1. Comparison between multiscale BNMs and other brain models.

Network Properties	Multiscale BNMs	Descriptive BNMs	DCM
Node Dynamics	Differential equations	NA	Differential equations
Network Connections	SC	SC FC EC	EC
Model Fitting	Static FC Dynamic FC BOLD signals	Static SC Static FC Static EC	Static FC Dynamic FC BOLD signals
Network Size	Large-scale	Large-scale	Relatively small networks
Biophysical Foundation	Firing rate Membrane potential Excitability Inhibitory	NA	NA

.

3.2. Comparison between Multiscale BNMs and Dynamic Causal Modeling

3.2.1. Dynamical Causal Modeling

SC and FC afford useful insights into the structure and dynamics of the brain but they are unidirectional. Another connectivity measure named effective connectivity (EC) refers to the directed interactions among brain regions and can describe how the activity of local network nodes transforms into macroscopic observations [86]. Dynamical causal modeling (DCM) is an analysis method that infers the EC at a single subject level using standard variational Laplace procedures [87,88]. A typical DCM contains a forward model that depicts the dynamics of interacted neuronal populations and a measurement model that transforms the neuronal activity into measurable observations such as fMRI, MEG, or EEG [89]. Additionally, the basic idea behind DCM is that neural activity propagates across brain networks in the order of input-state-output, where causal interactions are modulated by unobservable (hidden) neuronal dynamics [90]. Thus, DCM can be thought of as a generative framework to infer hidden neuronal states from observed neuroimaging data. Taking fMRI for example, DCM describes the dynamics in neuronal activity as a function of the EC between neuronal ensemble in the form:

$$\frac{dx}{dt}=\left(A+{{\displaystyle \sum }}_{j=1}^m{u}_j{B}^{\left(j\right)}\right)x+Cu$$

(6)

where $A$ denotes the network connection in the absence of an endogenous input, B indicates the perturbations of the endogenous input $u$, and $C$ represents how the input directly influences neuronal activity. The above model is coupled to a hemodynamical forward model to simulate BOLD time-series [91,92]. Then, EC can be inferred by the inversion of this generative model through a variational Bayesian approach under the Laplace approximation [93].

The primary DCM application to fMRI is only in small networks (in the order of 10 regions) and cannot scale to large networks for several reasons: First, estimating the likelihood function of DCM requires the integration of Equation (6) and the hemodynamic model, which is computationally costly. Second, the classical DCM deals with the data as a region * time-series vector and the error covariance matrix can become extremely large with increased numbers of regions. Thus, modified DCM is presented, such as the regression DCM. Regression DCM (rDCM) converts the numerically costly parameter estimations in differential equations into an efficiently solvable Bayesian linear regression in the frequency domain, enabling computationally highly efficient model inversion. The rDCM can estimate the EC of networks with more than 66 brain regions and, later, sparse rDCM is presented, which extends the estimated brain regions to large brain-wide numbers [94,95,96].

3.2.2. Comparison

Although DCM and its variants provide valuable analysis for human connectomics, they are inherently linear and have not incorporated more realistic biophysical models, which limits their applications in fundamental neuroscience problems. Multiscale BNMs share some common properties with DCM, such as they both embody a generative form to characterize neuronal dynamics and need a forward model to transform the neuronal activity to a BOLD signal, as well as an optimization scheme to estimate network connections. However, DCMs use a relatively simple bilinear neuronal model, while BNMs utilize more realistic biophysical models. BNMs often use SC as a proxy for a backbone of EC, while DCMs do not need SC necessarily. Besides, DCMs are often limited to smaller networks, while BNMs are used to simulate large-scale whole brain networks [89]. It should be noted that the latest development for DCMs and BNMs, such as the neural mass model-based DCM and multivariate Ornstein-Uhlenbeck-driven BNM, causes a convergence for DCMs and BNMs [89,97,98]. The detailed comparison between multiscale BNMs and DCM can be found in Table 1.

4. Applications of Multiscale BNMs in Understanding Neuropsychiatric Disorders

Advancements in network science and graph theory boost our understanding of the topology and function of the brain. As an effective modeling method for characterizing the structure and function of the brain, multiscale BNMs have provided great expectations for understanding brain disorders at a causal mechanistic level [19]. Many neuroimaging studies have reported altered structural and functional connectivity in brain disorders, but the underlying neuronal mechanisms are still not clear. Multiscale BNMs link the mesoscopic neuronal population to macroscopic functional dynamics through SC and may serve as an effective tool to provide a mechanistic explanation of the neuronal origin of brain dysfunctions. The detailed applications of multiscale BNMs in brain disorders can be found in Table 2.

4.1. Parkinson’s Disease

Parkinson’s disease (PD) is the second most common neurodegenerative disorder in the elderly and is characterized by the degeneration of dopaminergic neurons in the substantia nigra pars compacta with resulting striatal dopaminergic deficiency [99]. The striatum is the largest structure of the basal ganglia and dopaminergic deficiency in it causes a dysfunction within the basal ganglia. Thus, previous studies suggested that the pathophysiology of PD was associated with the local basal ganglia area. With the development of neuroimaging, several studies have shown that large-scale functional networks are affected, leading to different FC patterns when compared to those found in normal controls [100]. Van Hartevelt et al. used whole-brain models to reveal significant recovery of structural network connectivity as a result of deep brain stimulation to alleviate the symptoms of PD [101]. Saenger et al. uncovered the whole-brain dynamics of the deep brain stimulation for PD through a multiscale BNM and offered important insights into the underlying large-scale effects of deep brain stimulation [102]. In fact, in the context of PD, there exist not only local abnormal neuronal oscillations in the basal ganglia, but also large-scale brain dysfunction. Figuring out how local neuronal oscillations effect the large-scale brain functional dynamics across different temporal and spatial scales may provide a pathological understanding for PD and exploit the precise biomarker for PD classification and prediction.

4.2. Alzheimer’s Disease

Alzheimer’s disease (AD) is the most prevalent form of dementia and has become a major concern in developed countries [53]. Various resting-state fMRI studies showed altered FC in AD [103,104]. Multiscale neuronal oscillations are thought to be potential mechanisms of AD’s pathological foundation. Several multiscale BNMs are developed to study the mechanisms of AD such as Demirtas et al., who used a Hopf Normal model as its node dynamics to construct a multiscale BNM and explore the underlying mechanisms of the monotonously decreased synchronization in the whole brain during disease progression, as well as the significantly decreased FC strengths in the brain regions with high global connectivity [53]. Van Nifterick et al. explored whether neuronal hyperexcitability and inhibitory interneuron dysfunction explain large-scale magnetoencephalography activity through a computational network model interacting with 78 neural mass models and their findings indicate that neuronal hyperactivity can lead to slow oscillations [105]. Except for understanding mechanisms, whole-brain models are also used as a test platform for designing optimal network controllers for AD. As in [106], a control theory framework for adjusting the exogenous input that reverts the pathological electroencephalographic activity in AD as a minimal energetic cost is presented based on a multiscale BNM. The BNM is constructed using an anatomical network coupled with Duffing oscillators; then, based on this high-dimensional nonlinear neural system, the state-dependent Riccati equation control method is extended. By considering nonlinearities in the BNM, they identified the top target locations for stimulation in AD and predicted that the patients with low average shortest path lengths and high global efficiency in anatomical networks were the most suitable candidates for the propagation of stimuli and success on the control task [106].

4.3. Schizophrenia

Schizophrenia is a group of brain disorders thought to involve large-scale dysconnectivity as well as alterations in local cortical excitation-inhibition physiology [107,108,109,110]. Computational models that bridge from the level of synapses and neurons to that of spatiotemporal dynamics in distributed brain systems are very suited to explore this disease [37]. Cabral et al. used SC matrices combined with asynchronous attractors to analyze a multiscale model to examine how SC impacts functional dysconnectivity in Schizophrenia. Their studies suggest that FC is shaped by more than SC and that synaptic disruptions may play a profound role in disease-related dysconnectivity [111]. Yang et al. studied the large-scale impact of alterations in the excitation-inhibition ratio in cortical circuits on resting-state fMRI biomarkers in Schizophrenia based on a multiscale BNM and found that increased effective strength of connectivity at either the local or the long-range level would result in an elevated excitation-inhibition ratio that can capture the elevated local and global neural variability in Schizophrenia [112,113,114,115]. Anticevic et al. used multiscale models to identify the role for glutamate in establishing large-scale functional patterns related with Schizophrenia [116]. Zhang et al. used generative BNM to identify biological mechanisms of altered structural brain connectivity and suggested that spatial constraints and local topological structures are two interrelated mechanisms contributing to altered connectomes in Schizophrenia [117].

Table 2. Applications of multiscale BNMs in some brain disorders.

References	Node Dynamics	Parcellation	Model Fitting	SC Data	Diseases
Saenger et al. [102]	Normal form of Hopf	AAL atlas 90 regions	Static and dynamical FC, fMRI data	DTI	Parkinson
Van Nifterick et al. [105]	NMMs	AAL atlas 78 regions	Power spectrum, MEG data	DTI	Alzheimer
Sanchez-Rodriguez et al. [106]	Duffing oscillator	DK atlas 78 regions	Spectral measures, EEG data	DWI, T1-weighted MRIs	Alzheimer
Cabral et al. [111]	Mean-field approximation of IF models *	AAL atlas 90 regions	Static FC fMRI data	DTI	Schizophrenia
Yang et al. [112,113] Anticevic et al. [114], Cole et al. [115]	Mean-field models	66 regions	Static FC fMRI data	DWI	Schizophrenia

* IF models: Integrate-and-Fire models.

Table 2. Applications of multiscale BNMs in some brain disorders.

References	Node Dynamics	Parcellation	Model Fitting	SC Data	Diseases
Saenger et al. [102]	Normal form of Hopf	AAL atlas 90 regions	Static and dynamical FC, fMRI data	DTI	Parkinson
Van Nifterick et al. [105]	NMMs	AAL atlas 78 regions	Power spectrum, MEG data	DTI	Alzheimer
Sanchez-Rodriguez et al. [106]	Duffing oscillator	DK atlas 78 regions	Spectral measures, EEG data	DWI, T1-weighted MRIs	Alzheimer
Cabral et al. [111]	Mean-field approximation of IF models *	AAL atlas 90 regions	Static FC fMRI data	DTI	Schizophrenia
Yang et al. [112,113] Anticevic et al. [114], Cole et al. [115]	Mean-field models	66 regions	Static FC fMRI data	DWI	Schizophrenia

* IF models: Integrate-and-Fire models.

5. Discussion

5.1. Limitations

Multiscale BNMs have proven to be an effective tool to simulate brain dynamics and understand the mechanisms of brain disorders. The modeling pipeline mainly includes the estimation of structural matrices, selection of node dynamics, and model fitting to empirical data to find optimal model parameters. Thus far, there is no common rule for selecting a particular type of connectivity or mathematical equation when constructing multiscale models. Additionally, the specific models are related to the problem at hand, the background of the researchers, and the types of available data [118]. So, there still exist some challenges to construct optimal multiscale BNMs when confronted with specific problems. Knowing the brain parcellation before estimating the SC is of great importance because the level of parcellation granularity may strongly impact the topological properties of SC [27], meanwhile the multiscale BNMs are sensitive to the underlying network structure [119]. As mentioned above, the currently popular parcellations of brain regions include the Desikan-Killiany atlas or Hagmann atlas with 66 cortical regions and the automated anatomical labelling atlas with 116 regions [27,120,121]. Proix et al. suggested that under certain sets of assumptions, an atlas with approximately 140 brain regions may produce a good agreement with empirical data [122]. However, the proper choice of parcellation depends on many factors and the optimal parcellation of brain regions is not currently clear [123]. Fortunately, multiscale BNMs provide a test platform to compare the effects of different parcellation atlases on simulated brain dynamics; thus, in future modeling investigations, the effects of brain parcellation should be compared in advance.

The homogeneous node dynamics and coupling strength between nodes are used in most multiscale BNMs, but studies suggested that the hierarchical heterogeneity of local circuit parameters improves the fit of empirical FC compared with the homogeneous model or SC [37]. Heterogeneity in node dynamics can be introduced by assigning multiple oscillatory frequencies [32], while heterogeneity in SC is seldom explored. When constructing connectomes, a previous tractography analysis was performed to indicate the existence or absence of inter-areal connections. Typically, it is performed by selecting a threshold such that all the edges smaller than the threshold are set to zero or are otherwise set to one. However, determining an appropriate threshold is not straightforward and is often arbitrary, which makes such a binarized version an oversimplification not capable of reflecting the known heterogeneous distribution of fiber connection densities [124]. With the advancement in tractography techniques, such as tractogram filtering or microstructure-informed tractogram reconstruction, weighted connectomes are increasingly adopted as they can encode more biological features and offer more biological meaningful information [125,126,127,128,129]. On the other hand, currently one framework named dynamical neural model can estimate the SC using direct parameterization. Without prior SC information, one can obtain the SC using model inversion from the fMRI data. For example, Singh et al. presented the Mesoscale Individualized Neurodynamic (MINDy) modeling method to fit nonlinear dynamical neural models directly to fMRI data [130] and Li et al. used a Genetic algorithm to constitute a Multiscale Neural Model Inversion framework to infer the network connection [131]. Additionally, Sip et al. utilized the framework of amortized variational inference (variational autoencoders) to infer both the node dynamics and spatial heterogeneity [132]. All of these methods provide new solutions for SC heterogeneity.

Most multiscale BNMs utilize noise as a node input and are motivated by experimental findings that indicated that the envelope of the amplitudes of alpha and beta frequency oscillations of the electrophysiological signals exhibit correlation patterns similar to those fMRI signals at slow time scales [133,134], Schirner et al. presented a hybrid multiscale BNM that uses EEG as a source activity to be input into each node in the BNM [62]. Based on Schirner’s hybrid BNM, Rabuffo et al. presented neuronal cascades as the underlying neuronal underpinning of the whole-brain resting-state functional dynamics [135]. The hybrid BNM bridges the gap between the electrophysiology and neuroimages, which is promising in understanding neuronal mechanisms underlying fMRI dynamics. However, the fusion of the EEG and fMRI is in a simple way and, as we know, there are several ways to integrate EEG and fMRI. A more plausible fusion of EEG and fMRI should be introduced to multiscale BNMs [136,137,138].

5.2. Future Directions

Multiscale BNMs have proven an enormous potential for exploring neuronal mechanisms underlying large-scale brain functions. In neuroscience, understanding principles of the brain is not our ultimate aim, instead we aim to regulate the brain to enhance cognitive functions or improve neuropsychiatric diseases. Thus, models are not only for understanding information processing mechanisms of the brain, but also for exploring optimal brain stimulation techniques, including deep brain stimulation, transcranial direct current stimulation, intracranial cortical stimulation, and transcranial magnetic stimulation et al. [139,140,141,142]. To do this, multiscale BNMs should be combined with control theory to provide an in silico testbed for exploring and evaluating the efficacy of control strategies. In the context of control theory, the averaged firing rate or membrane potential of BNMs are considered as state variables of the system and the forward function (e.g., hemodynamical response function) is thought of as a measured function to map the state variables into the output of the system. The combination of control theory and neural networks produces network control theory; within this framework, the control properties of networks are very important for deciding whether or not certain networks can be controlled. Some metrics including average controllability, modal controllability, and so on should be estimated preceding the control application [143,144,145,146,147]. However, we have to note that the controllability metrics are based on the linearization of nonlinear systems, while the BNMs are nonlinear system that cannot be quantified by controllability. Thus, in the future, the BNMs should be improved to be more appropriate for network control theory through emerging neural technology and advances in numerical optimization [148] such as the system identification method presented in [149]. System identification methods have been successfully applied in areas where the fundamental mechanistic principles across variables are known [150,151]. However, in the brain, the high-dimensional measurements potentially affected by some hidden variables. Considering this, the combination of BNMs and system identification is likely to become a promising research area in the future.

6. Conclusions

With the rapid development of advanced neuroimaging, models from the whole-brain level have attracted more and more attention. The connectome is one of those results boosted by advanced neuroimaging techniques. Within this framework, the structure and function of the brain is described by SC and FC derived from neuroimaging data. Initial descriptive whole-brain models only consider SC or FC independently and statically and therefore cannot capture the dynamical properties of brain functions or the relationship between SC and FC. Recently, multiscale BNMs, also named communication models, generative models, mechanistic models, or whole-brain computational models in other literature, are gaining more attention. Although their applications are not widely developed, they indeed manifest great expectations for understanding the mechanisms of large-scale brain dynamics. In this brief review, we introduced a pipeline for implementing a multiscale BNM including the estimation of connections, choice of node dynamics, and model fitting. Furthermore, we put an emphasis on a machine learning (deep learning) application on the modeling fitting. Actually, some traditional machine learning algorithms, such as the Genetic Algorithm, are also applied in the parameter optimization process of multiscale BNMs and have exhibited excellent effects. We believe that in the development of BNMs, more and more intelligent algorithms will be applied to the parameter optimization of models, which will produce more biophysically meaningful models. At last, we compare multiscale BNMs with some popular brain models and present future developments. We think that combining the multiscale BNMs with control theory will provide a better potential for understanding cognitive and brain diseases as well as developing more effective and personalized treatments for neurological and psychiatric diseases.