Stability Analysis for Linear Systems with a Differentiable Time-Varying Delay via Auxiliary Equation-Based Method
Abstract
:1. Introduction
- (1)
- Motivated by the method in [33], the auxiliary equation is utilized to investigate the stability of the systems with a differentiable time-varying delay, and thus the information of delay derivative can be captured well and be used to derive a less conservative stability condition.
- (2)
- Inspired by the fact that , two state augmented zero equalities are introduced, which can help reduce the conservatism of the obtained stability condition.
- (3)
- On the basis of the system equation and the auxiliary equation, a new delay-product-type augmented LKF is constructed, which can utilize more system information, such as , and . Then, based on the LKF and by employing some vital lemmas, adding zero terms, and the convex analysis method, a relaxed stability condition is proposed. Finally, to illustrate the merit of the obtained stability condition, two typical numerical examples are given.
2. Problem Statement and Preliminaries
3. Stability Conditions
| Algorithm 1: Obtaining the optimal value of h based on Theorem 1 or Corollary 1. |
|
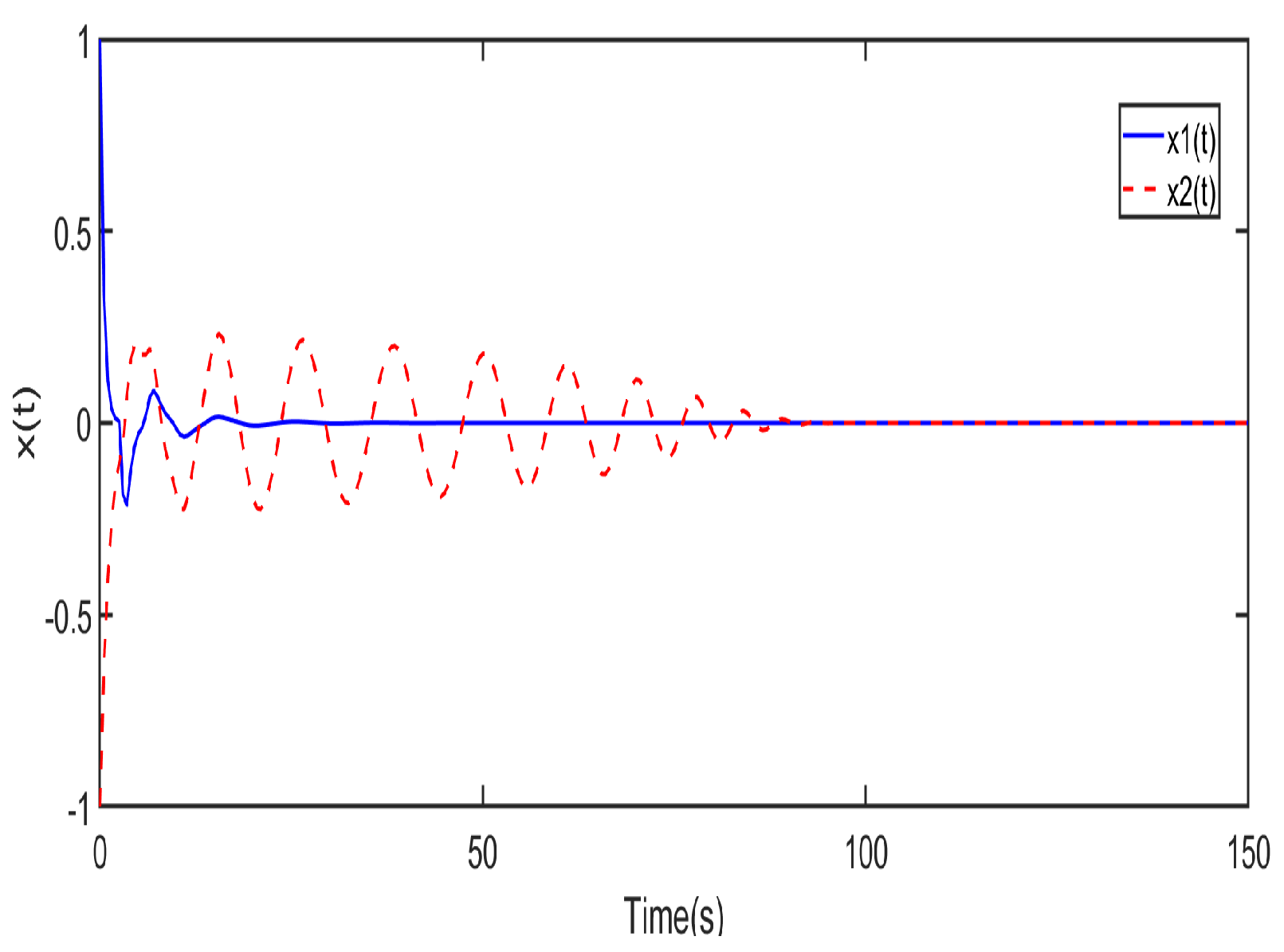
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gu, K.; Kharitonov, V.L.; Chen, J. Stability of Time-Delay Systems; Birkhäuser: Boston, MA, USA, 2003. [Google Scholar]
- Zhang, B.L.; Cheng, L.H.; Pan, K.J.; Zhang, X.M. Reducing conservatism of stability criteria for linear systems with time-varying delay using an improved triple-integral inequality. Appl. Math. Comput. 2020, 380, 125254. [Google Scholar] [CrossRef]
- Oliveira, D.; Fulvia, S.S.; Souza, F.O. Further refinements in stability conditions for time-varying delay systems. Appl. Math. Comput. 2020, 380, 124866. [Google Scholar] [CrossRef]
- Zhang, A.L.; Lin, Z.Y.; Wang, B.; Han, Z.M. Nonlinear model predictive control of single-link flexible-joint robot using recurrent neural network and differential evolution optimization. Electronics 2021, 10, 2426. [Google Scholar] [CrossRef]
- Zhang, X.M.; Han, Q.L.; Seuret, A.; Gouaisbaut, F. An improved reciprocally convex inequality and an augmented Lyapunov-Krasovskii functional for stability of linear systems with time-varying delay. Automatica 2017, 84, 221–226. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Liu, G.P.; Chen, J. Improved delay-range-dependent stability criteria for linear systems with time-varying delays. Automatica 2010, 46, 466–470. [Google Scholar] [CrossRef]
- Zhang, X.M.; Han, Q.L.; Seuret, A.; Gouaisbaut, F.; He, Y. Overview of recent advances in stability of linear systems with time-varying delays. IET Control Theory Appl. 2019, 13, 1–19. [Google Scholar] [CrossRef]
- Zeng, H.B.; Zhai, Z.L.; Wang, W. Hierarchical stability conditions of systems with time-varying delay. Appl. Math. Comput. 2021, 404, 126222. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Liu, H.B.; Li, X. A novel method for stability analysis of time-varying delay systems. IEEE Trans. Autom. Control 2021, 66, 1422–1428. [Google Scholar] [CrossRef]
- Sun, Y.; Li, N.; Shen, M.; Wei, Z.; Sun, G. Robust H∞ control of uncertain linear system with interval time-varying delays by using Wirtinger inequality. Appl. Math. Comput. 2018, 335, 1–11. [Google Scholar] [CrossRef]
- Chen, G.L.; Xia, J.W.; Zhang, Z.W.; Zhao, J.S. Improved delay-dependent stabilization for a class of networked control systems with nonlinear perturbations and two delay components. Appl. Math. Comput. 2018, 316, 1–17. [Google Scholar] [CrossRef]
- Park, M.J.; Kwon, O.M.; Park, J.H.; Lee, S.M.; Cha, E.J. Stability of time-delay systems via Wirtinger-based double integral inequality. Automatica 2015, 55, 204–208. [Google Scholar] [CrossRef]
- Jiang, X.F.; Yin, Z.M.; Wu, J.J. Stability analysis of linear systems under time-varying samplings by a non-standard discretization method. Electronics 2018, 7, 278. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.C.; Yan, H.C.; Peng, Y.; Park, J.H. Stability analysis of linear systems with time-varying delay via intermediate polynomial-based functions. Automatica 2020, 113, 108756. [Google Scholar] [CrossRef]
- Li, Z.C.; Yan, H.C.; Zhang, H.; Zhan, X.S. Huang, C.Z. Improved inequality based functions approach for stability analysis of time delay system. Automatica 2019, 108, 108416. [Google Scholar] [CrossRef]
- Zhang, X.M.; Han, Q.L.; Ge, X.H. Novel stability criteria for linear time-delay systems using Lyapunov-Krasovskii functionals with a cubic polynomial on time-varying delay. IEEE/CAA J. Autom. Sin. 2021, 8, 77–85. [Google Scholar] [CrossRef]
- Lin, H.C.; Zeng, H.B.; Wang, W. New Lyapunov-Krasovskii functional for stability analysis of linear systems with time-varying delay. J. Syst. Sci. Complex. 2021, 34, 632–641. [Google Scholar] [CrossRef]
- Kwon, O.M.; Lee, S.H.; Park, M.J. Some novel results on stability analysis of generalized neural networks with time-varying delays via augmented approach. IEEE Trans. Cybern. 2022, 52, 2238–2248. [Google Scholar] [CrossRef]
- Zhang, C.K.; He, Y.; Jiang, L.; Wu, M. Notes on stability of time-delay systems: Bounding inequalities and augmented Lyapunov-Krasovskii functional. IEEE Trans. Autom. Control 2017, 62, 5331–5336. [Google Scholar] [CrossRef] [Green Version]
- Lian, Z.; He, Y.; Zhang, C.K.; Shi, P.; Wu, M. Robust H∞ control for T-S fuzzy systems with state and input time-varying delays via delay-product-type functional method. IEEE Trans. Autom. Control 2019, 27, 1917–1930. [Google Scholar] [CrossRef]
- Lee, S.Y.; Lee, W.; Park, P.G. Improved stability criteria for linear systems with interval time-varying delays: Generalized zero equalities approach. Appl. Math. Comput. 2017, 292, 336–348. [Google Scholar] [CrossRef]
- Xiong, L.X.; Cheng, J.; Cao, J.D.; Liu, Z.X. Novel inequality with application to improve the stability criterion for dynamical systems with two additive time-varying delays. Appl. Math. Comput. 2018, 321, 672–688. [Google Scholar] [CrossRef]
- Zhang, R.M.; Zeng, D.Q.; Park, J.H.; Zhong, S.M.; Liu, Y.J.; Zhou, X. New approaches to stability analysis for time-varying delay systems. J. Frankl. Inst. 2019, 356, 4174–4189. [Google Scholar] [CrossRef]
- Seuret, A.; Gouaisbaut, F. Wirtinger-based integral inequality: Application to time-delay systems. Automatica 2013, 49, 2860–2866. [Google Scholar] [CrossRef] [Green Version]
- Seuret, A.; Gouaisbaut, F. Hierarchy of LMI conditions for the stability analysis of time-delay systems. Syst. Control Lett. 2015, 81, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Park, P.; Lee, W.I.; Lee, S.Y. Auxiliary function-based integral inequalities for quadratic functions and their applications to time-delay systems. J. Frankl. Inst. 2015, 352, 1378–1396. [Google Scholar] [CrossRef]
- Zeng, H.B.; He, Y.; Wu, M.; She, J.H. Free-matrix-based integral inequality for stability analysis of systems with time-varying delay. IEEE Trans. Autom. Control 2015, 60, 2768–2772. [Google Scholar] [CrossRef]
- Chen, J.; Xu, S.Y.; Zhang, B.Y. Single/multiple integral inequalities with applications to stability analysis of time-delay systems. IEEE Trans. Autom. Control 2017, 62, 3488–3493. [Google Scholar] [CrossRef]
- Zhang, X.M.; Han, Q.L.; Zeng, Z.G. Hierarchical type stability criteria for delayed neural networks via canonical Bessel-Legendre inequalities. IEEE Trans. Cybern. 2018, 48, 1660–1671. [Google Scholar] [CrossRef]
- Zhang, C.K.; He, Y.; Jiang, L.; Wu, M.; Wang, Q.C. An extended reciprocally convex matrix inequality for stability analysis of systems with time-varying delay. Automatica 2017, 85, 481–485. [Google Scholar] [CrossRef]
- Kwon, O.M.; Lee, S.H.; Park, M.J.; Lee, S.M. Augmented zero equality approach to stability for linear systems with time-varying delay. Appl. Math. Comput. 2020, 381, 125329. [Google Scholar] [CrossRef]
- Park, M.J.; Kwon, O.M.; Ryu, J.H. Advanced stability criteria for linear systems with time-varying delays. J. Frankl. Inst. 2018, 355, 520–543. [Google Scholar] [CrossRef]
- Zhi, Y.L.; He, Y.; Wu, M. Improved free matrix-based integral inequality for stability of systems with time-varying delay. IET Control Theory Appl. 2017, 11, 1571–1577. [Google Scholar] [CrossRef]
- Zhao, X.; Lin, C.; Chen, B.; Wang, Q.G. Stability analysis for linear time-delay systems using new inequality based on the second-order derivative. J. Frankl. Inst. 2019, 356, 8770–8784. [Google Scholar] [CrossRef]
- Souza, F.O. Critical frequencies of controlled second-order linear systems with delayed feedback. Mech. Syst. Signal Pr. 2022, 166, 108384. [Google Scholar] [CrossRef]
- Zhang, J.F.; Ouyang, H.J.; Zhang, K.E.; Liu, H.M. Stability test and dominant eigenvalues computation for second-order linear systems with multiple time-delays using receptance method. Mech. Syst. Signal Pr. 2020, 137, 106180. [Google Scholar] [CrossRef]
- Park, P.G.; Wan, K.J.; Changki, J. Reciprocally convex approach to stability of systems with time-varying delays. Automatica 2011, 47, 235–238. [Google Scholar] [CrossRef]
- Briat, C. Convergence and equivalence results for the Jensen’s inequality-application to time-delay and sampled-data systems. IEEE Trans. Autom. Control 2011, 56, 1660–1665. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.M. Study on Delay-Dependent Robust Control Based on an Integral Inequality Approach; Central South University: Changsha, China, 2006. [Google Scholar]
- Yin, Z.M.; Jiang, X.F.; Tang, L.; Wu, J.J. On stability and stabilization of T-S fuzzy systems with multiple random variables dependent time-varying delay. Neurocomputing 2020, 412, 91–100. [Google Scholar] [CrossRef]
- Yin, Z.M.; Jiang, X.F. Delay-derivative/distribution dependent stability and stabilization criteria for T-S fuzzy systems with random time-varying delay. IEEE Trans. Fuzzy Syst. 2022; to be published. [Google Scholar] [CrossRef]
- Long, F.; Zhang, C.H.; Jiang, L.; He, Y.; Wu, M. Stability analysis of systems with time-varying delay via improved Lyapunov-Krasovskii functionals. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 2457–2466. [Google Scholar] [CrossRef]
- Long, F.; Jiang, L.; He, Y.; Wu, M. Stability analysis of systems with time-varying delay via novel augmented Lyapunov-Krasovskii functionals and an improved integral inequality. Appl. Math. Comput. 2019, 357, 325–337. [Google Scholar] [CrossRef]
- Zeng, H.B.; Lin, H.C.; He, Y.; Zhang, C.K.; Teo, K.L. Improved negativity condition for a quadratic function and its application to systems with time-varying delay. IET Control Theory Appl. 2020, 14, 2989–2993. [Google Scholar] [CrossRef]
- Seuret, A.; Gouaisbaut, F. Stability of linear systems with time-varying delays using Bessel-Legendre inequalities. IEEE Trans. Autom. Control 2018, 63, 225–232. [Google Scholar] [CrossRef] [Green Version]
- Lee, T.H.; Park, J.H.; Xu, S. Relaxed conditions for stability of time-varying delay systems. Automatica 2017, 75, 11–15. [Google Scholar] [CrossRef]

| Methods/ | 0.1 | 0.5 | 0.8 | NoDVs |
|---|---|---|---|---|
| Theorem 3 [23] | 4.8562 | 3.1831 | 2.7391 | |
| Theorem 1 [14] | 4.867 | 3.12 | – | |
| Theorem 2(C1) [42] | 4.940 | 3.304 | 2.877 | |
| Theorem 1 [43] | 4.945 | 3.314 | 2.882 | |
| Corollary 1(II) [44] | 4.966 | 3.395 | 2.983 | |
| Theorem 1 [15] | 4.996 | 3.251 | 2.867 | |
| Theorem 8 (N = 4) [45] | 5.01 | 3.19 | 2.70 | |
| Corollary 1 | 4.8662 | 3.3349 | 2.9886 | |
| Theorem 1 | 5.0213 | 3.6032 | 3.2235 |
| Methods/ | 0.2 | 0.5 | 0.8 | NoDVs |
|---|---|---|---|---|
| Theorem 1 [46] | 4.5179 | 2.4158 | 1.8384 | |
| Theorem 3 [23] | 4.6380 | 2.5898 | 2.0060 | |
| Corollary 1(II) [44] | 4.947 | 2.801 | 2.137 | |
| Corollary 2 [3] | 4.969 | 2.774 | 2.117 | |
| Theorem 2 (N = 5) [8] | 4.985 | 2.806 | 2.148 | |
| Theorem 2 [17] | 4.997 | 2.814 | 2.149 | |
| Theorem 1 [2] | 5.0035 | 2.8096 | 2.1499 | |
| Corollary 1 | 4.9481 | 3.1531 | 2.7024 | |
| Theorem 1 | 5.1073 | 3.3984 | 2.9053 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, Z.; Jiang, X.; Zhang, N.; Zhang, W. Stability Analysis for Linear Systems with a Differentiable Time-Varying Delay via Auxiliary Equation-Based Method. Electronics 2022, 11, 3492. https://doi.org/10.3390/electronics11213492
Yin Z, Jiang X, Zhang N, Zhang W. Stability Analysis for Linear Systems with a Differentiable Time-Varying Delay via Auxiliary Equation-Based Method. Electronics. 2022; 11(21):3492. https://doi.org/10.3390/electronics11213492
Chicago/Turabian StyleYin, Zongming, Xiefu Jiang, Ning Zhang, and Weihua Zhang. 2022. "Stability Analysis for Linear Systems with a Differentiable Time-Varying Delay via Auxiliary Equation-Based Method" Electronics 11, no. 21: 3492. https://doi.org/10.3390/electronics11213492
APA StyleYin, Z., Jiang, X., Zhang, N., & Zhang, W. (2022). Stability Analysis for Linear Systems with a Differentiable Time-Varying Delay via Auxiliary Equation-Based Method. Electronics, 11(21), 3492. https://doi.org/10.3390/electronics11213492













