The MIMO Radar Transmit Beampattern Matching Design with Sidelobe Suppression

Abstract

In this paper, a novel method termed the cosine approach is proposed to address the sidelobe suppression problem in MIMO radar transmit beampattern matching design. In contrast to the traditional optimization algorithms that try to find the optimum solutions from feasible regions, the proposed method, starting from outside the feasible regions, aims to obtain a satisfactory solution from a series of optimal transmit beampatterns. We first standardized the sidelobe suppression problem in MIMO radar transmit beampattern matching design and put forward four criteria to guide the micro-adjustment to the desired beampattern. Then, the cosine method was proposed to adjust the desired beampattern as well as increase the main-to-sidelobe ratio (MSLR) of the transmit beampattern. Finally, several numerical examples were chosen to test the effectiveness and advantages of the proposed method.

1. Introduction

In attempts to solve the MIMO radar transmit beampattern matching design problem, many optimal algorithms have been developed to obtain transmit signals [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33], such as the gradient search algorithms [1,2], semi-definite programming algorithm [3,4,14,20], convex optimization techniques [5,23], cyclic minimization algorithm [6,7,9,10,11], and transmit beamspace processing techniques [8,12,13]. Although all these methods provide a comparatively good match to the desired beampattern, high sidelobes may still appear because the number of element positions is limited, or the desired beampattern cannot be expanded with finite Fourier series. Thus, it has become a challenge to design transmit signals to satisfy the constraint of the main-to-sidelobe ratio (i.e., the ratio of the maximum peak values of main lobe to sidelobe) as well as to match the desired beampattern as perfectly as possible.

Recently, several methods have been put forward to address the sidelobe suppression problem [29,34,35,36,37,38,39], in which various optimal models are established with the objective of reducing sidelobe peaks. In contrast with these optimal models, sidelobe suppression in transmit beampattern matching designs aims to minimize the errors between the desired and the transmit beampatterns, while accepting the constraint of the sidelobe. Thus far, there has been little discussion of this issue in the literature. Li and Stocia [3] provided a weighted optimization model to reduce the sidelobe peak in a MIMO radar transmit beampattern matching design; Hua and Abeysekera [22] developed another weighted optimization model to control the ripple levels within the energy focusing section and the transition bandwidth. However, in these approaches it is difficult to determine the weights, making it hard to balance the sidelobe suppression and the error between the desired and the transmit beampatterns.

In this paper, we propose a novel method termed the cosine method to address the sidelobe suppression problem in MIMO radar transmit beampattern matching design. Through matching the continually micro-adjusted desired beampattern, the final transmit beampattern can not only provide relatively good matching to the original desired beampattern but also has higher MSLR. In contrast to the traditional optimization algorithms which try to find the optimum solutions from feasible regions, the proposed cosine method, starting from the outside of a feasible region, obtains a satisfactory solution from a series of optimal transmit beampatterns.

This paper is organized as follows: Section 2 introduces the sidelobe suppression problem in transmit beampattern matching design, and establishes a sidelobe suppression model; Section 3 discusses the cosine method in detail, including its theoretical analysis and algorithm; Section 4 provides several examples to test the practicability and efficiency of the proposed method and conclusions are drawn in Section 5.

The notations in this paper are standard: ${(\cdot )}^T$ represents the transpose of a matrix or vector, ${(\cdot )}^H$ is the conjugate transpose of a matrix or vector, $E(\cdot )$ denotes the statistical expectation, and $\Vert \cdot \Vert$ means the Euclidean norm of a vector.

2. Sidelobe Suppression Model

Consider an M-element uniform linear array (ULA) with inter-element spacing $d=\lambda /2$ in a MIMO radar system and targets at the far field of the array. The transmit signals are defined as

$$S={\left[\begin{array}{cccc}{s}_1& s_2& \cdots & s_M\end{array}\right]}^T$$

(1)

where $s_m\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left(m=1,2,\dots ,M\right)$ means the mth transmit signal with the power equal to 1. The beampattern of $S$ can be written as

$$P\left(\varphi \right)=a^H\left(\varphi \right)Ra\left(\varphi \right)$$

(2)

where the steering vector $a\left(\varphi \right)$ is given by

$$a\left(\varphi \right)={\left[1,e^{-j\varphi },e^{-j2\varphi },\cdots ,e^{-j\left(M-1\right)\varphi }\right]}^T,\varphi =2\pi d\sin \theta /\lambda$$

(3)

where $\theta$ denotes the azimuth angle and $\theta \in \left[-\pi /2,\hspace{0.17em}\pi /2\right]$. The correlation matrix $R$ of $S$ can be written as

$$R=E\left[S*S^H\right]={\left[r_{m,n}\right]}_{M\times M}$$

(4)

where $R$ satisfies

$$R=R^H\hspace{0.17em}\Vert r_{mn}\Vert \le 1,\hspace{0.17em}{r}_{nn}=1;\hspace{0.17em}m,n=1,2,\cdots ,M$$

(5)

The sidelobe suppression problem in MIMO radar transmit beampattern matching design can be expressed as follows:

On condition of fixed transmit element positions and constant transmit energy for each element, and given a desired beampattern $\tilde{P}\left(\varphi \right)$ and sidelobe constraint (MSLR > $\delta$ dB), how can we produce the transmit signal $S$, making the transmit beampattern generated by $S$ match the desired beampattern $\tilde{P}\left(\varphi \right)$ as closely as possible? We may standardize this sidelobe suppression problem using the following model:

$$\left(\mathrm{I}\right)\{\begin{array}{l}\underset{S}{\min }\hspace{0.17em}{\displaystyle {\int }_{-\pi }^{\pi }{\left[a^H\left(\varphi \right)E\left[\left(S\ast S^H\right)\right]\hspace{0.17em}a\left(\varphi \right)-\tilde{P}\left(\varphi \right)\right]}^{2}d\varphi }\\ s.t.\\ s_n\cdot s_n^H=1,n=1,2,\cdots ,M\\ MSLR>\delta \hspace{0.17em}\mathrm{dB}\end{array}$$

3. Cosine Method for Sidelobe Suppression

For Model (I), due to the main lobe broadening in the solving process, it is often difficult to identify its feasible region. In this section, we propose a novel method, namely the cosine method, to obtain a satisfactory solution. The iterative method includes 3 steps:

Step 1:

Make the micro-adjustment to the desired beampattern to obtain a new desired beampattern;

Step 2:

Provide a minimum mean square error matching the new desired beampattern and obtain an optimal transmit beampattern;

Step 3:

Calculate the MSLR of the transmit beampattern. If it is not meet the MSLR constraint, go back to Step 1.

Indeed, since [27] has provided a minimum mean square approximation of the desired beampattern, our cosine method focuses on how to make the micro-adjustment to the desired beampattern. In the following sections, we will explain how to achieve this adjustment.

3.1. Criteria for Micro-Adjustment to the Desired Beampattern

The purpose of continual micro-adjustments to the desired beampattern is to ensure the final transmit beampattern not only has a relatively good match to the original desired beampattern, but also a higher MSLR. Therefore, the slightly adjusted desired beampattern should not only meet the basic requirements of the desired beampattern [27], but also meet the basic properties of the transmit beampattern. To guide these adjustments, we provide the following four criteria:

• $\widehat{P}\left(\varphi \right)\ge 0$;
• $\frac{1}{2\pi }{\displaystyle {\int }_{-\pi }^{\pi }\widehat{P}\left(\varphi \right)d\varphi }=M$;
• $\widehat{P}\left(\varphi \right)$ should be continuous and exists first order derivative;
• $\underset{M\to +\infty }{\lim }\frac{1}{2\pi }{\displaystyle {\int }_{-\pi }^{\pi }{\left[\tilde{P}\left(\varphi \right)-\widehat{P}\left(\varphi \right)\right]}^{2}d\varphi }=0$.

Where $\widehat{P}\left(\varphi \right)$ is micro-adjustments to the desired beampattern $\tilde{P}\left(\varphi \right)$. The criteria 1–2 derive from the basic requirements of the desired beampattern [27]; criteria 3 derives from the transmit beampattern that can be expanded with finite Fourier series; as M increases, the mean square error between transmit beampattern and $\tilde{P}\left(\varphi \right)$ will tend to zero, so we have criteria 4. In order to obtain a good matching transmit beampattern with higher MSLR, all four criteria are necessary for the micro-adjustment to the desired beampattern.

According to the above four criteria, we may find many approaches to adjust the desired beampattern. Among them, Fourier expansion is often used as an approximation to a function. Let the Fourier expansion of the desired beampattern $\tilde{P}\left(\varphi \right)$ be

$$\tilde{P}\left(\varphi \right)=a_0+{\displaystyle \sum _{k=1}^{+\infty }{a}_k\cos k\varphi +b_k\sin k\varphi }$$

(6)

Then the sum of the first M items is

$$\tilde{F}\left(\varphi \right)=a_0+{\displaystyle \sum _{k=1}^{M-1}{a}_k\cos k\varphi +b_k\sin k\varphi }$$

(7)

For $\tilde{F}\left(\varphi \right)$, we have the following conclusion:

Lemma 1. 

[40]: Let $\tilde{F}\left(\varphi \right)$ be the sum of the first M items of the Fourier expansions for the desired beampattern $\tilde{P}\left(\varphi \right)$, and $T\left(\varphi \right)$ be the arbitrary M-1 trigonometric polynomial, i.e.,

$$T\left(\varphi \right)=A_0+2{\displaystyle \sum _{k=1}^{M-1}{A}_k\cos k\varphi +B_k\sin k\varphi }$$

then we have

$${\delta }^2\left(\tilde{P},\tilde{F}\right)\le {\delta }^2\left(\tilde{P},T\right)$$

where

$${\delta }^2\left(\tilde{P},T\right)=\frac{1}{2\pi }{\displaystyle {\int }_{-\pi }^{\pi }{\left[\tilde{P}\left(\varphi \right)-T\left(\varphi \right)\right]}^{2}d\varphi }$$

Lemma 1 shows that $\tilde{F}\left(\varphi \right)$ is the minimum mean square approximation to $\tilde{P}\left(\varphi \right)$ in all M-1 trigonometric polynomial. It is obvious that $\tilde{F}\left(\varphi \right)$ satisfies criteria 2–4. However, according to [27], the desired beampattern $\tilde{P}\left(\varphi \right)$ and its finite Fourier expansion $\tilde{F}\left(\varphi \right)$ have the same optimal transmit beampattern $P\left(\varphi \right)$. Therefore, if $P\left(\varphi \right)$ cannot satisfy the MSLR constraint, we need to explore other approach to increase MSLR as well as meet the four criteria.

3.2. Cosine Method

In this study, a novel method termed the cosine method is proposed to make the micro-adjustment to the desired beampattern.

First, we identify the largest bias point ${\varphi }^{*}$ between the transmit beampattern $P\left(\varphi \right)$ and the desired beampattern $\tilde{P}\left(\varphi \right)$, i.e.,

$$\left|P\left({\varphi }^{*}\right)-\tilde{P}\left({\varphi }^{*}\right)\right|=\underset{-\pi \le \varphi \le \pi }{\max }\left|P\left(\varphi \right)-\tilde{P}\left(\varphi \right)\right|$$

(8)

where $P\left(\varphi \right)$ is the minimum mean square matching design of $\tilde{P}\left(\varphi \right)$ [27].

Then, we select the maximum monotone interval $\left[\alpha ,\hspace{0.17em}\beta \right]$ within ${\varphi }^{*}$ satisfying

$${\tilde{F}}^{\prime }\left(\alpha \right)={\tilde{F}}^{\prime }\left(\beta \right)=0,\hspace{0.17em}{\varphi }^{*}\in \left[\alpha ,\hspace{0.17em}\beta \right]$$

(9)

Finally, we use $\tilde{F}\left(\varphi \right)$ in $\left[\alpha ,\hspace{0.17em}\beta \right]$ to replace the corresponding part of $\tilde{P}\left(\varphi \right)$ as follows:

(a) In the case of ${\varphi }^{*}\in \left(\alpha ,\hspace{0.17em}\beta \right)$, we use $\tilde{F}\left(\varphi \right)$ in $\left[\alpha ,\hspace{0.17em}\beta \right]$ to replace the corresponding part of the desired beampattern $\tilde{P}\left(\varphi \right)$. Then the adjusted desired beampattern $\overline{P}\left(\varphi \right)$ is

$$\overline{P}\left(\varphi \right)=\{\begin{array}{cc}\frac{\tilde{P}\left(\beta \right)-\tilde{P}\left(\alpha \right)}{\tilde{F}\left(\beta \right)-\tilde{F}\left(\alpha \right)}\left[\tilde{F}\left(\varphi \right)-\tilde{F}\left(\alpha \right)\right]+\tilde{P}\left(\alpha \right)& \varphi \in \left[\alpha ,\beta \right]\\ \tilde{P}\left(\varphi \right)& \varphi \notin \left[\alpha ,\beta \right]\end{array}$$

(10)

(b) In the case of ${\varphi }^{*}=\beta$, we may adjust the desired beampattern in the strict monotone intervals $\left[\alpha ,\hspace{0.17em}\beta \right]$ and $\left[\beta ,\hspace{0.17em}\gamma \right]$. $\tilde{F}\left(\varphi \right)$ in $\left[\alpha ,\hspace{0.17em}\beta \right]$ and $\left[\beta ,\hspace{0.17em}\gamma \right]$ is used to replace the corresponding parts of the desired beampattern $\tilde{P}\left(\varphi \right)$. Then, the adjusted desired beampattern $\overline{P}\left(\varphi \right)$ is

$$\overline{P}\left(\varphi \right)=\{\begin{array}{cc}\frac{\tilde{P}\left(\beta \right)-\tilde{P}\left(\alpha \right)}{\tilde{F}\left(\beta \right)-\tilde{F}\left(\alpha \right)}\left[\tilde{F}\left(\varphi \right)-\tilde{F}\left(\alpha \right)\right]+\tilde{P}\left(\alpha \right)& \varphi \in \left[\alpha ,\beta \right]\\ \frac{\tilde{P}\left(\gamma \right)-\tilde{P}\left(\beta \right)}{\tilde{F}\left(\gamma \right)-\tilde{F}\left(\beta \right)}\left[\tilde{F}\left(\varphi \right)-\tilde{F}\left(\beta \right)\right]+\tilde{P}\left(\beta \right)& \varphi \in \left[\beta ,\gamma \right]\\ \tilde{P}\left(\varphi \right)& else\end{array}$$

(11)

(c) In the case of ${\varphi }^{*}=\alpha$, we may adjust the desired beampattern in the strict monotone intervals $\left[\gamma ,\hspace{0.17em}\alpha \right]$ and $\left[\alpha ,\hspace{0.17em}\beta \right]$. Similar to (b), the adjusted desired beampattern $\overline{P}\left(\varphi \right)$ is

$$\overline{P}\left(\varphi \right)=\{\begin{array}{cc}\frac{\tilde{P}\left(\alpha \right)-\tilde{P}\left(\gamma \right)}{\tilde{F}\left(\alpha \right)-\tilde{F}\left(\gamma \right)}\left[\tilde{F}\left(\varphi \right)-\tilde{F}\left(\gamma \right)\right]+\tilde{P}\left(\gamma \right)& \varphi \in \left[\gamma ,\alpha \right]\\ \frac{\tilde{P}\left(\beta \right)-\tilde{P}\left(\alpha \right)}{\tilde{F}\left(\beta \right)-\tilde{F}\left(\alpha \right)}\left[\tilde{F}\left(\varphi \right)-\tilde{F}\left(\alpha \right)\right]+\tilde{P}\left(\alpha \right)& \varphi \in \left[\alpha ,\beta \right]\\ \tilde{P}\left(\varphi \right)& else\end{array}$$

(12)

3.3. Four Criteria Examination

For the $\overline{P}\left(\varphi \right)$ in Equations (10)–(12), we may use stretch transformation to change $\overline{P}\left(\varphi \right)$

$$\widehat{P}\left(\varphi \right)=\frac{2\pi M}{{\displaystyle {\int }_{-\pi }^{\pi }\overline{P}\left(\varphi \right)d\varphi }}\overline{P}\left(\varphi \right)$$

(13)

Considering $\tilde{P}\left(\varphi \right)\ge 0$, it is obvious that $\widehat{P}\left(\varphi \right)\ge 0$, satisfying criterion 1.

From Equation (13), we have ${\displaystyle {\int }_{-\pi }^{\pi }\widehat{P}\left(\varphi \right)d\varphi }=2\pi M$. Thus $\widehat{P}\left(\varphi \right)$ also meets criterion 2.

Consider

$$\underset{M\to +\infty }{\lim }\tilde{F}\left(\varphi \right)=\tilde{P}\left(\varphi \right)$$

(14)

We have the following conclusions:

Lemma 2. 

For a sufficiently large M, if $\left[\alpha ,\hspace{0.17em}\beta \right]$ is a strict monotone interval of $\tilde{F}\left(\varphi \right)$, then$\left[\alpha ,\hspace{0.17em}\beta \right]$is also the monotone interval of$\tilde{P}\left(\varphi \right)$.

From Lemma 2, since

$${\widehat{P}}^{\prime }\left(\alpha \right)={\tilde{F}}^{\prime }\left(\alpha \right)={\tilde{P}}^{\prime }\left(\alpha \right)=0,{\widehat{P}}^{\prime }\left(\beta \right)={\tilde{F}}^{\prime }\left(\beta \right)={\tilde{P}}^{\prime }\left(\beta \right)=0$$

$\widehat{P}\left(\varphi \right)$ satisfies criterion 3.

Theorem 3. 

If the desired beampattern $\tilde{P}\left(\varphi \right)$ is a continuous function and $\widehat{P}\left(\varphi \right)$ is obtained from Equations (10)–(12), then

$$\underset{M\to +\infty }{\lim }{\delta }^2\left(\widehat{P},\tilde{P}\right)=0$$

Proof: 

Here, we only provide the proof in the case of ${\varphi }^{*}\in (\alpha ,\hspace{0.17em}\beta )$. The other cases are similar to this case. Since

$$\underset{M\to +\infty }{\lim }\tilde{F}\left(\varphi \right)=\tilde{P}\left(\varphi \right)$$

for $\forall \hspace{0.17em}\epsilon >0,\exists \hspace{0.17em}{M}^{*}>0$ when $M>M^{*}$, we have

$$\left|A\left(\varphi \right)\right|=\left|\frac{\tilde{P}\left(\beta \right)-\tilde{P}\left(\alpha \right)}{\tilde{F}\left(\beta \right)-\tilde{F}\left(\alpha \right)}\left[\tilde{F}\left(\varphi \right)-\tilde{F}\left(\alpha \right)\right]-\left[\tilde{P}\left(\varphi \right)-\tilde{P}\left(\alpha \right)\right]\right|\le \epsilon$$

By Equations (10) and (13)

$$\begin{array}{l}\frac{1}{2\pi }{\displaystyle {\int }_{-\pi }^{\pi }{\left[\widehat{P}\left(\varphi \right)-\tilde{P}\left(\varphi \right)\right]}^{2}d\varphi }\\ =\frac{1}{2\pi }{\displaystyle {\int }_{\alpha }^{\beta }{\left[\frac{2\pi M}{2\pi M+{\displaystyle {\int }_{\alpha }^{\beta }A\left(\varphi \right)d\varphi }}A\left(\varphi \right)+\frac{2\pi M}{2\pi M+{\displaystyle {\int }_{\alpha }^{\beta }A\left(\varphi \right)d\varphi }}\tilde{P}\left(\varphi \right)-\tilde{P}\left(\varphi \right)\right]}^{2}d\varphi }+\\ \frac{1}{2\pi }{\displaystyle {\int }_{-\pi }^{\alpha }{\left[\frac{2\pi M}{2\pi M+{\displaystyle {\int }_{\alpha }^{\beta }A\left(\varphi \right)d\varphi }}\tilde{P}\left(\varphi \right)-\tilde{P}\left(\varphi \right)\right]}^{2}d\varphi }+\frac{1}{2\pi }{\displaystyle {\int }_{\beta }^{\pi }{\left[\frac{2\pi M}{2\pi M+{\displaystyle {\int }_{\alpha }^{\beta }A\left(\varphi \right)d\varphi }}\tilde{P}\left(\varphi \right)-\tilde{P}\left(\varphi \right)\right]}^{2}d\varphi }\\ \le \frac{2}{2\pi }{\displaystyle {\int }_{\alpha }^{\beta }{\left[\frac{2\pi M}{2\pi M-\epsilon \left(\beta -\alpha \right)}\right]}^2{\epsilon }^{2}d\varphi }+\frac{2}{2\pi }{\displaystyle {\int }_{-\pi }^{\pi }{\left[\frac{{\displaystyle {\int }_{\alpha }^{\beta }A\left(\varphi \right)d\varphi }}{2\pi M+{\displaystyle {\int }_{\alpha }^{\beta }A\left(\varphi \right)d\varphi }}\right]}^2{\tilde{P}}^2\left(\varphi \right)d\varphi }\\ \le \frac{\pi {\left[2M\left(\beta -\alpha \right)\right]}^2}{{\left[2\pi M-\epsilon \left(\beta -\alpha \right)\right]}^2}{\epsilon }^2+\frac{{\left[\left(\beta -\alpha \right)\right]}^2{\displaystyle {\int }_{-\pi }^{\pi }{\tilde{P}}^2\left(\varphi \right)d\varphi }}{\pi {\left[2\pi M-\epsilon \left(\beta -\alpha \right)\right]}^2}{\epsilon }^2\\ \le 2\pi {\epsilon }^2\end{array}$$

that is,

$$\underset{M\to +\infty }{\lim }\frac{1}{2\pi }{\displaystyle {\int }_{-\pi }^{\pi }{\left[\tilde{P}\left(\varphi \right)-\widehat{P}\left(\varphi \right)\right]}^{2}d\varphi }=0$$

From Theorem 3, we know that $\widehat{P}\left(\varphi \right)$ satisfies criterion 4. □

3.4. Algorithm

According to the theoretical analysis above, given the sidelobe suppression level $MSLR>\delta \hspace{0.17em}\mathrm{dB}$, here we provide an algorithm to explain our proposed cosine method:

Step 1:

Let i = 0, ${\tilde{P}}_i\left(\varphi \right)=\tilde{P}\left(\varphi \right)$;

Step 2:

Use the one-step approach in [27] to obtain the transmit beampattern $P_i\left(\varphi \right)$ with minimum mean square error to the desired beampattern ${\tilde{P}}_i\left(\varphi \right)$;

Step 3:

If $MSLR>\delta \hspace{0.17em}\mathrm{dB}$, then go to end; otherwise, go to Step 4;

Step 4:

Solve ${\varphi }^{*}$, satisfying

$$\left|P_i\left({\varphi }^{*}\right)-{\tilde{P}}_i\left({\varphi }^{*}\right)\right|=\underset{-\pi \le \varphi \le \pi }{\max }\left|P_i\left(\varphi \right)-{\tilde{P}}_i\left(\varphi \right)\right|$$

and let ${\tilde{F}}_i\left(\varphi \right)$ be the first M items of ${\tilde{P}}_i\left(\varphi \right)$ Fourier expansion, identify the strict monopoly area $\left[{\alpha }_i,{\beta }_i\right]$ with ${\varphi }^{*}$ in ${\tilde{F}}_i\left(\varphi \right)$.

Step 5: 

If ${\varphi }^{*}\in (\alpha ,\hspace{0.17em}\beta )$, use Equation (10) to obtain ${\overline{P}}_i\left(\varphi \right)$;

If ${\varphi }^{*}=\beta$, use Equation (11) to obtain ${\overline{P}}_i\left(\varphi \right)$;

If ${\varphi }^{*}=\alpha$, use Equation (12) to obtain ${\overline{P}}_i\left(\varphi \right)$;

Step 6:

Implement stretch transformation to ${\overline{P}}_i\left(\varphi \right)$, let

$${\tilde{P}}_{i+1}\left(\varphi \right)=\frac{2\pi M}{{\displaystyle {\int }_{-\pi }^{\pi }{\overline{P}}_i\left(\varphi \right)d\varphi }}{\overline{P}}_i\left(\varphi \right)$$

Step 7:

Let i = i + 1, return to Step 2.

Note: If the desired beampattern is a symmetric figure, we may simultaneously adjust ${\tilde{P}}_i\left(\varphi \right)$ in the strict monopoly areas $\left[{\alpha }_i,\hspace{0.17em}{\beta }_i\right]$ and $\left[-{\beta }_i,\hspace{0.17em}-{\alpha }_i\right]$ for ${\tilde{F}}_i\left(\varphi \right)$.

4. Numerical Examples

Example 1.

Consider the following standardized symmetric triangle desired beampattern [4,29,34].

$$\tilde{P}\left(\varphi \right)=\{\begin{array}{cc}2M& -\frac{\pi }{9}\le \varphi \le \frac{\pi }{9}\\ 0& else\end{array}$$

(15)

Here, $MSLR\ge 16\hspace{0.17em}\mathrm{dB}$, $M=10$.

Figure 1 shows the optimal matching transmit beampattern $P\left(\varphi \right)=P_0\left(\varphi \right)$ with the first sidelobe peak, 2.6285. The MSLR = 12.334 dB is lower than the sidelobe suppression level $\delta$(16 dB), thereby not satisfying the sidelobe constraint. Hence, the cosine approach is employed to increase MSLR. As shown in Figure 1, since the bias between $\tilde{F}\left(\varphi \right)={\tilde{F}}_0\left(\varphi \right)$ and $\tilde{P}\left(\varphi \right)$ reaches the maximum at ${\varphi }^{*}=\pm \frac{\pi }{9}$, the monotone intervals $\left[-{\beta }_1,\hspace{0.17em}-{\alpha }_1\right]$ and $\left[{\alpha }_1,\hspace{0.17em}{\beta }_1\right]$ containing ${\varphi }^{*}=\pm \frac{\pi }{9}$ are chosen to adjust the desired beampattern $\tilde{P}\left(\varphi \right)$.

Figure 2 illustrates the optimal matching beampatterns after using the cosine method, where $P_1\left(\varphi \right),P_2\left(\varphi \right),P_3\left(\varphi \right)$ represents using the cosine method 1, 2, 3 times, respectively. As we can see, the first sidelobe peak of $P_3\left(\varphi \right)$ is 1.0912 with MSLR = 16.152 dB, satisfying the sidelobe constraint.

Table 1. Results of the cosine method for Example 1.

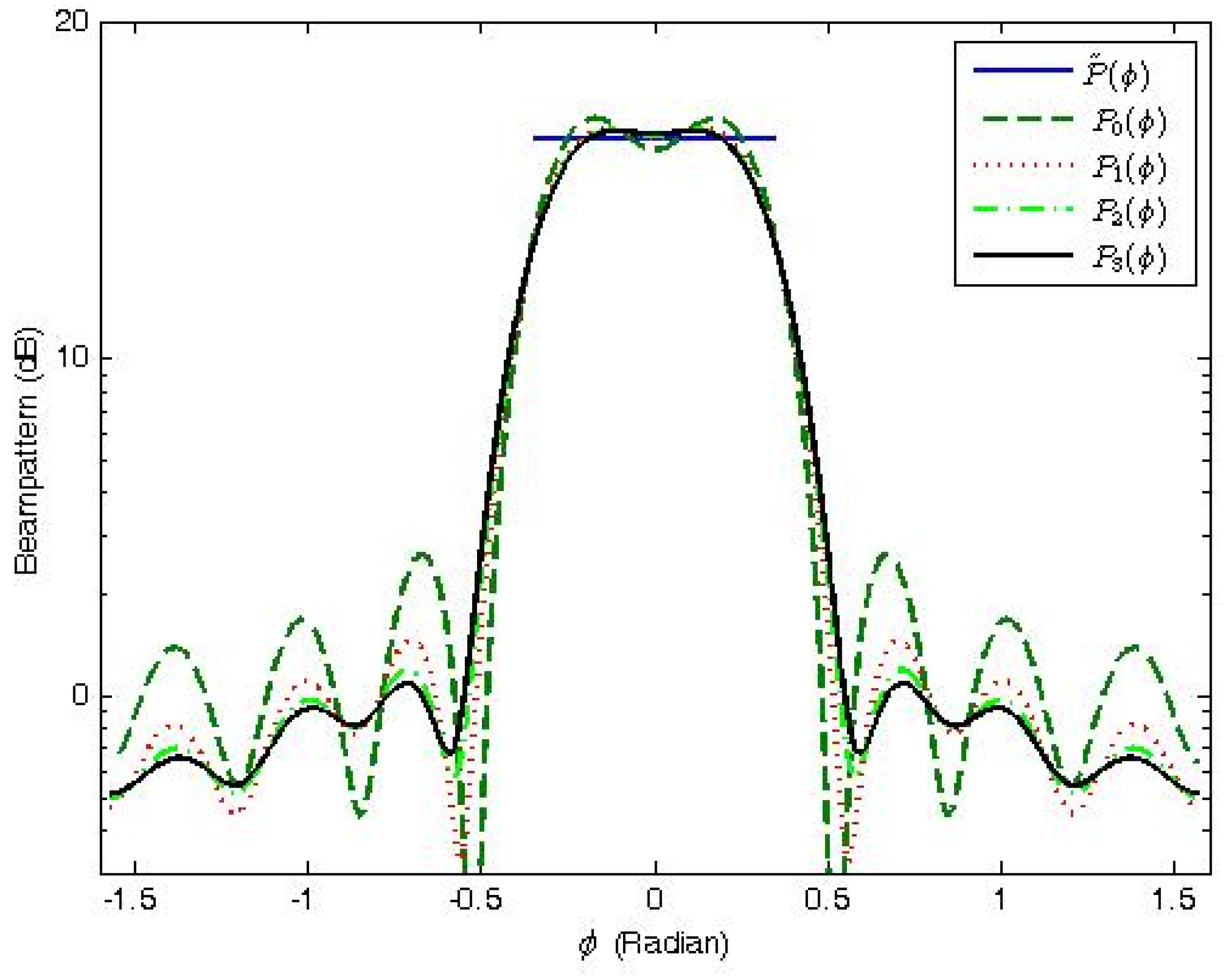
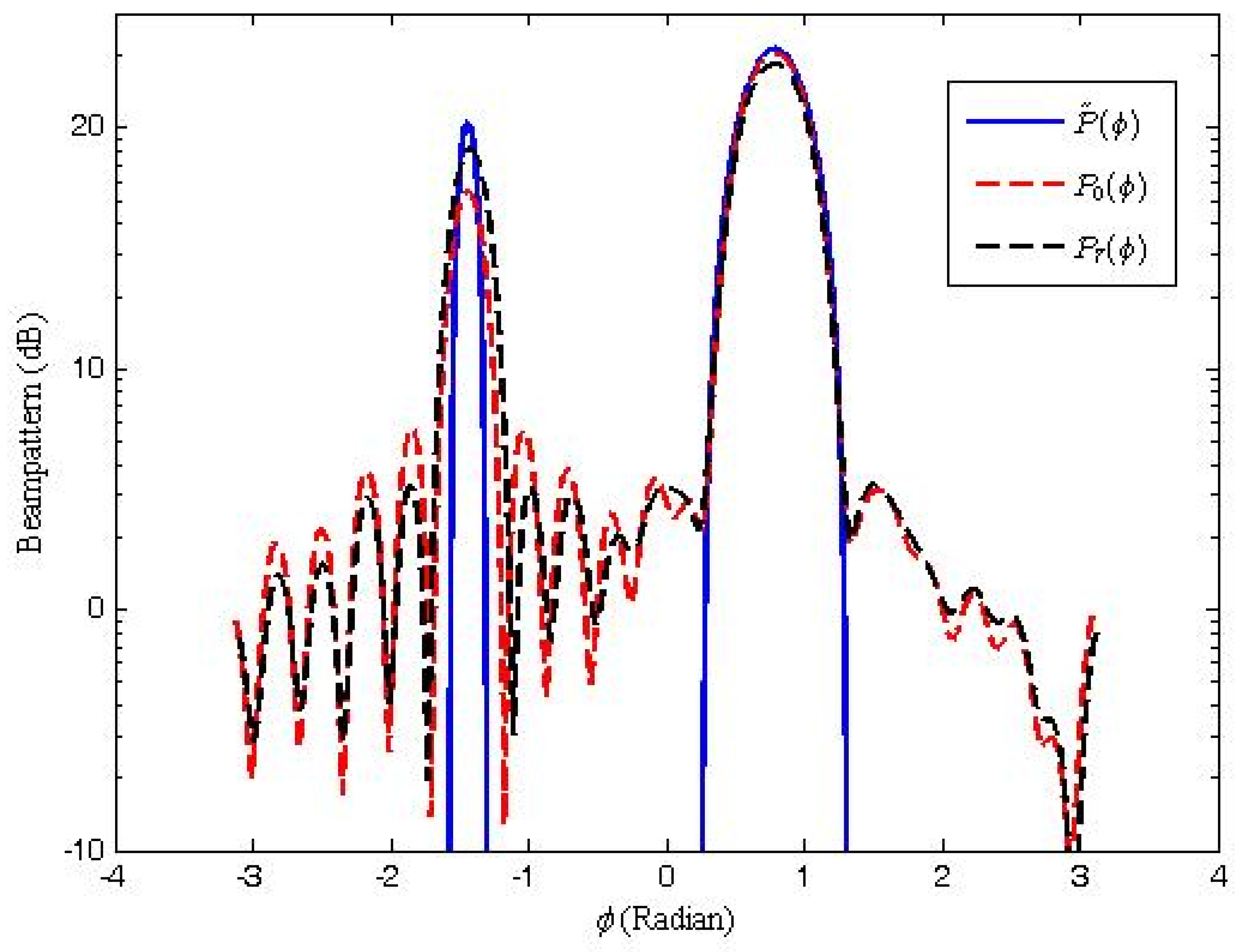
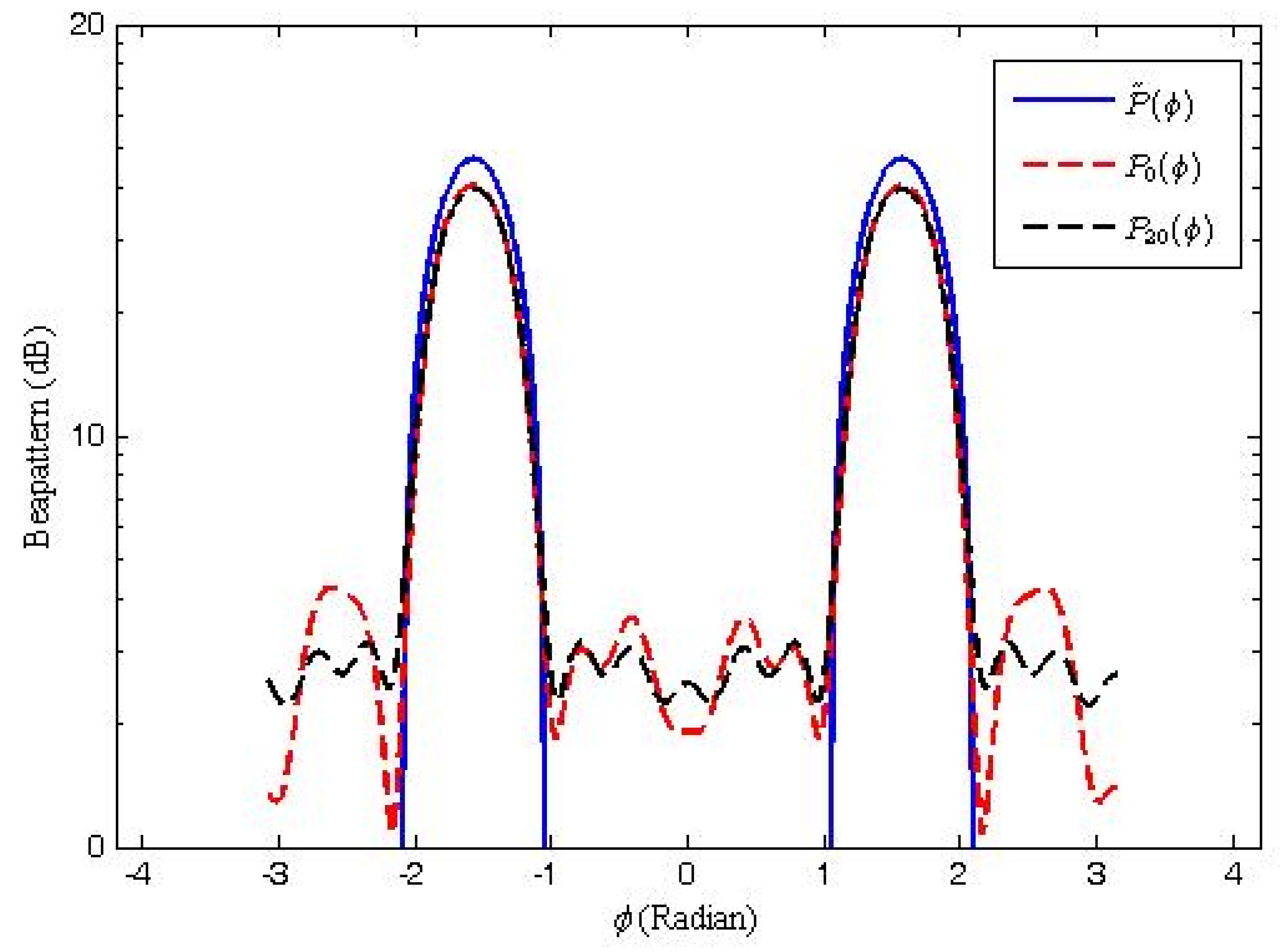
	Sidelobe Peak	MSLR	Mean Square Error
$P_0\left(\varphi \right)$	2.6285	12.334 dB	24.6343
$P_1\left(\varphi \right)$	1.4607	14.885 dB	26.7382
$P_2\left(\varphi \right)$	1.1994	15.741 dB	28.6358
$P_3\left(\varphi \right)$	1.0913	16.152 dB	29.7273

provides the results after using the cosine method each time.

As shown in Table 1, the sidelobe peaks of the transmit beampatterns $P_1\left(\varphi \right),P_2\left(\varphi \right),P_3\left(\varphi \right)$ are decreasing while their MSLR are increasing. After three adjustments, the MSLR increases 30.96% with only a 20.67% increase of the mean square error between the transmit beampattern and the original desired beampattern $\tilde{P}\left(\varphi \right)$. Thus, $P_3\left(\varphi \right)$ is a satisfactory solution of Example 1. As illustrated in Figure 2, the proposed cosine method can not only increase the MSLR significantly but also provide a comparatively good match to the desire beampattern.

Compared with [34], our cosine method can obtain a lower MSLR. For M = 16, Figure 3 illustrates the optimal matching beampatterns after using the cosine method, where $P_1\left(\varphi \right),P_5\left(\varphi \right),P_{10}\left(\varphi \right)$ represents using the cosine method 1, 5, and 10 times, respectively. After ten adjustments, the MSLR increased from 10.123 dB to 18.125 dB. Compared with [29], our cosine method also obtained a lower MSLR.

Example 2.

Consider an asymmetric desired beampattern.

$$\tilde{P}\left(\varphi \right)=\{\begin{array}{cc}\frac{8M}{3}\left(1-\cos \left(24\varphi \right)\right)& -\frac{\pi }{2}\le \varphi \le -\frac{5\pi }{12}\\ \frac{16M}{3}\left(1-\cos \left(6\varphi -\frac{\pi }{2}\right)\right)& \frac{\pi }{12}\le \varphi \le \frac{5\pi }{12}\\ 0& else\end{array}$$

(16)

Here, $MSLR\ge 14\hspace{0.17em}\mathrm{dB},\hspace{0.17em}\hspace{0.17em}M=20$.

Figure 4 illustrates the comparisons between the transmit beampattern $P_0\left(\varphi \right)$ and the transmit beampattern $P_7\left(\varphi \right)$ using the cosine method 7 times. For the $P_0\left(\varphi \right)$, the MSLR is 9.7842 dB, lower than the sidelobe suppression level $\delta$. However, after using the cosine method 7 times, the MSLR increased 43.24%, reaching 14.0183 dB, while the mean square error to the desired beampattern $\tilde{P}\left(\varphi \right)$ only increased 19.05% to 14.4256, showing the advantage of the cosine method for suppressing sidelobes in the beampattern matching design problem.

Example 3.

Consider a desired beampattern with a nonuniform linear array:

$$\tilde{P}\left(\varphi \right)=\{\begin{array}{cc}\frac{3\pi M}{2}\cos \left(3\varphi -\pi /2\right)& -\frac{2\pi }{3}\le \varphi <-\frac{\pi }{3}\\ \frac{3\pi M}{2}\cos \left(3\varphi +\pi /2\right)& \frac{\pi }{3}\le \varphi <\frac{2\pi }{3}\\ 0& else\end{array}$$

(17)

Here, $MSLR\ge 11\hspace{0.17em}\mathrm{dB},\hspace{0.17em}M=10$ and $D=7\lambda$. The positions of the elements are $\left[1,3,4,5,7,9,10,11,13,15\right]$.

Figure 5 compares $P_0\left(\varphi \right)$ and the transmit beampattern $P_{20}\left(\varphi \right)$. The MSLR of $P_0\left(\varphi \right)$ is 9.7754 dB, much lower than $\delta$. After 20 times adjustments by the cosine approach, the MSLR reached 11.0002 dB, satisfying the sidelobe suppression level $\delta$. Compared to the 12.53% increase in the MSLR, the mean square error between $P\left(\varphi \right)$ and $\tilde{P}\left(\varphi \right)$ only increased 1.26%, reaching 16.584.

From Examples 1–3, we may find that the proposed cosine method can not only significantly increase the MSLR, but also provide very good matching to the desired beampattern. In addition, this cosine method is suitable for both symmetric and asymmetric arrays. Therefore, the cosine method is an effective and efficient solution to the problem of sidelobe suppression in beampattern matching design.

5. Conclusions

In this paper, a novel method, the cosine method, is proposed for addressing the problem of sidelobe suppression in beampattern matching design, in which the MSLR is a constraint. The theoretical justification and algorithm for this method were provided and several numerical examples were tested to examine the advantages of the proposed method. Indeed, the cosine method showed significant improvement in MSLR but also increased the mean square error between the desired and transmit beampatterns. However, considering the trade-off between sidelobe level and total bias, the proposed method produces a substantial increase in the MSLR at the expense of a relatively small increase of the mean square error. In real application, we may combine this cosine method with more radar transmit arrays to increase the sidelobe suppression level as well as to obtain better matching beampattern.