Comparison between Piezoelectric Filter and Passive LC Filter in a Class L−Piezo Inverter
Abstract
:1. Introduction
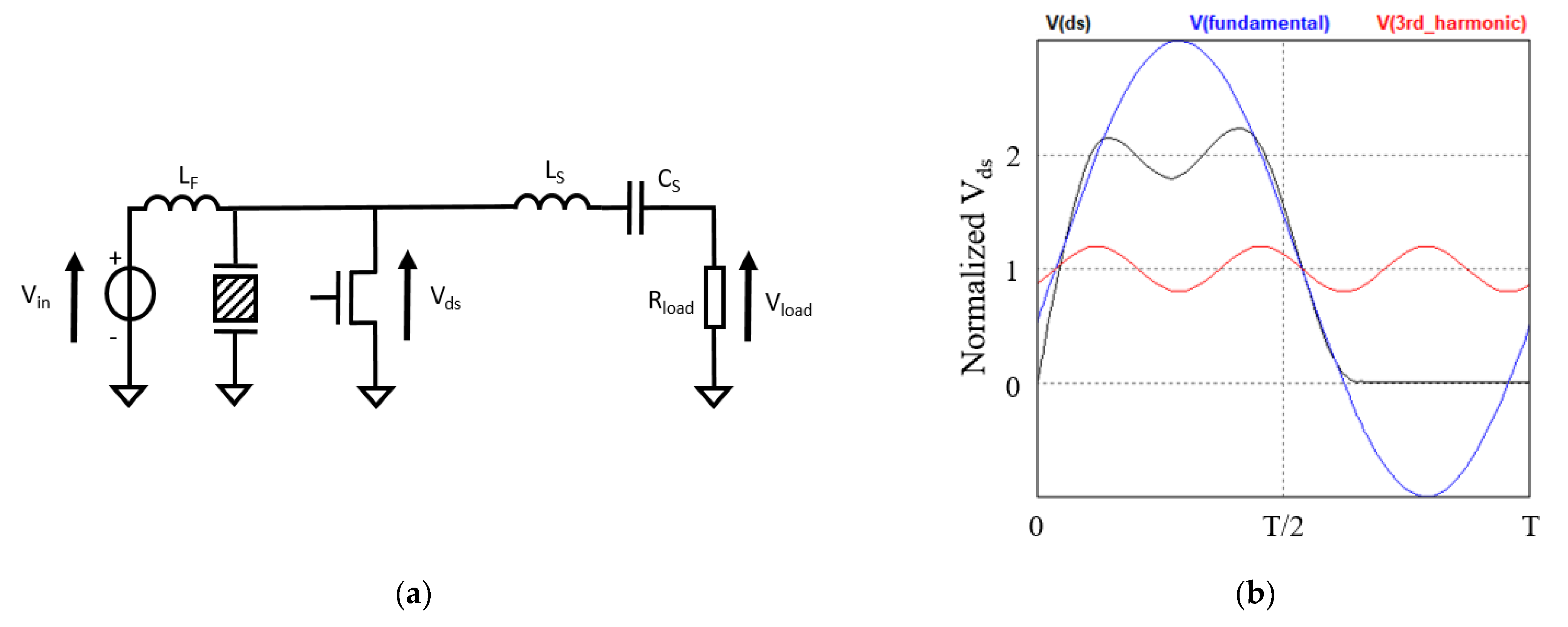
2. Class L−Piezo Inverter
2.1. Operating Principle and Design
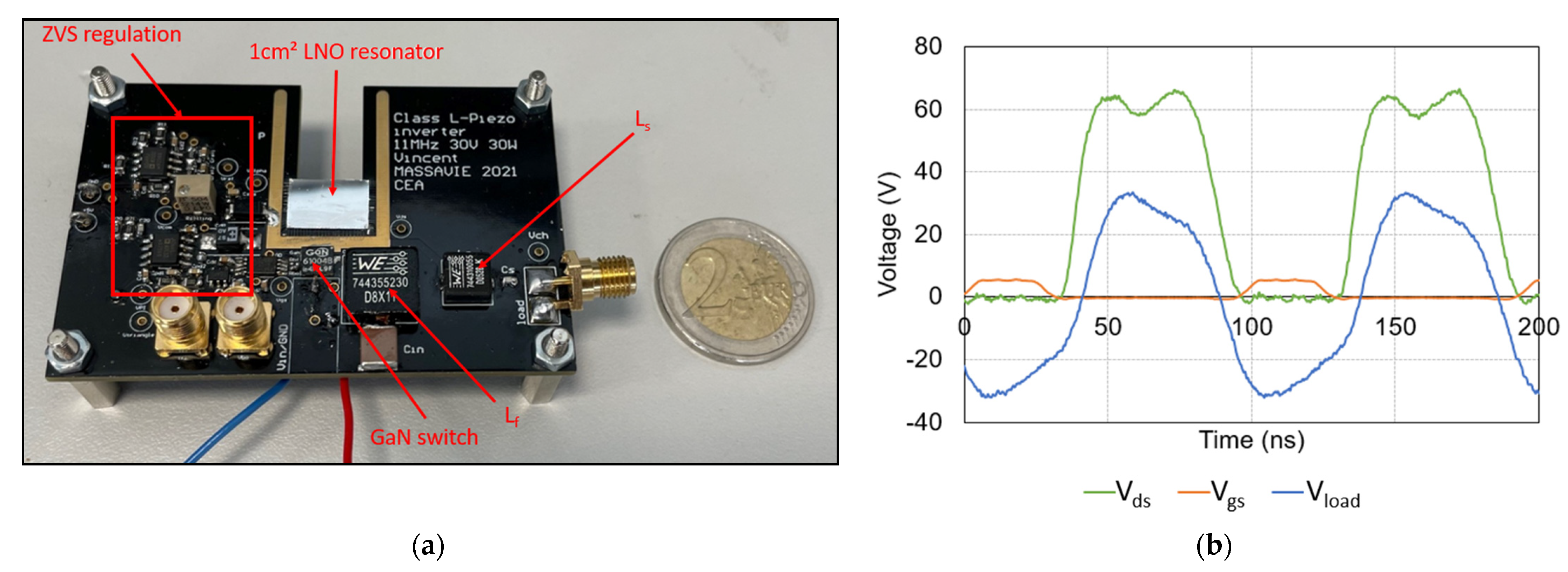
2.2. Zero Voltage Switching (ZVS)
- Characterization of a piezoelectric resonator;
- Calculate input inductance Lf with class φ2 equation;
- Tuning the inverter to reach the optimal behavior (ZVS, minimal voltage stress on the switch, etc.).
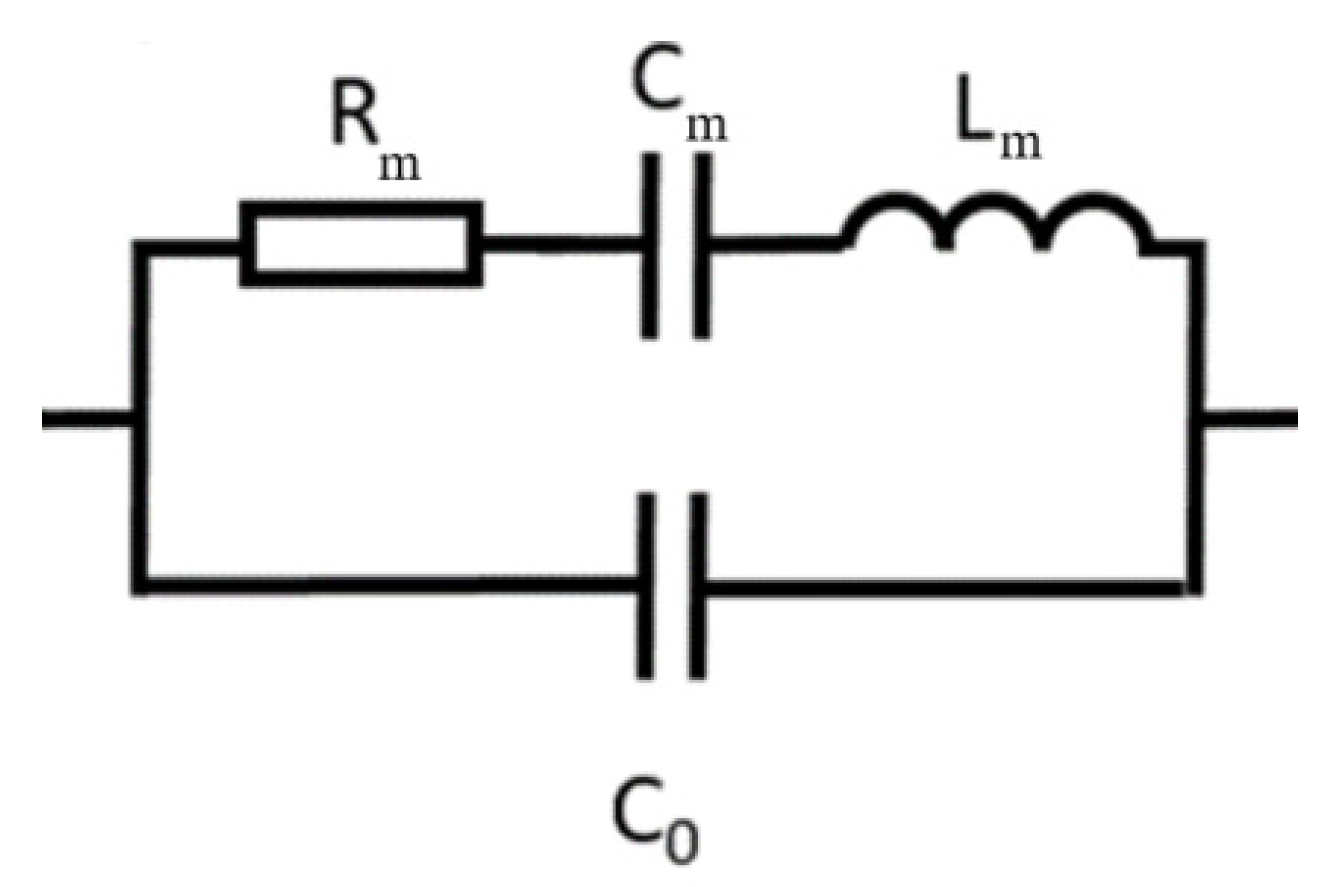
3. Piezoelectric Model Extraction
3.1. Determination of the Piezoelectric Resonator Model from Material Data and Size
3.2. Lithium Niobate Material Case (LNO)
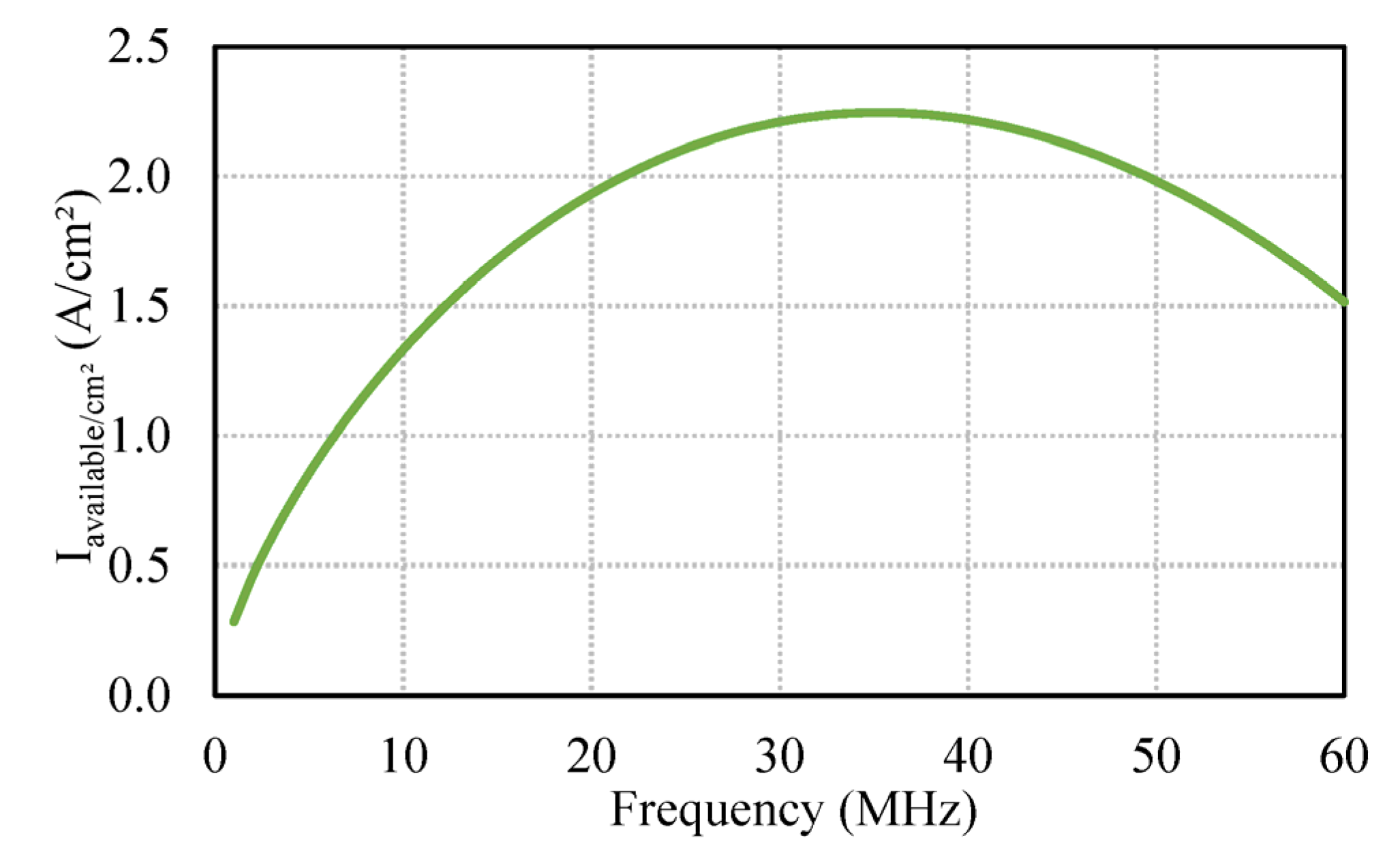
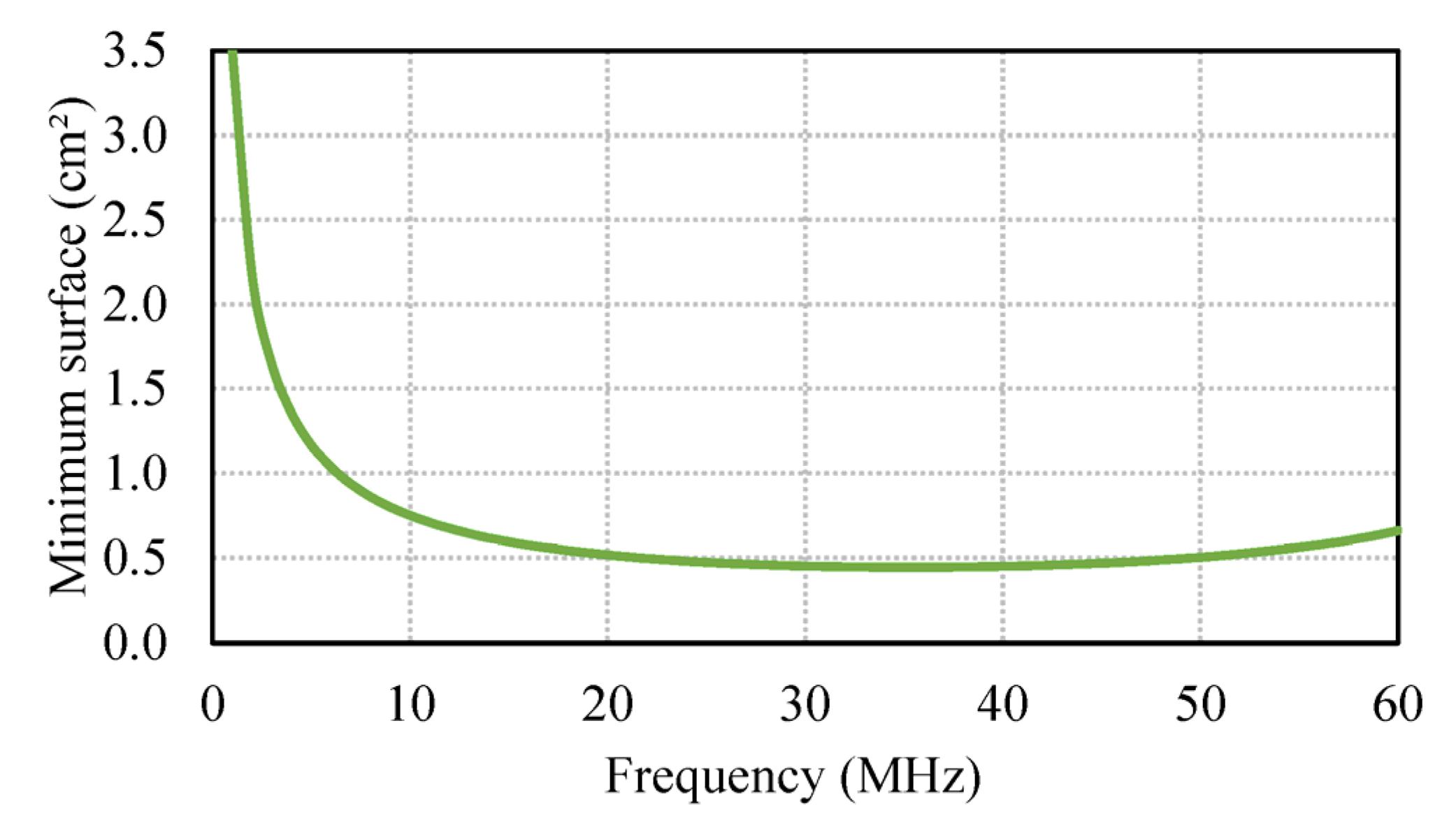
3.3. Current Density and Pre−Sizing Equations
4. Simulation of Class L−Piezo Inverter
4.1. Piezoelectric Resonator Characterisation
4.2. Design of a 10.4 MHz Class L−Piezo Inverter
- A maximum current of 2.48 A;
- A maximum voltage of 105.9 V.
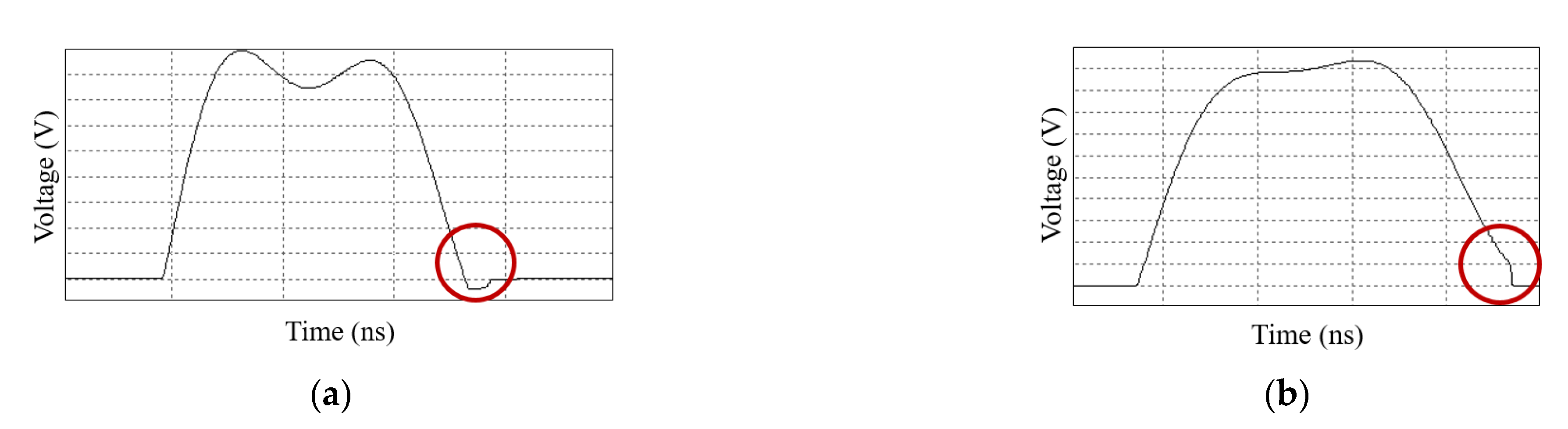
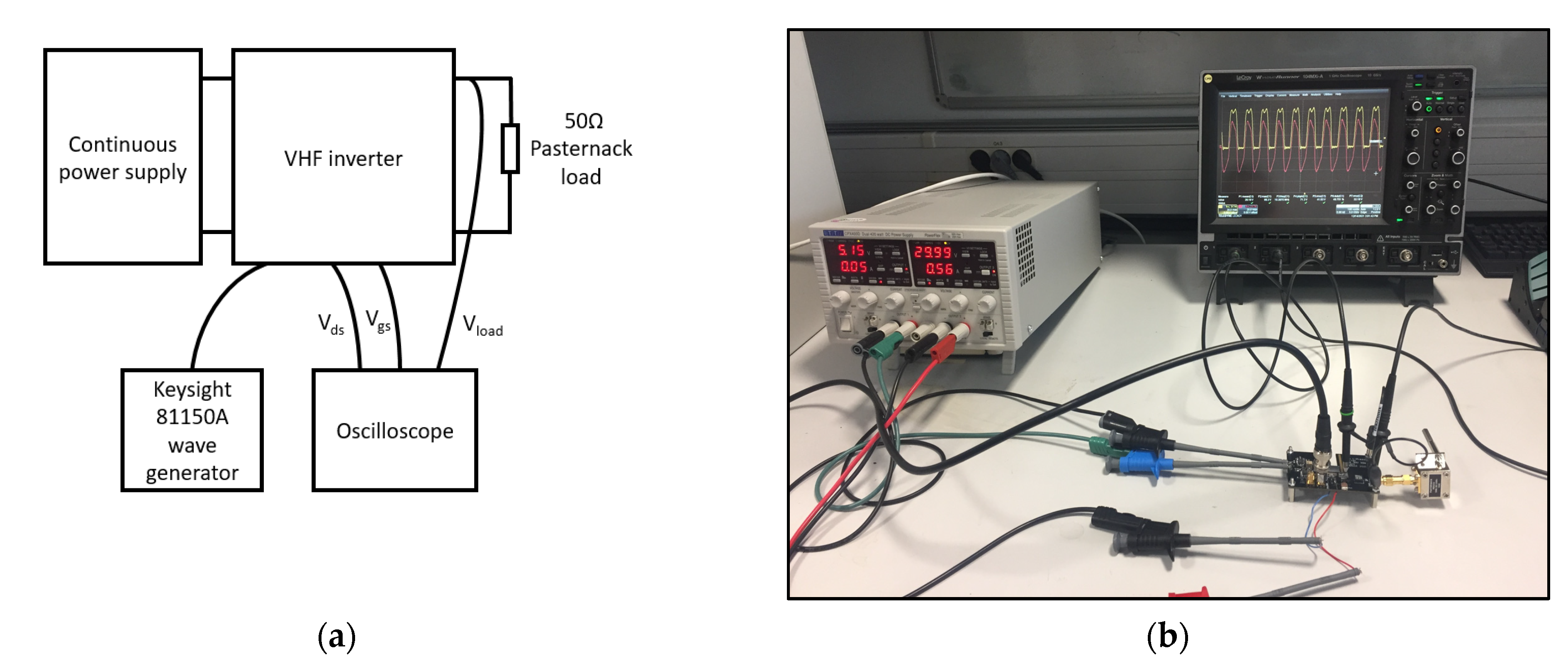
5. Experimental Results
5.1. Prototype including a Piezoelectric Material
- A double continuous power supply (for the input voltage and to supply the driver);
- A Keysight 81,150 A wave generator (to create and send the transistor gate control signal);
- An oscilloscope;
- A 50 Ω Pasternack load.
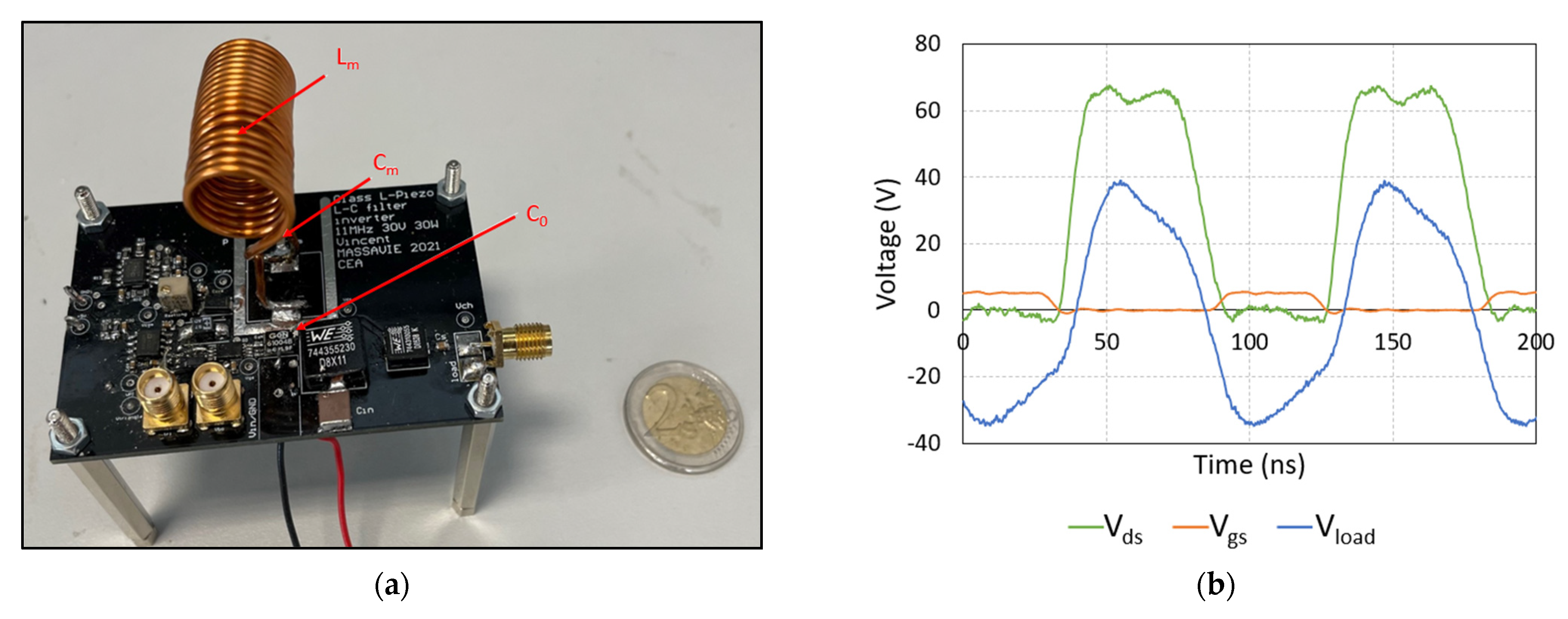
5.2. Prototype without Piezoelectric Material
- The current flowing in the filter oscillates at 20.8 MHz. At this frequency, magnetic core inductors have a low−quality factor, increasing component losses. Air core inductors are more interesting for very high frequencies. Currents through the other inductors in the inverter only oscillate at 10.4 MHz, which is still within the operating range of some magnetic core inductors;
- A hand−wound air inductor allows precise control over the actual value of the inductor.
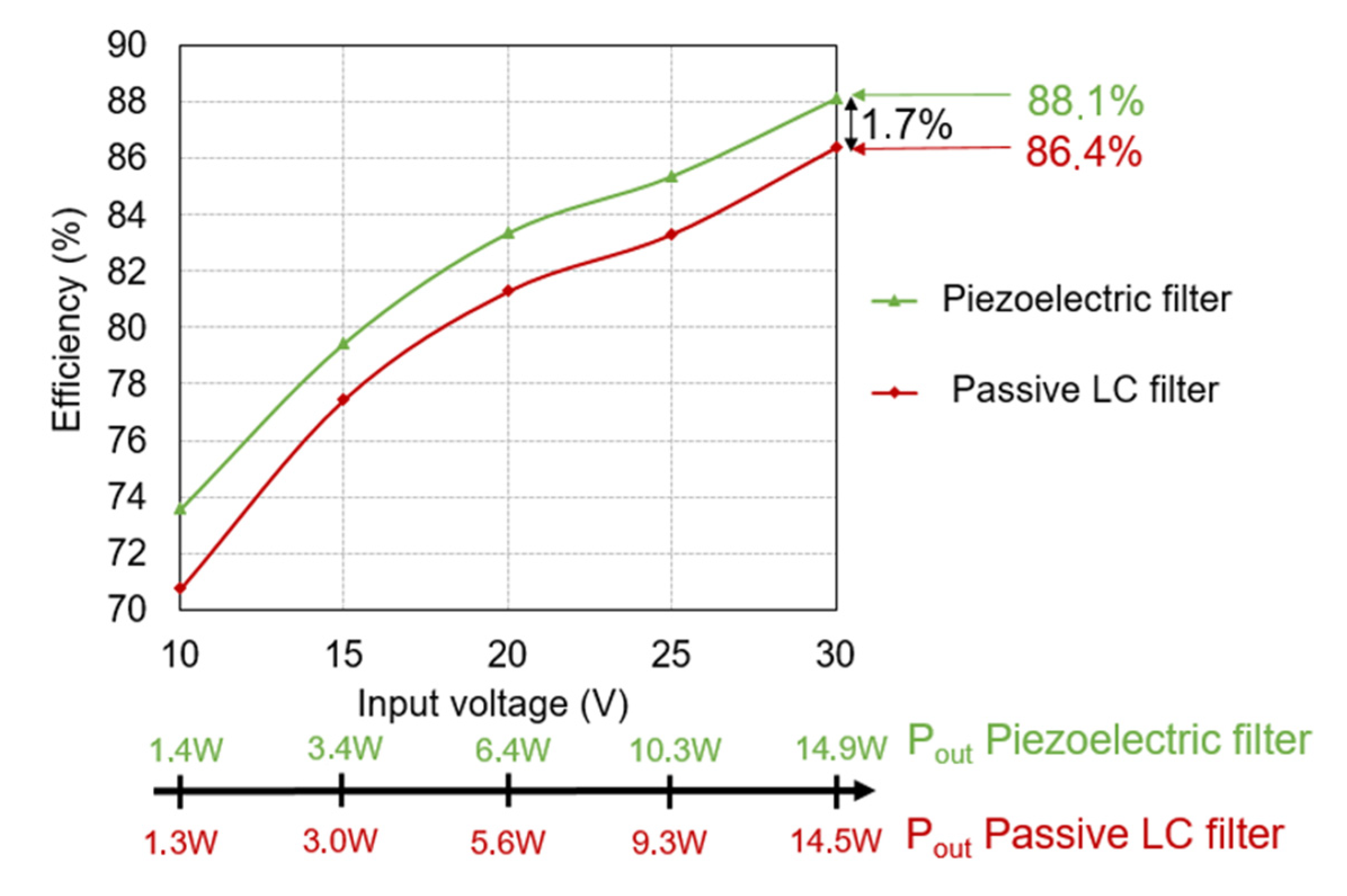
5.3. Efficiency Comparison
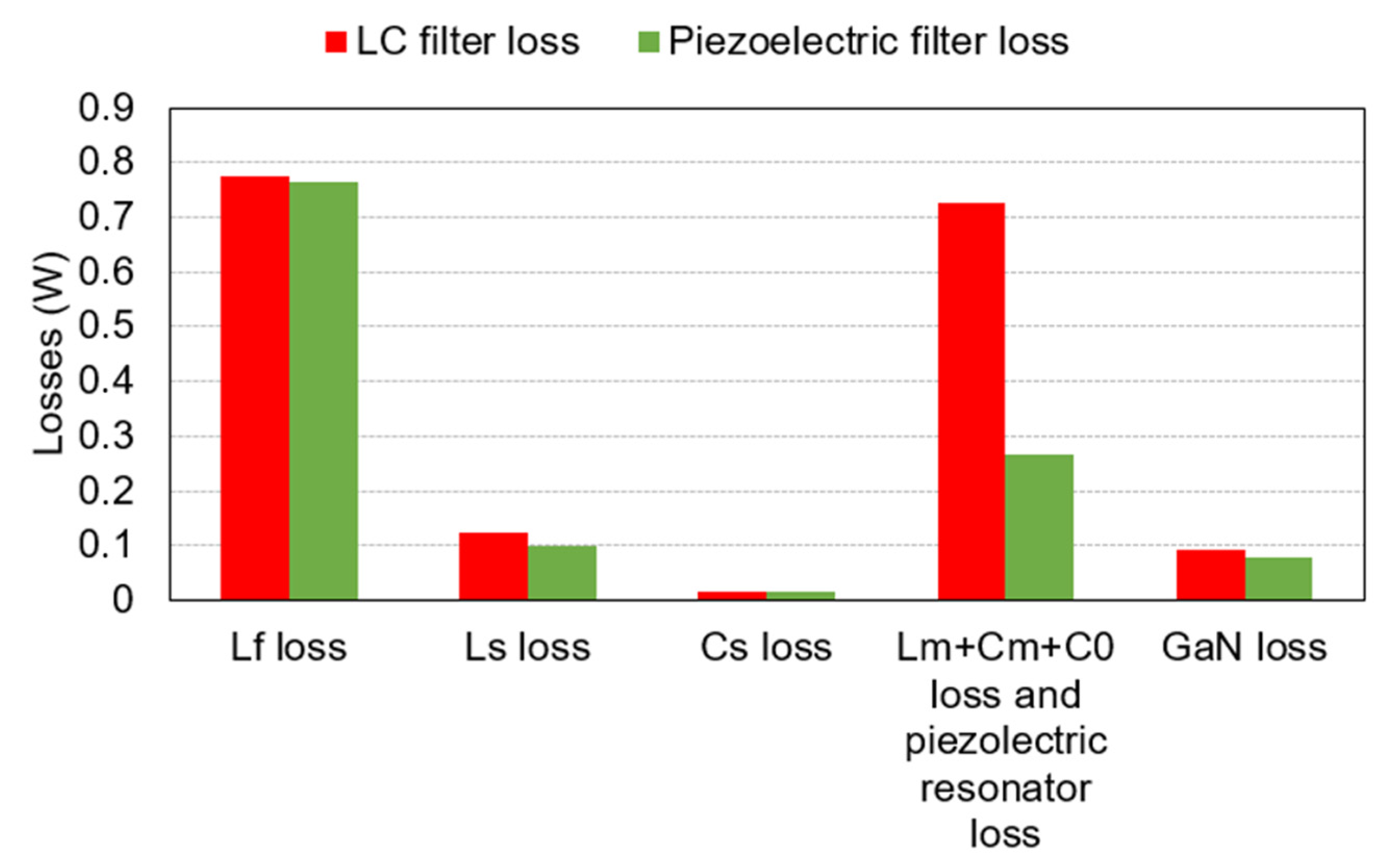
5.4. Losses Distribution
6. Conclusions
7. Patents
Author Contributions
Funding
Conflicts of Interest
References
- Peng, K.; Santi, E. Class E resonant inverter optimized design for high frequency (MHz) operation using eGaN HEMTs. In Proceedings of the 2015 IEEE Applied Power Electronics Conference and Exposition (APEC), Charlotte, NC, USA, 15–19 March 2015; pp. 2469–2473. [Google Scholar] [CrossRef]
- Kazimierczuk, M.K.; Czarkowski, D. Czarkowski, Resonant Power Converters; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Leitermann, O. Radio Frequency dc-dc Converters: Device Characterization, Topology Evaluation, and Design. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2008. [Google Scholar]
- Iwadare, M.; Mori, S.; Ikeda, K. Even harmonic resonant class E tuned power amplifier without RF choke. Electron. Commun. Jpn. Part Commun. 1996, 79, 23–30. [Google Scholar] [CrossRef]
- Rivas, J. Radio Frequency dc-dc Power Conversion. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2006. [Google Scholar]
- Stanford Energy, Juan Rivas|Emerging Applications in Power Electronics. Available online: https://www.youtube.com/watch?v=Op-aUvQG1ss (accessed on 26 May 2015).
- Glaser, J.S.; Nasadoski, J.; Heinrich, R. A 900W, 300V to 50V Dc-dc Power Converter with a 30MHz Switching Frequency. In Proceedings of the 2009 Twenty-Fourth Annual IEEE Applied Power Electronics Conference and Exposition, Washington, DC, USA, 15–19 February 2009; pp. 1121–1128. [Google Scholar] [CrossRef]
- Degel, C.; Fonfara, H.; Welsch, H.J.; Becker, F.J.; Hewener, H.; Fournelle, M.; Tretbar, S.H. 3D sonar system based on mills cross antenna configuration. In Proceedings of the 2014 Oceans-St. John’s, St. John’s, NL, Canada, 14–19 September 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Mason, W.P. Piezoelectricity, its history and applications. J. Acoust. Soc. Am. 1981, 70, 1561–1566. [Google Scholar] [CrossRef]
- Marrison, W.A. The evolution of the quartz crystal clock. Bell Syst. Tech. J. 1948, 27, 510–588. [Google Scholar] [CrossRef]
- Guyomar, D.; Badel, A.; Lefeuvre, E.; Richard, C. Toward energy harvesting using active materials and conversion improvement by nonlinear processing. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 584–595. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pollet, B.; Costa, F.; Despesse, G. A new inductorless DC-DC piezoelectric flyback converter. In Proceedings of the 2018 IEEE International Conference on Industrial Technology (ICIT), Lyon, France, 20–22 February 2018; pp. 585–590. [Google Scholar] [CrossRef]
- Touhami, M.; Despesse, G.; Costa, F. A New Topology of DC–DC Converter Based on Piezoelectric Resonator. IEEE Trans. Power Electron. 2022, 37, 6986–7000. [Google Scholar] [CrossRef]
- Braun, W.D.; Stolt, E.A.; Gu, L.; Segovia-Fernandez, J.; Chakraborty, S.; Lu, R.; Rivas-Davila, J.M. Optimized Resonators for Piezoelectric Power Conversion. IEEE Open J. Power Electron. 2021, 2, 212–224. [Google Scholar] [CrossRef]
- Touhami, M.; Despesse, G.; Hilt, T.; Bousquet, M.; Reinhardt, A.; Borel, E.; Breton, V.; Gneza, K.F.; Costa, F. Piezoelectric Materials for the DC-DC Converters Based on Piezoelectric Resonators. In Proceedings of the 2021 IEEE 22nd Workshop on Control and Modelling of Power Electronics (COMPEL), Cartagena, Colombia, 2–5 November 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Boles, J.D.; Piel, J.J.; Perreault, D.J. Enumeration and Analysis of DC–DC Converter Implementations Based on Piezoelectric Resonators. IEEE Trans. Power Electron. 2021, 36, 129–145. [Google Scholar] [CrossRef]
- Rivas, J.M.; Han, Y.; Leitermann, O.; Sagneri, A.; Perreault, D.J. A High-Frequency Resonant Inverter Topology with Low Voltage Stress. In Proceedings of the 2007 IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 17–21 June 2007; pp. 2705–2717. [Google Scholar] [CrossRef]
- Vincent, M.; Ghislain, D.; Sebastien, C.; Xavier, M. A new topology of resonant inverter including a piezoelectric component. In Proceedings of the 2021 23rd European Conference on Power Electronics and Applications (EPE’21 ECCE Europe), Ghent, Belgium, 6–10 September 2021; pp. P.1–P.10. [Google Scholar]
- Stolt, E.A.; Braun, W.D.; Daniel, C.Y.; Rivas-Davila, J.M. Piezoelectric Resonator Second Harmonic Cancellation in Class Φ2 Inverters. In Proceedings of the 2021 IEEE 22nd Workshop on Control and Modelling of Power Electronics (COMPEL), Cartagena, Colombia, 2–5 November 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Van Dyke, K.S. The Piezo-Electric Resonator and Its Equivalent Network. Proc. Inst. Radio Eng. 1928, 16, 742–764. [Google Scholar] [CrossRef]
- Lithium Niobate. Available online: http://www.roditi.com/SingleCrystal/LiNbO3/LiNbO3.html (accessed on 30 November 2022).
- Piezoelectric Ceramics. Available online: http://www.fujicera.co.jp/managed/wp-content/themes/fujicera/digitalbook/en/elements/index_h5.html#12 (accessed on 30 November 2022).
- Lithium Niobate Properties. Available online: http://www.roditi.com/SingleCrystal/LiNbO3/liNBO3-Properties.html (accessed on 30 November 2022).
- Braun, W.D.; Tong, Z.; Rivas-Davila, J. Inductorless Soft Switching DC-DC Converter with an Optimized Piezoelectric Resonator. In Proceedings of the 2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 15–19 March 2020; pp. 2272–2278. [Google Scholar] [CrossRef]
- GS61004B. GaN Systems. Available online: https://gansystems.com/gan-transistors/gs61004b/ (accessed on 30 November 2022).
- Massavie, V.; Despesse, G.; Carcouet, S.; Maynard, X. Class φ2 ZVS regulation applied to L−Piezo inverter. In Proceedings of the 2022 20th IEEE Interregional NEWCAS Conference (NEWCAS), Quebec City, QC, Canada, 19–22 June 2022; pp. 490–494. [Google Scholar] [CrossRef]



| LNO | |
|---|---|
| Frequency constant (MHz/m) | 3300 |
| Dielectric constant | 28.7 |
| Coupling factor k | 0.49 |
| Electrical quality factor Qe | 1000 |
| Mechanical quality factor Qm | 1.5 × 107 à 6.3 MHz [23] |
| Curie temperature | 1145 °C |
| Model | Value |
|---|---|
| C0 | 180 pF |
| Lm | 1.3 µH |
| Cm | 45 pF |
| Rm | 78 mΩ |
| Model | Value |
|---|---|
| Lf | 357 nH |
| Piezoelectric resonator model | C0 = 180 pF |
| Lm = 1.3 µH | |
| Cm = 45 pF | |
| Rm = 78 mΩ | |
| Switch | GaN HEMT model [25] |
| Ls | 520 nH |
| Cs | 500 pF |
| Rload | 50 Ω |
| Component | Component Characteristic | Measured Value |
|---|---|---|
| C0 | 1 × C0603C181F1GACTU | 182 pF |
| Lm | 18 turns of Ø1.56 mm copper wire with 11.88 mm/15 mm diam. | 1.394 µH |
| Cm | 1 × C1206C430JBGACTU | 41.2 pF |
| Components | Quality Factor for Prototype 1 | Quality Factor for Prototype 2 |
|---|---|---|
| Lf | 55 | 55 |
| Piezoelectric resonator | 802 | / |
| Lm | / | 203 |
| Cm | / | 998 |
| C0 | / | 1153 |
| Ls | 92 | 92 |
| Cs | 1024 | 1026 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Massavie, V.; Despesse, G.; Carcouet, S.; Maynard, X. Comparison between Piezoelectric Filter and Passive LC Filter in a Class L−Piezo Inverter. Electronics 2022, 11, 3983. https://doi.org/10.3390/electronics11233983
Massavie V, Despesse G, Carcouet S, Maynard X. Comparison between Piezoelectric Filter and Passive LC Filter in a Class L−Piezo Inverter. Electronics. 2022; 11(23):3983. https://doi.org/10.3390/electronics11233983
Chicago/Turabian StyleMassavie, Vincent, Ghislain Despesse, Sebastien Carcouet, and Xavier Maynard. 2022. "Comparison between Piezoelectric Filter and Passive LC Filter in a Class L−Piezo Inverter" Electronics 11, no. 23: 3983. https://doi.org/10.3390/electronics11233983
APA StyleMassavie, V., Despesse, G., Carcouet, S., & Maynard, X. (2022). Comparison between Piezoelectric Filter and Passive LC Filter in a Class L−Piezo Inverter. Electronics, 11(23), 3983. https://doi.org/10.3390/electronics11233983










