Implementation and Experimental Verification of Resistorless Fractional-Order Basic Filters
Abstract
:1. Introduction
- (i)
- Substituting the capacitors of the conventional (i.e., integer order) stages by fractional-order capacitors. At this point, there are two alternatives: (a) utilizing real fractional-order capacitors [12,13,14,15,16,17,18,19,20] or (b) utilizing RC networks for emulating the behavior of fractional-order capacitors [21,22,23,24,25,26,27], and their derivation is based on the utilization of approximation tools such as Charef, Oustaloup, Matsuda, continued fraction expansion, and partial fraction expansion [28,29,30,31,32]. The first alternative is straightforward, but the main obstacle is the absence of commercially available fractional-order capacitors. The second one is more practical, but requires an increased number of passive components.
- (ii)
- (a)
- Novel scheme for implementing fractional-order differentiator/ integrator and filter stages are proposed in this work, where the presented structures are constructed only by capacitors and, therefore, avoiding the utilization of passive resistors.
- (b)
- The realized time constants are formed as a ratio of a conventional and a pseudo-capacitance, overcoming the restriction of small-signal operation.
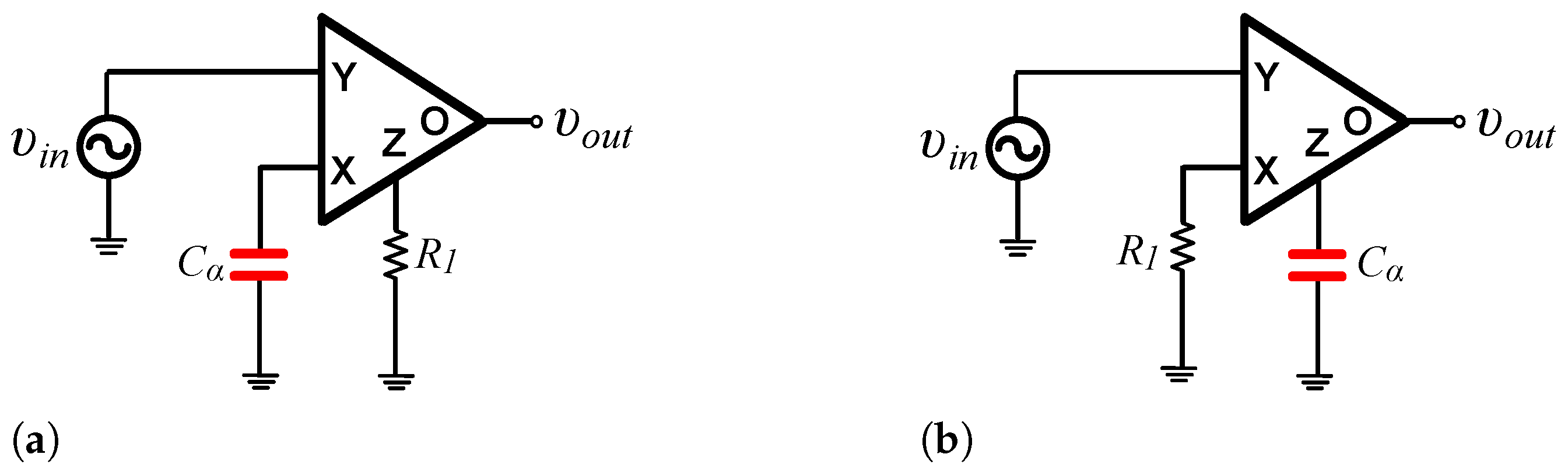
2. Novel Differentiation and Integration Stages
2.1. Proposed Topologies
2.2. Comparison with the Conventional Implementations
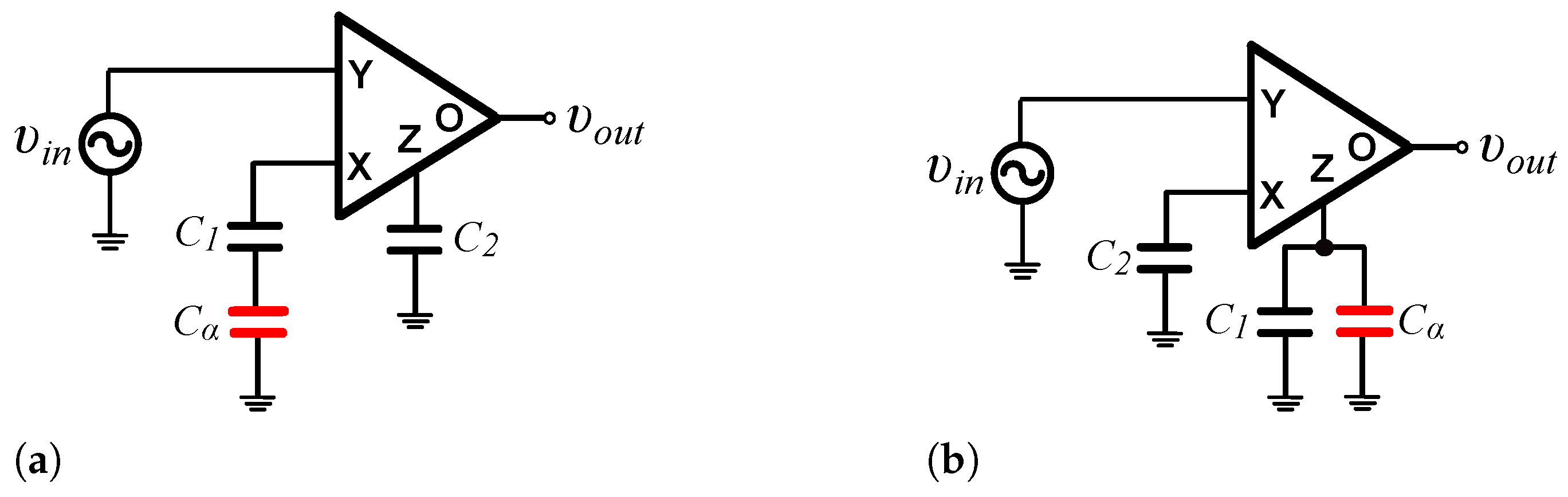
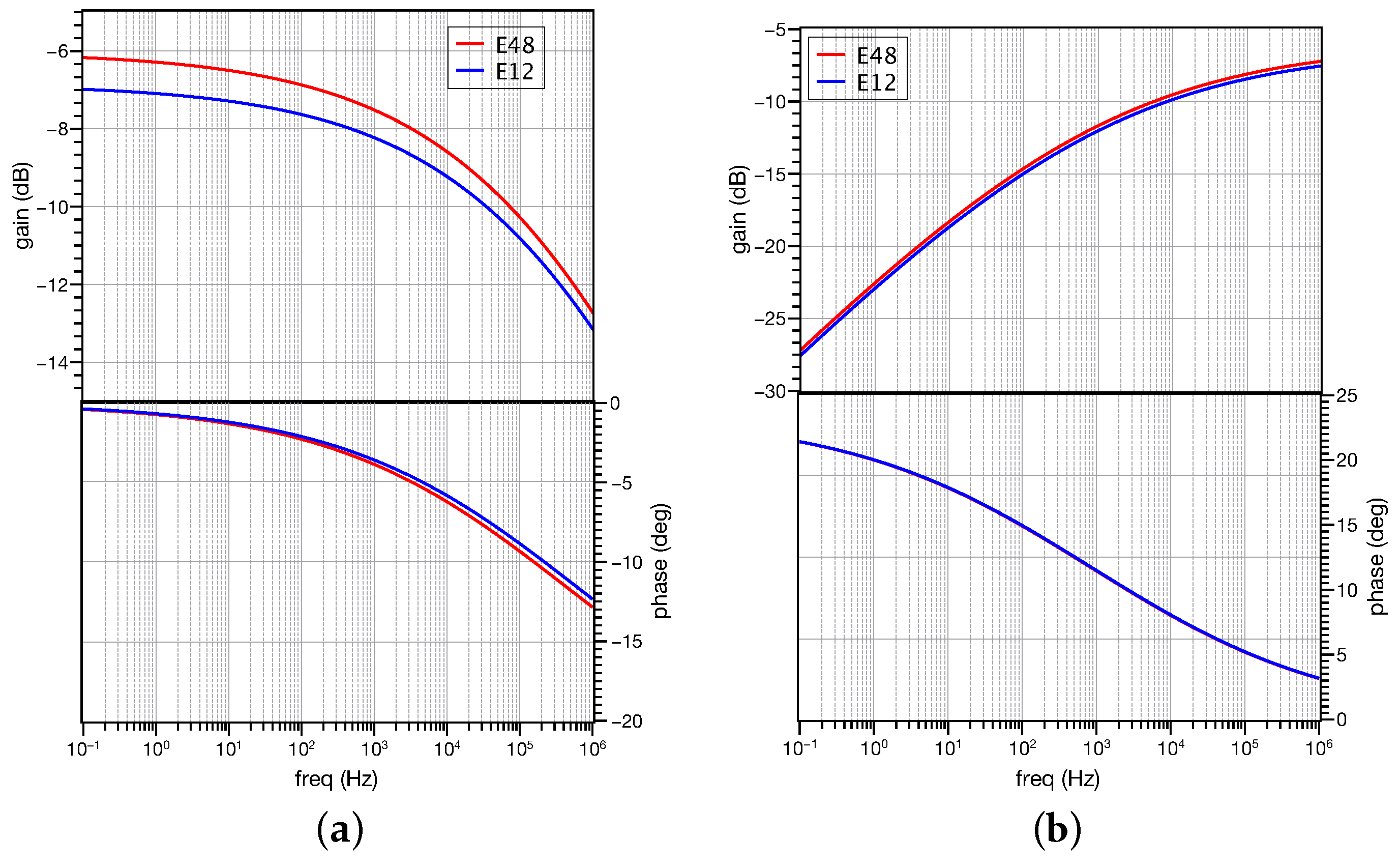
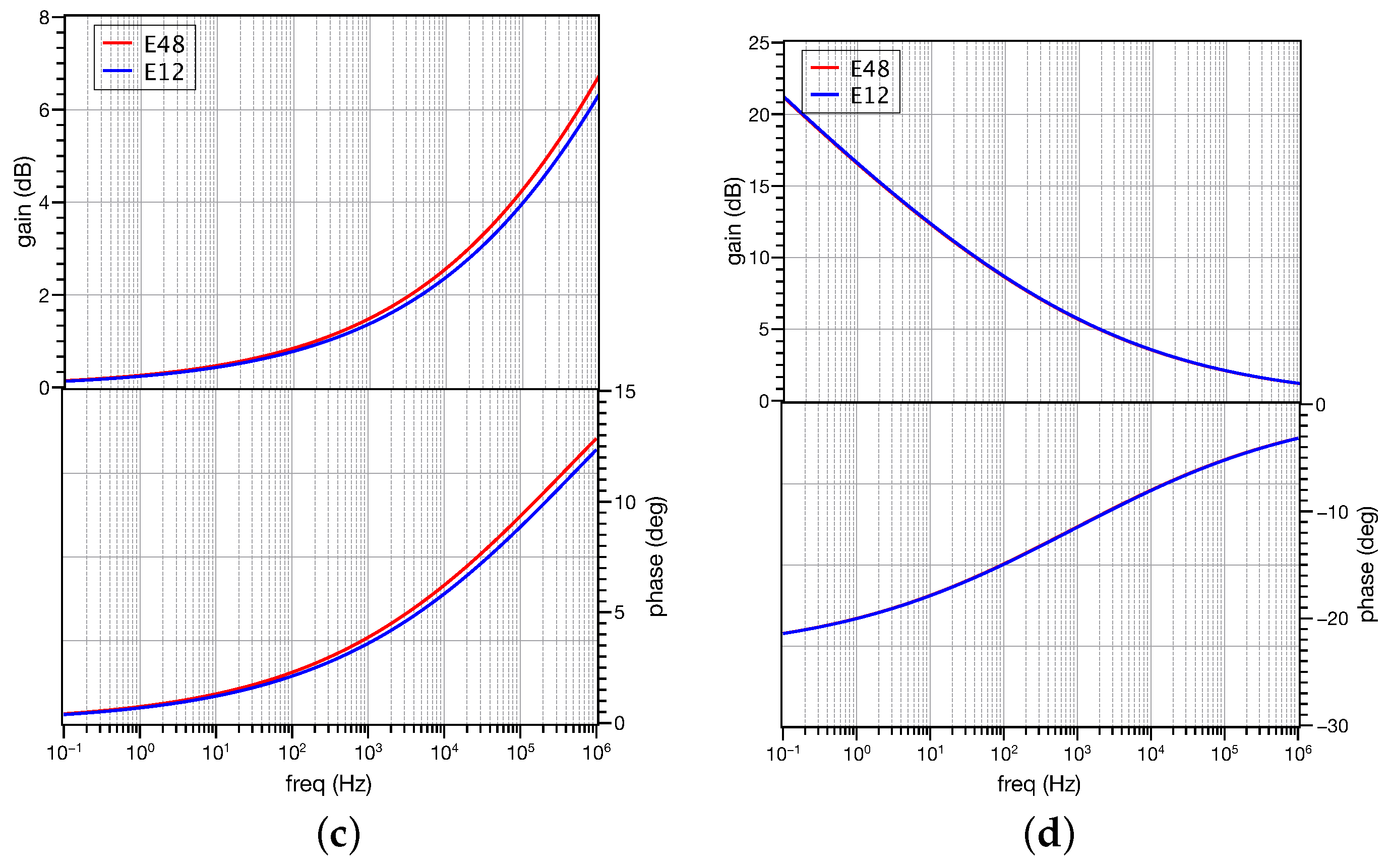
3. Filter Design Examples
3.1. Standard Filter Functions
3.2. Inverse Filter Functions
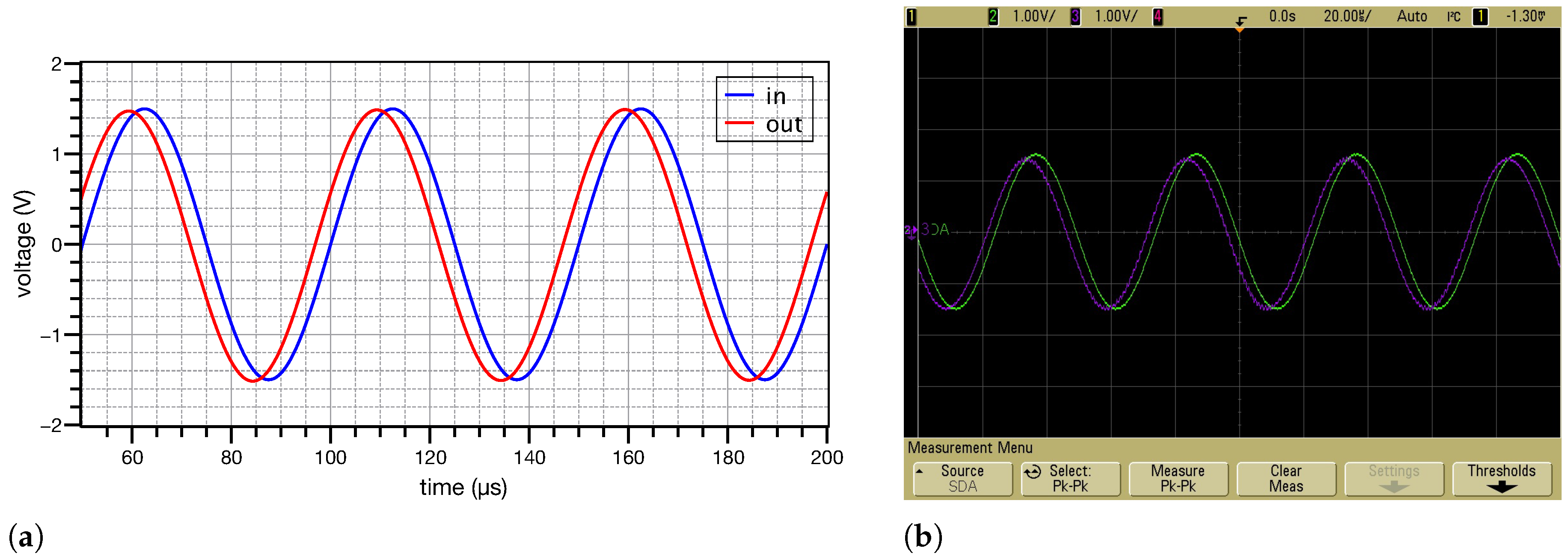
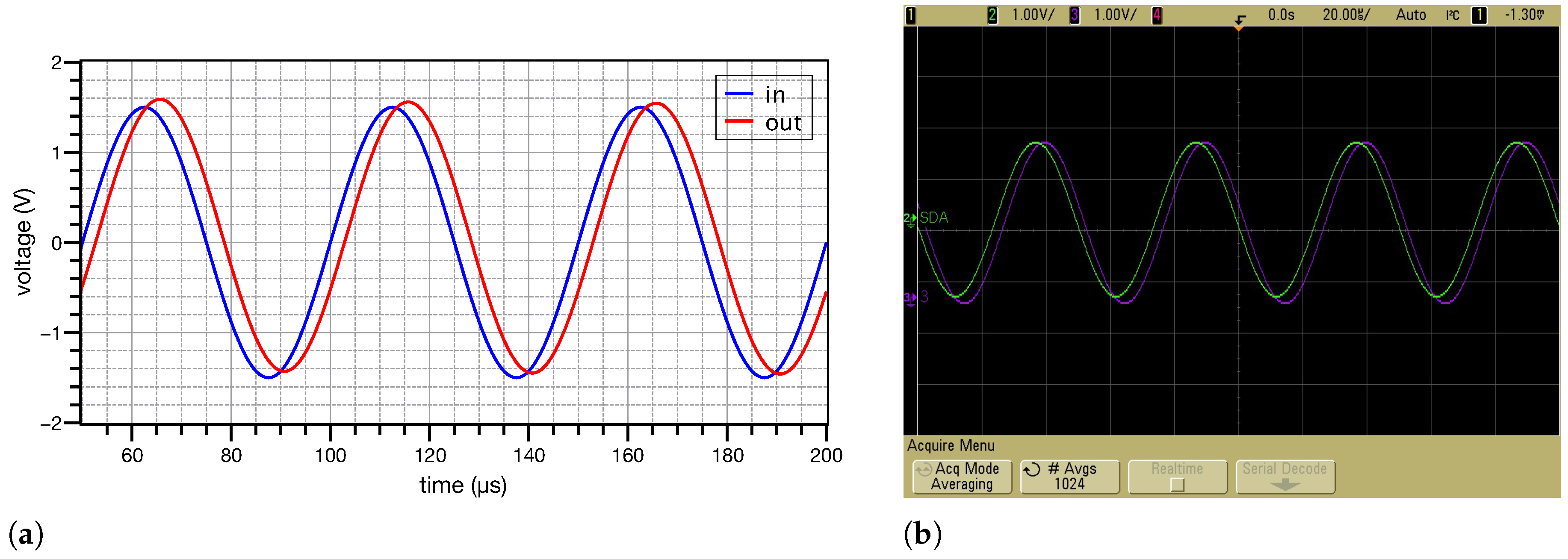
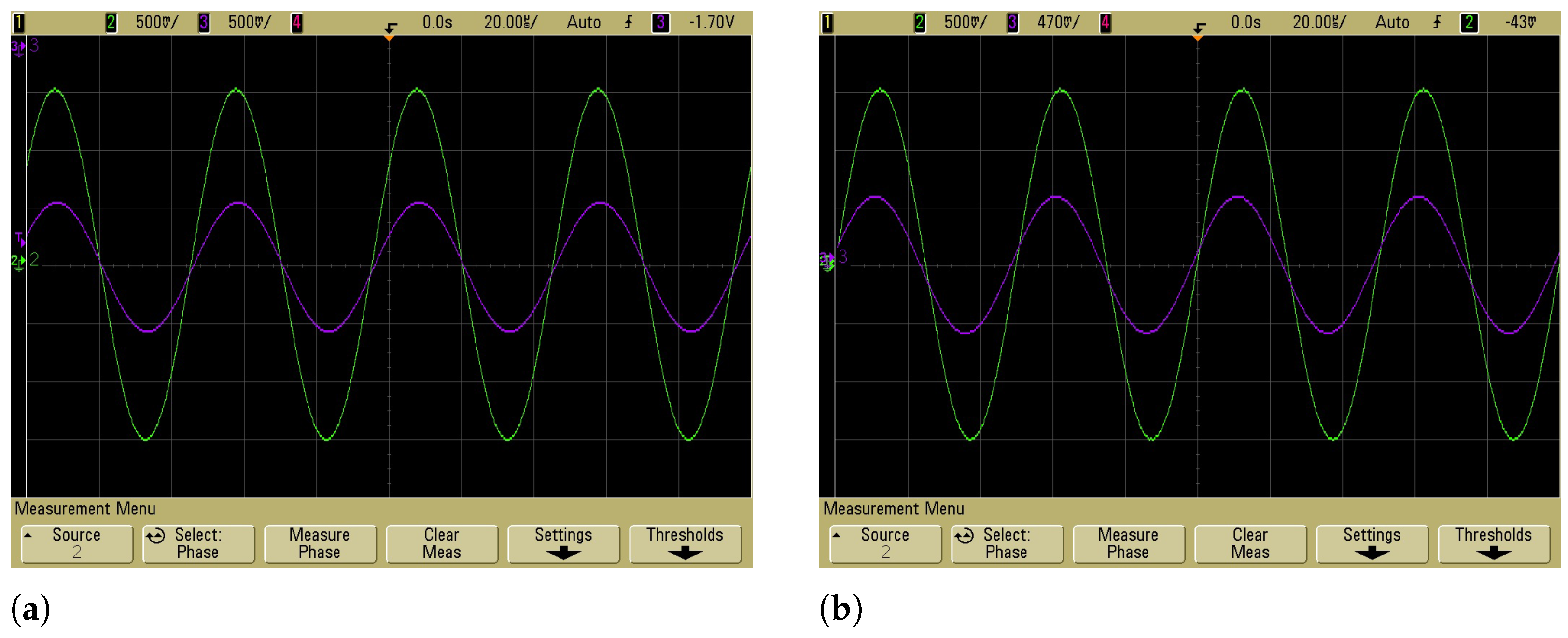
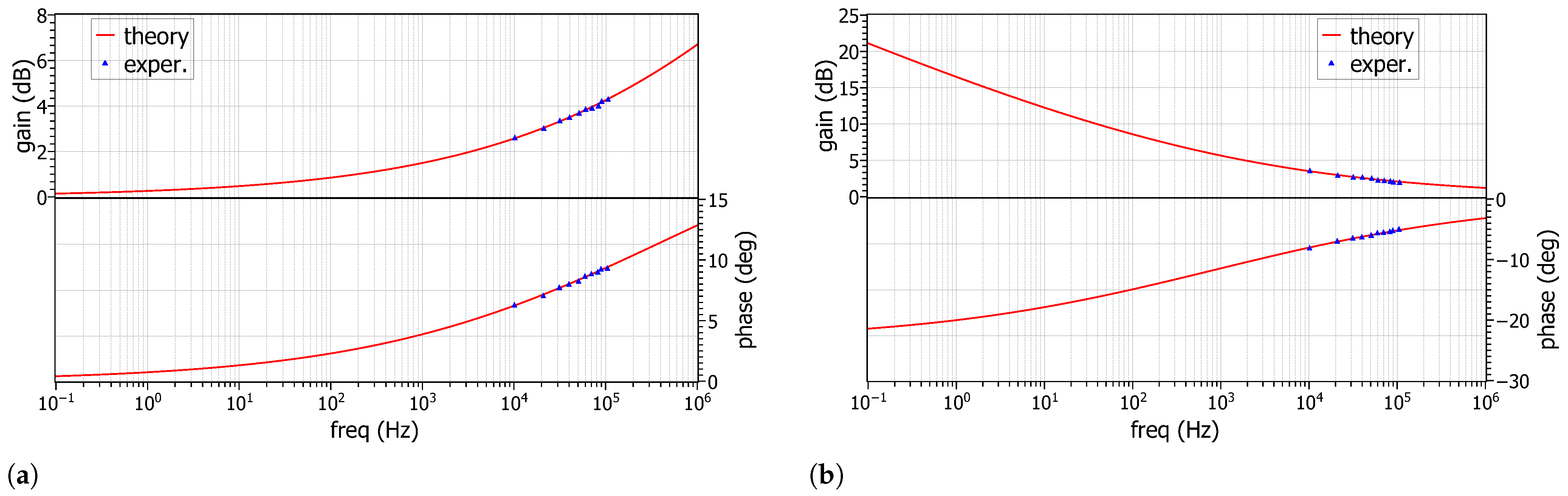
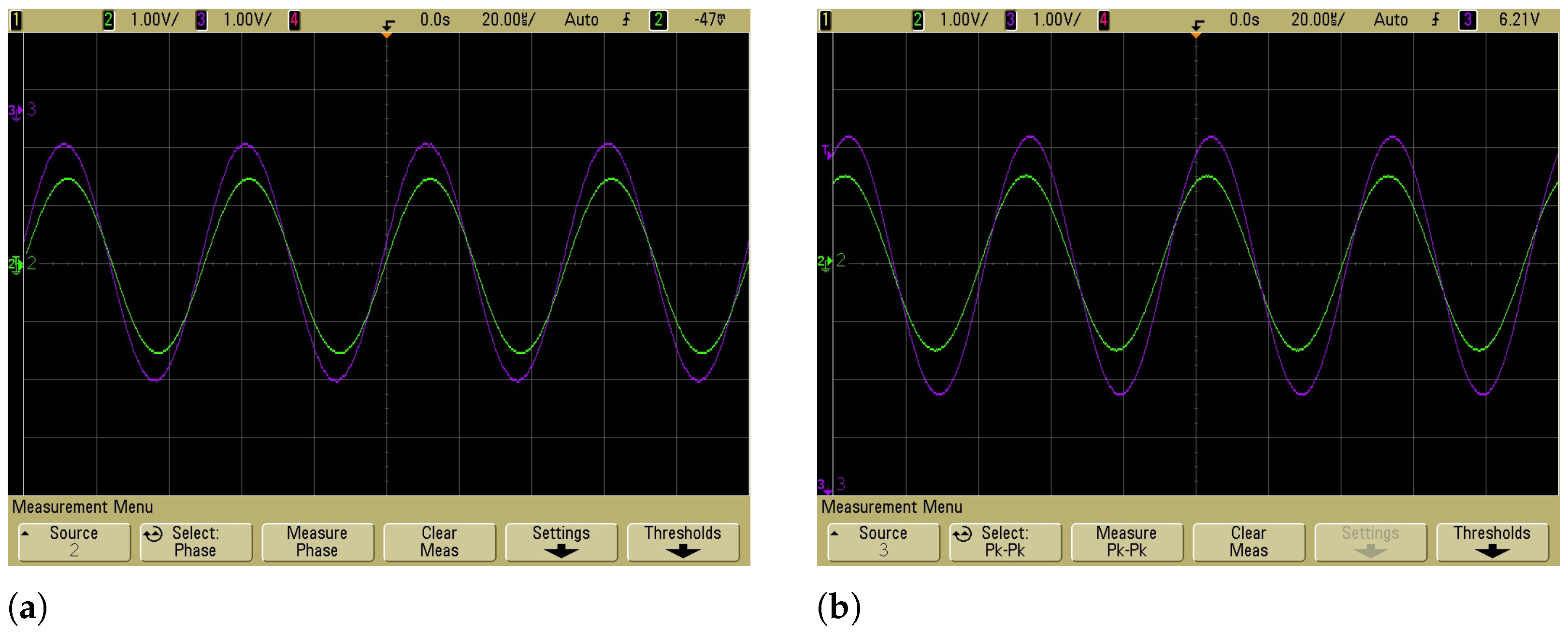
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFOA | Current Feedback Operational Amplifier |
| CNT | Carbon Nano-Tubes |
| MWCNT | Multi-Walled Carbon Nano-Tubes |
| RC | Resistor Capacitor |
References
- Podlubny, I. Fractional-order systems and PIλDμ controllers. IEEE Trans. Autom. Control 1999, 44, 208–214. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.; Yépez-Martínez, H.; Escobar-Jiménez, R.; Astorga-Zaragoza, C.; Reyes-Reyes, J. Analytical and numerical solutions of electrical circuits described by fractional derivatives. Appl. Math. Model. 2016, 40, 9079–9094. [Google Scholar] [CrossRef]
- Biswas, K.; Bohannan, G.; Caponetto, R.; Lopes, A.M.; Machado, J.A.T. Fractional-Order Devices; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Freeborn, T.J. A survey of fractional-order circuit models for biology and biomedicine. IEEE J. Emerg. Sel. Top. Crcuits Syst. 2013, 3, 416–424. [Google Scholar] [CrossRef]
- Tsirimokou, G.; Psychalinos, C.; Elwakil, A. Design of CMOS Analog Integrated Fractional-Order Circuits: Applications in Medicine And Biology; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Said, L.A.; Radwan, A.G.; Madian, A.H.; Soliman, A.M. Three fractional-order-capacitors-based oscillators with controllable phase and frequency. J. Circ. Syst. Comput. 2017, 26, 1750160. [Google Scholar] [CrossRef] [Green Version]
- Domansky, O.; Sotner, R.; Langhammer, L.; Jerabek, J.; Psychalinos, C.; Tsirimokou, G. Practical design of RC approximants of constant phase elements and their implementation in fractional-order PID regulators using CMOS Voltage Differencing Current Conveyors. Circ. Syst. Signal Process. 2019, 38, 1520–1546. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; Pano-Azucena, A.D.; Guillén-Fernández, O.; Silva-Juárez, A. Analog Implementations of Fractional-Order Chaotic Systems. In Analog/Digital Implementation of Fractional Order Chaotic Circuits and Applications; Springer: Berlin/Heidelberg, Germany, 2020; pp. 93–114. [Google Scholar]
- Tepljakov, A.; Alagoz, B.B.; Yeroglu, C.; Gonzalez, E.A.; Hosseinnia, S.H.; Petlenkov, E.; Ates, A.; Cech, M. Towards Industrialization of FOPID Controllers: A Survey on Milestones of Fractional-Order Control and Pathways for Future Developments. IEEE Access 2021, 9, 21016–21042. [Google Scholar] [CrossRef]
- Yousri, D.; AbdelAty, A.M.; Said, L.A.; AboBakr, A.; Radwan, A.G. Biological inspired optimization algorithms for cole-impedance parameters identification. AEU-Int. J. Electron. Commun. 2017, 78, 79–89. [Google Scholar] [CrossRef]
- Khalil, N.A.; Mohsen, M.; Ahmed, G.M.; Said, L.A.; Madian, A.H.; Radwan, A.G. Chapter Ten - Fractional-order oscillators based on a single Op-Amp. In Fractional Order Systems; Emerging Methodologies and Applications in Modelling; Radwan, A.G., Khanday, F.A., Said, L.A., Eds.; Academic Press: Cambridge, MA, USA, 2022; Volume 1, pp. 411–439. [Google Scholar] [CrossRef]
- Bertsias, P.; Psychalinos, C.; Elwakil, A.S.; Biswas, K. Single transistor fractional-order filter using a multi-walled carbon nanotube device. Analog. Integr. Circ. Signal Process. 2019, 100, 215–219. [Google Scholar] [CrossRef]
- Biswas, K.; Sen, S.; Dutta, P.K. Realization of a constant phase element and its performance study in a differentiator circuit. IEEE Trans. Circ. Syst. II Express Briefs 2006, 53, 802–806. [Google Scholar] [CrossRef]
- Biswas, K.; Caponetto, R.; Di Pasquale, G.; Graziani, S.; Pollicino, A.; Murgano, E. Realization and characterization of carbon black based fractional order element. Microelectron. J. 2018, 82, 22–28. [Google Scholar] [CrossRef]
- Buscarino, A.; Caponetto, R.; Di Pasquale, G.; Fortuna, L.; Graziani, S.; Pollicino, A. Carbon black based capacitive fractional order element towards a new electronic device. AEU-Int. J. Electron. Commun. 2018, 84, 307–312. [Google Scholar] [CrossRef]
- Buscarino, A.; Caponetto, R.; Graziani, S.; Murgano, E. Realization of fractional order circuits by a Constant Phase Element. Eur. J. Control 2020, 54, 64–72. [Google Scholar] [CrossRef]
- Caponetto, R.; Di Pasquale, G.; Graziani, S.; Murgano, E.; Pollicino, A. Realization of green fractional order devices by using bacterial cellulose. AEU-Int. J. Electron. Commun. 2019, 112, 152927. [Google Scholar] [CrossRef]
- John, D.A.; Banerjee, S.; Bohannan, G.W.; Biswas, K. Solid-state fractional capacitor using MWCNT-epoxy nanocomposite. Appl. Phys. Lett. 2017, 110, 163504. [Google Scholar] [CrossRef]
- John, D.A.; Aware, M.V.; Junghare, A.S.; Biswas, K. Performance Analysis of Solid-State Fractional Capacitor-Based Analog PIλDμ Controller. Circ. Syst. Signal Process. 2020, 39, 1815–1830. [Google Scholar] [CrossRef]
- Mohapatra, A.S.; Sarkar, S.; Biswas, K. Fabricating Solid State Fractional Capacitor in the Frequency Range of mHz to kHz. IEEE Trans. Comp. Packag. Manuf. Technol. 2021, 11, 2035–2038. [Google Scholar] [CrossRef]
- Tsirimokou, G.; Kartci, A.; Koton, J.; Herencsar, N.; Psychalinos, C. Comparative study of discrete component realizations of fractional-order capacitor and inductor active emulators. J. Circ. Syst. Comput. 2018, 27, 1850170. [Google Scholar] [CrossRef]
- Radwan, A.G.; Soliman, A.M.; Elwakil, A.S. First-order filters generalized to the fractional domain. J. Circ. Syst. Comput. 2008, 17, 55–66. [Google Scholar] [CrossRef]
- Bhaskar, D.; Kumar, M.; Kumar, P. Fractional order inverse filters using operational amplifier. Analog. Integr. Circ. Signal Process. 2018, 97, 149–158. [Google Scholar] [CrossRef]
- Bhaskar, D.; Kumar, M.; Kumar, P. Minimal realization of fractional-order inverse filters. IETE J. Res. 2020, 1–14. [Google Scholar] [CrossRef]
- Hamed, E.M.; Said, L.A.; Madian, A.H.; Radwan, A.G. On the approximations of CFOA-based fractional-order inverse filters. Circ. Syst. Signal Process. 2020, 39, 2–29. [Google Scholar] [CrossRef]
- Khali, N.A.; Said, L.A.; Radwan, A.G.; Soliman, A.M. Multifunction fractional inverse filter based on OTRA. In Proceedings of the 2019 Novel Intelligent and Leading Emerging Sciences Conference (NILES), Giza, Egypt, 28–30 October 2019; IEEE: Piscataway, NJ, USA, 2019; Volume 1, pp. 162–165. [Google Scholar] [CrossRef]
- Kumar, M.; Bhaskar, D.; Kumar, P. CFOA-Based New Structure of Fractional Order Inverse Filters. Int. J. Recent Technol. Eng 2020, 8, 2277–3878. [Google Scholar] [CrossRef]
- Matsuda, K.; Fujii, H. H∞ optimized wave-absorbing control-Analytical and experimental results. J. Guid. Control Dyn. 1993, 16, 1146–1153. [Google Scholar] [CrossRef]
- Oustaloup, A.; Levron, F.; Mathieu, B.; Nanot, F.M. Frequency-band complex noninteger differentiator: Characterization and synthesis. IEEE Trans. Circ. Syst. I Fund. Theory Appl. 2000, 47, 25–39. [Google Scholar] [CrossRef]
- Charef, A. Analogue realisation of fractional-order integrator, differentiator and fractional PIλDμ controller. IEE Proc.-Control Theory Appl. 2006, 153, 714–720. [Google Scholar] [CrossRef]
- Krishna, M.S.; Das, S.; Biswas, K.; Goswami, B. Fabrication of a fractional order capacitor with desired specifications: A study on process identification and characterization. IEEE Trans. Electron Devices 2011, 58, 4067–4073. [Google Scholar] [CrossRef]
- Bertsias, P.; Psychalinos, C.; Maundy, B.J.; Elwakil, A.S.; Radwan, A.G. Partial fraction expansion–based realizations of fractional-order differentiators and integrators using active filters. Int. J. Circuit Theory Appl. 2019, 47, 513–531. [Google Scholar] [CrossRef]
- Tsirimokou, G.; Psychalinos, C.; Elwakil, A.S.; Salama, K.N. Electronically tunable fully integrated fractional-order resonator. IEEE Trans. Circuits Syst. II Express Briefs 2017, 65, 166–170. [Google Scholar] [CrossRef]
- Jerabek, J.; Sotner, R.; Dvorak, J.; Polak, J.; Kubanek, D.; Herencsar, N.; Koton, J. Reconfigurable fractional-order filter with electronically controllable slope of attenuation, pole frequency and type of approximation. J. Circ. Syst. Comput. 2017, 26, 1750157. [Google Scholar] [CrossRef] [Green Version]
- Mahata, S.; Herencsar, N.; Kubanek, D. Further Generalization and Approximation of Fractional-Order Filters and Their Inverse Functions of the Second-Order Limiting Form. Fractal Fract. 2022, 6, 209. [Google Scholar] [CrossRef]
- Bertsias, P.; Tsirimokou, G.; Psychalinos, C.; Elwakil, A. Fully electronically tunable inverse fractional-order filter designs. In Proceedings of the 2019 Novel Intelligent and Leading Emerging Sciences Conference (NILES), Giza, Egypt, 28–30 October 2019; IEEE: Piscataway, NJ, USA, 2019; Volume 1, pp. 42–45. [Google Scholar]
- Analog Devices. AD844: Monolithic Op Amp with Quad Low Noise. Data Retrieved from Analog Devices. Available online: https://www.analog.com/media/en/technical-documentation/data-sheets/AD844.pdf (accessed on 19 November 2022).
- Psychalinos, C.; Elwakil, A.; Maundy, B.; Allagui, A. Analysis and realization of a switched fractional-order-capacitor integrator. Int. J. Circuit Theory Appl. 2016, 44, 2035–2040. [Google Scholar] [CrossRef]
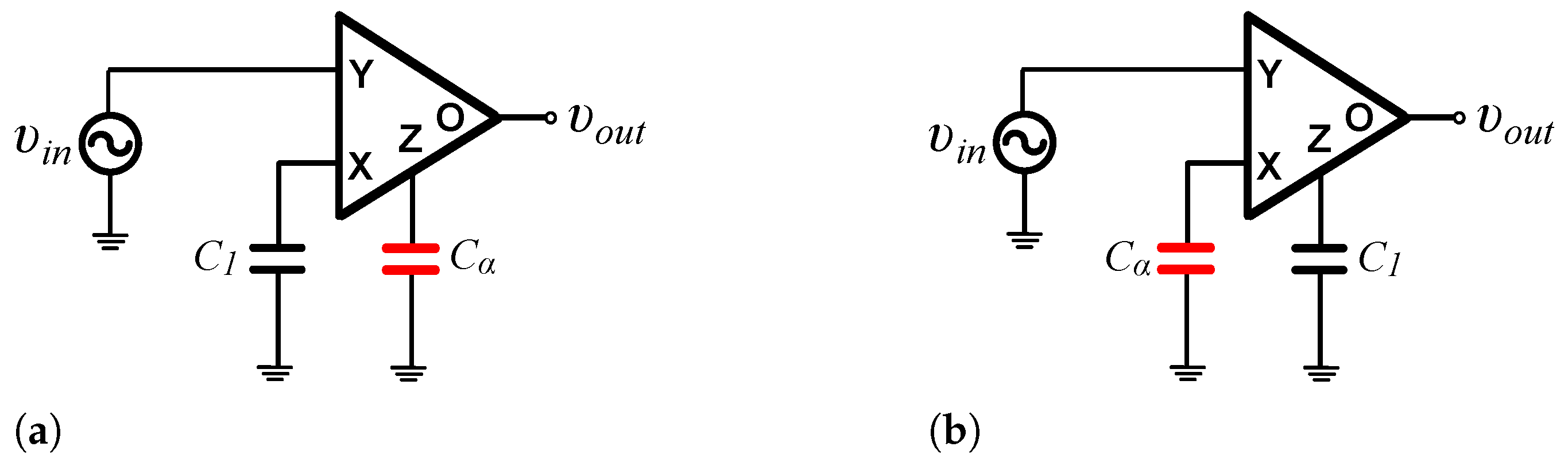
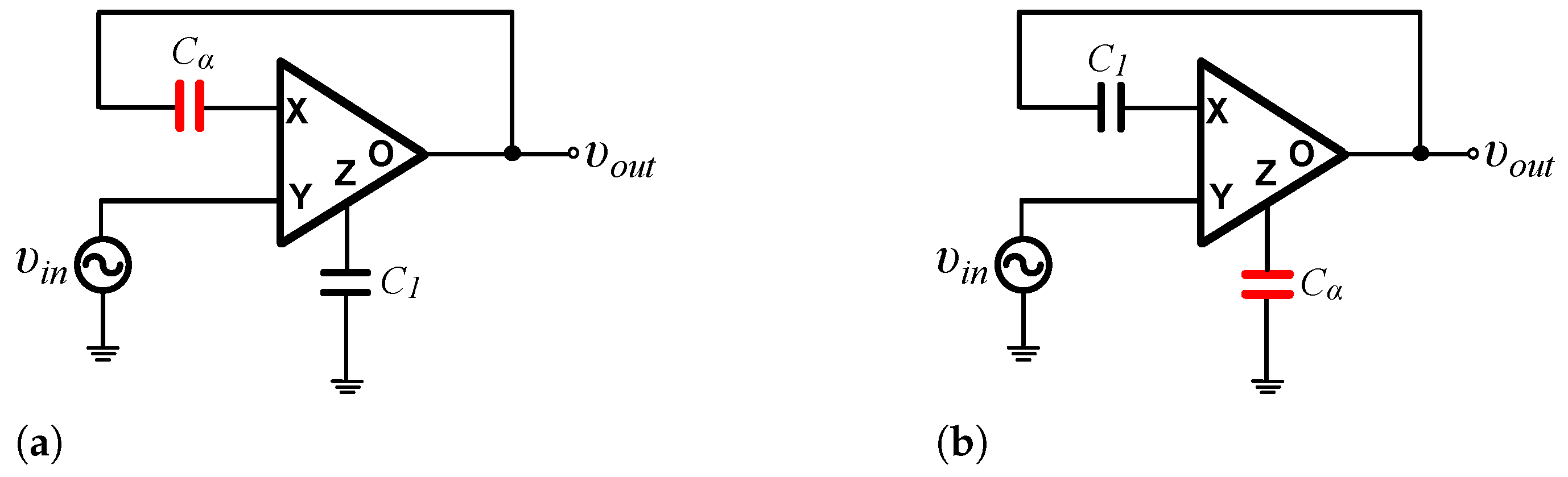





| Element | Value | Element | Value |
|---|---|---|---|
| 100 | - | - | |
| 348 | 332 nF | ||
| 3.48 k | 562 nF | ||
| 31.6 k | 953 nF | ||
| 301 k | 1.62 μF | ||
| 5.9 M | 1.27 μF |
| Element | Value | Element | Value |
|---|---|---|---|
| 100 k | - | - | |
| 71.5 | 0.75 nF | ||
| 127 k | 6.81 nF | ||
| 215 k | 61.9 nF | ||
| 383 k | 562 nF | ||
| 681 k | 4.87 μF |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patrinos, D.; Tsirmpas, G.; Bertsias, P.; Psychalinos, C.; Elwakil, A.S. Implementation and Experimental Verification of Resistorless Fractional-Order Basic Filters. Electronics 2022, 11, 3988. https://doi.org/10.3390/electronics11233988
Patrinos D, Tsirmpas G, Bertsias P, Psychalinos C, Elwakil AS. Implementation and Experimental Verification of Resistorless Fractional-Order Basic Filters. Electronics. 2022; 11(23):3988. https://doi.org/10.3390/electronics11233988
Chicago/Turabian StylePatrinos, Dimitrios, Georgios Tsirmpas, Panagiotis Bertsias, Costas Psychalinos, and Ahmed S. Elwakil. 2022. "Implementation and Experimental Verification of Resistorless Fractional-Order Basic Filters" Electronics 11, no. 23: 3988. https://doi.org/10.3390/electronics11233988








