Macro Model for Discrete-Time Sigma‒Delta Modulators
Abstract
1. Introduction
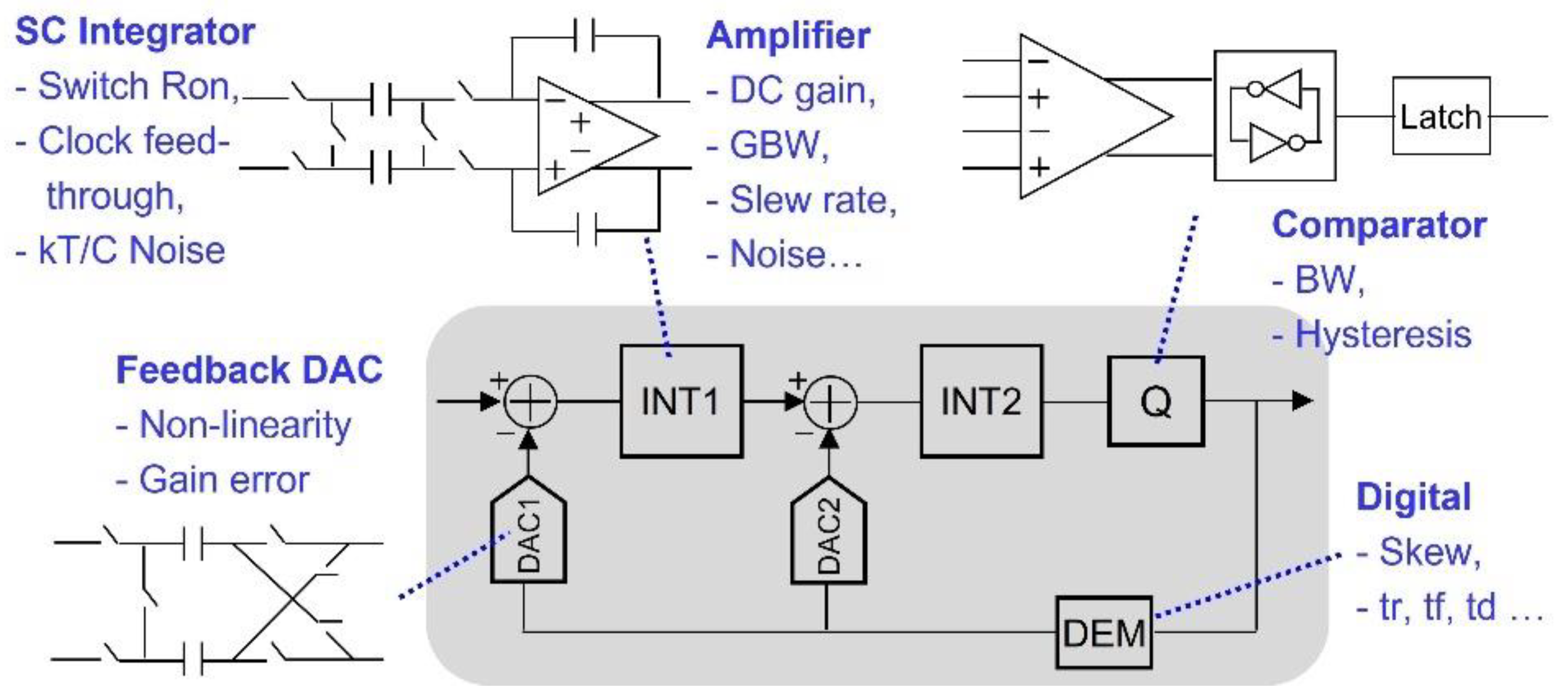
2. Proposed Macro Model
2.1. Sigma‒Delta Modulator Non-Idealities
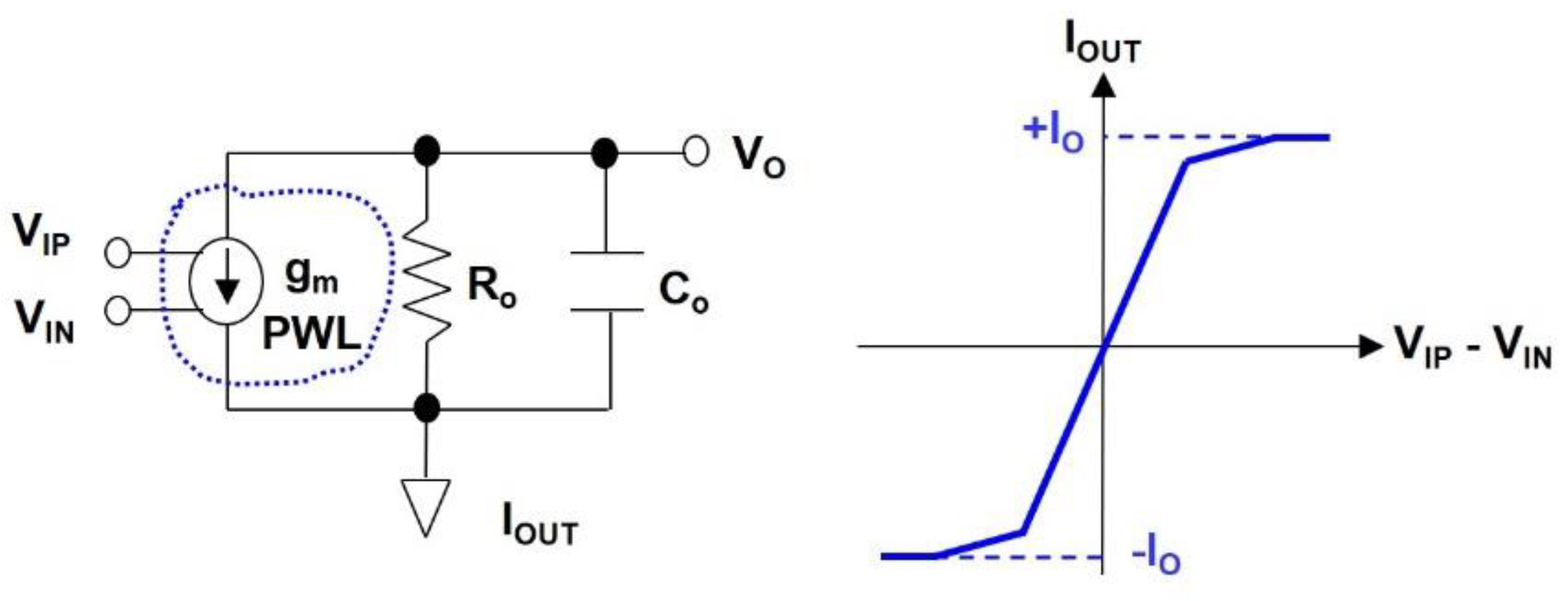
2.2. Amplifier Macro Model
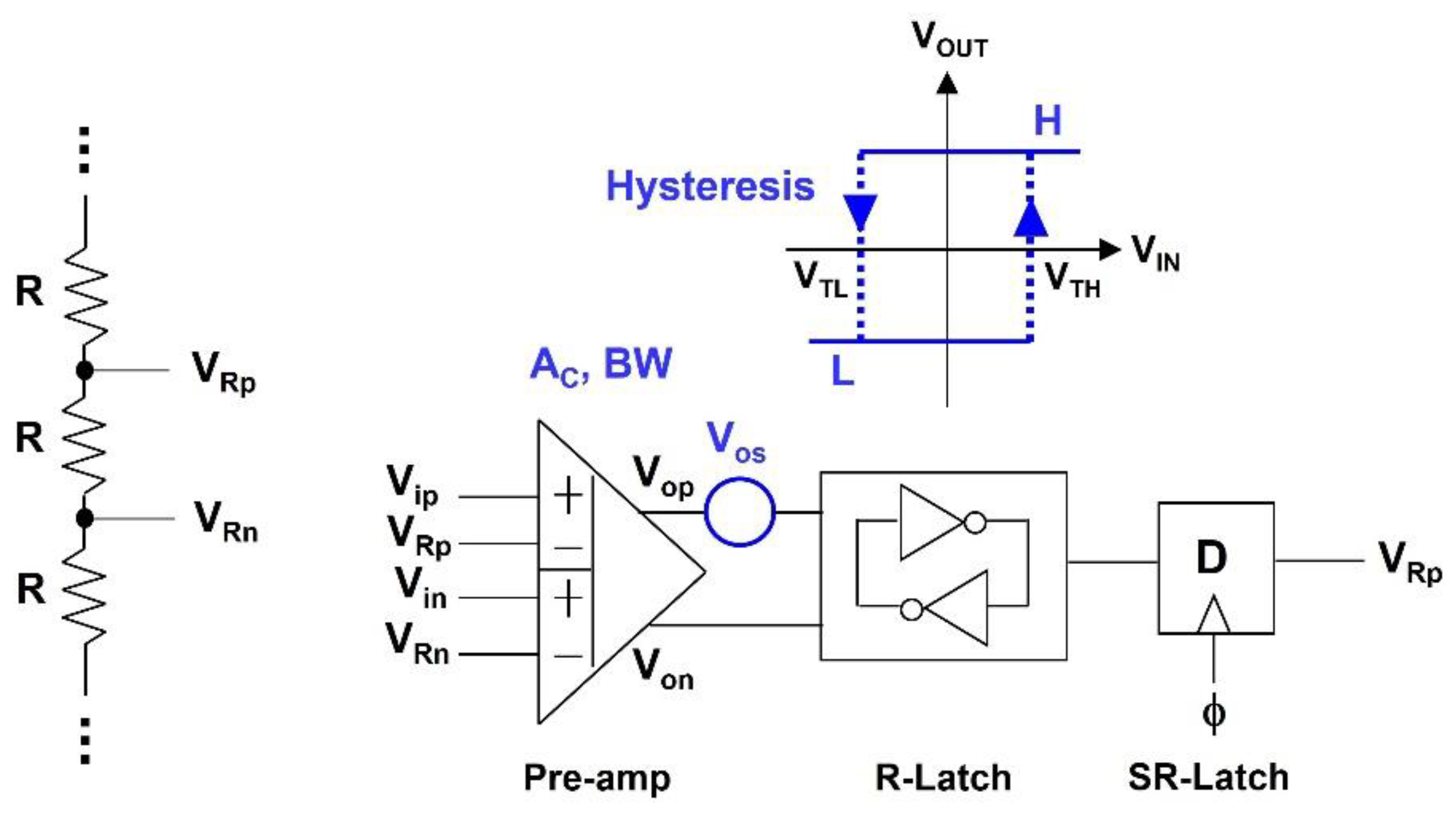
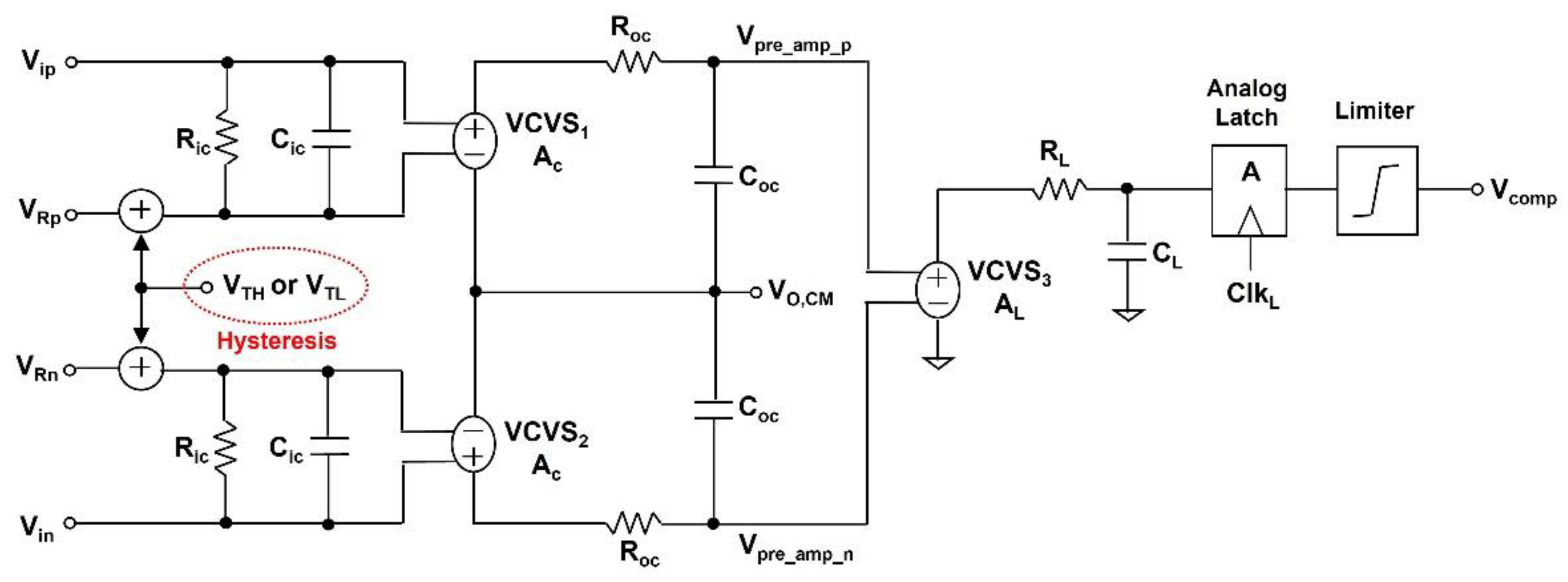
2.3. Comparator Macro Model
2.4. SC Integrator Macro Model
3. Macro Model Simulation Results
3.1. Simulation Setup
3.2. Effect of Amplifier Non-Idealities
3.3. Effect of Comparator Non-Idealities
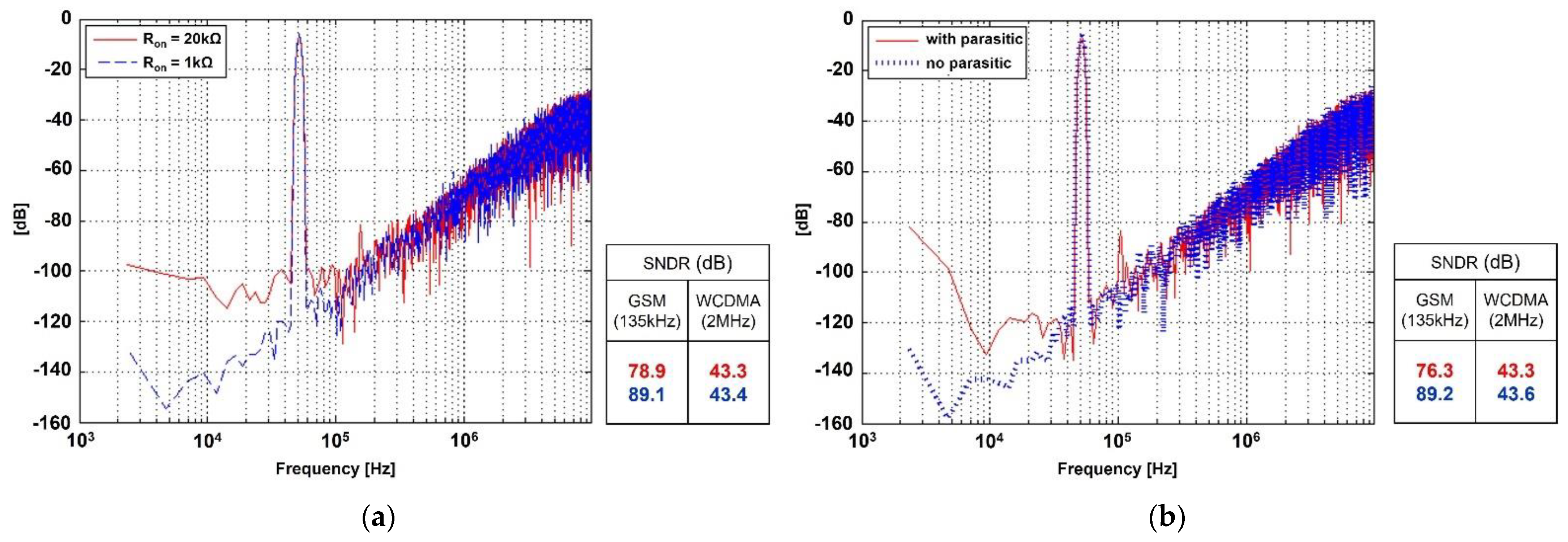
3.4. Effect of SC Integrator Non-Idealities
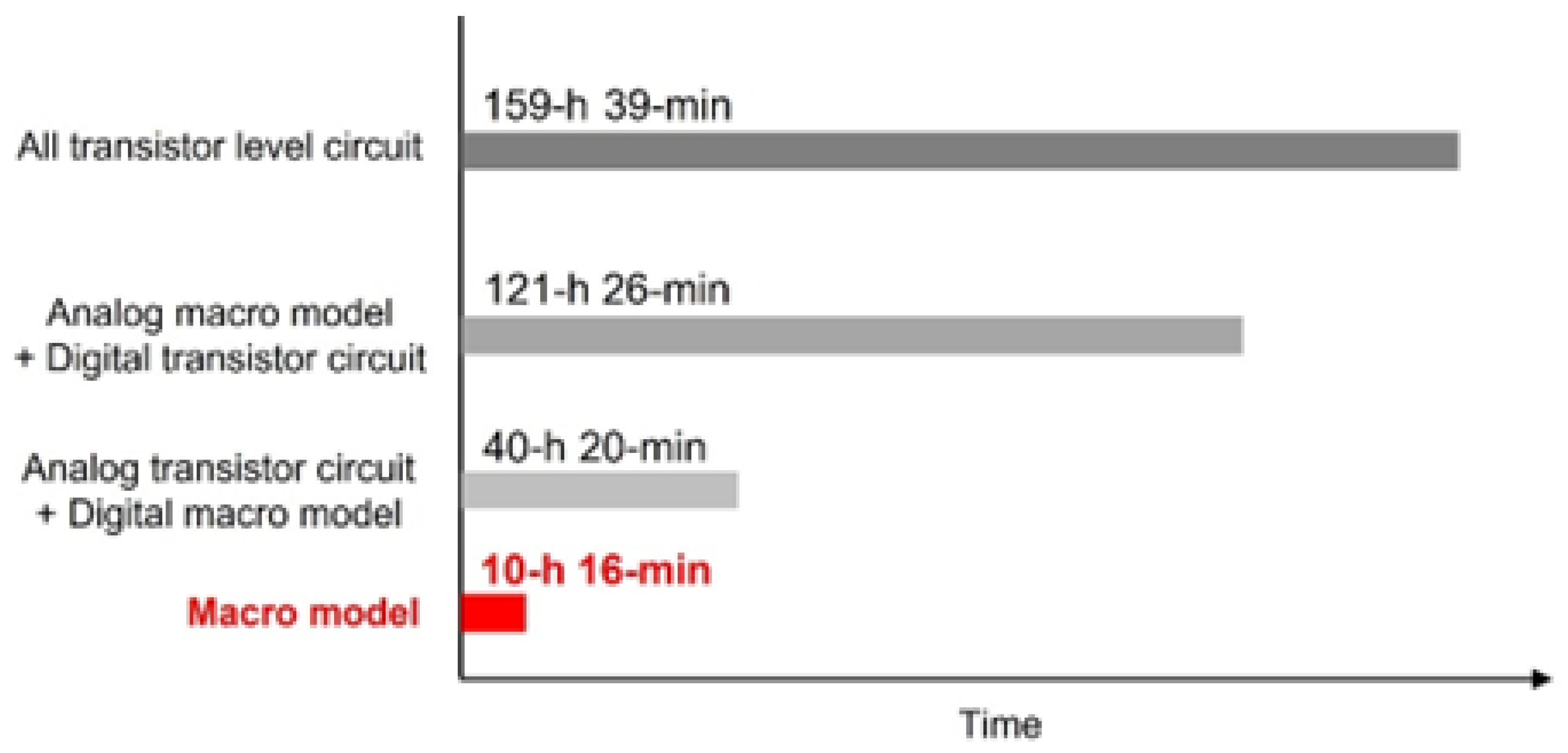
3.5. Simulation Time Comparison
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, D.; Qian, X.; Li, R.; Fei, C.; Jiang, L.; Chen, X.; Yang, Y.; Zhou, Q. High resolution ADC for ultrasound color doppler imaging based on MASH sigma-delta modulator. IEEE Trans. Biomed. Eng. 2020, 67, 1438–1449. [Google Scholar] [CrossRef]
- Boni, A.; Giuffred, L.; Pietrini, G.; Ronchi, M.; Caselli, M. A low-power sigma-delta modulator for healthcare and medical diagnostic applications. IEEE Trans. Circuits Syst. I Reg. Pap. 2022, 69, 207–219. [Google Scholar] [CrossRef]
- De la Rosa, J. Al-assisted sigma-delta converters—applications to cognitive radio. IEEE Trans. Circuits Syst. II Exp. Briefs 2022, 69, 2557–2563. [Google Scholar]
- Inose, H.; Yasuda, Y.; Murakami, J. A telemetering system by code modulation-Δ-Σ modulation. IRE Trans. Space Electron. Telem. 1962, SET-8, 204–209. [Google Scholar] [CrossRef]
- Sharifi, L.; Hashemipour, O. Multi-bit quantizer delta-sigma modulator with the feedback DAC mismatch error shaping. In Proceedings of the 27th Iranian Conference on Electrical Engineering (ICEE), Yazd, Iran, 1–2 May 2019; pp. 209–213. [Google Scholar]
- Pochet, C.; Hall, D.A. A pseudo-virtual ground feedforwarding technique enabling linearization and higher order noise shaping in VCO-based ΔΣ modulators. IEEE J. Solid-State Circuits 2022, 57, 3746–3756. [Google Scholar] [CrossRef]
- Zanbaghi, R.; Saxena, S.; Temes, G.C.; Fiez, T.S. A 75-dB SNDR, 5-MHz bandwidth stage-shared 2–2 MASH ΔΣ modulator dissipating 16 mW power. IEEE Trans. Circuits Syst. I Reg. Pap. 2012, 59, 1614–1625. [Google Scholar] [CrossRef]
- Colodro, F.; Torralba, A.; Laguna, M. Time-interleaved multirate sigma–delta modulators. IEEE Trans. Circuits Syst. II Exp. Briefs 2006, 53, 1026–1030. [Google Scholar] [CrossRef]
- Hoseini, Z.; Lee, K.S.; Kwon, C.K. Design of an 8-bit time-mode cyclic ADC based on macro modeling. Int. J. Circ. Theor. Appl. 2020, 48, 1839–1852. [Google Scholar] [CrossRef]
- Malcovati, P.; Brigati, S.; Francesconi, F.; Maloberti, F.; Cusinato, P.; Baschirotto, A. Behavioral modeling of switched-capacitor sigma-delta modulators. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2003, 69, 207–219. [Google Scholar] [CrossRef]
- Zare-Hoseini, H.; Kale, I.; Shoaei, O. Modeling of switched-capacitor delta-sigma modulators in SIMULINK. IEEE Trans. Instrum. Meas. 2005, 54, 1646–1653. [Google Scholar] [CrossRef]
- Suarez, G.; Jimenez, M.; Fernandez, F.O. Behavioral models for switched-capacitor ΣΔ modulators. IEEE Trans. Circuits Syst. I Reg. Pap. 2007, 54, 1236–1244. [Google Scholar] [CrossRef]
- Vázquez-Gutiérrez, A.E.; Ocampo-Hidalgo, J.J.; Molinar-Solís, J.E.; Pérez-Sánchez, G.G.; Ferreira-Medina, H. DSSim: A freeware tool for behavioral simulation of discrete-time ΣΔ modulators. IEEE Can. J. Elec. Comp. Eng. 2021, 44, 302–312. [Google Scholar] [CrossRef]
- Gonzalez-Diaz, V.R.; Pareschi, F. A 65 nm continuous-time sigma-delta modulator with limited OTA DC gain compensation. IEEE Access 2020, 8, 36464–36475. [Google Scholar] [CrossRef]
- Jiang, D.; Qi, L.; Sin, S.-W.; Maloberti, F.; Martins, R.P. A time-interleaved 2nd-order ΔΣ modulator achieving 5-MHz bandwidth and 86.1-dB SNDR using digital feed-forward extrapolation. IEEE J. Solid-State Circuits 2021, 56, 2375–2387. [Google Scholar] [CrossRef]
- Zhao, Y.; Shang, Z.; Lian, Y. A 2.55 NEF 76 dB CMRR DC-coupled fully differential difference amplifier based analog front end for wearable biomedical sensors. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 918–926. [Google Scholar] [CrossRef] [PubMed]
- An, X.; Wagner, J.; Ellinger, F. Fully differential ultra-wideband amplifier with 46 −dB gain and positive feedback for increased bandwidth. IEEE Trans. Circuits Syst. II: Exp. Briefs 2021, 68, 1083–1087. [Google Scholar] [CrossRef]
- Choksi, O.; Carley, L.R. Analysis of switched-capacitor common-mode feedback circuit. IEEE Trans. Circuits Syst II Analog Digit. Signal Process. 2003, 50, 906–917. [Google Scholar] [CrossRef]
- Yousefirad, M.; Yavari, M. Kick-back noise reduction and offset cancellation technique for dynamic latch comparator. In Proceedings of the 29th Iranian Conference on Electrical Engineering (ICEE), Tehran, Iran, 18–20 May 2021; pp. 149–153. [Google Scholar]
- Carusone, T.C.; Johns, D.A.; Martin, K. Analog Integrated Circuit Design, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2012; pp. 414–415. [Google Scholar]
- Abozeid, K.M.; Aboudina, M.M.; Khalil, A.H. Different configurations for dynamic latched comparators used in ultra low power analog to digital converters. In Proceedings of the International Conference on Engineering and Technology (ICET), Cairo, Egypt, 19–20 April 2014; pp. 1–6. [Google Scholar]
- Martin, K. Improved circuits for the realization of switched-capacitor filters. IEEE Trans. Circuits Syst. 1980, 27, 237–244. [Google Scholar] [CrossRef]
- Lee, K.S.; Kwon, S.; Maloberti, F. A power efficient time-interleaved ΣΔ modulator for broadband applications. IEEE J. Solid-State Circuits 2007, 42, 1206–1215. [Google Scholar]
- Ashtiani, S.J.; Shoaei, O.; Hasan, S.M.; Jannesari, A. On the parasitic-sensitivity of switched-capacitor summing-integrator structures for ΣΔ modulators. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 2003, 50, 634–640. [Google Scholar] [CrossRef]
- Sai, T.; Sugimoto, Y. Design of a 1-V operational passive sigma-delta modulator. Proceedings the of European Conference on Circuit Theory and Design, Antalya, Turkey, 23–27 August 2009; pp. 751–754. [Google Scholar]


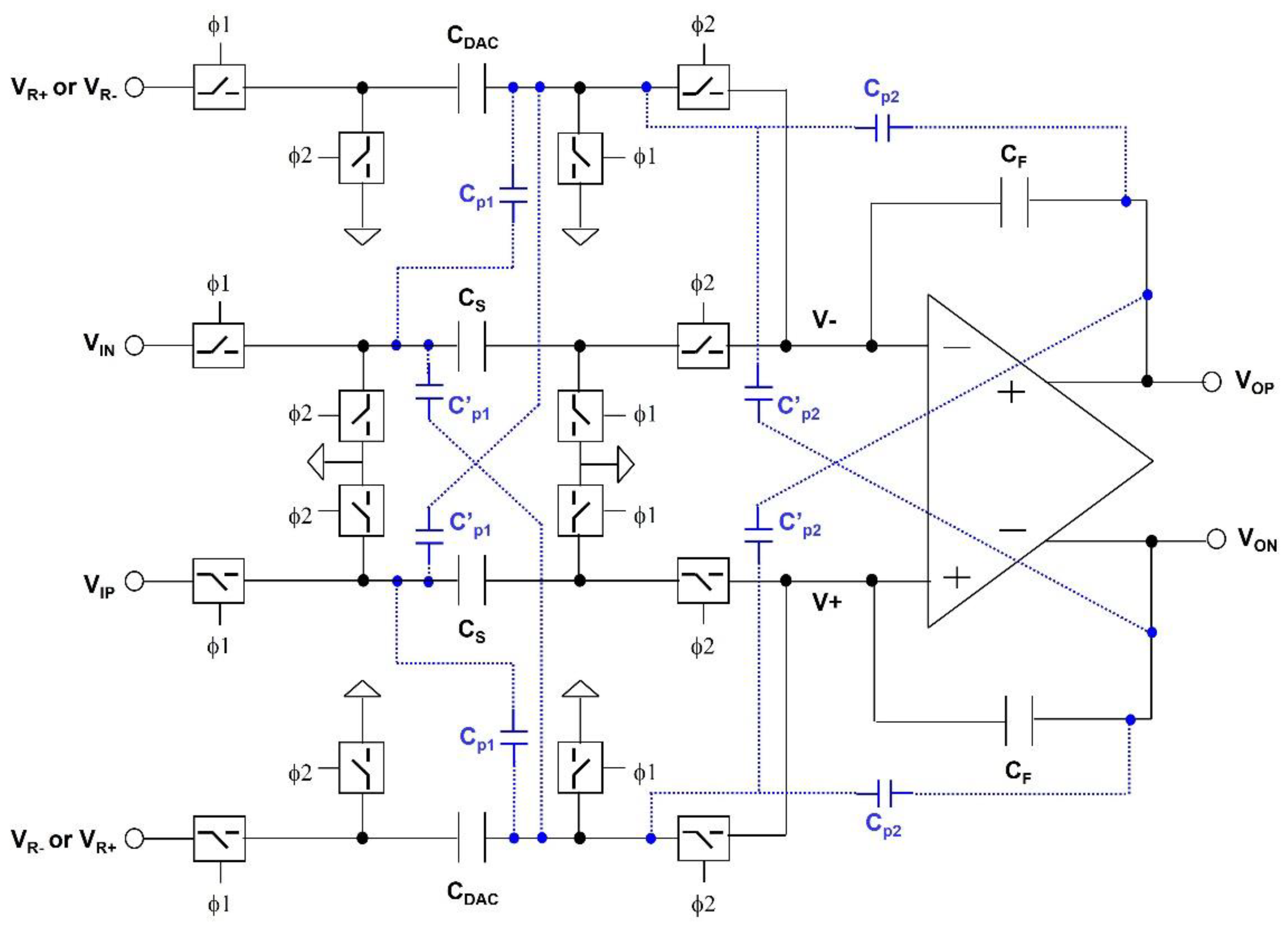
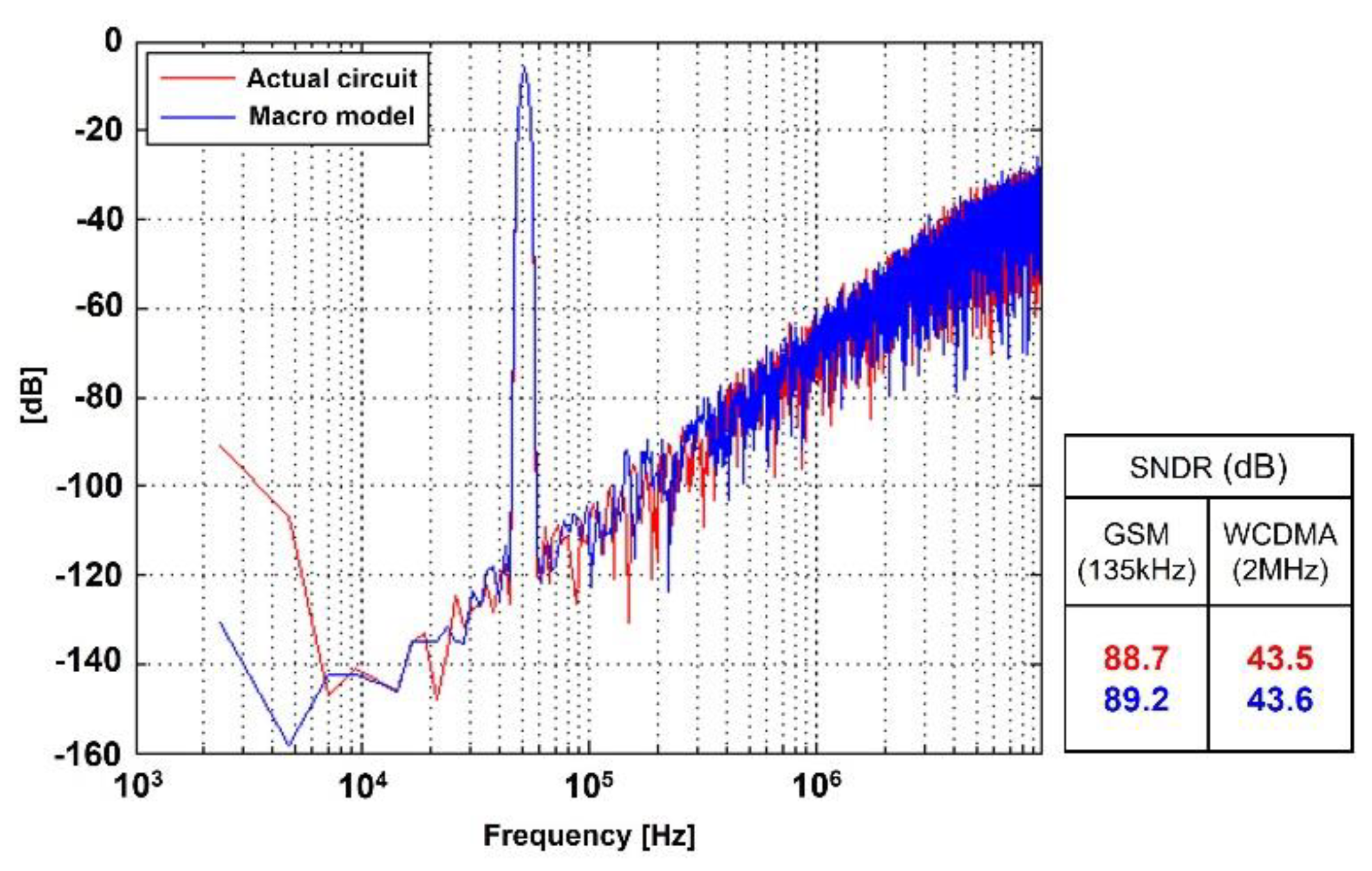
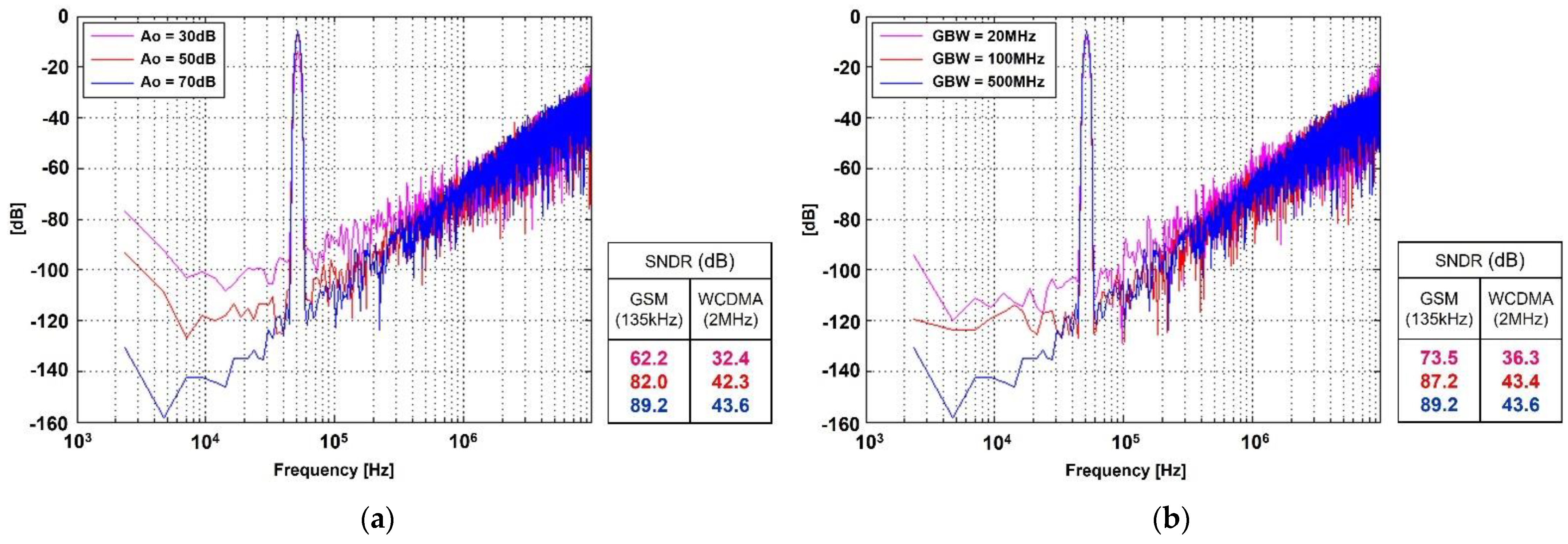

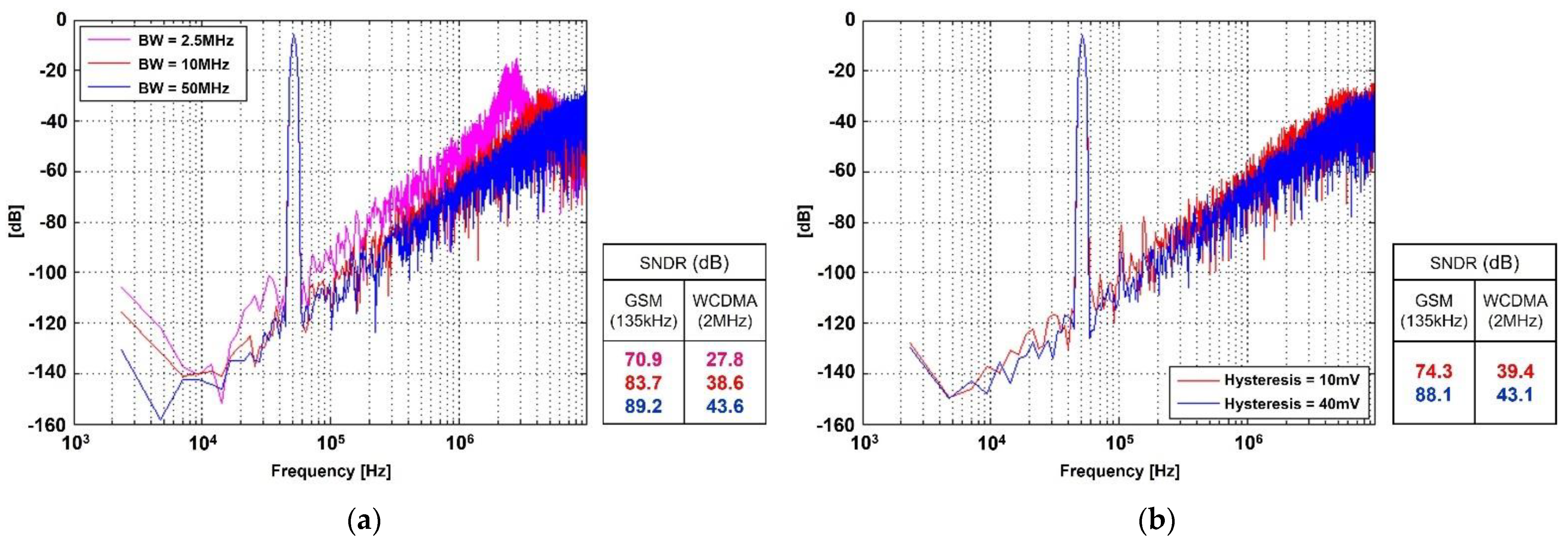
| Parameter [Unit] | Amplifier-1 | Amplifier-2 |
|---|---|---|
| gm [uA/V] Ro [MΩ] Ci [fF] Co [fF] Vos [mV] SR [V/us] | 200 10 50 25 1 100 | 100 10 25 10 2 50 |
| Integrator-1 | Integrator-2 | |
| CS [fF] CF [fF] Ron [Ω] Cp1 [fF] Cp2 [fF] C’p1 [fF] C’p2 [fF] | 250 500 1 k 3 2 1 0.5 | 200 100 1 k 3 2 1 0.5 |
| Comparator | ||
| Ac [V/V] Roc [MΩ] Coc [fF] VTL [mV] VTH [mV] AL [V/V] RL [MΩ ] CL [fF] | 5 0.3 10 −5 +5 20 0.2 10 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, K.-S. Macro Model for Discrete-Time Sigma‒Delta Modulators. Electronics 2022, 11, 3994. https://doi.org/10.3390/electronics11233994
Lee K-S. Macro Model for Discrete-Time Sigma‒Delta Modulators. Electronics. 2022; 11(23):3994. https://doi.org/10.3390/electronics11233994
Chicago/Turabian StyleLee, Kye-Shin. 2022. "Macro Model for Discrete-Time Sigma‒Delta Modulators" Electronics 11, no. 23: 3994. https://doi.org/10.3390/electronics11233994
APA StyleLee, K.-S. (2022). Macro Model for Discrete-Time Sigma‒Delta Modulators. Electronics, 11(23), 3994. https://doi.org/10.3390/electronics11233994





