Deep Learning-Based Modulation Recognition for Low Signal-to-Noise Ratio Environments
Abstract
1. Introduction
- We propose a novel modulation classification method based on deep learning, which considers time-frequency characteristics of signals as classifying features.
- We carry out time-frequency analysis of the signal and transform the original received signals into CWT images which are distinguishable and feature informative.
- We conduct experiments to test the performance of our proposed method and the experimental results show that the model reaches to 95% accuracy which demonstrates the effectiveness of our proposed method.
2. Related Work
3. Materials and Methods
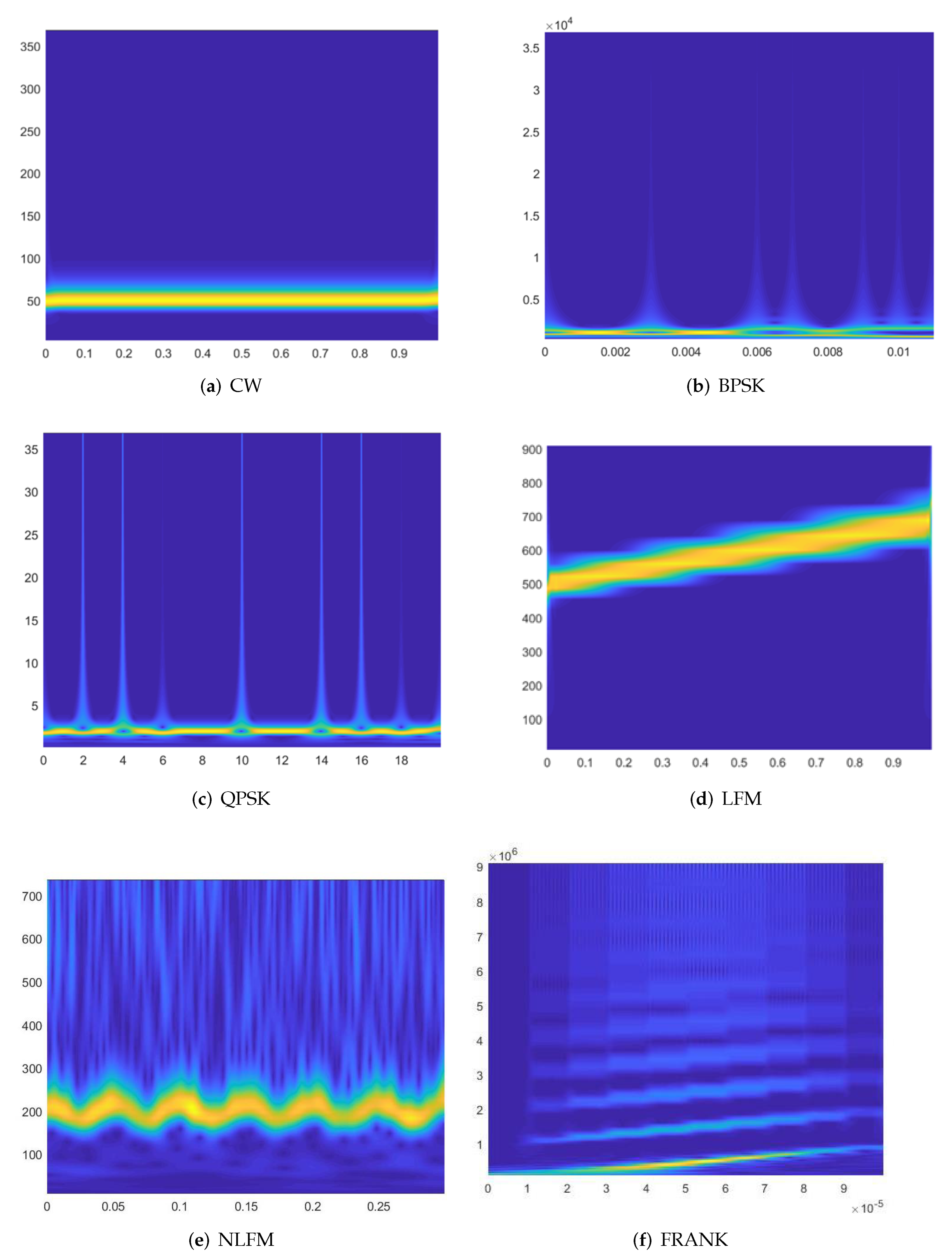
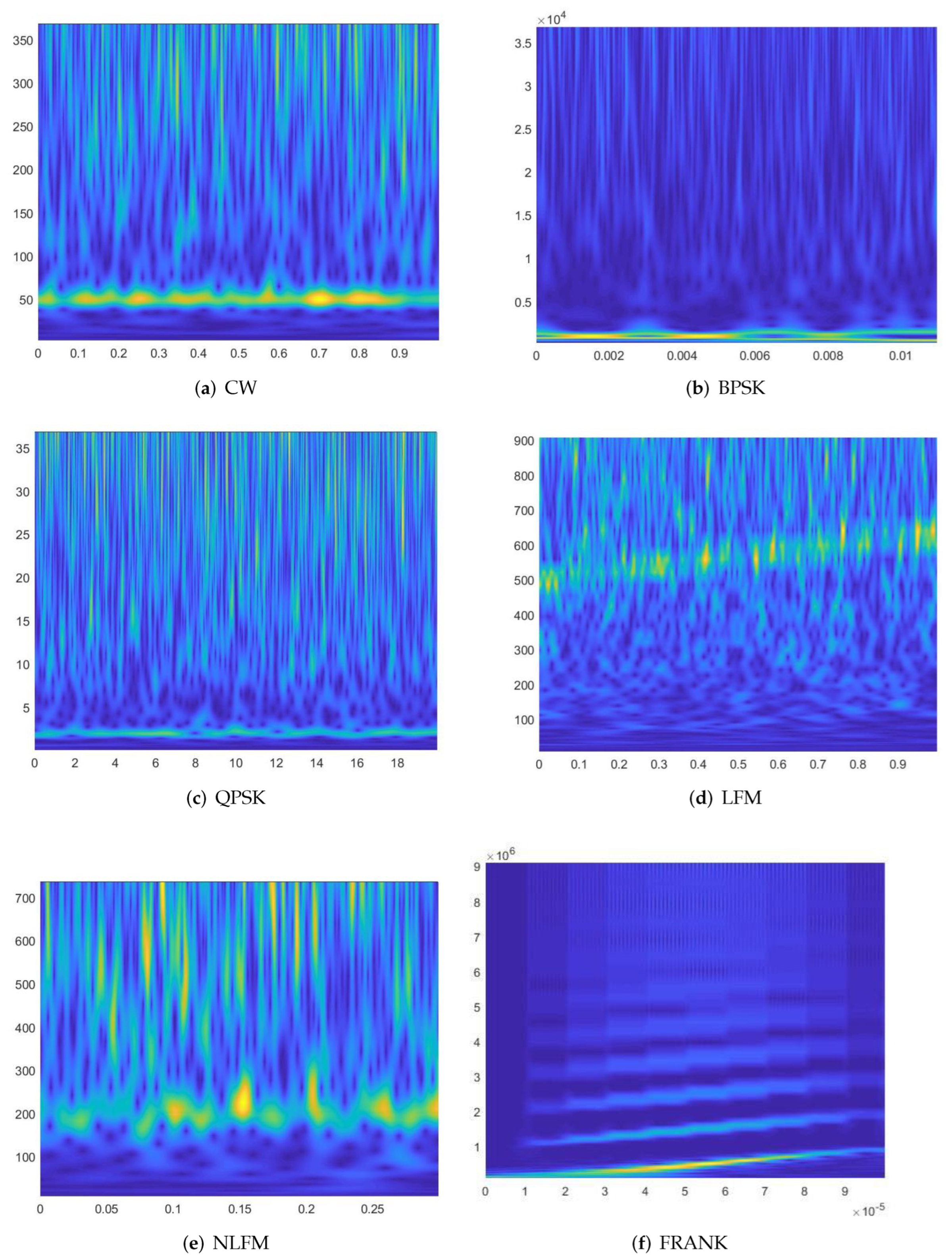
3.1. Time-Frequency Representation
3.2. System Model
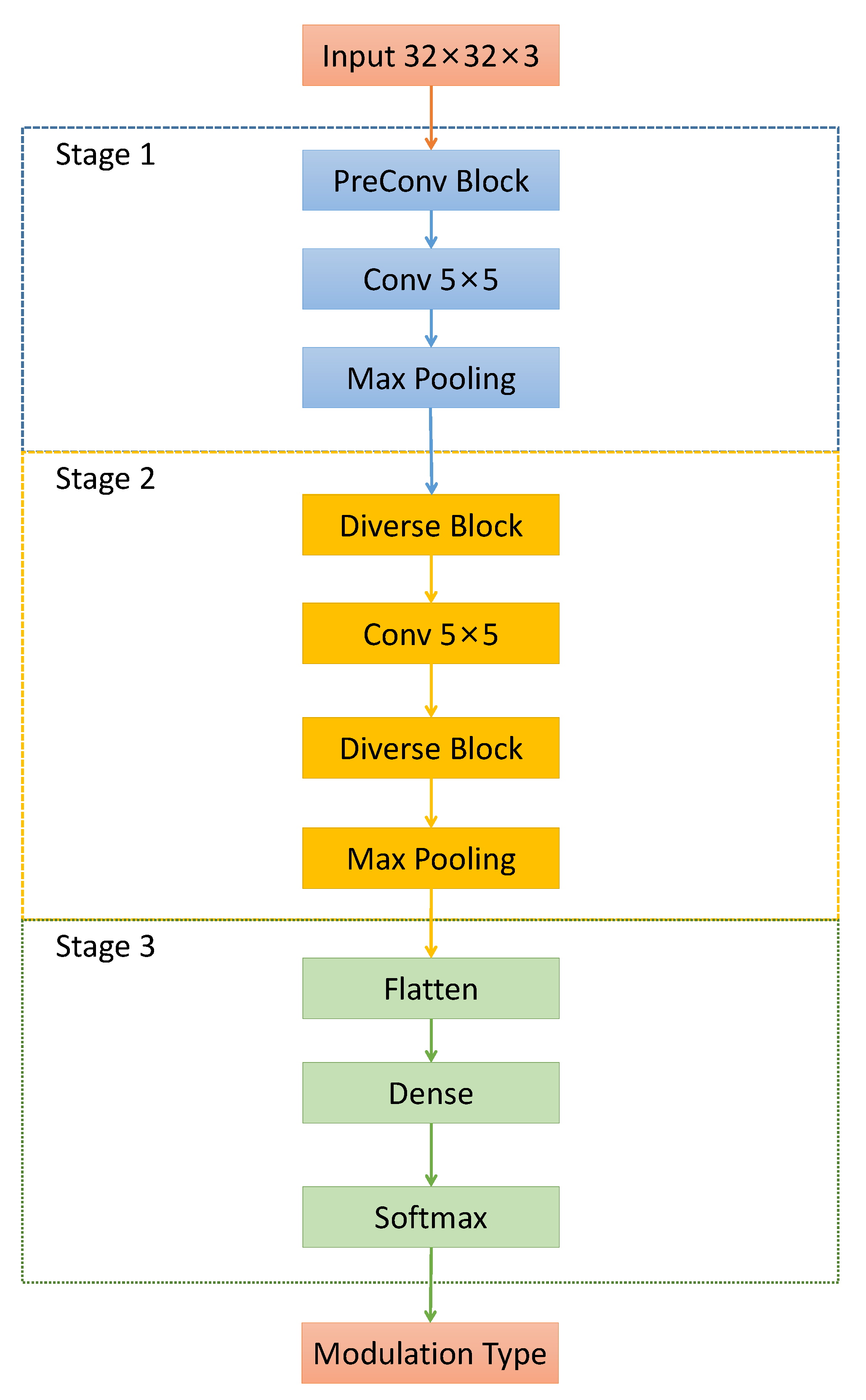
3.2.1. Overview
3.2.2. PreConv
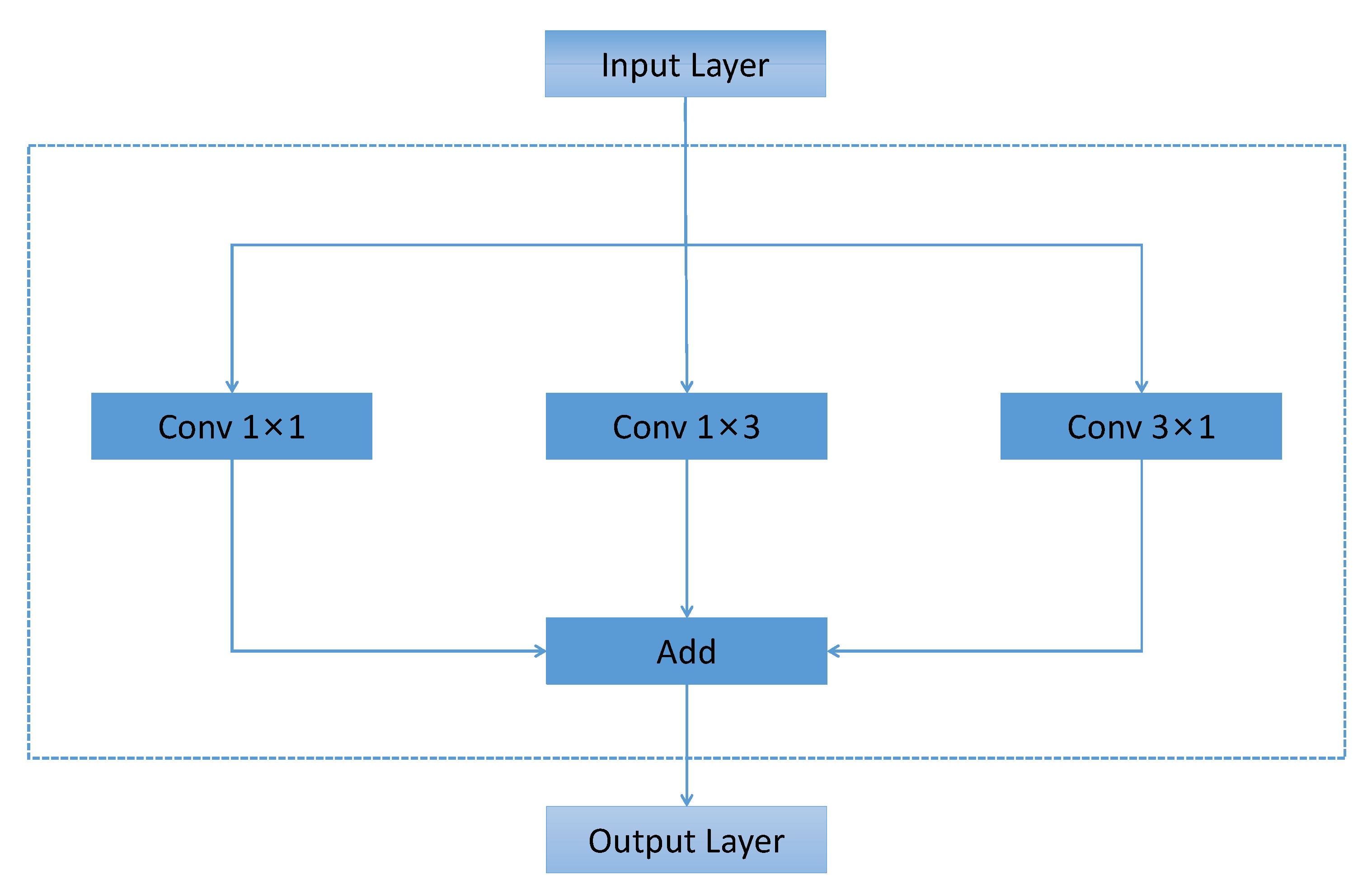
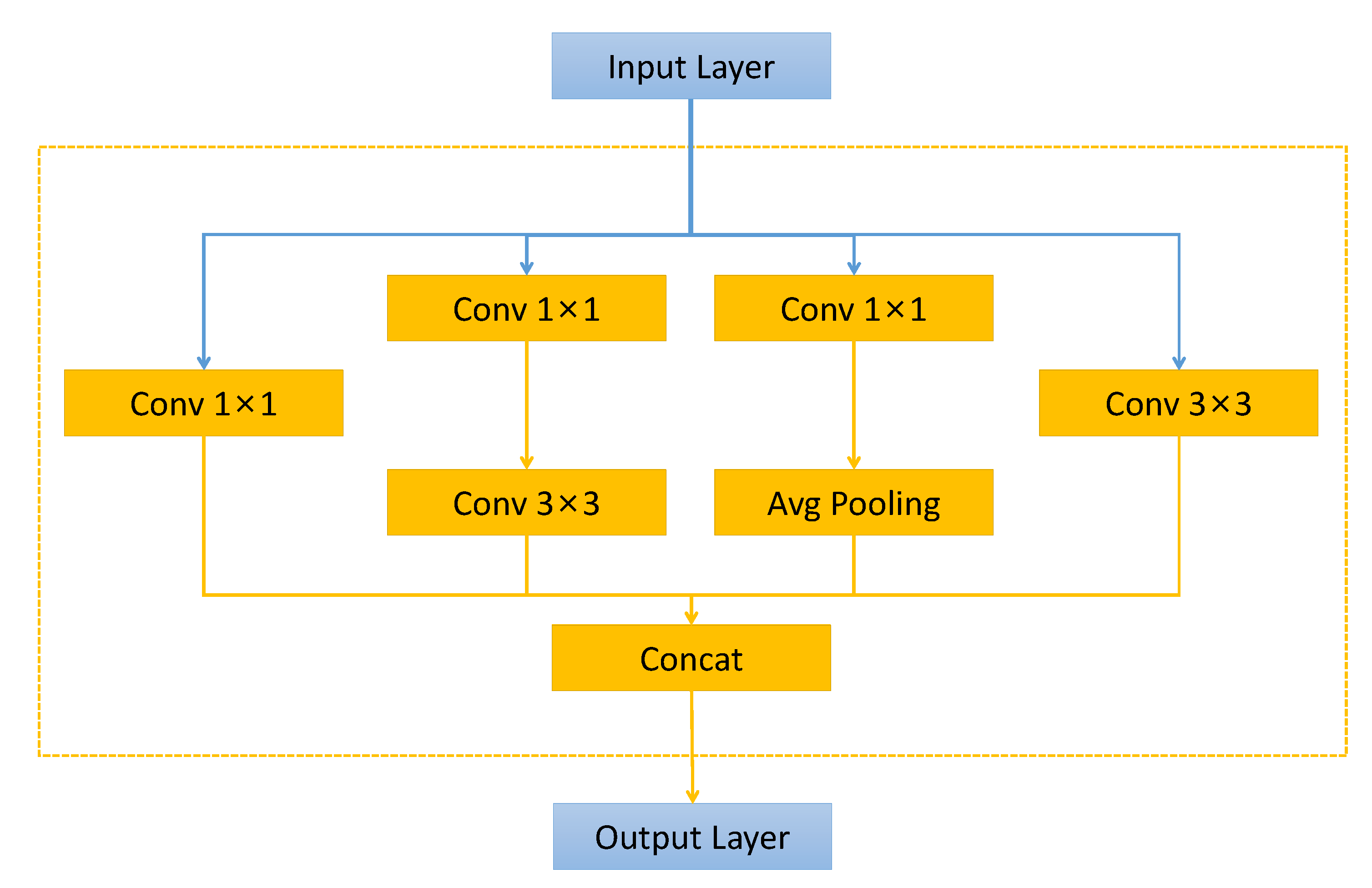
3.2.3. Diverse Block
3.2.4. Loss
4. Results and Discussion
4.1. Implementation Details
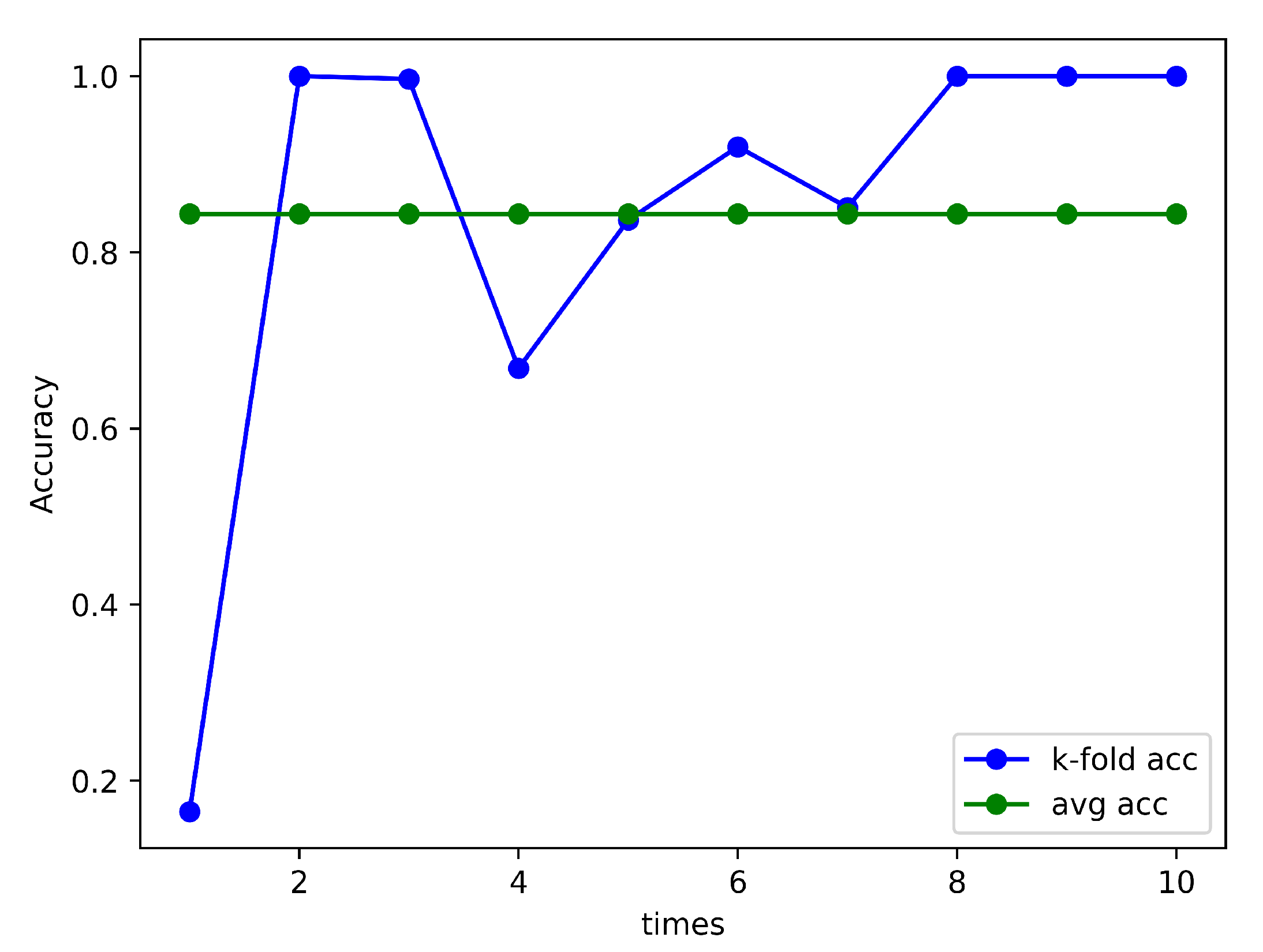
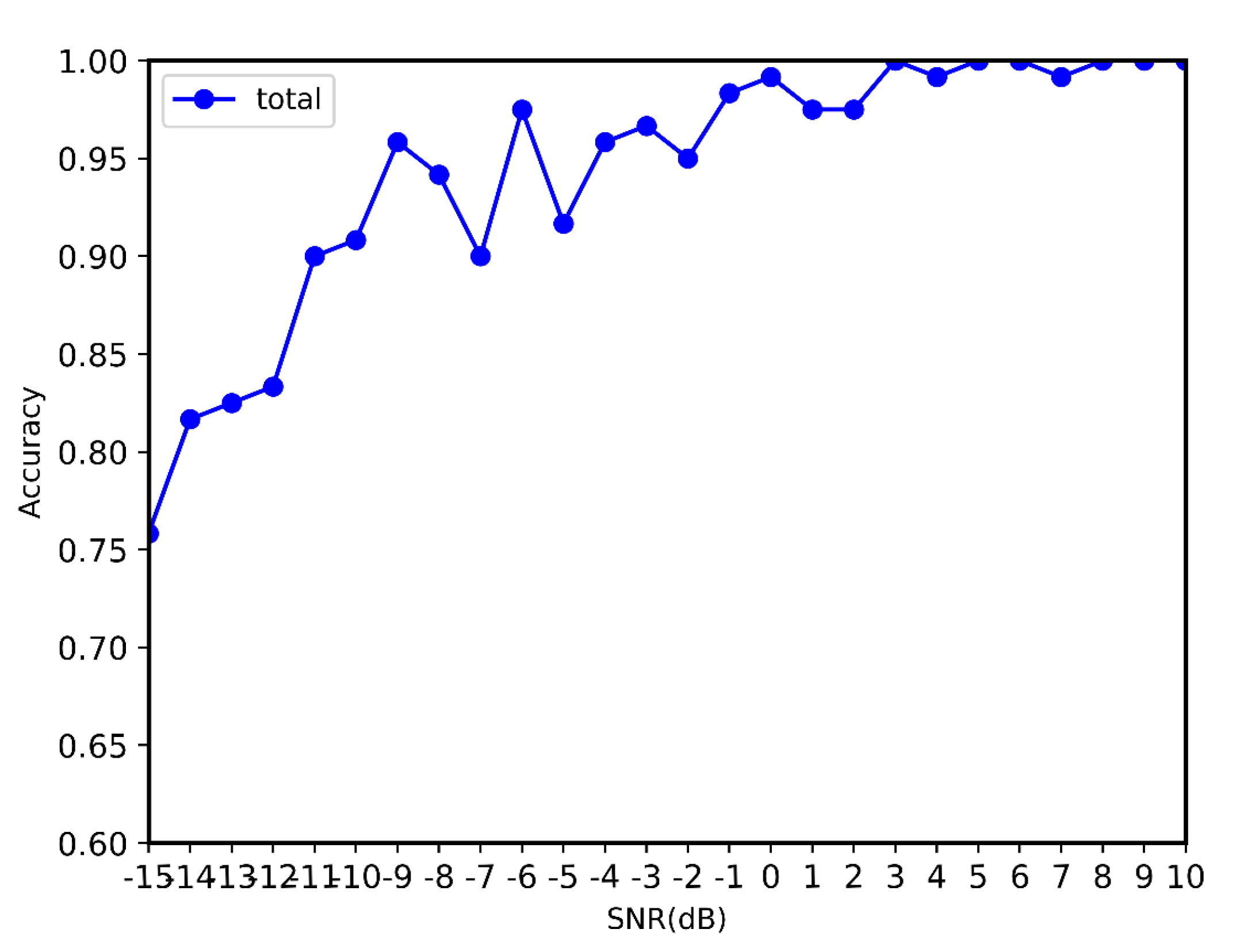
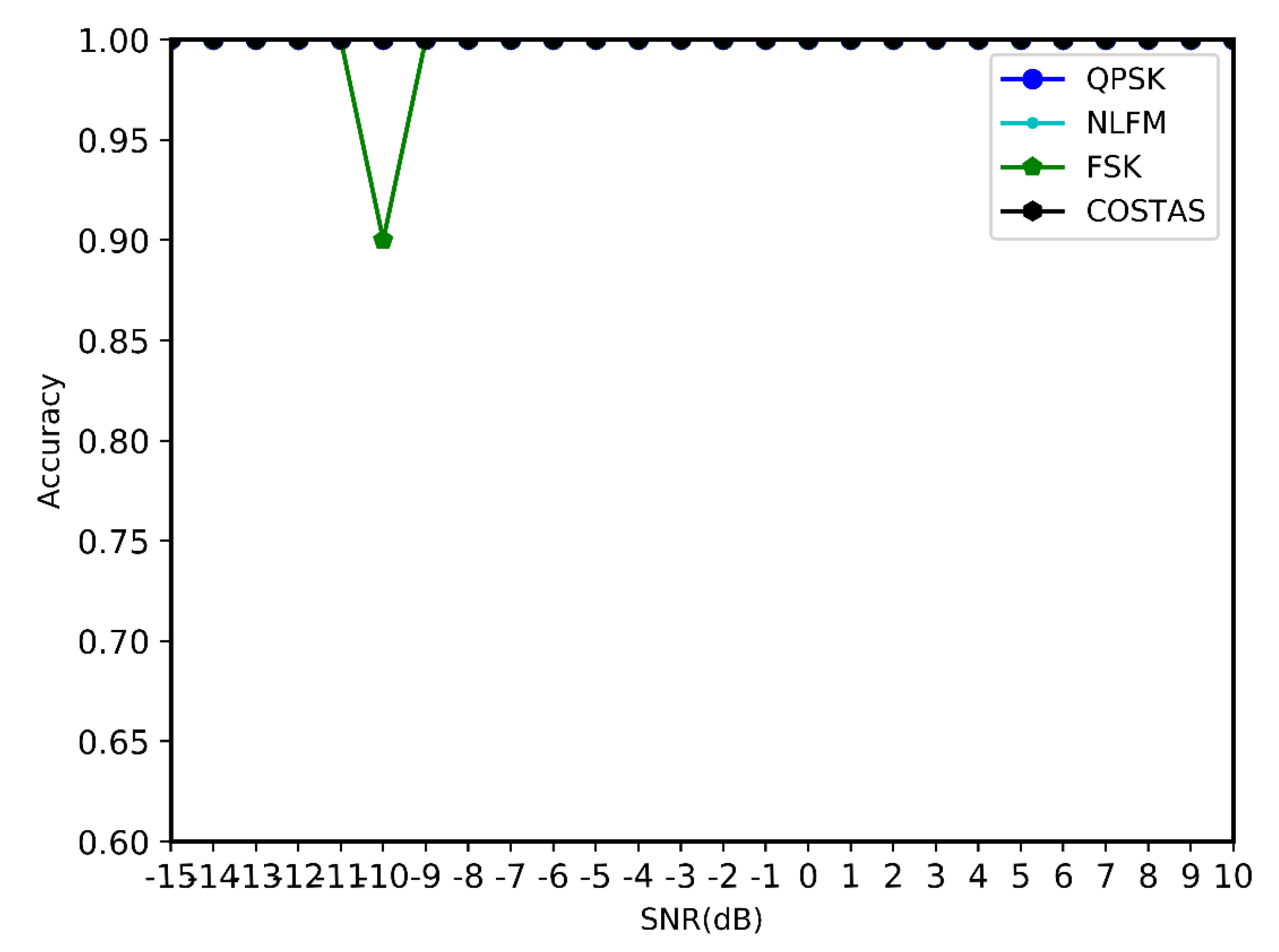
4.2. Experimental Section
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kozlenko, M.; Bosyi, A. Performance of spread spectrum system with noise shift keying using entropy demodulation. In Proceedings of the International Conference on Advanced Trends in Radioelecrtronics, Telecommunications and Computer Engineering (TCSET), Lviv-Slavske, Ukraine, 20–24 February 2018; IEEE: New York, NY, USA, 2018. [Google Scholar]
- Mohammad, A.S.; Reddy, N.; James, F.; Beard, C. Demodulation of faded wireless signals using deep convolutional neural networks. In Proceedings of the 2018 IEEE 8th Annual Computing and Communication Workshop and Conference (CCWC), Las Vegas, NV, USA, 8–10 January 2018; pp. 969–975. [Google Scholar] [CrossRef]
- Kozlenko, M.; Lazarovych, I.; Tkachuk, V.; Vialkova, V. Software Demodulation of Weak Radio Signals using Convolutional Neural Network. In Proceedings of the 2020 IEEE 7th International Conference on Energy Smart Systems (ESS), Kyiv, Ukraine, 12–14 May 2020; pp. 339–342. [Google Scholar] [CrossRef]
- Zheng, S.; Zhou, X.; Chen, S.; Qi, P.; Lou, C.; Yang, X. DemodNet: Learning Soft Demodulation from Hard Information Using Convolutional Neural Network. In Proceedings of the ICC 2022-IEEE International Conference on Communications, Seoul, Republic of Korea, 16–20 May 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Cretu-Ciocarlie, G.F.; Connolly, C.I.; Cheng, C.; Lindqvist, U.; Nováczki, S.; Sanneck, H.; Islam, M.N. Anomaly Detection and Diagnosis for Automatic Radio Network Verification. In Proceedings of the International Conference on Mobile Networks and Management (MONAMI), Würzburg, Germany, 14–18 July 2014; Springer: Cham, Switzerland, 2014. [Google Scholar]
- O’Shea, T.; Timothy, J.; Clancy, T.C.; Robert, W. McGwier. Recurrent neural radio anomaly detection. arXiv 2016, arXiv:1611.00301. [Google Scholar]
- Tandiya, N.; Jauhar, A.; Marojevic, V.; Reed, J.H. Deep Predictive Coding Neural Network for RF Anomaly Detection in Wireless Networks. In Proceedings of the 2018 IEEE International Conference on Communications Workshops (ICC Workshops), Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Zhou, X.; Xiong, J.; Zhang, X.; Liu, X.; Wei, J. A radio anomaly detection algorithm based on modified generative adversarial network. IEEE Wirel. Commun. Lett. 2021, 10, 1552–1556. [Google Scholar] [CrossRef]
- Tarongí, J.M.; Camps, A. Radio Frequency Interference Detection and Mitigation Algorithms Based on Spectrogram Analysis. Algorithms 2011, 4, 239–261. [Google Scholar] [CrossRef]
- Zhang, X.; Seyfi, T.; Ju, S.; Ramjee, S.; Gamal, A.E.; Eldar, Y.C. Deep Learning for Interference Identification: Band, Training SNR, and Sample Selection. In Proceedings of the IEEE 20th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Cannes, France, 2–5 July 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Pérez, A.; Querol, J.; Park, H.; Camps, A. Radio-frequency interference location, detection and classification using deep neural networks. In Proceedings of the IGARSS 2020–2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 6977–6980. [Google Scholar] [CrossRef]
- Octavia, A.O.; Abdi, A.; Bar-Ness, Y.; Su, W. Survey of automatic modulation classification techniques: Classical approaches and new trends. IET Commun. 2007, 1, 137–156. [Google Scholar]
- Panagiotou, P.; Anastasopoulos, A.; Polydoros, A. Likelihood ratio tests for modulation classification. In MILCOM 2000 Proceedings. 21st Century Military Communications. Architectures and Technologies for Information Superiority (Cat. No.00CH37155); IEEE: New York, NY, USA, 2000; Volume 2, pp. 670–674. [Google Scholar] [CrossRef]
- Abdi, A.; Dobre, O.A.; Choudhry, R.; Bar-Ness, Y.; Su, W. Modulation classification in fading channels using antenna arrays. In IEEE MILCOM 2004. Military Communications Conference, Monterey, CA, USA, 31 October–3 November 2004; IEEE: New York, NY, USA, 2004; Volume 1, pp. 211–217. [Google Scholar]
- Dobre, O.A.; Hameed, F. Likelihood-based algorithms for linear digital modulation classification in fading channels. In Proceedings of the 2006 Canadian Conference on Electrical and Computer Engineering, Ottawa, ON, Canada, 7–10 May 2006; pp. 1347–1350. [Google Scholar]
- Ghasemzadeh, P.; Banerjee, S.; Hempel, M.; Sharif, H. Accuracy analysis of feature-based automatic modulation classification with blind modulation detection. In Proceedings of the 2019 International Conference on Computing, Networking and Communications (ICNC), Honolulu, HI, USA, 18–21 February 2019; pp. 1000–1004. [Google Scholar]
- Zhang, Y.; Wu, G.; Wang, J.; Tang, Q. Wireless signal classification based on high-order cumulants and machine learning. In Proceedings of the 2017 International Conference on Computer Technology, Electronics and Communication (ICCTEC), Dalian, China, 19–21 December 2017; pp. 559–564. [Google Scholar]
- Yan, X.; Liu, G.; Wu, H.; Feng, G. New automatic modulation classifier using cyclic-spectrum graphs with optimal training features. IEEE Commun. Lett. 2018, 22, 1204–1207. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, M.; Yang, J.; Gui, G. Data-Driven Deep Learning for Automatic Modulation Recognition in Cognitive Radios. IEEE Trans. Veh. Technol. 2019, 68, 4074–4077. [Google Scholar] [CrossRef]
- Hui, Y.; Cheng, N.; Su, Z.; Huang, Y.; Zhao, P.; Luan, T.H.; Li, C. Secure and Personalized Edge Computing Services in 6G Heterogeneous Vehicular Networks. IEEE Internet Things J. 2022, 9, 5920–5931. [Google Scholar] [CrossRef]
- Hui, Y.; Su, Z.; Luan, T.H. Unmanned Era: A Service Response Framework in Smart City. IEEE Trans. Intell. Transp. Syst. 2022, 23, 5791–5805. [Google Scholar] [CrossRef]
- O’Shea, T.J.; Corgan, J.; Clancy, T.C. Convolutional Radio Modulation Recognition Networks. In Engineering Applications of Neural Networks. EANN 2016. Communications in Computer and Information Science; Jayne, C., Iliadis, L., Eds.; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Nie, S.; Yi, L.; Halim, Y.; Su, X.; Yapp, E.; Lee, K.; Yeh, H.; Chua, M. Incorporating convolutional neural networks and sequence graph transform for identifying multilabel protein Lysine PTM sites. Chemom. Intell. Lab. Syst. 2020, 206, 104171. [Google Scholar] [CrossRef]
- Le, N.Q.K.; Ho, Q.; Yapp, E.K.Y.; Ou, Y.; Yeh, H. DeepETC: A deep convolutional neural network architecture for investigating and classifying electron transport chain’s complexes. Neurocomputing 2020, 375, 71–79. [Google Scholar] [CrossRef]
- Arias-Vergara, T.; Klumpp, P.; Vasquez, J.; Noeth, E.; Orozco, J.R.; Schuster, M. Multi-channel spectrograms for speech processing applications using deep learning methods. Pattern Anal. Appl. 2021, 24, 423–431. [Google Scholar] [CrossRef]
- Khare, S.K.; Bajaj, V. Time-Frequency Representation and Convolutional Neural Network-Based Emotion Recognition. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 2901–2909. [Google Scholar] [CrossRef]
- Lopac, N.; Hržić, F.; Vuksanović, I.P.; Lerga, J. Detection of Non-Stationary GW Signals in High Noise From Cohen’s Class of Time–Frequency Representations Using Deep Learning. IEEE Access 2022, 10, 2408–2428. [Google Scholar] [CrossRef]
- Liu, M.; Liao, G.; Yang, Z.; Song, H.; Gong, F. Electromagnetic Signal Classification Based on Deep Sparse Capsule Networks. IEEE Access 2019, 7, 83974–83983. [Google Scholar] [CrossRef]
- Zhang, Z.; Tu, Y. A Pruning Neural Network for Automatic Modulation Classification. In Proceedings of the 2021 8th International Conference on Dependable Systems and Their Applications (DSA), Yinchuan, China, 5–6 August 2021; pp. 189–194. [Google Scholar] [CrossRef]
- Ji, H.; Xu, W.; Gan, L.; Xu, Z. Modulation Recognition Based on Lightweight Residual Network via Hybrid Pruning. In Proceedings of the 2021 7th International Conference on Computer and Communications (ICCC), Chengdu, China, 10–13 December 2021; pp. 142–146. [Google Scholar] [CrossRef]
- Xu, Y.; Xu, G.; Ma, C.; An, Z. An Advancing Temporal Convolutional Network for 5G Latency Services via Automatic Modulation Recognition. IEEE Trans. Circuits Syst. II Express Briefs 2022, 65, 3002–3006. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, F.; Wu, Q.; Wu, W.; Hu, R.Q. A Novel Automatic Modulation Classification Scheme Based on Multi-Scale Networks. IEEE Trans. Cogn. Commun. Netw. 2022, 8, 97–110. [Google Scholar] [CrossRef]
- Wei, S.; Qu, Q.; Zeng, X.; Liang, J.; Shi, J.; Zhang, X. Self-Attention Bi-LSTM Networks for Radar Signal Modulation Recognition. IEEE Trans. Microw. Theory Tech. 2021, 69, 5160–5172. [Google Scholar] [CrossRef]
- Liang, Z.; Tao, M.; Xie, J.; Yang, X.; Wang, L. A Radio Signal Recognition Approach Based on Complex-Valued CNN and Self-Attention Mechanism. IEEE Trans. Cogn. Commun. Netw. 2022, 8, 1358–1373. [Google Scholar] [CrossRef]
- Gupta, A.; Fernando, X. Automatic Modulation Classification for Cognitive Radio Systems using CNN with Probabilistic Attention Mechanism. In Proceedings of the 2022 IEEE 95th Vehicular Technology Conference: (VTC2022-Spring), Helsinki, Finland, 19–22 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Huynh-The, T.; Pham, Q.-V.; Nguyen, T.-V.; Nguyen, T.T.; Costa, D.B.D.; Kim, D.-S. RanNet: Learning Residual-Attention Structure in CNNs for Automatic Modulation Classification. IEEE Wirel. Commun. Lett. 2022, 11, 1243–1247. [Google Scholar] [CrossRef]
- Hao, Y.; Wang, X.; Lan, X. Frequency Domain Analysis and Convolutional Neural Network Based Modulation Signal Classification Method in OFDM System. In Proceedings of the 2021 13th International Conference on Wireless Communications and Signal Processing (WCSP), Changsha, China, 20–22 October 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Yakkati, R.R.; Tripathy, R.K.; Cenkeramaddi, L.R. Radio Frequency Spectrum Sensing by Automatic Modulation Classification in Cognitive Radio System Using Multiscale Deep CNN. IEEE Sens. J. 2022, 22, 926–938. [Google Scholar] [CrossRef]
- Liang, Z.; Wang, L.; Tao, M.; Xie, J.; Yang, X. Attention Mechanism Based ResNeXt Network for Automatic Modulation Classification. In Proceedings of the 2021 IEEE Globecom Workshops (GC Wkshps), Madrid, Spain, 7–11 December 2021; IEEE: New York, NY, USA, 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Li, K.; Shi, J. Modulation Recognition Algorithm based on Digital Communication Signal Time-Frequency Image. In Proceedings of the 2021 8th International Conference on Dependable Systems and Their Applications (DSA), Yinchuan, China, 5–6 August 2021; pp. 747–748. [Google Scholar] [CrossRef]
- Wang, Y.; Bai, J.; Xiao, Z.; Zhou, H.; Jiao, L. MsmcNet: A Modular Few-Shot Learning Framework for Signal Modulation Classification. IEEE Trans. Signal Process. 2022, 70, 3789–3801. [Google Scholar] [CrossRef]
- Huang, J.; Huang, S.; Zeng, Y.; Chen, H.; Chang, S.; Zhang, Y. Hierarchical Digital Modulation Classification Using Cascaded Convolutional Neural Network. J. Commun. Inf. Netw. 2021, 6, 72–81. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, H.; Zhu, H.; Adebisi, B.; Gui, G.; Gacanin, H.; Adachi, F. NAS-AMR: Neural Architecture Search-Based Automatic Modulation Recognition for Integrated Sensing and Communication Systems. IEEE Trans. Cogn. Commun. Netw. 2022, 8, 1374–1386. [Google Scholar] [CrossRef]
- Wang, Y.; Gui, G.; Gacanin, H.; Adebisi, B.; Sari, H.; Adachi, F. Federated Learning for Automatic Modulation Classification Under Class Imbalance and Varying Noise Condition. IEEE Trans. Cogn. Commun. Netw. 2022, 8, 86–96. [Google Scholar] [CrossRef]
- Tang, B.; Liu, W.; Song, T. Wind turbine fault diagnosis based on Morlet wavelet transformation and Wigner-Ville distribution. Renew. Energy 2010, 35, 2862–2866. [Google Scholar]
- Greco, A.; Costantino, D.; Morabito, F.C.; Versaci, M. A Morlet wavelet classification technique for ICA filtered sEMG experimental data. In Proceedings of the International Joint Conference on Neural Networks, Portland, OR, USA, 20–24 July 2003; pp. 166–171. [Google Scholar] [CrossRef]
- Gao, D.; Zhu, Y.; Wang, X.; Yan, K.; Hong, J. A Fault Diagnosis Method of Rolling Bearing Based on Complex Morlet CWT and CNN. In Proceedings of the 2018 Prognostics and System Health Management Conference (PHM-Chongqing), Chongqing, China, 26–28 October 2018; pp. 1101–1105. [Google Scholar] [CrossRef]
- Mgdob, H.M.; Torry, J.N.; Vincent, R.; Al-Naami, B. Application of Morlet transform wavelet in the detection of paradoxical splitting of the second heart sound. Comput. Cardiol. 2003, 2003, 323–326. [Google Scholar] [CrossRef]
- Le Cun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Handwritten digit recognition with a back-propagation network. Adv. Neural Inf. Process. Syst. 1989, 2, 396–404. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2016; pp. 770–778. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, P.; Zhang, Y.; Yang, X.; Xiao, X.; Wang, H.; Zhang, R. Deep Learning-Based Modulation Recognition for Low Signal-to-Noise Ratio Environments. Electronics 2022, 11, 4026. https://doi.org/10.3390/electronics11234026
He P, Zhang Y, Yang X, Xiao X, Wang H, Zhang R. Deep Learning-Based Modulation Recognition for Low Signal-to-Noise Ratio Environments. Electronics. 2022; 11(23):4026. https://doi.org/10.3390/electronics11234026
Chicago/Turabian StyleHe, Peng, Yang Zhang, Xinyue Yang, Xiao Xiao, Haolin Wang, and Rongsheng Zhang. 2022. "Deep Learning-Based Modulation Recognition for Low Signal-to-Noise Ratio Environments" Electronics 11, no. 23: 4026. https://doi.org/10.3390/electronics11234026
APA StyleHe, P., Zhang, Y., Yang, X., Xiao, X., Wang, H., & Zhang, R. (2022). Deep Learning-Based Modulation Recognition for Low Signal-to-Noise Ratio Environments. Electronics, 11(23), 4026. https://doi.org/10.3390/electronics11234026




