Multiple-Intelligent Reflective Surfaces (Multi-IRSs)-Based NOMA System
Abstract
:1. Introduction
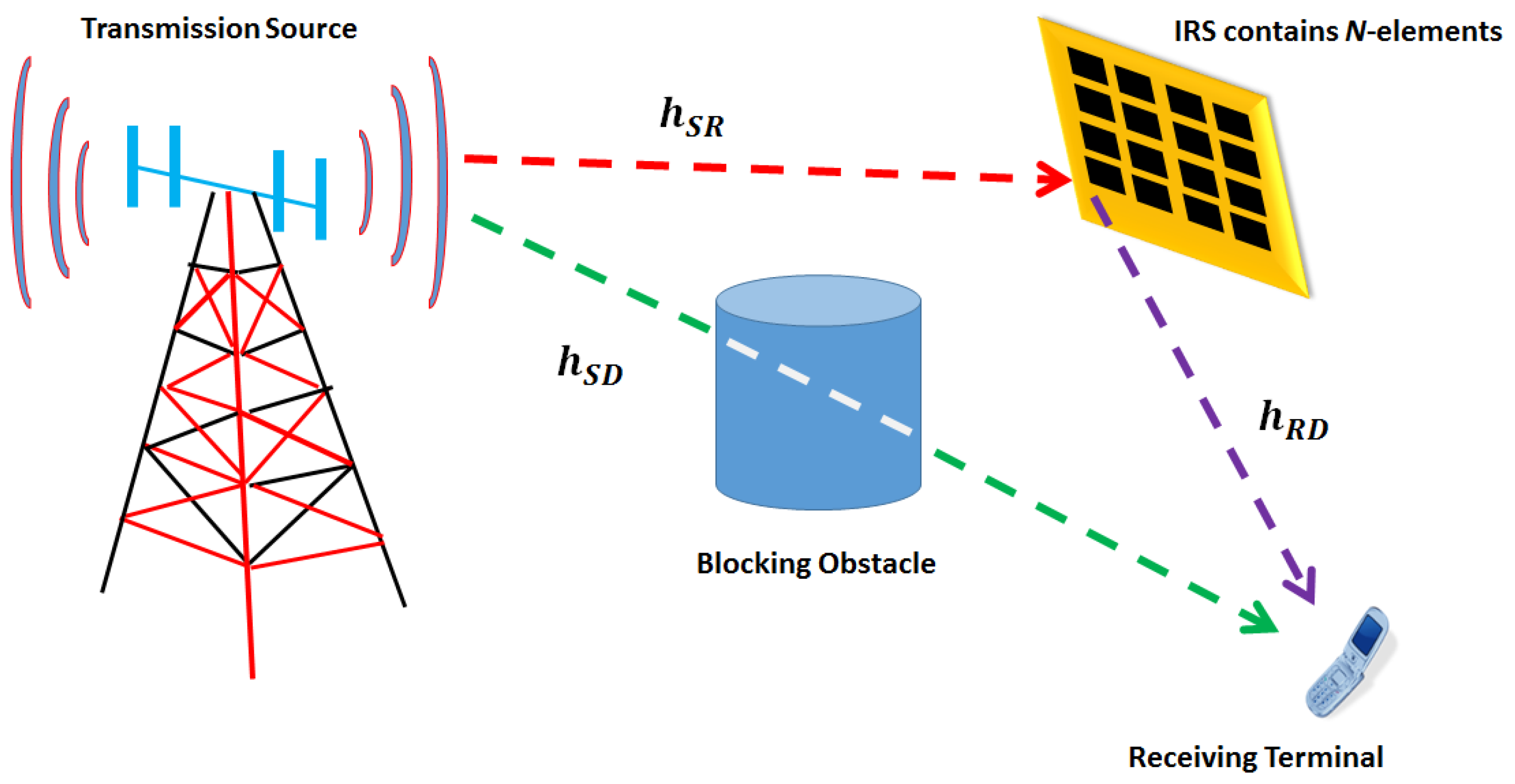
2. The Modeled IRS-NOMA System
3. The Proposed Closed Form Expression
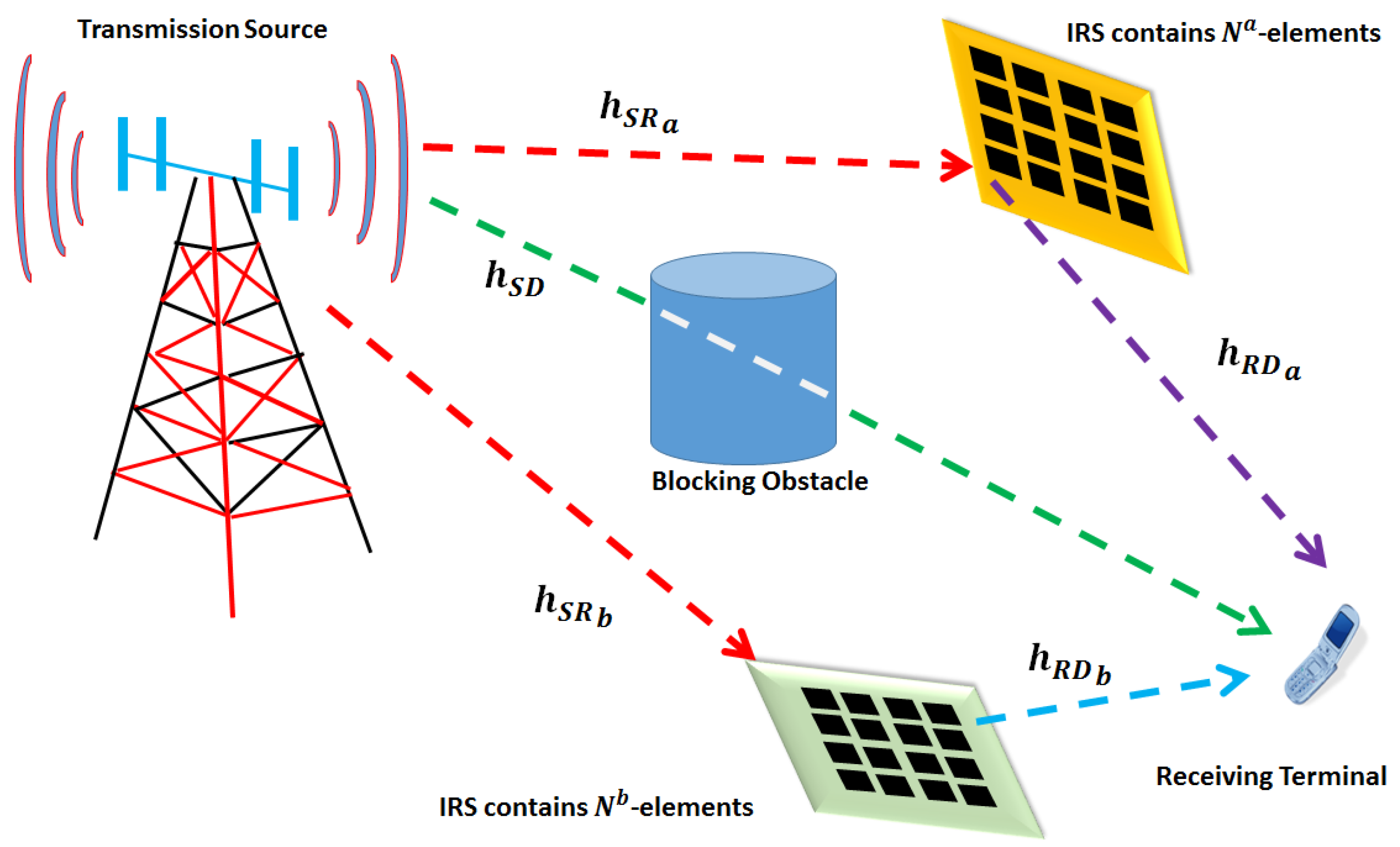
4. The Proposed Multi-IRS Approach
5. Simulation and Numerical Results
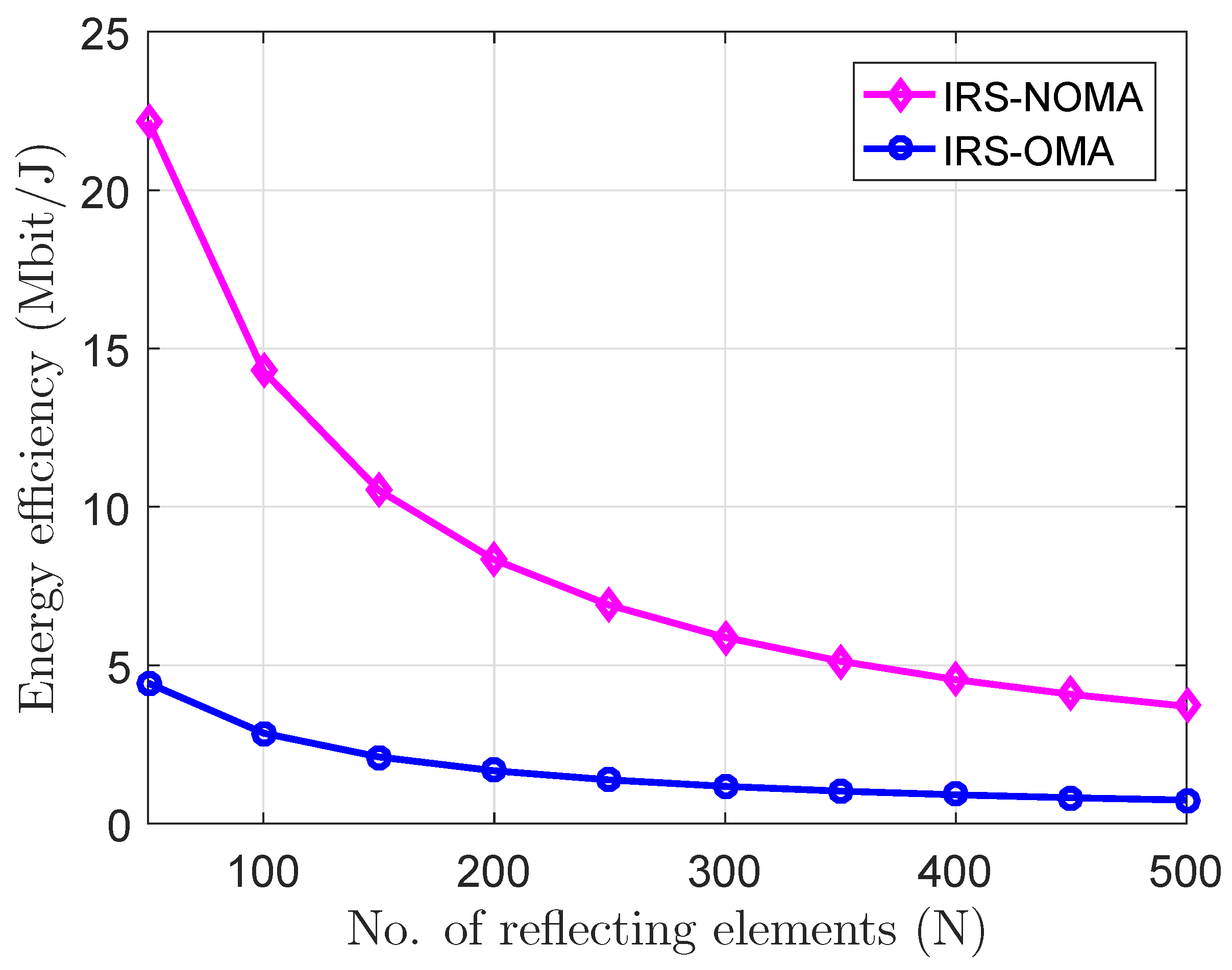
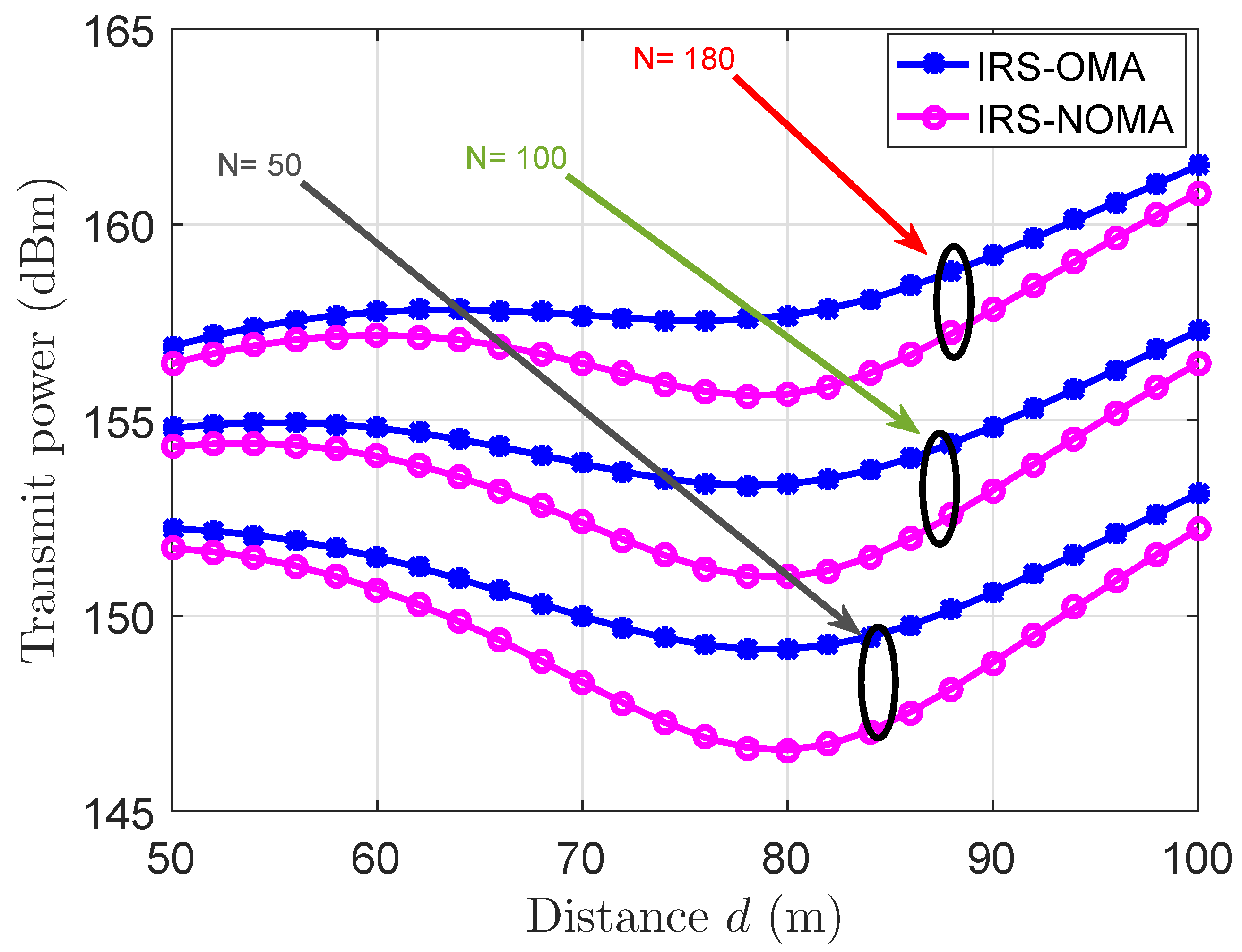
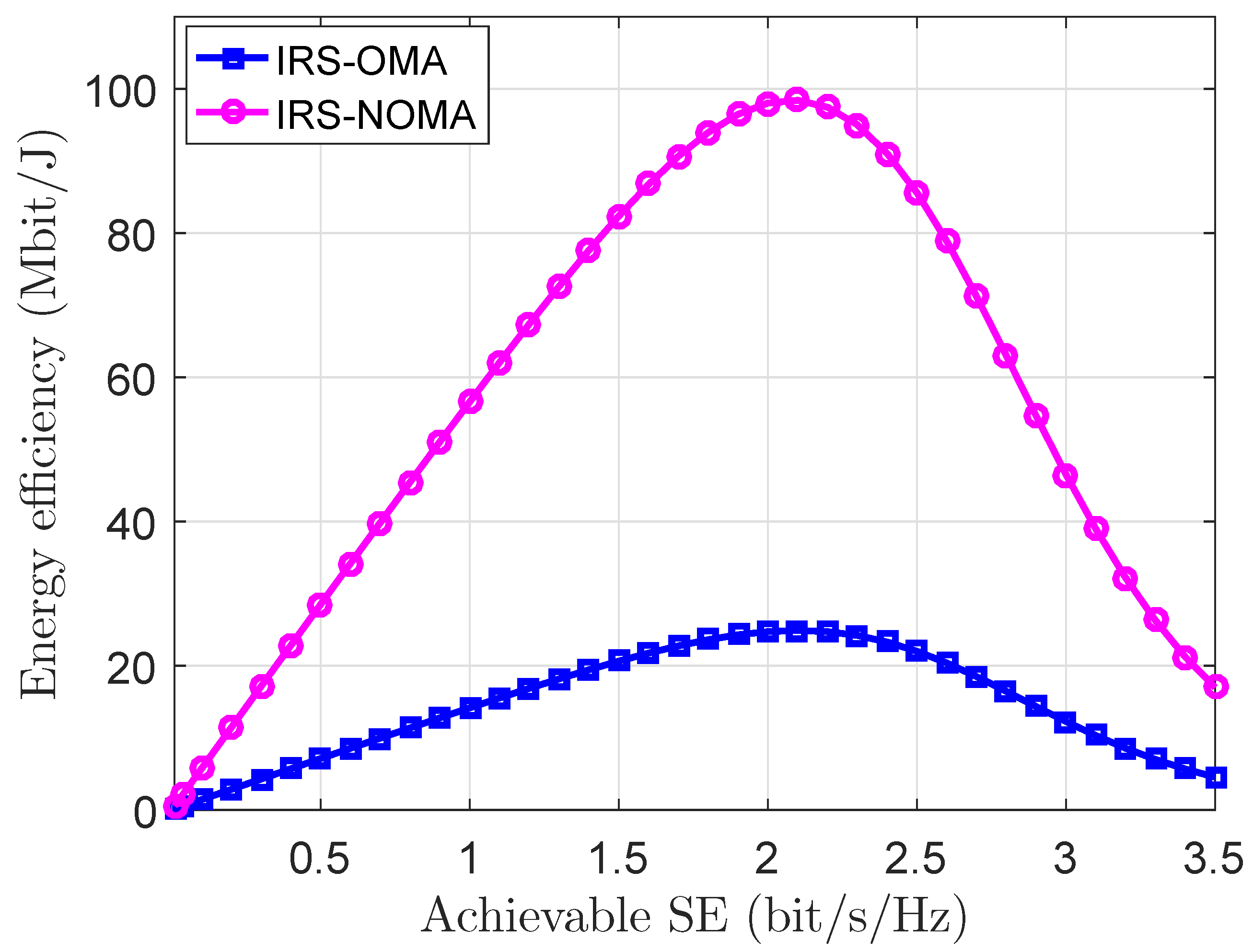
5.1. Numerical Results of a Single-Reflection Surface Scenario
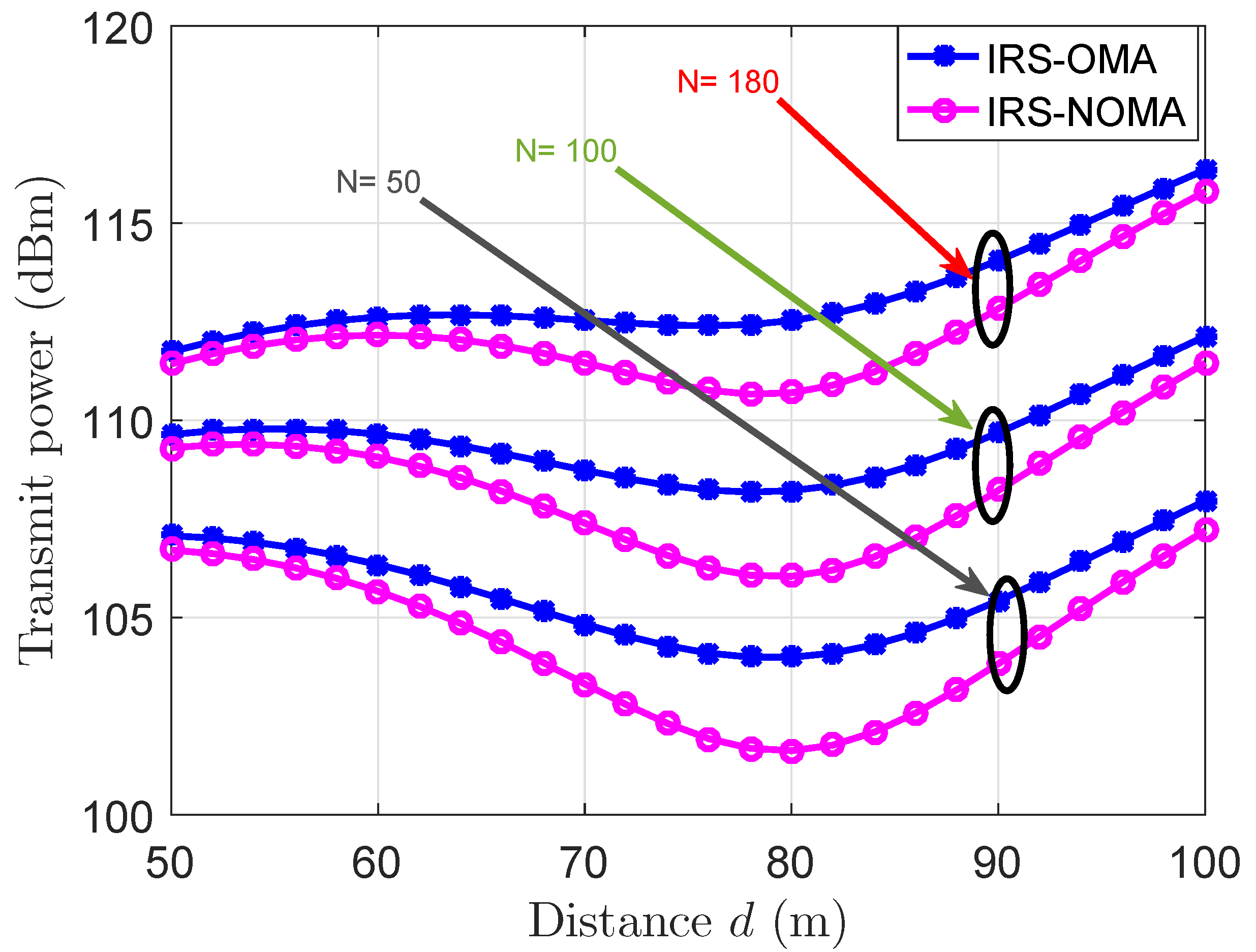
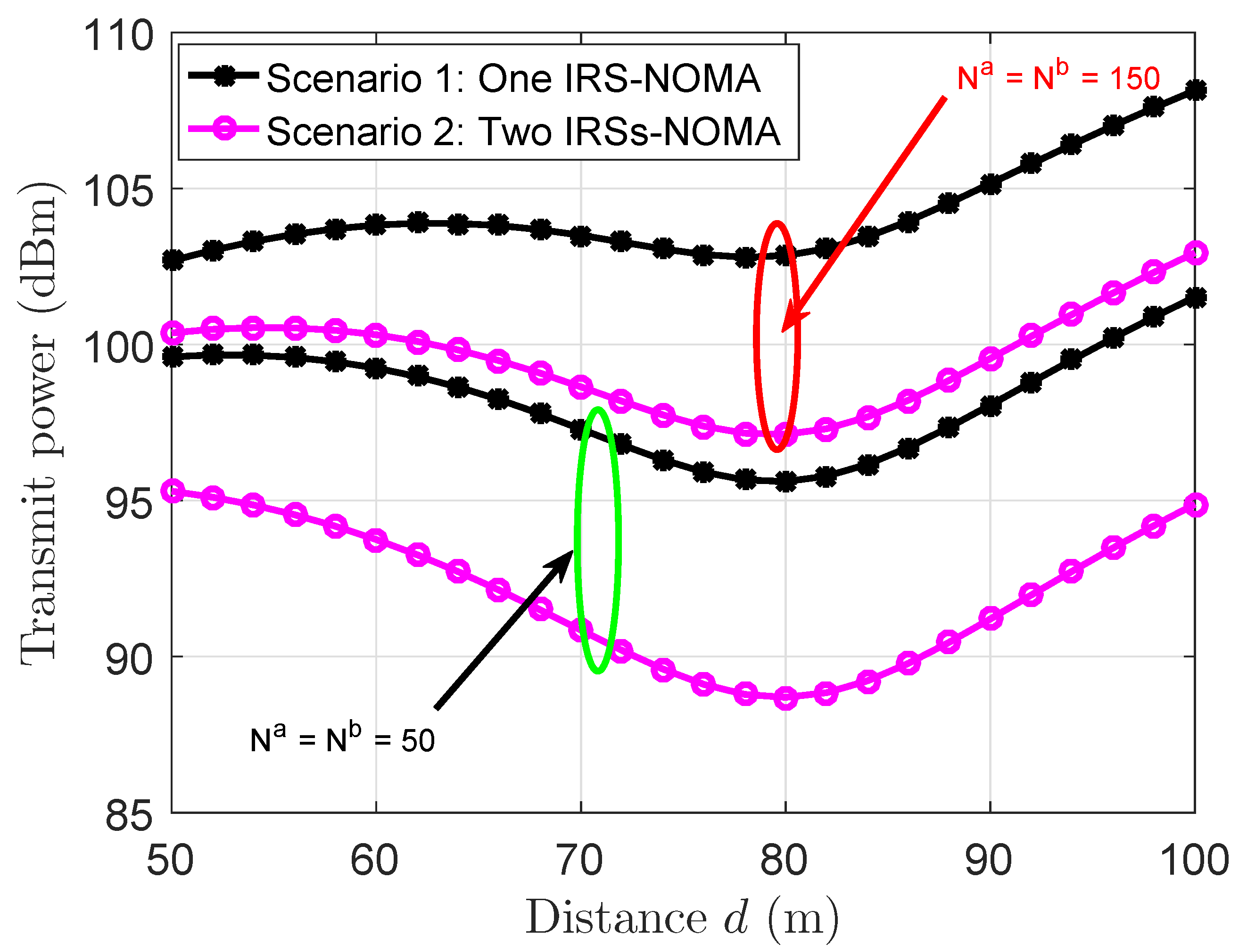
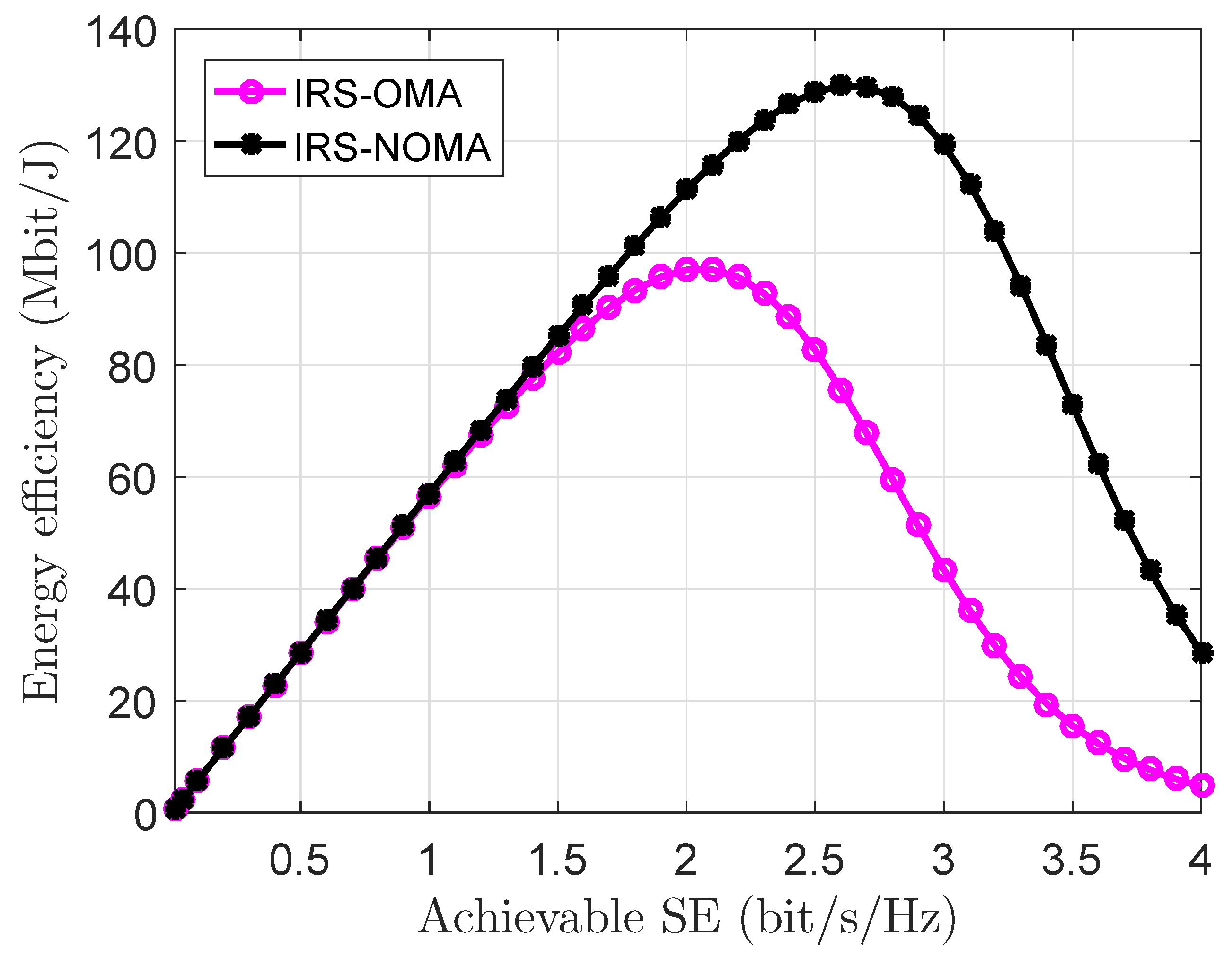
5.2. Numerical Results of a Two-Reflection-Surfaces-Assisted NOMA Scenario
6. Conclusions and Future Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Al-Abbasi, Z.Q.; So, D.K.C.; Tang, J. Energy Efficient Resource Allocation in Downlink Non-Orthogonal Multiple Access (NOMA) System. In Proceedings of the 2017 IEEE 85th Vehicular Technology Conference (VTC Spring), Sydney, Australia, 4–7 June 2017; pp. 1–5. [Google Scholar]
- Al-Abbasi, Z.Q.; So, D.K.C. Resource Allocation in Non-Orthogonal and Hybrid Multiple Access System with Proportional Rate Constraint. IEEE Trans. Wirel. Commun. 2017, 16, 6309–6320. [Google Scholar] [CrossRef] [Green Version]
- Luo, F.L.; Zhang, C. Signal Processing for 5G: Algorithms and Implementations; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Dai, Y.; Sheng, M.; Liu, J.; Cheng, N.; Shen, X.; Yang, Q. Joint Mode Selection and Resource Allocation for D2D-Enabled NOMA Cellular Networks. IEEE Trans. Veh. Technol. 2019, 68, 6721–6733. [Google Scholar] [CrossRef]
- Men, J.; Ge, J. Non-Orthogonal Multiple Access for Multiple-Antenna Relaying Networks. IEEE Commun. Lett. 2015, 19, 1686–1689. [Google Scholar] [CrossRef]
- Al-Abbasi, Z.Q.; So, D.K.C.; Tang, J. Resource allocation for MU-MIMO non-orthogonal multiple access (NOMA) system with interference alignment. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017. [Google Scholar] [CrossRef] [Green Version]
- Al-Abbasi, Z.Q.; Rabie, K.M.; So, D.K.C. EE Optimization for Downlink NOMA-Based Multi-Tier CRANs. IEEE Trans. Veh. Technol. 2021, 70, 5880–5891. [Google Scholar] [CrossRef]
- Liu, Y.; Pan, G.; Zhang, H.; Song, M. On the Capacity Comparison Between MIMO-NOMA and MIMO-OMA. IEEE Access 2016, 4, 2123–2129. [Google Scholar] [CrossRef]
- Martin-Vega, F.J.; Liu, Y.; Gomez, G.; Aguayo-Torres, M.C.; Elkashlan, M. Modeling and Analysis of NOMA Enabled CRAN with Cluster Point Process. In Proceedings of the GLOBECOM 2017—2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Dani, M.N.; Al-Abbasi, Z.Q.; So, D.K.C. Power Allocation for Layered Multicast Video Streaming in Non-Orthogonal Multiple Access System. In Proceedings of the 2017 IEEE Globecom Workshops (GC Wkshps), Singapore, 4–8 December 2017; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- De Sena, A.S.; Carrillo, D.; Fang, F.; Nardelli, P.H.; Da Costa, D.B.; Dias, U.S.; Ding, Z.; Papadias, C.B.; Saad, W. What role do intelligent reflecting surfaces play in multi-antenna non-orthogonal multiple access? IEEE Wirel. Commun. 2020, 27, 24–31. [Google Scholar] [CrossRef]
- Al-Abbasi, Z.Q.; Khamis, M.A. Spectral efficiency (SE) enhancement of NOMA system through iterative power assignment. Wirel. Netw. 2021, 279, 1309–1317. [Google Scholar] [CrossRef]
- Sun, Q.; Han, S.; I, C.L.; Pan, Z. On the Ergodic Capacity of MIMO NOMA Systems. IEEE Wirel. Commun. Lett. 2015, 4, 405–408. [Google Scholar] [CrossRef]
- Sun, Q.; Han, S.; I, C.L.; Pan, Z. Energy efficiency optimization for fading MIMO non-orthogonal multiple access systems. In Proceedings of the 2015 IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 2668–2673. [Google Scholar] [CrossRef]
- Li, Q.; Ren, P.; Xu, D. Security Enhancement and QoS Provisioning for NOMA-Based Cooperative D2D Networks. IEEE Access 2019, 7, 129387–129401. [Google Scholar] [CrossRef]
- Chen, J.; Jia, J.; Liu, Y.; Wang, X.; Aghvami, A.H. Optimal Resource Block Assignment and Power Allocation for D2D-Enabled NOMA Communication. IEEE Access 2019, 7, 90023–90035. [Google Scholar] [CrossRef]
- Fu, M.; Zhou, Y.; Shi, Y. Intelligent reflecting surface for downlink non-orthogonal multiple access networks. In Proceedings of the 2019 IEEE Globecom Workshops (GC Wkshps), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar]
- Al Abbasi, Z.Q.; Ahmed Khamis, M.; Rabie, K.M. Performance Evaluation of Downlink IRS-Assisted Multi-Cell Massive MIMO System. In Proceedings of the 2021 IEEE International Mediterranean Conference on Communications and Networking (MeditCom), Athens, Greece, 7–10 September 2021; pp. 138–143. [Google Scholar] [CrossRef]
- Özdogan, Ö.; Björnson, E.; Larsson, E.G. Intelligent reflecting surfaces: Physics, propagation, and pathloss modeling. IEEE Wirel. Commun. Lett. 2019, 9, 581–585. [Google Scholar] [CrossRef] [Green Version]
- Dampahalage, D.; Shashika Manosha, K.B.; Rajatheva, N.; Latva-aho, M. Intelligent Reflecting Surface Aided Vehicular Communications. In Proceedings of the 2020 IEEE Globecom Workshops (GC Wkshps), Taipei, Taiwan, 7–11 December 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Björnson, E.; Özdogan, Ö.; Larsson, E.G. Intelligent reflecting surface versus decode-and-forward: How large surfaces are needed to beat relaying? IEEE Wirel. Commun. Lett. 2019, 9, 244–248. [Google Scholar] [CrossRef] [Green Version]
- Mu, X.; Liu, Y.; Guo, L.; Lin, J.; Al-Dhahir, N. Exploiting intelligent reflecting surfaces in NOMA networks: Joint beamforming optimization. IEEE Trans. Wirel. Commun. 2020, 19, 6884–6898. [Google Scholar] [CrossRef]
- Ding, Z.; Poor, H.V. A simple design of IRS-NOMA transmission. IEEE Commun. Lett. 2020, 24, 1119–1123. [Google Scholar] [CrossRef]
- Ding, Z.; Schober, R.; Poor, H.V. On the impact of phase shifting designs on IRS-NOMA. IEEE Wirel. Commun. Lett. 2020, 9, 1596–1600. [Google Scholar] [CrossRef]
- Tekbıyık, K.; Kurt, G.K.; Yanikomeroglu, H. Energy-Efficient RIS-assisted Satellites for IoT Networks. arXiv 2021, arXiv:2101.07166. [Google Scholar] [CrossRef]
- Lin, Z.; An, K.; Niu, H.; Hu, Y.; Chatzinotas, S.; Zheng, G.; Wang, J. SLNR-based Secure Energy Efficient Beamforming in Multibeam Satellite Systems. IEEE Trans. Aerosp. Electron. Syst. 2022, 1–14. [Google Scholar] [CrossRef]
- Lin, Z.; Niu, H.; An, K.; Wang, Y.; Zheng, G.; Chatzinotas, S.; Hu, Y. Refracting RIS-Aided Hybrid Satellite-Terrestrial Relay Networks: Joint Beamforming Design and Optimization. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 3717–3724. [Google Scholar] [CrossRef]
- Lin, Z.; Lin, M.; Wang, J.B.; de Cola, T.; Wang, J. Joint Beamforming and Power Allocation for Satellite-Terrestrial Integrated Networks With Non-Orthogonal Multiple Access. IEEE J. Sel. Top. Signal Process. 2019, 13, 657–670. [Google Scholar] [CrossRef]
| Parameter Name | Value |
|---|---|
| Total number of active users | 3 |
| Carrier frequency | 5 GHz |
| Overall transmission bandwidth | 10 MHz |
| The standard deviation of shadowing | 8 dB |
| the total transmission power | 40 dBm |
| Dissipated power by each reflective element | 5 mW |
| Dissipated power by the source | 20 dBm |
| Dissipated power by the destination | 100 mW |
| Dissipated power by the rely | 100 mW |
| Noise power spectral density | −174 dBm/Hz |
| 3GPP LOS path-loss | |
| 3GPP LOS path-loss | |
| 3GPP NLOS path-loss | |
| Noise figure | 10 dB |
| The reflection coefficient | 1 |
| Transmitting antenna gain | 5 dB |
| Receiving antenna gain | 5 dB |
| Transmitting antenna gain | 1 dB |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Abbasi, Z.Q.; Farhan, L.; Alhumaima, R.S. Multiple-Intelligent Reflective Surfaces (Multi-IRSs)-Based NOMA System. Electronics 2022, 11, 4045. https://doi.org/10.3390/electronics11234045
Al-Abbasi ZQ, Farhan L, Alhumaima RS. Multiple-Intelligent Reflective Surfaces (Multi-IRSs)-Based NOMA System. Electronics. 2022; 11(23):4045. https://doi.org/10.3390/electronics11234045
Chicago/Turabian StyleAl-Abbasi, Ziad Qais, Laith Farhan, and Raad S. Alhumaima. 2022. "Multiple-Intelligent Reflective Surfaces (Multi-IRSs)-Based NOMA System" Electronics 11, no. 23: 4045. https://doi.org/10.3390/electronics11234045
APA StyleAl-Abbasi, Z. Q., Farhan, L., & Alhumaima, R. S. (2022). Multiple-Intelligent Reflective Surfaces (Multi-IRSs)-Based NOMA System. Electronics, 11(23), 4045. https://doi.org/10.3390/electronics11234045







