Experimental Validation and Applications of mm-Wave 8 × 8 Antenna-in-Package (AiP) Array Platform
Abstract
:1. Introduction
2. Mmwave 8 × 8 AiP Array Platform
2.1. Aip Array Platform Presentation
- (a)
- 64 patch antennas operating at 26.5 to 29.5 GHz.
- (b)
- 64 6-bit phase shifters with a phase shift range of 0° to 359°, and a control resolution of .
- (c)
- 64 6-bit attenuators with an attenuation range of 0 to 7.5 dB, and a control resolution of 0.5 dB.
- (d)
- 32 common attenuators with an attenuation range of 0 to 15 dB, and a control resolution of 1 dB.
- (e)
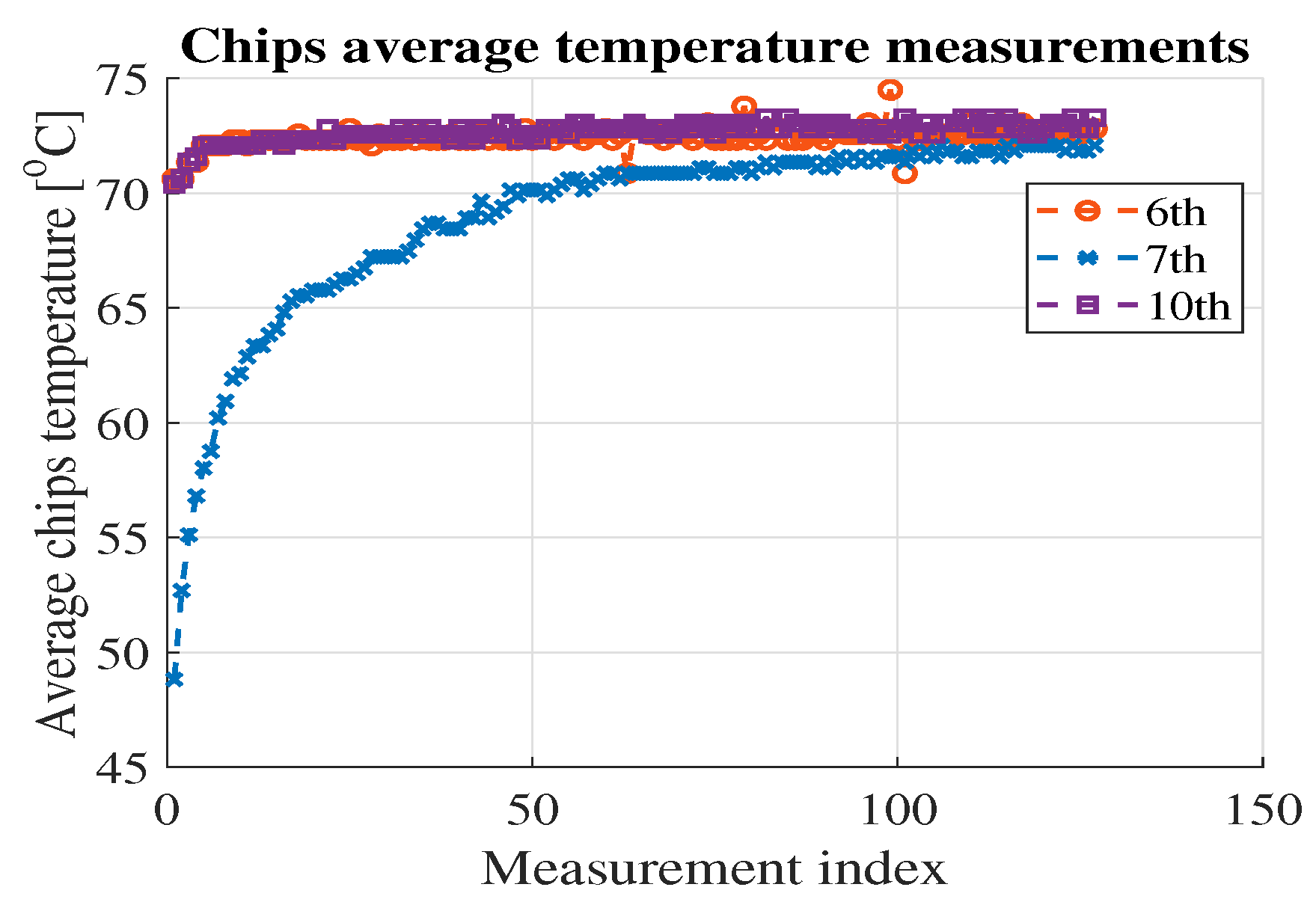
- 32 temperature variable attenuators (TVAs), which provide gain compensation for the disturbance of RF chains due to the variation of the AiP temperature.
- (f)
- 64 power amplifiers (PAs), which are tuned when the AiP is in Tx mode, and 64 low noise amplifiers (LNAs), which are tuned with the AiP in Rx mode.
- (g)
- 160 switches, which are swithed to set the operating mode (i.e., Tx or Rx) of the AiP.
- (h)
- 16 ANOKIAWAVE AWMF-0158 RFICs chips. Each RFIC on the AiP board has four control chains, each of which is connected to a patch antenna. A 6-bit phase shifter and a 6-bit attenuator are integrated in each control chain for the phase and amplitude control, respectively. Therefore, the excitation of the patch antenna is fed by controlling the phase shifter and attenuator in the RFIC.
- (i)
- One STM32F427VIT6 chip acts as the microprogrammed control unit (MCU) of the AiP board. The MCU interacts with the external control computer via a universal asynchronous receiver/transmitter (UART). The control of the AiP RFICs chips by the MCU, is achieved via the serial peripheral interphase (SPI).
- (a)
- Tx/Rx mode switching command for setting the AiP to work in Tx or Rx mode, respectively.
- (b)
- Element switch command for controlling each element of the AiP to turn on or off.
- (c)
- Chip temperature read command for reading the temperature of each chip of the AiP.
2.2. Aip Array Platform Experimental Validation
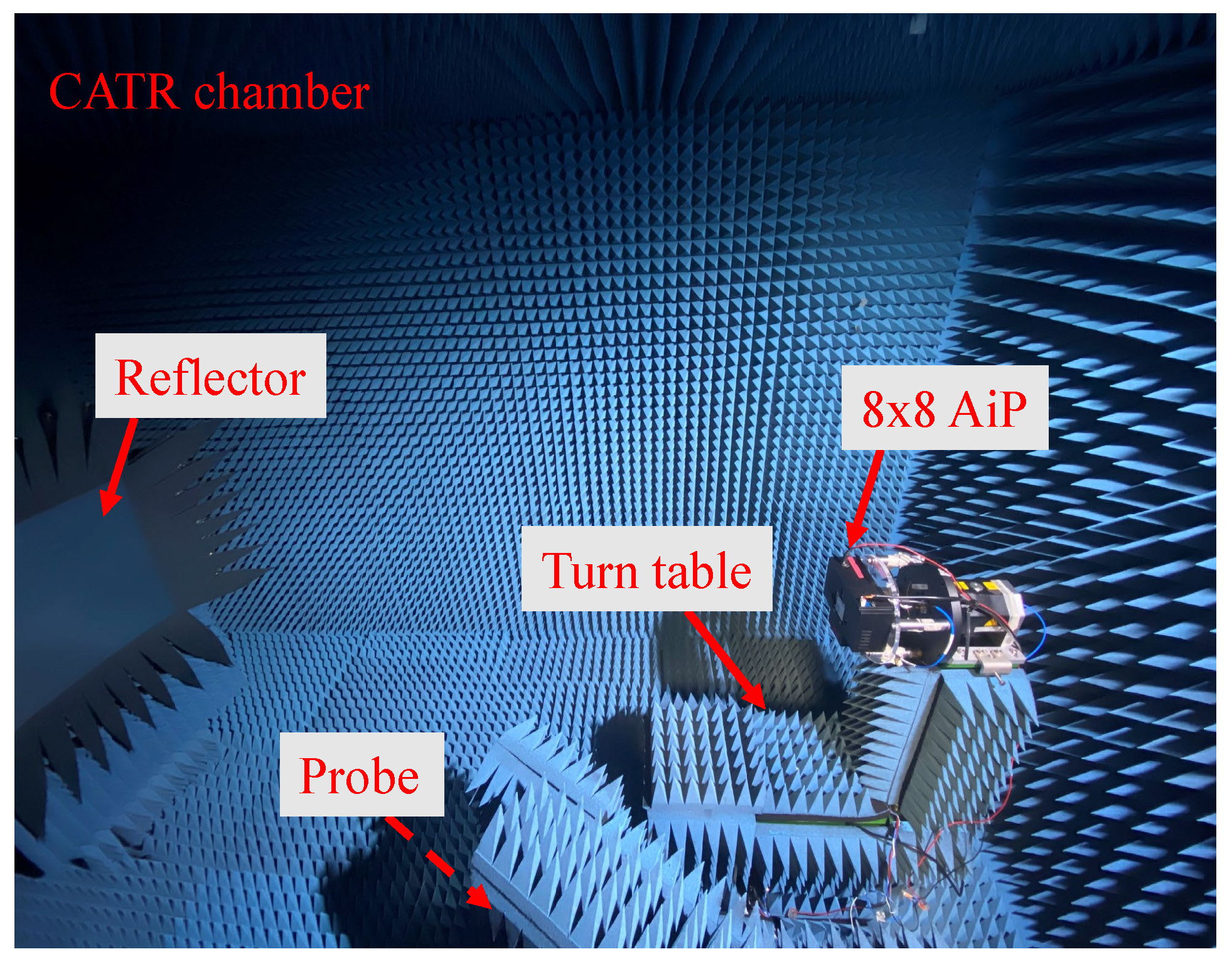
2.2.1. Stability Validation
- (a)
- A VNA operating from 10 MHz to 43.5 GHz.
- (b)
- A laptop as the control computer that controls the AiP and VNA.
- (c)
- An adjustable DC Power Supply working on 12 V for the AiP module.
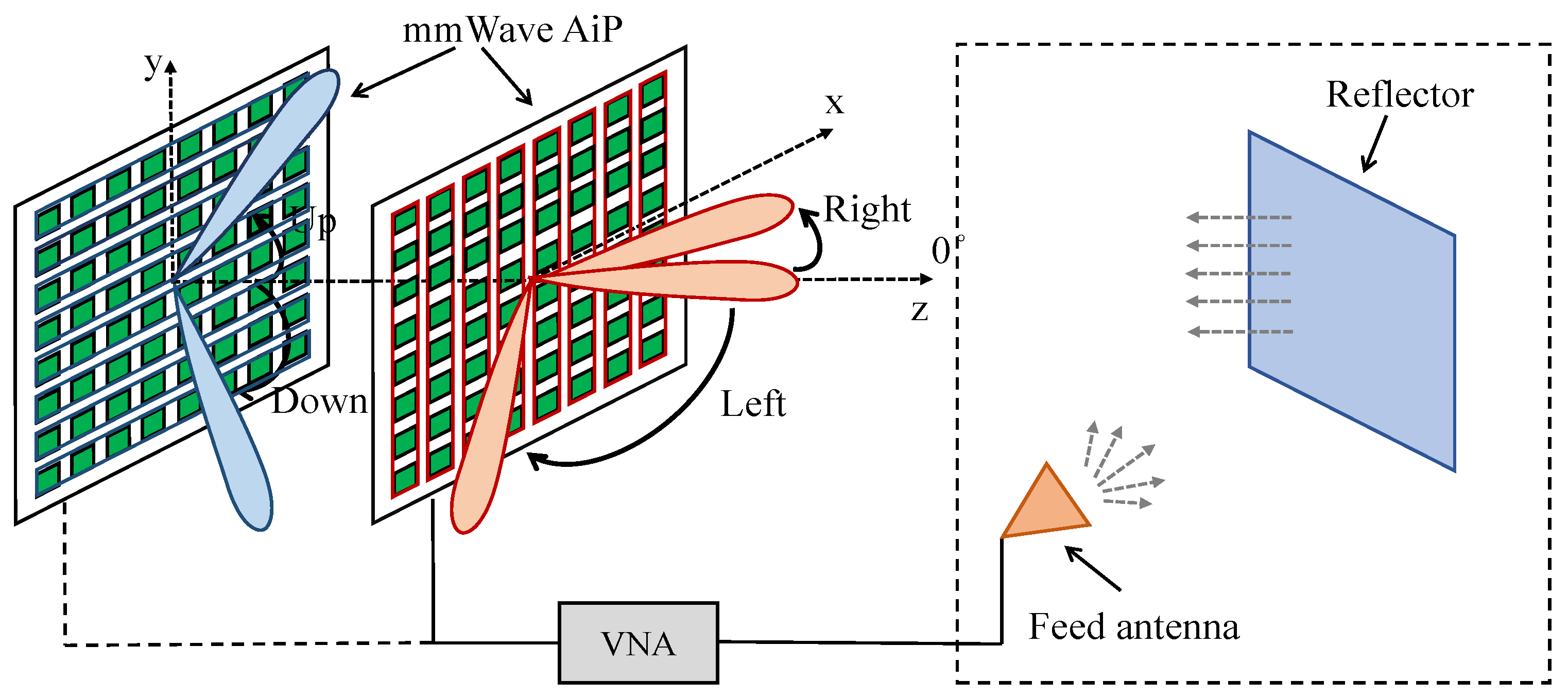
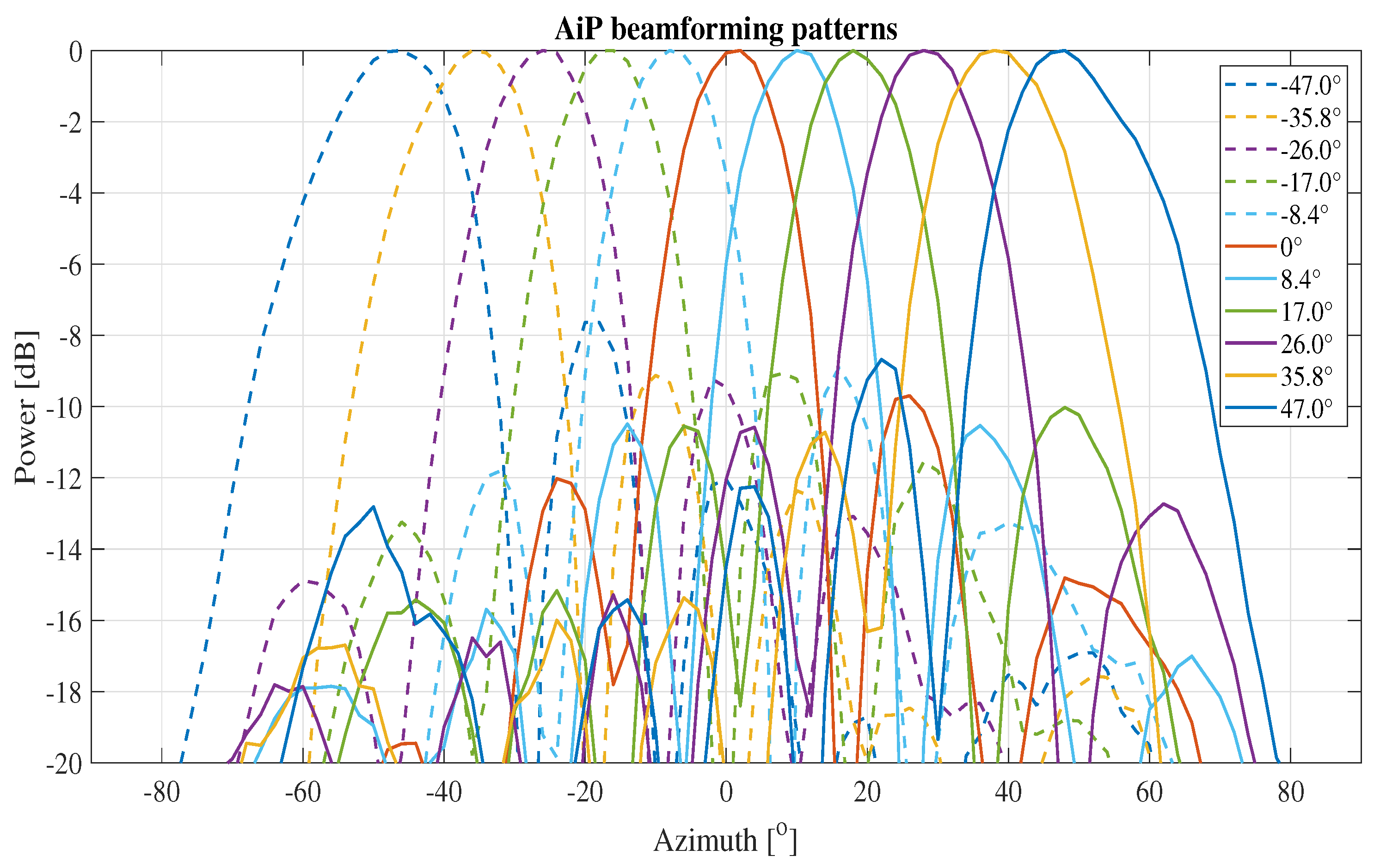
2.2.2. Aip Beamforming Performance Validation
3. Aip Array Platform Applications
3.1. Investigating the Effectiveness of Calibration Methods on Large Phased Array
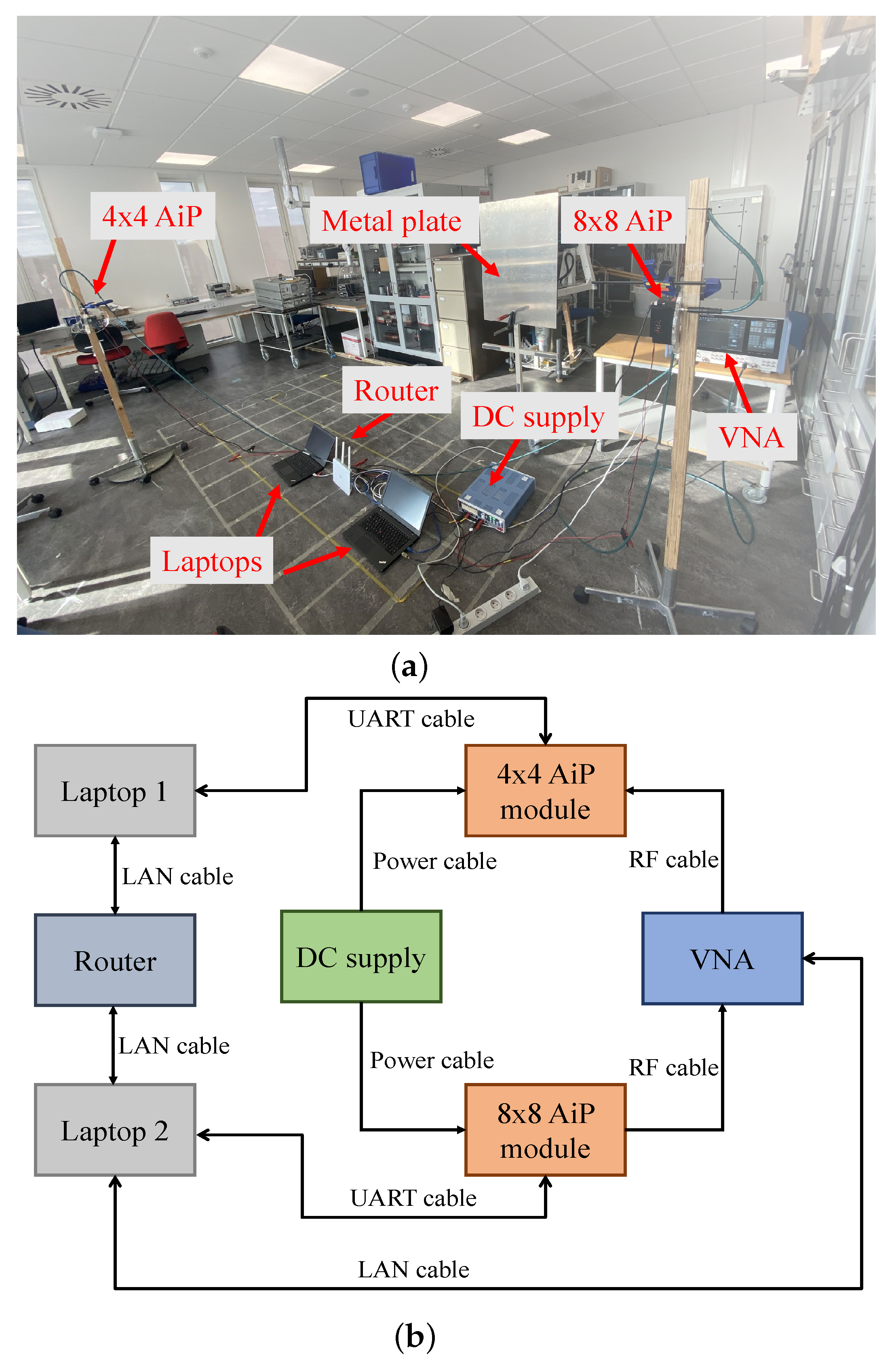
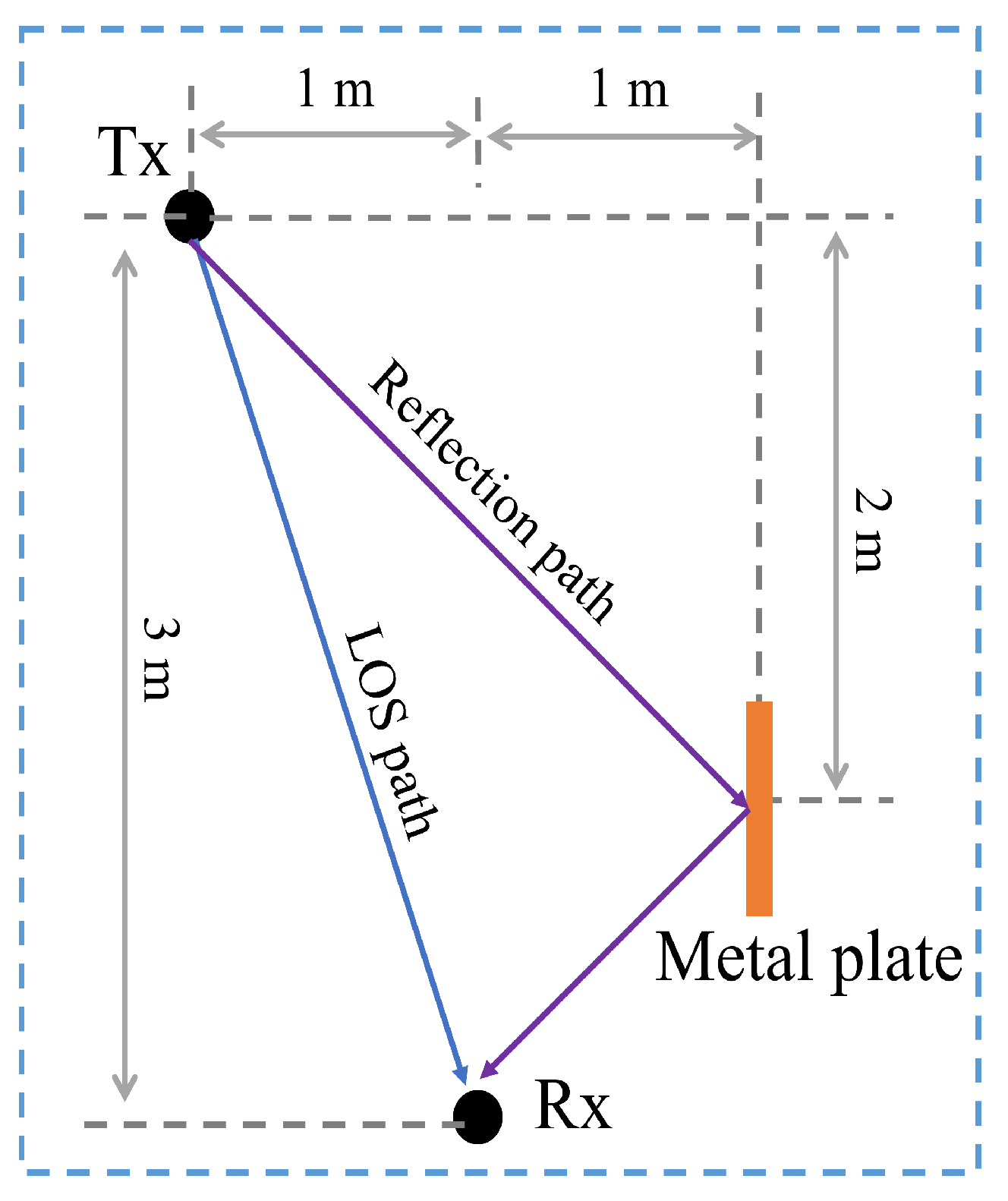
3.2. Mmwave Channel Sounding
Channel Sounding Measurements
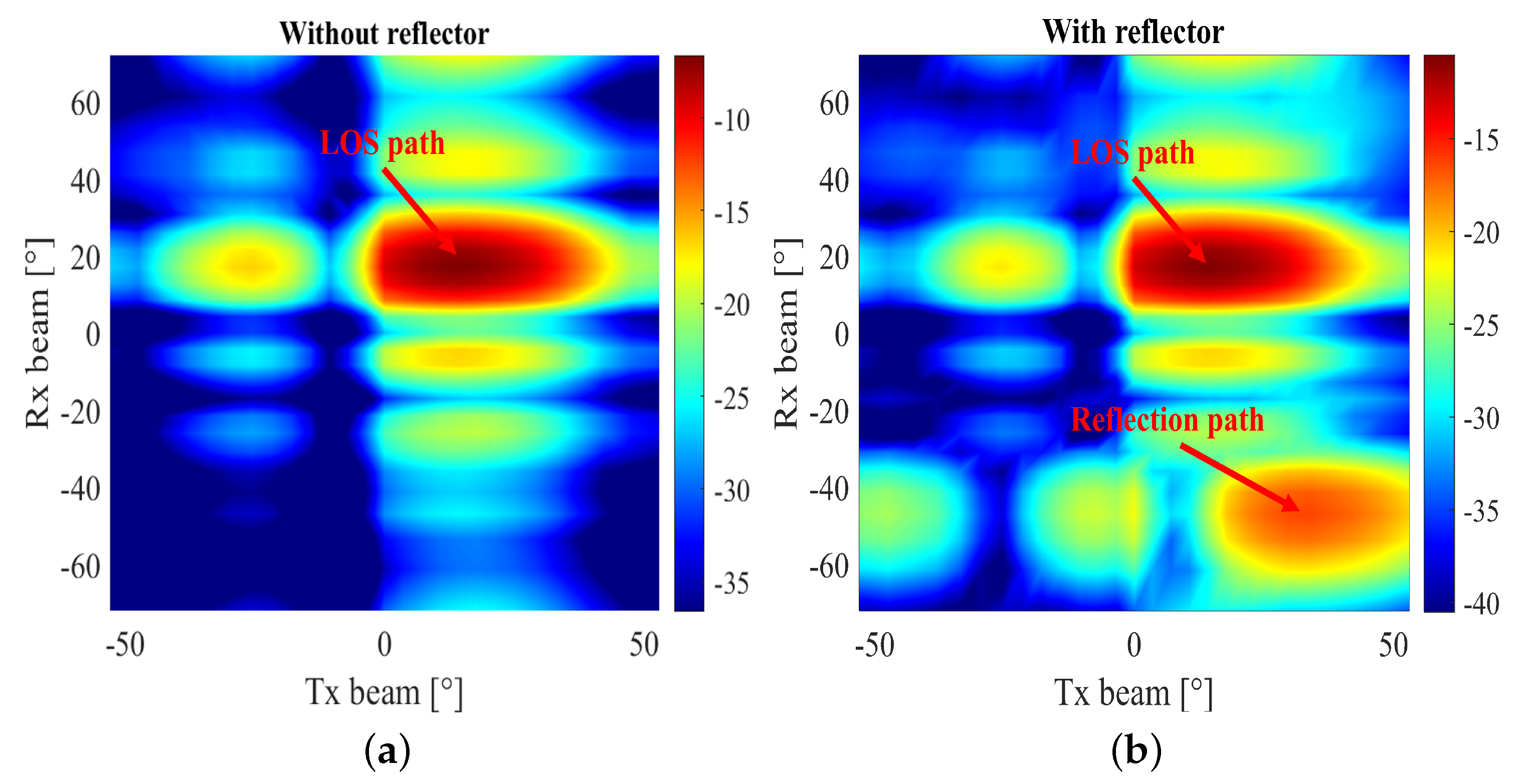
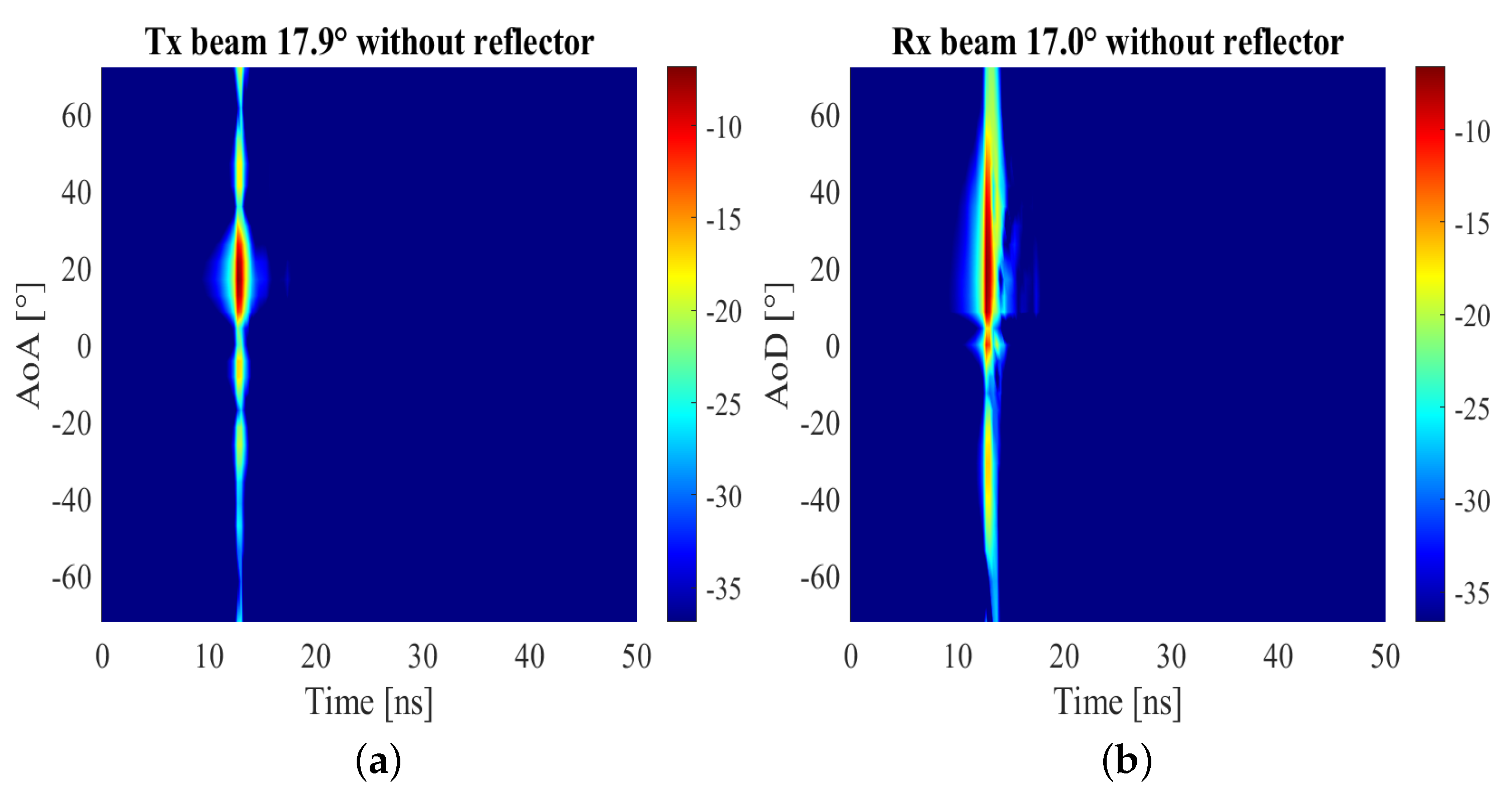
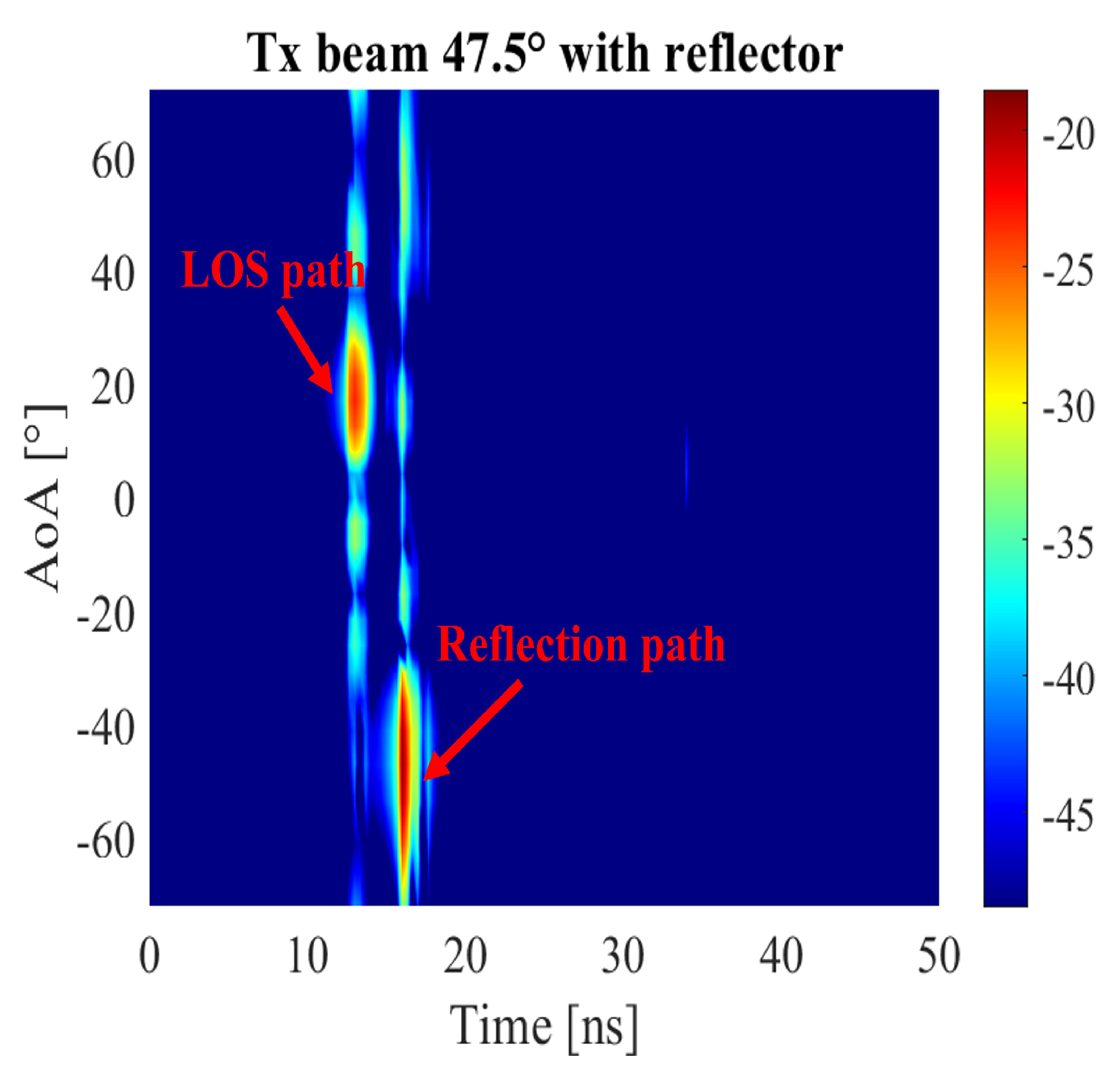
3.3. Channel Sounding Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hemadeh, I.A.; Satyanarayana, K.; El-Hajjar, M.; Hanzo, L. Millimeter-Wave Communications: Physical Channel Models, Design Considerations, Antenna Constructions, and Link-Budget. IEEE Commun. Surv. Tutor. 2018, 20, 870–913. [Google Scholar] [CrossRef] [Green Version]
- Choi, S.T.; Yang, K.S.; Nishi, S.; Shimizu, S.; Tokuda, K.; Kim, Y.H. A 60-GHz point-to-multipoint millimeter-wave fiber-radio communication system. IEEE Trans. Microw. Theory Tech. 2006, 54, 1953–1960. [Google Scholar] [CrossRef]
- Gao, H.; Wang, Z.; Zhang, X.; Kyösti, P.; Jing, Y.; Wang, W.; Wu, Y.; Pedersen, G.F.; Fan, W. Over-the-Air Performance Testing of 5G New Radio User Equipment: Standardization and Challenges. IEEE Commun. Stand. Mag. 2022, 6, 71–78. [Google Scholar] [CrossRef]
- Guan, K.; Ai, B.; Peng, B.; He, D.; Li, G.; Yang, J.; Zhong, Z.; Kürner, T. Towards Realistic High-Speed Train Channels at 5G Millimeter-Wave Band—Part I: Paradigm, Significance Analysis, and Scenario Reconstruction. IEEE Trans. Veh. Technol. 2018, 67, 9112–9128. [Google Scholar] [CrossRef]
- Joshi, K.C.; Niknam, S.; Prasad, R.V.; Natarajan, B. Analyzing the Tradeoffs in Using Millimeter Wave Directional Links for High Data-Rate Tactile Internet Applications. IEEE Trans. Ind. Inform. 2020, 16, 1924–1932. [Google Scholar] [CrossRef] [Green Version]
- Boccardi, F.; Heath, R.W.; Lozano, A.; Marzetta, T.L.; Popovski, P. Five disruptive technology directions for 5G. IEEE Commun. Mag. 2014, 52, 74–80. [Google Scholar] [CrossRef] [Green Version]
- Technical Report FCC-16-89; Further Notice of Proposed Rulemaking; Federal Communications Commission: Washington, DC, USA, July 2016.
- He, R.; Schneider, C.; Ai, B.; Wang, G.; Zhong, Z.; Dupleich, D.A.; Thomae, R.S.; Boban, M.; Luo, J.; Zhang, Y. Propagation Channels of 5G Millimeter-Wave Vehicle-to-Vehicle Communications: Recent Advances and Future Challenges. IEEE Veh. Technol. Mag. 2020, 15, 16–26. [Google Scholar] [CrossRef]
- Agiwal, M.; Roy, A.; Saxena, N. Next Generation 5G Wireless Networks: A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2016, 18, 1617–1655. [Google Scholar] [CrossRef]
- Ferreira, M.; Pinho, P. Propagation at mmWaves frequencies: Some considerations. In Proceedings of the 2021 Telecoms Conference (ConfTELE), Leiria, Portugal, 11–12 February 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Ghosh, A.; Thomas, T.A.; Cudak, M.C.; Ratasuk, R.; Moorut, P.; Vook, F.W.; Rappaport, T.S.; MacCartney, G.R.; Sun, S.; Nie, S. Millimeter-Wave Enhanced Local Area Systems: A High-Data-Rate Approach for Future Wireless Networks. IEEE J. Sel. Areas Commun. 2014, 32, 1152–1163. [Google Scholar] [CrossRef]
- Liao, S.; Wu, P.; Shum, K.M.; Xue, Q. Differentially Fed Planar Aperture Antenna With High Gain and Wide Bandwidth for Millimeter-Wave Application. IEEE Trans. Antennas Propag. 2015, 63, 966–977. [Google Scholar] [CrossRef]
- Briqech, Z.; Sebak, A.R.; Denidni, T.A. Wide-Scan MSC-AFTSA Array-Fed Grooved Spherical Lens Antenna for Millimeter-Wave MIMO Applications. IEEE Trans. Antennas Propag. 2016, 64, 2971–2980. [Google Scholar] [CrossRef]
- Guo, J.; Liao, S.; Xue, Q.; Xiao, S. Planar Aperture Antenna With High Gain and High Aperture Efficiency for 60-GHz Applications. IEEE Trans. Antennas Propag. 2017, 65, 6262–6273. [Google Scholar] [CrossRef]
- Rupakula, B.; Nafe, A.; Zihir, S.; Wang, Y.; Lin, T.W.; Rebeiz, G. 63.5–65.5-GHz Transmit/Receive Phased-Array Communication Link With 0.5–2 Gb/s at 100–800 m and ± 50° Scan Angles. IEEE Trans. Microw. Theory Tech. 2018, 66, 4108–4120. [Google Scholar] [CrossRef]
- Gu, X.; Liu, D.; Baks, C.; Tageman, O.; Sadhu, B.; Hallin, J.; Rexberg, L.; Parida, P.; Kwark, Y.; Valdes-Garcia, A. Development, Implementation, and Characterization of a 64-Element Dual-Polarized Phased-Array Antenna Module for 28-GHz High-Speed Data Communications. IEEE Trans. Microw. Theory Tech. 2019, 67, 2975–2984. [Google Scholar] [CrossRef]
- Wang, Y.; Chung, H.; Ma, Q.; Rebeiz, G.M. A 57.5–65.5 GHz Phased-Array Transmit Beamformer in 45 nm CMOS SOI With 5 dBm and 6.1 Linear PAE for 400 MBaud 64-QAM Waveforms. IEEE Trans. Microw. Theory Tech. 2021, 69, 1772–1779. [Google Scholar] [CrossRef]
- Herd, J.S.; Conway, M.D. The Evolution to Modern Phased Array Architectures. Proc. IEEE 2016, 104, 519–529. [Google Scholar] [CrossRef]
- Zhang, Y.P.; Liu, D. Antenna-on-Chip and Antenna-in-Package Solutions to Highly Integrated Millimeter-Wave Devices for Wireless Communications. IEEE Trans. Antennas Propag. 2009, 57, 2830–2841. [Google Scholar] [CrossRef]
- Zhang, Y.; Mao, J. An Overview of the Development of Antenna-in-Package Technology for Highly Integrated Wireless Devices. Proc. IEEE 2019, 107, 2265–2280. [Google Scholar] [CrossRef]
- Zwenger, C.; Chaudhry, V. Antenna in package (AiP) technology for 5G growth. Chip Scale Rev. March/April 2020, 351. Available online: https://www.chipscalereview.com/wp-content/uploads/2021/01/ChipScale_Mar-Apr_2020-wp.pdf (accessed on 28 November 2022).
- Gao, H.; Wang, W.; Fan, W.; Zhang, F.; Wang, Z.; Wu, Y.; Liu, Y.; Pedersen, G.F. Design and Experimental Validation of Automated Millimeter-Wave phased Array Antenna-in-Package (AiP) Experimental Platform. IEEE Trans. Instrum. Meas. 2021, 70, 1–11. [Google Scholar] [CrossRef]
- Zhang, F.; Fan, W.; Wang, Z.; Zhang, Y.; Pedersen, G.F. Improved Over-the-Air Phased Array Calibration Based on Measured Complex Array Signals. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 1174–1178. [Google Scholar] [CrossRef] [Green Version]
- Seiji, M.; Katagi, T. A method for measuring amplitude and phase of each radiating element of a phased array antenna. Electron. Commun. Jpn. Part Commun. 1982, J65-B, 555–560. [Google Scholar] [CrossRef]
- Takahashi, T.; Konishi, Y.; Chiba, I. A Novel Amplitude-Only Measurement Method to Determine Element Fields in Phased Arrays. IEEE Trans. Antennas Propag. 2012, 60, 3222–3230. [Google Scholar] [CrossRef]
- Long, R.; Ouyang, J.; Yang, F.; Han, W.; Zhou, L. Fast Amplitude-Only Measurement Method for Phased Array Calibration. IEEE Trans. Antennas Propag. 2017, 65, 1815–1822. [Google Scholar] [CrossRef]
- Hejselbæk, J.; Nielsen, J.; Fan, W.; Pedersen, G.F. Measured 21.5 GHz Indoor Channels With User-Held Handset Antenna Array. IEEE Trans. Antennas Propag. 2017, 65, 6574–6583. [Google Scholar] [CrossRef] [Green Version]
- Mbugua, A.W.; Fan, W.; Olesen, K.; Cai, X.; Pedersen, G.F. Phase-Compensated Optical Fiber-Based Ultrawideband Channel Sounder. IEEE Trans. Microw. Theory Tech. 2020, 68, 636–647. [Google Scholar] [CrossRef]
- Zwick, T.; Beukema, T.; Nam, H. Wideband channel sounder with measurements and model for the 60 GHz indoor radio channel. IEEE Trans. Veh. Technol. 2005, 54, 1266–1277. [Google Scholar] [CrossRef]
- Zhang, F.; Fan, W.; Pedersen, G.F. Frequency-Invariant Uniform Circular Array for Wideband mm-Wave Channel Characterization. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 641–644. [Google Scholar] [CrossRef] [Green Version]
- Lyu, Y.; Kyösti, P.; Fan, W. Sub-THz VNA-based Channel Sounder Structure and Channel Measurements at 100 and 300 GHz. In Proceedings of the 2021 IEEE 32nd Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Helsinki, Finland, 13–16 September 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Li, M.; Zhang, F.; Zhang, X.; Lyu, Y.; Fan, W. Omni-Directional Pathloss Measurement Based on Virtual Antenna Array With Directional Antennas. IEEE Trans. Veh. Technol. 2022, 1–5. [Google Scholar] [CrossRef]
- Caudill, D.; Chuang, J.; Jun, S.Y.; Gentile, C.; Golmie, N. Real-Time mmWave Channel Sounding Through Switched Beamforming With 3-D Dual-Polarized Phased-Array Antennas. IEEE Trans. Microw. Theory Tech. 2021, 69, 5021–5032. [Google Scholar] [CrossRef]
- Chopra, A.; Thornburg, A.; Kanhere, O.; Termos, A.; Ghassemzadeh, S.S.; Rappaport, T.S. Real-time Millimeter Wave Omnidirectional Channel Sounder Using Phased Array Antennas. In Proceedings of the GLOBECOM 2020-2020 IEEE Global Communications Conference, Taipei, Taiwan, 7–11 December 2020; pp. 1–7. [Google Scholar] [CrossRef]
- Wang, Y.; Phelps, T.; Kibaroglu, K.; Sayginer, M.; Ma, Q.; Rebeiz, G.M. 28 GHz 5G-Based Phased-Arrays for UAV Detection and Automotive Traffic-Monitoring Radars. In Proceedings of the 2018 IEEE/MTT-S International Microwave Symposium-IMS, Philadelphia, PA, USA, 10–15 June 2018; pp. 895–898. [Google Scholar] [CrossRef]
- Long, R.; Ouyang, J.; Yang, F.; Han, W.; Zhou, L. Multi-Element Phased Array Calibration Method by Solving Linear Equations. IEEE Trans. Antennas Propag. 2017, 65, 2931–2939. [Google Scholar] [CrossRef]
- Gao, H.; Wang, W.; Wu, Y.; Liu, Y.; Pedersen, G.F.; Fan, W. Experimental Comparison of On–Off and All-On Calibration Modes for Beam-Steering Performance of mmWave Phased Array Antenna-in-Package. IEEE Trans. Instrum. Meas. 2021, 70, 1–9. [Google Scholar] [CrossRef]


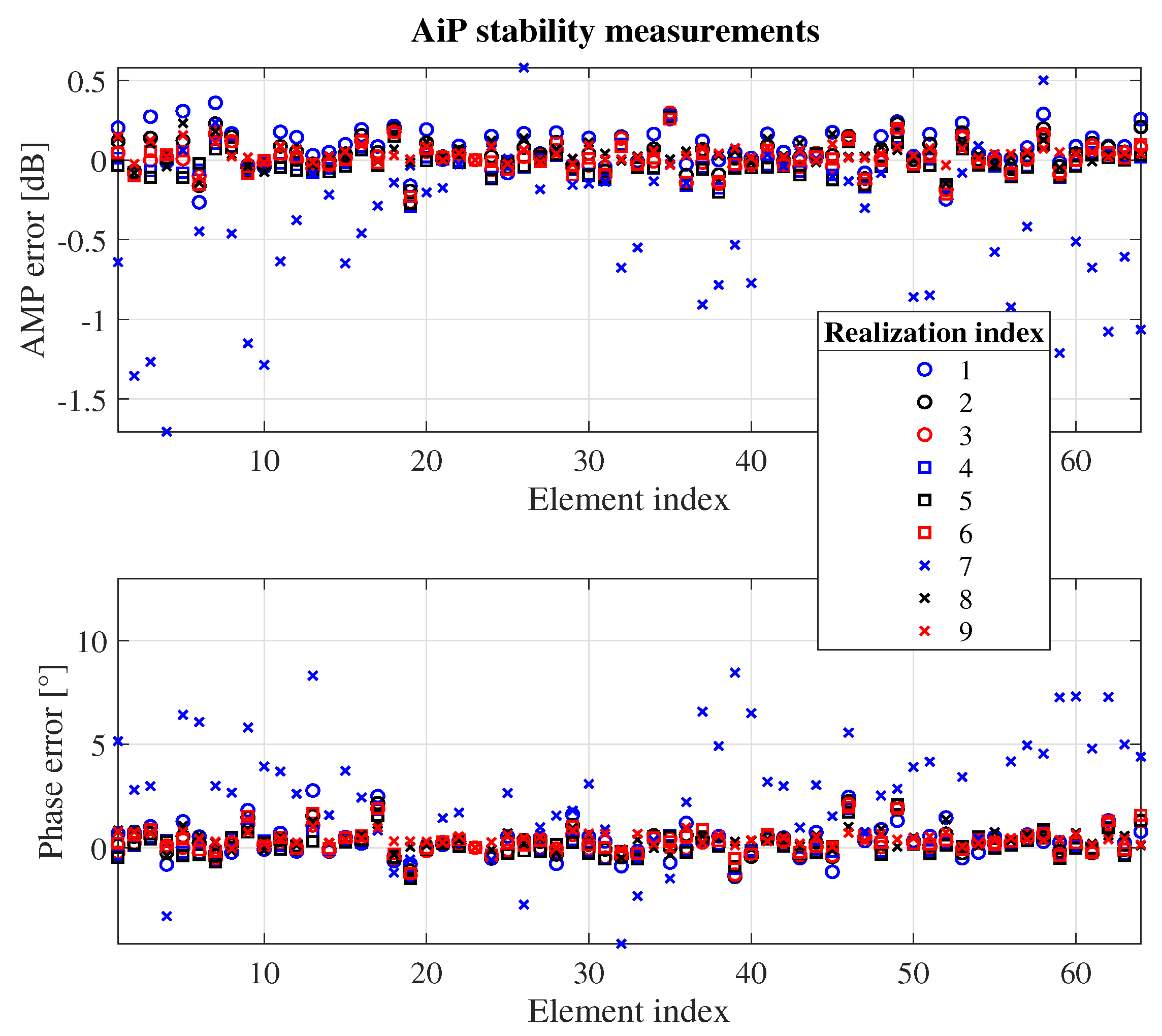
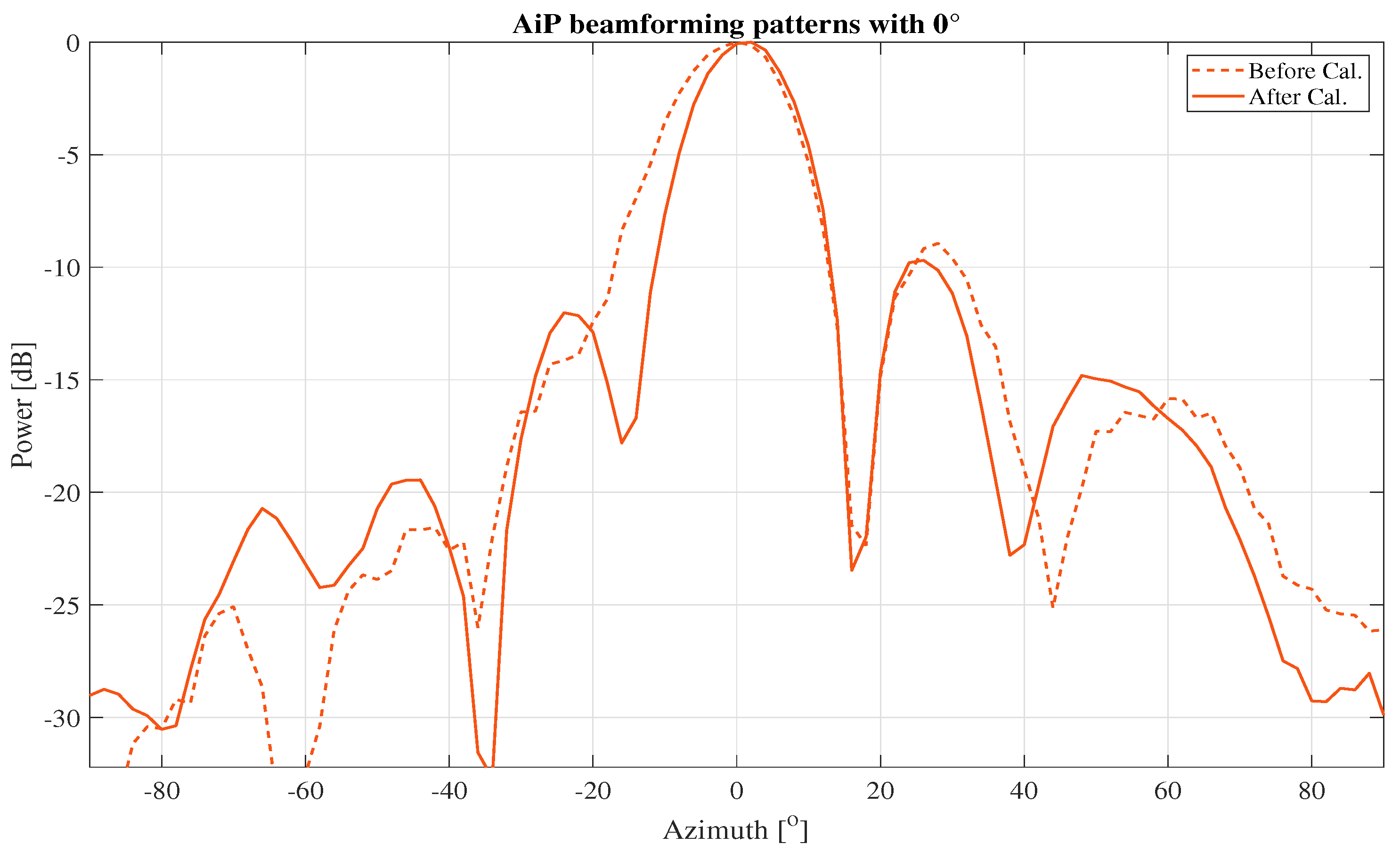

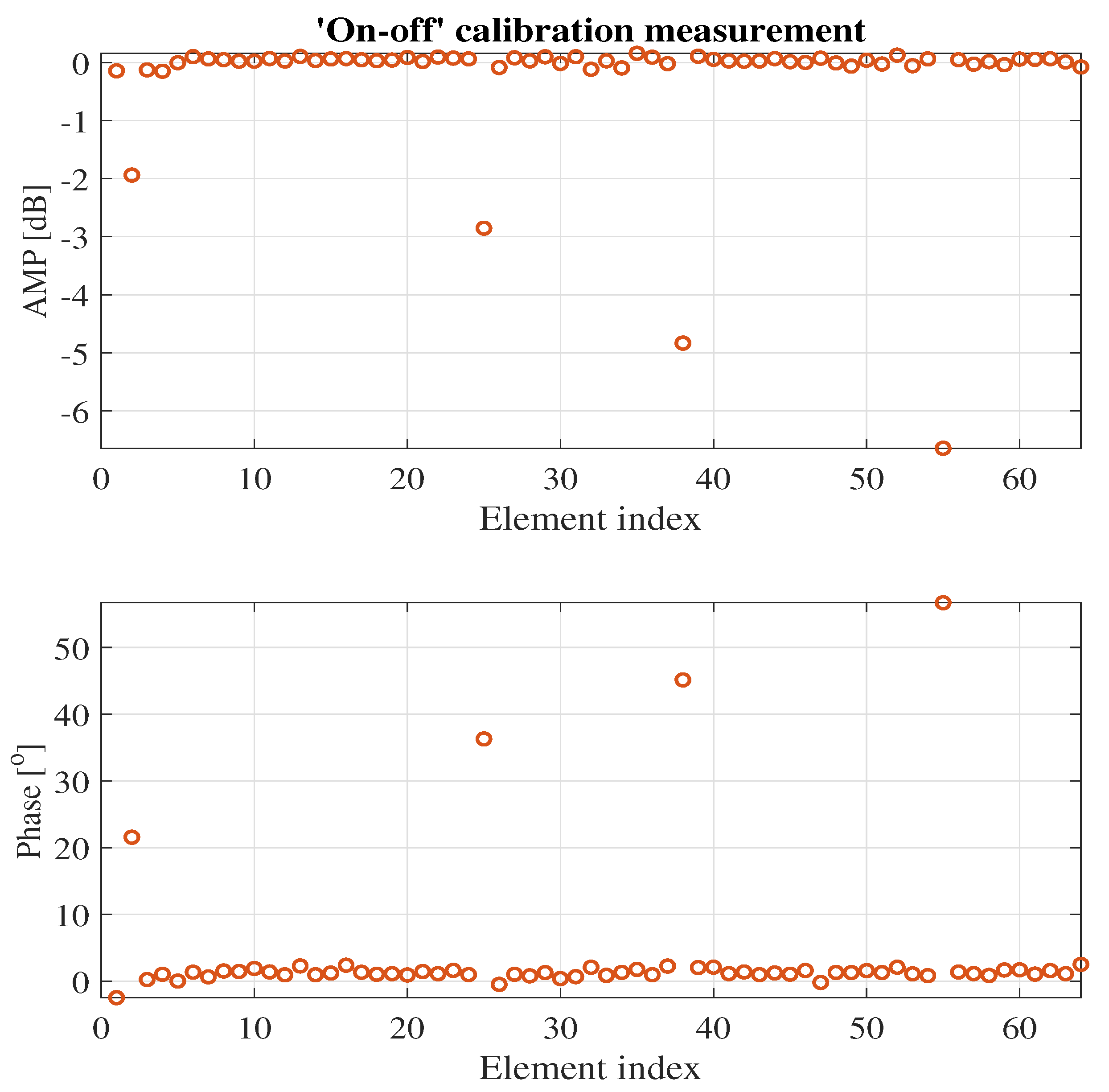
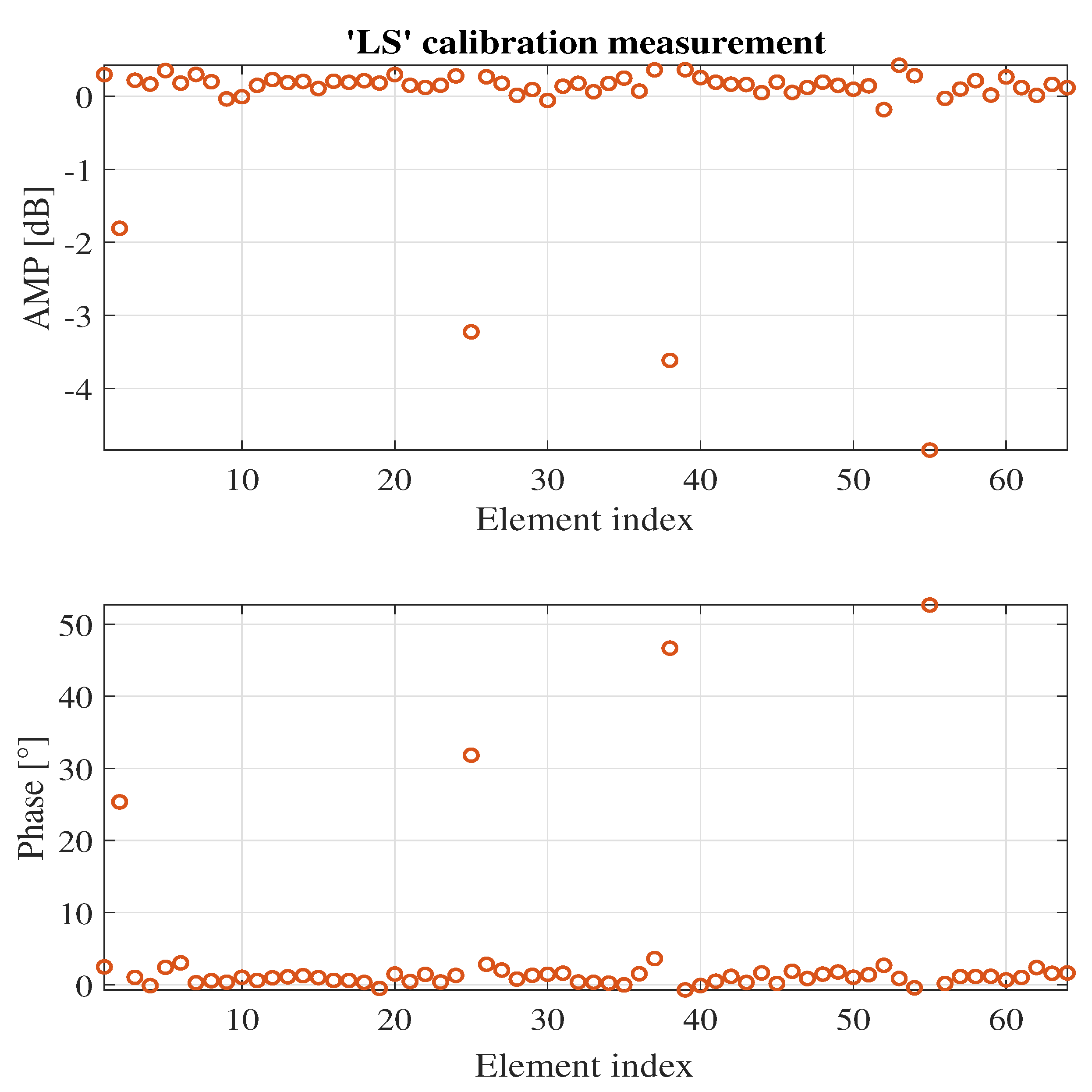
| Element | ‘On-off’ Amp. Err. [dB] | ‘LS’ Amp. Err. [dB] | ‘On-off’ Pha. Err. [°] | ‘LS’ Pha. Err. [°] |
|---|---|---|---|---|
| 1 | −0.2 | −0.2 | 1.6 | 2.8 |
| 2 | −0.3 | 0.2 | 5.0 | −1.9 |
| 3 | 0.7 | −0.4 | 2.6 | 1.7 |
| 4 | 1.5 | −0.2 | 2.9 | −3.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Fan, W.; Gao, H.; Zhang, F. Experimental Validation and Applications of mm-Wave 8 × 8 Antenna-in-Package (AiP) Array Platform. Electronics 2022, 11, 4055. https://doi.org/10.3390/electronics11234055
Li Y, Fan W, Gao H, Zhang F. Experimental Validation and Applications of mm-Wave 8 × 8 Antenna-in-Package (AiP) Array Platform. Electronics. 2022; 11(23):4055. https://doi.org/10.3390/electronics11234055
Chicago/Turabian StyleLi, Yifa, Wei Fan, Huaqiang Gao, and Fengchun Zhang. 2022. "Experimental Validation and Applications of mm-Wave 8 × 8 Antenna-in-Package (AiP) Array Platform" Electronics 11, no. 23: 4055. https://doi.org/10.3390/electronics11234055
APA StyleLi, Y., Fan, W., Gao, H., & Zhang, F. (2022). Experimental Validation and Applications of mm-Wave 8 × 8 Antenna-in-Package (AiP) Array Platform. Electronics, 11(23), 4055. https://doi.org/10.3390/electronics11234055







