An Improved Multimodal Trajectory Prediction Method Based on Deep Inverse Reinforcement Learning
Abstract
:1. Introduction
- (1)
- It is very necessary to accurately extract map features and historical sequence information, since it always directly affects the downstream feature analysis and trajectory prediction. In this paper, a fused dilated convolution module is introduced into the existing multimodal trajectory prediction network, which can make a streamlined improvement by expanding the perceptual field without ignoring local information of the traffic scene and retaining the same or even higher generalizability compared with the original network.
- (2)
- Since the inverse reinforcement learning policy extracts the reward function from expert presentation data, which can effectively solve the problem of the complexity and difficulty of setting the reward function manually, in this paper, an improved MaxEnt RL policy with inferred goals is applied into the existing multimodal trajectory prediction network, which can alleviate the need for a predefined goal state and induce distribution on possible goals.
- (3)
- It is very crucial to design a reasonable and effective sampling function that not only affects the optimization process of the neural network but also determines the effective utilization of feature information extracted from the dataset. In this paper, a proposed correction factor is added into the existing multimodal trajectory prediction network, which can encourage the generation of diverse trajectories by penalizing pairwise distances with small differences, and this is more in line with the multimodal characteristics of future trajectories.
2. Preliminaries
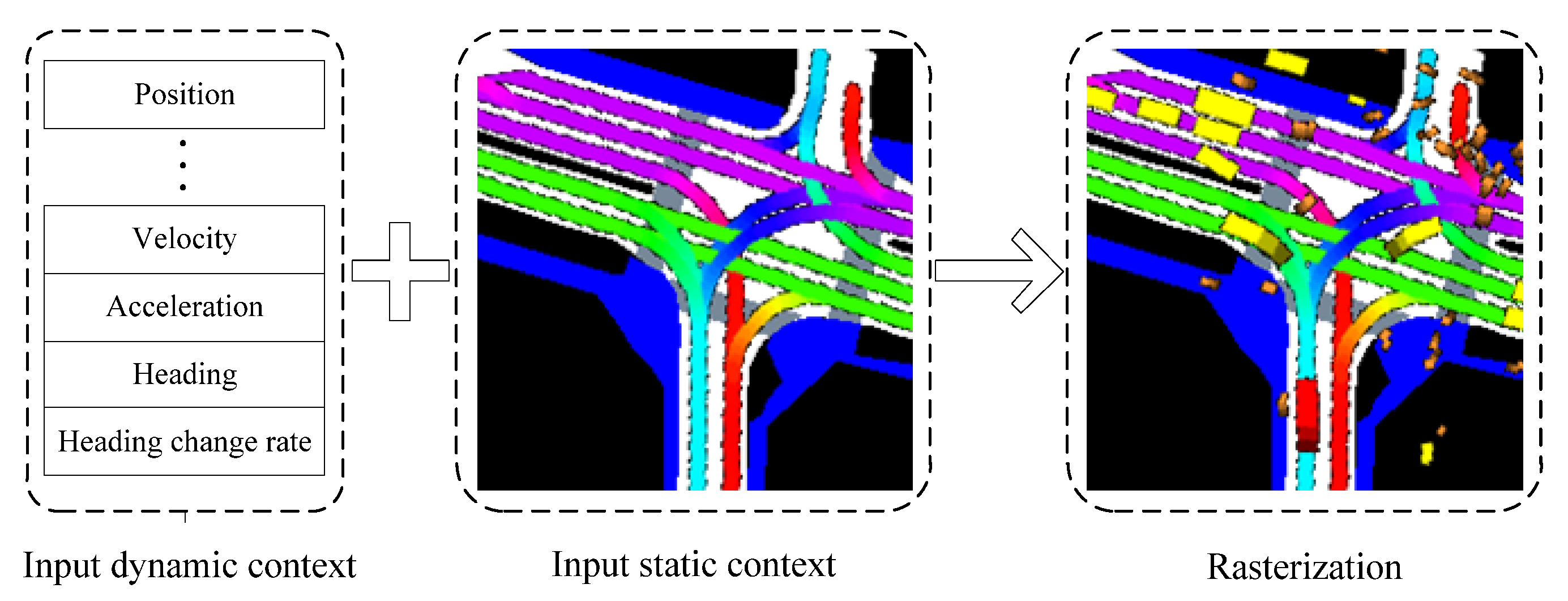
2.1. Rasterization for the Traffic Scene
2.2. Reward Initialization Based on Two-Stage Backbone
2.3. Reward Updating Based on MaxEnt RL Policy
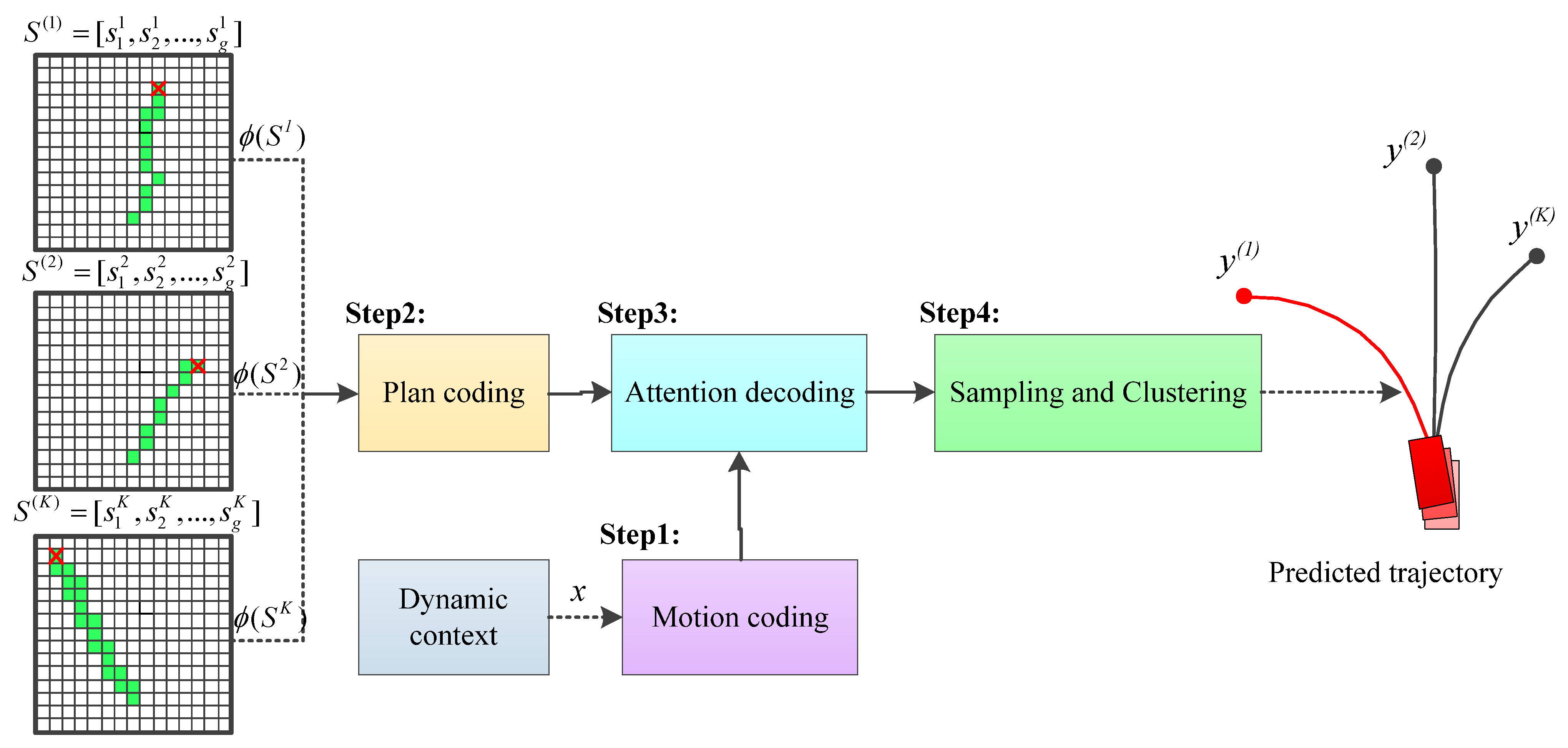
2.4. Trajectory Generation Based on Attention Mechanism
3. Proposed Method
3.1. Architecture
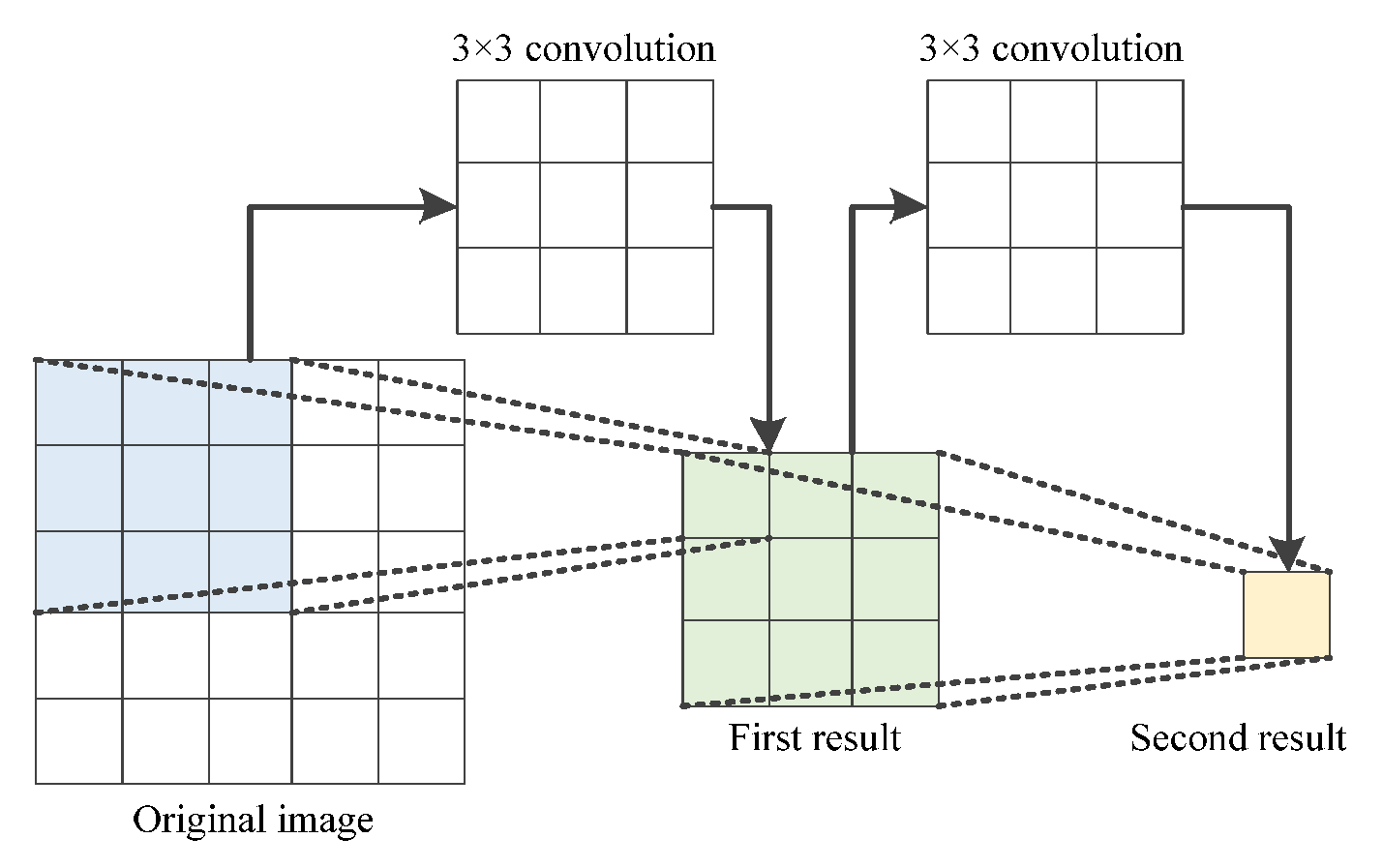
3.2. Improved Fused Dilated Convolution Module
3.3. Improved MaxEnt RL Policy Module with Inferred Goals
3.4. Improved Attention-Based Trajectory Generator with Correction Factor
4. Experimental Analysis
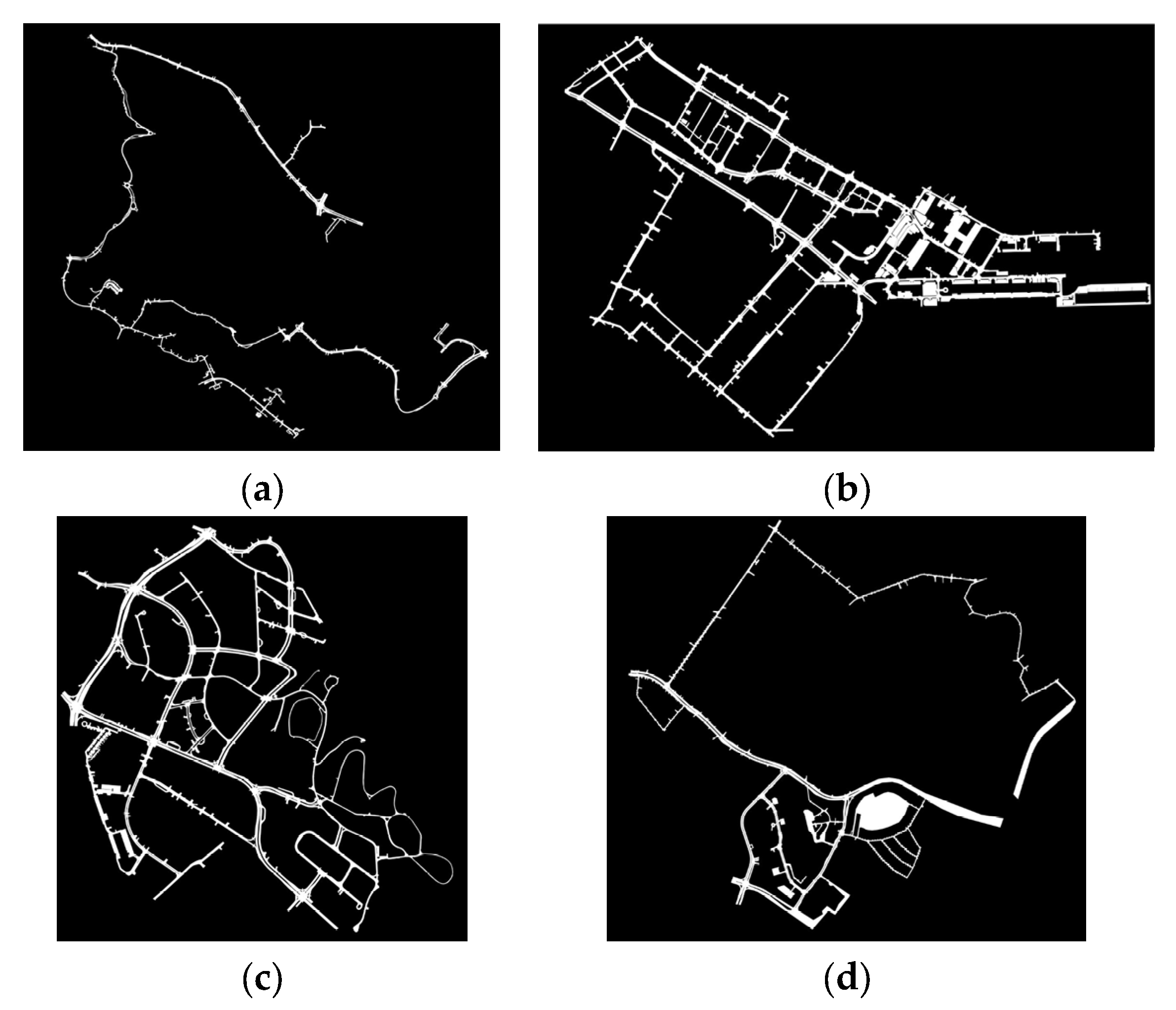
4.1. Dataset
4.2. Metrics
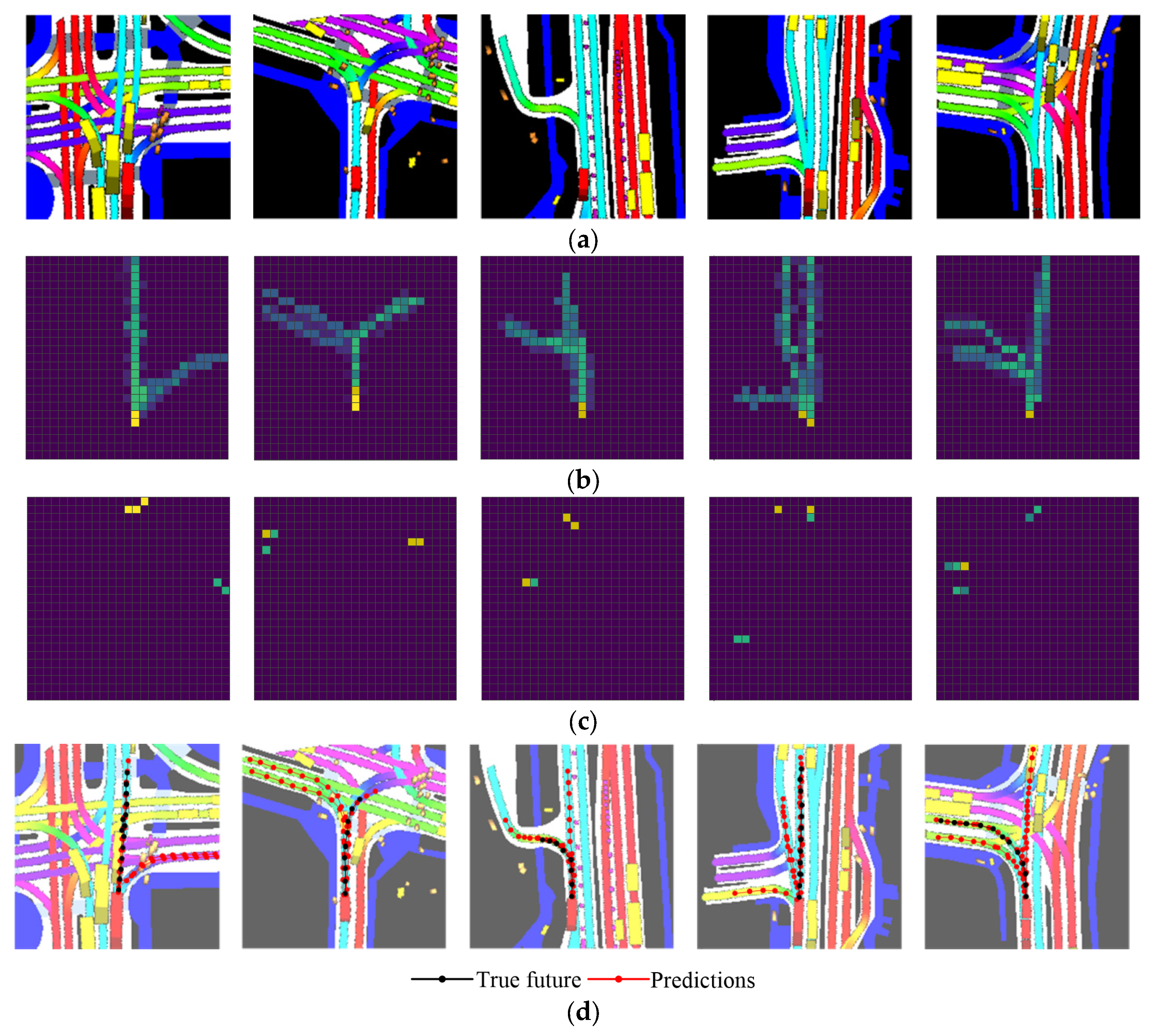
4.3. Experimental Comparison and Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, J.; Huang, H.; Zhi, P.; Sheng, Z.; Zhou, G. Review of development and key technologies in automatic driving. Appl. Electron. Tech. 2019, 6, 28–36. [Google Scholar] [CrossRef]
- Meng, X.; Zhang, C.; Su, C. Review of key technologies of autonomous vehicle systems. Auto Time 2019, 17, 4–5. [Google Scholar]
- Pei, Y.; Chi, B.; Lv, J.; Yue, Z. An overview of traffic management in “automatic + manual” driving environment. J. Transp. Inf. Saf. 2021, 5, 1–11. [Google Scholar]
- Gehlot, A.; Singh, R.; Kuchhal, P.; Kumar, A.; Singh, A.; Alsubhi, K.; Ibrahim, M.; Villar, S.G.; Brenosa, J. WPAN and IoT Enabled Automation to Authenticate Ignition of Vehicle in Perspective of Smart Cities. Sensors 2021, 21, 7031. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Wang, Y.; Deng, X.; Huang, Q.; Liao, K. A review on the study of impact of uncertainty on vehicle trajectory prediction. Automob. Technol. 2022, 7, 1–14. [Google Scholar] [CrossRef]
- Liu, W.; Hu, K.; Li, Y.; Liu, Z. A review of prediction methods for moving target trajectories. Chin. J. Intell. Sci. Technol. 2021, 2, 149–160. [Google Scholar]
- Leon, F.; Gavrilescu, M. A review of tracking and trajectory prediction methods for autonomous driving. Mathematics 2021, 6, 660. [Google Scholar] [CrossRef]
- Prevost, C.G.; Desbiens, A.; Gagnon, E. Extended Kalman filter for state estimation and trajectory prediction of a moving object detected by an unmanned aerial vehicle. In Proceedings of the 2007 American Control Conference, New York, NY, USA, 9–13 July 2007; pp. 1805–1810. [Google Scholar]
- Barth, A.; Franke, U. Where will the oncoming vehicle be the next second? In Proceedings of the 2008 IEEE Intelligent Vehicles Symposium, Eindhoven, The Netherlands, 4–6 June 2008; pp. 1068–1073. [Google Scholar]
- Qiao, S.; Han, N.; Zhu, X.; Shu, H.; Zheng, J.; Yuan, C. A dynamic trajectory prediction algorithm based on Kalman filter. Acta Electron. Sin. 2018, 02, 418–423. [Google Scholar]
- Vashishtha, D.; Panda, M. Maximum likelihood multiple model filtering for path prediction in intelligent transportation systems. Procedia Comput. Sci. 2018, 143, 635–644. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, G.; Hu, C.; Ma, X. Wavelet analysis based hidden Markov model for large ship trajectory prediction. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 2913–2918. [Google Scholar]
- Lim, Q.; Johari, K.; Tan, U.X. Gaussian process auto regression for vehicle center coordinates trajectory prediction. In Proceedings of the TENCON 2019-2019 IEEE Region 10 Conference (TENCON), Kochi, India, 17–20 October 2019; pp. 25–30. [Google Scholar]
- Wang, L.; Song, T. Ship collision trajectory planning and prediction for inland waterway. J. Hubei Univ. Technol. 2019, 2, 64–68. [Google Scholar]
- Yang, C. Research on the trajectory prediction method based on BP neural network. Pract. Electron. 2014, 20, 22. [Google Scholar] [CrossRef]
- Yang, B.; He, Z. Hypersonic vehicle track prediction based on GRNN. Comput. Appl. Softw. 2015, 7, 239–243. [Google Scholar]
- Gao, T.; Xu, L.; Jin, L.; Ge, B. Vessel trajectory prediction considering difference between heading and data changes. J. Transp. Syst. Eng. Inf. Technol. 2021, 1, 90–94. [Google Scholar] [CrossRef]
- Djuric, N.; Radosavljevic, V.; Cui, H.; Nguyen, T.; Chou, F.C.; Lin, T.H.; SINGH, N.; Schneider, J. Uncertainty-aware short-term motion prediction of traffic actors for autonomous driving. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Snowmass Village, CO, USA, 2–5 May 2020; pp. 2095–2104. [Google Scholar]
- Li, X.; Ying, X.; Chuah, M.C. Grip: Graph-based interaction-aware trajectory prediction. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 3960–3966. [Google Scholar]
- Luo, W.; Yang, B.; Urtasun, R. Fast and furious: Real time end-to-end 3d detection, tracking and motion forecasting with a single convolutional net. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 3569–3577. [Google Scholar]
- Gupta, A.; Johnson, J.; Fei-Fei, L.; Savarese, S.; Alahi, A. Social gan: Socially acceptable trajectories with generative adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 2255–2264. [Google Scholar]
- Lee, N.; Choi, W.; Vernaza, P.; Choy, C.B.; Torr, P.H.; Chandraker, M. Desire: Distant future prediction in dynamic scenes with interacting agents. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2018; pp. 336–345. [Google Scholar]
- Tang, C.; Salakhutdinov, R.R. Multiple futures prediction. Adv. Neural Inf. Processing Syst. 2019, 32, 1–11. [Google Scholar]
- Cui, H.; Radosavljevic, V.; Chou, F.C.; Lin, T.H.; Nguyen, T.; Huang, T.K.; Schneider, J.; Djuric, N. Multimodal trajectory predictions for autonomous driving using deep convolutional networks. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 2090–2096. [Google Scholar]
- Chai, Y.; Sapp, B.; Bansal, M.; Anguelov, D. Multipath: Multiple probabilistic anchor trajectory hypotheses for behavior prediction. arXiv 2019, arXiv:1910.05449. [Google Scholar]
- Phan-Minh, T.; Grigore, E.C.; Boulton, F.A.; Beijbom, O.; Wolff, E.M. Covernet: Multimodal behavior prediction using trajectory sets. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 14074–14083. [Google Scholar]
- Messaoud, K.; Deo, N.; Trivedi, M.M.; Nashashibi, F. Trajectory prediction for autonomous driving based on multi-head attention with joint agent-map representation. In Proceedings of the 2021 IEEE Intelligent Vehicles Symposium (IV), Nagoya, Japan, 11–17 July 2021; pp. 165–170. [Google Scholar]
- Luo, C.; Sun, L.; Dabiri, D.; Yuille, A. Probabilistic multi-modal trajectory prediction with lane attention for autonomous vehicles. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 2370–2376. [Google Scholar]
- Ivanovic, B.; Pavone, M. The trajectron: Probabilistic multi-agent trajectory modeling with dynamic spatiotemporal graphs. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 2375–2384. [Google Scholar]
- Salzmann, T.; Ivanovic, B.; Chakravarty, P.; Pavone, M. Trajectron++: Dynamically-feasible trajectory forecasting with heterogeneous data. In Proceedings of the European Conference on Computer Vision (ECCV), Online, 23–28 August 2020; pp. 683–700. [Google Scholar]
- Carrasco, S.; Llorca, D.F.; Sotelo, M.A. SCOUT: Socially-consistent and undersTandable graph attention network for trajectory prediction of vehicles and VRUs. In Proceedings of the 2021 IEEE Intelligent Vehicles Symposium (IV), Nagoya, Japan, 11–17 July 2021; pp. 1501–1508. [Google Scholar]
- Zhang, Y.; Wang, W.; Bonatti, R.; Maturana, D.; Scherer, S. Integrating kinematics and environment context into deep inverse reinforcement learning for predicting off-road vehicle trajectories. arXiv 2018, arXiv:1810.07225. [Google Scholar]
- Djuric, N.; Radosavljevic, V.; Cui, H.; Nguyen, T.; Chou, F.C.; Lin, T.H.; Schneider, J. Short-term motion prediction of traffic actors for autonomous driving using deep convolutional networks. arXiv 2018, arXiv:1808.05819. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural machine translation by jointly learning to align and translate. arXiv 2014, arXiv:1409.0473. [Google Scholar]
- Ahmed, M.; Seraj, R.; Islam, S.M.S. The k-means algorithm: A comprehensive survey and performance evaluation. Electronics 2020, 8, 1295. [Google Scholar] [CrossRef]
- Liu, J.; Li, C.; Liang, F.; Lin, C.; Sun, M.; Yan, J.; Ouyang, W.; Xu, D. Inception convolution with efficient dilation search. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Online, 19–25 June 2021; pp. 11486–11495. [Google Scholar]
- Sinha, D.; El-Sharkawy, M. Thin mobilenet: An enhanced mobilenet architecture. In Proceedings of the 2019 IEEE 10th Annual Ubiquitous Computing, Electronics & Mobile Communication Conference (UEMCON), New York, NY, USA, 10–12 October 2019; pp. 280–285. [Google Scholar]
- Iandola, F.N.; Han, S.; Moskewicz, M.W.; Ashraf, K.; Dally, W.J.; Keutzer, K. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <0.5 MB model size. arXiv 2016, arXiv:1602.07360. [Google Scholar]
- Ibrahim, M.; Iqbal, M.A.; Aleem, M.; Islam, M.A.; Vo, N.S. MAHA: Migration-based adaptive heuristic algorithm for large-scale network simulations. Clust. Comput. 2020, 2, 1251–1266. [Google Scholar] [CrossRef]
- Yuan, Y.; Kitani, K. Dlow: Diversifying latent flows for diverse human motion prediction. In Proceedings of the European Conference on Computer Vision (ECCV), Online, 23–28 August 2020; pp. 346–364. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Caesar, H.; Bankiti, V.; Lang, A.H.; Vora, S.; Liong, V.E.; Xu, Q.; Krishnan, A.; Pan, Y.; Baldan, G.; Beijbom, O. nuscenes: A multimodal dataset for autonomous driving. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 11621–11631. [Google Scholar]
- Greer, R.; Deo, N.; Trivedi, M. Trajectory prediction in autonomous driving with a lane heading auxiliary loss. IEEE Robot. Autom. Lett. 2021, 3, 4907–4914. [Google Scholar] [CrossRef]






| Parameter Name | Parameter Content |
|---|---|
| Computer model | Lenovo 30BBA8M0CW desktop computer |
| Operating system | Windows 10 Professional 64-bit |
| CPU | Intel Xeon Gold5118 @ 2.30 GHz (X2) |
| GPU | Nvidia Quadro RTX 5000 (16 GB) |
| Python | 3.8.8 |
| Pytorch | 1.10.0 |
| CUDA | 10.2 |
| cuDNN | 7.0 |
| Dataset | Release Time | Data Scale | Perspective | Scenes | Remark |
|---|---|---|---|---|---|
| NGSIM | 2006.12 | 4 scenes, 9206 vehicles, 5071 km driving distance, 174 h total recording time | top view | highway, city road | It used to be the most popular dataset in this field, but the research found that there are problems such as insufficient precision and coordinate drift, and it is rarely used at present. |
| ETH | 2008.6 | 3 video clips, 1804 images | vehicle view | city road | A classic pedestrian dataset, suitable for computer vision tasks and social behavior modeling. |
| Stanford Drone | 2016.8 | 8 scenes, 19,000 targets, 185,000 tagged target interaction messages | top view | campus | Video taken by drones across the Stanford campus, including pedestrians, vehicles, bicycles and other traffic participants. |
| HighD | 2018.10 | 6 scenes, 110,000 vehicles, 45,000 km driving distance, 447 h total recording time | top view | highway | A large dataset of natural vehicle trajectories on German highways, suitable for driver model parameterization, autonomous driving, and traffic pattern analysis. |
| nuScenes | 2019.3 | 1000 scenes, 1.4 million camera images, 390,000 LiDAR scans, 1.4 million radar scans | vehicle view | city road | The first publicly available full-sensor dataset, large enough for research on sensor suites. It is widely used in various fields of autonomous driving. |
| Method | Eave(5) | Eave(10) | Efinal(5) | Efinal(10) | Rmiss(5,2) | Rmiss(10,2) | Roff |
|---|---|---|---|---|---|---|---|
| Physics oracle [26] | 3.69 | 3.69 | 9.06 | 9.06 | 0.91 | 0.91 | 0.12 |
| CoverNet [26] | 2.62 | 1.92 | - | - | 0.76 | 0.64 | 0.13 |
| MTP [24] | 2.44 | 1.57 | 4.83 | 3.54 | 0.70 | 0.55 | 0.11 |
| M-SCOUT [31] | 1.92 | 1.92 | - | - | 0.78 | 0.78 | 0.10 |
| Trajectron++ [30] | 1.88 | 1.51 | - | - | 0.70 | 0.57 | 0.25 |
| Multipath [25] | 1.78 | 1.55 | 3.62 | 2.93 | 0.75 | 0.74 | 0.36 |
| MHA-JAM [27] | 1.81 | 1.24 | 3.72 | 2.21 | 0.59 | 0.45 | 0.07 |
| cxx [28] | 1.63 | 1.29 | - | - | 0.69 | 0.60 | 0.08 |
| Ours | 1.49 | 1.13 | 3.06 | 2.06 | 0.64 | 0.45 | 0.03 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.; Guo, C.; Li, H.; Gao, T.; Chen, L.; Tu, H.; Yang, J. An Improved Multimodal Trajectory Prediction Method Based on Deep Inverse Reinforcement Learning. Electronics 2022, 11, 4097. https://doi.org/10.3390/electronics11244097
Chen T, Guo C, Li H, Gao T, Chen L, Tu H, Yang J. An Improved Multimodal Trajectory Prediction Method Based on Deep Inverse Reinforcement Learning. Electronics. 2022; 11(24):4097. https://doi.org/10.3390/electronics11244097
Chicago/Turabian StyleChen, Ting, Changxin Guo, Hao Li, Tao Gao, Lei Chen, Huizhao Tu, and Jiangtian Yang. 2022. "An Improved Multimodal Trajectory Prediction Method Based on Deep Inverse Reinforcement Learning" Electronics 11, no. 24: 4097. https://doi.org/10.3390/electronics11244097
APA StyleChen, T., Guo, C., Li, H., Gao, T., Chen, L., Tu, H., & Yang, J. (2022). An Improved Multimodal Trajectory Prediction Method Based on Deep Inverse Reinforcement Learning. Electronics, 11(24), 4097. https://doi.org/10.3390/electronics11244097








