Speed-Gradient Adaptive Control for Parametrically Uncertain UAVs in Formation
Abstract
:1. Introduction
2. Point-Mass Model of UAV Dynamics
2.1. Feedback Linearization
2.2. Feedback Linearization for Variable Mass m Case
3. Adaptive Control of Single UAV
3.1. Problem Statement and Control Goal
3.2. Design of Main Control Loop
3.3. Synthesis of UAV Adaptation Law
- The scalar objective function is non-negative and satisfies the growth condition as . Note that this condition is met for function (19).
- Function should be convex on adjustable parameters , , , . This condition is met because is linear with respect to the adjustable parameters.
- The following reachability condition is satisfied: for any m from the range of its possible values , there exists a set of parameters , , , and a function ( as ) such that for all x, y, h, t, the inequalityis fulfilled, as follows from Proposition 1.
4. Control of Multi-Agent UAV Formation
4.1. Problem Description
4.2. Consensus Algorithm for Multi-Agent Formation Control
4.2.1. Basic Information on Consensus Algorithm
4.2.2. UAV Formation Control based on the Consensus Algorithm
- The scalar objective function is non-negative and satisfies the growth condition as . This is true for function (58).
- Function should be convex on the adjustable parameters , , , , . This condition is met because is linear with respect to the parameters.
- Reachability condition: for any set of values , from the ranges of possible values , there exists a set of parameters , , , and function ( as for which for all x, y, h, t hold:To prove this, we can consider the Lyapunov function:Because is the sum of the control objective functions for each UAV and the control signal based on the consensus algorithm enters additively into the overall control signal (61), by taking into account expressions (27) and (41) the proof of Proposition 1 implieswhere and is an addition to the derivative of the consensus algorithm (63). This function is as follows:By assumption, the associated communication digraph contains a spanning tree; therefore (see [76]), the Laplace matrix L is positive semi-definite, and hence all the matrices inside the parentheses of expression (67 ) are positive definite. Then, , and for (66) there always exists such thatis valid. Therefore, condition (64) is satisfied.
5. Simulation Results
5.1. General Data for Simulations
5.2. Control of Single UAV
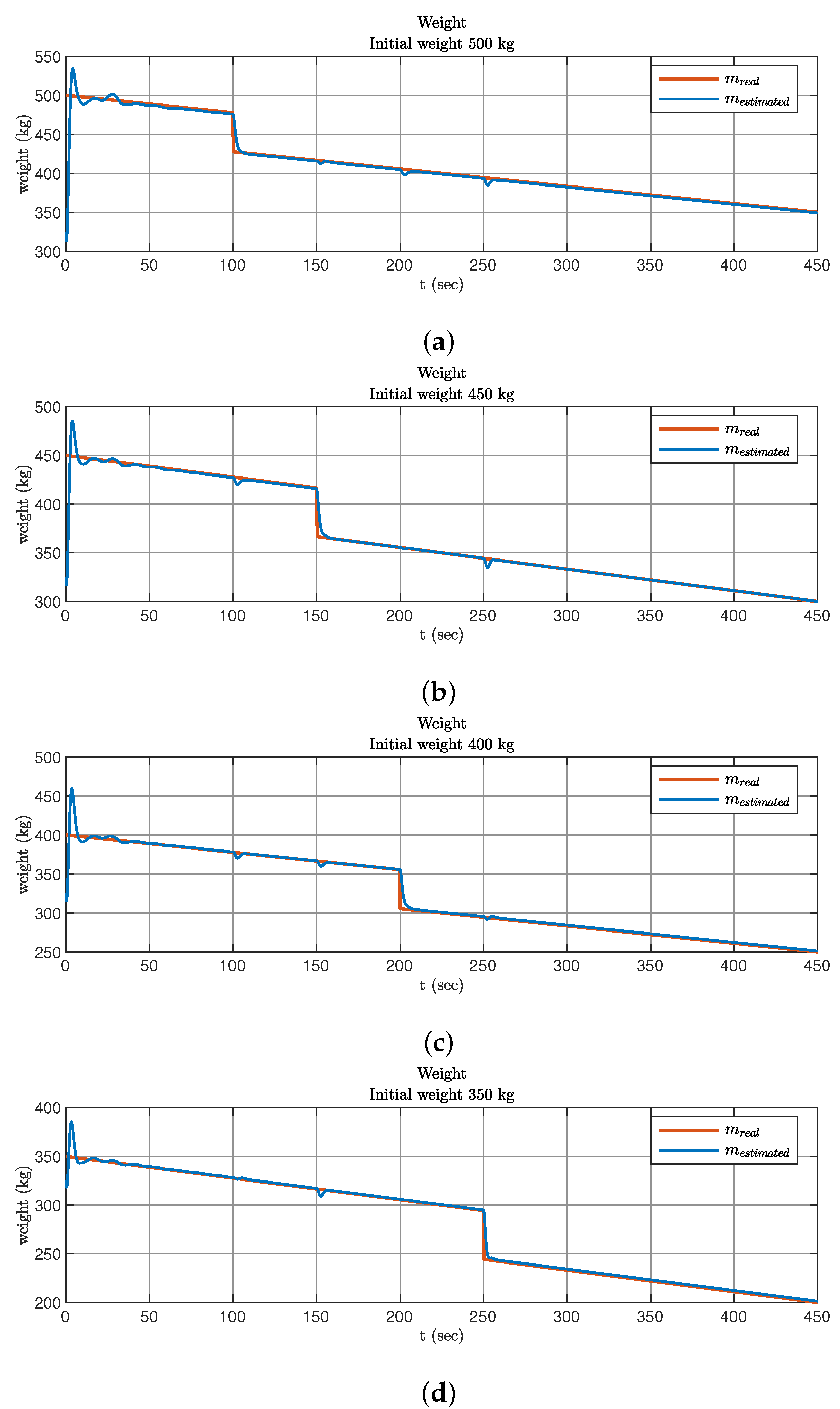
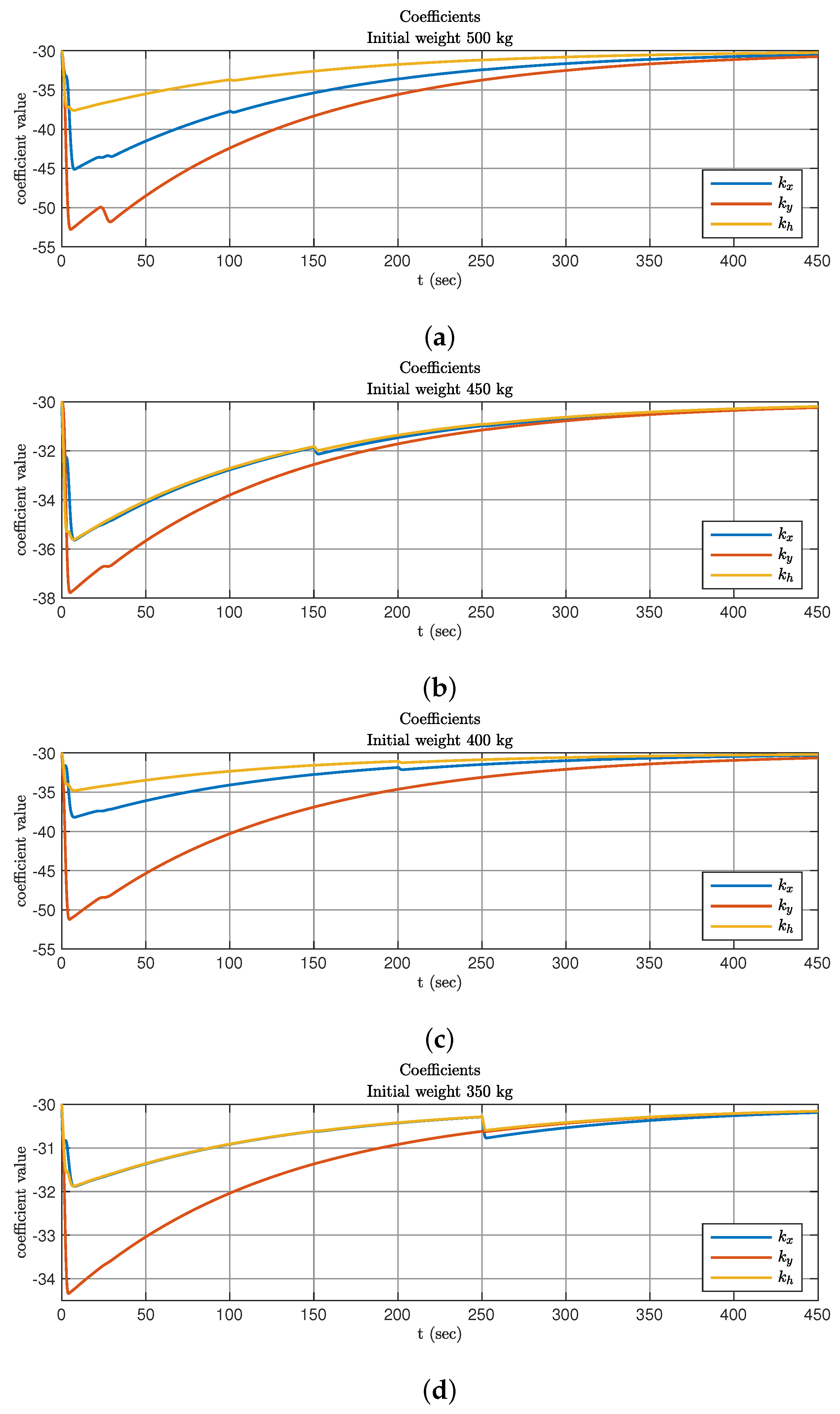
5.2.1. Control of Single UAV with Linearly Varying Mass
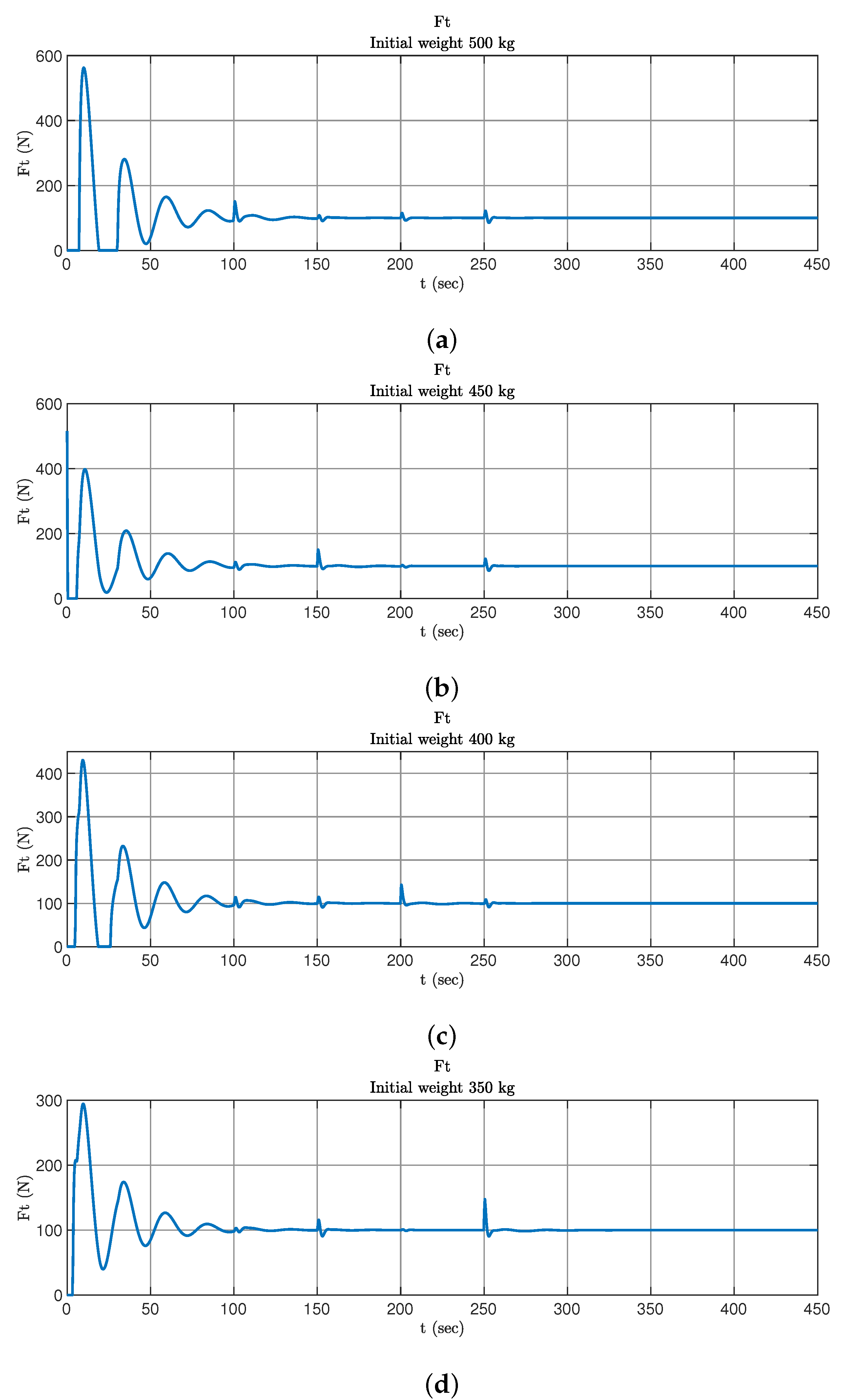
5.2.2. Control of Single UAV with Jump-changing Mass
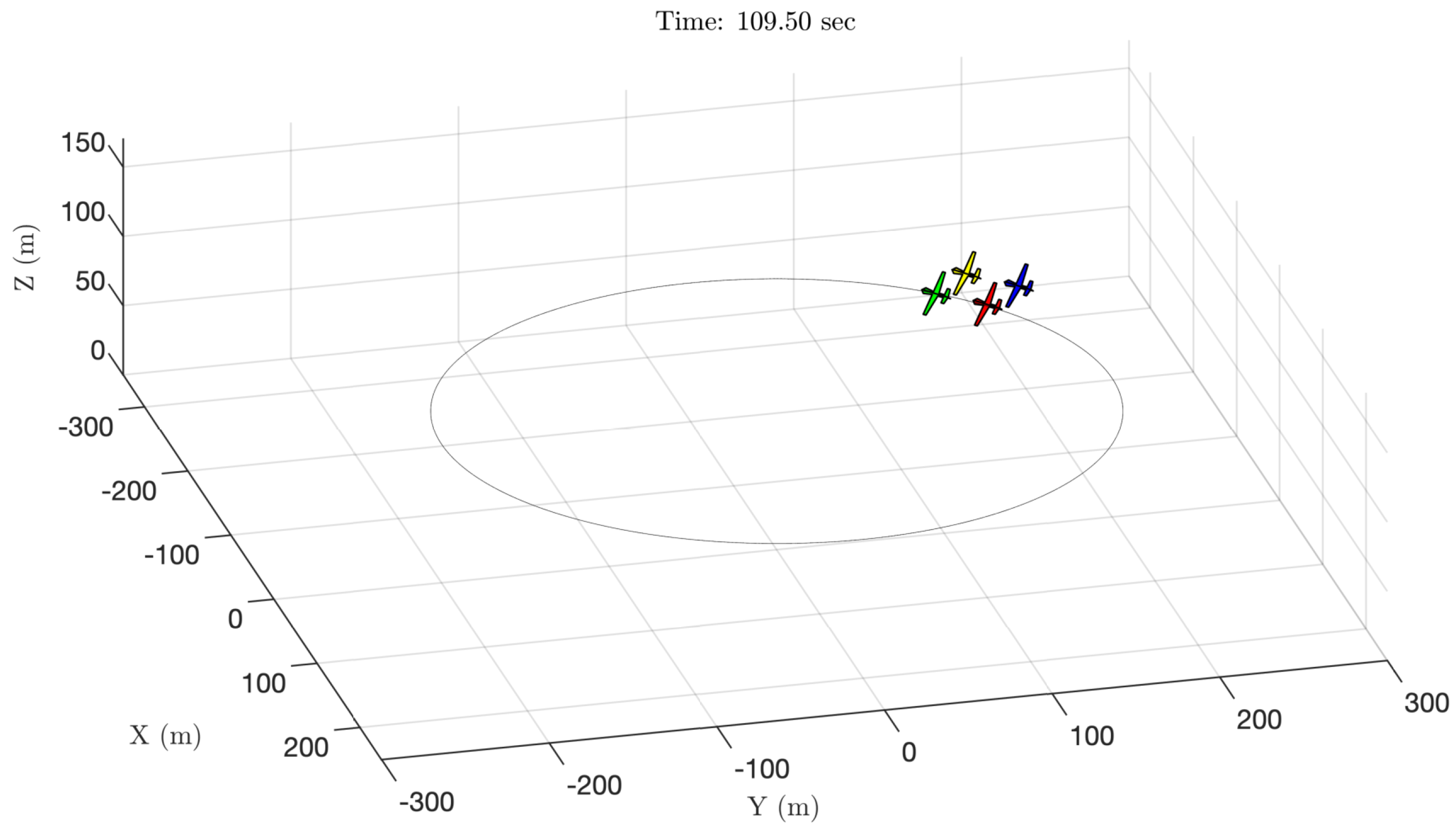
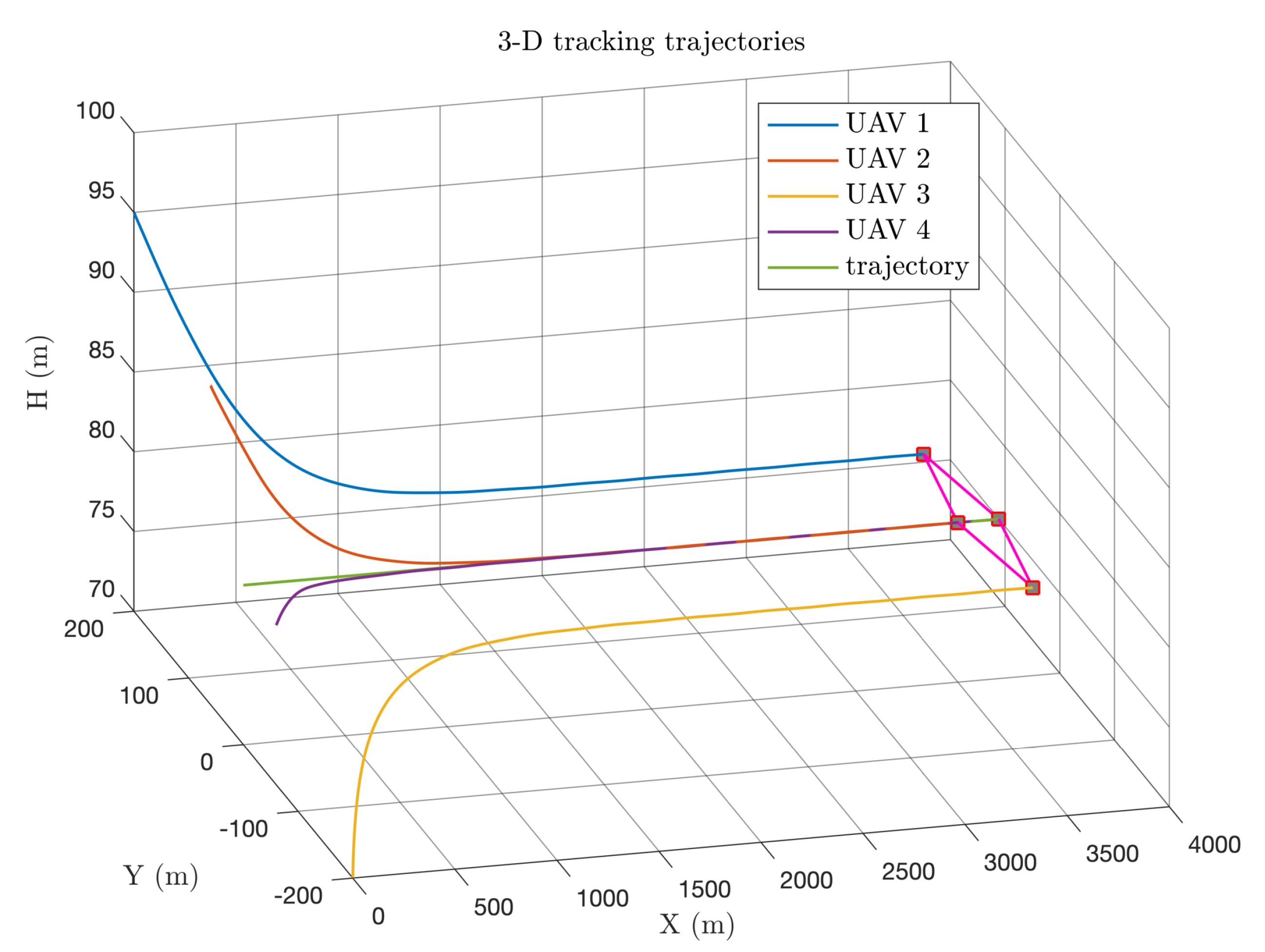
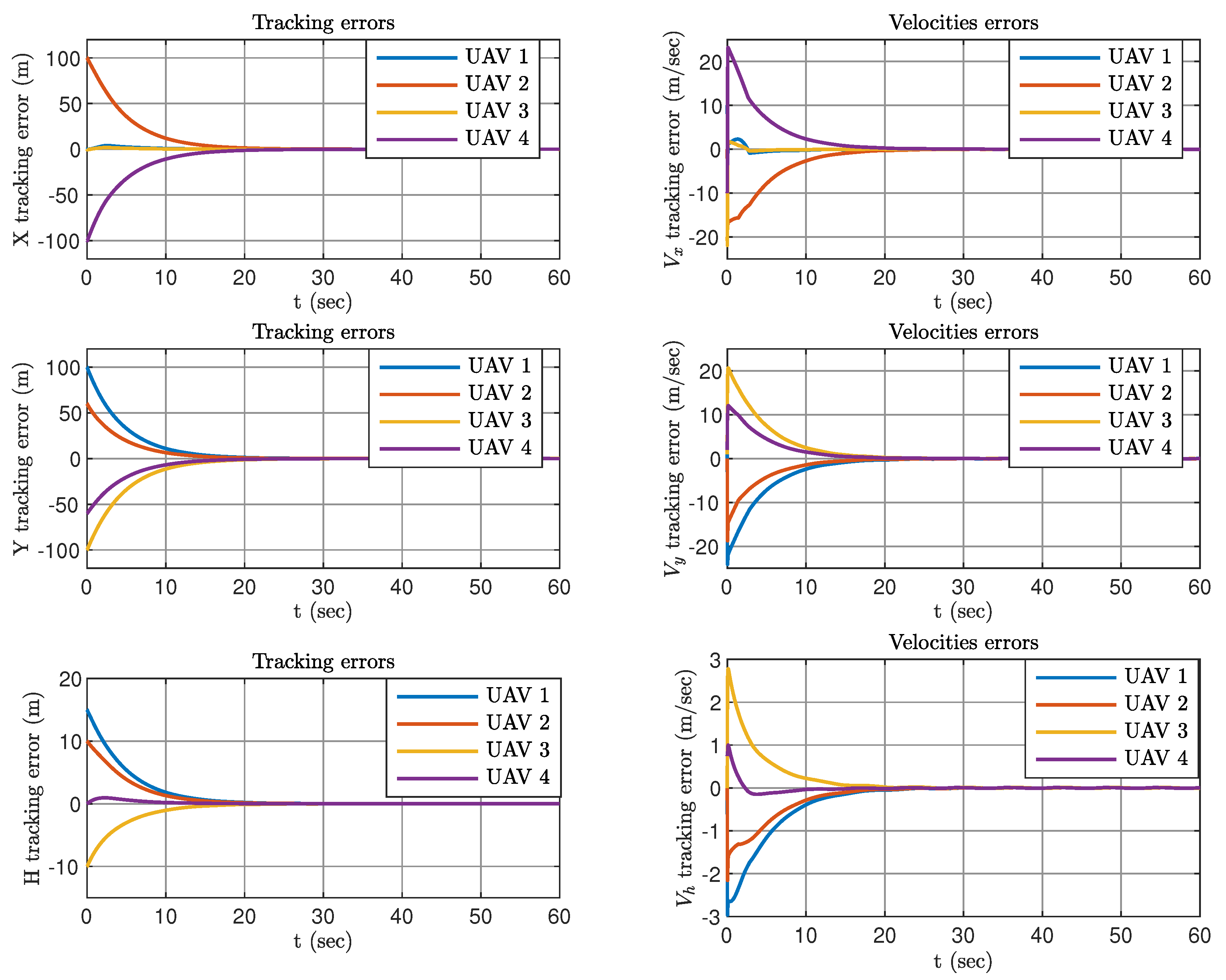
5.3. UAV Group Control
5.4. UAV Group Control under External Disturbances
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DMRRAC | Distributed Model Reference Robust Adaptive Controller |
| IRM | Implicit Reference Model |
| MRAC | Model Reference Adaptive Control |
| SG | Speed gradient |
| UAV | Unmanned Aerial Vehicle |
| Nomenclature | |
| x, y, h | UAV translational coordinates |
| flight-path angle | |
| heading angle | |
| bank angle | |
| UAV ground speed | |
| lift force | |
| drag force | |
| thrust force | |
| m | UAV mass |
| , | UAV mass , |
| g | gravity acceleration constant |
| S | wing platform area |
| air density | |
| lift coefficient | |
| drag coefficient | |
| zero-lift drag coefficient | |
| induced drag factor | |
| load factor | |
| u | vector of control signals |
| , , , , , | virtual controls |
| r | prescribed trajectory |
| , , | reference coordinates along the corresponding axes |
| , , | coordinate errors |
| vector of coordinate errors | |
| , , | speed errors |
| , , | implicit reference model outputs |
| vector of , , | |
| , , | implicit reference model parameters |
| goal function | |
| goal function for the group of UAVs | |
| , , | fixed control parameters |
| estimated mass | |
| , , | adjustable controller gains |
| , , , | stabilizing controller gains |
| , , , | “guessed” controller gains |
| , , , | adaptation gains |
| , , , | parametric feedback gains |
| N | number of UAVs (agents) |
| i | index of UAVs |
| relative position vector for i-th UAV | |
| , , | relative offset of i-th UAV in a group for corresponding axes |
| communication graph | |
| adjacency matrix | |
| L | Laplace matrix |
| , , | control signals based on the consensus algorithm |
| , , , , , , | consensus algorithm parameters |
| identity matrix | |
| , , | external perturbations |
| t | time |
| Subsripts | |
| x, y, h | UAV translational coordinates in the appropriate normal Earth’s reference frame |
| m | UAV mass |
| i | index of the UAV, |
References
- Du, N.; Zhou, Y.; Deng, W.; Luo, Q. Improved chimp optimization algorithm for three-dimensional path planning problem. Multimed. Tools Appl. 2022, 81, 27397–27422. [Google Scholar] [CrossRef]
- Sefati, S.; Halunga, S.; Farkhady, R. Cluster selection for load balancing in flying ad hoc networks using an optimal low-energy adaptive clustering hierarchy based on optimization approach. Aircr. Eng. Aerosp. Technol. 2022, 94, 1344–1356. [Google Scholar] [CrossRef]
- Trujillo, M.; Becerra, H.; Gómez-Gutiérrez, D.; Ruiz-León, J.; Ramírez-Treviño, A. Hierarchical task-based formation control and collision avoidance of UAVs in finite time. Eur. J. Control 2021, 60, 48–64. [Google Scholar] [CrossRef]
- Luo, L.; Wang, X.; Ma, J.; Ong, Y. GrpAvoid: Multigroup Collision-Avoidance Control and Optimization for UAV Swarm. IEEE Trans. Cybern. 2021. [Google Scholar] [CrossRef] [PubMed]
- Muslimov, T.; Munasypov, R. Multi-UAV cooperative target tracking via consensus-based guidance vector fields and fuzzy MRAC. Aircr. Eng. Aerosp. Technol. 2021, 93, 1204–1212. [Google Scholar] [CrossRef]
- Asami, K.; Bai, Y.; Svinin, M.; Hatayama, M. Survivor searching in a dynamically changing flood zone by multiple unmanned aerial vehicles. Artif. Life Robot. 2022, 27, 292–299. [Google Scholar] [CrossRef]
- Islam, S.; DIas, J.; Sunda-Meya, A. Distributed Tracking Synchronization Protocol for a Networked of Leader-follower Unmanned Aerial Vehicles with Uncertainty. In Proceedings of the Industrial Electronics Conference (IECON 2021), Toronto, Canada, 13–16 October 2021. [Google Scholar] [CrossRef]
- Cucker, F.; Smale, S. Emergent Behavior in Flocks. IEEE Trans. Autom. Control 2007, 52, 852–862. [Google Scholar] [CrossRef] [Green Version]
- Song, Y.; Gu, M.; Choi, J.; Oh, H.; Lim, S.; Shin, H.S.; Tsourdos, A. Using Lazy Agents to Improve the Flocking Efficiency of Multiple UAVs. J. Intell. Robot. Syst. Theory Appl. 2021, 103. [Google Scholar] [CrossRef]
- Zhou, P.; Chen, B. Semi-global leader-following consensus-based formation flight of unmanned aerial vehicles. Chin. J. Aeronaut. 2022, 35, 31–43. [Google Scholar] [CrossRef]
- Ahmed, A.; Naeem, M.; Al-Dweik, A. Joint Optimization of Sensors Association and UAVs Placement in IoT Applications With Practical Network Constraints. IEEE Access 2021, 9, 7674–7689. [Google Scholar] [CrossRef]
- Chen, L.; Zhao, R.; He, K.; Zhao, Z.; Fan, L. Intelligent ubiquitous computing for future UAV-enabled MEC network systems. Clust. Comput. 2022, 25, 2417–2427. [Google Scholar] [CrossRef]
- Mahmood, A.; Vu, T.; Khan, W.U.; Chatzinotas, S.; Ottersten, B. Optimizing Computational and Communication Resources for MEC Network Empowered UAV-RIS Communication. Preprint 2022. [Google Scholar] [CrossRef]
- Lin, Z.; Lin, M.; Wang, J.B.; de Cola, T.; Wang, J. Joint Beamforming and Power Allocation for Satellite-Terrestrial Integrated Networks With Non-Orthogonal Multiple Access. IEEE J. Sel. Top. Signal Process. 2019, 13, 657–670. [Google Scholar] [CrossRef] [Green Version]
- Güzey, H.; Güzey, N. Adaptive hybrid formation-search and track controller of UAVs. Int. J. Syst. Sci. 2022, 53, 2301–2317. [Google Scholar] [CrossRef]
- Mahfouz, M.; Hafez, A.; Ashry, M.; Elnashar, G. Target Assignment for Cooperative Quadrotors Unmanned Aerial Vehicles. J. Phys. Conf. Ser. 2021, 2128. [Google Scholar] [CrossRef]
- Han, Q.; Zhou, Y.; Liu, X.; Tuo, X. Event-Triggered Finite-Time Attitude Cooperative Control for Multiple Unmanned Aerial Vehicles. Appl. Bionics Biomech. 2022, 2022, 5875004. [Google Scholar] [CrossRef]
- Wu, X.; Wu, Y.; Xu, Z.; Chen, Q. Fixed-time flocking formation of nonlinear multi-agent system with uncertain state perturbation. Int. J. Control. 2022. [Google Scholar] [CrossRef]
- Gong, J.; Jiang, B.; Ma, Y.; Mao, Z. Distributed Adaptive Fault-Tolerant Formation Control for Heterogeneous Multiagent Systems With Communication Link Faults. IEEE Trans. Aerosp. Electron. Syst. 2022, 1–11. [Google Scholar] [CrossRef]
- Popov, A.M.; Kostin, I.; Fadeeva, J.; Andrievsky, B. Development and Simulation of Motion Control System for Small Satellites Formation. Electronics 2021, 10, 3111. [Google Scholar] [CrossRef]
- Popov, A.M.; Kostrygin, D.G.; Krashanin, P.V.; Shevchik, A.A. Development of Algorithm for Guiding the Swarm of Unmanned Aerial Vehicles. In Proceedings of the 29th Saint Petersburg International Conference on Integrated Navigation Systems (ICINS 2022), Saint Petersburg, Russia, 30 May–1 June 2022; Volume 1, pp. 1–4. [Google Scholar] [CrossRef]
- Gamagedara, K.; Lee, T. Geometric Adaptive Controls of a Quadrotor Unmanned Aerial Vehicle with Decoupled Attitude Dynamics. J. Dyn. Syst. Meas. Control. ASME 2022, 144, 031002. [Google Scholar] [CrossRef]
- Chatterjee, B.; Dutta, R. Studying the Effect of Network Latency on an Adaptive Coordinated Path Planning Algorithm for UAV Platoons. In Proceedings of the 2022 8th Workshop on Micro Aerial Vehicle Networks, Systems, and Applications (DroNet 2022), Part of MobiSys 2022, Portland, OR, USA, 27 June–1 July 2022; pp. 7–12. [Google Scholar] [CrossRef]
- Ullah, N.; Mehmood, Y.; Aslam, J.; Wang, S.; Phoungthong, K. Fractional order adaptive robust formation control of multiple quad-rotor UAVs with parametric uncertainties and wind disturbances. Chin. J. Aeronaut. 2022, 35, 204–220. [Google Scholar] [CrossRef]
- Liang, W.; Chen, Z.; Yao, B. Geometric Adaptive Robust Hierarchical Control for Quadrotors With Aerodynamic Damping and Complete Inertia Compensation. IEEE Trans. Ind. Electron. 2022, 69, 13213–13224. [Google Scholar] [CrossRef]
- Zhi, Y.; Liu, L.; Guan, B.; Wang, B.; Cheng, Z.; Fan, H. Distributed robust adaptive formation control of fixed-wing UAVs with unknown uncertainties and disturbances. Aerosp. Sci. Technol. 2022, 126, 107600. [Google Scholar] [CrossRef]
- Huang, Y.; Meng, Z. Bearing-Based Distributed Formation Control of Multiple Vertical Take-Off and Landing UAVs. IEEE Trans. Control Netw. Syst. 2021, 8, 1281–1292. [Google Scholar] [CrossRef]
- Andrievsky, B.; Tomashevich, S. Passification based signal-parametric adaptive controller for agents in formation. IFAC-PapersOnLine 2015, 48, 222–226. [Google Scholar] [CrossRef]
- Andrievskii, B.; Fradkov, A. Method of passification in adaptive control, estimation, and synchronization. Autom. Remote Control 2006, 67, 1699–1731. [Google Scholar] [CrossRef]
- Andrievskii, B.R.; Selivanov, A.A. New Results on the Application of the Passification Method. A Survey. Automat. Remote Control 2018, 79, 957–995. [Google Scholar] [CrossRef]
- Tomashevich, S.; Andrievsky, B. Adaptive control of quadrotors spatial motion in formation with implicit reference model. AIP Conf. Proc. 2018, 2046, 020103. [Google Scholar] [CrossRef]
- Tomashevich, S.; Andrievsky, B. High-order adaptive control in multi-agent quadrotor formation. Math. Eng. Sci. Aerosp. 2019, 10, 681–693. [Google Scholar]
- Furtat, I.B. Simple Adaptive Algorithm for Plants with Input Delay and Disturbances. IFAC-PapersOnLine 2017, 50, 4270–4275. [Google Scholar] [CrossRef]
- Tomashevich, S.I. Control for a system of linear agents based on a high order adaptation algorithm. Autom. Remote Control 2017, 78, 276–288. [Google Scholar] [CrossRef]
- Tomashevich, S.; Belyavskyi, A. 2DoF indoor testbed for quadrotor identification and control. In Proceedings of the 23rd Saint Petersburg International Conference Integrated Navigation Systems (ICINS 2016), Saint Petersburg, Russia, 30 May–1 June 2016; pp. 373–376. [Google Scholar]
- Andrievsky, B.; Popov, A.M.; Kostin, I.; Fadeeva, J. Modeling and Control of Satellite Formations: A Survey. Automation 2022, 3, 511–544. [Google Scholar] [CrossRef]
- Andrievsky, B.; Fradkov, A.; Kudryashova, E. Control of two satellites relative motion over the packet erasure communication channel with limited transmission rate based on adaptive coder. Electronics 2020, 9, 2032. [Google Scholar] [CrossRef]
- Kuznetsov, N.V.; Andrievsky, B.; Kudryashova, E.V.; Kuznetsova, O.A. Stability and hidden oscillations analysis of the spacecraft attitude control system using reaction wheels. Aerosp. Sci. Technol. 2022, 131, 107973. [Google Scholar] [CrossRef]
- Menon, P.K.A. Short-range nonlinear feedback strategies for aircraft pursuit-evasion. J. Guid. Control. Dyn. 1989, 12, 27–32. [Google Scholar] [CrossRef]
- Menon, P.K.; Sweriduk, G.D.; Sridhar, B. Optimal Strategies for Free-Flight Air Traffic Conflict Resolution. J. Guid. Control. Dyn. 1999, 22, 202–211. [Google Scholar] [CrossRef] [Green Version]
- Boskovic, J.D.; Chen, L.; Mehra, R.K. Adaptive Control Design for Nonaffine Models Arising in Flight Control. J. Guid. Control. Dyn. 2004, 27, 209–217. [Google Scholar] [CrossRef]
- Kim, S.; Kim, Y. Optimum design of three-dimensional behavioural decentralized controller for UAV formation flight. Eng. Optim. 2009, 41, 199–224. [Google Scholar] [CrossRef]
- Wang, J.; Xin, M. Integrated Optimal Formation Control of Multiple Unmanned Aerial Vehicles. IEEE Trans. Control Syst. Technol. 2013, 21, 1731–1744. [Google Scholar] [CrossRef]
- Beard, R.W.; McLain, T.W. Small Unmanned Aircraft: Theory and Practice; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Dobrokhodov, V. Kinematics and Dynamics of Fixed-Wing UAVs. In Handbook of Unmanned Aerial Vehicles; Springer Netherlands: Dordrecht, The Netherlands, 2015; pp. 243–277. [Google Scholar] [CrossRef]
- Miele, A. Flight Mechanics: Theory of Flight Paths; Dover Publications Inc.: New York, NY, USA, 2016. [Google Scholar]
- Zhao, Y.; Tsiotras, P. Time-Optimal Path Following for Fixed-Wing Aircraft. J. Guid. Control. Dyn. 2013, 36, 83–95. [Google Scholar] [CrossRef] [Green Version]
- Anderson, M.; Robbins, A. Formation flight as a cooperative game. In Proceedings of the Guidance, Navigation, and Control Conference and Exhibit; AIAA: Boston, MA, USA, 1998; p. 244. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Fliess, M.; Lévine, J.; Martin, P.; Rouchon, P. Flatness and defect of non-linear systems: Introductory theory and examples. Int. J. Control 1995, 61, 1327–1361. [Google Scholar] [CrossRef] [Green Version]
- Lévine, J. Analysis and Control of Nonlinear Systems A Flatness-Based Approach; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Fradkov, A.L. Speed-gradient scheme and its application in adaptive control problems. Autom. Remote Control 1980, 40, 1333–1342. [Google Scholar]
- Fradkov, A.L.; Miroshnik, I.V.; Nikiforov, V.O. Nonlinear and Adaptive Control of Complex Systems; Kluwer: Dordrecht, The Netherlands, 1999. [Google Scholar]
- Andrievsky, B.R.; Fradkov, A.L. Speed Gradient Method and Its Applications. Autom. Remote Control 2021, 82, 1463–1518. [Google Scholar] [CrossRef]
- Fradkov, A.L.; Andrievsky, B. Speed-Gradient Method in Mechanical Engineering. Adv. Struct. Mater. 2022, 164, 171–194. [Google Scholar] [CrossRef]
- Fradkov, A.L. Synthesis of an adaptive system for linear plant stabilization. Autom. Remote Control 1974, 35, 1960–1966. [Google Scholar]
- Fradkov, A. Lyapunov-Bregman functions for speed-gradient adaptive control of nonlinear time-varying systems. IFAC-PapersOnLine 2022, 55, 544–548. [Google Scholar] [CrossRef]
- Fradkov, A.; Andrievsky, B. Adaptive Synchronization of Time-Varying Non-linear Systems with Application to Signal Transmission. Stud. Syst. Decis. Control 2022, 414, 325–344. [Google Scholar] [CrossRef]
- Fradkov, A.; Tomashevich, S.; Andrievsky, B.; Amelin, K.; Kaliteevskiy, I. Adaptive Coding For Data Exchange Between Quadrotors In The Formation. IFAC-PapersOnLine 2016, 49, 275–280. [Google Scholar] [CrossRef]
- Marantos, P.; Koveos, Y.; Kyriakopoulos, K. UAV State Estimation Using Adaptive Complementary Filters. IEEE Trans. Control Syst. Technol. 2016, 24, 1214–1226. [Google Scholar] [CrossRef]
- Yu, Y.; Peng, S.; Li, Q.; Dong, X.; Ren, Z. Cooperative Navigation Method Based on Adaptive CKF for UAVs in GPS Denied Areas. In Proceedings of the IEEE CSAA Guidance, Navigation and Control Conference, CGNCC 2018, Xiamen, China, 10–12 August 2018. [Google Scholar] [CrossRef]
- Silantyev, A.; Tereshchenko, D.; Kazakov, L.; Selyanskaya, E. Adaptive system of mutual positioning for controlling the groups of unmanned aerial vehicles. In Proceedings of the 2018 Systems of Signal Synchronization, Generating and Processing in Telecommunications (SYNCHROINFO 2018), Minsk, Belarus, 4–5 July 2018. [Google Scholar] [CrossRef]
- Tomashevich, S.; Andrievsky, B.; Fradkov, A. Formation control of a group of unmanned aerial vehicles with data exchange over a packet erasure channel. In Proceedings of the 2018 IEEE Industrial Cyber-Physical Systems (ICPS 2018), Saint Petersburg, Russia, 15–18 May 2018; pp. 38–43. [Google Scholar] [CrossRef]
- Zhong, W.; Xu, L.; Liu, X.; Zhu, Q.; Zhou, J. Adaptive beam design for UAV network with uniform plane array. Phys. Commun. 2019, 34, 58–65. [Google Scholar] [CrossRef]
- Darabkh, K.; Alfawares, M.; Althunibat, S. MDRMA: Multi-data rate mobility-aware AODV-based protocol for flying ad-hoc networks. Veh. Commun. 2019, 18. [Google Scholar] [CrossRef]
- Tomashevich, S.; Andrievsky, B.; Dokuchaeva, A.; Emelyanov, V. Navigation data exchange between UAVs in the formation by means of the adaptive coding procedure. Math. Eng. Sci. Aerosp. 2019, 10, 463–478. [Google Scholar]
- Amelin, K.; Andrievsky, B.; Tomashevich, S.; Fradkov, A. Data Exchange with Adaptive Coding between Quadrotors in a Formation. Autom. Remote Control 2019, 80, 150–163. [Google Scholar] [CrossRef]
- Lim, S.; Song, Y.; Choi, J.; Myung, H.; Lim, H.; Oh, H. Decentralized Hybrid Flocking Guidance for a Swarm of Small UAVs. In Proceedings of the 2019 International Workshop on Research, Education and Development on Unmanned Aerial Systems, RED-UAS 2019, Cranfield, UK, 25–27 November 2019; pp. 287–296. [Google Scholar] [CrossRef]
- Lin, Z.; An, K.; Niu, H.; Hu, Y.; Chatzinotas, S.; Zheng, G.; Wang, J. SLNR-based Secure Energy Efficient Beamforming in Multibeam Satellite Systems. IEEE Trans. Aerosp. Electron. Syst. 2022, 1–4. [Google Scholar] [CrossRef]
- Lin, Z.; Lin, M.; de Cola, T.; Wang, J.B.; Zhu, W.P.; Cheng, J. Supporting IoT With Rate-Splitting Multiple Access in Satellite and Aerial-Integrated Networks. IEEE Internet Things J. 2021, 8, 11123–11134. [Google Scholar] [CrossRef]
- Lin, Z.; Niu, H.; An, K.; Wang, Y.; Zheng, G.; Chatzinotas, S.; Hu, Y. Refracting RIS-Aided Hybrid Satellite-Terrestrial Relay Networks: Joint Beamforming Design and Optimization. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 3717–3724. [Google Scholar] [CrossRef]
- Geraci, G.; Garcia-Rodriguez, A.; Azari, M.M.; Lozano, A.; Mezzavilla, M.; Chatzinotas, S.; Chen, Y.; Rangan, S.; Renzo, M.D. What Will the Future of UAV Cellular Communications Be? A Flight From 5G to 6G. IEEE Commun. Surv. Tutorials 2022, 24, 1304–1335. [Google Scholar] [CrossRef]
- Dovgal, V. Making decisions about the placement of unmanned aerial vehicles based on the implementation of an artificial immune system in relation to information processing. In Proceedings of the International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM 2021), Sochi, Russia, 17–21 May 2021; pp. 828–833. [Google Scholar] [CrossRef]
- Wu, P.; Xiao, F.; Huang, H.; Sha, C.; Yu, S. Adaptive and Extensible Energy Supply Mechanism for UAVs-Aided Wireless-Powered Internet of Things. IEEE Internet Things J. 2020, 7, 9201–9213. [Google Scholar] [CrossRef]
- Wei, X.; Yang, J.; Fan, X. Fully distributed guidance laws for unmanned aerial vehicles formation flight. Trans. Inst. Meas. Control 2020, 42, 965–980. [Google Scholar] [CrossRef]
- Ren, W.; Beard, R.W. Distributed Consensus in Multi-Vehicle Cooperative Control; Springer: London, UK, 2008. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Murray, R. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef] [Green Version]
- Olfati-Saber, R.; Fax, J.A.; Murray, R.M. Consensus and Cooperation in Networked Multi-Agent Systems. Proc. IEEE 2007, 95, 215–233. [Google Scholar] [CrossRef] [Green Version]
- Kabiri, M.; Atrianfar, H.; Menhaj, M. Formation control of VTOL UAV vehicles under switching-directed interaction topologies with disturbance rejection. Int. J. Control 2018, 91, 33–44. [Google Scholar] [CrossRef]





| # | Other Works | This Work |
|---|---|---|
| 1 | [5] – tracking the moving ground target in the real-time; method: fuzzy-logic model-reference adaptive control (FL MRAC) | – tracking the given reference trajectory; method: implicit reference model (IRM) adaptive control |
| 2 | [20] – UAV parameters are known; method: non-adaptive control | – uncertain parameters: m, , , S; method: IRM adaptive control |
| 3 | [27] – UAV type: VTOL; control vector: command forces and torques; UAV parameters are known; method: adaptive estimation of disturbance | – UAV type: fixed-wing aircraft; control vector: ; uncertain parameters: m, , , S; method: adaptive control with the IRM |
| 4 | [26] – control vector: ; uncertain parameters: , , S; method: robust adaptive controller | – control vector: ; uncertain parameters: , , , S; method: adaptive control with the IRM |
| 5 | [28,31,32] – the reference trajectory is known only to the leading UAV; no consensus is ensured; UAV type: rotating-wing (quadrotor) | – each UAV has an information about the desired trajectory; consensus is ensured; UAV type: fixed-wing aircraft |
| 6 | [41] – single UAV; regulation of , , tracking ; point-mass dynamics model without kinematic relations; control vector: ; uncertain parameters: ; method: adaptive control for non-affine plants | – group of UAVs; tracking the given reference trajectory; kinematic relations are included; control vector: ; uncertain parameters: , , , S; method: IRM adaptive control |
| 7 | [42] – mission: passing a waypoint by several UAVs;
control vector: ; parameters are known; method: optimal design of the behavioral approach of decentralized control; communication graph: undirected (ring topology) | – mission: tracking the given reference trajectory; control vector: ; uncertain parameters: , , , S; method: IRM adaptive control; communication graph: directed |
| 8 | [43]
– tracking the desired trajectory on the plane ; model: kinematic on the plane at constant height; control vector: ; parameters: estimated by the Gaussian Process Regression training procedure; – communication graph: undirected | – tracking the desired trajectory in 3-D space; model: 3-D nonlinear point model; control vector: ; uncertain parameters: , , , S; communication graph: directed |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Popov, A.M.; Kostrygin, D.G.; Shevchik, A.A.; Andrievsky, B. Speed-Gradient Adaptive Control for Parametrically Uncertain UAVs in Formation. Electronics 2022, 11, 4187. https://doi.org/10.3390/electronics11244187
Popov AM, Kostrygin DG, Shevchik AA, Andrievsky B. Speed-Gradient Adaptive Control for Parametrically Uncertain UAVs in Formation. Electronics. 2022; 11(24):4187. https://doi.org/10.3390/electronics11244187
Chicago/Turabian StylePopov, Alexander M., Daniil G. Kostrygin, Anatoly A. Shevchik, and Boris Andrievsky. 2022. "Speed-Gradient Adaptive Control for Parametrically Uncertain UAVs in Formation" Electronics 11, no. 24: 4187. https://doi.org/10.3390/electronics11244187
APA StylePopov, A. M., Kostrygin, D. G., Shevchik, A. A., & Andrievsky, B. (2022). Speed-Gradient Adaptive Control for Parametrically Uncertain UAVs in Formation. Electronics, 11(24), 4187. https://doi.org/10.3390/electronics11244187







