Integral Windup Resetting Enhancement for Sliding Mode Control of Chemical Processes with Longtime Delay
Abstract
1. Introduction
2. Problem Formulation
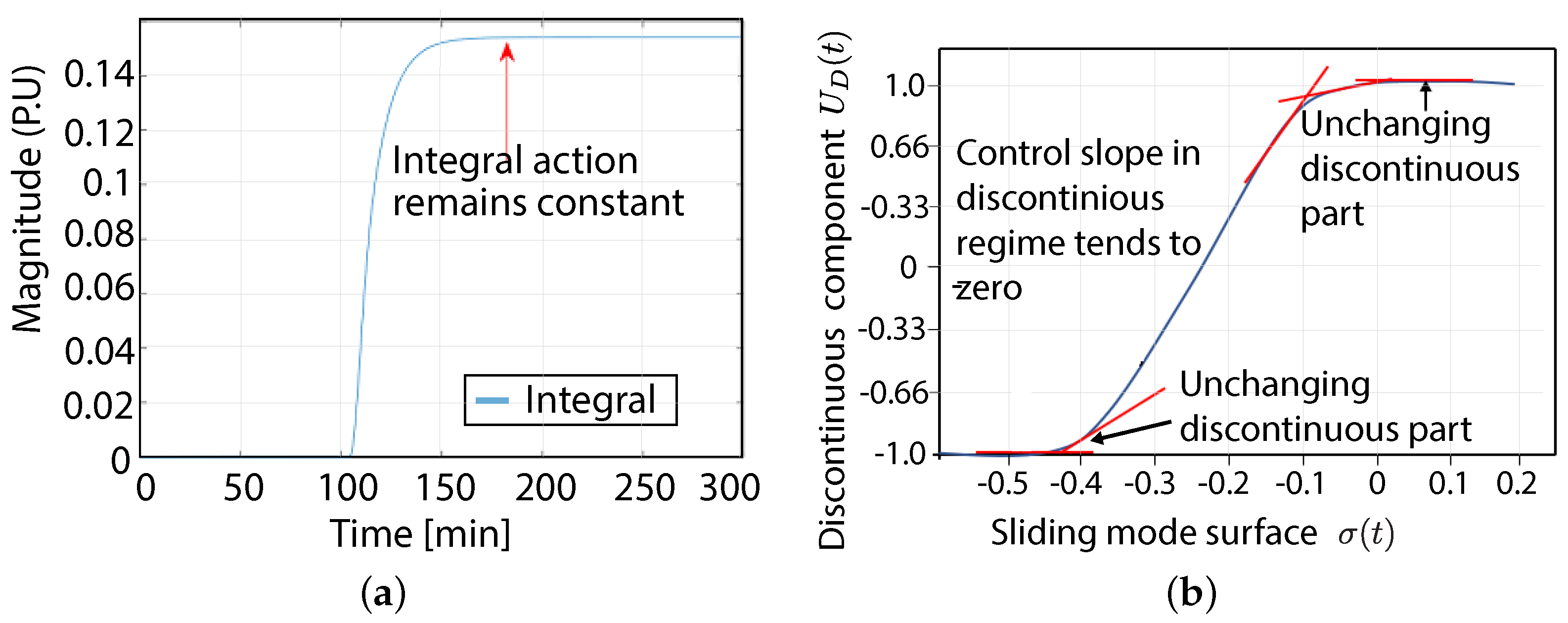
2.1. Integral Control Law for the SMC
2.2. Stability Analysis
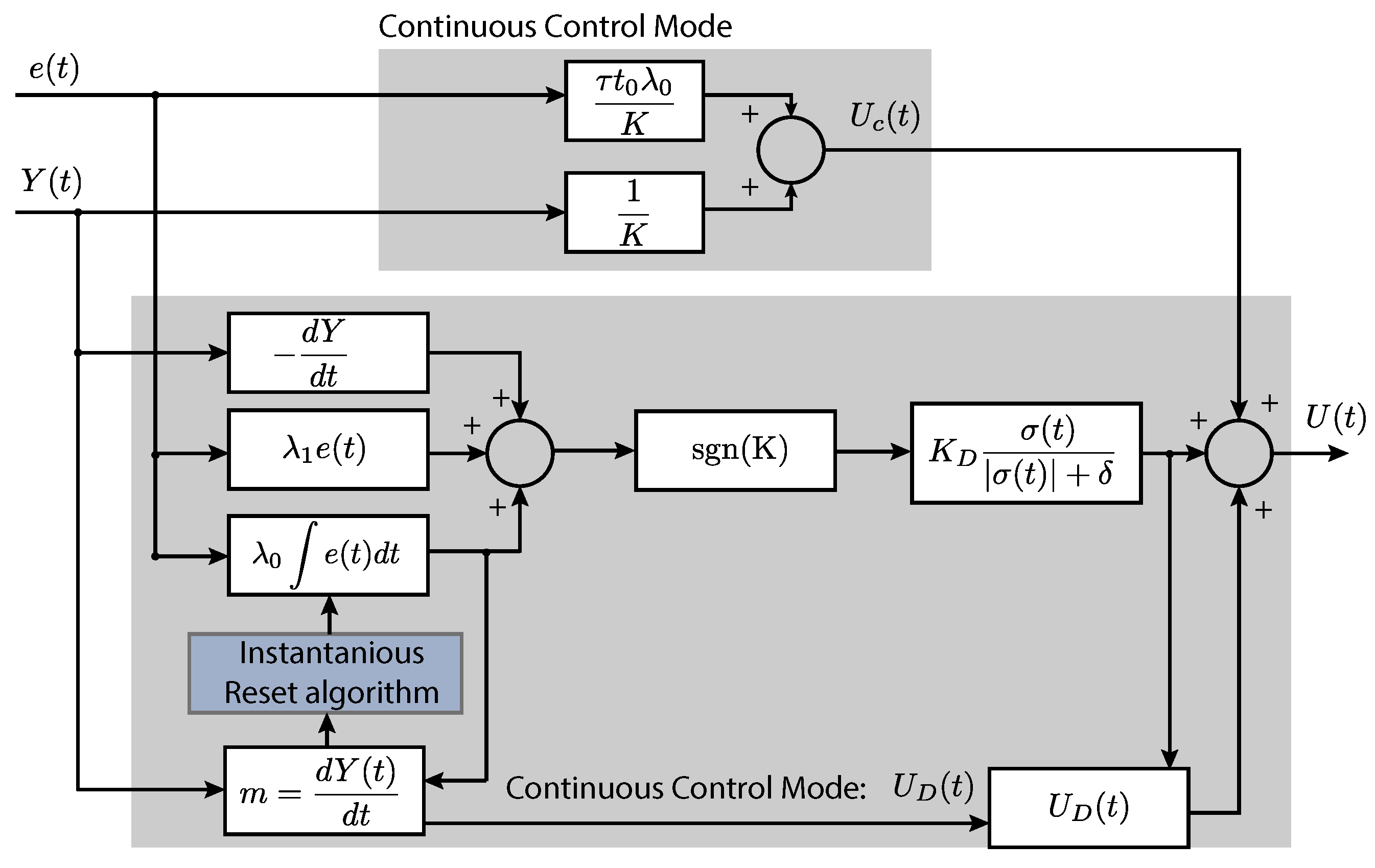
3. Anti-Windup Algorithms
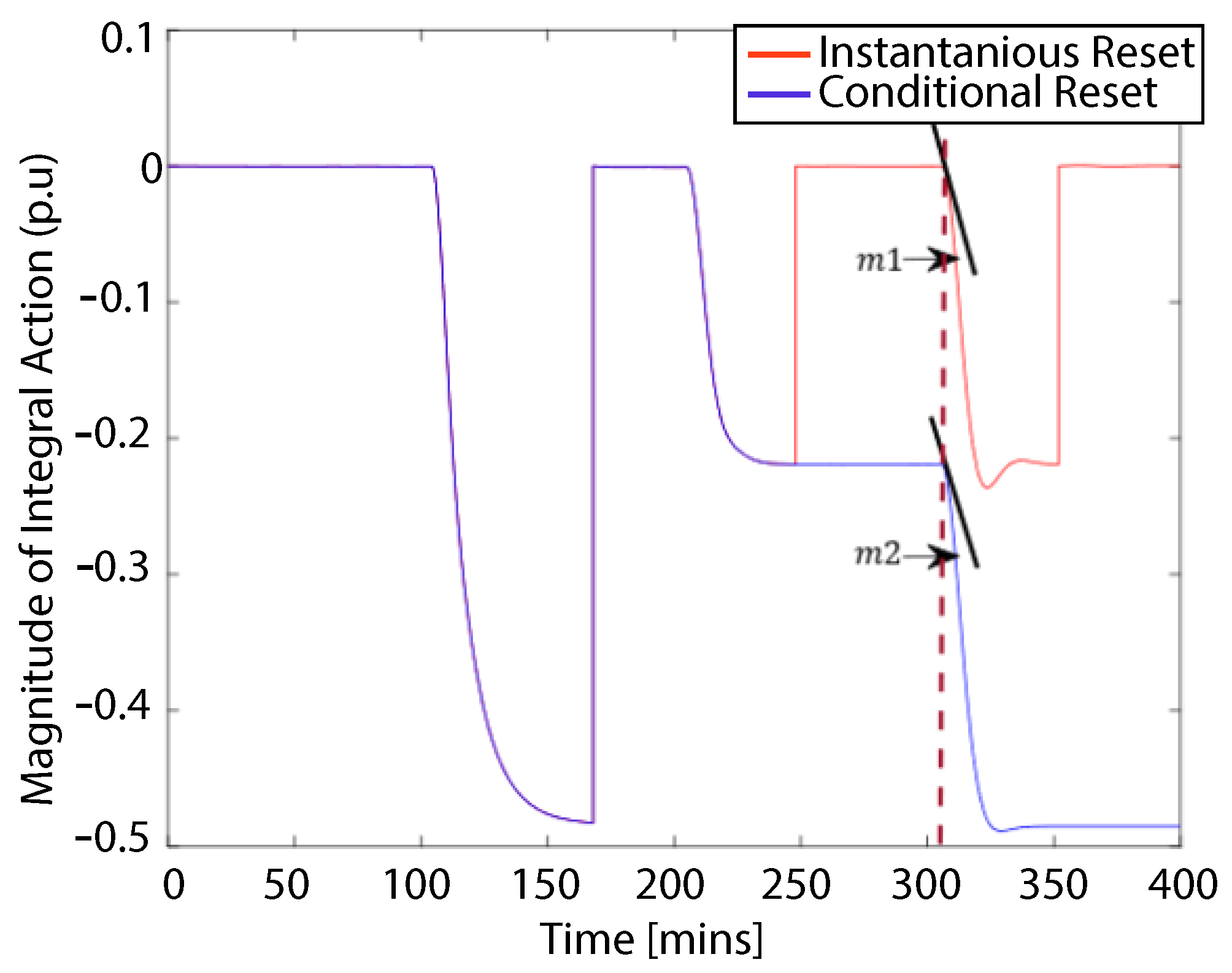
3.1. SMC with Windup Instantaneous Reset
3.2. SMC with Windup Conditional Reset
| Algorithm 1 Windup Instantaneous Reset—WIR. Anti-windup algorithm to instantaneously reboot the integral control action in an SMC |
|
| Algorithm 2 Windup Conditional Reset—WCR. Anti-windup algorithm to reboot the integrator in a controller by conditionally evaluating the process output derivative |
|
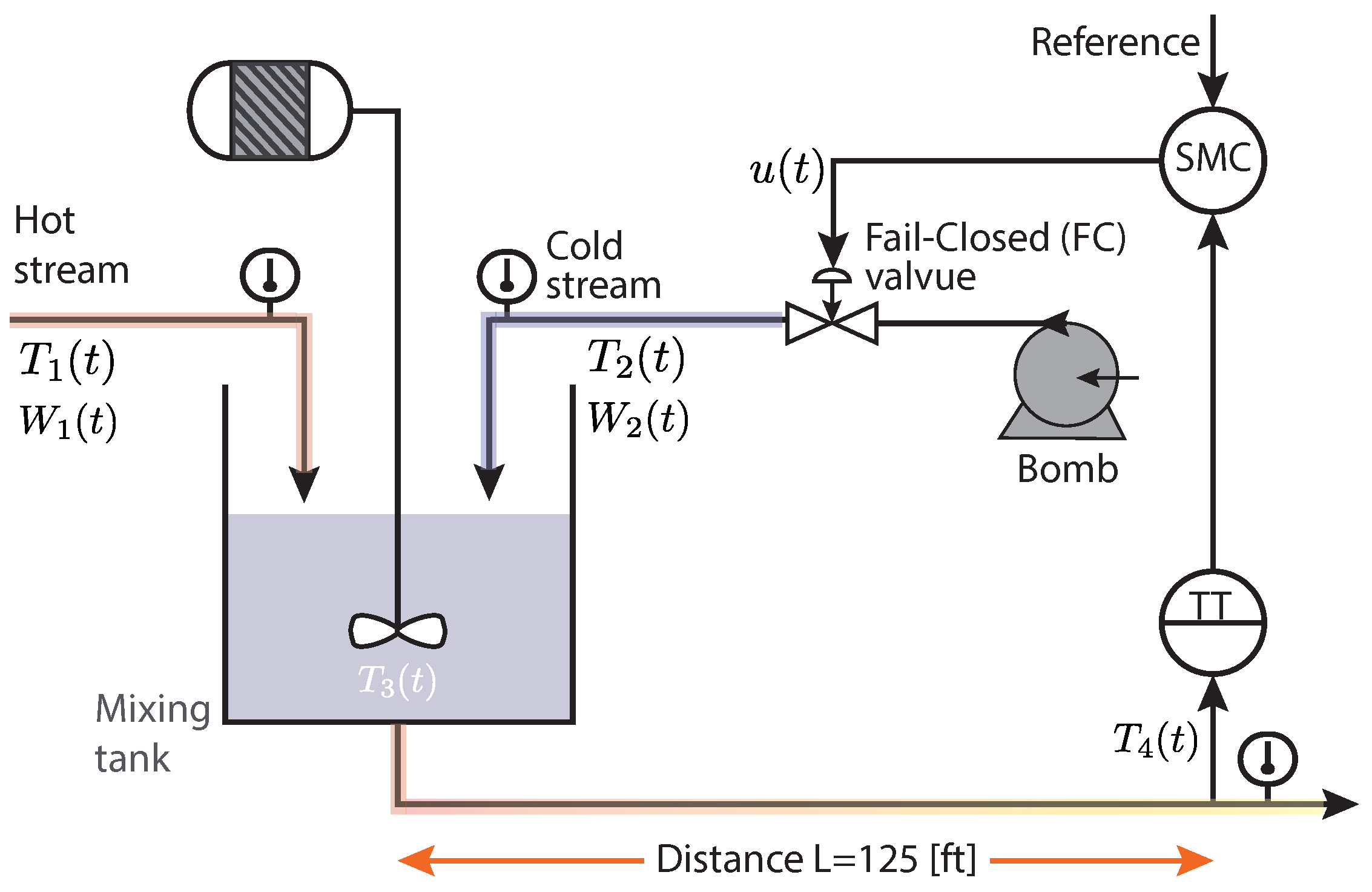
4. Modeling of the Mixing Process
4.1. Mixing Tank Process with Long Time-Delay
- The mixing tank and the entire guidance pipe are ideally isolated.
- The product within the repository is completely homogenized.
- The TT is calibrated in an operating range [100, 200] ºF.
- The TT is assumed to provide variations of the process temperature output.
- The height and volumetric properties of the product inside the mixing tank remain constant during the whole test due to its internal control system.
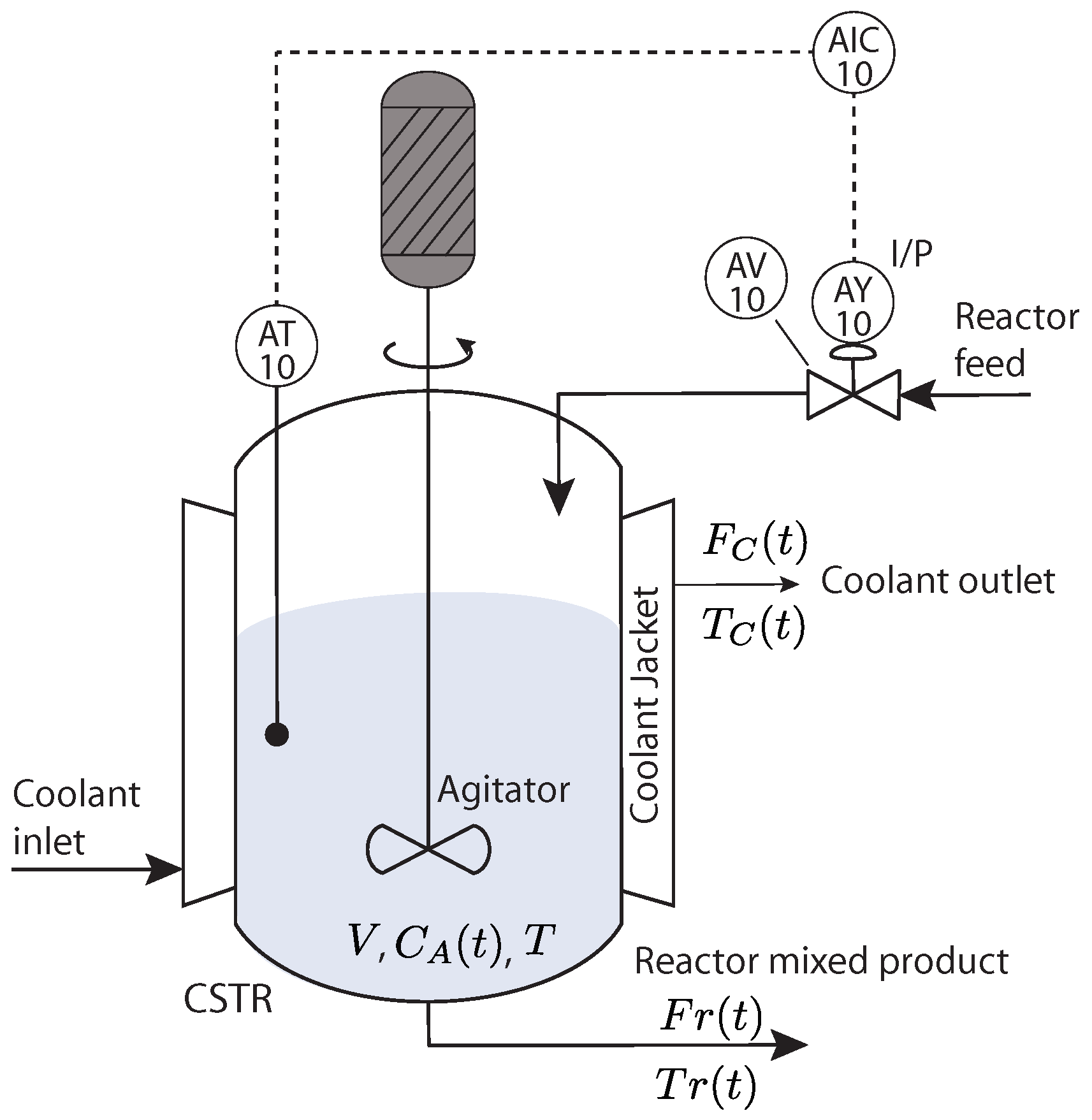
4.2. Continuous Stirred Tank Reactor Process with Long Time-Delay
- Heat and density capacities of the reactants are constant;
- The heat loss in a coolant jacket is considered negligible;
- The reaction heat and volume remain constant;
- The reaction and reacted material are uniformly mixed.
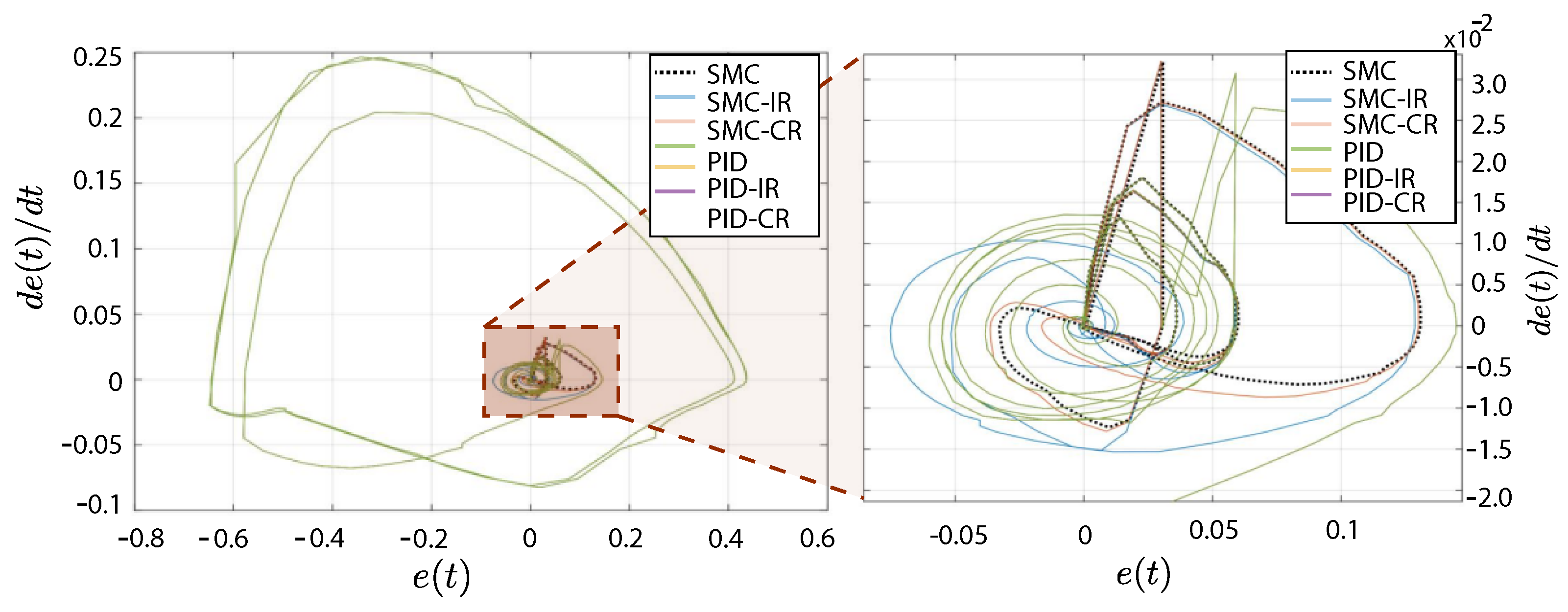
5. Results for the VHMT Process
5.1. System Response against Disturbances
5.2. System Response against Reference Changes
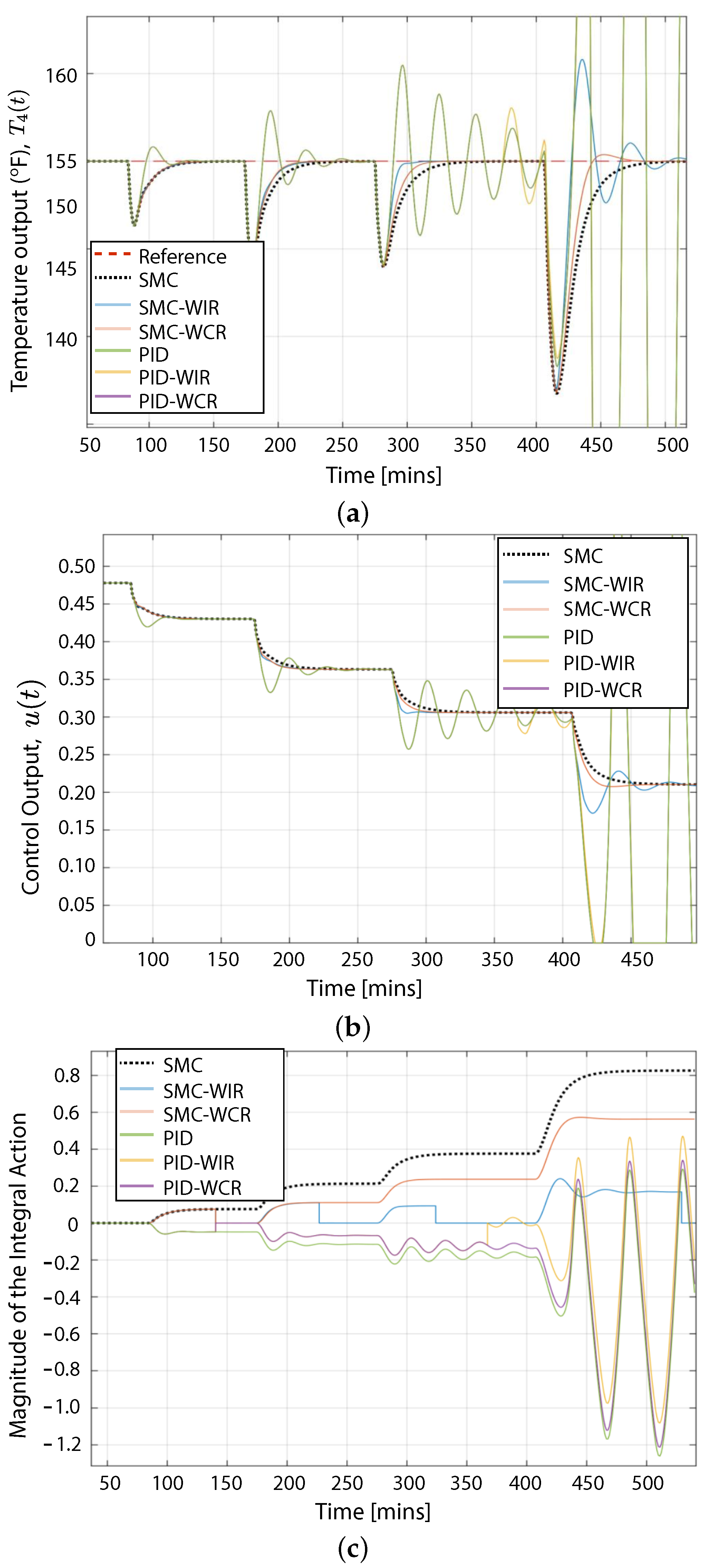
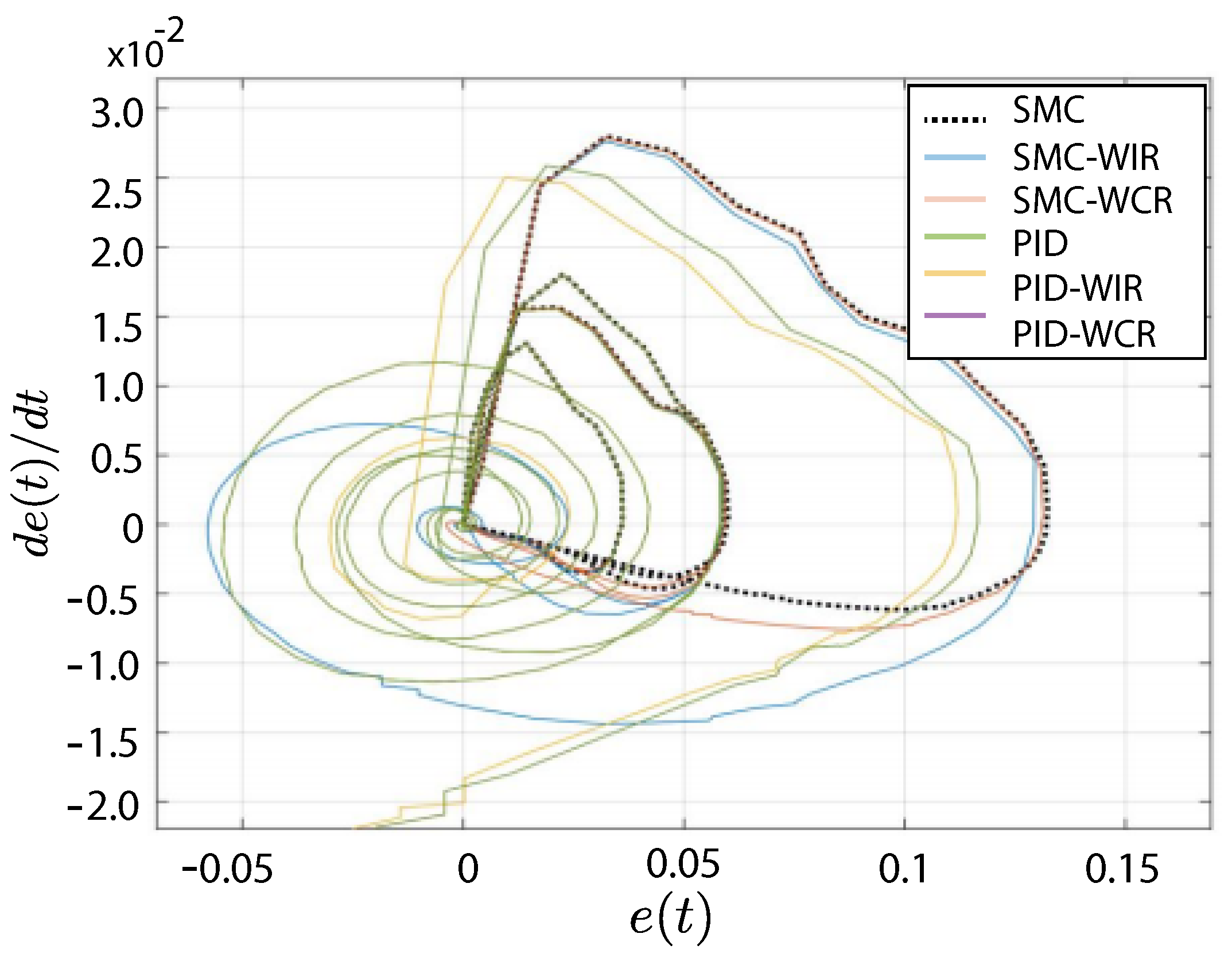
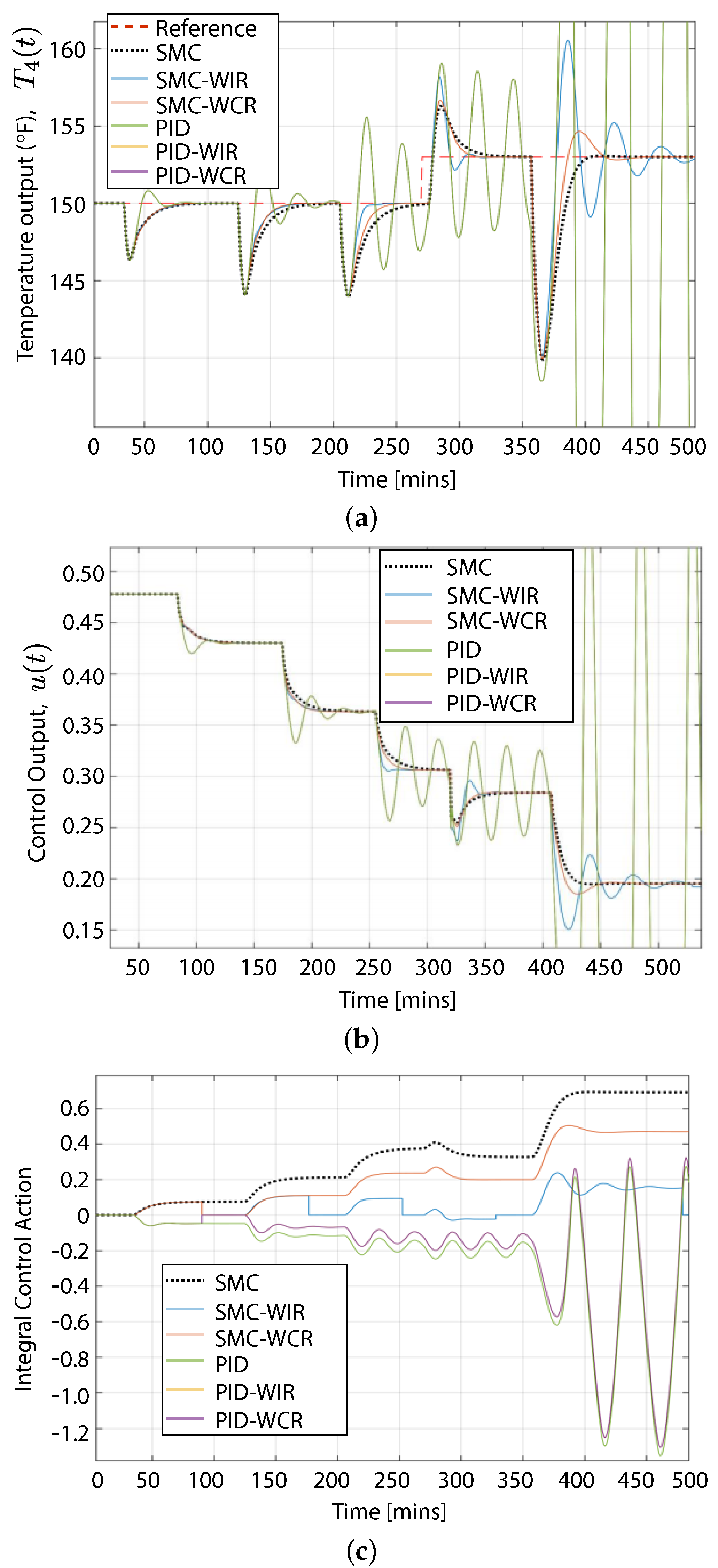
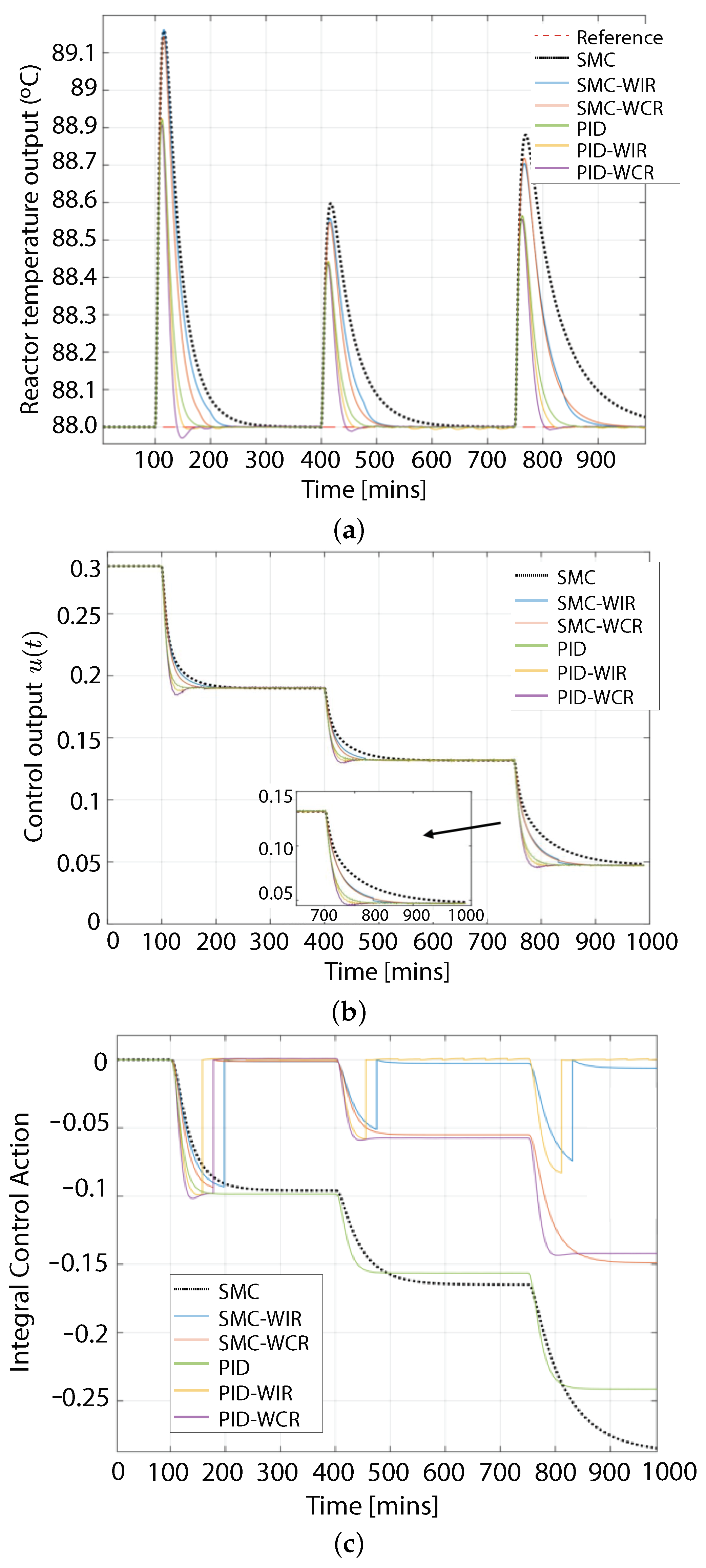
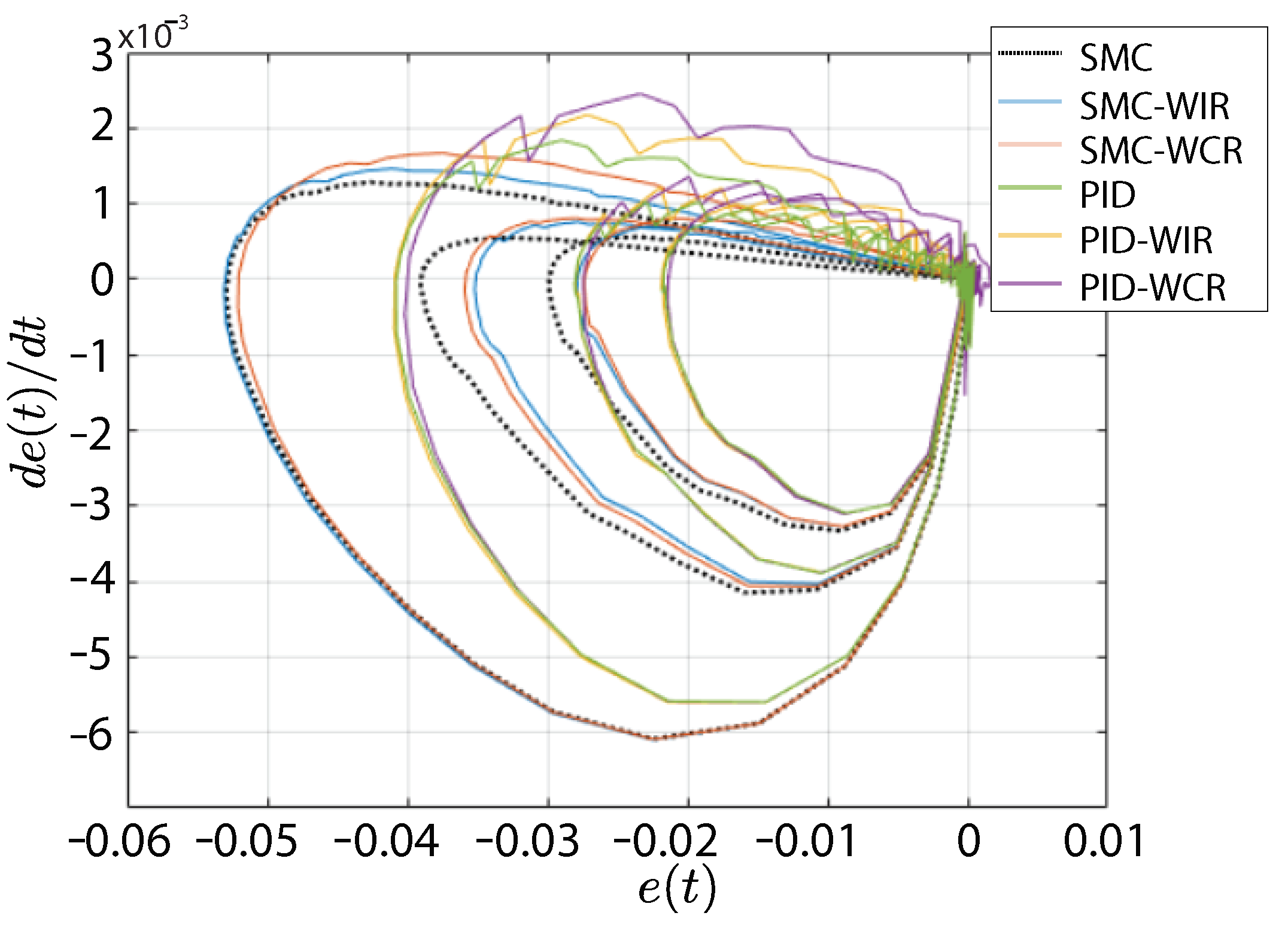
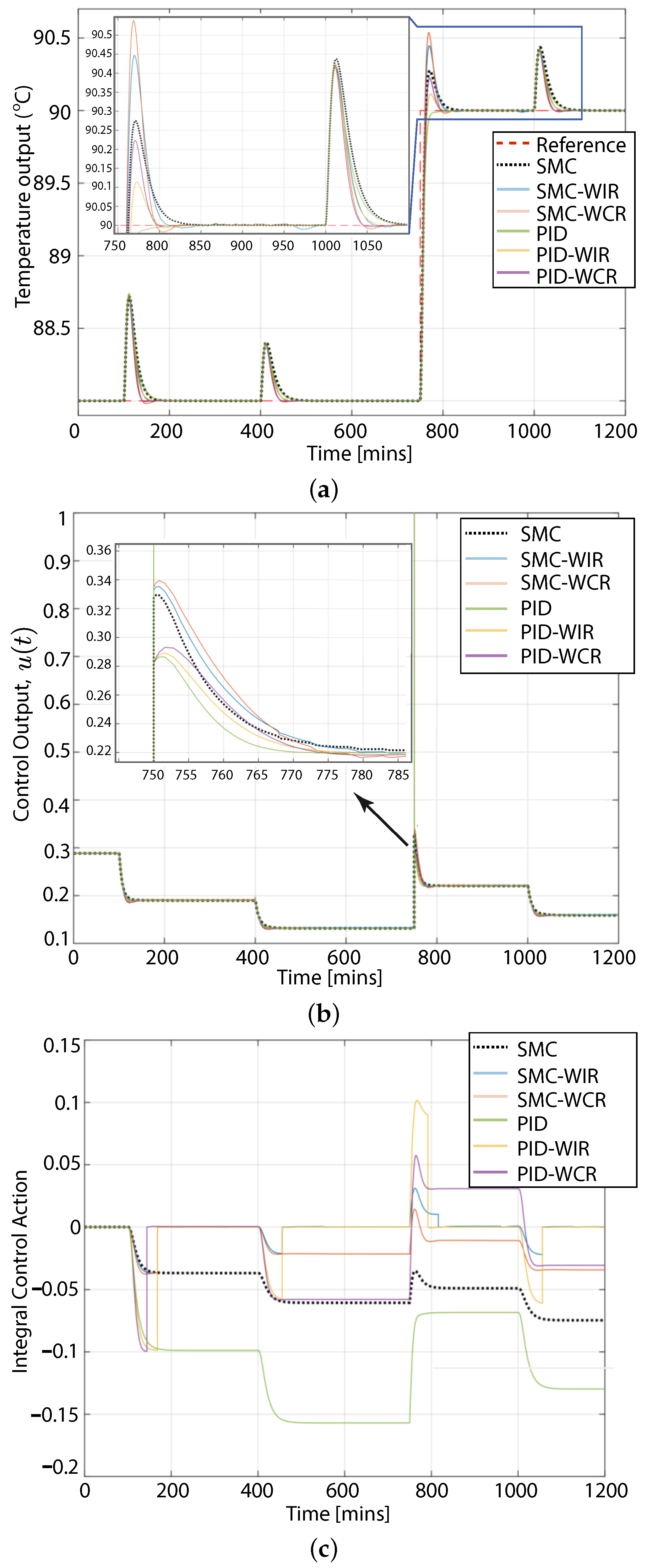
6. Results for the CSTR Process
6.1. System Response against Disturbances
6.2. System Response against Reference Changes
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Discontinuous control action | |
| Continuous control action. | |
| Sliding mode surface. | |
| Sign of the control gain K. | |
| Tuning gain for discontinuous control. | |
| Tuning parameter for discontinuous control. | |
| Y, | Output and reference of the process output, respectively |
| U | Process control input. |
| Process model in transfer function of variable s. | |
| Time constant of the process (min). | |
| Time delay of the process (min). | |
| Adjustable parameters of the sliding surface. | |
| Allowable tracking error boundary. | |
| m | Derivative of the process output. |
| Anti-windup saturation function. | |
| Hot and cold product flow, respectively, (lb/min). | |
| Hot and cold stream temperature, respectively, (°C). | |
| Temperature of the process output with and without delay (°C). | |
| Stream heat capacity at constant pressure, Btu/lb−°F. | |
| Stream heat capacity at constant volume (Btu/lb−°F). | |
| Density of the mixing tank content in lb/ft. | |
| Cross section of the mixing tank (ft). | |
| Product level in the mixing tank (ft). | |
| Manual valve flow coefficient (gpm/ft). | |
| Control valve flow coefficient in (gpm/psi). | |
| Valve position from 0 (valve closed) to 1 (valve open). | |
| Output signal of the temperature transmitter (0 to 1 p.u). | |
| Mass of the process to control (0 to 1 p.u). | |
| Specific gravity, dimensionless. | |
| Pressure loss through the control valve (psi). | |
| Control valve time constant (min). | |
| A | Cross section of the transportation pipe (ft). |
| L | Length of the transportation pipe (ft). |
| Flow through the reactor (m/min) | |
| V | Reactor volume that will remain constant during operation (m) |
| Concentration of A or B in the reactor (mol L) | |
| Concentration of or in steady-state (mol L) | |
| Coolant flow (m/s) | |
| Normalized output signal of the transmitter (0 to 1 p.u) | |
| Coolant temperature (°C). | |
| Reaction rate constants for three reactions. |
References
- Mejía, C.; Salazar, E.; Camacho, O. A comparative experimental evaluation of various Smith predictor approaches for a thermal process with large dead time. Alex. Eng. J. 2022, 61, 9377–9394. [Google Scholar] [CrossRef]
- Yan, H.; Zhou, X.; Zhang, H.; Yang, F.; Wu, Z.-G. A Novel Sliding Mode Estimation for Microgrid Control With Communication Time Delays. IEEE Trans. Smart Grid 2019, 10, 1509–1520. [Google Scholar] [CrossRef]
- Liu, Z.X.; Wang, Z.Y.; Wang, Y.; Ji, Z.-C. Optimal Zonotopic Kalman Filter-based State Estimation and Fault-diagnosis Algorithm for Linear Discrete-time System with Time Delay. Int. J. Control Autom. Syst. 2022, 20, 1757–1771. [Google Scholar] [CrossRef]
- Qi, X.; Liu, W.; Lu, J. Observer-based Finite-time Adaptive Prescribed Performance Control for Nonlinear Systems with Input Delay. Int. J. Control Autom. Syst. 2022, 20, 1428–1438. [Google Scholar] [CrossRef]
- Camacho, O.; Leiva, H. Impulsive semilinear heat equation with delay in control and in state. Asian J. Control 2020, 22, 1075–1089. [Google Scholar] [CrossRef]
- Espín, J.; Castrillon, F.; Leiva, H.; Camacho, O. A modified Smith predictor based-sliding mode control approach for integrating processes with dead time. Alex. Eng. J. 2022, 61, 10119–10137. [Google Scholar] [CrossRef]
- Mancisidor, I.; Pena-Sevillano, A.; Dombovari, Z.; Barcena, R.; Munoa, J. Delayed feedback control for chatter suppression in turning machines. Mechatronics 2019, 63, 102276. [Google Scholar] [CrossRef]
- Gao, F.; Chen, W. Disturbance Rejection in Singular Time-delay Systems with External Disturbances. Int. J. Control Autom. Syst. 2022, 20, 1841–1848. [Google Scholar] [CrossRef]
- Cajamarca, B.; PatiñO, K.; Camacho, O.; Chavez, D.; Leica, P.; Pozo, M. A comparative analysis of sliding mode controllers based on internal model for a nonminimum phase buck and boost converter. In Proceedings of the 2019 International Conference on Information Systems and Computer Science (INCISCOS), Quito, Ecuador, 20–22 November 2019; pp. 189–195. [Google Scholar] [CrossRef]
- Salinas, L.R.; Santiago, D.; Slawiñski, E.; Mut, V.; Chavez, D.; Leica, P.; Camacho, O. P+ d plus sliding mode control for bilateral teleoperation of a mobile robot. Int. J. Control Autom. Syst. 2018, 16, 1927–1937. [Google Scholar] [CrossRef]
- Báez, E.; Bravo, Y.; Leica, P.; Chávez, D.; Camacho, O. Dynamical sliding mode control for nonlinear systems with variable delay. In Proceedings of the 2017 IEEE 3rd Colombian Conference on Automatic Control (CCAC), Cartagena, Colombia, 18–20 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Owais, K.; Mahmood, P.; Ejaz, A.; Jamshed, I. On the derivation of novel model and sophisticated control of flexible joint manipulator. Rev. Roum. Sci. Tech.-Ser. Electrotech. Energ. 2017, 62, 103–108. [Google Scholar]
- Prado, A.J.; Cheein, F.A.; Torres-Torriti, M. Probabilistic approaches for self-tuning path tracking controllers using prior knowledge of the terrain. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; pp. 3095–3100. [Google Scholar] [CrossRef]
- Wu, X.; Lin, Z. On Immediate, Delayed and Anticipatory Activation of Anti-Windup Mechanism: Static Anti-Windup Case. IEEE Trans. Autom. Control 2012, 57, 771–777. [Google Scholar] [CrossRef]
- Peng, Y.; Vrancic, D.; Hanus, R. Anti-windup, bumpless, and conditioned transfer techniques for PID controllers. IEEE Control Syst. Mag. 1996, 16, 48–57. [Google Scholar] [CrossRef]
- Chen, L.; Fang, J. Adaptive Continuous Sliding Mode Control for Fractional-order Systems with Uncertainties and Unknown Control Gains. Int. J. Control Autom. Syst. 2022, 20, 1509–1520. [Google Scholar] [CrossRef]
- Iqbal, J. Modern Control Laws for an Articulated Robotic Arm: Modeling and Simulation. Eng. Technol. Appl. Sci. Res. 2019, 9, 4057–4061. [Google Scholar] [CrossRef]
- Herrera, M.; Morales, L.; Rosales, A.; Garcia, Y.; Camacho, O. Processes with variable dead time: Comparison of hybrid control schemes based on internal model. In Proceedings of the 2017 IEEE Second Ecuador Technical Chapters Meeting (ETCM), Salinas, Ecuador, 16–20 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Prado, J.; Yandun, F.; Torres Torriti, M.; Auat Cheein, F. Overcoming the Loss of Performance in Unmanned Ground Vehicles Due to the Terrain Variability. IEEE Access 2018, 6, 17391–17406. [Google Scholar] [CrossRef]
- Torres, J.; Chavez, D.; Aboukheir, H.; Herrera, M.; Prado, J.; Camacho, O. Anti-Windup Algorithms for Sliding Mode Control in Processes with Variable Dead-Time. In Proceedings of the 2020 IEEE ANDESCON, Quito, Ecuador, 13–16 October 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Camacho, O.; Díaz, R.; Obando, C. Hardware in the loop simulation for sliding mode control schemes for deadtime systems. In Proceedings of the International Conference on Information Systems and Computer Science (INCISCOS), Quito, Ecuador, 20–22 November 2019; pp. 183–188. [Google Scholar] [CrossRef]
- Aichi, B.; Bourahla, M.; Kendouci, K. Real-Time Hybrid Control of Induction Motor Using Sliding Mode and PI Anti-Windup. In Proceedings of the 2018 International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM), Algiers, Algeria, 28–31 October 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Guo, X.-G.; Ahn, C.K. Adaptive Fault-Tolerant Pseudo-PID Sliding-Mode Control for High-Speed Train with Integral Quadratic Constraints and Actuator Saturation. IEEE Trans. Intell. Transp. Syst. 2021, 22, 7421–7431. [Google Scholar] [CrossRef]
- Zhang, X.; Su, C. Stability Analysis and Antiwindup Design of Switched Linear Systems with Actuator Saturation. Int. J. Control Autom. Syst. 2018, 16, 1247–1253. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, Y.; Xu, L.; Wu, H. Adaptive Robust Control for a Class of Uncertain Neutral Systems with Time Delays and Nonlinear Uncertainties. Int. J. Control Autom. Syst. 2021, 19, 1215–1227. [Google Scholar] [CrossRef]
- Prusty, S.B.; Seshagiri, S.; Pati, U.C.; Mahapatra, K.K. Sliding mode control of coupled tank systems using conditional integrators. IEEE/CAA J. Autom. Sin. 2020, 7, 118–125. [Google Scholar] [CrossRef]
- Sun, T.; Liu, C.; Wang, X. Anti-windup neural network-sliding mode control for dynamic positioning vessels. In Proceedings of the 2021 8th International Conference on Information, Cybernetics, and Computational Social Systems (ICCSS), Beijing, China, 10–12 December 2021; pp. 356–361. [Google Scholar] [CrossRef]
- Scholl, T.H.; Groll, L. Stability Criteria for Time-Delay Systems from an Insightful Perspective on the Characteristic Equation. IEEE Trans. Autom. Control, 2022; ahead of print. [Google Scholar] [CrossRef]
- Sajjadi-Kia, S.; Jabbari, F. Modified Anti-windup compensators for stable plants: Dynamic Anti-windup case. In Proceedings of the 48h IEEE Conference on Decision and Control (CDC) held jointly with 2009 28th Chinese Control Conference, Shanghai, China, 15–18 December 2009; pp. 2795–2800. [Google Scholar] [CrossRef]
- Camacho, O.; Smith, C. Sliding mode control: An approach to regulate nonlinear chemical processes. ISA Trans. 2000, 39, 205–218. [Google Scholar] [CrossRef]
- Nath, K.; Bera, M.K. Adaptive Integral Sliding Mode Control: An Event-Triggered Approach. IFAC-PapersOnLine 2022, 55, 604–609. [Google Scholar] [CrossRef]
- Nath, U.M.; Dey, C.; Mudi, R.K. Designing of anti-windup feature for internal model controller with real-time performance evaluation on temperature control loop. In Proceedings of the 2019 2nd International Conference on Intelligent Computing, Instrumentation and Control Technologies (ICICICT), Kannur, India, 5–6 July 2019; pp. 787–790. [Google Scholar] [CrossRef]
- Bandyopadhyay, B.; Deepak, F.; Park, Y.J. A Robust Algorithm Against Actuator Saturation using Integral Sliding Mode and Composite Nonlinear Feedback. IFAC Proc. Vol. 2008, 41, 14174–14179. [Google Scholar] [CrossRef]
- Septanto, H.; Syaichu-Rohman, A.; Mahayana, D. Static anti-windup compensator design of linear Sliding Mode Control for input saturated systems. In Proceedings of the 2011 International Conference on Electrical Engineering and Informatics, Bandung, Indonesia, 17–19 July 2011; pp. 1–4. [Google Scholar] [CrossRef]
- Guanghui, Z.; Huihe, S. Anti-windup design for the controllers of integrating processes with long delay. J. Syst. Eng. Electron. 2007, 18, 297–303. [Google Scholar] [CrossRef]
- Proaño, P.; Capito, L.; Rosales, A.; Camacho, O. Sliding Mode Control: Implementation Like PID for Trajectory-Tracking for Mobile Robots. In Proceedings of the 2015 Asia-Pacific Conference on Computer Aided System Engineering, Quito, Ecuador, 14–16 July 2015; pp. 220–225. [Google Scholar] [CrossRef]
- Coronel, W.; Camacho, O. A Dynamic Sliding Mode Controller using a Rotating Type Moving Sliding Surface for Chemical Processes with Variable Delay. In Proceedings of the 2021 IEEE CHILEAN Conference on Electrical, Electronics Engineering, Information and Communication Technologies (CHILECON), Valparaiso, Chile, 6–9 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Utkin, V.; Poznyak, A.; Orlov, Y.V.; Polyakov, A. Road Map for Sliding Mode Control Design; Springer: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Smith, C.; Corripio, A.B. Principles and Practices of Automatic Process Control, 3rd ed.; Wiley: Hoboken, NJ, USA, 2005; ISBN 978-0-471-43190-9. [Google Scholar]
- Dogu, T.; Dogu, G. Fundamentals of Chemical Reactor Engineering: A Multi-Scale Approach; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Victor, M.A.; Pedro, B.; Orlando, A. Robustness Considerations on PID Tuning for Regulatory Control of Inverse Response Processes. IFAC Proc. Vol. 2012, 45, 193–198. [Google Scholar] [CrossRef]

| Model Parameters | Values | Units |
|---|---|---|
| . | ||
| 10 | ||
| V | 700 | L |
| 2.9175 | ||
| 1.1 | ||
| 60 | % |
| ISE | ITSE | Variation of ISE (Percentage) | Variation of ITSE (Percentage) | |
|---|---|---|---|---|
| SMC | 0.357 | 95.454 | - | - |
| SMC-WIR | 0.270 | 67.343 | 24.35% (of reduction) | 29.51% (of reduction) |
| SMC-WCR | 0.302 | 79.301 | 17.05% (of reduction) | 88.7% (of reduction) |
| PID | 2.394 | 933.536 | - | - |
| PID-WIR | 2.259 | 933.235 | 532.77% (of increase) | 497.18% (of increase) |
| PID-WCR | 2.569 | 935.781 | 619.19% (of increase) | 548.06% (of increase) |
| ISE | ITSE | Variation of ISE (Percentage) | Variation of ITSE (Percentage) | |
|---|---|---|---|---|
| SMC | 0.56 | 161.34 | - | - |
| SMC-WIR | 0.41 | 139.02 | 27.78% (of reduction) | 13.83% (of reduction) |
| SMC-WCR | 0.53 | 143.08 | 5.36% (of reduction) | 21.31% (of reduction) |
| PID | 23.66 | 1166.08 | - | - |
| PID-WIR | 23.64 | 1155.66 | 0.05% (of reduction) | 0.89% (of reduction) |
| PID-WCR | 23.69 | 1160.73 | 0.05% (of increase) | 0.45% (of reduction) |
| ISE | ITSE | Variation of ISE (Percentage) | Variation of ITSE (Percentage) | |
|---|---|---|---|---|
| SMC | 0.786 | 139.111 | - | - |
| SMC-WIR | 0.137 | 101.557 | 82.57% (of reduction) | 26.99% (of reduction) |
| SMC-WCR | 0.124 | 92.736 | 84.22% (of reduction) | 3.34% (of reduction) |
| PID | 0.867 | 95.188 | - | - |
| PID-WIR | 0.815 | 89.528 | 10.31% (of increase) | 35.64% (of reduction) |
| PID-WCR | 0.603 | 85.901 | 23.28% (of reduction) | 38.25% (of reduction) |
| ISE | ITSE | Variation of ISE (Percentage) | Variation of ITSE (Percentage) | |
|---|---|---|---|---|
| SMC | 0.9 | 128.22 | - | - |
| SMC-WIR | 0.17 | 78.18 | 81.11% (of reduction) | 39.03% (of reduction) |
| SMC-WCR | 0.24 | 83.21 | 73.33% (of reduction) | 35.10% (of reduction) |
| PID | 0.33 | 99.76 | - | - |
| PID-WIR | 0.21 | 87.91 | 76.67% (of reduction) | 31.44% (of reduction) |
| PID-WCR | 0.38 | 89.26 | 57.78% (of reduction) | 30.39% (of reduction) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prado, A.J.; Herrera, M.; Dominguez, X.; Torres, J.; Camacho, O. Integral Windup Resetting Enhancement for Sliding Mode Control of Chemical Processes with Longtime Delay. Electronics 2022, 11, 4220. https://doi.org/10.3390/electronics11244220
Prado AJ, Herrera M, Dominguez X, Torres J, Camacho O. Integral Windup Resetting Enhancement for Sliding Mode Control of Chemical Processes with Longtime Delay. Electronics. 2022; 11(24):4220. https://doi.org/10.3390/electronics11244220
Chicago/Turabian StylePrado, Alvaro Javier, Marco Herrera, Xavier Dominguez, Jose Torres, and Oscar Camacho. 2022. "Integral Windup Resetting Enhancement for Sliding Mode Control of Chemical Processes with Longtime Delay" Electronics 11, no. 24: 4220. https://doi.org/10.3390/electronics11244220
APA StylePrado, A. J., Herrera, M., Dominguez, X., Torres, J., & Camacho, O. (2022). Integral Windup Resetting Enhancement for Sliding Mode Control of Chemical Processes with Longtime Delay. Electronics, 11(24), 4220. https://doi.org/10.3390/electronics11244220









