Path Tracking for Car-like Robots Based on Neural Networks with NMPC as Learning Samples
Abstract
:1. Introduction
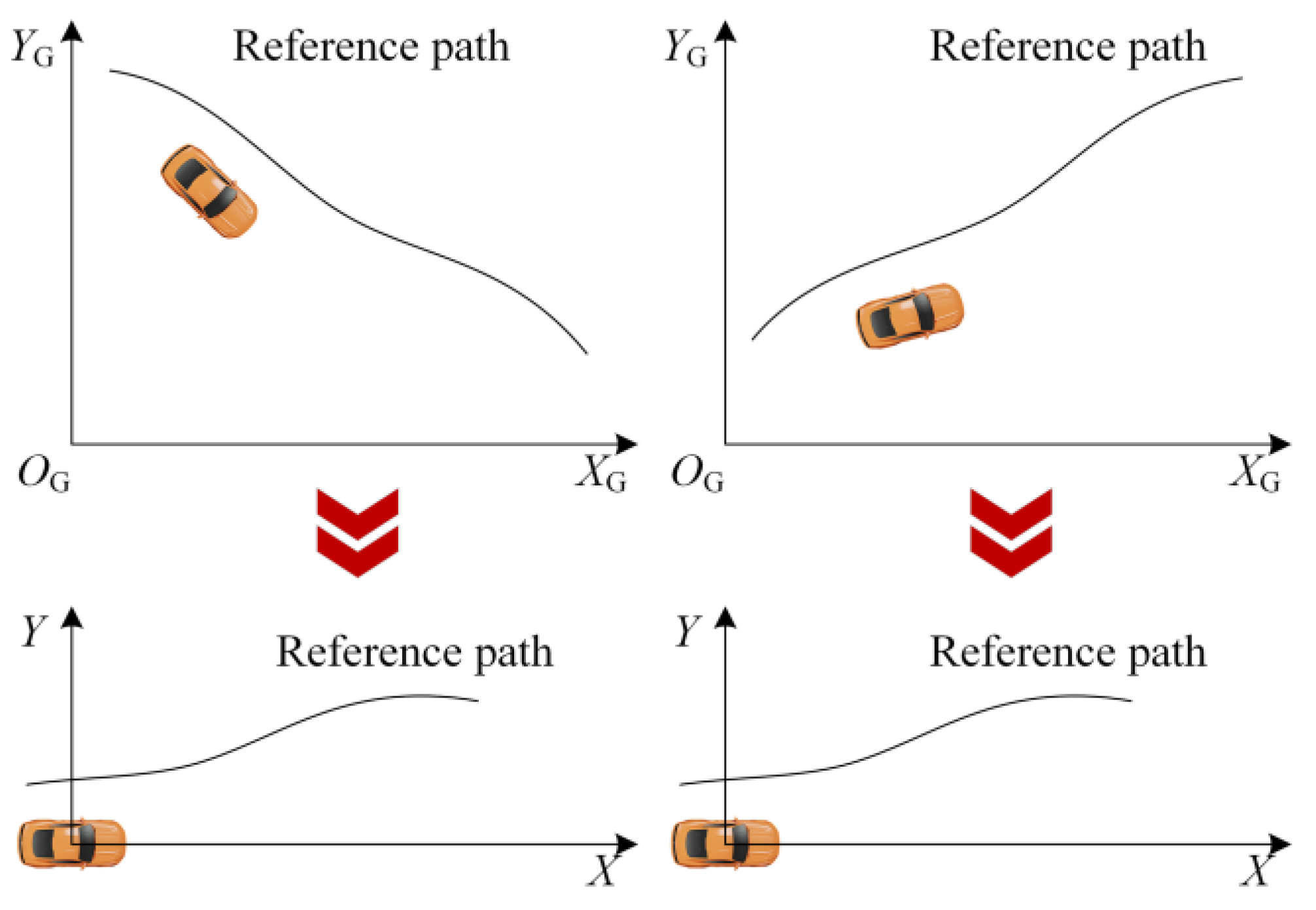
2. Reference Path and Coordinate System
3. NMPC Controller Based on the Time-Varying Local Model
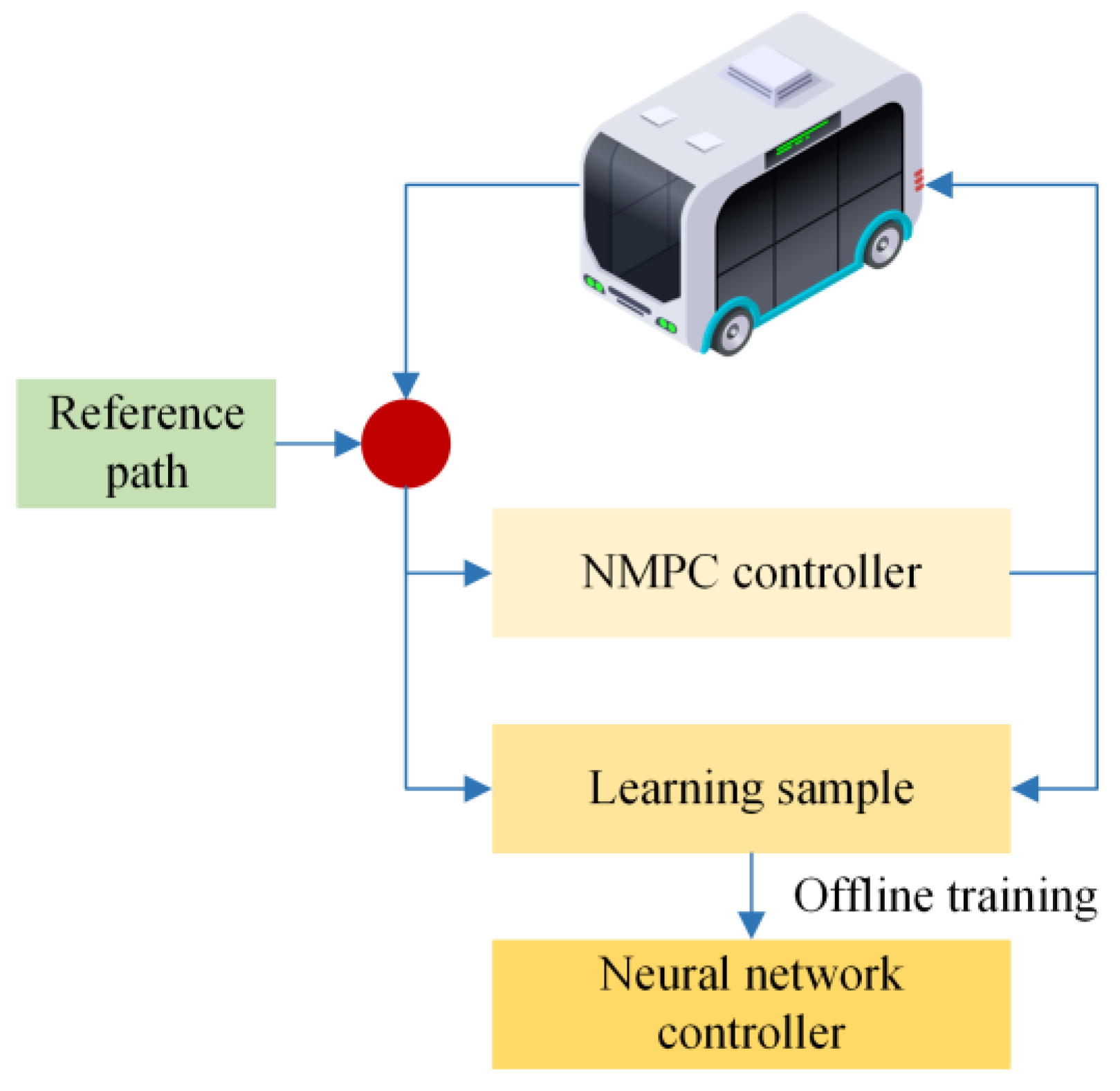
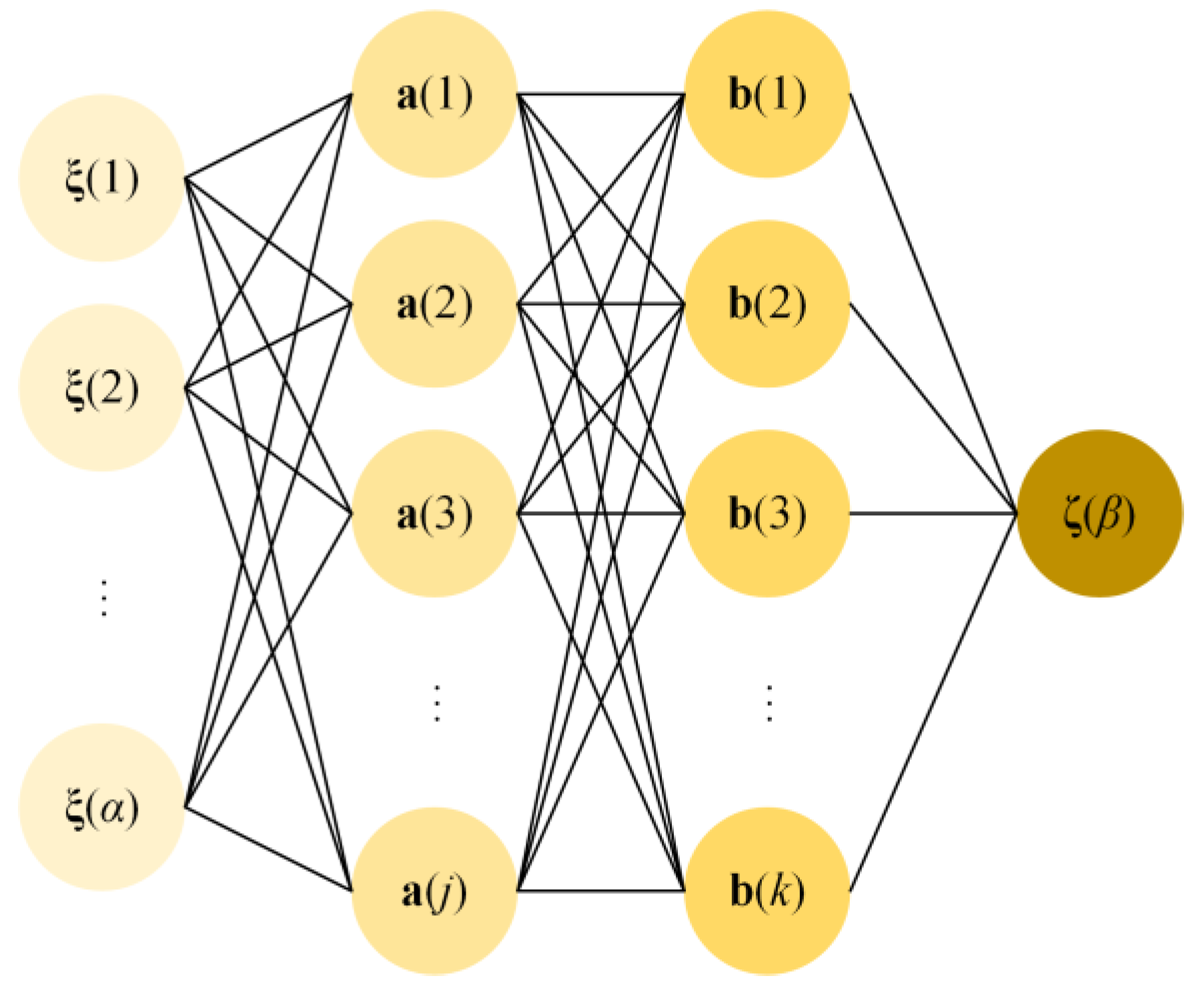
4. Neural Network Controller with NMPC as Learning Samples
5. Joint Simulation and Results
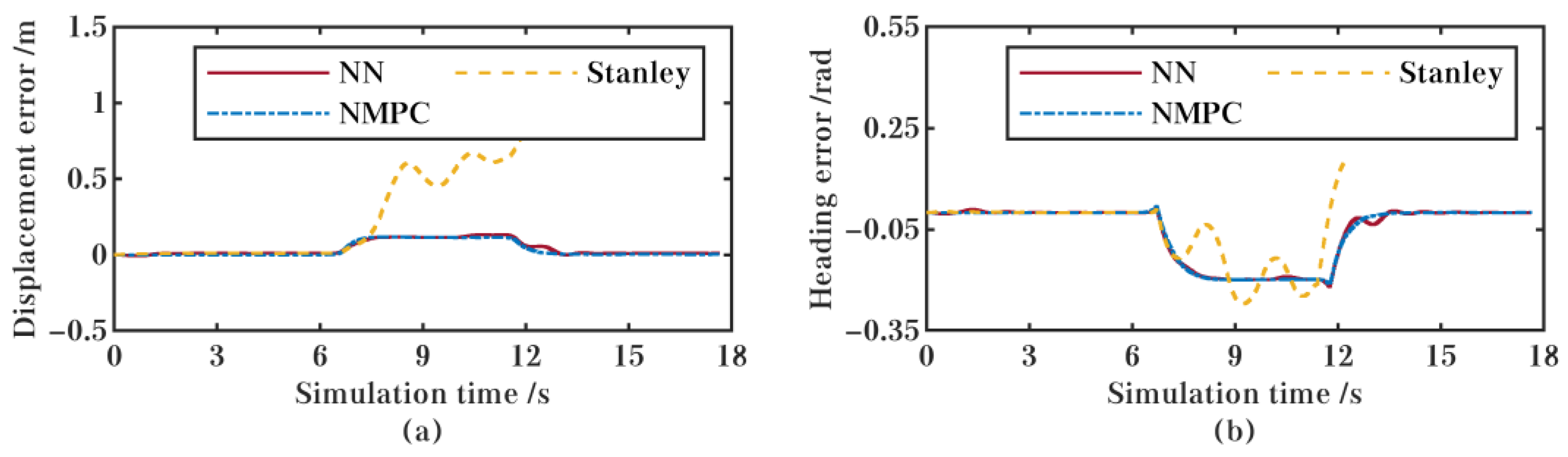
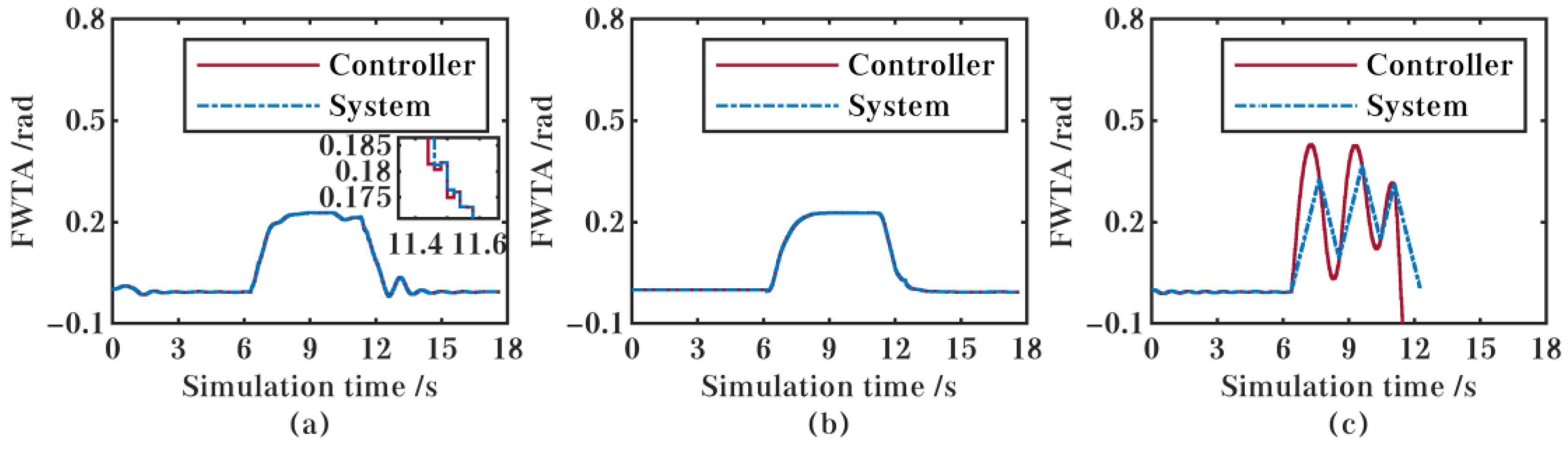
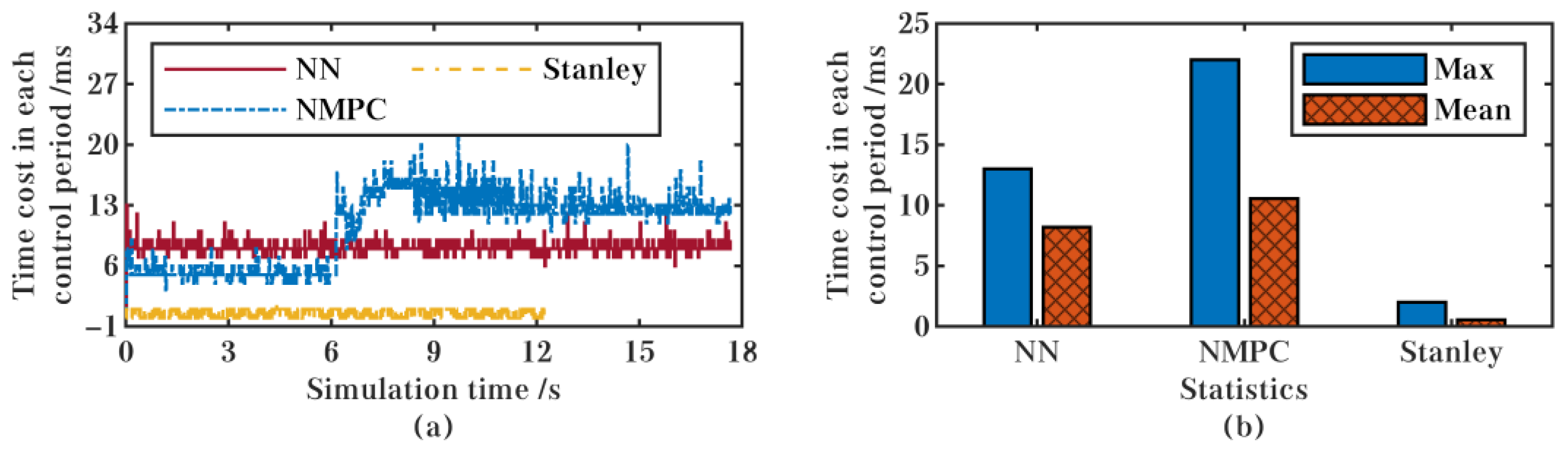
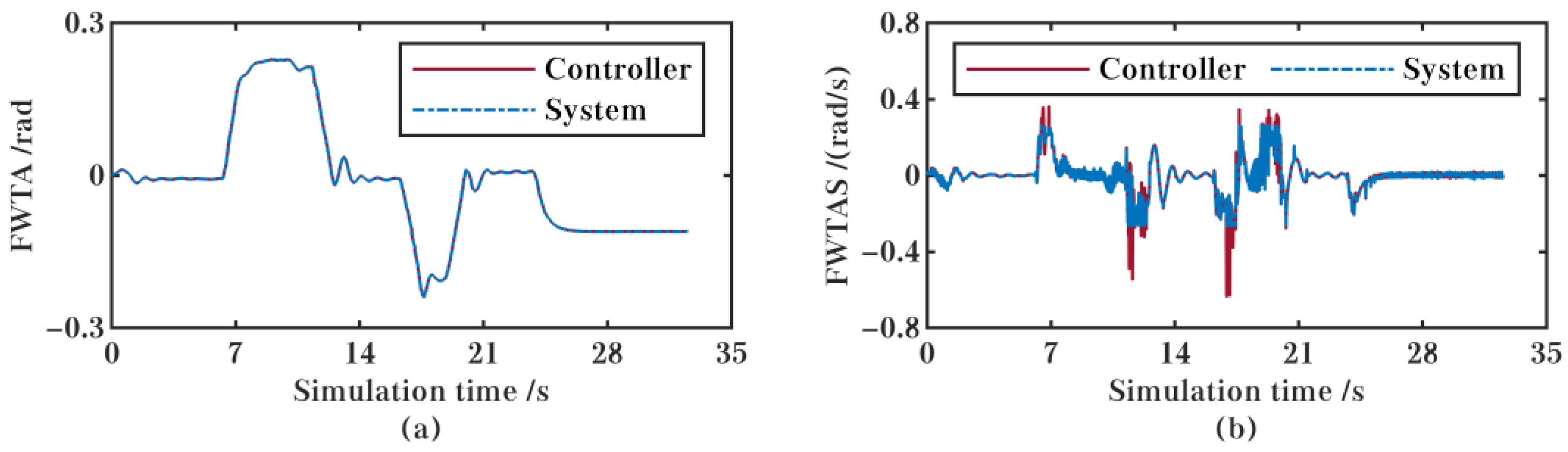
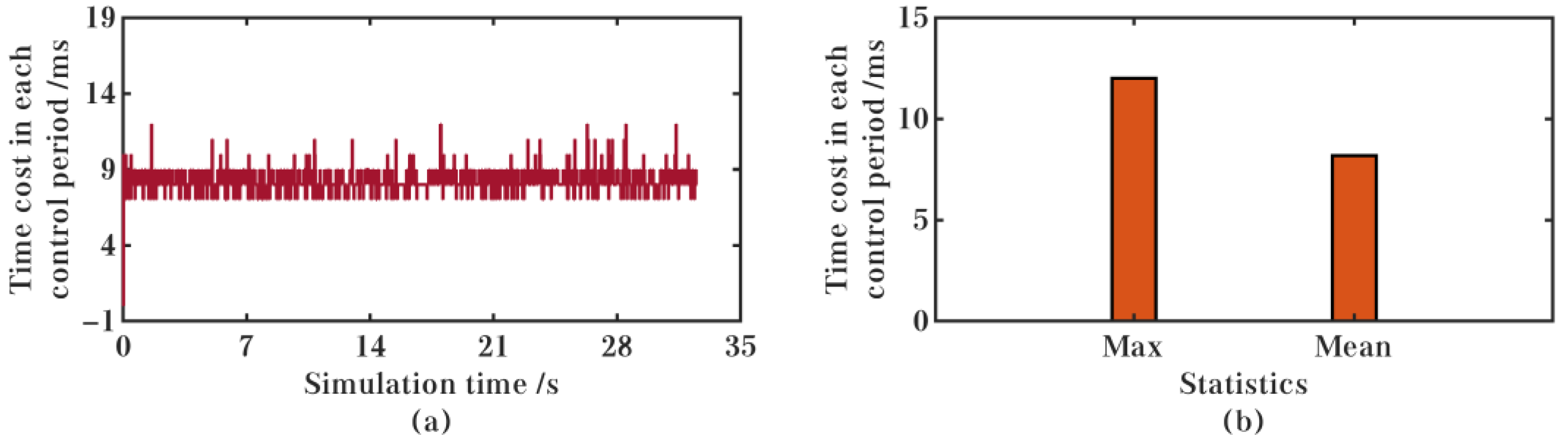
5.1. Comparison with Other Controllers
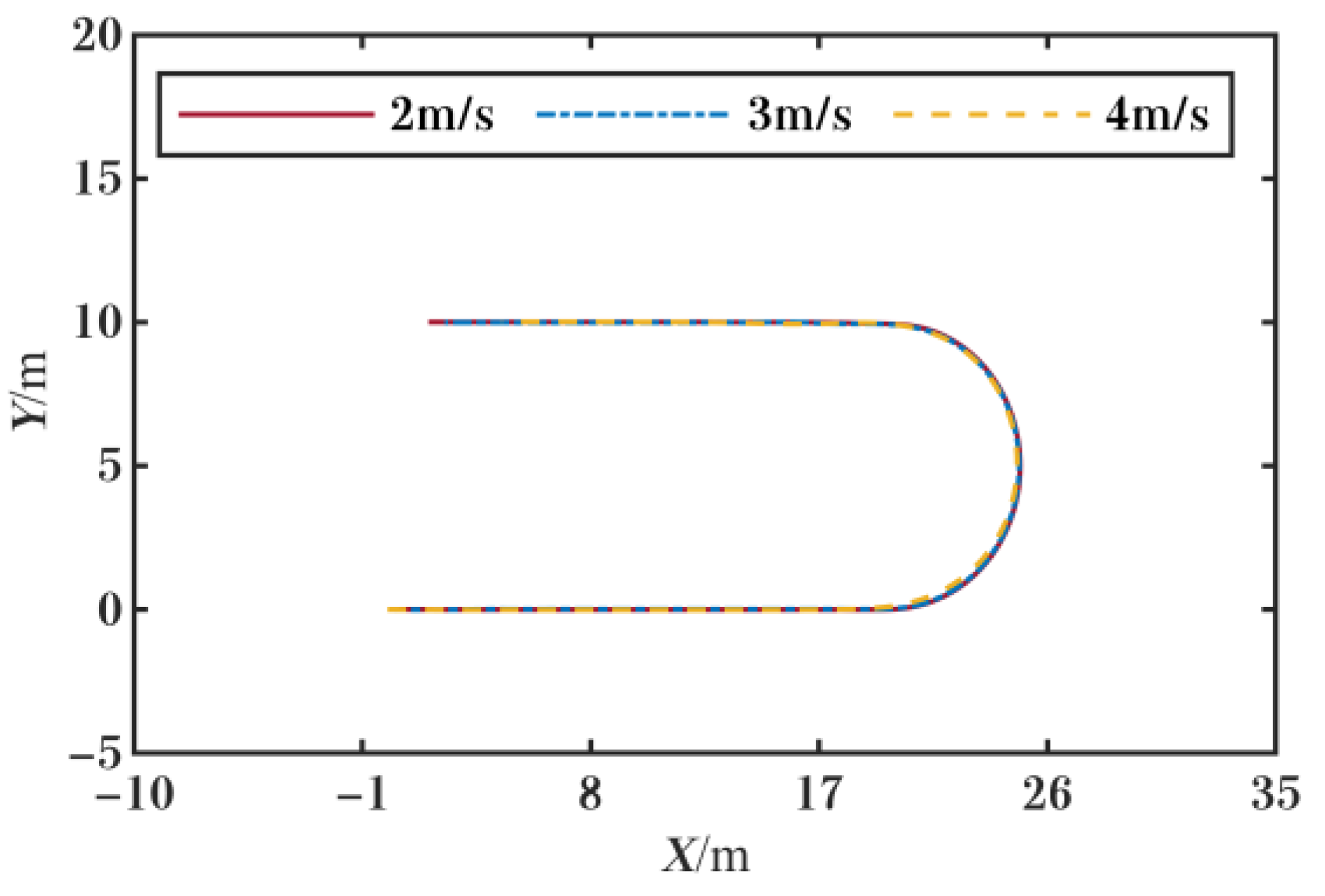
5.2. Simulation at Different Speeds
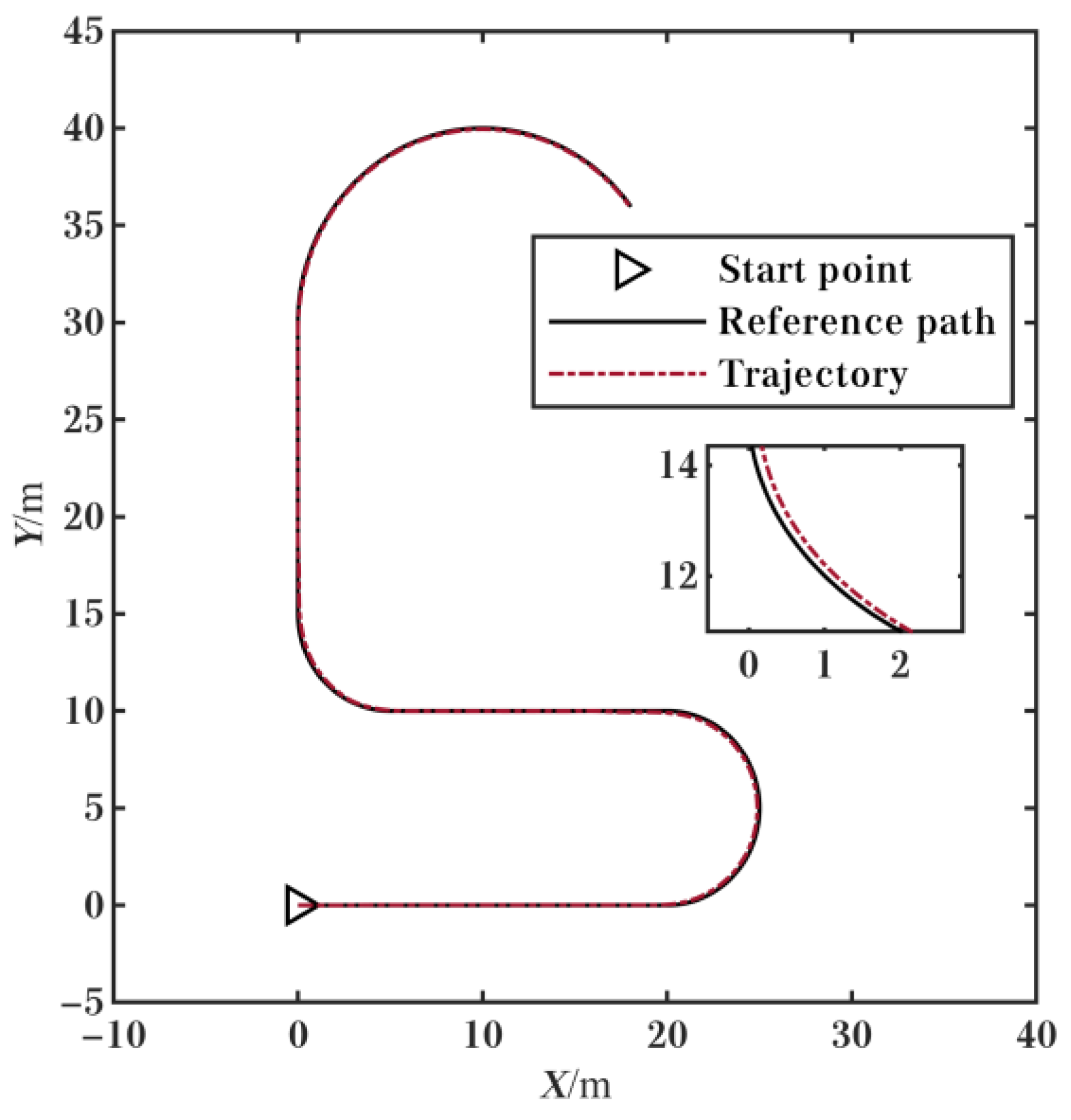
5.3. Simulation When Tracking the Complex Reference Path
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ortega, J.; Lengyel, H.; Szalay, Z. Overtaking maneuver scenario building for autonomous vehicles with PreScan software. Transp. Eng. 2020, 2, 100029. [Google Scholar] [CrossRef]
- Naderi Samani, N.; Danesh, M.; Ghaisari, J. Parallel parking of a car-like mobile robot based on the P-domain path tracking controllers. IET Control Theory Appl. 2016, 10, 564–572. [Google Scholar] [CrossRef]
- Hwang, C.L. Comparison of path tracking control of a car-like mobile robot with and without motor dynamics. IEEE ASME Trans. Mechatron. 2016, 21, 1801–1811. [Google Scholar] [CrossRef]
- Abd Latip, N.B.; Omar, R. Car-like robot path tracker with kinematic constraints. In Proceedings of the 2016 6th IEEE International Conference on Control System, Computing and Engineering (ICCSCE), Penang, Malaysia, 25–27 November 2016. [Google Scholar]
- Ballinas, E.; Montiel, O.; Castillo, O.; Rubio, Y.; Aguilar, L.T. Automatic Parallel Parking Algorithm for a Carlike Robot using Fuzzy PD+ I Control. Eng. Lett. 2018, 26, 447–454. [Google Scholar]
- Ghaffari, S.; Homaeinezhad, M.R. Autonomous path following by fuzzy adaptive curvature-based point selection algorithm for four-wheel-steering car-like mobile robot. Proc. Inst. Mech. Eng. C J. Eng. Mech. Eng. Sci. 2018, 232, 2655–2665. [Google Scholar] [CrossRef]
- Ljungqvist, O.; Evestedt, N.; Axehill, D.; Cirillo, M.; Pettersson, H. A path planning and path-following control framework for a general 2-trailer with a car-like tractor. J. Field Robot. 2019, 36, 1345–1377. [Google Scholar] [CrossRef] [Green Version]
- Kamran, D.; Zhu, J.; Lauer, M. Learning path tracking for real car-like mobile robots from simulation. In Proceedings of the 2019 European Conference on Mobile Robots (ECMR), Prague, Czech Republic, 4–6 September 2019. [Google Scholar]
- Wu, H.M. Nonlinear trajectory-tracking control of a car-like mobile robot in the presence of input saturations and a pulse disturbance. In Proceedings of the 2019 58th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), Hiroshima, Japan, 10–13 September 2019. [Google Scholar]
- Mohan Rayguru, M.; Rajesh Elara, M.; Ramalingam, B.; Muthugala, M.V.J.; Samarakoon, S.B.P. A path tracking strategy for car like robots with sensor unpredictability and measurement errors. Sensors 2020, 20, 3077. [Google Scholar] [CrossRef]
- Prokopyev, I.; Sofronova, E. Study on synthesis methods for real-time control of car-like mobile robot. In Artificial Intelligence and Evolutionary Computations in Engineering Systems; Dash, S., Lakshmi, C., Das, S., Panigrahi, B., Eds.; Springer: Singapore, 2020; pp. 431–441. [Google Scholar]
- Elobaid, M.; Mattioni, M.; Monaco, S.; Normand-Cyrot, D. Digital path-following for a car-like robot. IFAC-PapersOnLine 2021, 54, 174–179. [Google Scholar] [CrossRef]
- Yeom, K. Design of deep neural network based model predictive controller for a car-like mobile robot. Int. J. Mech. Eng. Robot. Res. 2022, 11, 606–613. [Google Scholar] [CrossRef]
- Gong, J.W.; Xu, W.; Jiang, Y.; Liu, K.; Guo, H.F.; Sun, Y.J. Multi-constrained model predictive control for autonomous ground vehicle trajectory tracking. J. Beijing. Inst. Technol. 2015, 24, 441–443. [Google Scholar]
- Bai, G.; Meng, Y.; Liu, L.; Luo, W.; Gu, Q.; Liu, L. Review and comparison of path tracking based on model predictive control. Electronics 2019, 8, 1077. [Google Scholar] [CrossRef] [Green Version]
- Rokonuzzaman, M.; Mohajer, N.; Nahavandi, S.; Mohamed, S. Review and performance evaluation of path tracking controllers of autonomous vehicles. IET Intell. Transp. Syst. 2021, 15, 646–670. [Google Scholar] [CrossRef]
- Bai, G.X.; Luo, W.D.; Liu, L.; Meng, Y.; Gu, Q.; Li, K.L. Current status and progress of path tracking control of mining articulated vehicles. Chin. J. Eng. 2021, 43, 193–204. (In Chinese) [Google Scholar]
- Bai, G.X.; Meng, Y.; Liu, L.; Gu, Q.; Wang, G.D.; Zhou, B.N. Current status of path tracking control of unmanned driving vehicles. Chin. J. Eng. 2021, 43, 475–485. (In Chinese) [Google Scholar]
- Zhang, K.; Wang, J.; Xin, X.; Li, X.; Sun, C.; Huang, J.; Kong, W. A survey on learning-based model predictive control: Toward path tracking control of mobile platforms. Appl. Sci. 2022, 12, 1995. [Google Scholar] [CrossRef]
- Wang, X.; Taghia, J.; Katupitiya, J. Adaptive min-max model predictive control for field vehicle guidance in the presence of wheel slip. In Robotics and Mechatronics for Agriculture; Zhang, D., Wei, B., Eds.; CRC Press: Boca Raton, FL, USA, 2017; pp. 157–184. [Google Scholar]
- Bai, G.; Liang, C.; Meng, Y.; Liu, L.; Luo, W.; Gu, Q. Obstacle avoidance of semi-trailers based on nonlinear model predictive control. World Electr. Veh. J. 2019, 10, 72. [Google Scholar] [CrossRef] [Green Version]
- Bai, G.; Meng, Y.; Liu, L.; Gu, Q.; Luo, W.; Gan, X. Path tracking control of vehicles based on variable prediction horizon and velocity. China Mech. Eng. 2020, 31, 1277–1284. (In Chinese) [Google Scholar]
- Bai, G.; Liu, L.; Meng, Y.; Gu, Q.; Wang, G.; Dong, G. Path tracking of vehicles on urban roads based on fuzzy control and NMPC. In Proceedings of the 2021 China Automation Congress (CAC), Beijing, China, 22–24 October 2021. [Google Scholar]
- Bai, G.X.; Zhou, L.; Meng, Y.; Liu, L.; Gu, Q.; Wang, G.D. Path tracking of unmanned vehicles based on the time-varying local model. Chin. J. Eng. 2022. in press. (In Chinese) [Google Scholar]
- Bai, G.; Meng, Y.; Liu, L.; Luo, W.; Gu, Q.; Li, K. Anti-sideslip path tracking of wheeled mobile robots based on fuzzy model predictive control. Electron. Lett. 2020, 56, 490–493. [Google Scholar] [CrossRef]
- Bai, G.; Meng, Y.; Gu, Q.; Wang, G.; Dong, G.; Zhou, L. An anti-sideslip path tracking control method of wheeled mobile robots. In Proceedings of the International Conference on Intelligent Robotics and Applications, Harbin, China, 1–3 August 2022. [Google Scholar]
- Yin, C.; Xu, B.; Chen, X.; Qin, Z.; Bian, Y.; Sun, N. Nonlinear model predictive control for path tracking using discrete previewed points. In Proceedings of the 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), Rhodes, Greece, 20–23 September 2020. [Google Scholar]
- Barzegar, A.; Doukhi, O.; Lee, D.J.; Jo, Y.H. Nonlinear model predictive control for self-driving cars trajectory tracking in GNSS-denied environments. In Proceedings of the 2020 20th International Conference on Control, Automation and Systems (ICCAS), Busan, Republic of Korea, 13–16 October 2020. [Google Scholar]
- Farag, W. Real-time NMPC path tracker for autonomous vehicles. Asian J. Control 2021, 23, 1952–1965. [Google Scholar] [CrossRef]
- Chen, L.; Zhou, K.; Teng, C.; Sun, X.; Wang, H. Longitudinal and lateral comprehensive trajectory tracking control of intelligent vehicles based on NMPC. Autom. Eng. 2021, 43, 153–161. (In Chinese) [Google Scholar]
- Franco, I.J.P.B.; Ribeiro, T.T.; Conceição, A.G.S. A novel visual lane line detection system for a NMPC-based path following control scheme. J. Intell. Rob. Syst. Theor. Appl. 2021, 101, 12. [Google Scholar] [CrossRef]
- Hang, P.; Lou, B.; Lv, C. Nonlinear predictive motion control for autonomous mobile robots considering active fault-tolerant control and regenerative braking. Sensors 2022, 22, 3939. [Google Scholar] [CrossRef]
- Lee, J.; Choi, S. Nonlinear model predictive control for path tracking in high-speed corner entry situations. Int. J. Automot. Technol. 2022, 23, 1373–1381. [Google Scholar] [CrossRef]
- Bai, G.X.; Liu, L.; Meng, Y.; Liu, S.Y.; Liu, L.; Luo, W.D. Real-time path tracking of mobile robot based on nonlinear model predictive control. Trans. Chin. Soc. Agric. Mach. 2020, 51, 47–52, 60. (In Chinese) [Google Scholar]
- Bai, G.; Meng, Y.; Gu, Q.; Li, K.; Li, S. Some rules for setting the horizon parameters of NMPC-based vehicle path tracking. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020. [Google Scholar]
- Wang, H.W.; Liu, C.Y.; Li, L.; Zhang, H.T. Research on trajectory tracking control of unmanned vehicle based on efficient NMPC algorithm. Autom. Eng. 2022, 44, 1494–1502, 1618. (In Chinese) [Google Scholar]
- Gómez-Ortega, J.; Camacho, E.F. Neural network MBPC for mobile robot path tracking. Rob. Comput. Integr. Manuf. 1994, 11, 271–278. [Google Scholar] [CrossRef]
- Gómez-Ortega, J.; Camacho, E.F. Neural predictive control for mobile robot navigation in a partially structured static environment. IFAC Proc. 1996, 29, 8125–8130. [Google Scholar] [CrossRef]
- Gómez-Ortega, J.; Camacho, E.F. Mobile robot navigation in a partially structured static environment, using neural predictive control. Control Eng. Pract. 1996, 4, 1669–1679. [Google Scholar] [CrossRef]
- Liu, L. Path Tracking Control of Handling Robot Based on Neural Network. Master’s Thesis, University of Science and Technology Beijing, Beijing, China, 11 December 2019. (In Chinese). [Google Scholar]
- Ji, X.; He, X.; Lv, C.; Liu, Y.; Wu, J. A vehicle stability control strategy with adaptive neural network sliding mode theory based on system uncertainty approximation. Veh. Syst. Dyn. 2018, 56, 923–946. [Google Scholar] [CrossRef] [Green Version]
- Ji, X.; Yang, K.; Na, X.; Lv, C.; Liu, Y.; Liu, Y. Feedback game-based shared control scheme design for emergency collision avoidance: A fuzzy-linear quadratic regulator approach. J. Dyn. Syst. Meas. Control Trans. ASME 2019, 141, 081005. [Google Scholar] [CrossRef]
- Chen, Y.; Song, L.; Liu, Y.; Yang, L.; Li, D. A review of the artificial neural network models for water quality prediction. Appl. Sci. 2020, 10, 5776. [Google Scholar] [CrossRef]
- Hemeida, A.M.; Hassan, S.A.; Mohamed, A.A.A.; Alkhalaf, S.; Mahmoud, M.M.; Senjyu, T.; El-Din, A.B. Nature-inspired algorithms for feed-forward neural network classifiers: A survey of one decade of research. Ain Shams Eng. J. 2020, 11, 659–675. [Google Scholar] [CrossRef]
- Lippmann, R. An introduction to computing with neural nets. IEEE ASSP Mag. 1987, 4, 4–22. [Google Scholar] [CrossRef]







| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Wheelbase | 1 m | Distance from the center of mass to the front axle | 0.5 m |
| Mass | 1230 kg | Rotational inertia around the vertical direction | 1343.1 kg∙m−2 |
| 30° | Ground adhesion coefficient | 0.8 | |
| 15°/s | Tire type | 185/65 R15 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 30 | 2 | ||
| Q | [0.01] | ||
| 20 | 10 | ||
| 0.85 | 0.73 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, G.; Meng, Y.; Liu, L.; Gu, Q.; Huang, J.; Liang, G.; Wang, G.; Liu, L.; Chang, X.; Gan, X. Path Tracking for Car-like Robots Based on Neural Networks with NMPC as Learning Samples. Electronics 2022, 11, 4232. https://doi.org/10.3390/electronics11244232
Bai G, Meng Y, Liu L, Gu Q, Huang J, Liang G, Wang G, Liu L, Chang X, Gan X. Path Tracking for Car-like Robots Based on Neural Networks with NMPC as Learning Samples. Electronics. 2022; 11(24):4232. https://doi.org/10.3390/electronics11244232
Chicago/Turabian StyleBai, Guoxing, Yu Meng, Li Liu, Qing Gu, Jianxiu Huang, Guodong Liang, Guodong Wang, Li Liu, Xinrui Chang, and Xin Gan. 2022. "Path Tracking for Car-like Robots Based on Neural Networks with NMPC as Learning Samples" Electronics 11, no. 24: 4232. https://doi.org/10.3390/electronics11244232
APA StyleBai, G., Meng, Y., Liu, L., Gu, Q., Huang, J., Liang, G., Wang, G., Liu, L., Chang, X., & Gan, X. (2022). Path Tracking for Car-like Robots Based on Neural Networks with NMPC as Learning Samples. Electronics, 11(24), 4232. https://doi.org/10.3390/electronics11244232






