Package-Scale Galvanic Isolators Based on Radio Frequency Coupling: Micro–Antenna Design
Abstract
:1. Introduction
2. Galvanic Isolators Based on RF Planar Coupling
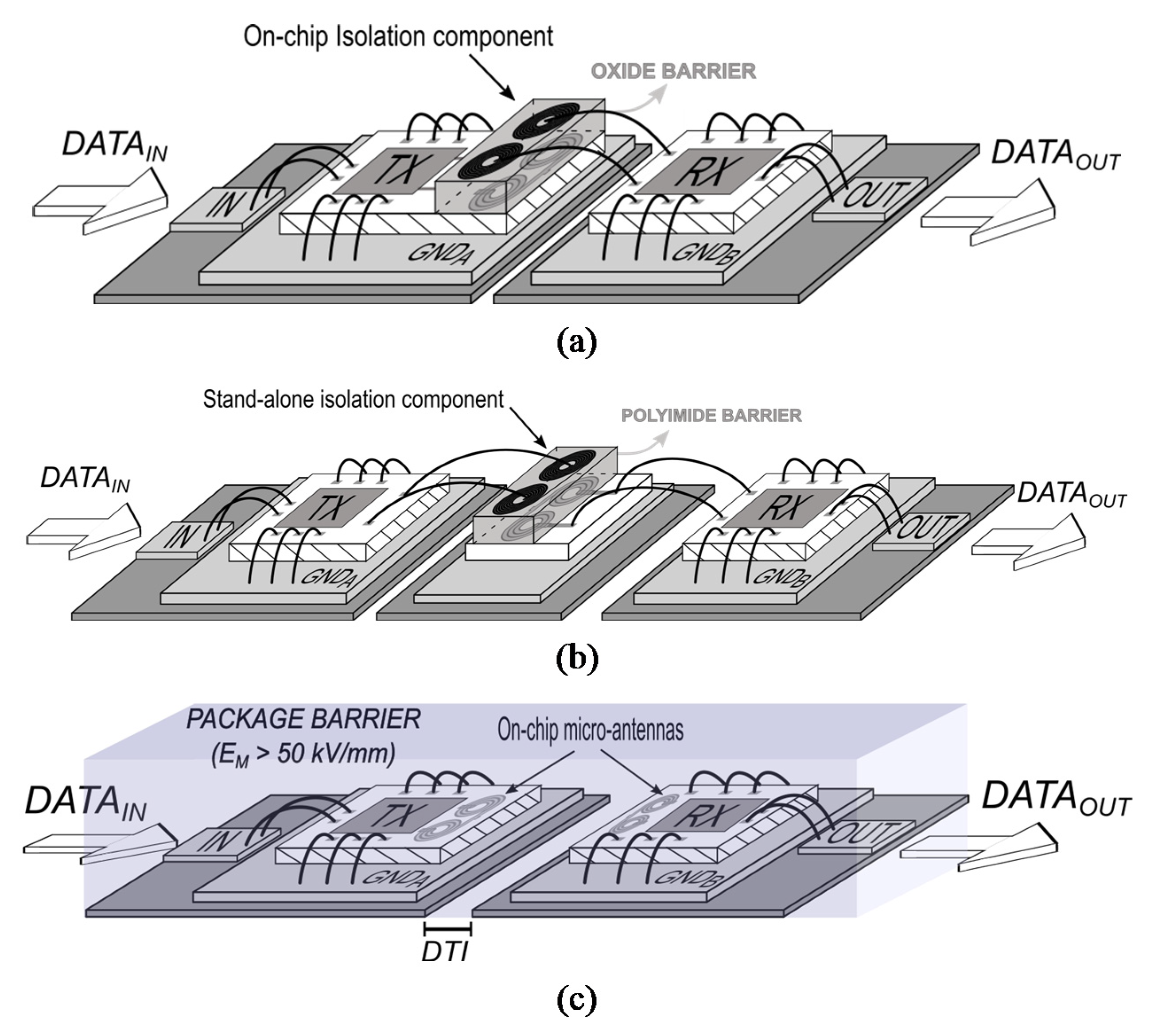
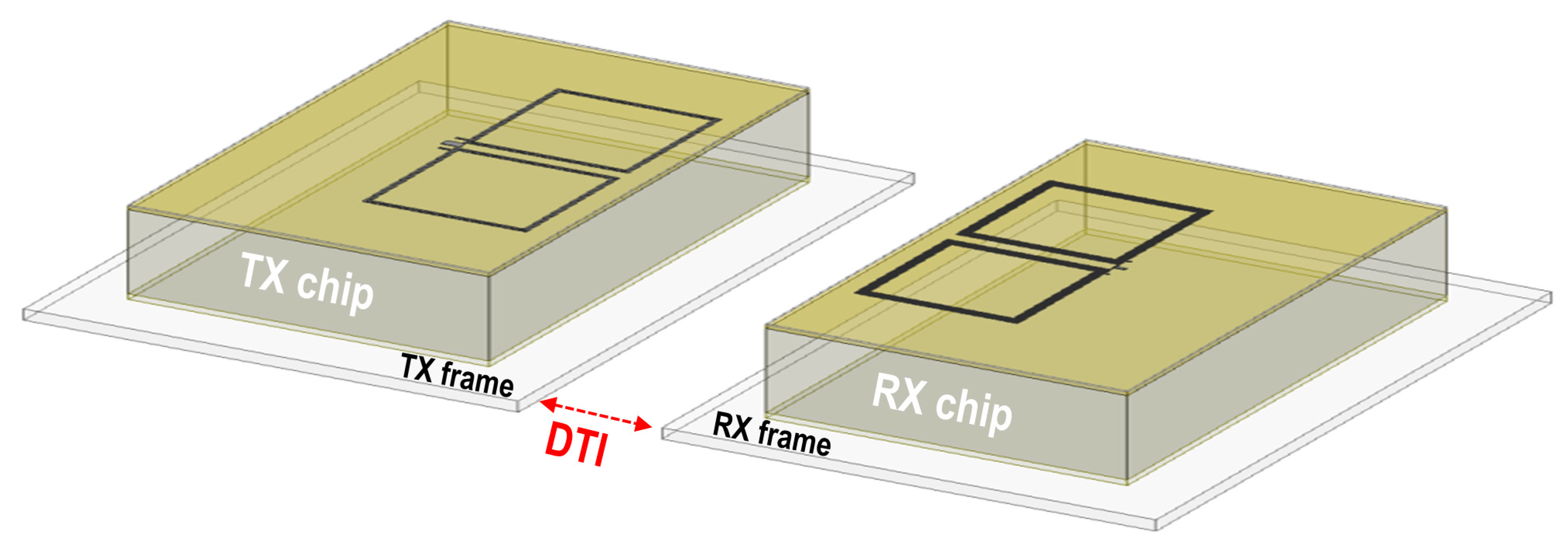
2.1. Chip-Scale Isolation vs. Package-Scale Isolation
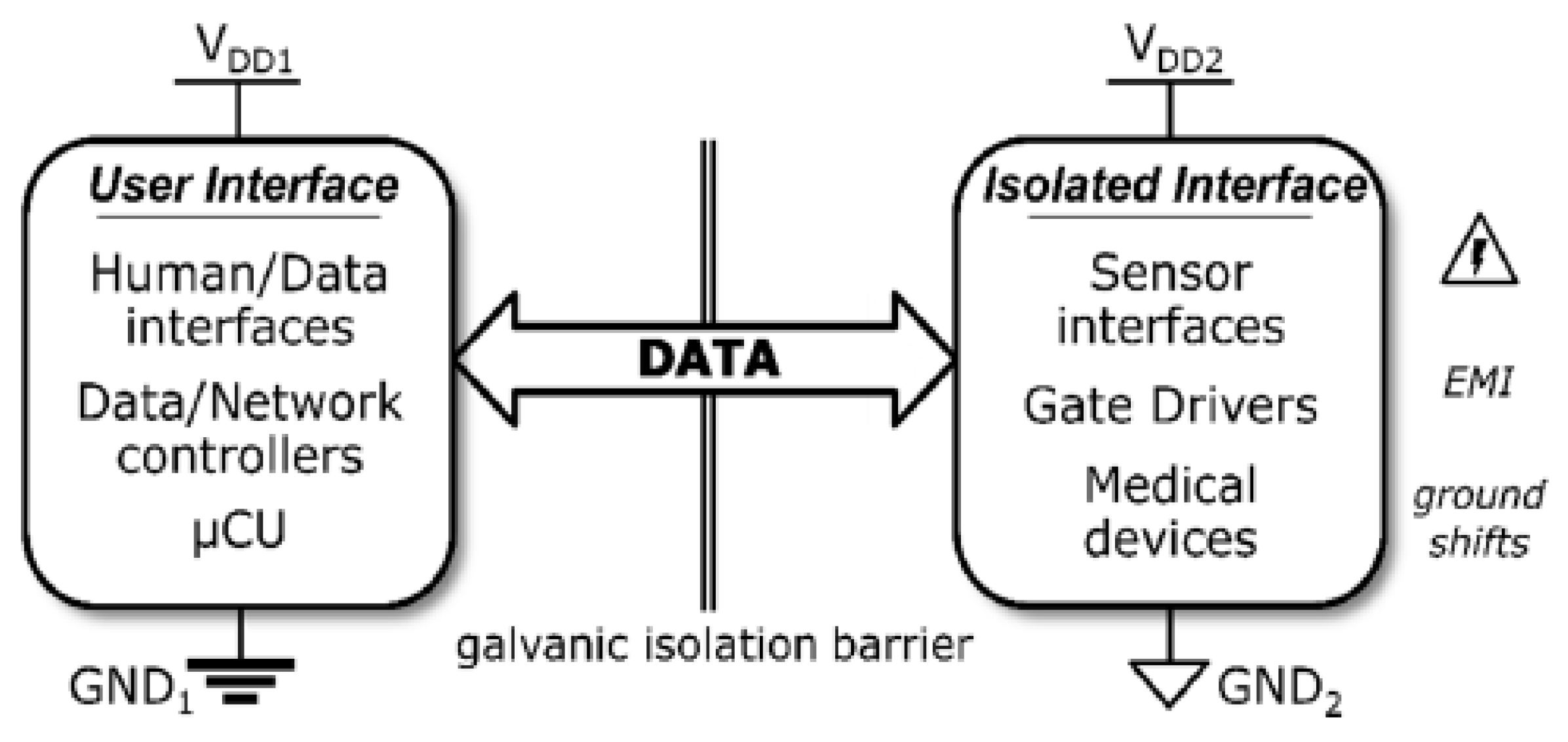
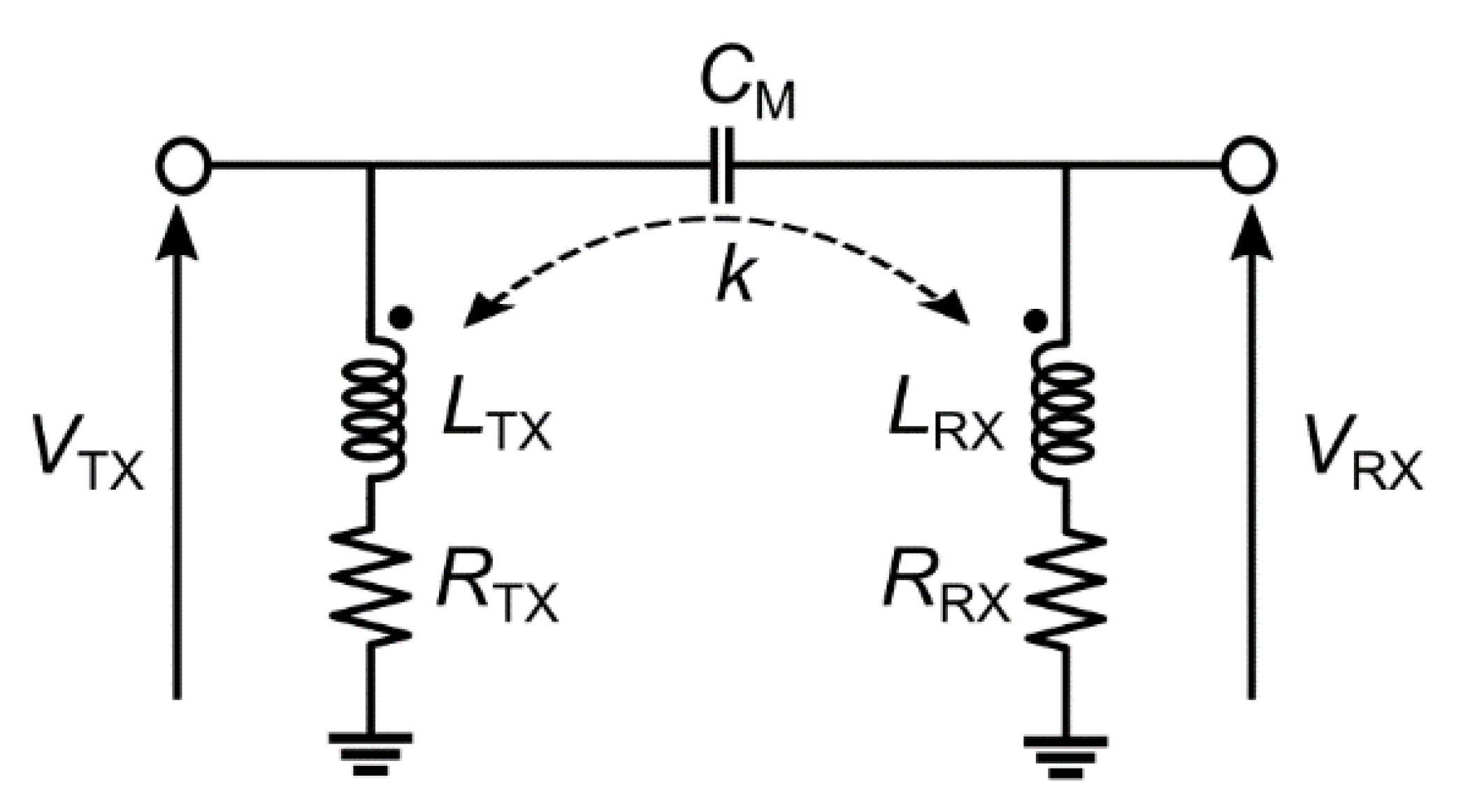
2.2. System Architecture and Circuit Description
2.3. On-Chip Micro-Antenna Design Guidelines
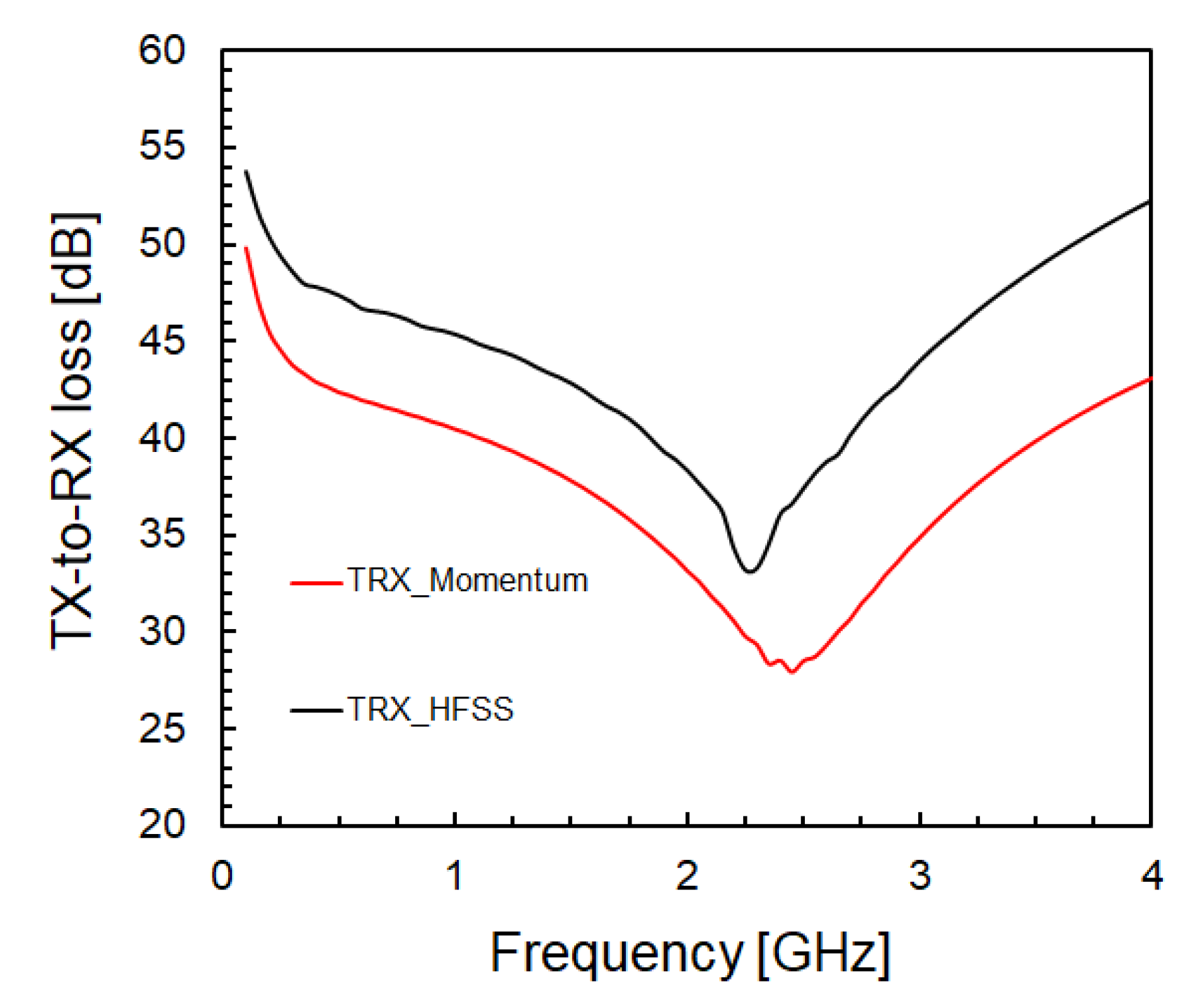
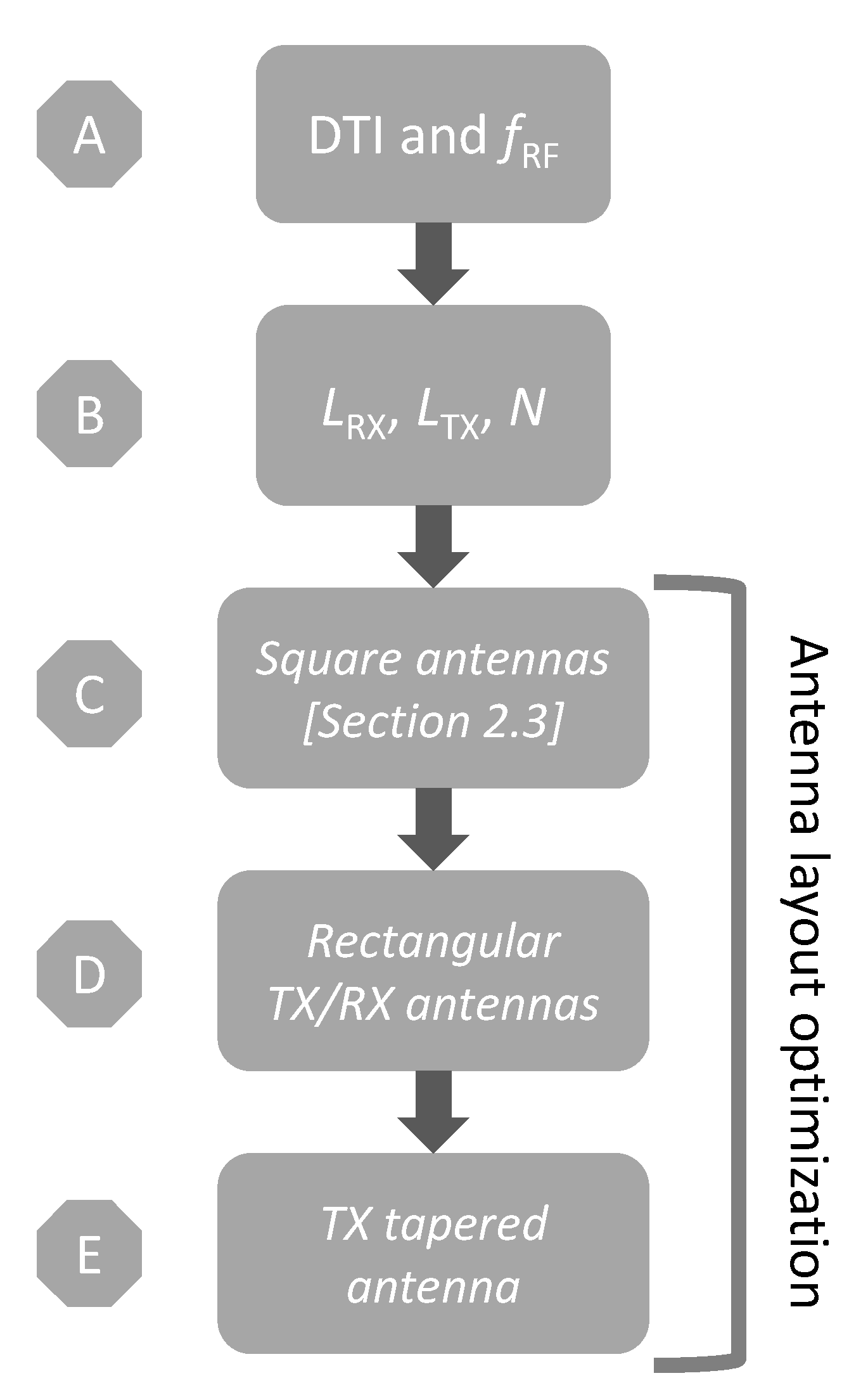
3. Micro-Antenna Optimization
3.1. On-Chip Micro-Antenna Design Guidelines
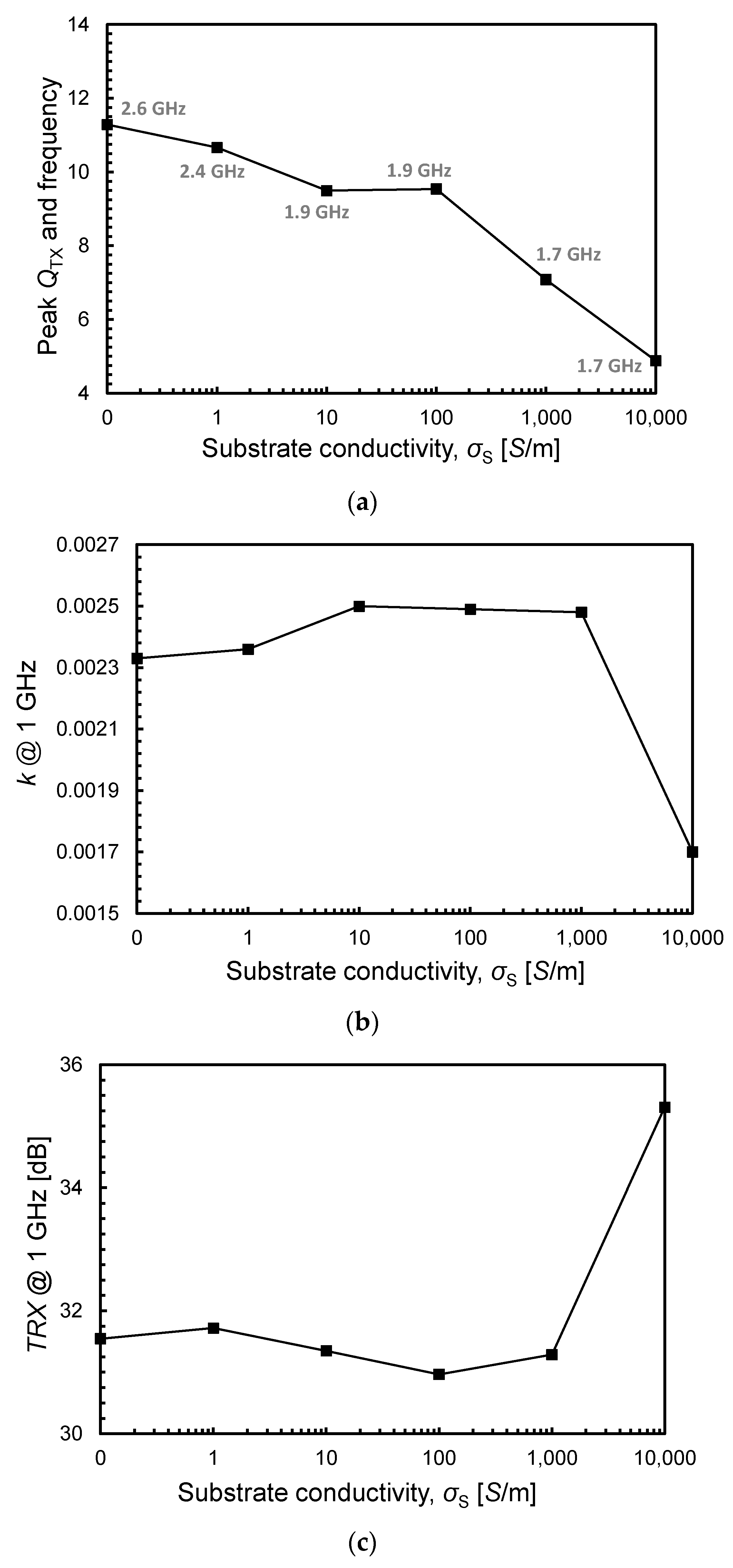
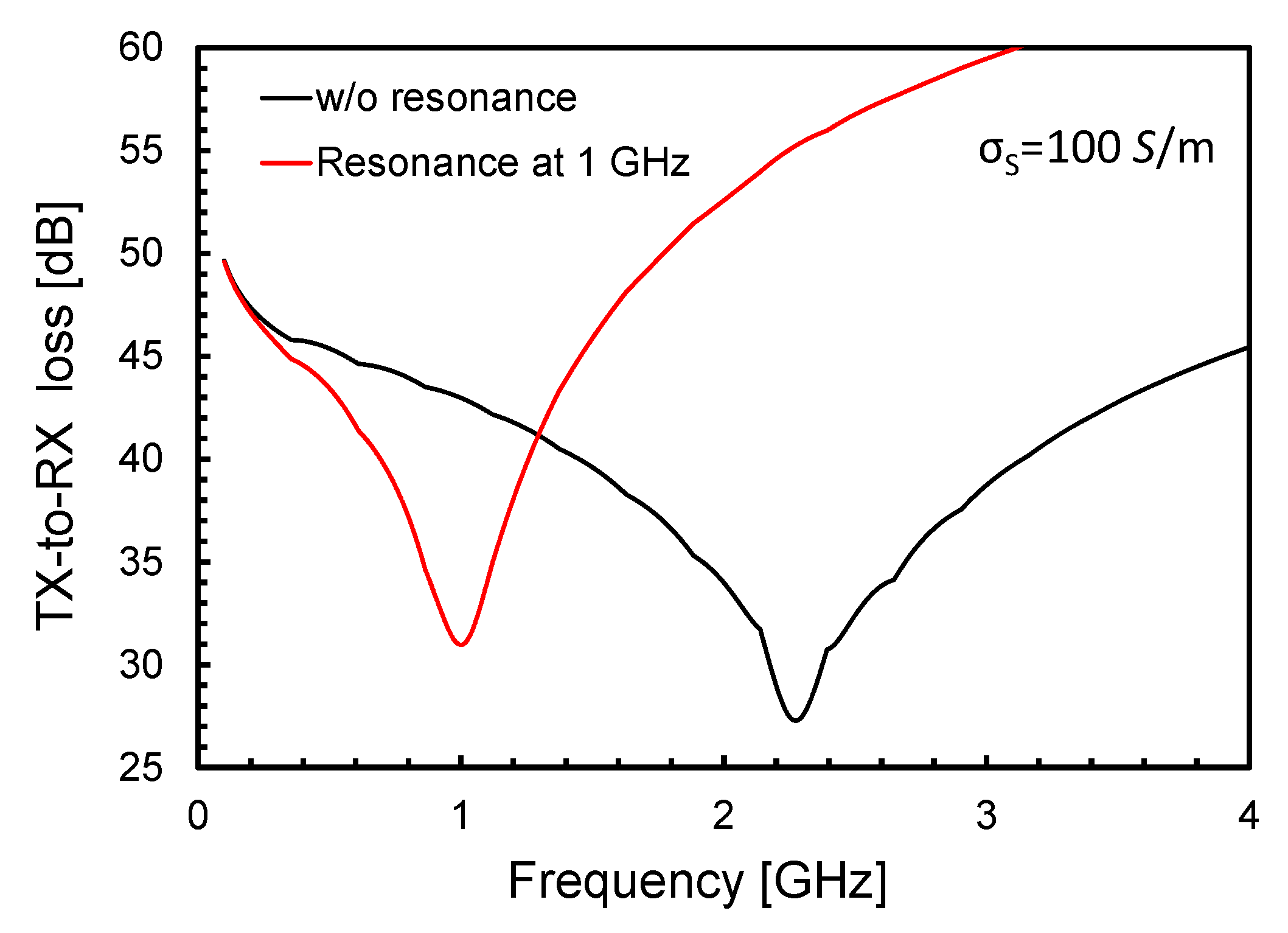
3.2. Optimization Flow for TX and RX Antennas
4. Conclusions
- (1)
- a significant improvement of the EM coupling in terms of magnetic coupling factor (i.e., 19% in the reported design example)
- (2)
- a consequent reduction of the TX-RX coupling loss (i.e., 1.7 dB in the reported design example).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- DIN VDE Semiconductor Devices-Magnetic and Capacitive Coupler for Basic and Reinforced Isolation, VDE Verlag VDE V 0884-11. January 2017. Available online: https://www.vde-verlag.de/standards/0800375/dinvde-v-0884-11-vde-v-0884-11-2017-01.html (accessed on 8 December 2021).
- Kazanbas, M.; Schittler, A.; Araújo, S.; Zacharias, P. High-Side Driving under High-Switching Speed: Technical Challenges and Testing Methods. In Proceedings of the PCIM Europe 2015; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 19–20 May 2015. [Google Scholar]
- Ragonese, E.; Palmisano, G.; Parisi, A.; Spina, N. Highly Integrated Galvanically Isolated Systems for Data/Power Transfer. In Proceedings of the 2019 26th IEEE International Conference on Electronics, Circuits and Systems, ICECS 2019, Genoa, Italy, 27–29 November 2019; pp. 518–521. [Google Scholar]
- Shi, G.; Yan, R.; Xi, J.; He, L.; Ding, W.; Pan, W.; Liu, Z.; Yang, F.; Chen, D. A Compact 6 Ns Propagation Delay 200 Mbps 100 KV/μs CMR Capacitively Coupled Direction Configurable 4-Channel Digital Isolator in Standard CMOS. In Proceedings of the 2018 25th IEEE International Conference on Electronics Circuits and Systems, ICECS 2018, Bordeaux, France, 9–12 December 2018; pp. 721–724. [Google Scholar]
- Texas Instruments. ISO7841x High-Performance, 8000-VPK Reinforced Quad-Channel Digital Isolator. Available online: http://www.ti.com (accessed on 8 December 2021).
- Fiore, V.; Ragonese, E.; Palmisano, G. A Fully Integrated Watt-Level Power Transfer System with On-Chip Galvanic Isolation in Silicon Technology. IEEE Trans. Power Electron. 2017, 32, 1984–1995. [Google Scholar] [CrossRef]
- Ragonese, E.; Spina, N.; Castorina, A.; Lombardo, P.; Greco, N.; Parisi, A.; Palmisano, G. A Fully Integrated Galvanically Isolated DC-DC Converter with Data Communication. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 1432–1441. [Google Scholar] [CrossRef]
- Erlbacher, T. Lateral Power Transistors in Integrated Circuits; Power Systems; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Moscatelli, A.; Merlini, A.; Croce, G.; Galbiati, P.; Contiero, C. LDMOS Implementation in a 0.35 Μm BCD Technology (BCD6). In Proceedings of the IEEE International Symposium on Power Semiconductor Devices and ICs (ISPSD), Toulouse, France, 22–25 May 2000; pp. 323–326. [Google Scholar]
- Riccardi, D.; Causio, A.; Filippi, I.; Paleari, A.; Pregnolato, L.V.A.; Galbiati, P.; Contiero, C. BCD8 from 7V to 70V: A New 0.18μm Technology Platform to Address the Evolution of Applications towards Smart Power ICs with High Logic Contents. In Proceedings of the International Symposium on Power Semiconductor Devices and ICs, Jeju, Island, 27–31 May 2007; pp. 73–76. [Google Scholar]
- Parisi, A.; Ragonese, E.; Spina, N.; Palmisano, G. Galvanically Isolated DC-DC Converter Using a Single Isolation Transformer for Multi-Channel Communication. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 4434–4444. [Google Scholar] [CrossRef]
- Chen, B. iCoupler® Products with isoPower™ Technology: Signal and Power Transfer across Isolation Barrier Using Microtransformers. Technical Article, Analog Devices, USA. Available online: http://www.analog.com/media/cn/technical-documentation/technical-articles/isoPower.pdf?doc=CN0185.pdf (accessed on 8 December 2021).
- Qin, W.; Yang, X.; Ma, S.; Liu, F.; Zhao, Y.; Zhao, T.; Chen, B. 15.5 An 800 mW Fully Integrated Galvanic Isolated Power Transfer System Meeting CISPR 22 Class-B Emission Levels with 6 dB Margin. In Proceedings of the Digest of Technical Papers—IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 17–21 February 2019; pp. 246–248. [Google Scholar]
- Tan, Z.; Mueck, M.; Du, X.H.; Getzin, L.; Guidry, M.; Keating, S.; Xing, X.; Zhao, F.; Chen, B. A Fully Isolated Delta-Sigma ADC for Shunt Based Current Sensing. IEEE J. Solid-State Circuits 2016, 51, 2232–2240. [Google Scholar] [CrossRef]
- Greco, N.; Parisi, A.; Lombardo, P.; Spina, N.; Ragonese, E.; Palmisano, G. A Double-Isolated DC-DC Converter Based on Integrated LC Resonant Barriers. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 4423–4433. [Google Scholar] [CrossRef]
- Mukherjee, S.; Bhat, A.N.; Shrivastava, K.A.; Bonu, M.; Sutton, B.; Gopinathan, V.; Thiagarajan, G.; Patki, A.; Malakar, J.; Krishnapura, N. A 500 Mb/s 200 pJ/b Die-to-Die Bidirectional Link with 24 kV Surge Isolation and 50 kV/Μs CMR Using Resonant Inductive Coupling in 0.18 µm CMOS. In Proceedings of the Digest of Technical Papers—IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 5–9 February 2017; Volume 60, pp. 434–435. [Google Scholar]
- Ragonese, E.; Spina, N.; Parisi, A.; Palmisano, G. Reinforced Galvanic Isolation: Integrated Approaches to Go Beyond 20-kV Surge Voltage (invited). In Applications in Electronics Pervading Industry, Environment and Society; Saponara, S., De Gloria, A., Eds.; ApplePies 2019. Lecture Notes in Electrical Engineering; Springer: Cham, Switzerland, 2020; Volume 627, pp. 277–283. [Google Scholar]
- Ragonese, E.; Spina, N.; Parisi, A.; Palmisano, G. A Cmos Data Transfer System Based on Planar RF Coupling for Reinforced Galvanic Isolation with 25-Kv Surge Voltage and 250-Kv/Μs CMTI. Electronics 2020, 9, 943. [Google Scholar] [CrossRef]
- Mahalingam, P.; Guiling, D.; Lee, S. Manufacturing Challenges and Method of Fabrication of On-Chip Capacitive Digital Isolators. In Proceedings of the 2007 International Symposium on Semiconductor Manufacturing, Santa Clara, CA, USA, 15–17 October 2007; pp. 1–4. [Google Scholar]
- Paye, J.; Claudi, A.; Stecher, M. High Voltage Robustness of Mold Compounds under Different Environmental Conditions. In Proceedings of the IEEE International Reliability Physics Symposium Proceedings, Monterey, CA, USA, 19–23 April 2015; pp. CP51–CP56. [Google Scholar]
- Paye, J.; Claudi, A.; Stecher, M. High Voltage Robustness of Mold Compounds after Different Treatments. In Proceedings of the 34th Electrical Insulation Conference, EIC 2016, Montreal, QC, Canada, 19–22 June 2016; pp. 162–165. [Google Scholar]
- Fanori, L.; Andreani, P. Class-D CMOS Oscillators. IEEE J. Solid-State Circuits 2013, 48, 3105–3119. [Google Scholar] [CrossRef]
- Fiore, V.; Ragonese, E.; Palmisano, G. Low-Power ASK Detector for Low Modulation Indexes and Rail-to-Rail Input Range. IEEE Trans. Circuits Syst. II Express Briefs 2016, 63, 458–462. [Google Scholar] [CrossRef]
- Spataro, S.; Ragonese, E. Design and Optimization of Silicon-Integrated Inductive Components for Automotive Radar Applications in k-and w-Bands. In Proceedings of the 2020 AEIT International Conference of Electrical and Electronic Technologies for Automotive, AEIT AUTOMOTIVE 2020, Turin, Italy, 18–20 November 2020. [Google Scholar]
- Chaki, S.; Aono, S.; Andoh, N.; Sasaki, Y.; Tanino, N.; Ishihara, O. Experimental Study on Spiral Inductors. In Proceedings of the 1995 IEEE MTT-S International Microwave Symposium, Orlando, FL, USA, 16–20 May 1995; Volume 2, pp. 753–756. [Google Scholar]
- Mohan, S.S. The Design, Modeling and Optimization of on Chip Inductor and Transformer Circuit. Ph.D. Thesis, Department of Electrical Engineering, Stanford University, Stanford, CA, USA, 1999. [Google Scholar]
- Craninckx, J.; Steyaert, M.S.J. A 1.8-GHz Low-Phase-Noise CMOS VCO Using Optimized Hollow Spiral Inductors. IEEE J. Solid-State Circuits 1997, 32, 736–744. [Google Scholar] [CrossRef] [Green Version]
- Mohan, S.S.; Hershenson, M.D.M.; Boyd, S.P.; Lee, T.H. Simple Accurate Expressions for Planar Spiral Inductances. IEEE J. Solid-State Circuits 1999, 34, 1419–1420. [Google Scholar] [CrossRef] [Green Version]
- McAndrew, C.C.; Lorenzo-Cassagnes, A.; Goyhenetche, P.; Pigott, J.; Yao, W.; Gildenblat, G.; Victory, J. Advances in LDMOS Compact Modeling for IC Design: The SP-HV Model and Its Capabilities. IEEE Solid-State Circuits Mag. 2014, 6, 35–46. [Google Scholar] [CrossRef]





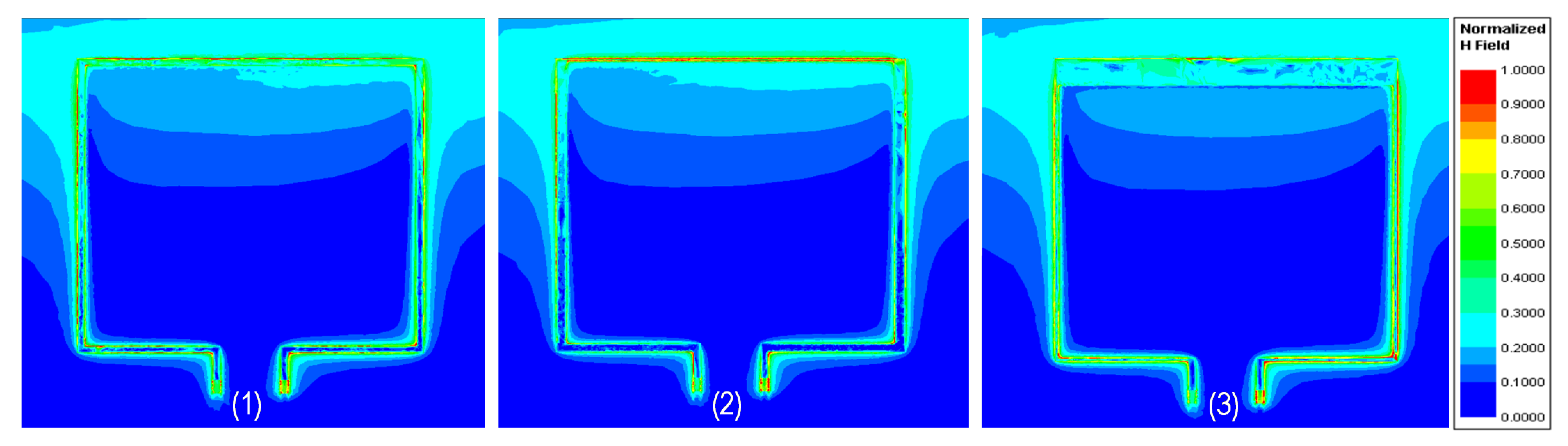
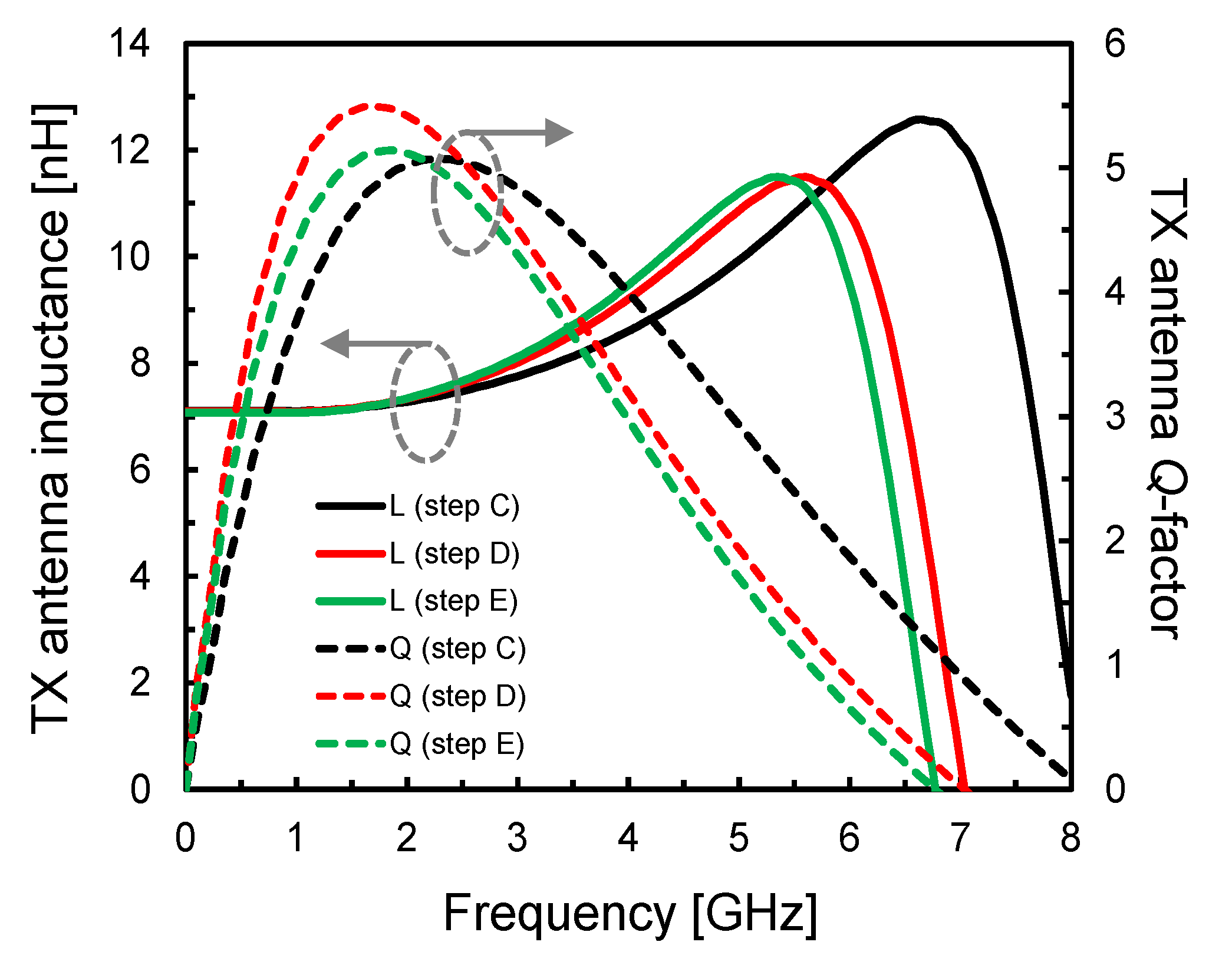
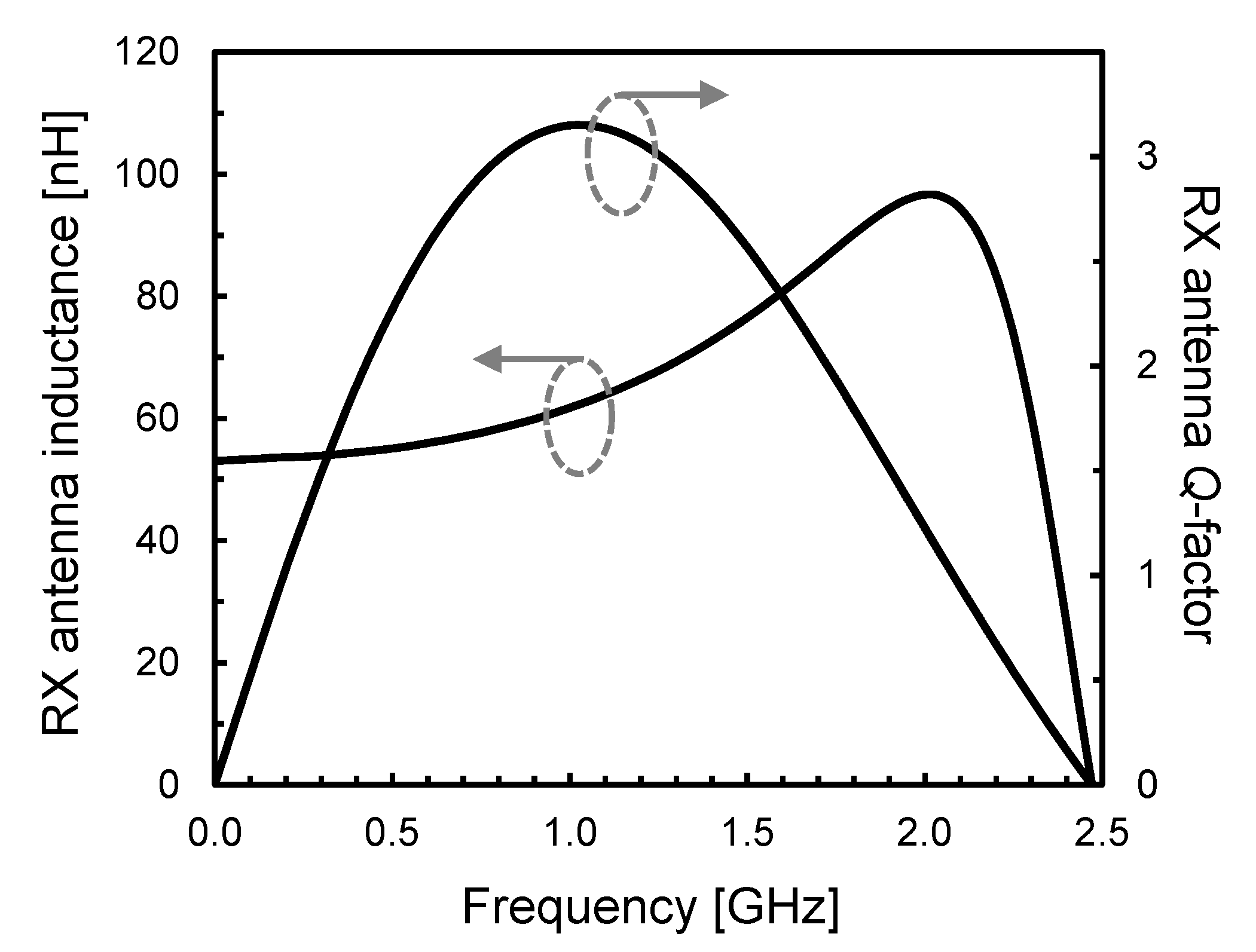

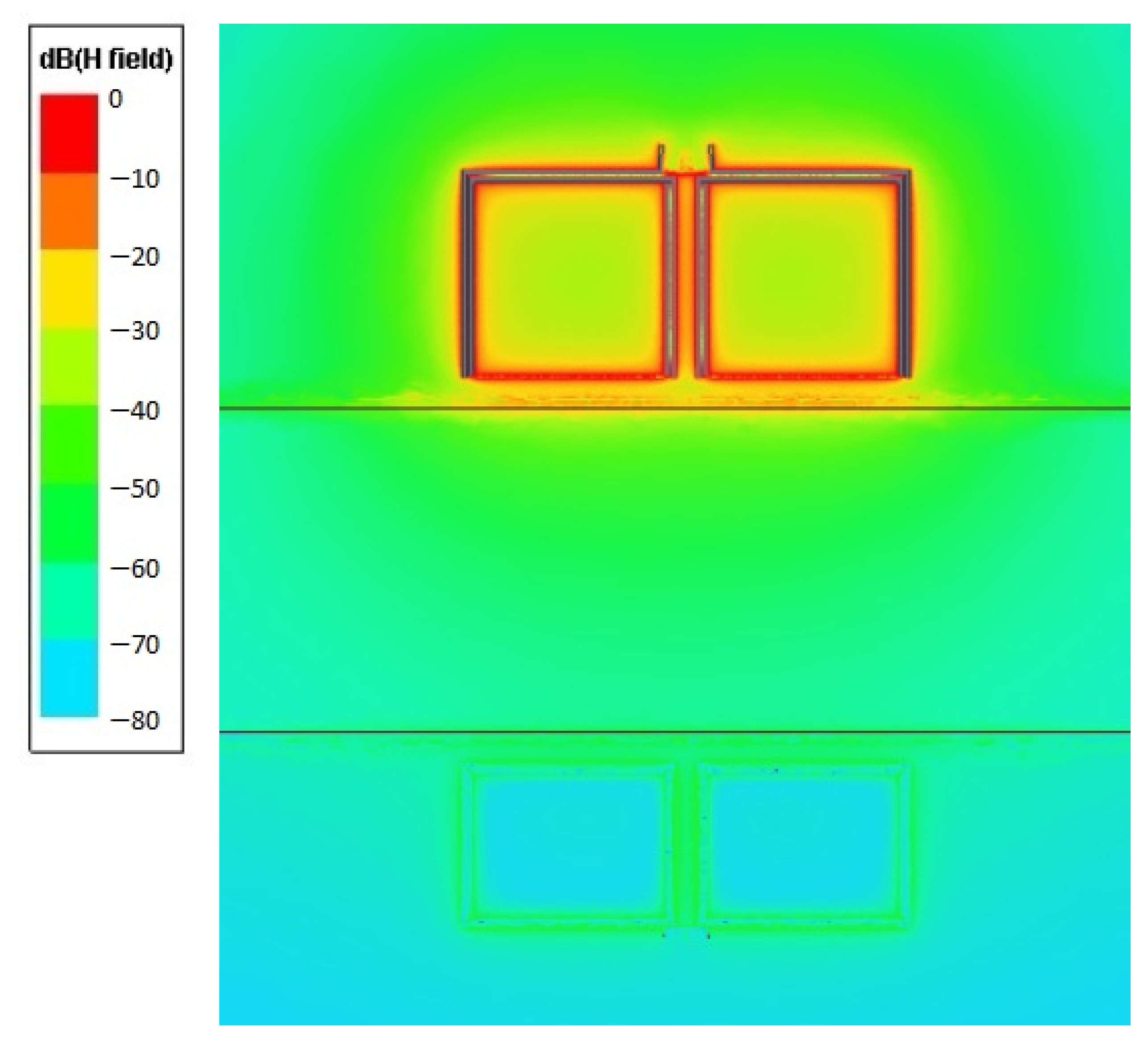
| Isolation Approach | Isolation Layer | No. Chips | Isolation Scale | Custom Technology | Modulation | Power | Design Flexibility | DTI [µm] | Isolation [kV] | CMTI [kV/μs] | Si Area |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Inductive | SiO2/Polyimide | 2/3 | Chip | Required | Impulsive/ Carrier-based OOK | YES | Low | 10–30 | 5–20 | 75–200 | Medium |
| Capacitive | SiO2/Polyimide | 2/3 | Chip | Required | Impulsive | NO | Low | 10–30 | 5–10 | 50–150 | Low |
| RF coupling | Molding compound | 2 | Package | Not required | Carrier-based OOK | NO | High | 300–700 | 10–25 | 200–250 | Medium/high |
| Antenna Layout | dout, max [μm] | TX Antenna | RX Antenna | ||||||
|---|---|---|---|---|---|---|---|---|---|
| AR | W [μm] | s [μm] | n | AR | w [μm] | s [μm] | n | ||
| C | 306 | 1 | 4 | 1.5 | 2 | 1 | 1.6 | 1.7 | 6 |
| D | 345 | 1.03 | 7 | 1.5 | 2 | 1.30 | 1.6 | 1.7 | 6 |
| E | 345 | 1.03 | 1.6 (*)/9.8 | 1.5 | 2 | 1.30 | 1.6 | 1.7 | 6 |
| Test Case | Geometrical Parameters | Electrical Parameters @ 8 GHz | ||||
|---|---|---|---|---|---|---|
| n | dIN [μm] | wMIN [μm] | wMAX [μm] | L [nH] | k | |
| 1 | 1 | 340 | 8 | 8 | 1.07 | 5.3 × 103 |
| 2 | 1 | 340 | 2 (*) | 11.4 | 1.08 | 5.7 × 103 |
| 3 | 1 | 340 | 4.6 | 32 (*) | 1.04 | 4.5 × 103 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spataro, S.; Spina, N.; Ragonese, E. Package-Scale Galvanic Isolators Based on Radio Frequency Coupling: Micro–Antenna Design. Electronics 2022, 11, 291. https://doi.org/10.3390/electronics11030291
Spataro S, Spina N, Ragonese E. Package-Scale Galvanic Isolators Based on Radio Frequency Coupling: Micro–Antenna Design. Electronics. 2022; 11(3):291. https://doi.org/10.3390/electronics11030291
Chicago/Turabian StyleSpataro, Simone, Nunzio Spina, and Egidio Ragonese. 2022. "Package-Scale Galvanic Isolators Based on Radio Frequency Coupling: Micro–Antenna Design" Electronics 11, no. 3: 291. https://doi.org/10.3390/electronics11030291
APA StyleSpataro, S., Spina, N., & Ragonese, E. (2022). Package-Scale Galvanic Isolators Based on Radio Frequency Coupling: Micro–Antenna Design. Electronics, 11(3), 291. https://doi.org/10.3390/electronics11030291







