Progress on Second-Generation High-Temperature Superconductor Tape Targeting Resistive Fault Current Limiter Application
Abstract
:1. Introduction
2. Experimental Details
2.1. Preparation of Samples
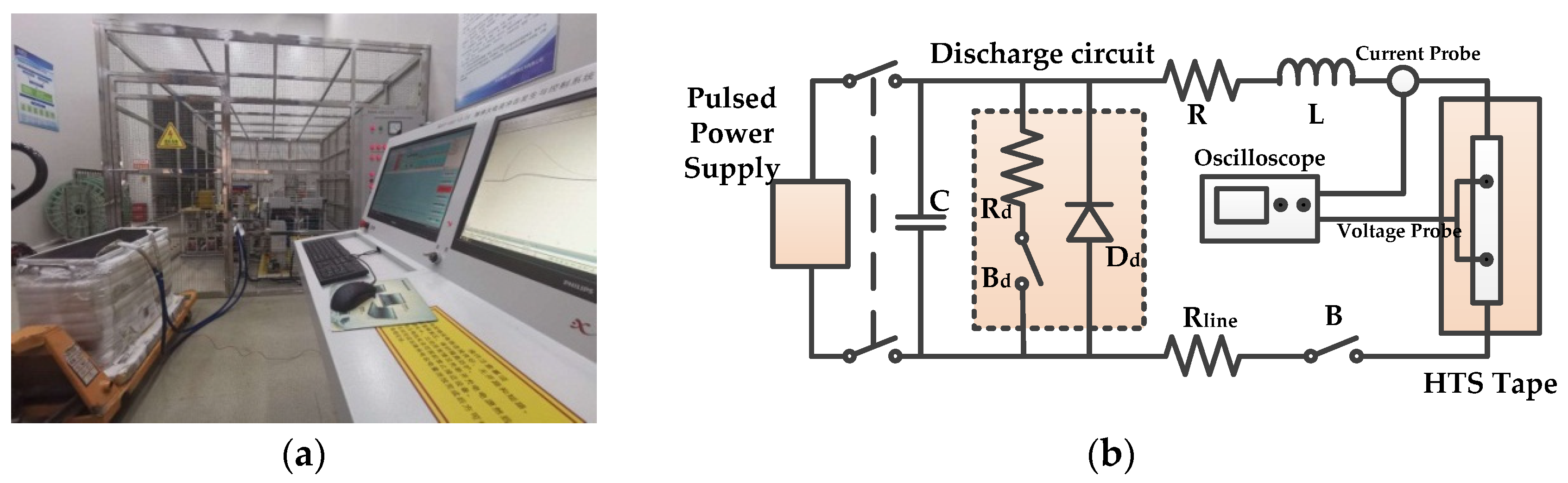
2.2. Test Platform
3. Results and Discussion
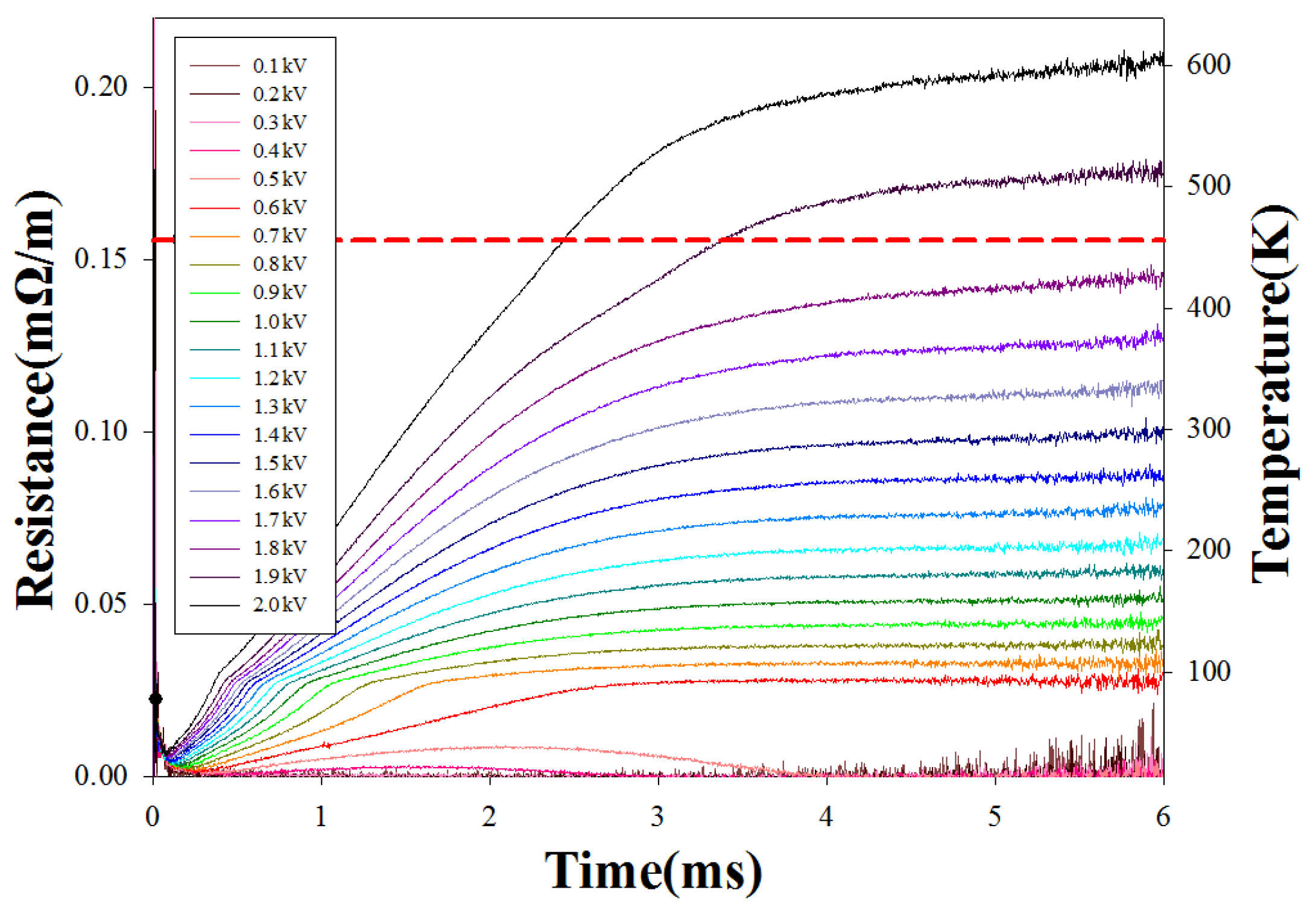
3.1. Experimental Results and Analysis for Typical Samples
3.2. Comparison of Impact Tolerance
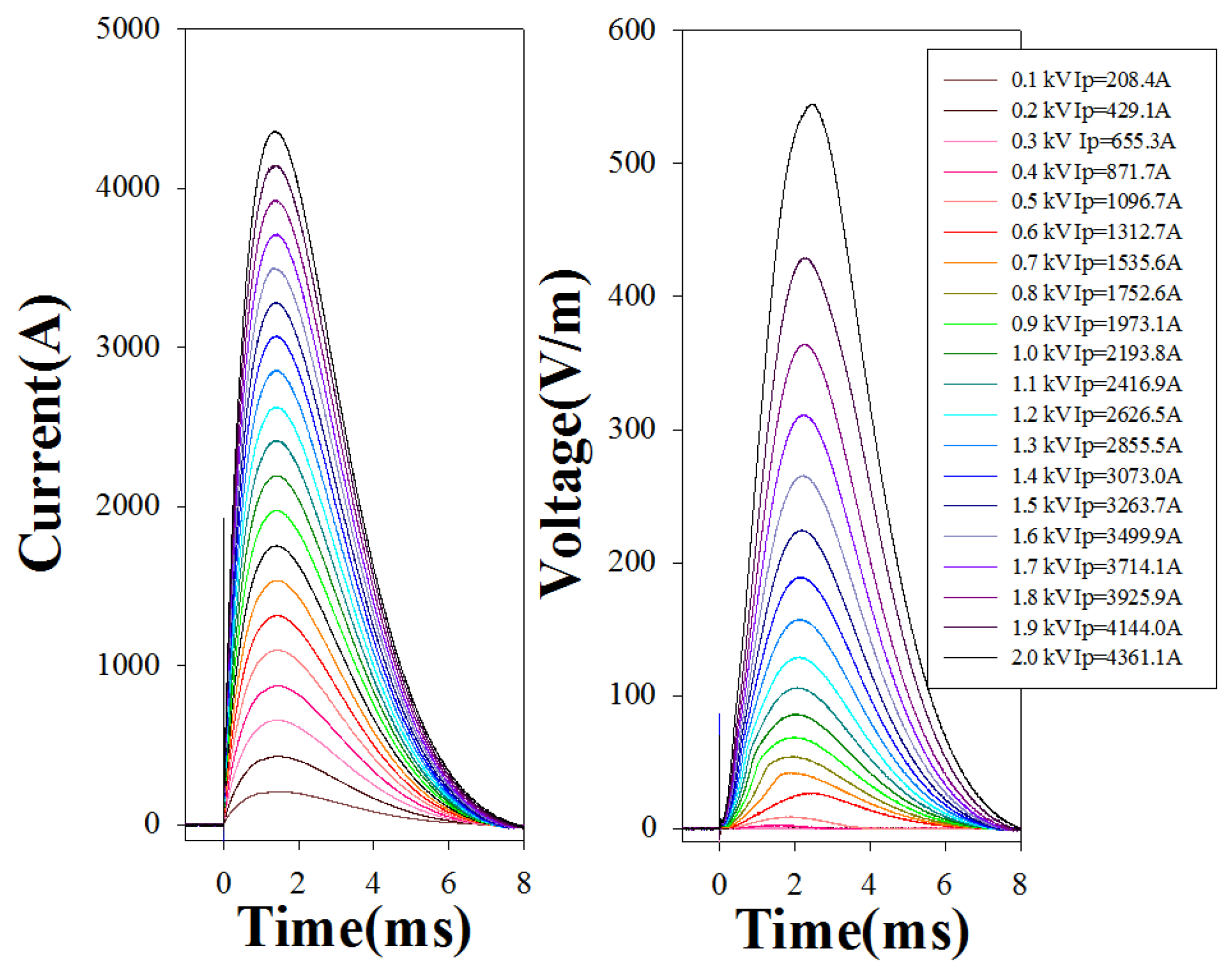
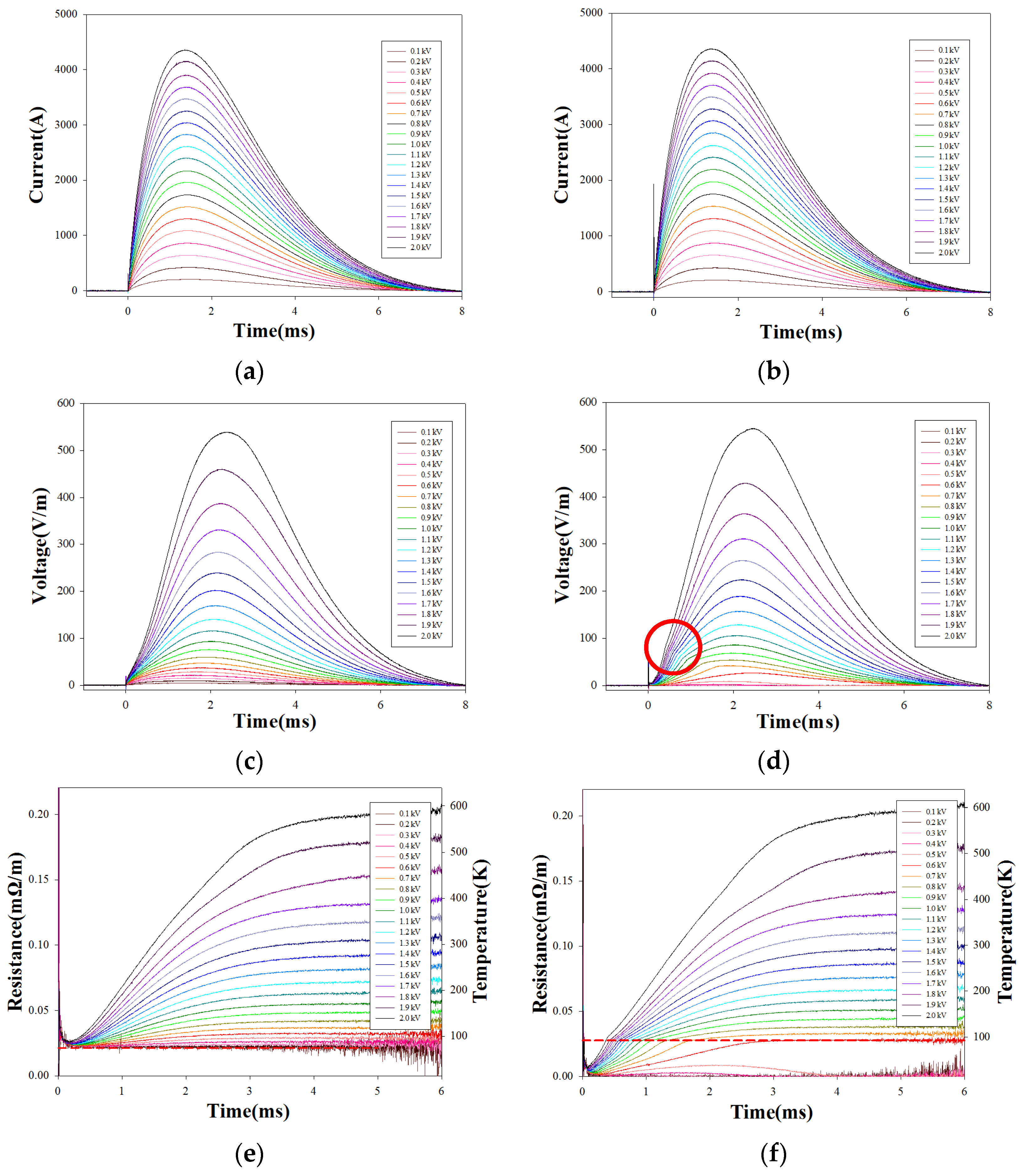
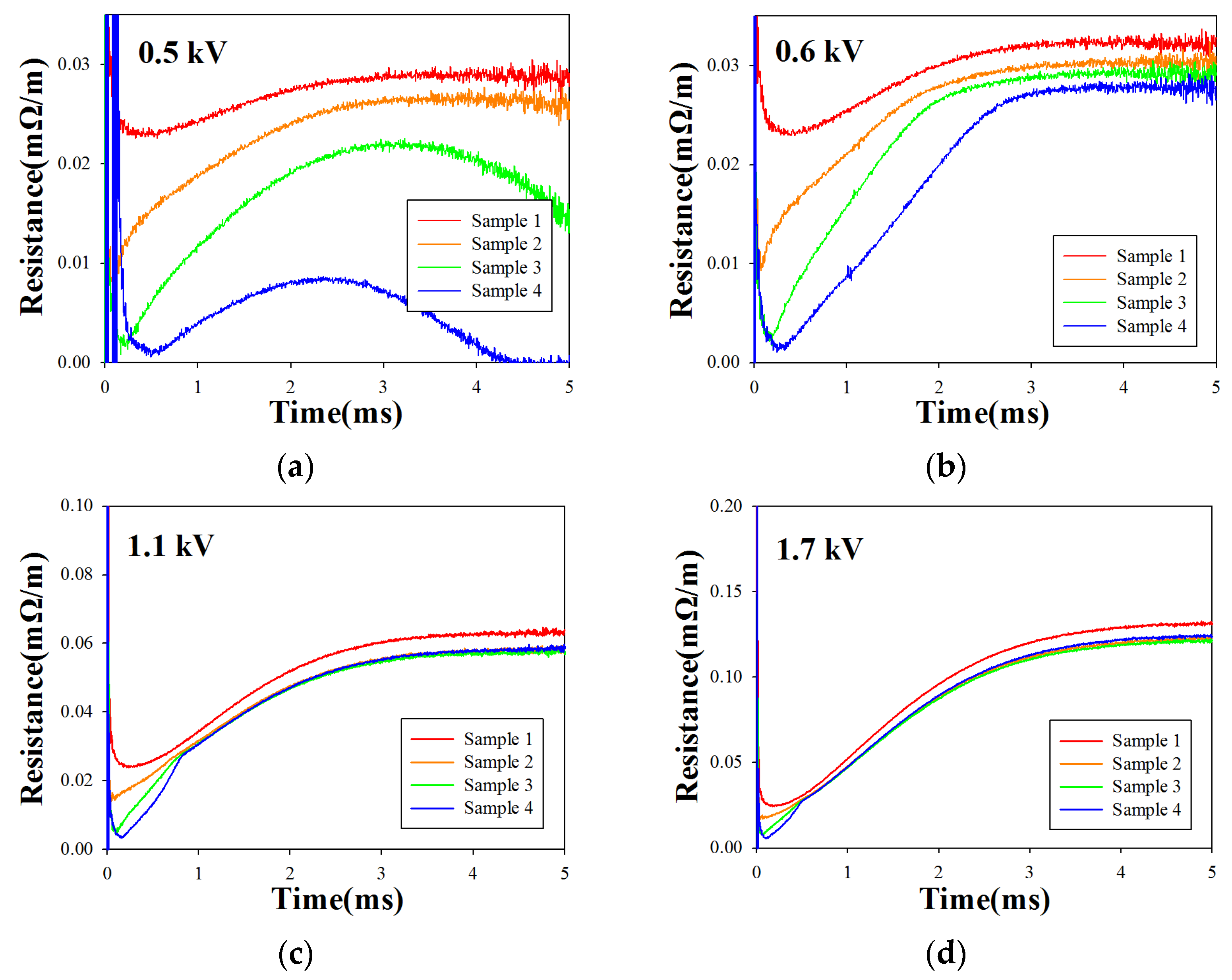
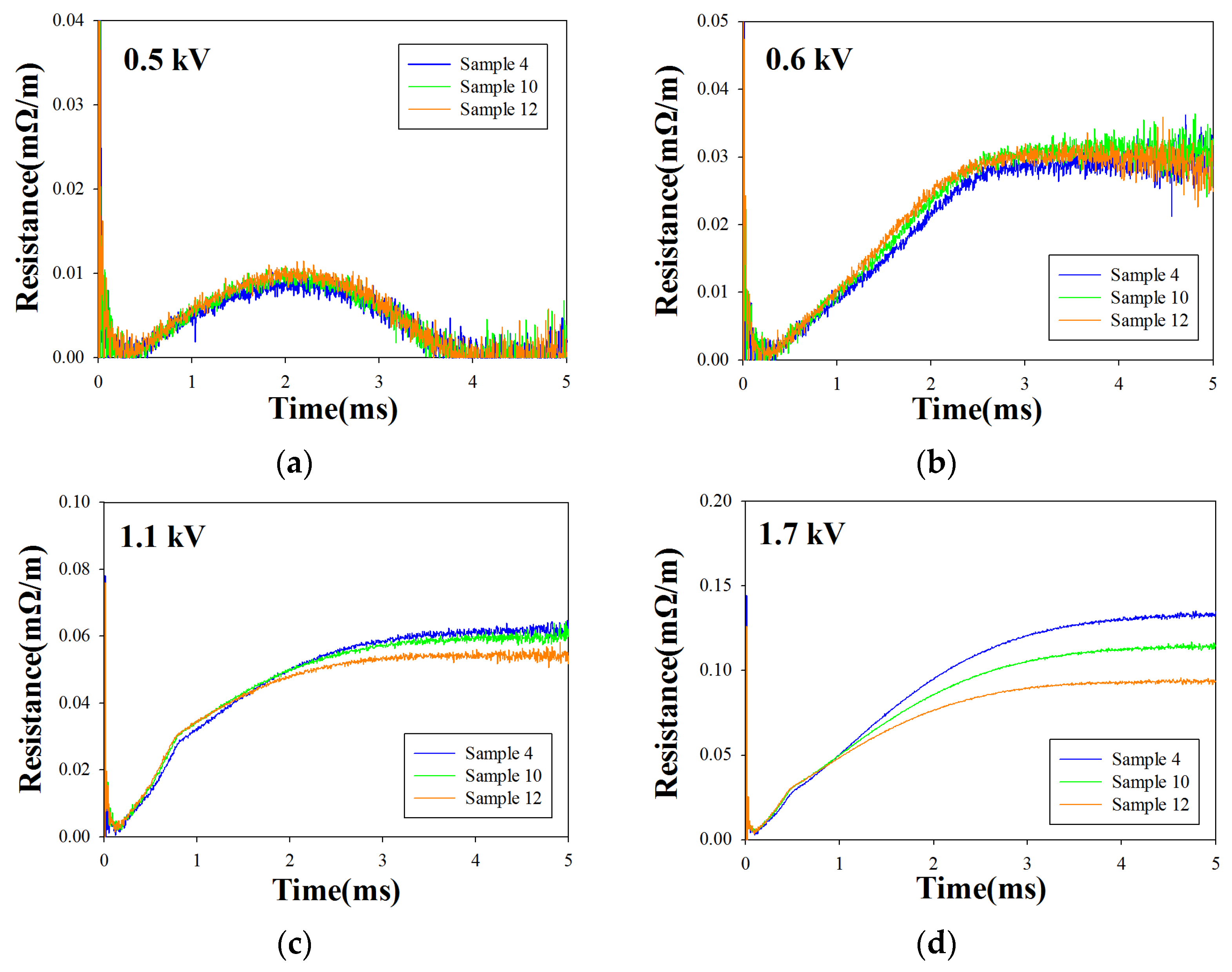
3.2.1. Effect of Critical Current of the HTS Tapes
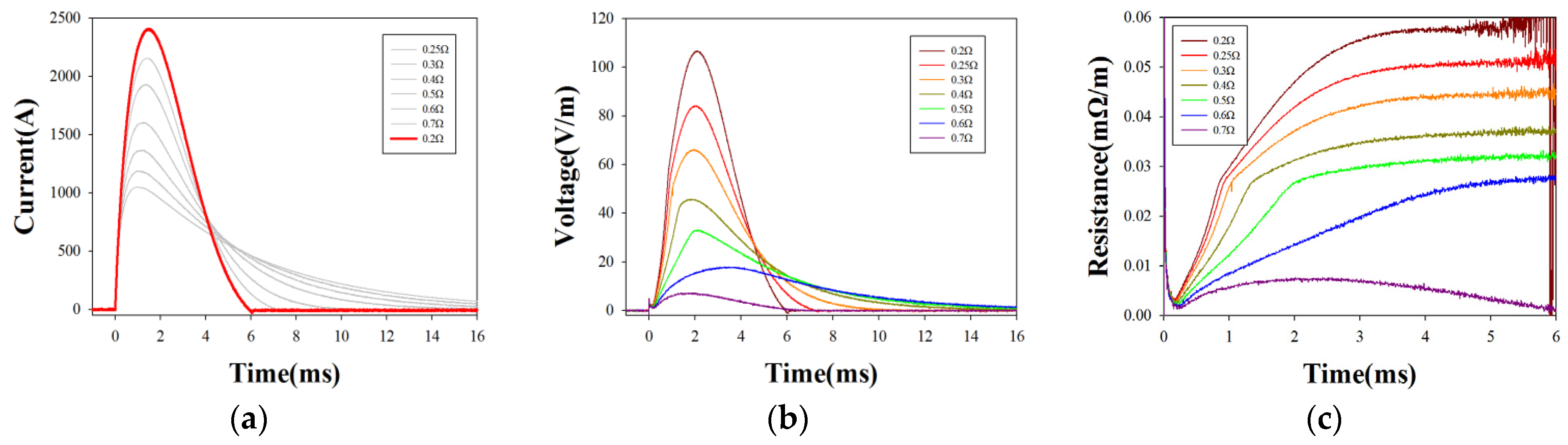
3.2.2. Effect of Room-Temperature Resistance of the HTS Tapes
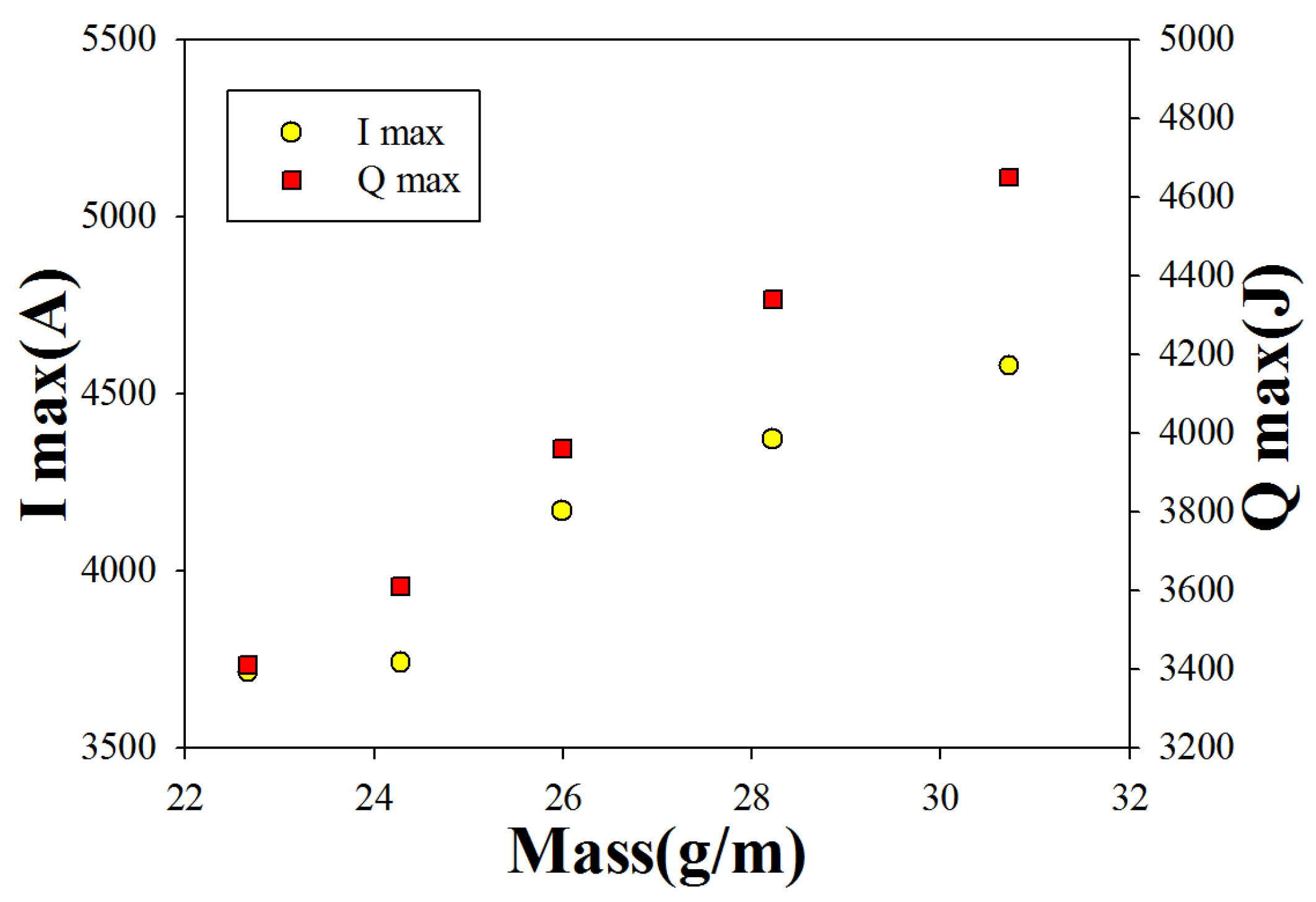
3.2.3. Effect of Mass of the HTS Tapes
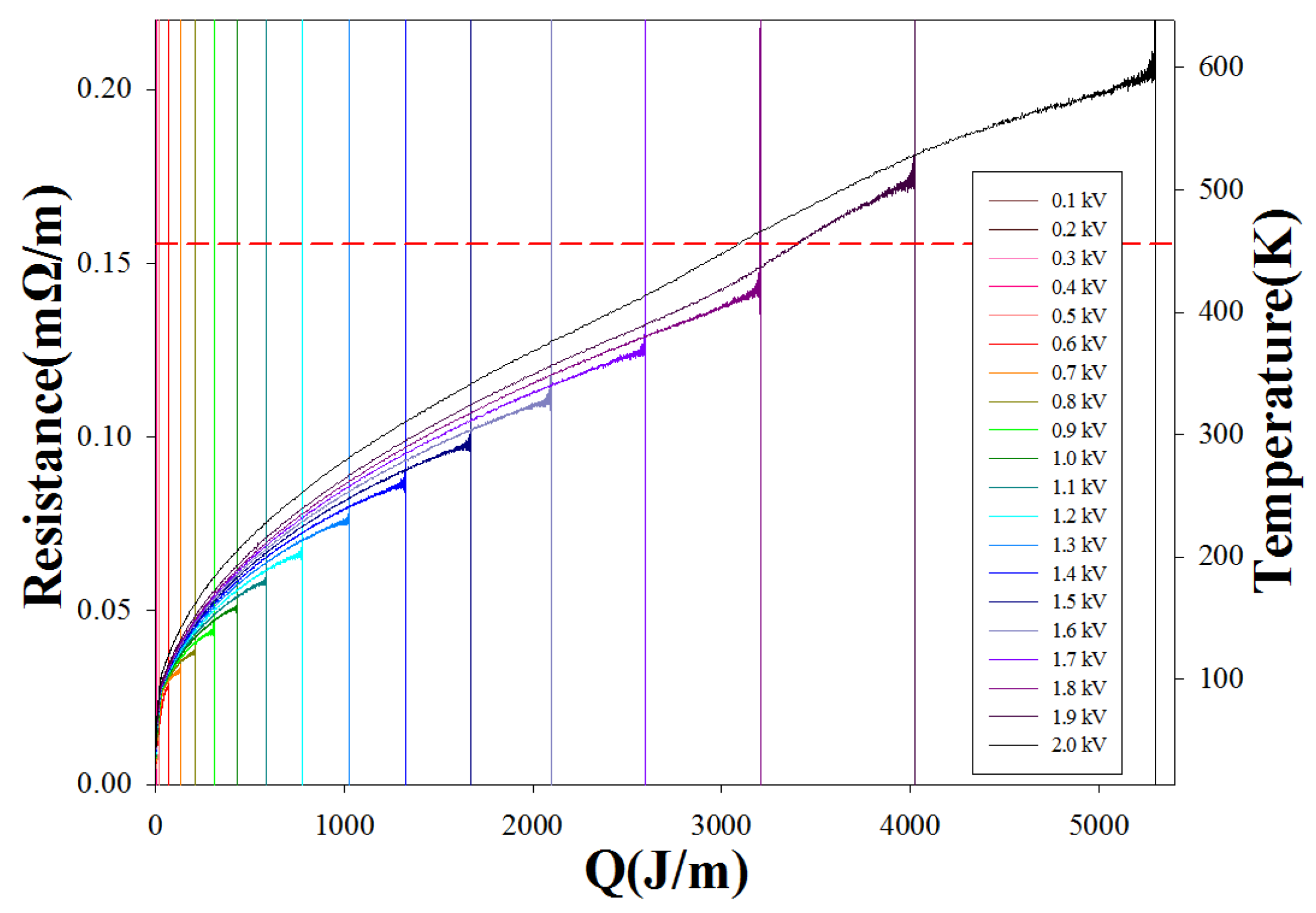
3.3. Resistance Response to Impulses
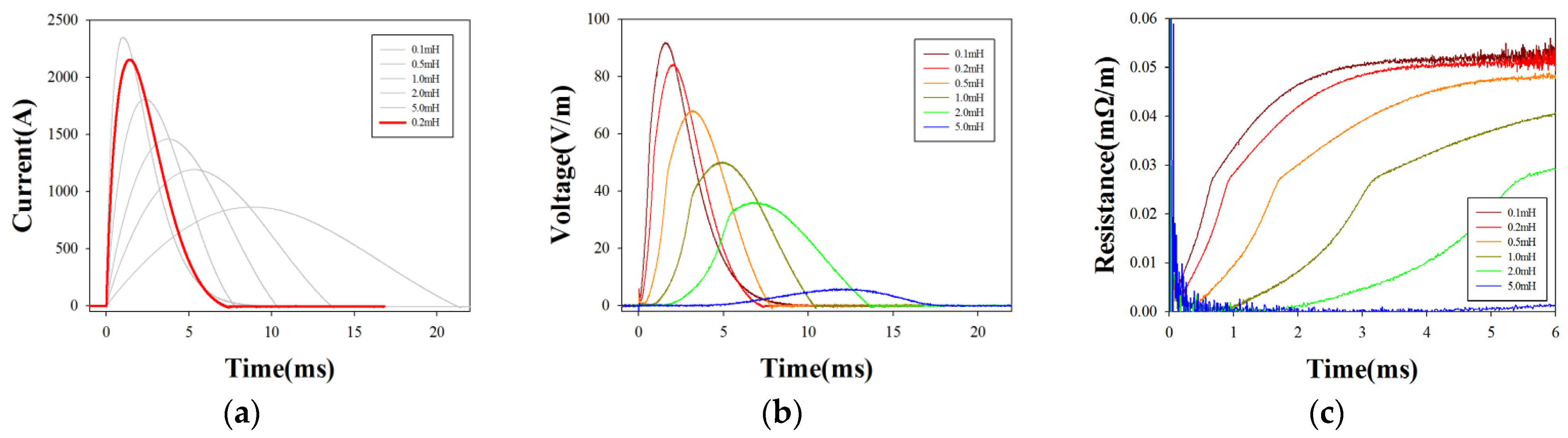
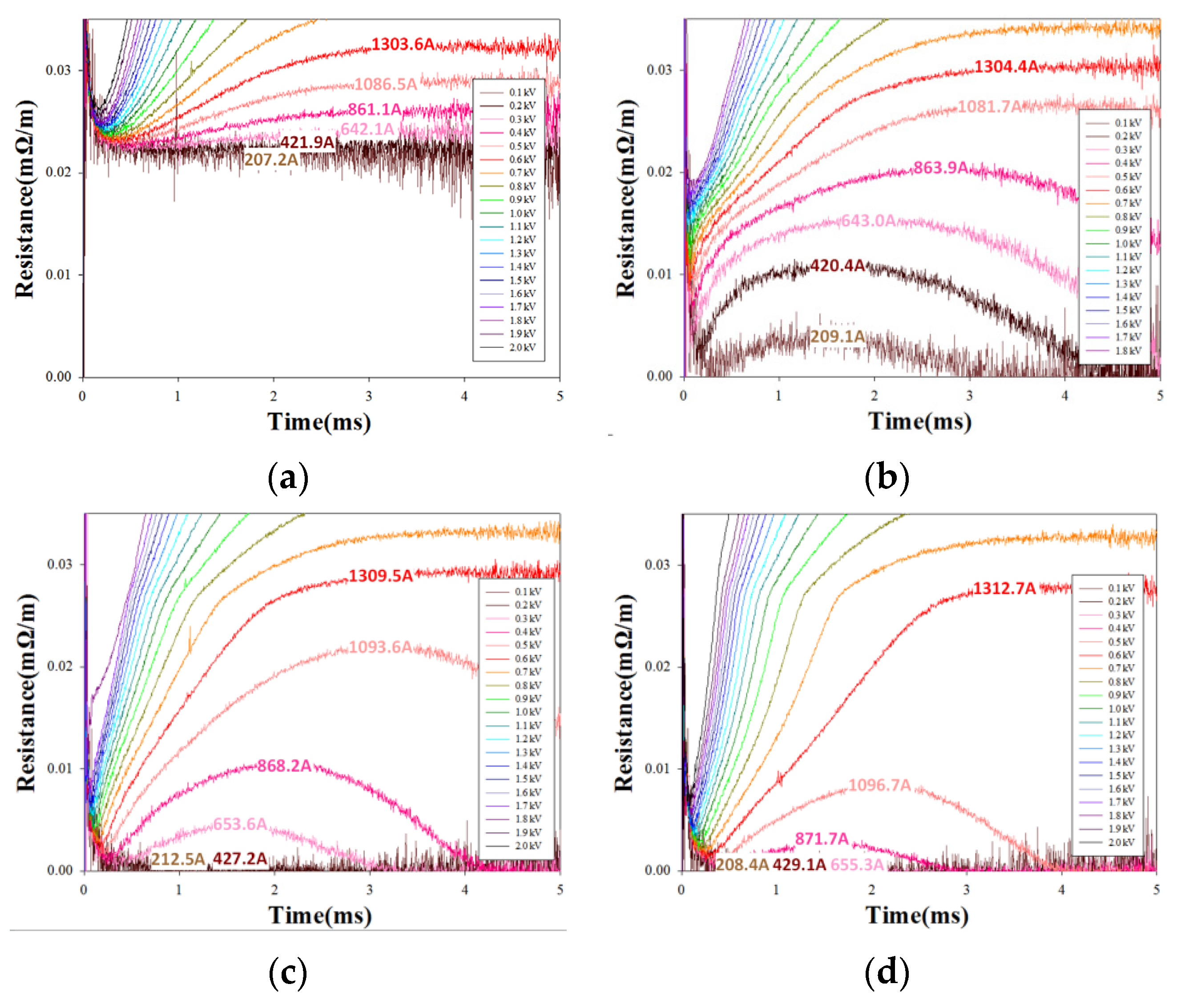
3.3.1. Impact of HTS Characteristics on Resistance Response to Impulses
3.3.2. Impact of Critical Current on Resistance Response to Impulses
3.3.3. Impact of Mass on Resistance Response to Impulses
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dommerque, R.; Krämer, S.; Hobl, A.; Böhm, R.; Bludau, M.; Bock, J.; Klaus, D.; Piereder, H.; Wilson, A.; Krüger, T.; et al. First commercial medium voltage superconducting fault-current limiters: Production, test and installation. Supercond. Sci. Technol. 2010, 23, 034020. [Google Scholar] [CrossRef] [Green Version]
- Hobl, A.; Elschner, S.; Bock, J.; Kramer, S.; Janke, C.; Schramm, J. Superconducting fault current limiters: A new tool for the “grid of the future”. In Proceedings of the CIRED 2012 Workshop: Integration of Renewables into the Distribution Grid, Lisbon, Portugal, 9–30 May 2012. [Google Scholar]
- Stemmle, M.; Merschel, F.; Noe, M.; Hobl, A. AmpaCity—Advanced superconducting medium voltage system for urban area power supply. In Proceedings of the 2014 IEEE PES T&D Conference and Exposition, Chicago, IL, USA, 14–17 April 2014. [Google Scholar]
- McGuckin, P.; Burt, G. Overview and assessment of superconducting technologies for power grid applications. In Proceedings of the 2018 53rd International Universities Power Engineering Conference (UPEC), Glasgow, UK, 4–7 September 2018. [Google Scholar]
- Safaei, A.; Zolfaghari, M.; Gilvanejad, M.; Gharehpetian, G.B. A survey on fault current limiters: Development and technical aspects. Int. J. Electr. Power Energy Syst. 2020, 118, 105729. [Google Scholar] [CrossRef]
- Rupich, M.W.; Li, X.; Sathyamurthy, S.; Thieme, C.L.; DeMoranville, K.; Gannon, J.; Fleshler, S. Second generation wire development at AMSC. IEEE Trans. Appl. Supercond. 2012, 23, 6601205. [Google Scholar] [CrossRef]
- Selvamanickam, V.; Chen, Y.; Xiong, X.; Xie, Y.Y.; Reeves, J.L.; Zhang, X.; Qiao, Y.; Lenseth, K.P.; Schmidt, R.M.; Rar, A.; et al. Recent progress in second-generation HTS conductor scale-up at SuperPower. IEEE Trans. Appl. Supercond. 2007, 17, 3231–3234. [Google Scholar] [CrossRef]
- Usoskin, A.; Betz, U.; Gnilsen, J.; Noll-Baumann, S.; Schlenga, K. Long-length YBCO coated conductors for ultra-high field applications: Gaining engineering current density via pulsed laser deposition/alternating beam-assisted deposition route. Supercond. Sci. Technol. 2019, 32, 094005. [Google Scholar] [CrossRef]
- Stafford, B.H.; Sieger, M.; Ottolinger, R.; Meledin, A.; Strickland, N.M.; Wimbush, S.C.; Van Tendeloo, G.; Hühne, R.; Schultz, L. Tilted BaHfO3 nanorod artificial pinning centres in REBCO films on inclined substrate deposited-MgO coated conductor templates. Supercond. Sci. Technol. 2017, 30, 055002. [Google Scholar] [CrossRef]
- Molodyk, A.; Samoilenkov, S.; Markelov, A.; Degtyarenko, P.; Lee, S.; Petrykin, V.; Gaifullin, M.; Mankevich, A.; Vavilov, A.; Sorbom, B.; et al. Development and large volume production of extremely high current density YBa2Cu3O7 superconducting wires for fusion. Sci. Rep. 2021, 11, 2084. [Google Scholar] [CrossRef] [PubMed]
- Fujita, S.; Muto, S.; Hirata, W.; Yoshida, T.; Kakimoto, K.; Iijima, Y.; Daibo, M.; Kiss, T.; Okada, T.; Awaji, S. Flux-pinning properties of BaHfO 3-doped EuBCO-coated conductors fabricated by hot-wall PLD. IEEE Trans. Appl. Supercond. 2019, 29, 8001505. [Google Scholar] [CrossRef]
- Lee, J.H.; Lee, H.; Lee, J.W.; Choi, S.M.; Yoo, S.I.; Moon, S.H. RCE-DR, a novel process for coated conductor fabrication with high performance. Supercond. Sci. Technol. 2014, 27, 044018. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhu, J.M.; Jiang, G.Y.; Chen, C.S.; Wu, W.; Zhang, Z.W.; Chen, S.; Hong, Y.; Hong, Z.; Jin, A.; et al. Progress in fabrication of second generation high temperature superconducting tape at Shanghai Superconductor Technology. Supercond. Sci. Technol. 2019, 32, 044004. [Google Scholar] [CrossRef]
- Bock, J.; Hobl, A.; Schramm, J.; Krämer, S.; Jänke, C. Resistive superconducting fault current limiters are becoming a mature technology. IEEE Trans. Appl. Supercond. 2014, 25, 5600604. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, H.; Qiu, Q.; Zhang, Z.; Xiao, L.; Lin, L. Recent progress of superconducting fault current limiter in China. Supercond. Sci. Technol. 2020, 34, 013001. [Google Scholar] [CrossRef]
- Neumueller, H.W.; Schmidt, W.; Kraemer, H.P.; Otto, A.; Maguire, J.; Yuan, J.; Folts, D.; Romanosky, W.; Gamble, B.; Madura, D.; et al. Development of resistive fault current limiters based on YBCO coated conductors. IEEE Trans. Appl. Supercond. 2009, 19, 1950–1955. [Google Scholar] [CrossRef]
- Kraemer, H.P.; Schmidt, W.; Cai, H.; Gamble, B.; Madura, D.; MacDonald, T.; McNamara, J.; Romanosky, W.; Snitchler, G.; Lallouet, N.; et al. Superconducting fault current limiter for transmission voltage. Phys. Procedia 2012, 36, 921–926. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.R.; Lee, J.J.; Yoon, J.; Kang, Y.W.; Hur, J. Protection scheme of a 154-kV SFCL test transmission line at the KEPCO power testing center. IEEE Trans. Appl. Supercond. 2017, 27, 5401305. [Google Scholar] [CrossRef]
- Lee, S.R.; Ko, E.Y.; Lee, J.J.; Dinh, M.C. Development and HIL Testing of a Protection System for the Application of 154-kV SFCL in South Korea. IEEE Trans. Appl. Supercond. 2019, 29, 5401305. [Google Scholar] [CrossRef]
- Moyzykh, M.; Gorbunova, D.; Ustyuzhanin, P.; Sotnikov, D.; Baburin, K.; Maklakov, A.; Magommedov, E.; Shumkov, A.; Telnova, A.; Shcherbakov, V.; et al. First Russian 220 kV superconducting fault current limiter (SFCL) for application in city grid. IEEE Trans. Appl. Supercond. 2021, 31, 5601707. [Google Scholar] [CrossRef]
- Hong, Z.; Sheng, J.; Zhang, J.; Lin, B.; Ying, L.; Li, Y.; Jin, Z. The development and performance test of a 10 kV resistive type superconducting fault current limiter. IEEE Trans. Appl. Supercond. 2011, 22, 5600504. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, X.; Sheng, J.; Cai, L.; Jin, Z.; Gu, J.; An, Z.; Yang, X.; Hong, Z. Design and application of a superconducting fault current limiter in DC systems. IEEE Trans. Appl. Supercond. 2013, 24, 5601305. [Google Scholar] [CrossRef]
- Dai, S.; Ma, T.; Xue, C.; Zhao, L.; Huang, Y.; Hu, L.; Wang, B.; Zhang, T.; Xu, X.; Cai, L.; et al. Development and test of a 220 kV/1.5 kA resistive type superconducting fault current limiter. Phys. C Supercond. Its Appl. 2019, 565, 1253501. [Google Scholar] [CrossRef]
- Song, M.; Dai, S.; Sheng, C.; Zhong, L.; Duan, X.; Yan, G.; Huang, Y.; Chen, C.; Li, L.; Cai, L.; et al. Design and performance tests of a 160 kV/1.0 kA DC superconducting fault current limiter. Phys. C Supercond. Its Appl. 2021, 585, 1353871. [Google Scholar] [CrossRef]
- Llambes, J.C.; Hazelton, D.; Duval, J.; Albertini, M.; Repnoy, S.; Selvamanickam, V.; Majkic, G.; Kesign, I.; Langston, J.; Steurer, M.; et al. Performance of 2G HTS tapes in sub-cooled LN2 for superconducting fault current limiting applications. IEEE Trans. Appl. Supercond. 2011, 21, 1206–1208. [Google Scholar] [CrossRef]
- Hajdasz, S.; Kempski, A.; Rusinski, J. Study of HTS 2G superconductor tapes properties for applications in SFCL. In Proceedings of the 2018 Innovative Materials and Technologies in Electrical Engineering, Sulecin, Poland, 18–20 April 2018. [Google Scholar]
- Schmidt, W.; Gamble, B.; Kraemer, H.P.; Madura, D.; Otto, A.; Romanosky, W. Design and test of current limiting modules using YBCO-coated conductors. Supercond. Sci. Technol. 2009, 23, 014024. [Google Scholar] [CrossRef]
- Baldan, C.A.; Shigue, C.Y.; Lamas, J.S.; Ruppert Filho, E. Test results of a superconducting fault current limiter using YBCO coated conductor. IEEE Trans. Appl. Supercond. 2007, 17, 1903–1906. [Google Scholar] [CrossRef]
- Baldan, C.A.; Lamas, J.S.; Shigue, C.Y.; Ruppert Filho, E. Fault current limiter using YBCO coated conductor—The limiting factor and its recovery time. IEEE Trans. Appl. Supercond. 2009, 19, 1810–1813. [Google Scholar] [CrossRef]
- Ahn, M.C.; Yang, S.E.; Park, D.K.; Kang, H.; Seok, B.Y.; Ko, T.K. Current limiting characteristics of coated conductors with various stabilizers. Cryogenics 2007, 47, 425–430. [Google Scholar] [CrossRef]
- Park, D.K.; Kim, M.J.; Yang, S.E.; Kim, Y.J.; Chang, K.S.; Na, J.B.; Ko, T.K. A study on the short circuit characteristic of metallic stabilizer free coated conductor for FCL application. Prog. Supercond. Cryog. 2007, 9, 37–40. [Google Scholar]
- Sheng, J.; Zeng, W.; Ma, J.; Yao, Z.; Li, Z.; Jin, Z.; Hong, Z. Study of recovery characteristics of 2nd generation HTS tapes with different stabilizers for resistive type superconducting fault current limiters. Phys. C Supercond. Its Appl. 2016, 521, 33–37. [Google Scholar] [CrossRef]
- Lacroix, C.; Sirois, F. Concept of a current flow diverter for accelerating the normal zone propagation velocity in 2G HTS coated conductors. Supercond. Sci. Technol. 2014, 27, 035003. [Google Scholar] [CrossRef]
- Lacroix, C.; Lapierre, Y.; Coulombe, J.; Sirois, F. High normal zone propagation velocity in 2G HTS coated conductors with a current flow diverter architecture. Supercond. Sci. Technol. 2014, 27, 055013. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, J.; Qiu, Q.; Zhang, G.; Lin, L. Research on resistance characteristics of YBCO tape under short-time DC large current impact. Cryogenics 2017, 84, 53–59. [Google Scholar] [CrossRef]
- Liu, S.; Xia, D.; Qiu, Q.; Zhang, Z.; Wang, H.; Liu, Q. Threshold value analysis of YBCO tapes under transient DC over-current impulse. Phys. C Supercond. Its Appl. 2018, 554, 32–37. [Google Scholar] [CrossRef]
- Sheng, J.; Zeng, W.; Yao, Z.; Zhao, A.; Hu, D.; Hong, Z. Recovery time of high temperature superconducting tapes exposed in liquid nitrogen. Phys. C Supercond. Its Appl. 2016, 527, 50–54. [Google Scholar] [CrossRef]
- Maeda, C.; Yanai, S.; Shirai, Y.; Shiotsu, M.; Honda, G.; Isojima, S. Recovery characteristics of GdBCO tape in a pressurized liquid nitrogen for a resistive SFCL. IEEE Trans. Appl. Supercond. 2019, 29, 5602505. [Google Scholar] [CrossRef]
- Xiang, B.; Gao, L.; Junaid, M.; Liu, Z.; Geng, Y.; Wang, J.; Yanabu, S. Effects of Magnetic Fields on Quench Characteristics of Superconducting Tape for Superconducting Fault Current Limiter. Appl. Sci. 2019, 9, 1466. [Google Scholar] [CrossRef] [Green Version]
- Rusiński, J.; Hajdasz, S.; Kempski, A. Analysis of recovery time under load conditions and energy dissipation of superconducting tapes with electrical insulation for SFCL applications. In Proceedings of the 2019 Progress in Applied Electrical Engineering, Koscielisko, Poland, 17–21 June 2019. [Google Scholar]
- Jiang, Z.; Wang, Y.; Dai, S.; Ma, T.; Peng, C.; Liu, M.; Chen, H. Influence of Insulation on Quench and Recovery of YBCO Tape Under DC Impact. IEEE Trans. Appl. Supercond. 2018, 29, 7700305. [Google Scholar] [CrossRef]
- Liang, S.; Tang, Y.; Ren, L.; Xu, Y.; Wang, W.; Hu, Z.; Zhang, B.; Jiao, F. A novel simplified modeling method based on R–Q curve of resistive type SFCL in power systems. Phys. C Supercond. Its Appl. 2019, 563, 82–87. [Google Scholar] [CrossRef]
- Liang, S.; Ren, L.; Ma, T.; Xu, Y.; Tang, Y.; Tan, X.; Li, Z.; Chen, G.; Yan, S.; Cao, Z.; et al. Study on quenching characteristics and resistance equivalent estimation method of second-generation high temperature superconducting tape under different overcurrent. Materials 2019, 12, 2374. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lv, Y.; Jiang, J.; Yao, L.; Ryu, K.; Li, Z.; Hong, Z.; Jin, Z. Experimental results of various optical fibers encapsulated HTS tapes under impulse currents for the SFCL application. IEEE Trans. Appl. Supercond. 2020, 30, 9001605. [Google Scholar] [CrossRef]






| Material | Density (kg/m3) | Specific Heat J/(kg·K) | Resistivity × 10−8 Ω·m | ||
|---|---|---|---|---|---|
| 77 K | 295 K | 77 K | 295 K | ||
| Silver (Ag) | 1.05 × 104 | 187 | 236 | 0.27 | 1.60 |
| Copper (Cu) | 8.93 × 103 | 254 | 386 | 0.23 | 1.73 |
| Hastelloy (Has) | 8.89 × 103 | 251 | 427 | 124.00 | 127.00 |
| SS 316L (Sus) | 7.98 × 103 | 251 | 490 | 56.80 | 77.10 |
| Solder 63/37 (Sn) | 8.78 × 103 | 155 | 182 | 3.00 | 15.00 |
| Nominal IC | Actual IC | Cu Thickness Calculated Value | Lamination Thickness | Nominal Resistance at RT | Actual Resistance at RT | Mass, Calculated Value | Mass, Actual Value | |
|---|---|---|---|---|---|---|---|---|
| Sample 1 | 0 A | 0 A | 3.29 μm | (80 + 80) μm | 100 mΩ/m | 101.0 mΩ/m | 22.6 g/m | 22.6 g/m |
| Sample 2 | 100 A | 101 A | 3.50 μm | (80 + 80) μm | 100 mΩ/m | 98.5 mΩ/m | 22.7 g/m | 22.9 g/m |
| Sample 3 | 300 A | 288 A | 3.41 μm | (80 + 80) μm | 100 mΩ/m | 99.6 mΩ/m | 22.6 g/m | 22.9 g/m |
| Sample 4 | 500 A | 510 A | 3.38 μm | (80 + 80) μm | 100 mΩ/m | 100.0 mΩ/m | 22.6 g/m | 22.6 g/m |
| Sample 5 | 500 A | 501 A | 4.34 μm | (80 + 80) μm | 90 mΩ/m | 89.8 mΩ/m | 22.8 g/m | 22.7 g/m |
| Sample 6 | 500 A | 502 A | 5.45 μm | (80 + 80) μm | 80 mΩ/m | 80.2 mΩ/m | 23.1 g/m | 22.9 g/m |
| Sample 7 | 500 A | 500 A | 6.97 μm | (80 + 80) μm | 70 mΩ/m | 70.0 mΩ/m | 23.4 g/m | 23.2 g/m |
| Sample 8 | 500 A | 498 A | 9.51 μm | (80 + 80) μm | 60 mΩ/m | 58.1 mΩ/m | 23.8 g/m | 24.1 g/m |
| Sample 9 | 500 A | 506 A | 2.96 μm | (80 + 100) μm | 100 mΩ/m | 101.9 mΩ/m | 24.5 g/m | 24.3 g/m |
| Sample 10 | 500 A | 511 A | 2.78 μm | (100 + 100) μm | 100 mΩ/m | 101.1 mΩ/m | 26.3 g/m | 26.0 g/m |
| Sample 11 | 500 A | 510 A | 2.47 μm | (100 + 120) μm | 100 mΩ/m | 101.1 mΩ/m | 28.6 g/m | 28.2 g/m |
| Sample 12 | 500 A | 510 A | 2.45 μm | (120 + 120) μm | 100 mΩ/m | 98.1 mΩ/m | 30.5 g/m | 30.7 g/m |
| Actual Resistance at RT | Calculated Resistance at 77 K | Actual Resistance at 77 K | Calculated Resistance at 456 K | Actual Resistance at 456 K | Peak Current During Impact | Heat Generated During Impact | |
|---|---|---|---|---|---|---|---|
| Sample 1 | 101.0 mΩ/m | 22.6 mΩ/m | 24.5 mΩ/m | 157.1 mΩ/m | 156.0 mΩ/m | 3687.2 A | 3410 J |
| Sample 2 | 98.5 mΩ/m | 21.7 mΩ/m | 25.3 mΩ/m | 153.6 mΩ/m | 150.3 mΩ/m | 3694.8 A | 3440 J |
| Sample 3 | 99.6 mΩ/m | 22.1 mΩ/m | 25.0 mΩ/m | 155.1 mΩ/m | 156.4 mΩ/m | 3694.0 A | 3450 J |
| Sample 4 | 100.0 mΩ/m | 22.2 mΩ/m | 25.4 mΩ/m | 155.6 mΩ/m | 153.7 mΩ/m | 3714.0 A | 3410 J |
| Sample 5 | 89.8 mΩ/m | 18.7 mΩ/m | 21.9 mΩ/m | 140.6 mΩ/m | 139.7 mΩ/m | 3923.1 A | 3510 J |
| Sample 6 | 80.2 mΩ/m | 15.9 mΩ/m | 17.0 mΩ/m | 126.2 mΩ/m | 126.0 mΩ/m | 4395.5 A | 3540 J |
| Sample 7 | 70.0 mΩ/m | 13.1 mΩ/m | 14.0 mΩ/m | 110.7 mΩ/m | 110.6 mΩ/m | 4849.9 A | 3560 J |
| Sample 8 | 58.1 mΩ/m | 10.1 mΩ/m | 9.7 mΩ/m | 92.4 mΩ/m | 92.9 mΩ/m | 5314.2 A | 3570 J |
| Sample 9 | 101.9 mΩ/m | 23.9 mΩ/m | 28.0 mΩ/m | 157.7 mΩ/m | 152.5 mΩ/m | 3741.7 A | 3610 J |
| Sample 10 | 101.1 mΩ/m | 24.6 mΩ/m | 29.0 mΩ/m | 155.7 mΩ/m | 152.9 mΩ/m | 4169.2 A | 3960 J |
| Sample 11 | 101.1 mΩ/m | 26.0 mΩ/m | 29.6 mΩ/m | 154.7 mΩ/m | 153.6 mΩ/m | 4372.6 A | 4340 J |
| Sample 12 | 98.1 mΩ/m | 25.8 mΩ/m | 32.6 mΩ/m | 150.0 mΩ/m | 143.9 mΩ/m | 4579.9 A | 4650 J |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Chen, S.; Jin, Z. Progress on Second-Generation High-Temperature Superconductor Tape Targeting Resistive Fault Current Limiter Application. Electronics 2022, 11, 297. https://doi.org/10.3390/electronics11030297
Zhu J, Chen S, Jin Z. Progress on Second-Generation High-Temperature Superconductor Tape Targeting Resistive Fault Current Limiter Application. Electronics. 2022; 11(3):297. https://doi.org/10.3390/electronics11030297
Chicago/Turabian StyleZhu, Jiamin, Sikan Chen, and Zhijian Jin. 2022. "Progress on Second-Generation High-Temperature Superconductor Tape Targeting Resistive Fault Current Limiter Application" Electronics 11, no. 3: 297. https://doi.org/10.3390/electronics11030297
APA StyleZhu, J., Chen, S., & Jin, Z. (2022). Progress on Second-Generation High-Temperature Superconductor Tape Targeting Resistive Fault Current Limiter Application. Electronics, 11(3), 297. https://doi.org/10.3390/electronics11030297





